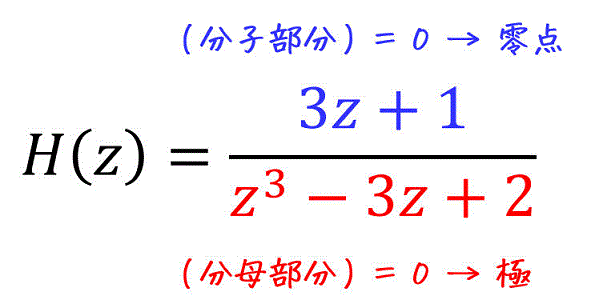スポンサードリンク
※ 動的システムではなく、ディジタルシステムの極と安定性について知りたい方は、この記事ではなく、下のリンク先の記事をご覧ください。
こんにちは、ももやまです。
前回は、
- ある動的システムをラプラス変換して伝達関数を求める
- 求めた伝達関数からインパルス応答やステップ応答などを用いてシステムの振る舞いを確認する
ということををしましたね。
↓↓↓前回の内容はこちら!!
今回は前回に引き続き動的システムの振る舞い、その中でもシステムの安定性についての仕組み、および判定方法についてみていきましょう。
目次
スポンサードリンク
1. 伝達関数の極と零点
伝達関数 \( G(s) \) は、分数で出てきますね。その分数の分子を \( N(s) \)、分母を \( D(s) \) としましょう。\[
G(s) = \frac{ \textcolor{blue}{N(s)} }{ \textcolor{red}{D(s)} }
\]
※ 分子を英語で Numerator、分母を英語で Denominator と呼ぶため、\( N(s) \)、\( D(s) \) と名付けています。
この分子部分 \( N(s) \) が0となる点を零点、分母部分 \( D(s) \) が0となる点を極と呼びます。
※ 必ず因数分解し、分子分母が同じ分数のものを約分してから判定しましょう。

さっそくなので、例題で確認してみましょう。
次の伝達関数 \( G_1 (s) \), \( G_2 (s) \) の振る舞いをする2つのシステムにおいて、極と零点をすべて答えなさい。
(1)\[
G_1(s) = \frac{s(s+2)}{(s-1)(s+3)}
\]
(2)\[
G_2(s) = \frac{s^2-4s+3}{s^3-2s-11s+12}
\]
[解答1]
(1) 与えられた伝達関数\[
G_1 (s) = \frac{ \textcolor{blue}{ s(s+2) } }{ \textcolor{red}{ (s-1)(s+3) } }
\]はすでに約分できない形になっていますね。なので、極と零点を確認していきましょう。
(i) 極 → (分母) = 0 となる \( s \)\[
(s-1)(s+3)=0
\]を満たす \( s \) を求めればOK。よって、 \( s = 1, -3 \) が極。
(ii) ゼロ点 → (分子) = 0 となる \( s \)\[
s(s+2) = 0
\]を満たす \( s \) を求めればOK、よって、\( s = 0, -2 \) が零点。
(2) 与えられた伝達関数\[
G_2 (s) = \frac{s^2-4s+3}{s^3-2s-11s+12 }
\]の分子、分母部分をまず因数分解、および分子分母で出てくる同じ因数を約分していきましょう。\[\begin{align*}
\frac{ s^2-4s+3 }{ s^3-2s-11s+12 } & = \frac{ (s-1)(s-3) }{ (s-1)(s^2-s-12) }
\\ & = \frac{ (s-1)(s-3) }{ (s-1)(s+3)(s-4) }
\\ & = \frac{ \textcolor{blue}{ s-3 } }{ \textcolor{red}{ (s+3)(s-4) } }
\end{align*}\]
ここまでの形に変形できたら、極と零点を見ていきましょう。
(i) 極 → (分母) = 0 となる \( s \) は\[
(s+3)(s-4) =0
\]を満たす \( s \) を求めればOK。よって、 \( s = -3, 4 \) が極。
(ii) 零点 → (分子) = 0 となる \( s \) は \( s-3 = 0 \) を満たす \( s \) を求めればOK、よって、\( s = 3 \) が零点。
ある伝達関数\[
G(s) = \frac{ \textcolor{blue}{N(s)} }{ \textcolor{red}{D(s)} }
\]で表される動的システムの極と零点は以下のように求められる。
(1) 極 → \( D(s) = 0 \) となる点
(分母部分が0になる点)
(2) 零点 → \( N(s) = 0 \) となる点
(分子部分が0になる点)
★超適当な覚え方★
極 → 分母 \( D(s) = 0 \) となる極限まで近づけることにより発散する点
(極限が出てきそうな方が極)
零点 → 分子 \( N(s) = 0 \) となり、名前の通り値が0(零)になる点
(伝達関数の値が0になるのが零点)
スポンサードリンク
2. 動的システムの安定性
安定という言葉は、普段の会話でもたまに使います。例えば、下のような感じに…。
- 今月の給料は安定している
- メンタルが最近安定してきた。
- その授業を取るのが安定だわ!
この3つの会話に出てくる安定は、シチュエーションこそ違いますが、共通して「落ち着いた状態」や「激しい変動がない」ことを表しています。
制御の世界でも安定という言葉が出てきます。具体的には、ある(動的)システムが安定か不安定かを判別する場面で登場します。
(1) 動的システムの「安定」とは
ある動的システムが安定であるというのは、システムの入力後、十分な時間 \( t \) を経過させたときにシステムの振る舞い \( y(t) \) が0に収束することを指します。
数式で書くと、下の式を満たすようなシステムが安定であるといえますね。\[
\lim_{t \to \infty} y(t) = 0
\]
反対に、十分に時間 \( t \) を経過させた際に振る舞い \( y(t) \) が無限大に発散してしまうシステムは、不安定といえます。
(2) 伝達関数から安定性を判定するには?
いちいち伝達関数 \( G(s) \) を逆ラプラス変換して、\( t \to \infty \) の極限をとってから安定性を判定するのは少しめんどくさいですね。
そこで、伝達関数 \( G(s) \) を見るだけで安定性を調べる方法を考えてみましょう。
(i) 安定性を考えるときに使う入力は?
安定性は、時間 \( t \to \infty \) が十分に経過したときに出力 \( y(t) \) が0に収束するかで判定するのでしたね。
すると、入力 \( u(t) \) がどんなものであっても十分に時間がたってしまえば微小な差となりますね。そこで、安定性を考えるときは最も簡単な入力で考えることにします。
ここで、システムの入力の中で最も簡単なものは、ラプラス変換上では1( \( U(s) = 1 \) )である単位インパルス関数を入力とした、インパルス応答でしたね。
なので、安定性を考える際には最も単純な入力であるインパルス応答で考えることにしましょう。
インパルス応答を考えることで、伝達関数 \( G(s) \) を逆ラプラス変換したときの結果をそのまま出力結果とすることができます[1]伝達関数 \( G(s) \) はラプラス変換上での入力 \( U(s) \)、出力 \( Y(s) \) に対し、\( Y(s) = G(s) U(s) \) … Continue reading。
(i) \( y(t) \) を収束させるには…?
伝達関数 \( G(s) \) は、逆ラプラス変換すると\[
f(t) = 2 e^{-3t} - 3 e^{-2t} + 4 e^{-t}
\]\[
f(t) = e^{-t} ( \sin 2t + 3 \cos 2t )
\]\[
f(t) = t e^{-2t} + e^{-2t} + e^{3t} + 4
\]のように、「\( t^n \)、指数関数 \( e^{-at} \)、三角関数 \( \sin bt \), \( \cos bt \)」を何倍かしたもの和で表されますね[2]線形代数を習っている皆さんであれば、\( f(t) \) は \( t^n \)、\( e^{-at} \)、\( \sin bt \)、\( \cos bt \) … Continue reading。
ここで、\( f(t) \) を0に収束させるためには、\( f(t) \) で出てくるすべての項が0に収束する必要がありますね。例えば、\[
f(t) = \underbrace{ 2e^{-3t} }_{0 \mathrm{に収束} } - \underbrace{ 3 e^{-2t} }_{0 \mathrm{に収束} } + \underbrace{ 4 e^{-t} }_{0 \mathrm{に収束} }
\]は式内にある3つの項が0に収束しますね。そのため、\( t \to \infty \) のとき、\( f(t) \) も0に収束します。
同じように\[
\underbrace{ e^{-t} }_{0 \mathrm{に収束}} \underbrace{ ( \sin 2t + 3 \cos 2t ) }_{\mathrm{- \sqrt{10} \sim \sqrt{10} となる} }
\]も項が0に収束するため、\( f(t) \) も0に収束します。
一方\[
f(t) = \underbrace{ t e^{-2t} }_{0 \mathrm{に収束} } + \underbrace{ e^{-2t} }_{0 \mathrm{に収束} } + \underbrace{ e^{3t} }_{ \mathrm{無限大に発散} } + 4
\]は1つ以上の項が無限大に発散してしまいます。そのため、 \( t \to \infty \) のときに \( f(t) \) が発散してしまいます。
具体的には、\( e^{at} \) が \( a > 0 \) となるときに \( f(t) \) が発散してしまうといえますね。
(ii) 定数はちっぽけな存在
逆ラプラス変換をする際には、関数 \( G(s) \) を\[
\frac{c_1}{s-2} + \frac{c_2}{s+1}
\]のように部分分数分解してから、それぞれの係数 \( c_1 \), \( c_2 \), … の値を代入法などで決定していきますね。
安定性を判断する場合は、\( t \to \infty \) にしたときに0に収束するかどうかだけを確認すればOKです。ここで \( t \to \infty \) のときは、係数 \( c_1 \), \( c_2 \), … , はただの定数、ちっぽけな値ですよね。
なので、安定性の判断では定数を無視、つまり部分分数分解のめんどくさいステップである「係数の決定」をスキップすることができます。
(iii) ラプラス変換上の世界で、条件を書き換えてみよう
(i), (ii) より、以下の2つを行うことで安定性を判断できることがわかります。
- \( G(s) \) を部分分数分解する(係数の決定は不要)
- すべての項が \( t \to \infty \) のときに0に収束することを確認する
(項の中に \( e^{at} \)、\( a > 0 \) となる項がないか確認する)
ここからは、安定性の条件を簡単なものに書き換えていきたいと思います。
まず、1の部分分数分解ですが、下のような伝達関数をそれぞれの因数ごとにばらしてあげることができますね。\[\begin{align*}
G(s) & = \frac{ G_s (s) }{(s - a_1) (s - a_2) (s - a_3) \cdots}
\\ & = \frac{ c_1 }{s - a_1} + \frac{ c_2 }{s - a_2 } + \frac{ c_3 }{s - a_3} \cdots
\end{align*}\]
このばらした項それぞれが0に収束するかを確認しましょう。ここで、逆ラプラス変換公式\[
\mathcal{L}^{-1} \left[ e^{\textcolor{red}{a}t} \right] = \frac{1}{s - \textcolor{red}{a}}
\]を思い出しましょう。
すると、\( G(s) \) を逆ラプラス変換した結果が\[
f(t) = \underbrace{ c_1 e^{a_1 t} }_{ a_1 < 0 \mathrm{で収束} } + \underbrace{ c_2 e^{a_2 t} }_{ a_2 < 0 \mathrm{で収束} } + \underbrace{ c_3 e^{a_3 t} }_{ a_3 < 0 \mathrm{で収束} } + \cdots
\]となることがわかります。
そのため、\( a_1 \), \( a_2 \), \( a_3 \), … がすべて0未満であれば \( y(t) \) が0に収束することがわかりますね[3]\( a_1 \), \( a_2 \), … に0が含まれていた場合、収束こそしますが \( y(t) \) が0にはならないため、安定であるとはいえません。。
言い換えると、\[
G(s) = \frac{N(s)}{D(s)}
\]の分母部分が0になるような \( s \)、つまり\( D(s) = 0 \) を求めるだけで安定性を判断できるといえますね!
信号処理的に言い換えると、すべての極が負であることと言い換えられますね。
伝達関数\[
G(s) = \frac{N(s)}{\textcolor{red}{D(s)}}\]に対して、\( \textcolor{red}{D(s)} = 0 \) となる \( s \) がすべて負のとき、システムが安定であるといえる。
言い換えると、伝達関数の極がすべて負のとき、システムが安定であるといえる。
一方、伝達関数の極に正が含まれるとき、システムは不安定であえるといえる。
( \( D(s) = 0 \) となる \( s \) が重解のときでも同じように判定ができる)
(iv) 複素数が絡むと…?
条件をもう少し深堀りしてみましょう。
例えば、\( D(s) = 0 \) となるような \( s \)、つまり極に複素数 \( s = a + bi \) が入るとします。
すると、\( G(s) \) を部分分数分解した後の項に\[
G(s) = \frac{c_1}{s - (a+bi)}
\]が含まれますね。これを逆ラプラス変換すると、\[\begin{align*}
\mathcal{L}^{-1} \left[ \frac{c_1}{s - (a+bi)} \right] & = e^{(a+bi)t}
\\ & = e^{at} e^{ibt}
\\ & = e^{at} \underbrace{ \left( \cos bt + i \sin bt \right) }_{\mathrm{値の範囲が-1から1}}
\end{align*}\]となりますね。
ここで、\[
-1 \leqq \cos bt \leqq 1 , \ \ -1 \leqq \sin bt \leqq 1
\]なので、\( \cos bt + i \sin bt \) は \( e^{at} \) が無限大に発散しようが、0に収束しようが無視できるほど小さい値ですね[4]厳密には実数と複素数が両方とも含まれているものに対して一度に極限を取るのはまずいのですが、今回は証明ではないので無視します。。
そのため、極の虚部 \( bi \) の値にかかわらず実部が負 ( \( a < 0 \) ) であればシステムが安定であるということができますね。
極に複素数が含まれていた場合でも、虚部を無視して実部部分に着目してシステムの安定性を確認できる。
具体的には、極 \( \textcolor{red}{a_1} + \textcolor{blue}{b_1} i \), \( \textcolor{red}{a_2} + \textcolor{blue}{b_2} i \), \( \textcolor{red}{a_3} + \textcolor{blue}{b_3} i \), … に対して、\[
\textcolor{red}{a_1} < 0, \ \ \textcolor{red}{a_2} < 0, \ \ \textcolor{red}{a_3} < 0, \cdots
\]が成り立てばシステムが安定であるといえる。
(極の実部がすべて負であれば安定! 1つでも実部が正の極があれば不安定!)
(v) 極が重解となるとき
最後に、極が \( n \) 重解となるとき、つまり \( G(s) \) を部分分数分解したときに\[
G(s) = \frac{c_1}{(s-a)^n}
\]の項が出てきたときにでも、同じく「すべての極が0未満」という条件で安定性が確認できるかを確認しましょう。
ここで、逆ラプラス変換公式\[
\mathcal{L}^{-1} \left[ \frac{n!}{ (s-a)^{n+1} } \right] = t^n e^{at}
\]を思い出しましょう。
さらに、係数を \( c_1 = n! \cdot d_1 \) とおきます。すると、\[\begin{align*}
\mathcal{L}^{-1} \left[ \frac{c_1}{(s-a)^n} \right] & = \mathcal{L}^{-1} \left[ \frac{n! \cdot d_1}{(s-a)^n} \right]
\\ & = d_1 t^n e^{at}
\end{align*}\]と書き換えられますね。
ここで、\[
\lim_{t \to \infty} d_1 t^n e^{at}
\]としたときに、\( t^n \) は \( e^{at} \) に比べて十分小さいと考えることができます。
そのため、\( a < 0 \) であれば\[
\lim_{t \to \infty} d_1 t^n e^{at} = 0
\]となり、安定であるといえます[5]厳密に解く場合は、ロピタルの定理などで \( a<0 \) のときに\[ \lim_{t \to \infty} \frac{t^n}{e^{-at}} = 0 … Continue reading。
よって、極に重解があったとしても安定性の判定方法は変わらないことがわかりましたね。
スポンサードリンク
3. 不安定であることを一瞬で確認する方法
2章では、伝達関数 \( G(s) \) の極を見てから安定性を判定する方法について見ていきました。
でも、もう少し早く安定性について確認したいですよね。そこで、限定的ですが安定性の確認をさらに高速にする方法を見ていきましょう。
(1) 負の数を他の数の積で表してみよう
例えば、-24という数を他の数字の掛け算で表すことを考えましょう。
例えば\[ -2 \times 12 , \ \ \ (-2) \times (-3) \times (-4) \]など、様々な組み合わせがありますが、1つ共通して言えることは、負の数を他の数字の掛け算で表す際には、最低でも1つは負の数を入れる必要があるということです。
(2) 正の数の場合は?
一方、正の数は負の数だけで表すことができます。例えば、24 であれば\[
(-4) \times (-6)
\]と表現することができます。
(3) 不安定性は一瞬でわかる!
あるシステムが不安定であるということは、システムの極に正が含まれるといえますね。つまり、伝達関数 \( G(s) \) の分母に \( s-a \) の因数 ( \( a > 0 \) ) が含まれるといえますね。
ここで、伝達関数\[
G(s) = \frac{N(s)}{D(s)}
\]の分母 \( D(s) \) に \( s^3 + 3s^2 \textcolor{red}{-} 4s + 5 \) のような係数が負となる項が含まれていることを考えましょう。
負の項が含まれているということは、(1)のように分解(因数分解)すると必ず \( s-a \) ( \( a > 0 \) ) の項が出てきますね。
つまり、伝達関数の分母を見たときに1つでも係数が負となる項が存在すれば一瞬でシステムが不安定であることを見抜くことができるのです!
ただし、2点注意が必要です。
- 伝達関数の係数がすべて正だからといって、システムが安定であるとは限りません。
(正の数は、負の数の積で表すことが可能だからです。) - 必ず分子、分母に共通因数がなく、約分ができない状態かを確認してください。
(約分後に、分母 \( D(s) \) の負の数の係数が消える可能性があるため)
\[
G(s) = \frac{2s+1}{s^3 + 3s^2 \textcolor{red}{-} 4s + 5}\]のように、伝達関数の分母に負の係数が1つでも含まれている場合、必ずそのシステムは不安定となる。
※1 分子・分母に共通因数がある場合は約分後に確認すること!!
※2 伝達関数の分母の係数がすべて正だからといって、安定であるとは言えない点に注意!
4. 例題で安定性について考えよう
それでは、システムの安定性についての例題を実際に解いてみましょう!
次の \( G_1(s) \)、\( G_2(s) \)、\( G_3 (s) \) の伝達関数で表される3つのシステムがある。\[
G_1(s) = \frac{1}{s^3 + 8}
\]\[
G_2(s) = \frac{23s-67}{s^5 + 46s^4 - 8 s^3 + 27s^2 + 41s - 30}
\]\[
G_3(s) = \frac{s+3}{s^3+7s^2+14s+8}
\]
この中で1つだけ安定なシステムがある。それはどれか。
[解説2]
それぞれの伝達関数を因数分解して、(分母部分) = 0 となる \( s \)、つまり極を求めましょう。
さらに求めた極の実部がすべて負になるかを確認しましょう。(負になれば安定、そうでなければ不安定)
(1) \( G_1(s) \) → 不安定
\( s^3 + 8 \) を因数分解すると、\[
s^3 + 8 = (s-2)(s^2 - 2s+4)
\]となるため、解は \( s = 2 \), \( s = \textcolor{red}{1} \pm \sqrt{3} i \) となります。
よって、実部が正となる極が存在するため、不安定。
※
(2) \( G_2(s) \) → 不安定
分母部分に\[ s^5 + 46s^4 \textcolor{red}{-} 8 s^3 + 27s^2 + 41s \textcolor{red}{-} 30 \]と、負の係数が存在しますね。
よって、不安定。
(3) \( G_3 (s) \) → 安定
\( s^3+7s^2+14s+8 \) を因数分解すると、\[\begin{align*}
s^3+7s^2+14s+8 & = (s+1)(s^2+6s+8)
\\ & = (s+1)(s+2)(s+4)
\end{align*}\]となるため、解は \( s = -1 \), \( s = -2 \), \( s = -4 \) となります。
※ 極を求める場合、分子部分の因数 \( s+3 \) で割り切れないことも答案に書きましょう。今回は安定性の判定のため不要です。
よって、すべての極(の実部)が負なため、安定である。
(1)~(3)より、安定なシステムは \( G_3 (s) \) である。
5. さいごに
今回は、伝達関数 \( G(s) \) の分母部分(極など)に着目したシステムの安定性について説明していきました。
次回は、また別の観点から伝達関数 \( G(s) \) 表記されているシステムの振る舞いを見ていきましょう!
注釈
| ↑1 | 伝達関数 \( G(s) \) はラプラス変換上での入力 \( U(s) \)、出力 \( Y(s) \) に対し、\( Y(s) = G(s) U(s) \) と表されるように定義されているから。ここにインパルス応答を入力としているため \( U(s) = 1 \) となり、\( Y(s) = G(s) \) となる。 |
|---|---|
| ↑2 | 線形代数を習っている皆さんであれば、\( f(t) \) は \( t^n \)、\( e^{-at} \)、\( \sin bt \)、\( \cos bt \) の線形結合で表現される、と言った方がわかりやすいかもしれません。 |
| ↑3 | \( a_1 \), \( a_2 \), … に0が含まれていた場合、収束こそしますが \( y(t) \) が0にはならないため、安定であるとはいえません。 |
| ↑4 | 厳密には実数と複素数が両方とも含まれているものに対して一度に極限を取るのはまずいのですが、今回は証明ではないので無視します。 |
| ↑5 | 厳密に解く場合は、ロピタルの定理などで \( a<0 \) のときに\[ \lim_{t \to \infty} \frac{t^n}{e^{-at}} = 0 \]を確認すること十分小さいことを確認することができます。 |
関連広告・スポンサードリンク