スポンサードリンク
※ ディジタルシステムではなく、動的システムについて(伝達関数、インパルス応答、ステップ応答の求め方など)知りたい人は、こちらの記事ではなく、下のリンク先の記事をご覧ください。
こんにちは、ももやまです。
信号処理(制御数学)の第01羽、第02羽では、z変換の基礎や、漸化式(差分方程式)の解き方について学んでいいきましたね。
今回は、学んだz変換の知識を応用してディジタルシステム[1]余談ですが、何故デジタルじゃなくてディジタルって書かれてる本やサイトが多いんでしょうかね…を2回にわたって解読してみましょう!!
z変換の計算に慣れていない人は、下の記事で練習してからこちらの記事を読むことをおすすめします!
目次
スポンサードリンク
1. ディジタルシステムとは
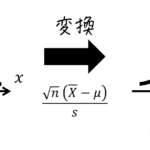
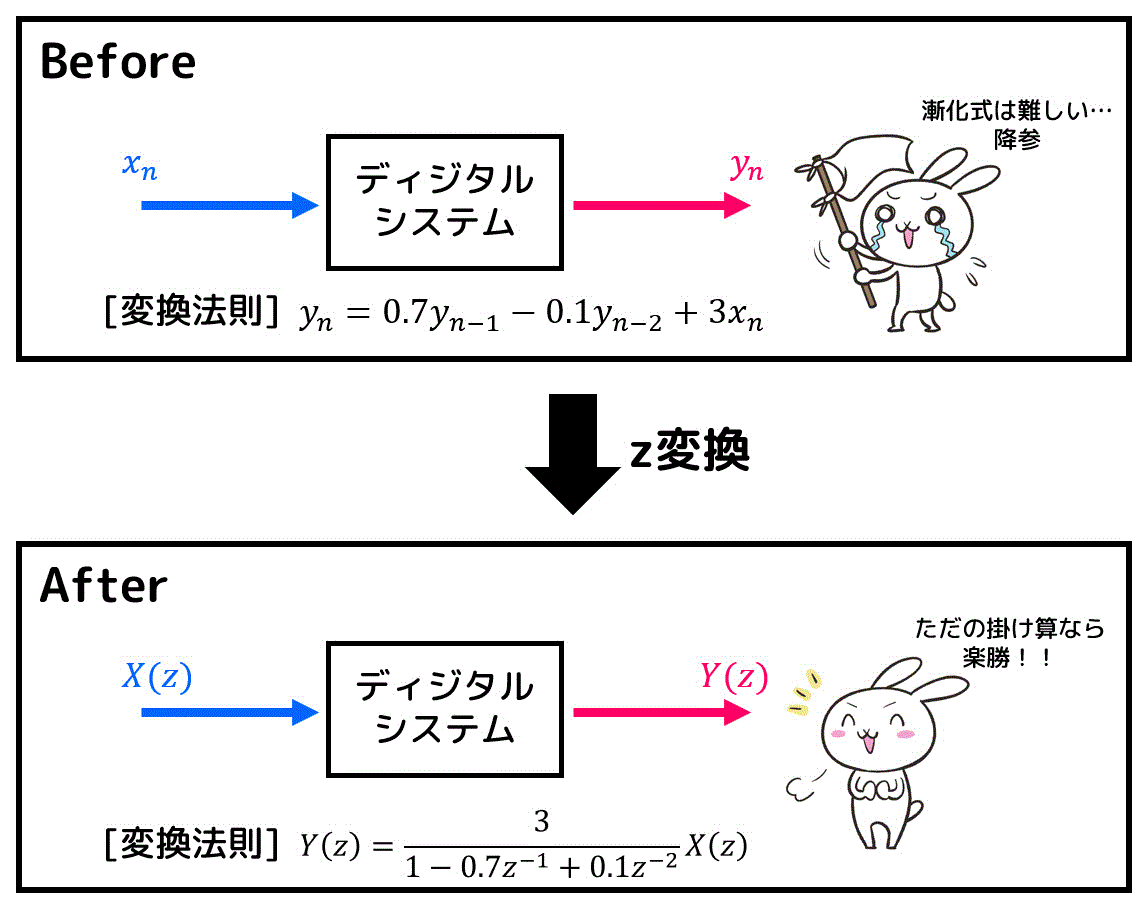
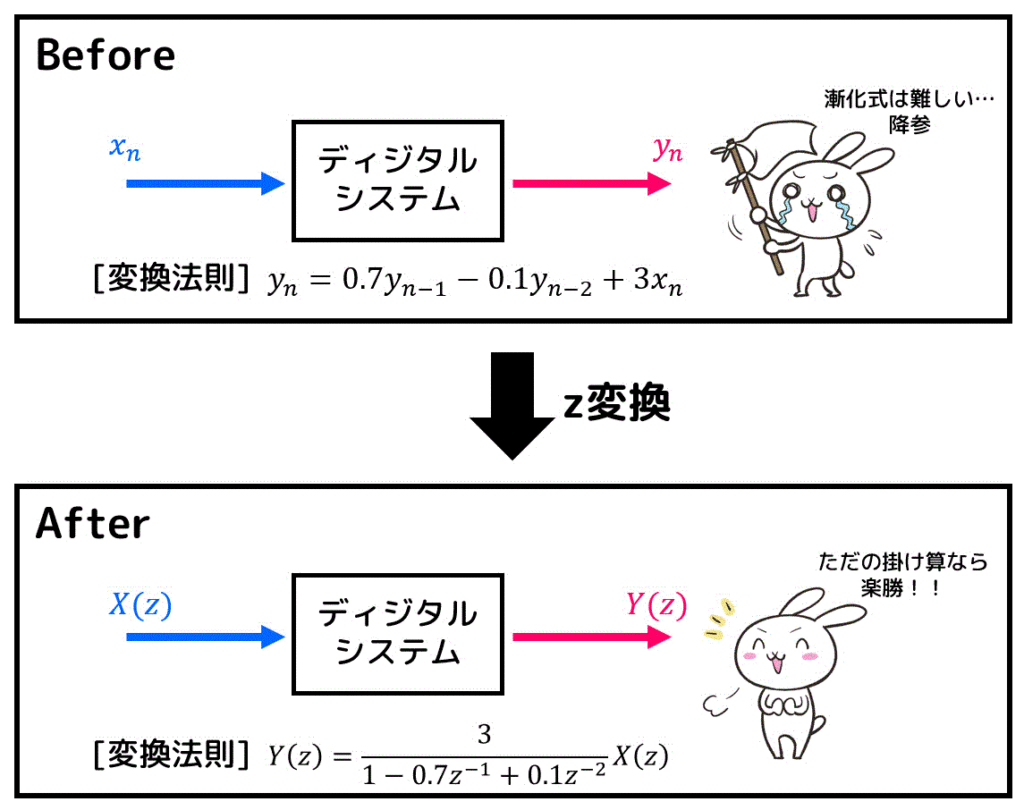
ディジタルシステムを簡単に説明すると、信号 \( x_n \) を決められた仕組みに従って \( y_n \) に変換する魔法の箱です。関数が進化したものだと思って頂いてOKです。

ただし、ディジタルシステム(魔法の箱)の中身は漸化式(差分方程式)で書かれています。そのため、解読するのが少し大変です。
1つ漸化式で表されたディジタルシステムの例を挙げてみましょう。例えばこんな式だとどうでしょう。\[
y_n = 0.7 y_{n-1} - 0.1 y_{n-2} + 3 x_{n}
\]
この式では、出力 \( y_n \) が、1つ前の出力 \( y_{n-1} \)、2つ前の出力 \( y_{n-2} \)、および現在の入力 \( x_n \) の3つで表されていますね[2]ちなみに数2Bで習う漸化式は、\[a_{n+1} = 2 a_{n} + … Continue reading。
これだと、\( y_{n} \) がどんな法則で決まるかは少し想像しづらいですよね。
そこで、ディジタルシステムを単純にする魔法を次の章で紹介しましょう!
スポンサードリンク
2. ディジタルシステムを解読する魔法・z変換
第01羽・第02羽では、z変換の基礎について学びましたね。
ですが念の為、z変換について復習をしておきましょう。
(1) z変換の法則の復習
ここで、第02羽で習った線形の法則(定数倍・足し算の法則)、シフトの法則について復習しましょう。
z変換、逆z変換の計算の際、積分計算と同じように定数倍、および足し算引き算を分離することができる。
\[\begin{align*}
\mathcal{Z} \left[ \textcolor{magenta}{a} x_n + \textcolor{deepskyblue}{b} y_n \right] & = \textcolor{magenta}{a} \mathcal{Z} \left[ x_n \right] + \textcolor{ deepskyblue }{b} \mathcal{Z} \left[ y_n \right]
\end{align*}\]
\[\begin{align*}
\mathcal{Z}^{-1} \left[ \textcolor{magenta}{a} X(z) + \textcolor{deepskyblue}{b} Y(z) \right] & = \textcolor{magenta}{a} \mathcal{Z}^{-1} \left[ X(z) \right] + \textcolor{ deepskyblue }{b} \mathcal{Z}^{-1} \left[ Y(z) \right]
\end{align*}\]
※ 数列 \( x_n \) を \( z \) 変換したものを \( X(z) \)、\( y_n \) を \( z \) 変換したものを \( y_n \) とする。つまり、\[
\mathcal{Z} \left[ x_{n} \right] = X(z), \ \ \ \mathcal{Z} \left[ y_{n} \right] = Y(z)
\]である。
\[\begin{align*}
\mathcal{Z} \left[ x_{n-1} \right] & = z^{-1} X(z) + x_{-1}
\\ \mathcal{Z} \left[ x_{n-2} \right] & = z^{-2} X(z) + z^{-1} x_{-1} + x_{-2}
\\ \mathcal{Z} \left[ x_{n-3} \right] & = z^{-3} X(z) + z^{-2} x_{-1} + z^{-1} x_{-2} + x_{-3}
\\ \mathcal{Z} \left[ x_{n-k} \right] & = z^{-k} X(z) + z^{-(k-1)} x_{-1} + \cdots + x_{-k}
\end{align*}\]
※ 数列 \( x_n \) を \( z \) 変換したものを \( X(z) \) とする。つまり、\[
\mathcal{Z} \left[ x_{n} \right] = X(z)
\]である。
(2) ディジタルシステムで出てくる数列の初期値は…?
漸化式(差分方程式)では必ず初期値が与えられていましたね。例えば\[
a_{n} = 2 a_{n-1} + 3 , \ \ \ a_0 = 2
\]であれば、初期値は \( a_0 = 2 \) となります。しかし、今回のディジタルシステムでは初期値が何も書かれていません。
実は、ディジタルシステムを解読する際[3]正確には、伝達関数やインパルス応答を求めるときのことです。には、全ての初期値 \( x_k \) を0として考えてOKなのです[4] … Continue reading!
なので、解読時にはディジタルシステムで出てくる数列の初期値は \( x_{-1} = x_{-2} = \cdots = 0 \), \( y_{-1} = y_{-2} = \cdots = 0 \) として考えます。
よって、z変換のシフト法則は下のように簡略化して表記することができます。
ディジタルシステムでは出てくる数列 \( x_k \), \( y_k \) の初期値を0として考える。
そのため、z変換のシフト法則は以下のように簡略化できる。
\[\begin{align*}
\mathcal{Z} \left[ x_{n} \right] & = X(z)
\\ \mathcal{Z} \left[ x_{n-\textcolor{red}{1}} \right] & = z^{- \textcolor{red}{1} } X(z)
\\ \mathcal{Z} \left[ x_{n- \textcolor{red}{2} } \right] & = z^{- \textcolor{red}{2} } X(z)
\\ \mathcal{Z} \left[ x_{n- \textcolor{red}{3} } \right] & = z^{- \textcolor{red}{3} } X(z)
\\ & \vdots
\\ \mathcal{Z} \left[ x_{n- \textcolor{red}{k} } \right] & = z^{- \textcolor{red}{k} } X(z)
\end{align*}\]
スポンサードリンク
3. z変換を使って伝達関数を求めてみよう
さてz変換の復習が終わったところで、実際に先ほどのディジタルシステムの中身をz変換にかけてみましょう。
次の漸化式で表されるディジタルシステムがある。\[
y_n = 0.7 y_{n-1} - 0.1 y_{n-2} + 3 x_{n}
\]
このシステムの伝達関数 \( H(z) \) を求めなさい。
まず線形の法則を使い、それぞれの項ごとに分離をしましょう。\[\begin{align*}
\mathcal{Z} \left[ y_{n} \right] & = \mathcal{Z} \left[ 0.7 y_{n-1} - 0.1 y_{n-2} + 3 x_{n} \right]
\\ \mathcal{Z} \left[ y_{n} \right] & = 0.7 \ \mathcal{Z} \left[ y_{n-1} \right] - 0.1 \ \mathcal{Z} \left[ y_{n-2} \right] + 3 \ \mathcal{Z} \left[ x_{n} \right]
\end{align*}\]
ここで、\( x_n \) をz変換した結果を \( X(z) \)、\( y_n \) をz変換した結果を \( Y(z) \) とすると、シフト法則より、以下の式が成り立ちますね。\[\begin{align*}
\mathcal{Z} \left[ y_{n-1} \right] & = z^{-1} Y(z) \\
\mathcal{Z} \left[ y_{n-2} \right] & = z^{-2} Y(z)
\end{align*}\]
よって、\[\begin{align*}
Y(z) & = \mathcal{Z} \left[ y_{n} \right]
\\ & = 0.7 \ \mathcal{Z} \left[ y_{n-1} \right] - 0.1 \ \mathcal{Z} \left[ y_{n-2} \right] + 3 \ \mathcal{Z} \left[ x_{n} \right]
\\ & = 0.7 z^{-1} Y(z) - 0.1 z^{-2} Y(z) + 3 X(z)
\end{align*}\]となりますね。
ここで式の整理をすると、\[\begin{align*}
Y(z) - 0.7 z^{-1} Y(z) + 0.1 z^{-2} Y(z) & = 3 X(z) \\
\left( 1 - 0.7 z^{-1} + 0.1 z^{-2} \right) Y(z) & = 3 X(z) \end{align*}\]となります。
さらに、\( Y(z) = \) の形になるように整理すると\[
Y(z) = \textcolor{green}{ \frac{3}{1 - 0.7z^{-1} + 0.1 z^{-2}} } X(z)
\]と変形することができますね。
するとどうでしょう。
今までは漸化式という難しい表記をしていたディジタルシステムが、z変換を行うことで入力 \( X(z) \) と出力 \( Y(z) \) の関係を四則演算だけで表現することができました!!
式を見ると、元の入力をz変換したもの \( X(z) \) と \( z \) の関数 \( H(z) \) を掛けたものが、出力をz変換したもの \( Y(z) \) になっていますね。
この掛けられている \( H(z) \) のことを伝達関数と呼び、ディジタルシステムの仕組み(魔法の箱)がどうなっているのかを把握するための大きな手がかりとなります。

元の入力をz変換したもの \( X(z) \) と出力をz変換したもの \( Y(z) \) の関係を表すz変換上の関数のことを伝達関数と呼び、\[
Y(z) = H(z) X(z) , \ \ \ H(z) = \frac{Y(z)}{X(z)}
\]の形で表される。
4. インパルス応答を求めてみよう
伝達関数は、ディジタルシステムの仕組み(魔法の箱の中身)がどうなっているのかを把握するための大きな手がかりとなるのでしたね。ですが、z変換の世界で仕組みが表されていてもちょっとよくわかりませんよね。
例えばですが、「この品物の価値は1,000,000イランリアルだ!」って言われてもよくわかりませんよね。できれば「この品物の価値は2,650円だ!」のように自分に馴染みのある単位、表記で知りたいですよね。
そこで、ディジタルシステムの仕組み(魔法の箱の中身)をz変換を使わずに表す方法について考えてみましょう。
(1) (単位)インパルス信号とは
インパルス信号とは、ごく一瞬だけ値を持ち、それ以外のときは0となる信号のことです。
さらに、ごく一瞬の値が1の信号のことを単位インパルス信号と呼びます。
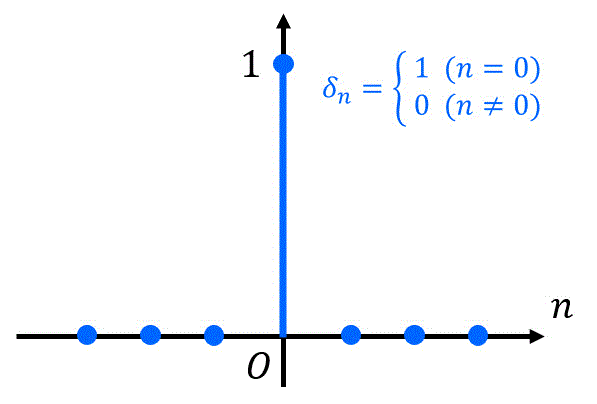
ディジタルシステムの世界では、単位インパルス信号を入力としたときの出力の値でディジタルシステムがどのような振る舞いをするのかを表します。
このとき(単位インパルス信号を入力としたとき)の出力値のことをインパルス応答と呼び、\( \delta_n \) と表記します。
インパルス応答は試験で頻出するので、必ず計算方法まで理解をしましょう!
(2) なぜ、単位インパルス信号を使うの?
単位インパルス応答を入力したときの出力値を指標にする大きな理由は、z変換したときの値のわかりやすさです。
なんと、z変換後の値が1となるのです。
数式で書くと \( \mathcal{Z} \left[ \delta_n \right] = 1 \) ですね。
「z変換後の値が1になる」という特性がどれだけ便利なのかを、実際に先程計算したディジタルシステム\[
y_n = 0.7 y_{n-1} - 0.1 y_{n-2} + 3 x_{n}
\]の例で体感してもらいましょう。
このシステムの両辺をz変換すると、\[\begin{align*}
Y(z) & = \frac{3}{1 - 0.7z^{-1} + 0.1 z^{-2}} X(z)
\\ & = H(z) X(z)
\end{align*}\]となるのでしたね。(※ \( H(z) \) は伝達関数)
ここで、入力 \( x_n \) をインパルス応答 \( \delta_n \) とします。
すると、\( \mathcal{Z} \left[ \delta_n \right] = 1 \) より、\( x_n \) をz変換した結果は1となりますね。
よって、\( X(z) = 1 \) となりますね。これを先程の式に代入すると、\[\begin{align*}
Y(z) & = \frac{3}{1 - 0.7z^{-1} + 0.1 z^{-2}}
\\ & = H(z)
\end{align*}\]となるため、伝達関数 \( H(z) \) をそのまま逆z変換することで、出力値 \( y_n \) の値(インパルス応答)を求められることがわかりますね。
単位インパルス信号 \( \delta_n \) を入力としたときの出力のことをインパルス応答と呼び、\( H(z) \) の逆z変換で求めることができる。
ただし、\( n < 0 \) のときは \( h_n < 0 \) となるので注意。
(3) インパルス応答を計算してみよう
ここからは、実際にインパルス応答を計算していきましょう!
次の漸化式で表されるディジタルシステムがある。\[
y_n = 0.7 y_{n-1} - 0.1 y_{n-2} + 3 x_{n}
\](例題1と同じ)
このシステムの伝達関数\[
Y(z) = \frac{3}{1 - 0.7z^{-1} + 0.1 z^{-2}}
\]を利用して、システムのインパルス応答 \( h_n \) を求めなさい。
インパルス応答を計算するためには、\( H(z) \) を逆z変換すればOKでしたね。\[
H(z) = \frac{3}{1 - 0.7z^{-1} + 0.1 z^{-2}}
\]
(i) 逆z変換で使う公式
ここで、ディジタルシステムの逆z変換でよく使う公式は、下の2種類です。
必ず頭に入れておきましょう。
★線形の法則★\[
\mathcal{Z}^{-1} \left[ \textcolor{magenta}{a} X(z) + \textcolor{deepskyblue}{b} Y(z) \right] = \textcolor{magenta}{a} \ \mathcal{Z}^{-1} \left[ X(z) \right] + \textcolor{deepskyblue}{b} \ \mathcal{Z}^{-1} \left[ Y(z) \right]
\]
★重要な2つの変形公式★\[\begin{align*}
\mathcal{Z}^{-1} \left[ \frac{1}{1 - \textcolor{red}{a} z^{-1} } \right] & = \textcolor{red}{a}^n \\
\mathcal{Z}^{-1} \left[ \frac{\textcolor{red}{a} z^{-1}}{(1 - \textcolor{red}{a} z^{-1})^2 } \right] & = n \textcolor{red}{a}^n
\end{align*}\]
(ii) 逆z変換と部分分数分解
次に、逆z変換の変形公式に当てはまるように部分分数分解を行います。
ここで、\[
1 - 0.7 z^{-1} + 0.1z^{-2} = (1 - 0.5 z^{-1})(1 - 0.2 z^{-1})
\]と因数分解できるので、今回の場合\[\begin{align*}
\frac{3}{1 - 0.7z^{-1} + 0.1 z^{-2}} & = \frac{3}{(1 - 0.5 z^{-1})(1 - 0.2 z^{-1})}
\\ & = \frac{a}{1 - 0.5 z^{-1}} + \frac{b}{1 - 0.2 z^{-1}}
\end{align*}\]の \( a \), \( b \) を求めればOKです。
\( a \), \( b \) を求める際、信号処理の教科書では「ヘビサイドの展開公式」を使うことも多いのですが、今回はもっと簡単な方法で求めてみましょう。
まず、両辺を \( (1 - 0.5 z^{-1})(1 - 0.2 z^{-1}) \) 倍します。すると、\[
3 = a ( 1 - 0.2 z^{-1} ) + b (1 - 0.5 z^{-1} )
\]となりますね。
次に、\( a \), \( b \) のうちの片方を消すように \( z \) に具体的な値を求めます。
(i) \( z = 0.2 \) を代入(つまり \( z^{-1} = \frac{1}{0.2} \))
\( z = 0.2 \) を代入すると、\[\begin{align*}
3 & = a \left( 1 - \frac{0.2}{0.2} \right) + b \left( 1 - \frac{0.5}{0.2} \right)
\\ & = b \left( 1 - \frac{5}{2} \right)
\\ & = - \frac{3}{2} b
\end{align*}\]となります。
よって、\( - \frac{3}{2} b = 3 \)、つまり\( b = -2 \) と求められます。
(ii) \( z = 0.5 \) を代入(つまり \( z^{-1} = \frac{1}{0.5} \))
\( z = 0.5 \) を代入すると、\[\begin{align*}
3 & = a \left( 1 - \frac{0.2}{0.5} \right) + b \left( 1 - \frac{0.5}{0.5} \right)
\\ & = a \left( 1 - \frac{2}{5} \right)
\\ & = \frac{3}{5} a
\end{align*}\]となります。
よって、\( \frac{3}{5} a = 3 \) より、\( a = 5 \) と求められます。
(i), (ii)より、\( Y(z) \) を下のように部分分数分解することができます。\[\begin{align*}
\frac{3}{1 - 0.7z^{-1} + 0.1 z^{-2}} & = \frac{5}{1 - 0.5 z^{-1}} + \frac{-2}{1 - 0.2 z^{-1}}
\\ & = \frac{5}{1 - 0.5 z^{-1}} - \frac{2}{1 - 0.2 z^{-1}}
\end{align*}\]
(iii) あとは公式に当てはめて逆z変換!
ここまでくればあとは公式に当てはめるだけでOKです!
求めるインパルス応答を \( h_n \) としましょうか。\[\begin{align*}
h_n & = \mathcal{Z}^{-1} \left[ Y(z) \right]
\\ & = \mathcal{Z}^{-1} \left[ \frac{5}{1 - 0.5 z^{-1}} - \frac{2}{1 - 0.2 z^{-1}} \right]
\\ & = 5 \mathcal{Z}^{-1} \left[ \frac{1}{1 - \textcolor{red}{0.5} z^{-1}} \right] - 2 \mathcal{Z}^{-1} \left[ \frac{2}{1 - \textcolor{red}{0.2} z^{-1}} \right]
\\ & = 5 \cdot \textcolor{red}{0.5}^n - 2 \cdot \textcolor{red}{0.2}^n
\end{align*}\]
となり、(単位)インパルス応答は\[
h_n = 5 \cdot 0.5^n - 2 \cdot 0.2^n
\]となります。(※ただし \( n \geqq 0 \) のとき。\( n < 0 \) のときは \( h_n \) は0となる。)
単位ステップ応答 \( u_n \) を用いた答えの書き方
インパルス応答を解答する際にいちいち\[
h_n = \left\{ \begin{array}{cc} 5 \cdot 0.5^n - 2 \cdot 0.2^n & (n \geqq 0 ) \\ 0 & (n < 0) \end{array} \right.
\]と場合分けして書くのはめんどくさいですね。
そこで、信号処理の世界では、下の図および、数式\[
u_n = \left\{ \begin{array}{ll} 1 & ( n \geqq 0 ) \\ 0 & (n < 0) \end{array} \right.
\]となる関数(数列)で表記します。この \( u_n \) のことを単位ステップ信号(関数)と呼びます。
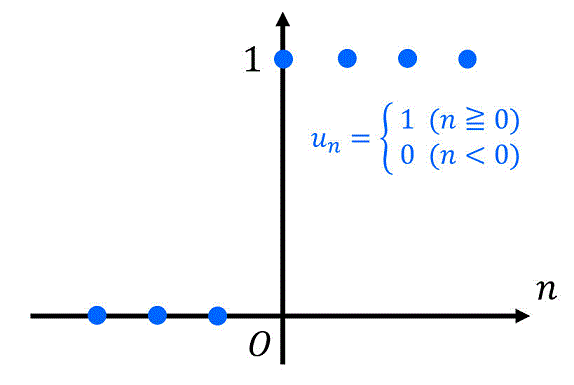
単位ステップ信号 \( u_n \) を使うことで、インパルス応答を\[
h_n = \left( 5 \cdot 0.5^n - 2 \cdot 0.2^n \right) u_n
\]と場合分けなしで書くことができます。
5. 伝達関数からステップ応答を求めてみよう
信号処理(ディジタルシステム)の世界では、インパルス応答のほかにも、\( n \geqq 0 \) で常に一定(1)の値を持つステップ信号を入力としたときの出力である「ステップ応答」をつかってディジタルシステムの仕組みを表現することがあります。
そこで、インパルス応答に加えてステップ応答の求め方を説明していきます。
(1) ステップ応答の求め方
単位ステップ信号\[
u_n = \left\{ \begin{array}{ll} 1 & ( n \geqq 0 ) \\ 0 & (n < 0) \end{array} \right.
\]を入力としたときの出力をステップ応答と呼びます。本記事では、ステップ応答の記号を \( s_n \) としましょう。
ステップ応答の求め方は、
- 伝達関数から求める方法
- インパルス応答から求める方法
の2通りありますが、まずは伝達関数から地道に求める方法を紹介します。
ステップ信号の \( z \) 変換は、\[
\mathcal{Z} \left[ u_n \right] = \frac{1}{1-z^{-1}}
\]と計算できるので[5]公式的には1を \( z \) 変換する場合と同じです。、ステップ信号を入力、つまり \( x_n = u_n \) としたときの出力を \( z \) 変換上の世界 \( Y(z) \) で表すと、\[\begin{align*}
Y(z) & = H(z) X(z)
\\ & = H(z) \cdot \frac{1}{1-z^{-1}}
\\ & = \frac{1}{1-z^{-1}} H(z)
\end{align*}\]となり、この \( Y(z) \) を逆 \( z \) 変換することで出力 \( y_n \) が求めることができ、この値がステップ応答 \( s_n \) となります。
(2) 例題で計算してみよう
それでは、実際にステップ応答 \( s_n \) の計算を例題でしてみましょう。
次の漸化式で表されるディジタルシステムがある。\[
y_n = 0.7 y_{n-1} - 0.1 y_{n-2} + 3 x_{n}
\](例題1, 2と同じ)
このシステムの伝達関数\[
H(z) = \frac{3}{1 - 0.7z^{-1} + 0.1 z^{-2}}
\]を利用して、システムのステップ応答 \( s_n \) を求めなさい。
ステップ応答は、\[\begin{align*}
Y(z) & = \frac{1}{1-z^{-1}} H(z)
\\ & = \frac{3}{(1 - 0.7z^{-1} + 0.1 z^{-2}) ( 1 - z^{-1} ) }
\end{align*}\]を \( z \) 変換することで計算できる。
ここで、\[
(1 - 0.7z^{-1} + 0.1 z^{-2}) = (1 - 0.2z^{-1} )(1 - 0.5z^{-1})
\]と因数分解できるため、\[\begin{align*}
Y(z) & = \frac{3}{(1 - 0.7z^{-1} + 0.1 z^{-2}) ( 1 - z^{-1} ) }
\\ & = \frac{3}{(1 - 0.2z^{-1} )(1 - 0.5z^{-1}) ( 1 - z^{-1} ) }
\\ & = \frac{a}{1 - 0.2 z^{-1}} + \frac{b}{1 - 0.5 z^{-1}} + \frac{c}{1 - z^{-1}}
\end{align*}\]と部分分数分解の形にできる。
さらに、\[
\frac{3}{(1 - 0.7z^{-1} + 0.1 z^{-2}) ( 1 - z^{-1} ) } = \frac{a}{1 - 0.2 z^{-1}} + \frac{b}{1 - 0.5 z^{-1}} + \frac{c}{1 - z^{-1}}
\]の両辺を \( (1 - 0.7z^{-1} + 0.1 z^{-2}) ( 1 - z^{-1} ) \) 倍し、\[
3 = a (1 - 0.5z^{-1} )(1 - z^{-1} ) + b (1 - 0.2z^{-1} )(1 - z^{-1}) + c (1 - 0.2z^{-1} )(1 - 0.5z^{-1})
\]としてから \( a \), \( b \), \( c \) を求める。
- \( z = 0.2 \) のとき、\[\begin{align*}
3 & = a \left( 1 - \frac{0.5}{0.2} \right) \left( 1 - \frac{1}{0.2} \right)
\\ & = a \left( 1 - \frac{5}{2} \right) \cdot (-4)
\\ & = 6 a
\end{align*}\]となるため、\( a = 1/2 \)。 - \( z = 0.5 \) のとき、\[\begin{align*}
3 & = b \left( 1 - \frac{0.2}{0.5} \right) \left( 1 - \frac{1}{0.5} \right)
\\ & = b \left( 1 - \frac{2}{5} \right) \cdot (-1)
\\ & = - \frac{3}{5} b
\end{align*}\]となるため、\( b = -5 \)。 - \( z = 1 \) のとき、\[\begin{align*}
3 & = c \left( 1 - 0.2 \right) \left( 1 - 0.5 \right)
\\ & = c \cdot 0.8 \cdot 0.5
\\ & = \frac{2}{5} c
\end{align*}\]より、\( c = 15/2 \)
よって、\[
Y(z) = \frac{1}{2} \cdot \frac{1}{1 - 0.2 z^{-1}} - \frac{5}{1 - 0.5 z^{-1}} + \frac{15}{2} \cdot \frac{1}{1 - z^{-1}}
\]と部分分数分解できる。
あとは、部分分数分解したものを逆 \( z \) 変換したものが \( s_n \) となる。\[\begin{align*}
s_n & = \mathcal{Z}^{-1} \left[ Y(z) \right]
\\ & = \mathcal{Z}^{-1} \left[ \frac{1}{2} \cdot \frac{1}{1 - 0.2 z^{-1}} - \frac{5}{1 - 0.5 z^{-1}} + \frac{15}{2} \cdot \frac{1}{1 - z^{-1}} \right]
\\ & = \frac{1}{2} \mathcal{Z}^{-1} \left[ \frac{1}{1 - \textcolor{red}{0.2} z^{-1}} \right] - 5 \mathcal{Z}^{-1} \left[ \frac{1}{1 - \textcolor{red}{0.5} z^{-1}} \right] + \frac{15}{2} \mathcal{Z}^{-1} \left[ \frac{1}{1 - z^{-1}} \right]
\\ & = \frac{1}{2} \cdot \textcolor{red}{0.2}^n - 5 \cdot \textcolor{red}{0.5}^n + \frac{15}{2}
\end{align*}\]ただし、これは \( n \geqq 0 \) のとき。
\( n < 0 \) のときは常に \( s_n = 0 \) なので、ステップ応答は\[
s_n = \left\{ \begin{array}{cc} \frac{1}{2} \cdot 0.2^n - 5 \cdot 0.5^n + \frac{15}{2} & ( n \geqq 0 ) \\ 0 & (n < 0) \end{array} \right.
\]となる。
※ インパルス応答のときと同じように単位ステップ信号 \( u_n \) を用いてステップ応答を\[
s_n = \left( \frac{1}{2} \cdot 0.2^n - 5 \cdot 0.5^n + \frac{15}{2} \right) u_n
\]と答えてもOK。
例題を解いてみた方はわかると思うのですが、部分分数分解関連の計算が少し重いです。
もし部分分数分解の計算が嫌だなぁと思った方は、本記事の第6章まで飛んでください。インパルス応答を利用して部分分数分解なしに計算する方法を紹介しています。
単位ステップ信号 \( s_n \) を入力としたときの出力のことをステップ応答と呼び、\[
\frac{1}{1-z^{-1}} H(z)
\]を逆 \( z \) 変換することで求められる。
※1 \( H(z) \) は伝達関数
※2 \( n < 0 \) のときは \( h_n < 0 \) となるので注意。
6. インパルス応答から入力信号に対する出力信号を求めてみよう
インパルス応答 \( h_n \) を求めることで、様々な入力 \( x_n \) に対する出力 \( y_n \) を求めることができます。
そこで、実際にインパルス応答を使って出力 \( y_n \) を計算してみましょう。
(1) 数列・信号のたたみ込み演算
(i) たたみ込み演算の定義
2つの信号(数列)\( x_n * y_n \) とは、下の図のように一方の数列 \( x_n \) を0番目(つまり \( n = 0 \) を基準に左から右方向に、もう一方の数列 \( y_n \) を \( k \) 番目(つまり \( n = k \))を基準にを右から左方向に読んでいき、対応する2つの数列を掛けたものをすべて足す演算を表します。別名コンボリューションとも呼びます。
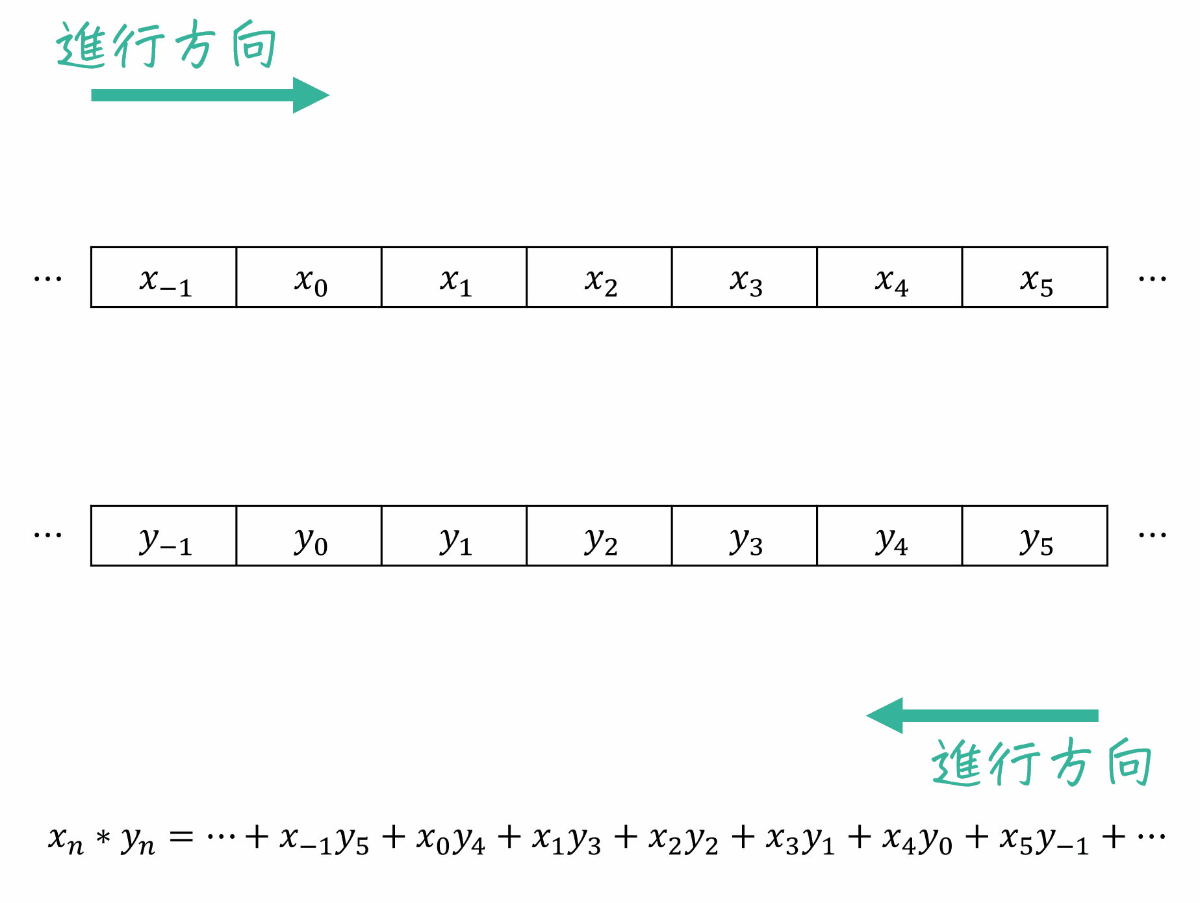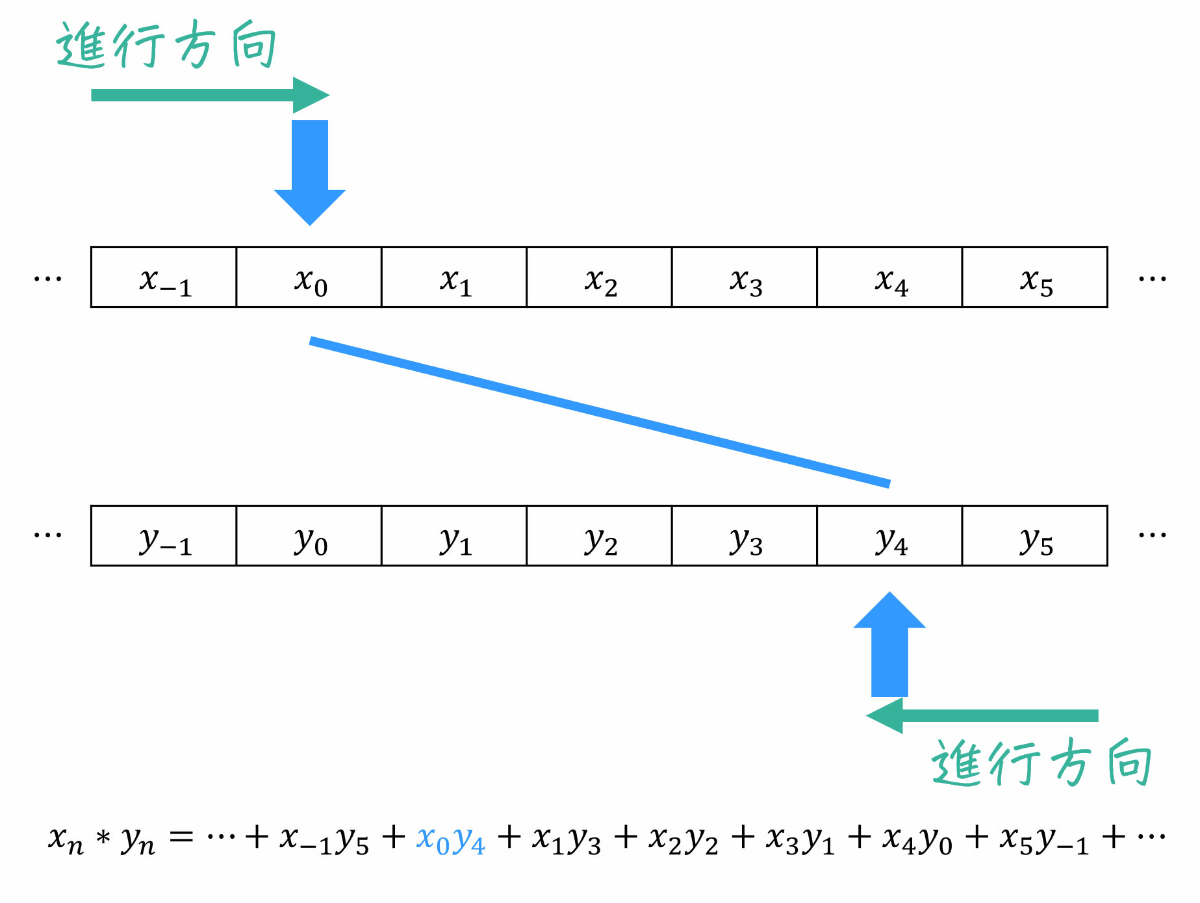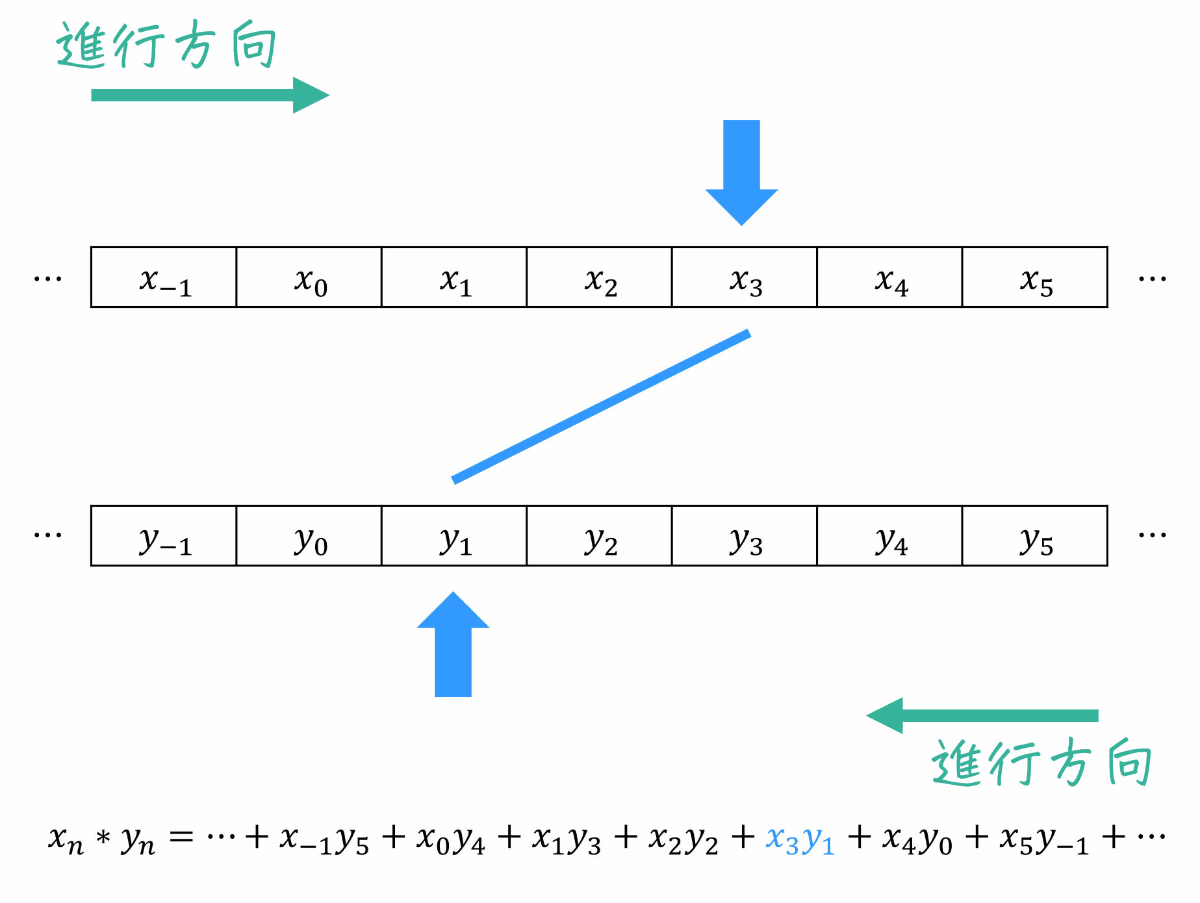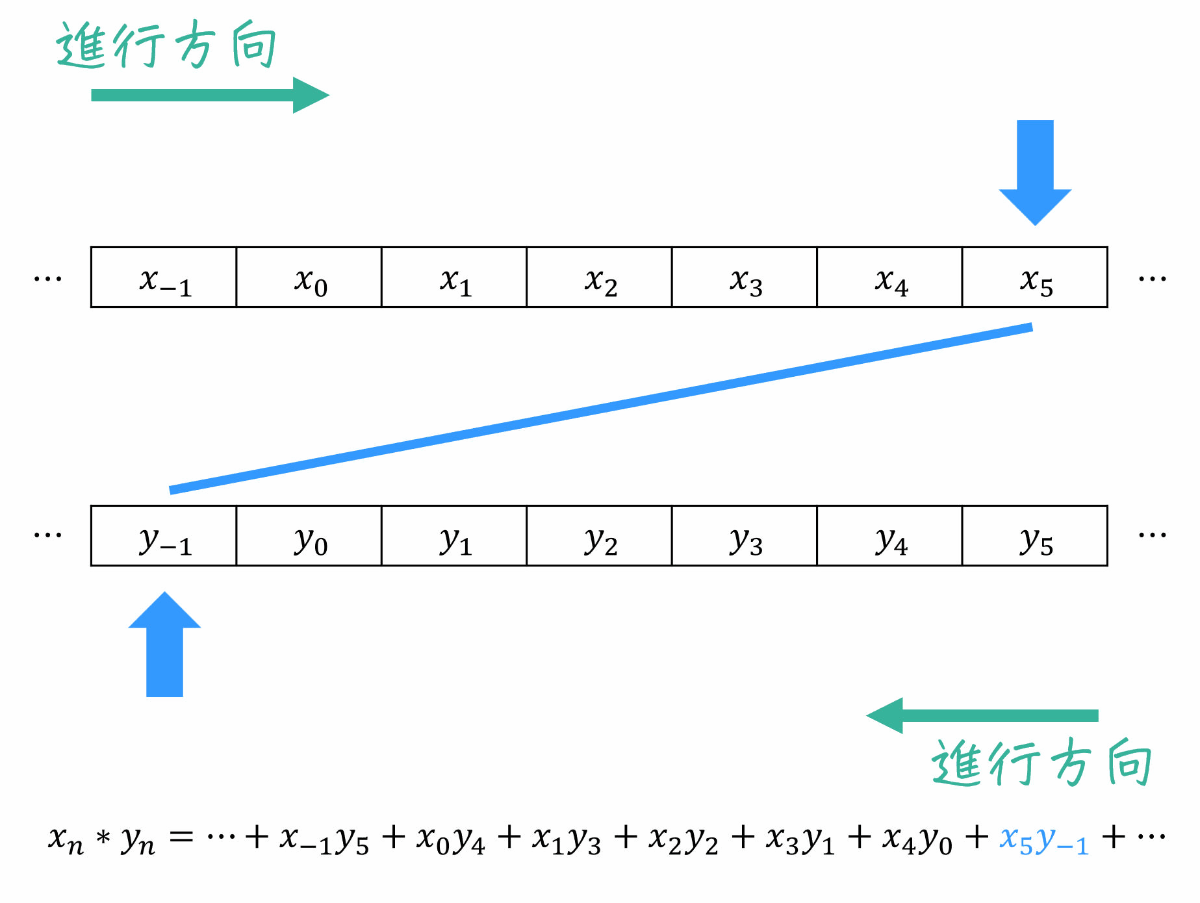
式で表すと、\[
\cdots + x_{-1} y_{n+1} + x_0 y_n + x_1 y_{n-1} + x_2 y_{n-2} + \cdots + x_{n-1} y_{1} + x_{n} y_{0} + x_{-1} y_{n+1}+ \cdots
\]となります。
また、シグマ記号を使って\[
\sum^{\infty}_{k = - \infty} x_k y_{n-k}
\]と表すこともできます。
(ii) たたみ込み演算と因果系システム
数列 \( x_k \) のマイナス項目(例えば \( x_{-4} \) や \( y_{-5} \) など)の値がすべて0、つまり\[ x_k = 0 \ \ \ ( k < 0 ) \]となるシステムのことを因果系システムと呼びます。
例えば、単位ステップ信号(関数)\[
u_n = \left\{ \begin{array}{ll} 1 & ( n \geqq 0 ) \\ \textcolor{red}0 & \textcolor{red}{(n < 0)} \end{array} \right.
\]は、マイナス項目(\( u_{-1}, u_{-2}, \cdots \))では必ず0となりますね。なので単位ステップ信号(関数)で表されるシステムは因果系システムと言えますね。
因果系システム、つまり \( k < 0 \) のとき、必ず \( x_k = 0 \) を満たす数列(信号)同士のたたみ込み演算は、\( x_n \), \( y_n \) のマイナス項目が0で掛けあわされ、打ち消される形となります。
(i)の例でも出した \( n = 4 \) の例だと、下のような形となります。
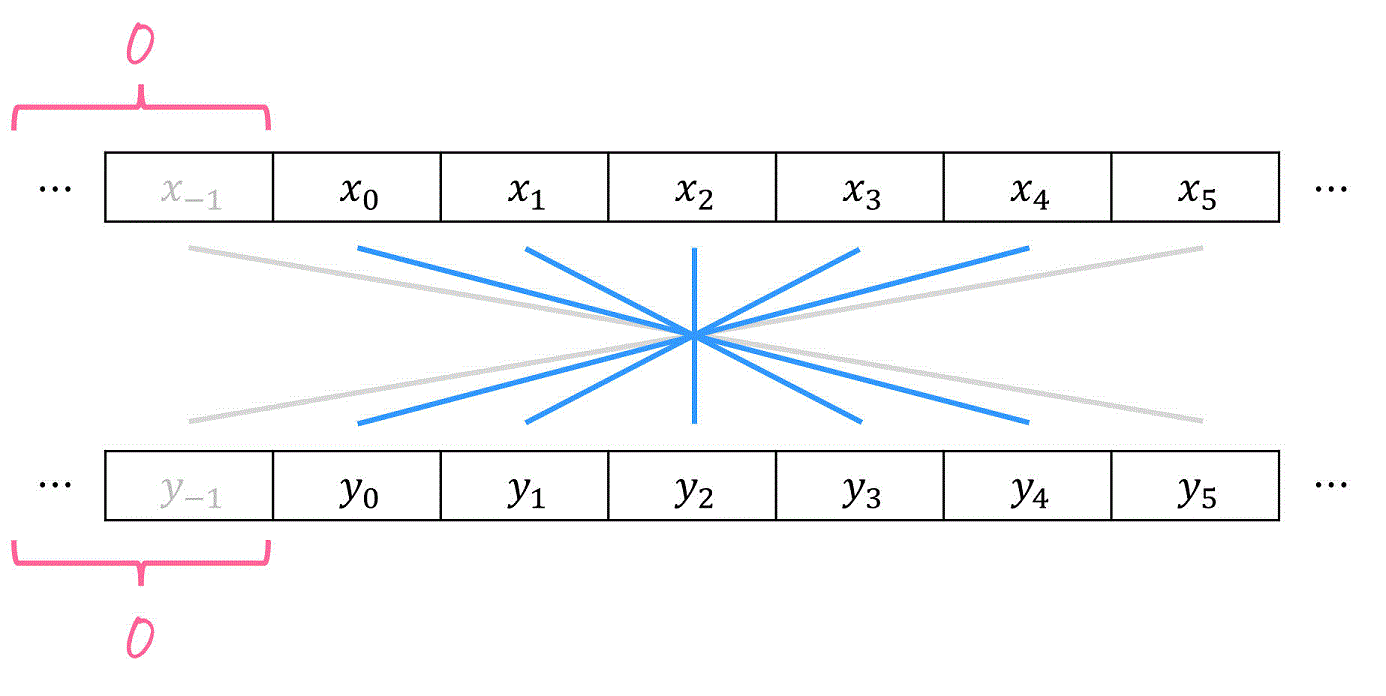
また、数式で書くと、計算が必要な部分は下の青色部分だけとなります。(※ 例えば \( n = 4 \) の場合 )

そのため、残るのは \( 0 \leqq k \leqq n \) 部分のたたみ込み、つまり\[\begin{align*}
x_n * y_n & = x_0 y_n + x_1 y_{n-1} + x_2 y_{n-2} + \cdots + x_{n-1} y_1 + x_n y_0
\\ & = \sum^{n}_{k=0} x_k y_{n-k}
\end{align*}\]となるため、無限大の計算がなくなり、だいぶ簡単になります。
x_n * y_n & = \sum^{\infty}_{k = - \infty} x_k y_{n-k} \\ & = \cdots + x_{-1} y_{n+1} + x_0 y_n + \cdots + x_n y_0 + x_{n+1} y_{-1} + \cdots
\end{align*}\] [\( x_n \), \( y_n \) ともに因果系システムの場合]\[\begin{align*}
x_n * y_n & = \sum^{n}_{k = 0} x_k y_{n-k} \\ & = x_0 y_n + x_1 y_{n-1} + \cdots + x_{n-1} y_1 + x_n y_0
\end{align*}\]
※ 数列(信号) \( x_n \) のマイナス項目の値がすべて0になるシステム\[
x_{k} = 0 \ \ \ (k < 0)
\]のことを因果系システムと呼ぶ。
(2) たたみ込みと入出力信号の関係
(i) z変換とたたみ込み
2つの数列 \( x_n \), \( y_n \) の畳み込み \( x_n * y_n \) をz変換した結果は、数列をそれぞれz変換した結果 \( X(z) \), \( Y(z) \) の積になります。数式で書くと、\[
\mathcal{Z} \left[ x_n * y_n \right] = X(z) Y(z)
\]となります。
(ちなみに計算順序を入れ替えて \( Y(z) X(z) \) としてもOKです)
(ii) たたみ込みと伝達関数
ディジタルシステムは、z変換をすることで\[
Y(z) = H(z) X(z)
\]と、伝達関数 \( H(z) \) を用いて表すことができましたね。
この \( H(z) X(z) \) というのがまさにたたみこみの形ですね。つまり、\[
\mathcal{Z}^{-1} \left[ H(z) X(z) \right] = h_n * x_n = x_n * h_n
\]が成立します。
そのため、\( y_n = h_n * x_n = x_n * h_n \) の関係式も成立します。
(iii) インパルス応答とたたみ込み
インパルス応答 \( h_n \) さえわかれば、入力信号 \( x_n \) とのたたみ込み演算 \( h_n * x_n \) をすることにより、出力信号 \( y_n \) を求めることができます。
しかし、この計算が出来るのはインパルス応答 \( h_n \) と入力信号 \( x_n \) がともに因果系システム、つまり「すべての \( n < 0 \) において、\( h_n = x_n = 0 \) を満たすシステム」の場合のみです。
(なお、インパルス応答が有限な区間内(0〜n)のみで終わるようにしたフィルタをFIRフィルタ(finite impulse response)と呼ばれます。一方、インパルス応答が無限の範囲で続くフィルタはIIRフィルタ(infinite impulse response)と呼ばれます。)
(3) たたみこみを使って出力を求めてみよう!
では、たたみ込みを使って実際にある入力 \( x_n \) に対する出力 \( y_n \) を求めてみましょう。
次の漸化式で表されるディジタルシステムがある。\[
y_n = 0.7 y_{n-1} - 0.1 y_{n-2} + 3 x_{n}
\]
このシステムに \( x_0 = 5 \), \( x_1 = -1 \) の入力、つまり\[
x_n = 5 \delta_n - \delta_{n-1}
\]を与える。このときの出力 \( y_n \) を単位インパルス信号を用いて表しなさい。
[解説4]
例題2で、インパルス応答 \( h_n \) が\[
h_n = 5 \cdot 0.5^n - 2 \cdot 0.2^n
\]と求められてるので、これをつかいます。
また、\( n < 0 \) を満たすどんな \( n \) に対しても、\( h_n = 0 \) および \( x_n = 0 \) を満たすため、例題3のシステム、および入力信号は因果的である。
よって、出力 \( y_n \) は、たたみこみ\[\begin{align*}
y_n & = h_n * x_n
\\ & = \sum^{n}_{k = 0} h_k \cdot x_{n-k}
\end{align*}\]で計算できる。
ここで、\( h_n * x_n \) を計算すると、\[\begin{align*}
y_n & = h_n * x_n
\\ & = \sum^{n}_{k = 0} h_k \cdot x_{n-k}
\\ & = h_0 \cdot x_n + h_{1} \cdot x_{n-1} + \cdots + h_{n-1} \cdot x_1 + h_n \cdot x_0
\\ & = h_{n} \cdot x_0 + h_{n-1} \cdot x_1
\\ & = 5 ( 5 \cdot 0.5^n - 2 \cdot 0.2^n) - ( 5 \cdot 0.5^{n-1} - 2 \cdot 0.2^{n-1} )
\\ & = 25 \cdot 0.5^n - 10 \cdot 0.2^n - ( 10 \cdot 0.5^n - 10 \cdot 0.2^n )
\\ & = 15 \cdot 0.5^n
\end{align*}\]となるため、出力は\[
y_n = 15 \cdot 0.5^n
\]となります。(ただし \( n \geqq 0 \) )
入力信号 \( x_n \)、出力信号 \( y_n \)、インパルス応答 \( h_n \) は以下の関係が成立する。\[
y_n = h_n * x_n = x_n * h_n
\]※ \( * \) はたたみ込み積(コンボリューション)を表す。
7. インパルス応答からステップ応答を求めてみよう
そこで、第6章ではステップ信号(関数)\[
u_n = \left\{ \begin{array}{ll} 1 & ( n \geqq 0 ) \\ 0 & (n < 0) \end{array} \right.
\]を入力にしたときの出力 \( s_n \) であるステップ応答の求め方を確認しましょう。
(1) インパルス応答とステップ応答の関係(計算方法)
インパルス応答 \( h_n \) さえわかれば、入力信号 \( x_n \) とのたたみ込み演算 \( h_n * x_n \) をすることにより、出力信号 \( y_n \) を求めることができるのでしたね。
さらにたたみ込み演算 \( h_n * x_n \) は、因果系システム同士、つまりどのような \( n \) に対しても、\( h_n < 0 \)、\( x_n < 0 \) をともに満たす場合は\[\begin{align*}
h_n * x_n & = h_0 x_n + h_1 x_{n-1} + \cdots + h_{n-1} x_1 + h_n x_0
\\ & = \sum^{n}_{k = 0} h_k x_{n-k}
\end{align*}\]と少し簡単に計算ができるのでしたね。
ここで、ステップ信号は \( n < 0 \) のときは常に \( u_n < 0 \) なので、インパルス応答も \( n < 0 \) のときに \( h_n < 0 \) を満たすのであれば、ステップ応答 \( s_n \) は、\[\begin{align*}
s_n & = h_n *u_n
\\ & = h_0 \underbrace{ u_n }_{1} + h_1 \underbrace{ u_{n-1} }_{1} + h_2 \underbrace{ u_{n-2} }_{1} + \cdots + h_{n-1} \underbrace{ u_1 }_{1} + h_n \underbrace{ u_0 }_{1}
\\ & = h_0 + h_1 + h_2 + \cdots + h_{n-1} + h_n
\\ & = \sum^{n}_{k = 0} h_k
\end{align*}\]で簡単に計算ができます。
(2) 等比数列の計算方法
インパルス応答は、\[
h_n = 5 \cdot 0.5^n - 2 \cdot 0.2^n
\]のようにべき乗 \( a^n \) の足し算と定数倍の組み合わせで出来ています。
なので、因果系システムに対するステップ応答\[
s_n = \sum^{n}_{k = 0} h_k
\]を求める際には、このべき乗 \( a^n \) の和を計算する必要が出てきます。
ここで、べき乗 \( a^n \) に \( n = 0 , 1, 2 , \cdots \) と代入してみると、\[
1, a, a^2, a^3, \cdots, a^{n-1}, a^n
\]と、「初項1、公比 \( a \) の \( n+1 \) 項の等比数列の和」となっていますね。
さらに、項数は \( k = 0 \) から \( k = n \) までの \( n + 1 \) 項あるので、べき乗 \( a^n \) の和 の公式は、\[
S = \frac{1 - a^{n+1}}{1-a} = \frac{a^{n+1} - 1}{a-1}
\]と求めることができます[6]数2Bで習う等比数列の公式は、初項 \( a_1 \), 公比 \( r \) の第 \( n \) 項までの和 \( S_n \) の公式\[ S_n = \frac{a(1 - r^n)}{1 - r} = \frac{a(r^n - 1)}{r - … Continue reading。
インパルス応答 \( h_n \) が因果的システム、つまり \( n < 0 \) を満たすどのような \( n \) 対しても、\( h_n = 0 \) を満たすとき、単位ステップ応答 \( s_n \) は\[\begin{align*}
s_n & = h_0 + h_1 + \cdots + h_{n-1} + h_n
\\ & = \sum^{n}_{k = 0} h_k
\end{align*}\]と計算できる。ただし、\( n \geqq 0 \)。
※1 和を \( 0 \leqq k \leqq n \) の範囲でのみ計算しているため、\( n < 0 \) のときは \( s_n = 0 \) となる。
※2 試験で計算させてくるシステムは、ほぼ確実に因果系システムなので、基本的に公式が適用できると思ってもらってOKです)
また、インパルス応答は \( h_n = t_1 a^n + t_2 b^n \) のようなべき乗の和、定数倍の形になっていることが非常に多い。
このような場合、ステップ応答 \( s_n \) を計算する際には\[\begin{align*}
s_n & = \sum^{n}_{k = 0} h_k
\\ & = \sum^{n}_{k = 0} t_1 a^n + t_2 b^n
\\ & = t_1 \sum^{n}_{k =0} a^n + t_2 \sum^{n}_{k =0} b^n
\end{align*}\]のようにまずは和とべき乗を隔離し、隔離した後に\[
\sum^{n}_{k =0} a^n = \frac{1-a^{n+1}}{1-a} = \frac{a^{n+1}-1}{a-1}
\]と等比数列の公式を適用する。
(3) 例題
それでは、早速インパルス応答からステップ応答を求める練習をしてみましょう!
次の漸化式で表されるディジタルシステムがある。\[
y_n = 0.7 y_{n-1} - 0.1 y_{n-2} + 3 x_{n}
\]
このディジタルシステムのインパルス応答は例題2より、\[
h_n = \left\{ \begin{array}{cc} 5 \cdot 0.5^n - 2 \cdot 0.2^n & ( n \geqq 0 ) \\ 0 & ( n < 0 ) \end{array} \right.
\]と求められている。
例題2の答えを使って、ステップ応答 \( s_n \) を求めなさい。
[解説5]
\( n < 0 \) を満たすどんな \( n \) に対しても、\( h_n = 0 \) を満たすため、例題3のシステムは因果的システムと言える。
そのため、ステップ応答 \( s_n \) はインパルス応答 \( h_n \) を用いて\[\begin{align*}
s_n & = h_0 + h_1 + h_2 \cdots + h_{n-1} + h_n
\\ & = \sum^{n}_{k = 0} h_k
\end{align*}\]と計算できる。
ここで、\( a_n = 0.5^n \) と \( b_n = 0.2^n \) とし、第0項から第 \( n \) 項までの総和を求める。
すると、\[\begin{align*}
\sum^{n}_{k = 0} a_n & = \sum^{n}_{k = 0} 0.5^n
\\ & = \frac{1 - 0.5^{n+1}}{1-0.5}
\\ & = 2 ( 1 - 0.5^{n+1} )
\end{align*}\]
\[\begin{align*}
\sum^{n}_{k = 0} b_n & = \sum^{n}_{k = 0} 0.2^n
\\ & = \frac{1 - 0.2^{n+1}}{1-0.2}
\\ & = 1.25 ( 1 - 0.2^{n+1} )
\end{align*}\]と求められる。
よって、\( s_n \) を\[\begin{align*}
s_n & = \sum^{n}_{k = 0} h_n
\\ & = \sum^{n}_{k = 0} 5 \cdot 0.5^n - 2 \cdot 0.2^n
\\ & = 5 \sum^{n}_{k = 0} a_n - 2 \sum^{n}_{k = 0} b_n
\\ & = 5 \cdot 2 ( 1 - 0.5^{n+1} ) - 2 \cdot 1.25 ( 1 - 0.2^{n+1} )
\\ & = 10 ( 1 - 0.5^{n+1} ) - 2.5 (1 - 0.2^{n+1} )
\\ & = 7.5 - 10 \cdot 0.5^{n+1} + 2.5 \cdot 0.2^{n+1}
\end{align*}\]と計算できる。ただし、\( n \geqq 0 \)。
また、\( n < 0 \) のときは、\( s_n = 0 \) なので、ステップ応答 \( s_n \) は\[\begin{align*}
s_n = \left\{ \begin{array}{cc} 7.5 - 10 \cdot 0.5^{n+1} + 2.5 \cdot 0.2^{n+1} & ( n \geqq 0 ) \\ 0 & ( n < 0 ) \end{array} \right.
\end{align*}\]となる。
少し形は違いますが、伝達関数からステップ応答を求めた例題3の答え\[
s_n = \left\{ \begin{array}{cc} \frac{1}{2} \cdot 0.2^n - 5 \cdot 0.5^n + \frac{15}{2} & ( n \geqq 0 ) \\ 0 & (n < 0) \end{array} \right.
\]と同じ形になることが確認できましたね。
このように、たたみ込みとインパルス応答を使うことで、ステップ応答も少し簡単に計算することができます。
ただし、インパルス応答を間違えてしまうとステップ応答も連動して間違えてしまうので、計算は慎重に…。
7. 練習問題
では、今回習った内容が定着できているかを練習問題で確認しましょう!
次の漸化式\[
y_n = \frac{9}{4} y_{n-1} - \frac{9}{8} y_{n-2} + x_n + \frac{3}{2} x_{n-1}
\]で表されるシステムがある。
(1) 伝達関数 \( H(z) \) を求めなさい。
(2) インパルス応答 \( h_n \) を求めなさい。
(3) ステップ応答 \( s_n \) を求めなさい。
(4) 入力を \( x_n = \delta_n + 3 \delta_{n-1} - 9 \delta_{n-2} \) とする。このときの出力 \( y_n \) を答えなさい。
8. 練習問題の答え
(1) 伝達関数の計算
\( y_n \) をz変換すると、\[\begin{align*}
Y(z) & = \mathcal{Z} \left[ y_n \right]
\\ & = \mathcal{Z} \left[ \frac{9}{4} y_{n-1} - \frac{9}{8} y_{n-2} + x_n + \frac{3}{2} x_{n-1} \right]
\\ & = \frac{9}{4} \mathcal{Z} \left[ y_{n-1} \right] - \frac{9}{8} \mathcal{Z} \left[ y_{n-2} \right] + \mathcal{Z} \left[ x_n \right] + \frac{3}{2} \mathcal{Z} \left[ x_{n-1} \right]
\\ & = \frac{9}{4} z^{-1} Y(z) - \frac{9}{8} z^{-2} Y(z) + X(z) + \frac{3}{2} z^{-1} X(z)
\end{align*}\]
となる。両辺を整理すると\[\begin{align*}
Y(z) - \frac{9}{4} z^{-1} Y(z) + \frac{9}{8} z^{-2} Y(z) & = X(z) + \frac{3}{2} z^{-1} X(z) \\
8 Y(z) - 18 z^{-1} Y(z) + 9 z^{-2} Y(z) & = 8 X(z) + 12 z^{-1} X(z) \\
(8 - 18 z^{-1} + 9 z^{-2}) Y(z) & = (8 + 12z^{-1}) X(z)
\end{align*}\]となるため、
\[
Y(z) = \frac{8 + 12z^{-1} }{ 8 - 18 z^{-1} + 9 z^{-2} } X(z)
\]となる。
よって、伝達関数 \( H(z) \) は\[
H(z) = \frac{8 + 12z^{-1} }{ 8 - 18 z^{-1} + 9 z^{-2} }
\]となる。
(2) インパルス応答の計算
インパルス応答 \( h_n \) は、伝達関数 \( H(z) \) を逆z変換することで求めることができる。
ここで、\[\begin{align*}
\frac{8 + 12z^{-1} }{ 8 - 18 z^{-1} + 9 z^{-2} } & = \frac{8 + 12z^{-1} }{ (2-3z^{-1})(4-3z^{-1}) }
\\ & = \frac{ a }{ 2 - 3z^{-1} } + \frac{ b }{ 4 - 3z^{-1} }
\end{align*}\]と部分分数分解をすることを考える。
両辺を \( (2-3z^{-1})(4-3z^{-1}) \) 倍すると、\[
8 + 12 z^{-1} = a (4 - 3z^{-1} ) + b ( 2 - 3z^{-1} )
\]となる。
(i) \( z^{-1} = \frac{4}{3} \) のとき(つまり \( z = \frac{3}{4} \) )
\[
8 + 12 \cdot \frac{4}{3} = a ( 4 - 4) +b \left( 2 - 4 \right)
\]より、\(8 + 16 = -2b \)、\( b = -12 \) となる。
(ii) \( z^{-1} = \frac{2}{3} \) のとき(つまり \( z = \frac{3}{2} \) )
\[
8 + 12 \cdot \frac{2}{3} = a (4 - 2) + b (2 - 2)
\]より、\( 16 = 2a \)、\( a = 8 \) となる。
したがって、\[
H(z) = \frac{8}{2 - 3z^{-1}} - \frac{12}{4 - 3z^{-1}}
\]と部分分数分解できる。
よって、インパルス応答 \( h_n \) は、\( n \geqq 0 \) のとき、\[\begin{align*}
h_n & = \mathcal{Z}^{-1} \left[ H(z) \right]
\\ & = \mathcal{Z}^{-1} \left[ \frac{8}{2 - 3z^{-1}} - \frac{12}{4 - 3z^{-1}} \right]
\\ & = 4 \mathcal{Z}^{-1} \left[ \frac{1}{1- \textcolor{red}{1.5} z^{-1}} \right] - 3 \mathcal{Z}^{-1} \left[ \frac{1}{1 - \textcolor{red}{0.75} z^{-1} } \right]
\\ & = 4 \cdot \textcolor{red}{1.5}^n - 3 \cdot \textcolor{red}{0.75}^n
\end{align*}\]となる。
\( n < 0 \) のときは \( h_n = 0 \) なので、インパルス応答は\[
h_n = \left\{ \begin{array}{cc} 4 \cdot 1.5^n - 3 \cdot 0.75^n & ( n \geqq 0 ) \\ 0 & ( n < 0 ) \end{array} \right.
\]となる。
※ 単位ステップ信号 \( u_n \) を用いてインパルス応答を\[
h_n = \left( 4 \cdot 1.5^n - 3 \cdot 0.75^n \right) u_n
\]と答えてもOK。
(3) ステップ応答の計算
[推奨] インパルス応答から求める方法
(2)より、\( n < 0 \) を満たすどんな \( n \) に対しても、\( h_n = 0 \) を満たすため、題意のシステムは因果的システムと言える。
そのため、ステップ応答 \( s_n \) はインパルス応答 \( h_n \) を用いて\[\begin{align*}
s_n & = h_0 + h_1 + h_2 \cdots + h_{n-1} + h_n
\\ & = \sum^{n}_{k = 0} h_k
\end{align*}\]と計算できる。
ここで、\( a_n = 1.5^n \) と \( b_n = 0.75^n \) とし、第0項から第 \( n \) 項までの総和を求める。
すると、\[\begin{align*}
\sum^{n}_{k = 0} a_n & = \sum^{n}_{k = 0} 1.5^n
\\ & = \frac{1.5^{n+1} - 1}{1.5 - 1}
\\ & = 2 ( 1.5^{n+1} - 1 )
\end{align*}\]
\[\begin{align*}
\sum^{n}_{k = 0} b_n & = \sum^{n}_{k = 0} 0.75^n
\\ & = \frac{1 - 0.75^{n+1}}{1-0.75}
\\ & = 4 ( 1 - 0.75^{n+1} )
\end{align*}\]と求められる。
よって、\[\begin{align*}
s_n & = \sum^{n}_{k = 0} h_n
\\ & = \sum^{n}_{k = 0} 4 \cdot 1.5^n - 3 \cdot 0.75^n
\\ & = 4 \sum^{n}_{k = 0} a_n - 3 \sum^{n}_{k = 0} b_n
\\ & = 4 \cdot 2 ( 1.5^{n+1} - 1 ) - 3 \cdot 4 ( 1 - 0.75^{n+1} )
\\ & = 8 ( 1.5^{n+1} - 1 ) - 12 ( 1 - 0.75^{n+1} )
\\ & = 8 \cdot 1.5^{n+1} + 12 \cdot 0.75^{n+1} - 20
\end{align*}\]と \( s_n \) を計算できる。
また、\( n < 0 \) のときは、\( s_n = 0 \) なので、ステップ応答 \( s_n \) は\[\begin{align*}
s_n = \left\{ \begin{array}{cc} 8 \cdot 1.5^{n+1} + 12 \cdot 0.75^{n+1} - 20 & ( n \geqq 0 ) \\ 0 & ( n < 0 ) \end{array} \right.
\end{align*}\]
※ インパルス応答のときと同じように単位ステップ信号 \( u_n \) を用いてステップ応答を\[
s_n = \left( 8 \cdot 1.5^{n+1} + 12 \cdot 0.75^{n+1} - 20 \right) u_n
\]と答えてもOK。
伝達関数から求める方法
ステップ応答は、\[\begin{align*}
Y(z) & = \frac{1}{1-z^{-1}} H(z)
\\ & = \frac{8 + 12z^{-1}}{(2-3z^{-1})(4-3z^{-1})( 1 - z^{-1} ) }
\end{align*}\]を \( z \) 変換することで計算できる。
まず\[\begin{align*}
Y(z) & = \frac{8 + 12z^{-1}}{(2-3z^{-1})(4-3z^{-1})( 1 - z^{-1} ) }
\\ & = \frac{a}{2 - 3 z^{-1}} + \frac{b}{4 - 3 z^{-1}} + \frac{c}{1 - z^{-1}}
\end{align*}\]と部分分数分解の形にする。
さらに、\[
\frac{8 + 12z^{-1}}{(2-3z^{-1})(4-3z^{-1})( 1 - z^{-1} ) } = \frac{a}{2 - 3 z^{-1}} + \frac{b}{4 - 3 z^{-1}} + \frac{c}{1 - z^{-1}}
\]の両辺を \( (2-3z^{-1})(4-3z^{-1})( 1 - z^{-1} ) \) 倍し、\[
8 + 12z^{-1} = a (4-3z^{-1})( 1 - z^{-1} ) + b (2-3z^{-1})( 1 - z^{-1} ) + c (2-3z^{-1})( 4 -3 z^{-1} )
\]としてから \( a \), \( b \), \( c \) を求める。
- \( z = 3/2 \) のとき、(つまり \( z^{-1} = 2/3 \))\[\begin{align*}
8 + 12 \cdot \frac{2}{3} & = a \left( 4 - 3 \cdot \frac{2}{3} \right) \left( 1 - \frac{2}{3} \right)
\\ & = a \cdot 2 \cdot \frac{1}{3}
\\ & = \frac{2}{3} a
\end{align*}\]となるため、\( 16 = \frac{2}{3} a \) より、\( a = 24 \)。 - \( z = 3/4 \) のとき(つまり \( z^{-1} = 4/3 \))\[\begin{align*}
8 + 12 \cdot \frac{4}{3} & = b \left( 2 - 3 \cdot \frac{4}{3} \right) \left( 1 - \frac{4}{3} \right)
\\ & = b \left( -2 \right) \cdot \left( - \frac{1}{3} \right)
\\ & = \frac{2}{3} b
\end{align*}\]となるため、\( 24 = \frac{2}{3} b \) より、 \( b = 36 \)。 - \( z = 1 \) のとき、(つまり \( z^{-1} = 1 \))\[\begin{align*}
8 + 12 & = c \left( 2 - 3 \right) \left( 4-3 \right)
\\ & = - c
\end{align*}\]より、\( c = -20 \)
よって、\[
Y(z) = \frac{24}{2 - 3 z^{-1}} + \frac{36}{4 - 3 z^{-1}} - \frac{20}{1 - z^{-1}}
\]と部分分数分解できる。
あとは、部分分数分解したものを逆 \( z \) 変換したものが \( s_n \) となる。\[\begin{align*}
s_n & = \mathcal{Z}^{-1} \left[ Y(z) \right]
\\ & = \mathcal{Z}^{-1} \left[ \frac{24}{2 - 3 z^{-1}} + \frac{36}{4 - 3 z^{-1}} - \frac{20}{1 - z^{-1}} \right]
\\ & = \mathcal{Z}^{-1} \left[ \frac{12}{1 - 1.5 z^{-1}} + \frac{9}{1 - 0.75 z^{-1}} - \frac{20}{1 - z^{-1}} \right]
\\ & = 12 \mathcal{Z}^{-1} \left[ \frac{1}{1 - \textcolor{red}{ 1.5 } z^{-1}} \right] + 9 \mathcal{Z}^{-1} \left[ \frac{1}{1 - \textcolor{red}{0.75} z^{-1}} \right] - 20 \mathcal{Z}^{-1} \left[ \frac{1}{1 - z^{-1}} \right]
\\ & = 12 \cdot \textcolor{red}{1.5}^n + 9 \cdot \textcolor{red}{0.75}^n - 20
\end{align*}\]ただし、これは \( n \geqq 0 \) のとき。
\( n < 0 \) のときは常に \( s_n = 0 \) なので、ステップ応答は\[
s_n = \left\{ \begin{array}{cc} 12 \cdot 1.5^n + 9 \cdot 0.75^n - 20 & ( n \geqq 0 ) \\ 0 & (n < 0) \end{array} \right.
\]となる。
※ インパルス応答のときと同じように単位ステップ信号 \( u_n \) を用いてステップ応答を\[
s_n = \left( 12 \cdot 1.5^n + 9 \cdot 0.75^n - 20 \right) u_n
\]と答えてもOK。
(4) 任意の入力に対する出力計算
入力 \( x_n \)、インパルス応答 \( h_n \)、出力 \( y_n \) には \( y_n = h_n * x_n \) の関係がある。また、(2)より、題意のシステムは因果的システムである。
そのため、\[\begin{align*}
y_n & = h_n * x_n
\\ & = \sum^{n}_{k = 0} h_k x_{n-k}
\\ & = h_0 x_n + h_1 x_{n-1} + \cdots + h_{n-2} x_2 + h_{n-1} x_1 + h_n x_0
\\ & = h_n x_0 + h_{n-1} x_1 + h_{n-2} x_2
\\ & = (4 \cdot 1.5^n - 3 \cdot 0.75^n) + 3 (4 \cdot 1.5^{n-1} - 3 \cdot 0.75^{n-1}) - 9 (4 \cdot 1.5^{n-2} - 3 \cdot 0.75^{n-2})
\\ & = 4 \cdot 1.5^n - 3 \cdot 0.75^n + 3 \left( \frac{8}{3} \cdot 1.5^{n} - 4 \cdot 0.75^n \right) - 9 \left( \frac{16}{9} \cdot 1.5^n - \frac{16}{3} \cdot 0.75^n \right)
\\ & = (4+8-16) 1.5^n + (-3-12+48) 0.75^n
\\ & = -4 \cdot 1.5^n + 33 \cdot 0.75^n
\end{align*}\]とステップ応答を計算できる。
9. さいごに
今回は、ディジタルシステムの解読の前編として、
- z変換の復習
- 伝達関数について
- インパルス応答
- たたみ込み計算
- インパルス応答と入力から出力を求める方法
- ステップ応答の求め方
の説明をしていきました。
引き続き、ディジタルシステムの理論を中編、後編にて書いてく予定なので、よろしくお願いいたします!
注釈
| ↑1 | 余談ですが、何故デジタルじゃなくてディジタルって書かれてる本やサイトが多いんでしょうかね… |
|---|---|
| ↑2 | ちなみに数2Bで習う漸化式は、\[ a_{n+1} = 2 a_{n} + 3 \]のように1つの変数に対して1つの式しか出てきません。一方、ディジタルシステムで出てくる漸化式は今回のように2つの変数 \( y \), \( x \) が出てきます。そのため、ディジタルシステム出てくる漸化式は余計に解くのが困難なのです。 |
| ↑3 | 正確には、伝達関数やインパルス応答を求めるときのことです。 |
| ↑4 | ディジタルシステムの解読では、将来的にどのような振る舞いをするかを調べる。そのため、十分先の未来においては、初期値の値が0だろうが1だろうがほとんど関係がない。なら、最初から全部初期値を0にして考えてしまおうというわけ。 |
| ↑5 | 公式的には1を \( z \) 変換する場合と同じです。 |
| ↑6 | 数2Bで習う等比数列の公式は、初項 \( a_1 \), 公比 \( r \) の第 \( n \) 項までの和 \( S_n \) の公式\[ S_n = \frac{a(1 - r^n)}{1 - r} = \frac{a(r^n - 1)}{r - 1}\]です。忘れてしまった人は、この機会に思い出しましょう。 |
関連広告・スポンサードリンク






![[基本情報・応用情報] うさぎでもわかる情報理論 第3羽 ハフマン符号化](https://www.momoyama-usagi.com/wp-content/uploads/joho3-2-3-150x150.jpg)