1週間で完成！　うさぎでもわかる確率分布と統計的な推測　6日目　母平均・母比率の推定

こんにちは、ももやまです。

今回は、数Bの「確率分布と統計的な推測」で頻繁に出てくる「母平均・母比率の推定」について説明していきたいと思います。

「母平均・母比率の推定」に関する問題は共通テスト（センター試験）でほぼ毎年どちらかが出てくるので、必ず勉強しておきましょう！

 

 

前回の「うさぎでもわかる確率分布と統計的な推測」5日目はこちら↓

www.momoyama-usagi.com

スポンサードリンク

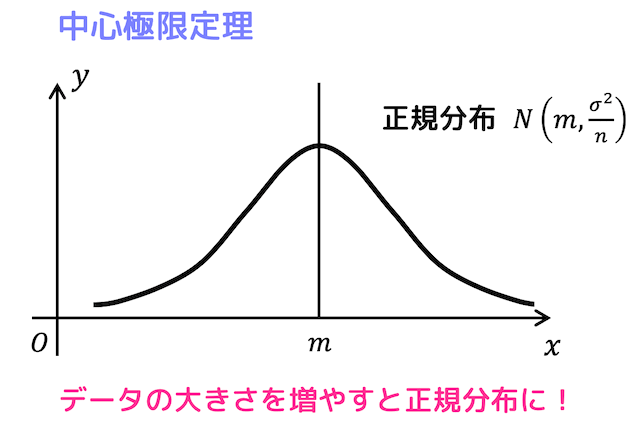
１．中心極限定理（復習）

まずは、前回説明した中心極限定理の復習をしましょう。

 

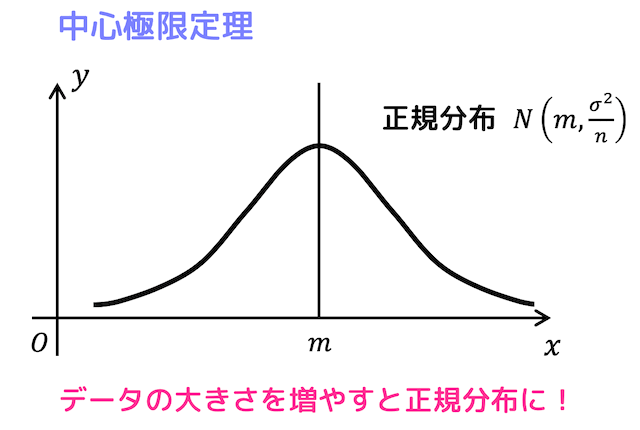
母集団が（分散が0ではない）どんな分布であっても、母平均が \( m \)、母分散が \( \sigma^2 \) の母集団から、大きさ \( n \) の標本を選んだときの標本平均 \( \overline{X} \) は正規分布 \( N \left( m, \frac{\sigma^2}{n} \right) \) に従うのが中心極限定理です。

スポンサードリンク

２．信頼度

(1) 信頼度とは

標本調査では母集団の一部のデータを抽出し、抽出したデータから母集団のデータを予測するため、正確なデータ（母平均など）を求めることができません。

そこで、ある範囲内に正確なデータが確率はどれくらいかを表したものが信頼度となり、ある範囲のことを信頼区間と呼びます。

例

信頼度95%：信頼区間内に正しいデータがある確率が95%
信頼度99%：信頼区間内に正しいデータがある確率が99%

(2) 正規分布と信頼区間

数Bの「確率分布と統計的な推測」では、標本を正規分布とみなし、標本から計算された平均、標準偏差から信頼区間を求めます*1。

具体的には、平均が信頼区間の中央となり、そこから標準偏差と信頼度によって信頼区間が決定します。

 

ここからは、平均から標準偏差何個分離れたら信頼度95%（99%）に相当するのかを確認していきましょう。

 

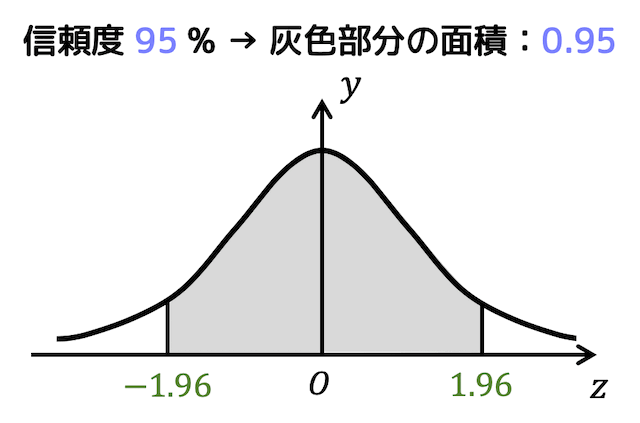
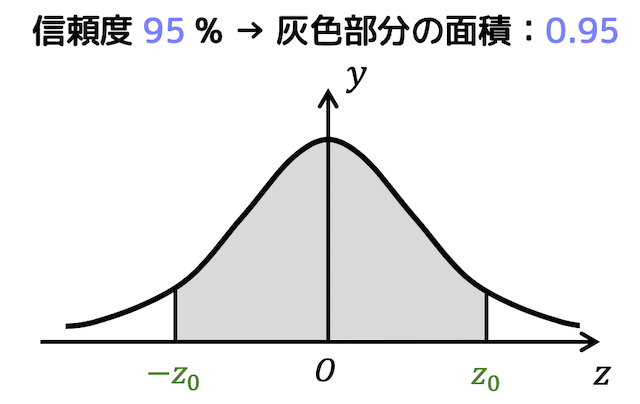
信頼度95％ということは、信頼区間内に正しいデータがある確率が95%ということでしたね。

つまり、下の図のように、\( y \) 軸（平均）を中心にした灰色部分の面積が0.95になるということですね。

上の図（標準正規分布）は \( y \) 軸に対して対称*2なので、正の部分の面積と負の部分の面積が等しくなりますよね。

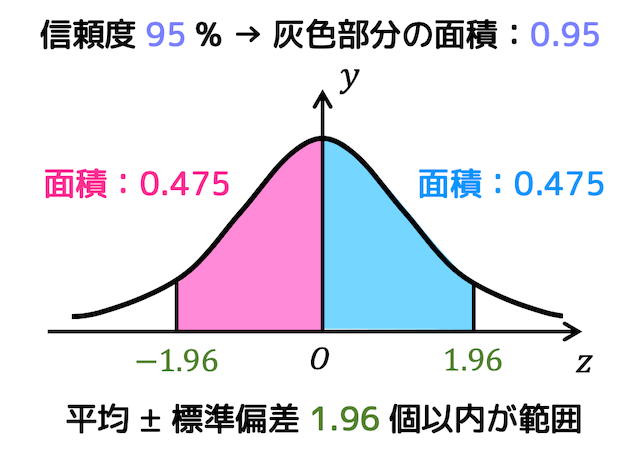
つまり、青色部分の面積が0.475（0.95÷2）になるとき、\( 0 \leqq z \leqq z_0 \) の \( z_0 \) がどうなるかを求めればいいですね。

これを正規分布表から求めると……

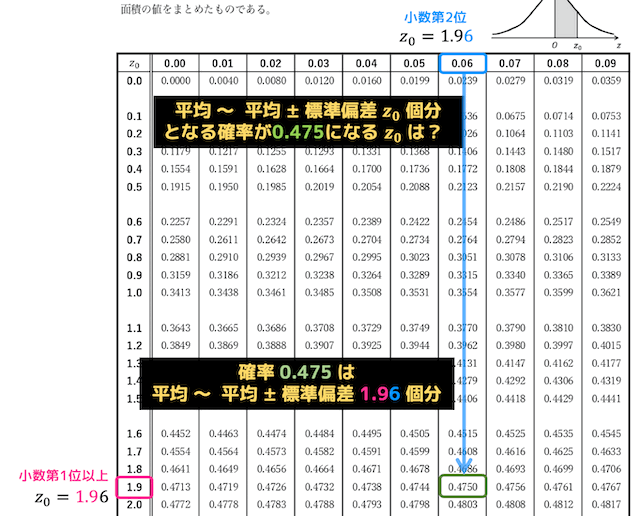
\( z_0 = 1.96 \) と求めることができますね。

これを日本語で表すと、「平均 ± 標準偏差1.96個以内」が信頼度95%の範囲に相当することがわかりますね。

 

同様に信頼度99%の場合、\( - z_0 \leqq z \leqq z_0 \) となる確率が0.99、つまり\( 0 \leqq z \leqq z_0 \) となる確率が0.495（0.99÷2）となる \( z_0 \) を求めればいいですね。

上と同じようにして正規分布表から0.495となる \( z_0 \) を探すと、\( z_0 = 2.58 \) と求めることができます。

日本語で表すと、「平均 ± 標準偏差2.58個以内」が信頼度99%の範囲に相当することがわかりますね。

スポンサードリンク

２．母平均の推定

簡単に求めることができる標本平均 \( \overline{X} \) と標本分散 \( s \) から母平均 \( m \) を推定する方法について説明していきましょう。

(1) 信頼度・信頼区間

母平均 \( m \) がある範囲内 \( A \leqq m \leqq B \) となる確率が \( c \) %となる区間のことを母平均 \( m \) に対する信頼度 \( c \) %の信頼区間と呼びます。

(2) 母平均の推定方法

母分散が \( \sigma^2 \) の母集団から、十分に大きい大きさ \( n \) の標本を選び、その標本の標本平均が \( \overline{X} \)、標本分散が \( s^2 \) だとします。

上の情報だけから、母集団の母平均 \( m \) を信頼度95%で推定してみましょう。

 

まず、標本の大きさ \( n \) が十分に大きいので、標本平均 \( \overline{X} \) は平均が \( m \)、分散が \( \frac{\sigma^2}{n} \) の正規分布に従いますね。

ここで、標準偏差の形がややこしいくなるので\[
\sigma' = \frac{\sigma}{\sqrt{n} }
\]とし、さらに \( z \) を\[
z = \frac{ \overline{X} - m}{\sigma'}
\]とすることで \( z \) は標準正規分布に従いますね。

ここで、\(  -z_0 \leqq z \leqq z_0 \)（対称なのがポイント）を変形すると、\[
-z_0 \leqq \frac{ \overline{X} - m}{\sigma'} \leqq z_0 \\
-z_0 \sigma' \leqq \overline{X} - m \leqq z_0 \sigma' \\
\overline{X} - z_0 \sigma' \leqq m \leqq \overline{X} + z_0 \sigma'
\]と変形することができます。

 

ここで、信頼度95％となる \( z_0 \)、つまり\(  -z_0 \leqq z \leqq z_0 \) となる確率が95％になるような \( z_0 \) を求めます。

つまり、標準正規分布の灰色部分の面積が0.95になるような \( z_0 \) を求めればいいですね。

また、下の図の青色面積部分と赤色面積部分はともに等しくなります。

あとは青色面積部分が0.475（0.95÷2）となるための \( z_0 \)、つまり標準偏差何個分かを正規分布表から読み取ればOKです。

よって、\( z_0 = 1.96 \)（標準偏差1.96個分）となるので、信頼度95%における母平均 \( m \) の信頼区間は\[
\overline{X} - z_0 \sigma' \leqq m \leqq \overline{X} + z_0 \sigma'
\]と求められます。

 

1問例題を解いてみましょう。

例題1

生徒が25人いるあるクラスの数学の平均点が70点だった。学年全体の分散が \( 10^2 \ 点^2 \) だとわかっているときに信頼区間95%、98%で母平均 \( m \) をそれぞれ推定したときの信頼区間を小数第2位まで求めなさい。

解説1

母分散が \( 10^2 \) とわかっており、標本の大きさ \( n = 25 \) は十分大きいので、\( \overline{X} \) は平均 \( m = 70 \)、分散 \( \sigma' = \frac{10}{\sqrt{25}} = 2 \) の正規分布に従う。

 

ここで \( z \) を\[
z = \frac{ \overline{X} - 70 }{2}
\]とおくと、\( z \) は標準正規分布に従う。

（ \( z \) は標準偏差何個分離れているかを表すものなので、なれてきたらおかなくてもOK）

 

さらに、\( y \) 軸に対称な \( - z_0 \leqq z \leqq z_0 \) を \( z \) が満たす確率が95%、98%となる \( z_0 \) をそれぞれ求める。

すると 95%のとき \( z_0 = 1.96 \)、98%のとき \( z_0 = 2.33 \) となることがわかる。

 

つまり、信頼度95%のときの母平均 \( m \) に対する信頼区間は、平均点70点 ± 標準偏差1.96個分（\( z_0 = 1.96 \)）となるので、\[
70 - 1.96 \cdot 2 \leqq m \leqq 70 + 1.96 \cdot 2 \\
66.08 \leqq m \leqq 73.92
\]と求められる。

同じように信頼度98%のときの母平均 \( m \) に対する信頼区間は、平均点70点 ± 標準偏差2.33個分（\( z_0 = 2.33 \)）となるので、\[
70 - 2.33 \cdot 2 \leqq m \leqq 70 + 2.33 \cdot 2 \\
65.34 \leqq m \leqq 74.66
\]と求められる。

 

３．母比率の推定

いよいよ「確率分布と統計的な推測」 の最終項目「母比率の推定」にやってきました。

この項目では、「母集団の中である事象が起こる確率」を比較的容易に計算ができる「標本の中である事象が起こる確率」から推定する方法について説明していきたいと思います。

(1) 母比率・標本比率

母集団（つまり調べたい対象全体）の中で、ある事象Aを満たす確率のことを母比率と呼び、標本（母集団の一部をとってきたもの）の中で事象Aを満たす確率のことを標本比率と呼びます。

標本の大きさが \( n \)、標本の中から事象Aを満たす個数を \( X \) とすると、標本比率 \( R \) は\[
R = \frac{X}{n}
\]で求めることができます。

 

例えば、100人の標本の中から、事象を満たしている人が35人いたとすると、標本比率は\[
\frac{35}{100} = 0.35
\]となります。

実際に数字を入れて計算してみると全然大した計算じゃないなってことがわかるかと思います。

(2) 大数の法則

母集団全体を調べるのは非常に大変なので、母比率 \( p \) はわからないことがほとんどです。

そこで、標本の大きさ \( n \) が十分に大きいときは、母比率 \( p \) は標本比率 \( R \) にほぼ等しい ( \( p \fallingdotseq R \)) と考えます。

この法則のことを大数の法則と呼びます。

大数の法則を使うことで、母比率をいったん \( p = R \) と代入してから母比率の信頼区間（母比率がだいたいどれくらいになるのか）を計算していきます。

 

なお、共通テストでは問題文に \(  p \fallingdotseq R \) とするタイミングが必ず書かれてあるので、誘導に従いましょう。

(3) 信頼度・信頼区間

母平均とほぼ同じですが、念のためもう1度説明します。

母比率 \( p \) がある範囲内 \( A \leqq p \leqq B \) となる確率が \( c \) %となる区間のことを母比率 \( p \) に対する信頼度 \( c \) %の信頼区間と呼びます。

(4) 二項分布と標本比率

標本において、ある事象Aが起こるか起こらないかは独立と考えることができます*3。

（ただし、標本は十分大きく、母集団は標本よりもさらに十分に大きいことが条件ですが基本的に標本調査では満たしているので問題ありません。）

 

さらに標本から1つ1つのデータを抽出すると考えるます。すると、抽出したデータはある事象Aが「起こる」か「起こらない」か*4の2通りですね。

つまり、抽出したデータの中からある事象を満たしている個数 \( X \) は、二項分布に従うと考えられますね。

 

二項分布に従うと考えられれば、平均、分散、標準偏差はあっという間に求められますね。

（もし二項分布ってなんだっけと思った人はこちらの記事で早急に復習しましょう。）

 

標本の大きさ \( n \) 、標本比率 \( R = p \)（母比率と仮定）のときのある事象を満たしている個数  \( X \) の平均 \( E(X) \) は\[
E(X) = np
\]となり、分散 \( V(X) \) は\[\begin{align*}
V(X) & = E(X) \cdot (1-p)
\\ & = np(1-p)
\end{align*} \]となりますね。

また、母集団から抽出した標本の大きさ \( n \) は十分大きいと考えられるので、ある事象が起こる回数 \( X \) は正規分布にも従いますね。

 

さらに、標本比率 \( R \) は\[
R = \frac{X}{n}
\]で求めることができるので、\( R \) の期待値 \( E(R) \) は\[\begin{align*}
E(R) & = E \left( \frac{X}{n} \right)
\\ & = \frac{1}{n} E(X) \ \ \left( \because E(aX) = a E(X) \right)
\\ & = \frac{1}{n} \cdot np
\\ & = p
\end{align*} \]となり、分散 \( V(R) \) は\[\begin{align*}
V(R) & = V \left( \frac{X}{n} \right)
\\ & = \frac{1}{n^2} V(X) \ \ \left( \because V(aX) = a^2 V(X) \right)
\\ & = \frac{1}{n^2} \cdot np(1-p)
\\ & = \frac{p(1-p)}{n}
\end{align*} \]と求められますね。

\( X \) が正規分布に従うので、\(  R = \frac{X}{n} \) とおいた \( R \) も正規分布に従います*5。

そのため、標本比率 \( R \) は、平均が \( p \)、分散が \(  \frac{p(1-p)}{n} \) の正規分布 \( N \left( p,\frac{p(1-p)}{n} \right) \) に近似的に従います。

 

この性質を用いてから、標本比率 \( R \) を用いて母平均 \( p \) を推定することができます。

(5) 母比率の推定の流れ  

では、簡単に求めることができる標本の大きさ \( n \) の標本比率 \( R \) から母比率 \( p \) を信頼度95%で推定する方法について説明していきましょう。

上の情報だけから、母集団の母平均 \( m \) を信頼度95%で推定してみましょう。

 

まず、標本の大きさ \( n \) が十分に大きいので、標本比率 \( R \) は平均 \( p \)、分散 \(   \frac{p(1-p)}{n} \) の正規分布に近似的に従いますね。

ここで、標準偏差の形がややこしいくなるので\[
\sigma' = \frac{\sigma}{\sqrt{n} }
\]とし、さらに \( z \) を\[
z = \frac{ \overline{X} - m}{\sigma'}
\]とすることで \( z \) は標準正規分布に従いますね。

 

ここから先は母平均の推定のときと流れが一緒です。

ここで、\(  -z_0 \leqq z \leqq z_0 \)（対称なのがポイント）を変形すると、\[
-z_0 \leqq \frac{ R - p}{\sigma'} \leqq z_0 \\
-z_0 \sigma' \leqq R - p \leqq z_0 \sigma'
R - z_0 \sigma' \leqq p \leqq R + z_0 \sigma'
\]と変形することができます。

 

ここで、信頼度95％となる \( z_0 \)、つまり\(  -z_0 \leqq z \leqq z_0 \) となる確率が95％になるような \( z_0 \) を求めます。

母平均と同じように正規分布表から読み取ると、\( z _0 = 1.96 \) とわかります。

あとは、代入することで、母比率 \( p \) の信頼度95%における信頼区間を\[
R - 1.96 \sigma' \leqq p \leqq R + 1.96 \sigma'
\]と求めることができます。

（標本比率 \( R \) ± 標準偏差 (\( \sigma' \)) 1.96個分が信頼区間）

 

例題2

某大学の大学生400人を無作為に調査したところ、40人が北九州市出身だった。

このとき、某大学の北九州市出身の母比率 \( p \) に対する信頼度95％の信頼区間を小数第2位まで推定しなさい。

解説2

標本比率 \( R \)（ある調査における北九州市出身の割合）は、\[
R = \frac{40}{400} = 0.1
\]となる。すると \( R \) は平均 \( p \)、分散 \( \frac{p(1-p)}{400} \) の正規分布に従う。

ここで、\( p = 0.1 \) に等しいので、平均 \( E(R) \) を\[
E(R) = 0.1
\]標準偏差 \( \sigma (R) \) を\[\begin{align*}
\sigma (R) & = \sqrt{ \frac{p(1-p)}{400} }
\\ & = \sqrt{ \frac{0.1 \cdot 0.9}{400} }
\\ & = \frac{ \sqrt{ 0.09 } }{ \sqrt{ 400 } }
\\ & = \frac{ 0.3 }{20}
\\ & = 0.015 = \sigma'
\end{align*} \]としてよい。

 

ここで \( z \) を\[
z = \frac{ R - p }{\sigma'} = \frac{ R - 0.1 }{0.015}
\]とおくと、\( z \) は標準正規分布に従う。

（標準偏差何個分かを表す \( z \) に変換。慣れてきたら書かなくてOK。）

 

さらに、\( y \) 軸に対称な \( - z_0 \leqq z \leqq z_0 \) を \( z \) が満たす確率が95%となる \( z_0 \) をそれぞれ求める。

すると 95%のとき \( z_0 = 1.96 \) となる。

（平均 ± 標準偏差1.96個分が信頼度95％の信頼区間となる）

 

よって、信頼度95%のときの母比率 \( p \) に対する信頼区間は、平均 0.1 ± 標準偏差1.96個分（\( z_0 = 1.96 \)）となるので、\[
0.1 - 1.96 \cdot 0.015 \leqq p \leqq 0.1 + 1.96 \cdot 0.015 \\
0.07 \leqq p \leqq 0.13
\]と求められる。

 

４．練習問題

では、母平均推定・母比率推定の練習をしてみましょう。

必要であればこちらから正規分布表をダウンロードし、使用してください。

※注意

小数の形で解答する場合、指定された桁数の1つ下の桁を四捨五入して解答してください。また、必要に応じて、確定された桁まで⓪をマークしてください。

例えば、[　ア　] . [　イウ　] に 2.5 と答えたいとき → 2.50 とする。

練習1　母平均の推定

 

練習2　母比率の推定

 

 

５．練習問題の答え

練習1

母分散がわからないが、問題文から母分散が標本分散に等しいと考えてよいので、母分散を標本偏差と同じ36とする。

また、標本の大きさ \( n = 100 \) は十分大きいので、\( \overline{X} \) は平均 \( m = 30 \)、標準偏差 \( \sigma' = \frac{ \sqrt{36} }{\sqrt{100}} = 0.6 \) の正規分布に従う。

（ア.イ = 0.6）

 

ここで \( z \) を\[
z = \frac{ \overline{X} - 30 }{0.6}
\]とおくと、\( z \) は標準正規分布に従う。

 

また、\( |z| \leqq 1.96 \) となる確率は、\( 0 \leqq z \leqq 1.96 \) となる確率を正規分布表から読み取って2倍すれば求められる。

正規分布表より、\( 0 \leqq z \leqq 1.96 \) となる確率は0.475と求められるので、\( |z| \leqq 1.96 \) となる確率は 0.95となる。

（ウエ：95）

 

よって、信頼度95%のときの母平均 \( m \) に対する信頼区間は、平均 30 ± 標準偏差1.96個分（\( z_0 = 1.96 \)）となるので、\[
30 - 1.96 \cdot 0.6 \leqq m \leqq 30 + 1.96 \cdot 0.6 \\
28.8 \leqq m \leqq 31.2
\]と求められる。

（オカキ：288　クケコ：312）

練習2

(1)

 標本比率 \( R \)（ある調査における北九州市出身の割合）は、\[
R = \frac{20}{100} = 0.2
\]となる。（ア：2）

 

ここで、問題文の通りに母比率 \( p = 0.2 \) とすると、\( X \) の平均 \( E(X) \) は、\[\begin{align*}
E(X) & = 100 \cdot 0.2
\\ & = 20
\end{align*}\]となる。（イウ：20）

 

また、分散 \( V(X) \) は\[\begin{align*}
V(X) & = E(X) \cdot (1 - 0.2)
\\ & = 16
\end{align*}\]と求められるので、標準偏差 \( \sigma (X) \) は\[\begin{align*}
\sigma (X) & = \sqrt{ 16 }
\\ & = 4
\end{align*}\]となる。（エ：4）

 

ここで、標本比率 \( R \) は\[
R = \frac{X}{n} = \frac{X}{100}
\]で求められるので、平均 \( E(R) \) は\[\begin{align*}
E(R) & = E \left( \frac{X}{100} \right)
\\ & = \frac{1}{100} E (X)
\\ & = 0.2
\end{align*}\]となる。（オ：2）

また、標準偏差 \( \sigma (R) \) は\[\begin{align*}
\sigma (R) & = \sigma \left( \frac{X}{100} \right)
\\ & = \frac{1}{100} \sigma (X)
\\ & = 0.04
\end{align*}\]となる。（カキ：04）

※ 解説なので丁寧に書いていますが、共通テストなどで解く際には、「1/100になるから平均、標準偏差も1/100になるな〜」くらいの勢いで解いてください。

 

ここで、\( z \) を\[
z = \frac{ \overline{X} - 0.2 }{0.04}
\]とすることで \( z \) は標準正規分布に従う。

  

信頼度95％となる \( z_0 \)、つまり\(  -z_0 \leqq z \leqq z_0 \) となる確率が95％になるような \( z_0 \) を正規分布表から読み取ると、\( z _0 = 1.96 \) とわかる。

（平均 ± 標準偏差1.96個分が信頼度95%に対する信頼区間）

 

よって、信頼度95%のときの母比率 \( p \) に対する信頼区間は、平均 0.2 ± 標準偏差1.96個分（\( z_0 = 1.96 \)）となるので、\[
0.2 - 1.96 \cdot 0.04 \leqq p \leqq 0.1 + 1.96 \cdot 0.04 \\
0.12 \leqq p \leqq 0.28
\]と求められる。

（クケ：12　コサ：28）

 

(2)

母比率 \( p \) の信頼区間の幅、正規分布から読み取った \( z_0 \)、および \( R \) の標準偏差 \( \sigma' \) を用いて\[
\overline{X} - z_0 \sigma' \leqq m \leqq \overline{X} + z_0 \sigma'
\]と計算できるので、信頼区間の幅 \( L \) は、\[\begin{align*}
L & = \left( \overline{X} + z_0 \sigma' \right) - \left( \overline{X} - z_0 \sigma' \right)
\\ & = 2 z_0 \sigma'
\end{align*}\]となるので、信頼区間の幅は、信頼度によって決まる \( z_0 \) （標準偏差何個分に相当するか）と標準偏差 \( \sigma' \) によって決まることがわかる。

よって信頼区間の幅の大小を比べる際には、\( z_0 \cdot \sigma' \) の大小を比べればよい。

\( L_1 \) の信頼区間の幅の基準値

標準偏差0.04 × 1.96個分（\( |z| \leqq 1.96 \)）が信頼区間の大きさの基準となる。

\( L_2 \) の信頼区間の幅の基準値

\( L_1 \) と異なるのは信頼度が99%となる点である。

\( |z| \leqq z_0 \) が99%となる \( z_0 \)、つまり \( 0 \leqq z \leqq z_0 \) となる確率が0.495となるような \( z_0 \) を探せばよい。

すると、正規分布表より \( z_0 = 2.58 \) となる。

 

よって、標準偏差0.04 × 2.58個分（\( |z| \leqq 2.58 \)）が信頼区間の大きさの基準となる。

\( L_3 \) の信頼区間の幅の基準値

\( L_1 \) と異なるのは標本比率 \( R = 0.5 \) である点である。標本比率が変わると、\( R \) の標準偏差も変化するので、\( R \) の標準偏差がいくらになるかを求める。

 

標本の大きさ \( n = 100 \)、標本比率 \( R = 0.5 \) の場合、回数 \( X \) の標準偏差 \( \sigma(X) \)は \[\begin{align*}
\sigma (X) & = \sqrt{ 100 \cdot \frac{1}{2} \cdot \left( 1 - \frac{1}{2} \right) }
\\ & = 5
\end{align*} \]となるため、\( R \) の標準偏差は \[\begin{align*}
\sigma (R) & = \sigma \left( \frac{X}{100} \right)
\\ & = \frac{1}{100} \sigma (X)
\\ & = 0.05
\end{align*}\]となる。

よって、標準偏差0.05 × 1.96個分（\( |z| \leqq 1.96 \)）が信頼区間の大きさの基準となる。

 

下の3つの信頼区間の幅の基準値を比べると、信頼区間の幅の大小は\[
L_1 < L_3 < L_2
\]となる。（シ：1）

\( L_1 \)：標準偏差0.04 × 1.96個分（信頼度95％）
\( L_2 \)：標準偏差0.04 × 2.58個分（信頼度99％）
\( L_3 \)：標準偏差0.05 × 1.96個分（信頼度95％）

 

信頼区間の幅を比べる問題は過去のセンター試験にも出題されているため、共通テストでも出題される可能性があります。

なので、信頼区間の幅の比べ方は頭に入れておくと安心です。

 

 

５．さいごに

今回は、「確率分布と統計的な推測」の分野における「母平均・母比率の推定」について行っていきました。

共通テストでは推定を行って信頼区間を出す問題は頻出するので、必ず信頼区間の出し方を確認・復習しておきましょう。

 

これで数B「確率分布と統計的な推測」の試験範囲はすべてです！

おつかれさまでした！！

 

7日目（最終日）は、総復習問題を用意する予定です。

復習（推定の流れ）

母平均・母比率の推定は以下のような手順で行う。

• 平均（基準値、信頼区間の真ん中の値） \( \vec{X} \) と標準偏差 \( \sigma \) を求める
  母平均 \( m \) の場合
  → 平均 \( m \)、標準偏差 \(   \frac{\sigma}{ \sqrt{n} } \)
  母比率 \( p \) の場合
  → 平均 \( p \)、標準偏差 \( \sqrt{ \frac{p(1-p)}{ n } } \)

• 信頼度 c %、つまり\(  -z_0 \leqq z \leqq z_0 \) となる確率が c ％になるような \( z_0 \) を正規分布表から読み取る。
  （信頼度95％ → \( z_0 = 1.96 \)、信頼度99% → \( z_0 = 2.58 \)）
• 推定したいもの（母平均 or 母比率）\( x \) の信頼区間を\[
  \overline{X} - z_0 \sigma \leqq x \leqq \overline{X} + z_0 \sigma 
  \]と求めることができる。