スポンサードリンク
今回から3回に分けて、統計学や確率・統計でよく出てくる分布の1つである「カイ2乗分布」について勉強していきましょう。
カイ2乗分布は、
- 母分散の区間推定
- 適合度の検定
- 独立性の検定
などに使える道具であり、確率・統計の期末試験や統計検定(2級以上)で頻出の項目です。
カイ2乗分布の1回目では、カイ2乗分布の定義を説明した後、母分散を推定できる仕組みについて見ていきます。
目次
スポンサードリンク
1. カイ2乗分布の定義
最初に、カイ2乗分布の定義を確認していきましょう。
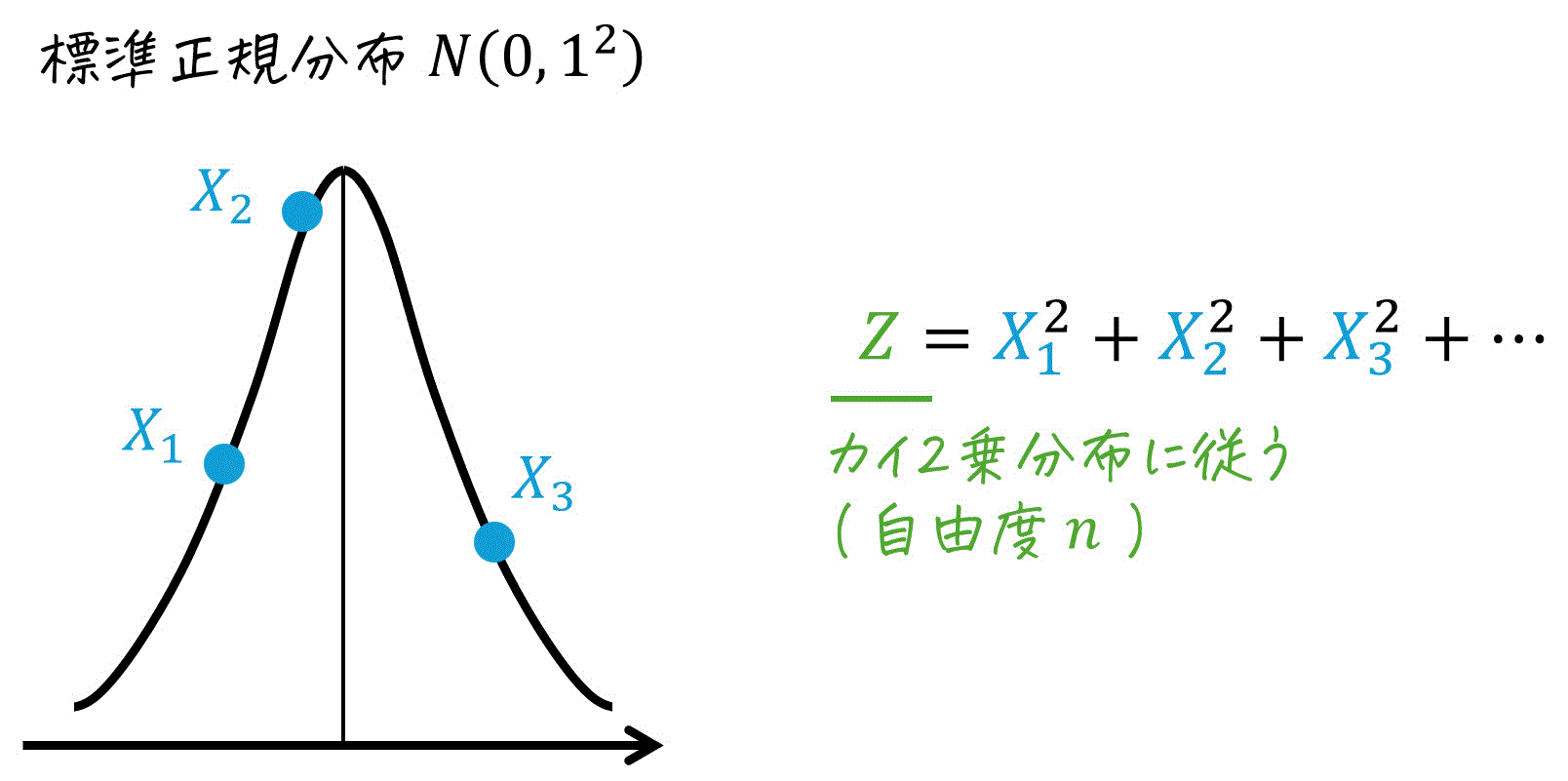
まず、このように標準正規分布に従う確率変数 \( X_1 \), \( X_2 \), \( X_3 \), … を取り出してみましょう。
取り出した \( X_1 \), \( X_2 \), \( X_3 \), … をそれぞれ2乗してすべて足したもの、つまり\[
Z = X_1^2 + X_2^2 + X_3^2 + \cdots
\]の \( Z \) が従う分布のことを、カイ2乗分布と呼びます。

標準正規分布に従う独立な確率変数 \( X_1 \), \( X_2 \), … \( X_n \) をそれぞれ2乗したものの和\[\begin{align*}
Z & = X_1^2 + X_2^2 + \cdots + X_n^2
\\ & = \sum^{n}_{k = 1} X_k^2
\end{align*}\]はカイ2乗分布に従う。(自由度: \( n \))
※ 2乗したものの和を取っているため、\( Z \) は0以上(負にならない)です。
スポンサードリンク
2. カイ2乗分布表の使い方
カイ2乗分布を用いて推定や仮説検定をする際には、t分布や正規分布のときと同じように専用の表(カイ2乗分布表)を使用します。
しかし、t分布や正規分布のときとは異なり、カイ2乗分布表を使う際には2点ほど注意するべきポイントがあります。
ここでは、その2つのポイントを紹介していきます。
例題、練習問題を解く際にお使いください。
注意点1. グラフが左右対称ではない
カイ2乗分布のグラフは、正規分布やt分布のように左右対称ではありません。
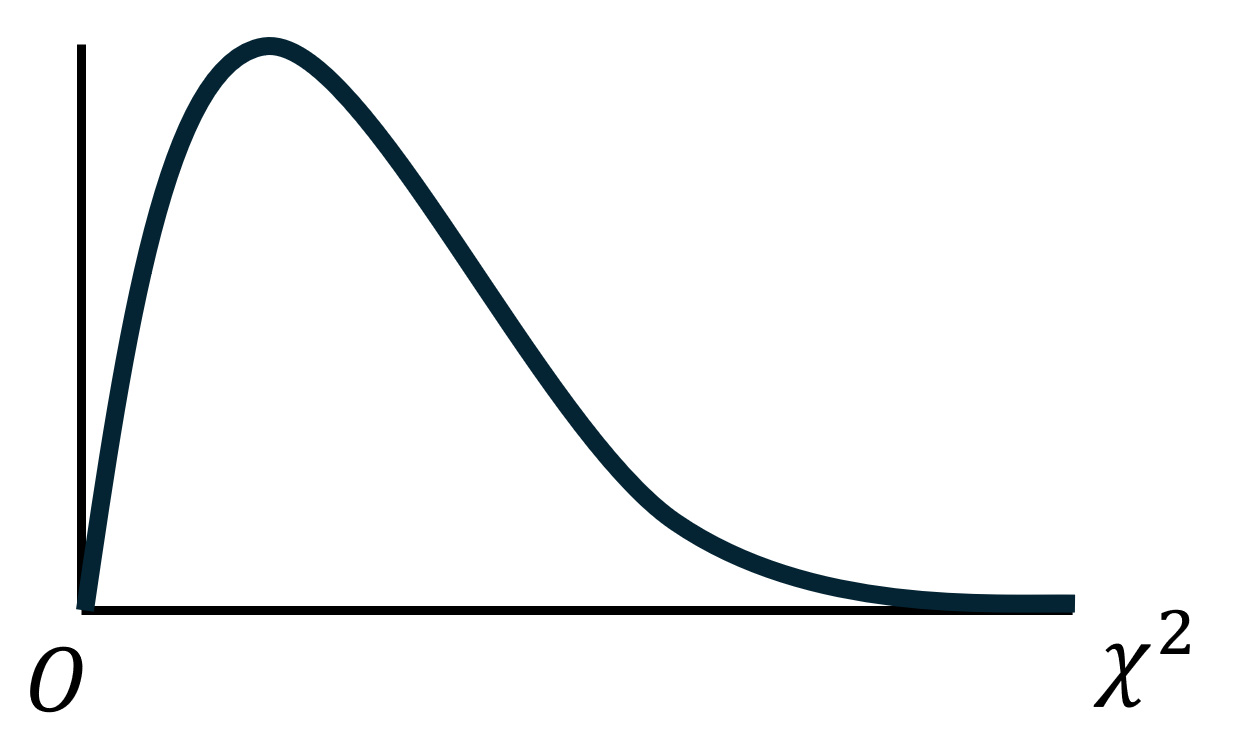
そのため、カイ2乗分布を用いた区間推定や両側検定をする際には、2つの値(上側の点、下側の点)を確認する必要があります[1]正規分布やt分布では、左右対称という性質を利用することで、片方の値を求めればその値をもう片方に適用することが出来ました。。
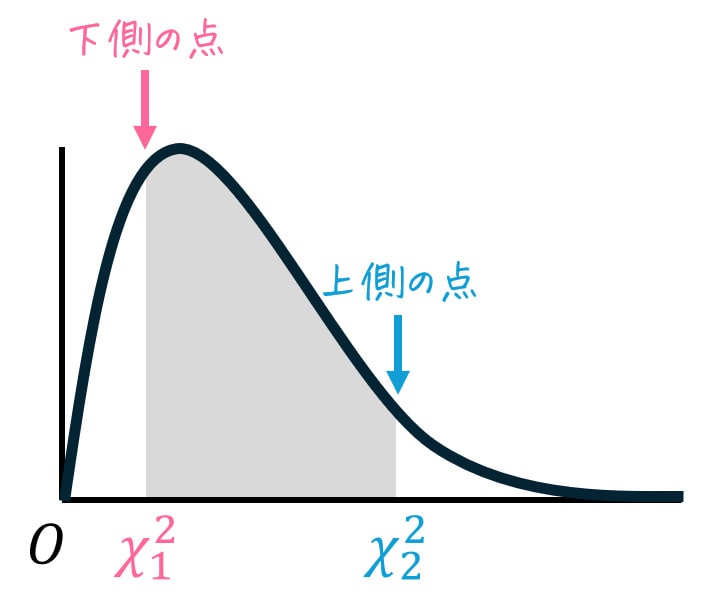
下側の点 \( \chi_2^2 \)、上側の点 \( \chi_1^2 \) を確認する
※ 上側、下側は上位、下位みたいなものだと思ってください。例えば、上側5%の点というのは、ある値が上位5%に属するときの値を指しています。
※ 実際に区間推定や両側検定をする際に、再度詳細を詳しく説明します。
注意点2. 自由度によってグラフの概形が変わる
カイ2乗分布のグラフは、自由度によってグラフの概形が変化します。(t分布と同じ)
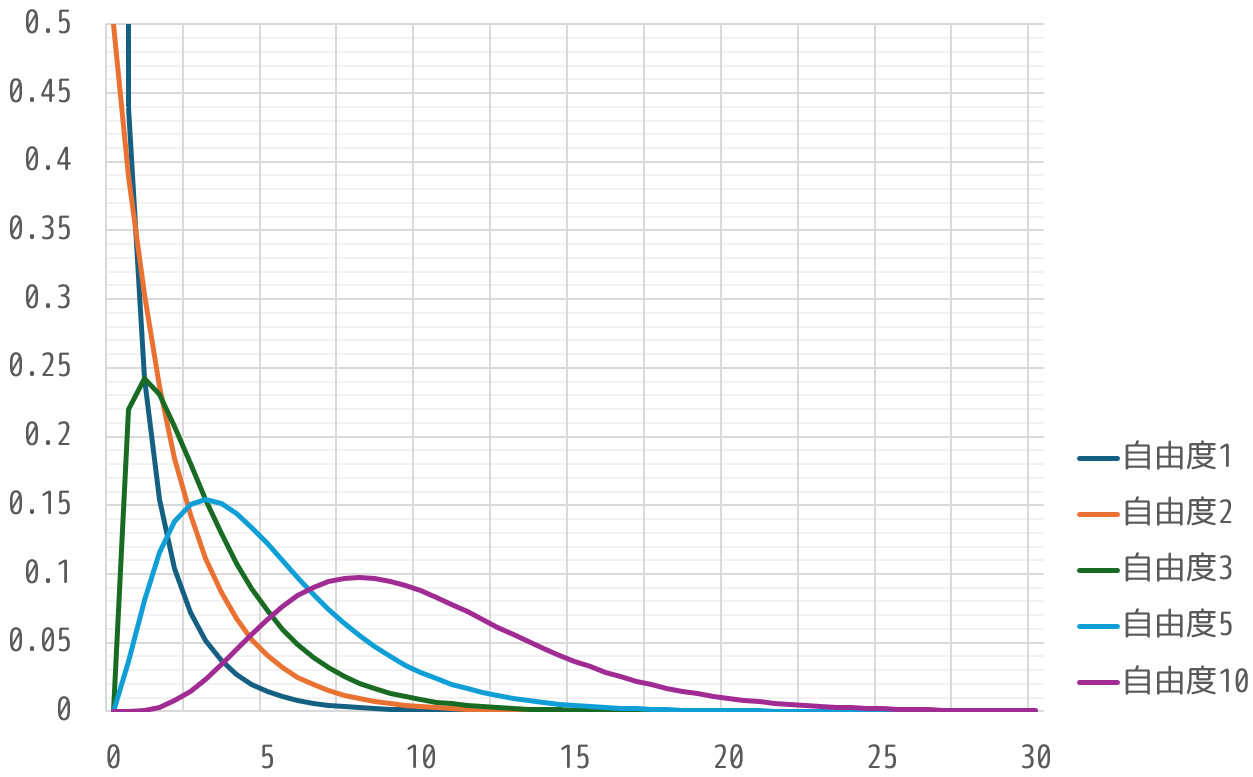
そのため、カイ2乗分布表を使用する際には、t分布のときと同じように自由度も併せて把握する必要があります。
カイ2乗分布表の読み方
では、実際にカイ2乗分布表を読んでみましょう。
例えば、自由度が5、上側5%点(=カイ2乗値が上位5%となるときの値)をカイ2乗分布表から読み取ってみましょう。
読み取る際には、自由度 \( k = 5 \)、確率 \( \alpha = 0.050 \) の部分を見ます。
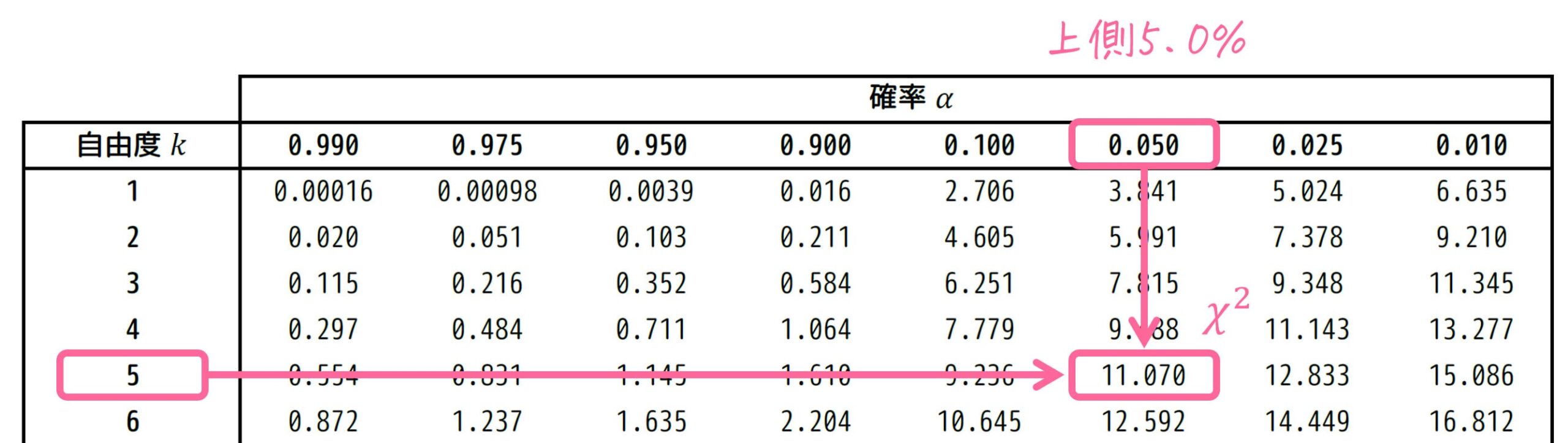
すると、11.070と読み取れますね。つまり、自由度が5のとき、カイ2乗値が上位5%となるときの値は11.070であることが分かります。
スポンサードリンク
3. カイ2乗分布を用いて母分散推定が出来る仕組み
カイ2乗分布を使うことで、次の式での母分散 \( \sigma^2 \) 推定が可能となります。
信頼度 \( a \) % で、母分散 \( \sigma^2 \) を区間推定は、\[
\frac{ (n-1) s^2 }{ \chi_2^2 } \leqq \sigma^2 \leqq \frac{ (n-1) s^2 }{ \chi_1^2 }
\]を計算することで推定が可能。(自由度 \( n - 1 \) のカイ2乗分布を使用)
【変数の意味】
- \( n \) … 標本サイズ(データの数)
- \( s^2 \) … 不偏分散
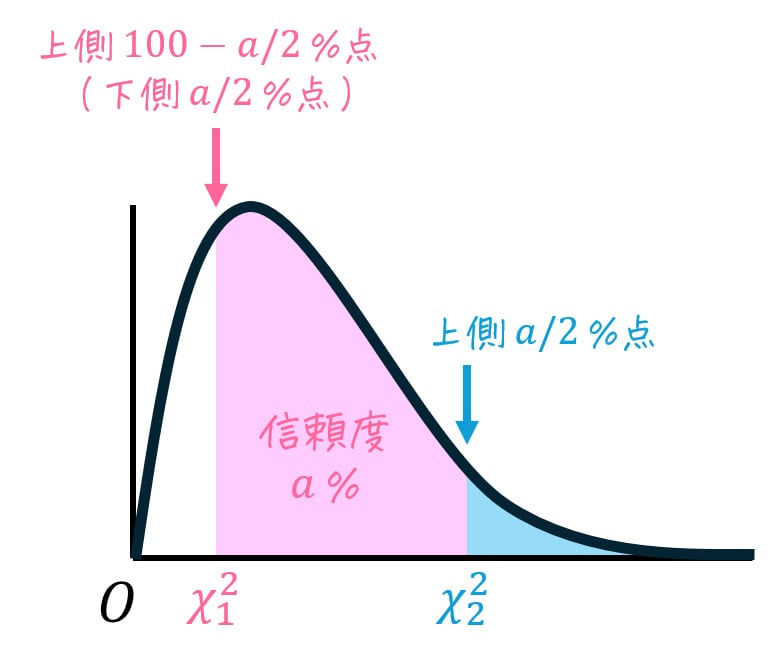
- \( \chi_1^2 \) … 上側 \( 100 - a/2 \) %点(下側 \( a/2 \) %点)でのカイ2乗値(カイ2乗分布表から読み取る)
- \( \chi_2^2 \) … 上側 \( a/2 \) % 点でのカイ2乗値(カイ2乗分布表から読み取る)
※ 補足
標本分散\[
S^2 = \frac{1}{n} \left\{ ( X_1 - \overline{X} )^2 + ( X_2 - \overline{X} )^2 + \cdots + ( X_n - \overline{X} )^2 \right\}
\]を使う場合、母分散の推定式は\[
\frac{ n S^2 }{ \chi_2^2 } \leqq \sigma^2 \leqq \frac{ n S^2 }{ \chi_1^2 }
\]となる。
この章では、上の公式が実際にどのように導出されるかを見ていきましょう。
※ 導出なんてどうでもいい、実際に母分散推定練習がしたい!という人は4章まで飛ばしてください。
手順1.正規分布に従う標本の用意
まず、正規分布(平均: \( \mu \)、分散 \( \sigma^2 \))に従う母集団から、\( n \) 個の標本 \( X_1 \), \( X_2 \), … , \( X_n \) を取りましょう。
手順2.正規分布から標準正規分布への変換確認
正規分布(平均: \( \mu \)、分散 \( \sigma^2 \))に従う変数は、標準正規分布ではないため、そのままでは各変数を2乗したものの和\[
Z = X_1^2 + X_2^2 + \cdots + X_n^2
\]取っても、カイ2乗分布には従いません。
しかし、平均: \( \mu \)、分散 \( \sigma^2 \) に従う \( X \) に対して、\[
Y = \frac{X - \mu}{ \sigma }
\]のように平均1、分散0になるように標準化してあげることで、正規分布に従う変数を標準正規分布に従わせることが出来ます。
つまり、正規分布(平均: \( \mu \)、分散 \( \sigma^2 \))に従う母集団から選んだ標本 \( X_1 \), \( X_2 \), … , \( X_n \) は、以下のように標準化することで \( Z \) をカイ2乗分布に従わせることが出来ます。\[\begin{align*}
Z & = Y_1^2 + Y_2^2 + \cdots + Y_n^2 \\
\\ & = \left( \frac{X_1 - \mu}{ \sigma } \right)^2 + \left( \frac{X_2 - \mu}{ \sigma } \right)^2 + \cdots + \left( \frac{X_n - \mu}{ \sigma } \right)^2
\\ & = \sum^{n}_{k = 1} \left( \frac{X_k - \mu}{ \sigma } \right)^2
\end{align*}\]この形は、後ほど使うのでいったん片隅に置いておきます。
手順3.不偏分散の計算式確認
\( X_1 \), \( X_2 \), … \( X_n \) の不偏分散 \( s^2 \) は、標本平均 \( \overline{X} \) を用いて、\[\begin{align*}
s^2 & = \frac{1}{n-1} \left\{ ( X_1 - \overline{X} )^2 + ( X_2 - \overline{X} )^2 + \cdots + ( X_n - \overline{X} )^2 \right\}
\\ & = \frac{1}{n-1} \sum^{n}_{k=1} ( X_k - \overline{X} )^2
\end{align*}\]
手順4. 手順3の式を変形
ここからは、手順3の式\[
s^2 = \frac{1}{n-1} \sum^{n}_{k=1} ( X_k - \overline{X} )^2
\]を手順2の形に持っていきます。まず、両辺を \( n - 1 \) 倍して\[
(n-1) s^2 = \sum^{n}_{k=1} ( X_k - \overline{X} )^2
\]とします。
この形から、\[\begin{align*}
(n-1) s^2 & = \sum^{n}_{k=1} ( X_k - \overline{X} )^2
\\ & = \sum^{n}_{k=1} ( X_k - \mu + \mu - \overline{X} )^2
\\ & = \sum^{n}_{k=1} \left\{ \underbrace{ (X_k - \mu) }_{A} - \underbrace{ (\overline{X} - \mu) }_{B} \right\}^2
\\ & = \sum^{n}_{k=1} ( A^2 - 2AB + B^2 )
\\ & = \sum^{n}_{k=1} A^2 - 2 \sum^{n}_{k=1} AB + \sum^{n}_{k=1} B^2
\\ & = \sum^{n}_{k=1} (X_k - \mu)^2 - 2 \sum^{n}_{k=1} (X_k - \mu) (\overline{X} - \mu) + \sum^{n}_{k=1} (\overline{X} - \mu)^2
\\ & = \sum^{n}_{k=1} (X_k - \mu)^2 - 2 (\overline{X} - \mu) \sum^{n}_{k=1} (X_k - \mu) + (\overline{X} - \mu)^2 \textcolor{deepskyblue}{ \sum^{n}_{k=1} 1 }
\\ & = \sum^{n}_{k=1} (X_k - \mu)^2 - 2 (\overline{X} - \mu) \left( \textcolor{magenta}{ \sum^{n}_{k=1} X_k } - \mu \textcolor{deepskyblue}{ \sum^{n}_{k=1} 1 } \right) + \textcolor{deepskyblue}{n} (\overline{X} - \mu)^2
\\ & = \sum^{n}_{k=1} (X_k - \mu)^2 - 2 (\overline{X} - \mu) \left( \textcolor{magenta}{ n \overline{X} } - \textcolor{deepskyblue}{n} \mu \right) + n (\overline{X} - \mu)^2
\\ & = \sum^{n}_{k=1} (X_k - \mu)^2 - 2 (\overline{X} - \mu) \cdot n (\overline{X} - \mu) + n (\overline{X} - \mu)^2
\\ & = \sum^{n}_{k=1} (X_k - \mu)^2 - 2n (\overline{X} - \mu)^2 + n (\overline{X} - \mu)^2
\\ & = \sum^{n}_{k=1} (X_k - \mu)^2 - n (\overline{X} - \mu)^2
\end{align*}\]と変形をします。
※ 変形時に、\[
\textcolor{deepskyblue}{ \sum^{n}_{k = 1} 1 = n }
\]であること、および標本平均が\[\begin{align*}
\overline{X} & = \frac{1}{n} ( X_1 + X_2 + \cdots + X_n )
\\ & = \frac{1}{n} \sum^{n}_{k=1} X_k
\end{align*}\]で計算できるので、両辺を \( n \) 倍して\[\begin{align*}
\textcolor{magenta}{n \overline{X} = \sum^{n}_{k=1} X_k}
\end{align*}\]が成立することを途中変換で使っています。
手順5. カイ2乗分布が成り立つ形にする
手順4で、\[
(n-1) s^2 = \sum^{n}_{k=1} (X_k - \mu)^2 - n (\overline{X} - \mu)^2
\]の式を導出しました。
この式の両辺を \( \sigma^2 \) で割ると、\[\begin{align*}
\frac{ (n-1) s^2 }{ \sigma^2 } & = \frac{1}{ \sigma^2 } \left\{ \sum^{n}_{k=1} (X_k - \mu)^2 - n (\overline{X} - \mu)^2 \right\}
\\ & = \frac{1}{ \sigma^2 } \sum^{n}_{k=1} (X_k - \mu)^2 - \frac{n}{ \sigma^2} (\overline{X} - \mu)^2
\\ & = \sum^{n}_{k=1} \left( \frac{X_k - \mu}{\sigma} \right)^2 - \left( \frac{\overline{X} - \mu}{ \frac{ \sigma }{ \sqrt{n} } } \right)^2
\end{align*}\]と変形できます。
ここで、右辺の\[
\sum^{n}_{k = 1} \left( \frac{X_k - \mu}{ \sigma } \right)^2
\]の部分は、手順3で標準化した式、つまり「標準正規分布を2乗したものの和」となっていますね。
また、\[
\left( \frac{\overline{X} - \mu}{ \frac{ \sigma }{ \sqrt{n} } } \right)^2
\]も、以下の3つの理由により「標準正規分布を2乗したものの和」となっていると言えます。
- \( \overline{X} \) は、平均 \( \mu \)、分散 \( \frac{ \sigma^2 }{n} \) の正規分布に従っている(=中心極限定理)
- 以下の式\[
\frac{\overline{X} - \mu}{ \frac{ \sigma }{ \sqrt{n} } }
\]は、平均1、分散0の標準正規分布に標準化している。 - 標準化した標準正規分布を2乗している
よって、右辺が「標準正規分布を2乗したもの」の和の形になっているため、左辺\[
\frac{ (n-1) s^2 }{ \sigma^2 }
\]はカイ2乗分布に従います。
手順6. 自由度の確認
手順5で導出したカイ2乗分布に従う以下の式の、自由度を確認します。\[
\frac{ (n-1) s^2 }{ \sigma^2 }
\]
手順5の式の左辺で出てきた\[
\textcolor{deepskyblue}{ \sum^{n}_{k=1} \left( \frac{X_k - \mu}{\sigma} \right)^2 } - \textcolor{magenta}{ \left( \frac{\overline{X} - \mu}{ \frac{ \sigma }{ \sqrt{n} } } \right)^2 }
\]の水色部分は \( n \) 個の標本 \( X_1 \), \( X_2 \), …, \( X_n \) が出てくるため、自由度は \( n \) となります。
しかし、桃色部分に標本平均 \( \overline{X} \) が入っているため、標本の情報量が1つ減ってしまいます[2]標本平均が分かっている場合、( n \) 個の標本の各値 \( X_1 \), \( X_2 \), …, \( X_n \) … Continue reading。
よって、\[
\frac{ (n-1) s^2 }{ \sigma^2 }
\]は、自由度 \( n-1 \) のカイ2乗分布に従うと言えます。
手順6. 母分散\( \sigma^2 \) に対する不等式の形とする
あとは、信頼区間に対応する下側の点 \( \chi_1^2 \) と上側の点 \( \chi_2^2 \) を読み取り、\[
\chi_1^2 \leqq \frac{ (n-1) s^2 }{ \sigma^2 } \leqq \chi_2^2
\]となる \( \sigma^2 \) の範囲を見つければOKです。
ここで、この不等式を\[
\chi_1^2 \leqq \frac{ (n-1) s^2 }{ \sigma^2 } , \ \ \ \frac{ (n-1) s^2 }{ \sigma^2 } \leqq \chi_2^2
\]と2つに分離します。
つぎに、各不等式の両辺を \( \sigma^2 \) で掛けます。つまり、\[
\sigma^2 \chi_1^2 \leqq (n-1) s^2, \ \ \ (n-1) s^2 \leqq \sigma^2 \chi_2^2
\]とします。
さらに、\[
\sigma^2 \chi_1^2 \leqq (n-1) s^2,
\]に対しては \( \chi_1^2 \) を割り、\[
\sigma^2 \leqq \frac{ (n-1) s^2 }{ \chi_1^2 }
\]とします。同じように、\[
(n-1) s^2 \leqq \sigma^2 \chi_2^2
\]に対しては \( \chi_2^2 \) を割り、\[
\frac{ (n-1) s^2 }{ \chi_2^2 } \leqq \sigma^2
\]とします。
あとは、この2式を合わせて\[
\frac{ (n-1) s^2 }{ \chi_2^2 } \leqq \sigma^2 \leqq \frac{ (n-1) s^2 }{ \chi_1^2 }
\]とすれば、母分散の推定式の導出完了です!
4. 例題にチャレンジ
では、実際に母分散の推定をする問題を、例題で解いてみましょう。
正規母集団から10個の標本を抽出したところ、標本平均が64、不偏分散が36であった。
このとき、信頼度95%で母分散を区間推定しなさい。区間推定の結果は、小数第2位まで示すこと。
解説.
Step1. 自由度を確認する
今回は、10個の標本を抽出(=標本サイズが10)なので、自由度は 10 - 1 = 9 となります。
Step2. カイ2乗分布から値を読み取る
今回は、信頼度95%の推定を実施するため、下の図のように分布の中心から両端に合計95%の確率が含まれるようにします。
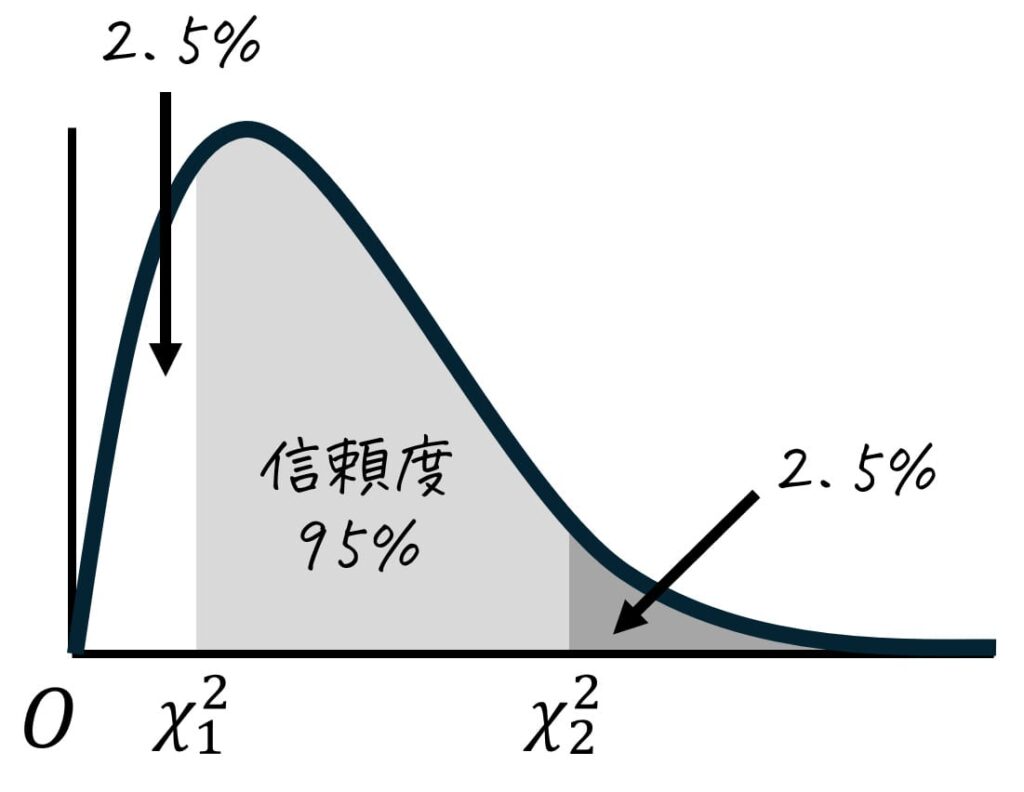
ここで、分布の中心から両端に取った薄い灰色部分の面積は95%なので、残りの5%は半分(2.5%)ずつ上側2.5%と下側2.5%に分けられます。
さらに、上側97.5%(=下側2.5%)部分のカイ2乗値の境界値を \( \chi_1^2 \)、上側2.5%のカイ2乗値の境界値を \( \chi_2^2 \) とおきます。つまり、\( \chi_1^2 \) は上位97.5%点(=下位2.5%点)、\( \chi_2^2 \) は上位2.5%点となります。
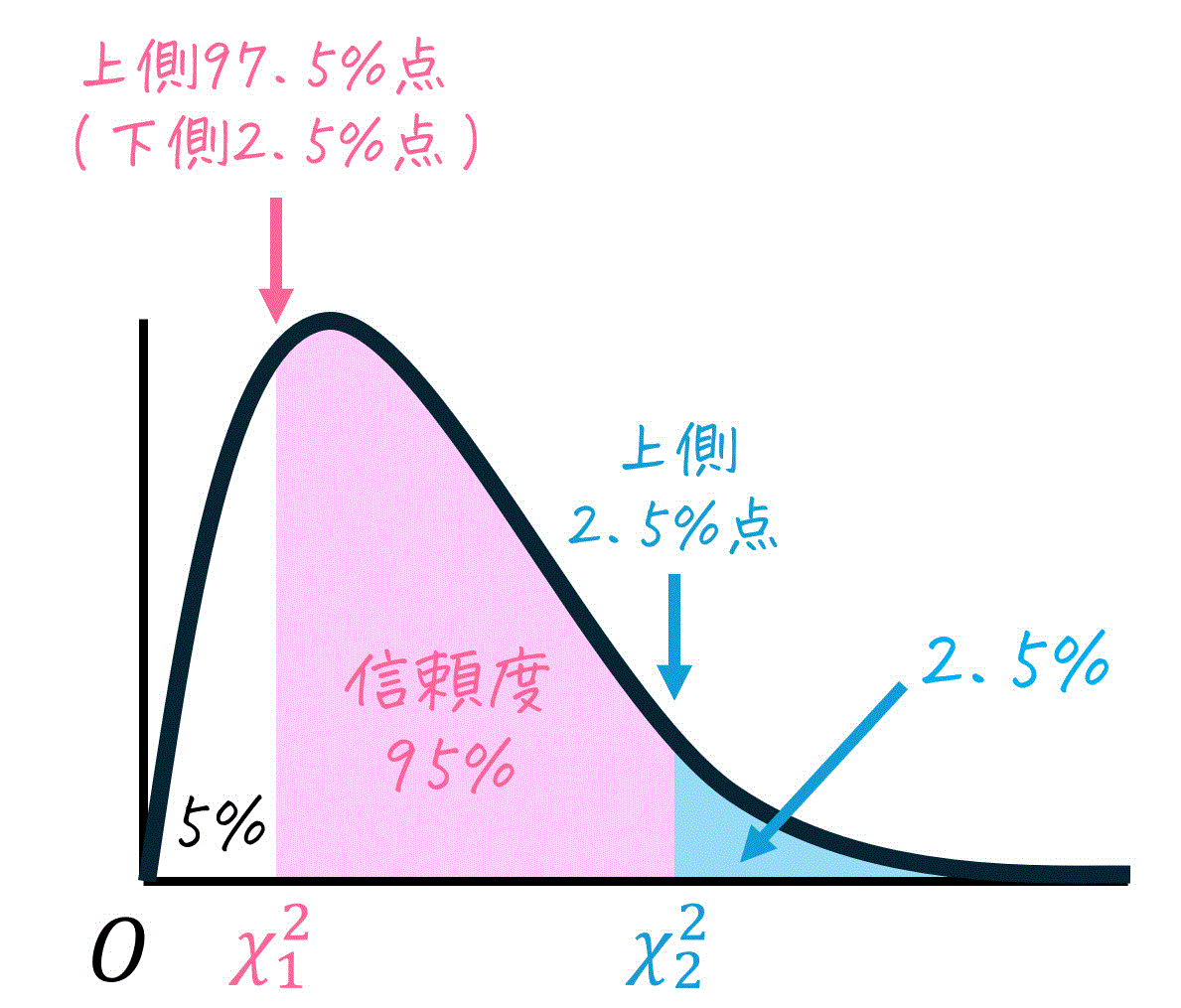
カイ2乗分布表は、上側確率 \( \alpha \) と自由度毎のカイ2乗値を記載しているため、\( \chi_1^2 \), \( \chi_2^2 \) は以下の部分の値を読めばOKです。
- \( \chi_1^2 \) … 上側97.5%、自由度9。つまり \( \alpha = 0.975 \), \( k = 9 \)
- \( \chi_2^2 \) … 上側2.5%、自由度9。つまり \( \alpha = 0.025 \), \( k = 9 \)
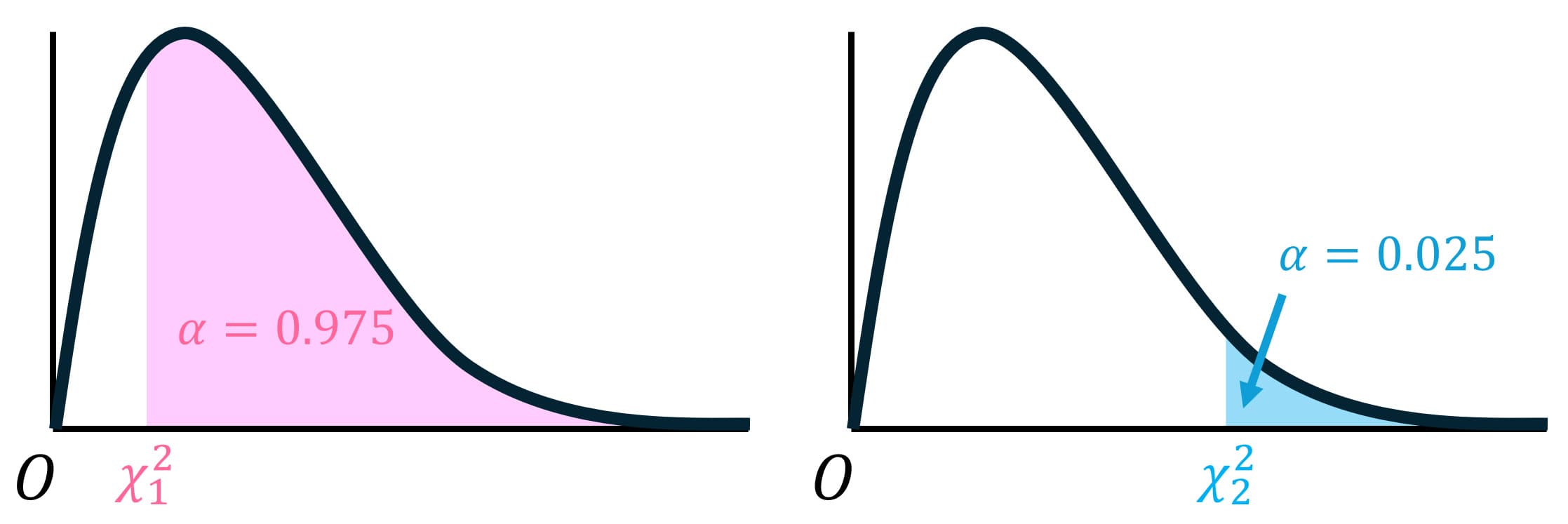
実際に表から読みってみましょう。
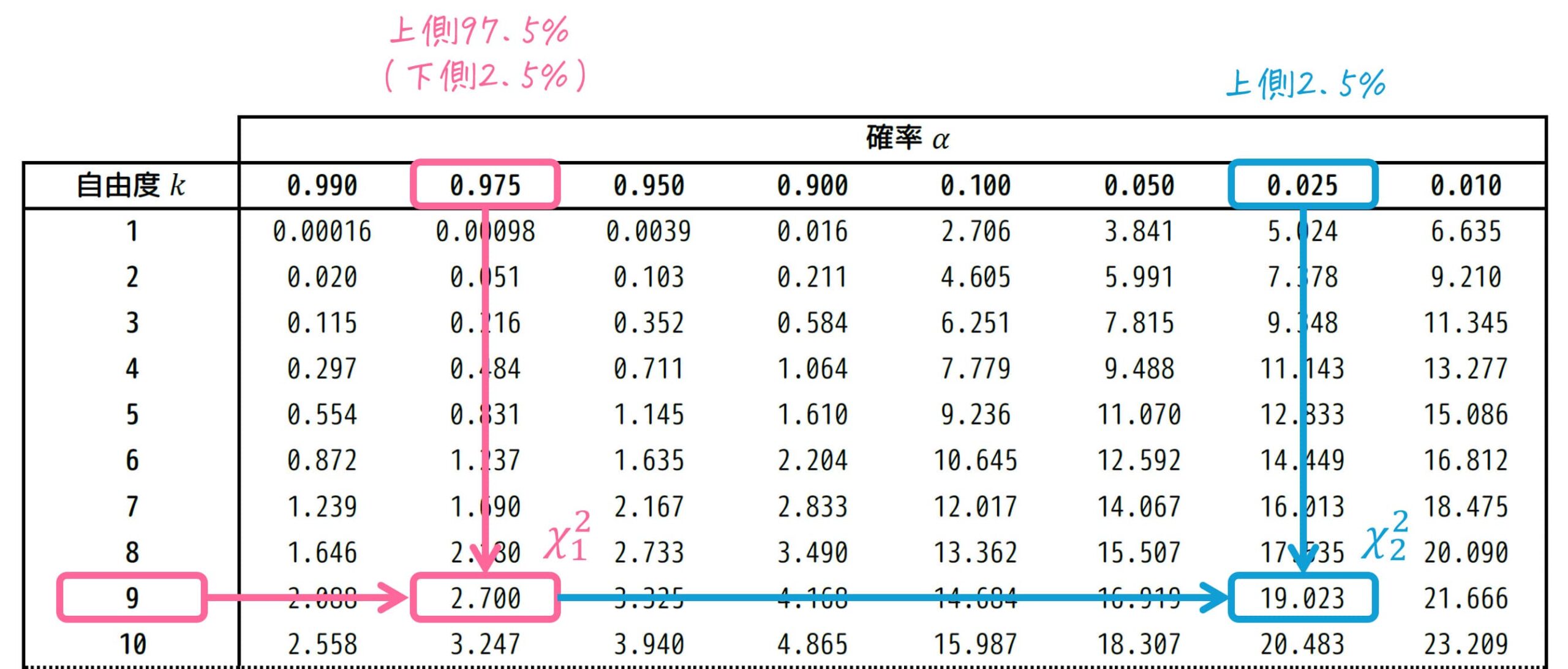
結果、\( \chi_1^2 = 2.700 \)、\( \chi_2^2 = 19.023 \) とわかりますね。
Step3. 区間推定の公式に代入
あとは、標本サイズ \( n = 10 \)、不偏分散 \( s^2 = 36 \)、カイ2乗分布表から読み取った値\( \chi_1^2 = 2.700 \)、\( \chi_2^2 = 19.023 \) を区間推定公式\[
\frac{ (n-1) s^2 }{ \chi_2^2 } \leqq \sigma^2 \leqq \frac{ (n-1) s^2 }{ \chi_1^2 }
\]に代入すればOKです。
実際に代入すると、\[
\frac{ 9 \cdot 36 }{ 19.023 } \leqq \sigma^2 \leqq \frac{ 9 \cdot 36 }{ 2.700 }
\]\[
\frac{ 3 \cdot 36 }{ 6.341 } \leqq \sigma^2 \leqq \frac{ 9 \cdot 3 \cdot 12 }{ 27 \cdot 0.100 }
\]\[\frac{ 3 \cdot 36 }{ 6.341 } \leqq \sigma^2 \leqq \frac{ 12 }{ 0.100 }
\]\[
17.032 \leqq \sigma^2 \leqq 120.000
\]となります。小数第2位まで求めればOKなので、信頼度95%にて母分散を推定した結果は\[
17.03 \leqq \sigma^2 \leqq 120.00
\]となります。
5. 練習問題で確認!
最後に、練習問題を解くことで母分散の区間推定の復習をしましょう。
※ 練習問題のデータは、「うさぎでもわかる確率・統計 t分布のいろは① 母平均の推定」の練習問題と同じものを使っています。
ある中学生の1年生全体が対象の、数学の期末テストが行われた。その中で、特定の塾に通っている4人(佐藤くん、西尾くん、池田さん、竹本さん)の期末テストの点数は、次の通りだった。
| 佐藤くん | 西尾くん | 池田さん | 竹本さん | |
|---|---|---|---|---|
| 期末テストの点数 | 72 | 60 | 84 | 76 |
(1) 4人のテスト結果の平均点、および不偏分散を求めなさい。
(2) この4人のテスト結果から、1年生全体の数学の点数の母分散を信頼度90%で区間推定しなさい。
6. 練習問題の答え
(1)
標本の平均\[\begin{align*}
\overline{X} & = \frac{1}{4} (72 + 60 + 84 + 76)
\\ & = 73
\end{align*}\]
計算ミスを減らすテクニックとして、いったん \( a = 70 \) とおいて、\[\begin{align*}
\overline{X} & = \frac{1}{4} \left\{ (a+2) + (a-10) + (a+14) + (a+6) \right\}
\\ & = \frac{1}{4} (4a + 12)
\\ & = a + 3
\\ & = 73
\end{align*}\]のように計算すると計算ミスを減らせる。
不偏分散
\[\begin{align*}
s^2 & = \frac{1}{4-1} \left\{ (73-72)^2 + (73-60)^2 + (73-84)^2 + (73-76)^2 \right\}
\\ & = \frac{1}{3} \left\{ 1^2 + 13^2 + (-11)^2 + (-3)^2 \right\}
\\ & = \frac{1}{3} \cdot 300
\\ & = 100
\end{align*}\]※ 不偏分散は割る数が \( n \) ではなく \( n-1 \) なので注意!
(2)
Step1. 自由度の確認
今回は、4個の標本を抽出(=標本サイズが4)なので、自由度は 4 - 1 = 3 となります。
Step2. カイ2乗分布から値を読み取る
信頼度90%の推定を実施するため、下の図のように分布の中心から両端に合計90%の確率が含まれるようにします。
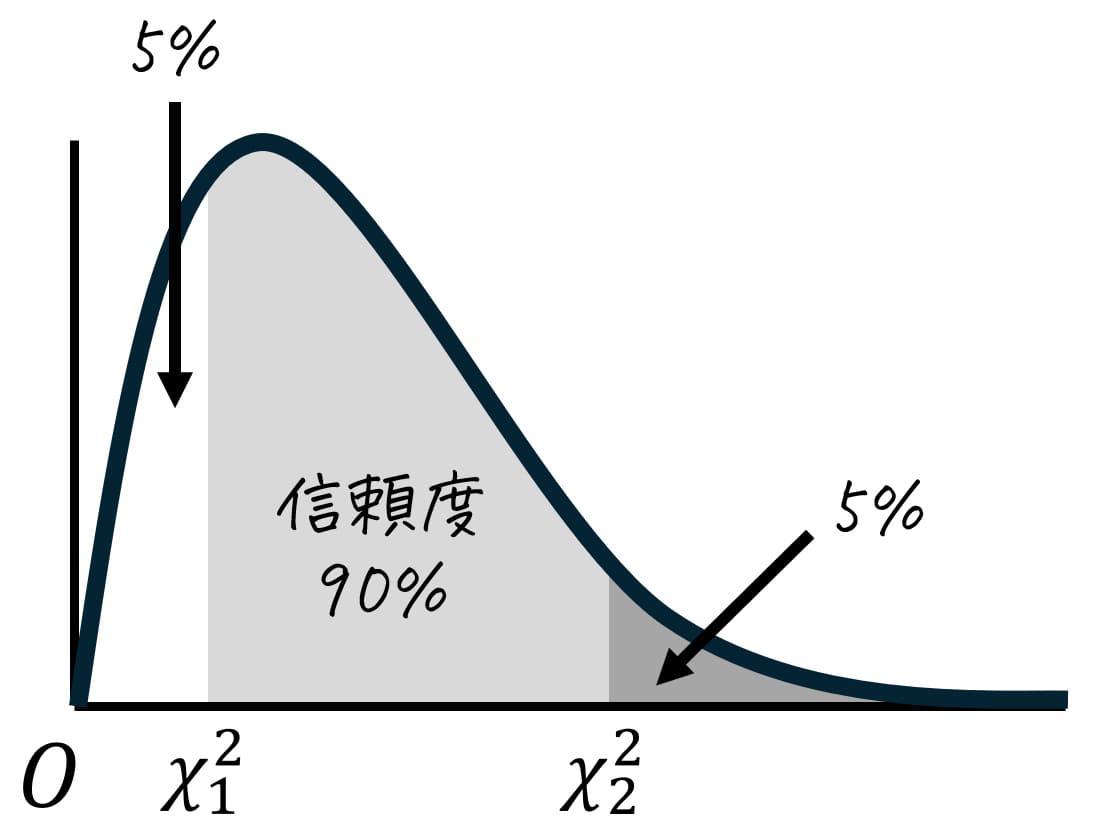
分布の中心から両端に取った薄い灰色部分の面積は90%なので、残りの10%は半分(5%)ずつ上側5%と下側5%に分けられます。
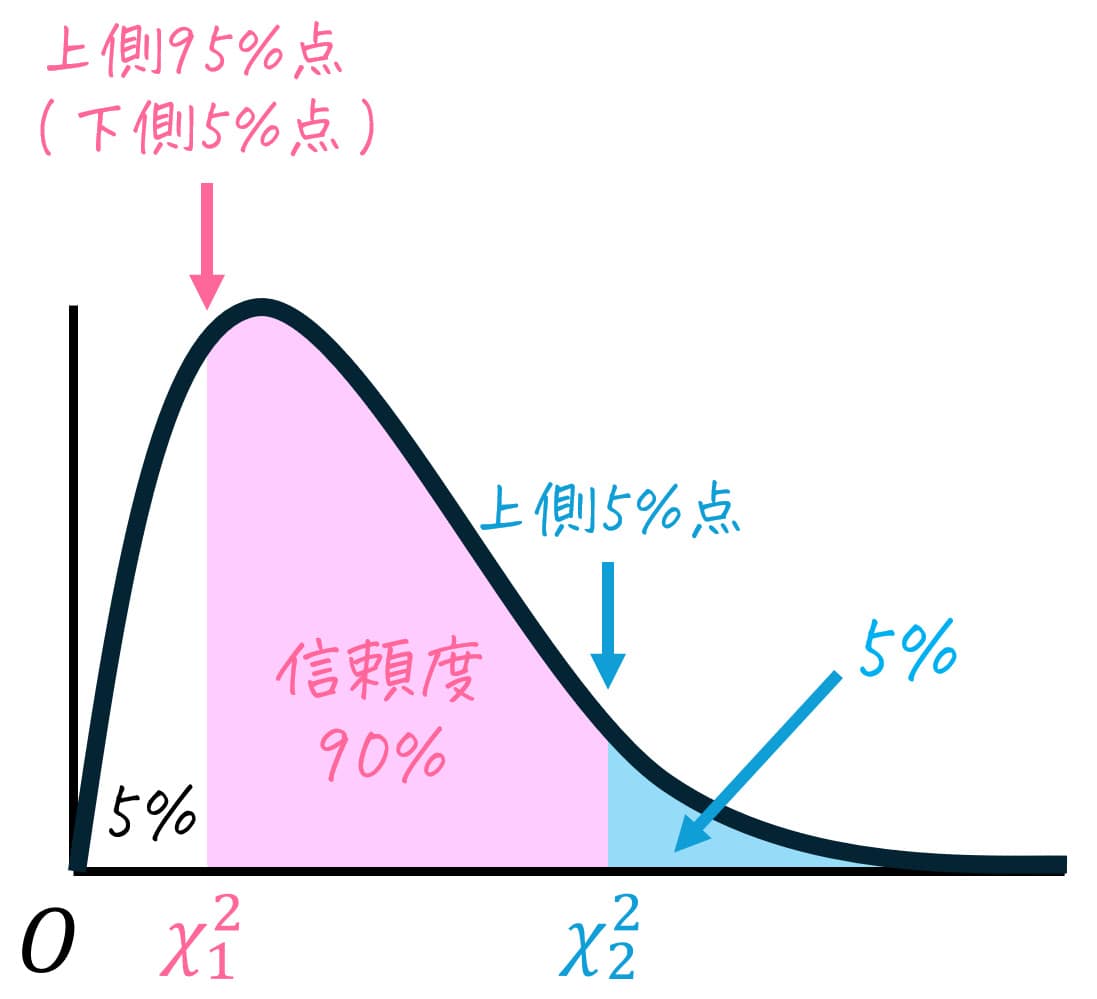
ここで、下側5%(=上側95%)部分のカイ2乗値の境界値を \( \chi_1^2 \)、上側5%のカイ2乗値の境界値を \( \chi_2^2 \) とおきます。つまり、\( \chi_1^2 \) は上位95%点(=下位5%点)、\( \chi_2^2 \) は上位5%点となります。
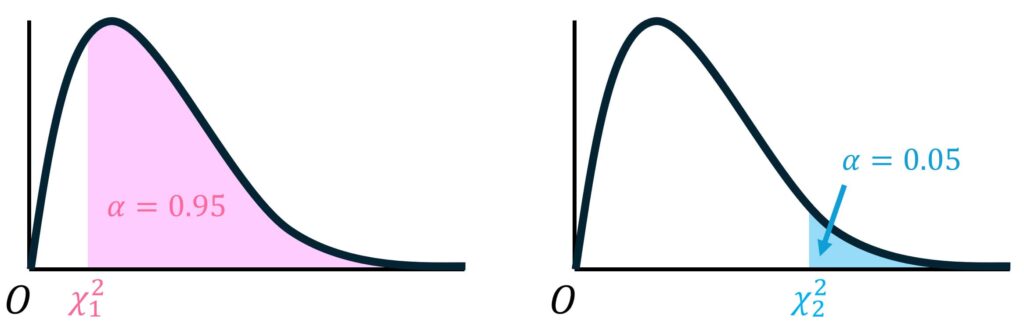
あとは、\( \chi_1^2 \) , \( \chi_2^2 \) を表から読み取ればOKです。
- \( \chi_1^2 \) … 上側95.0%、自由度3。つまり \( \alpha = 0.950 \), \( k = 3 \)
- \( \chi_2^2 \) … 上側5.0%、自由度3。つまり \( \alpha = 0.050 \), \( k = 3 \)
実際に表から読みってみましょう。
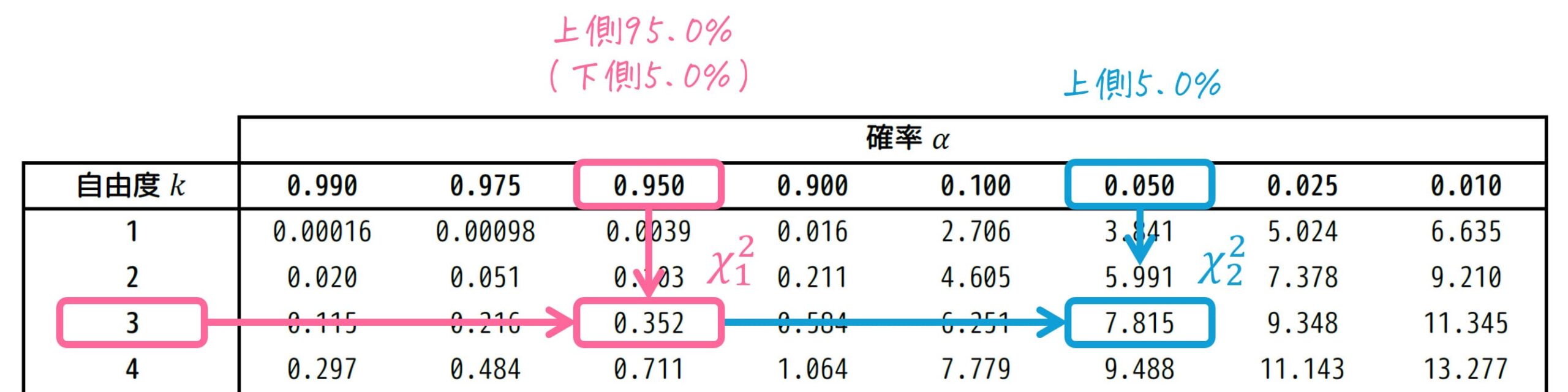
結果、\( \chi_1^2 = 0.352 \)、\( \chi_2^2 = 7.815 \) とわかりますね。
Step3. 区間推定の公式に代入
あとは、標本サイズ \( n = 4 \)、不偏分散 \( s^2 = 100 \)、カイ2乗分布表から読み取った値\( \chi_1^2 = 0.352 \)、\( \chi_2^2 = 7.815 \) を区間推定公式\[
\frac{ (n-1) s^2 }{ \chi_2^2 } \leqq \sigma^2 \leqq \frac{ (n-1) s^2 }{ \chi_1^2 }
\]に入れていきましょう。
代入すると、\[
\frac{ 3 \cdot 100 }{ 7.815 } \leqq \sigma^2 \leqq \frac{ 3 \cdot 100 }{ 0.352 }
\]\[
\frac{ 100 }{ 2.605 } \leqq \sigma^2 \leqq \frac{ 3 \cdot 100 }{ 0.352 }
\]\[
38.388 \leqq \sigma^2 \leqq 852.273
\]となります。小数第2位まで求めればOKなので、信頼度90%にて母分散を推定した結果は\[
38.39 \leqq \sigma^2 \leqq 852.27
\]となります。
※ 標本サイズが小さいと、信頼区間の幅がかなり大きくなりますね。
関連広告・スポンサードリンク