スポンサードリンク
こんにちは、ももやまです。
F分布のいろは①では、「F分布とはどんなものなのか」というところから、「F分布を用いて母分散の比率の区間推定」について勉強しました。
また、F分布のいろは②では、F分布を使って2つのグループ(標本)の分散が等しいかどうかを検定する「等分散性の検定」の方法について勉強しました。
今回のF分布のいろは③では、3グループ以上の母平均がすべて等しいか否かを判定することができる「一元配置分散分析」について勉強していきましょう!
例題、練習問題を解く際にお使いください。
例題、練習問題を解く際にお使いください。
※ 使っている参考書や授業に合わせて、両側t分布表、片側t分布表を選択することをおすすめします。なお、統計検定の場合、与えられる表は片側t分布表です。
目次
スポンサードリンク
1. 一元配置分散分析とは?
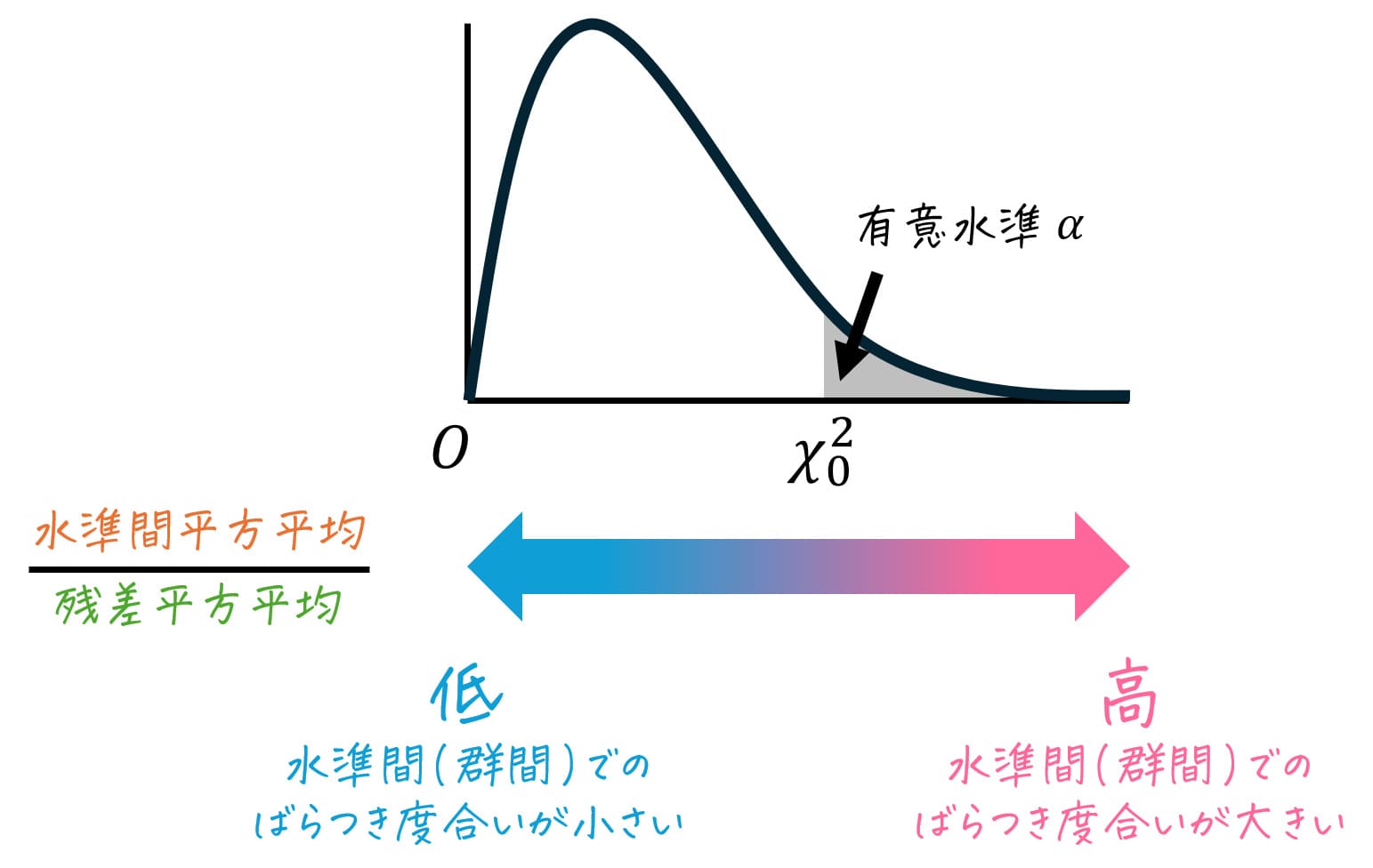
一元配置分散分析とは、3つ以上の異なるグループ(標本)の母平均がすべて等しいかどうかを、各データのばらつき度合いから検定する方法です。
具体的には、各データのばらつきを「グループ間のばらつき」と「グループ内のばらつき」に分解し、「グループ間のばらつき」に対する「グループ内のばらつき」の比率から、3つ以上の異なるグループ(標本)の母平均がすべて等しいとみなせるかを検定します。
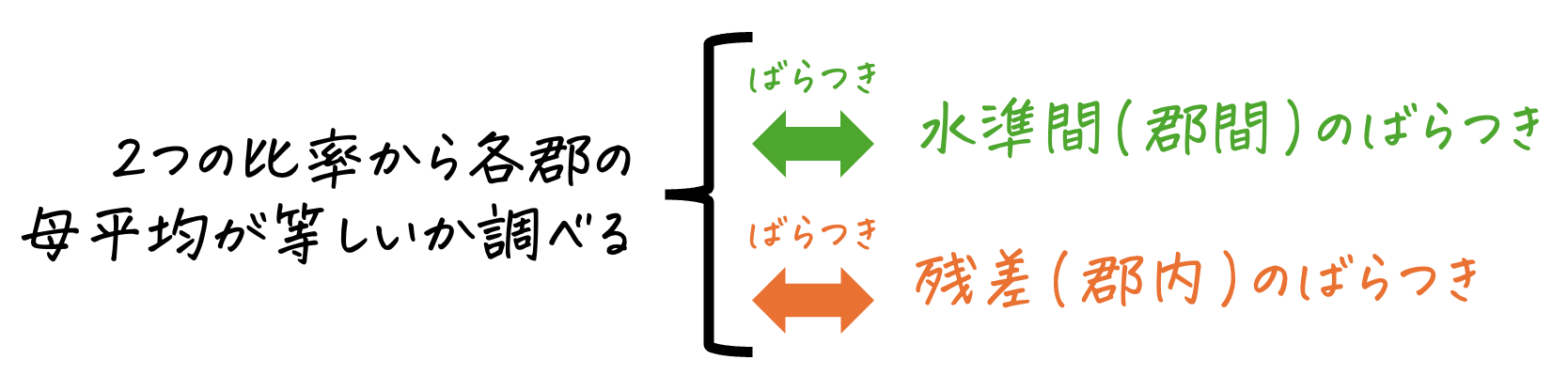
※ 「郡」はグループのことだと思ってください。グループと表記している箇所もあれば、郡と表記している箇所もあります。
スポンサードリンク
2. 一元配置分散分析で出てくる用語解説
例題を見る前に、一元配置分散分析をする上で、覚えておきたい用語を見ておきましょう。
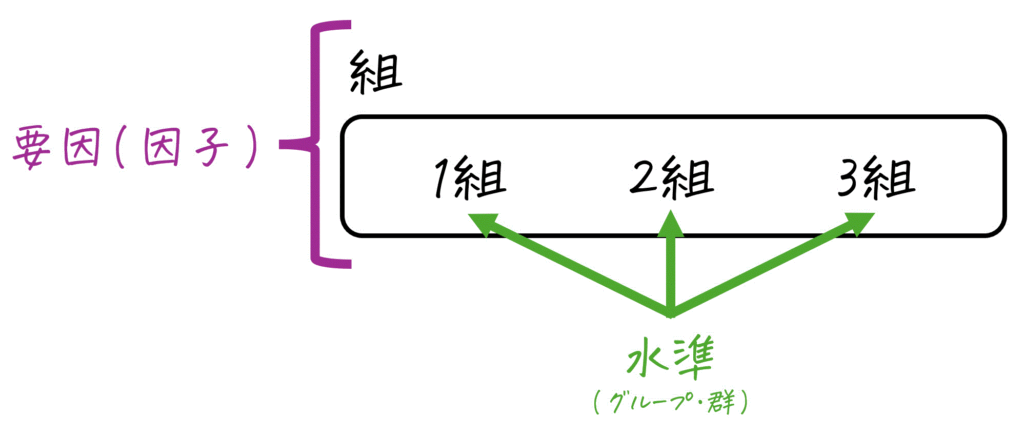
(1) 要因(因子)
要因は、データの値に変化を与えるグループ全体のことを表します。分析対象のものが要因になるという認識でOKです[1] … Continue reading。
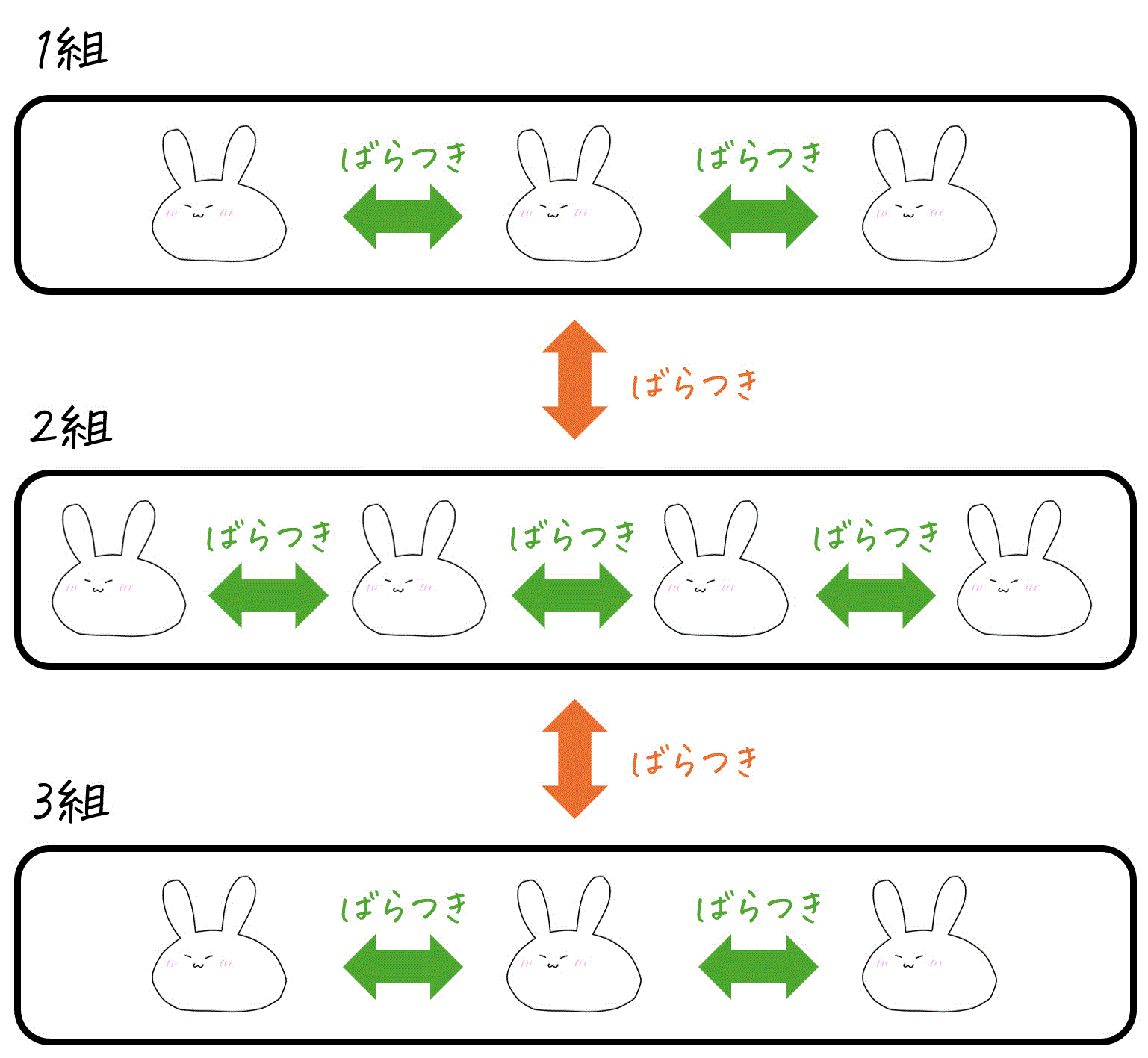
例えば、1組、2組、3組の平均点(母平均)が等しいかどうかを一元配置分散分析で調べる場合、このときの要因は「組」全体を指します。
(2) 水準
水準は、要因を異なる状態やカテゴリーに分けてグループ(郡)化したものです。グループ間のことを「水準間」と表現することが多いので覚えておきましょう。
例えば、1組、2組、3組の平均点(母平均)を等しいとみなしてよいかを一元配置分散分析で調べるとき、このときの水準は「1組」、「2組」、「3組」となります。
(3) 残差
残差とは、各データのばらつきを「グループ間のばらつき」と「グループ内のばらつき」に分解した際に、グループ内のばらつきに相当する部分を指します。
全体のばらつきから、グループ間(水準間)のばらつきを取り除いた後に残ったものだから「残差」という解釈でOKです。
スポンサードリンク
3. 例題で一元配置分散分析の流れを確認しよう!
ここからは、実際に例題を使って、一元配置分散分析の流れを確認していきましょう。
桃山高校の1年生を対象とし、1組、2組、3組で数学の小テストを実施した。
ここで、3つの異なるクラスの成績を比較するために、1組、2組、3組の中から数人(4〜5人程度)のテスト結果を確認したところ、以下の結果が得られた。
| 組 | 1人目 (点) | 2人目 (点) | 3人目 (点) | 4人目 (点) | 5人目 (点) |
|---|---|---|---|---|---|
| 1組 | 13 | 20 | 20 | 19 | - |
| 2組 | 7 | 17 | 11 | 12 | 8 |
| 3組 | 19 | 18 | 20 | 11 | - |
※ 表内の "−" は、該当するデータが存在しないことを表す。言い換えると、1組、3組からは4人、2組からは5人のデータを抽出している。
この結果をもとに、1組、2組、3組の平均点(母平均)を等しいとみなしてよいか、分散分析によって調べたい。つぎの
表. 分散分析表
| 要因 | 平方和 | 自由度 | 平方平均 | \( F \) 値 |
|---|---|---|---|---|
| 水準間 [郡間] | ||||
| 残差 [郡内] | − | |||
| 合計 | − | − |
(1) 帰無仮説 \( H_0 \) と対立仮説 \( H_1 \) を述べなさい。
(2) 抽出したデータ内における、全体(1組、2組、3組すべて)の平均点(標本平均) と、各組の平均点(標本平均)を求めなさい。
(3) 分散分析表の空欄を埋めなさい。ただし、" − " の箇所は埋めなくて良い。また、平方平均は小数第1位まで、F値は小数第3位まで求めること。
(4) 有意水準(危険率)5%で検定を行う。この検定で使う臨界値をすべて求めなさい。値は小数第3位まで記すこと。
(5) 有意水準(危険率)5%で検定を行い、結果およびその理由を記しなさい。
※ 臨界値:仮説の採択/棄却が変わる境界値のこと。片側検定であれば1つ、両側検定であれば2つある。
※ 必要であれば、こちらからF分布表をダウンロードできます。
(1) 帰無仮説と対立仮説の設定
一元配置分散分析では、帰無仮説で「出てくるすべてのグループ(郡)の母平均が等しいこと」を仮定します。
また、対立仮説は、帰無仮説の否定、つまり「少なくとも1つのグループの母平均が、他のグループの母平均とは異なる」とします[2] … Continue reading。
今回の例題の場合、帰無仮説 \( H_0 \)、対立仮説 \( H_1 \) は、つぎの通りとなります。
帰無仮説 \( H_0 \): 仮説検定をするための「仮定」
テストの点数(1組)の母平均 \( \mu_1 \)、小テストの点数(2組)の母平均 \( \mu_2 \)、小テストの点数(3組)の母平均 \( \mu_3 \) がすべて等しい、つまり \( \mu_1 = \mu_2 = \mu_3 \)。
対立仮説 \( H_1 \): 仮説検定を否定することで示したいもの
テストの点数(1組)の母平均 \( \mu_1 \)、小テストの点数(2組)の母平均 \( \mu_2 \)、小テストの点数(3組)の母平均 \( \mu_3 \) のうち、少なくとも1つの母平均が異なる。つまり、 \( \mu_1 = \mu_2 = \mu_3 \) が成り立たない。
(2) グループ全体の標本平均、各グループの標本平均を求める
求めたいグループ (or グループ全体)内 の点数の合計を、人数で割って標本平均を求めていきましょう。
| 組 | 1人目 (点) | 2人目 (点) | 3人目 (点) | 4人目 (点) | 5人目 (点) |
|---|---|---|---|---|---|
| 1組 | 13 | 20 | 20 | 19 | - |
| 2組 | 7 | 17 | 11 | 12 | 8 |
| 3組 | 19 | 18 | 20 | 11 | - |
全体の平均点 \( \overline{X} \)
\( a = 15 \) と仮定して計算するのがおすすめです。
\[\begin{align*}
\overline{X} & = \frac{1}{13} (13+20+20+19+7+17+11+12+8+19+18+20+11)
\\ & = \frac{1}{13} \left\{ (a-2) + (a+5) + (a+5) + (a+4) + (a-8)+ (a+2) + (a-4) + (a-3) + (a-7) + (a+4) + (a+3) + (a+5) - (a-4) \right\}
\\ & = \frac{1}{13} \cdot 13a
\\ & = a
\\ & = 15
\end{align*}\]
1組の平均点 \( \overline{X}_1 \)
\( a = 15 \) と仮定して計算するのがおすすめです。
\[\begin{align*}
\overline{X}_1 & = \frac{1}{4} (13+20+20+19)
\\ & = \frac{1}{4} \left\{ (a-2) + (a+5) + (a+5) + (a+4) \right\}
\\ & = \frac{1}{4} (4a+12)
\\ & = a + 3
\\ & = 18
\end{align*}\]
2組の平均点 \( \overline{X}_2 \)
こちらも、\( a = 15 \) と仮定して計算するのがおすすめです。
\[\begin{align*}
\overline{X}_2 & = \frac{1}{5} (7+17+11+12+8)
\\ & = \frac{1}{5} \left\{ (a-8)+(a+2)+(a-4)+(a-3)+(a-7) \right\}
\\ & = \frac{1}{5} (5a-20)
\\ & = a - 4
\\ & = 11
\end{align*}\]
3組の平均点 \( \overline{X}_3 \)
同じように、\( a = 15 \) と仮定して計算しましょう。
\[\begin{align*}
\overline{X}_3 & = \frac{1}{4} (19+18+20+11)
\\ & = \frac{1}{4} \left\{ (a+4)+(a+3)+(a+5)+(a-4) \right\}
\\ & = \frac{1}{4} (4a+8)
\\ & = a + 2
\\ & = 17
\end{align*}\]
(3) 分散分析表の穴埋め
[i] 平方和(水準間平方和、残差平方和、全体平方和)
分散分析表の、(a)〜(c)を埋める操作に相当します。
| 要因 | 平方和 | 自由度 | 平方平均 | \( F \) 値 |
|---|---|---|---|---|
| 水準間 [郡間] | (a) \( S_A \) | |||
| 残差 [群内] | (b) \( S_E \) | − | ||
| 全体 | (c) \( S_T \) | − | − |
(a) 水準間平方和・群間平方和 \( S_A \) [SSB]
水準間平方和は、「グループ間のばらつき度合い」をすべて足したものです。群間平方和とも呼ばれます。
水準間平方和は、各グループのデータが、仮にそのグループの平均値だった場合の、全体の平均からのずれの2乗和で計算ができます。
今回の例題の場合は、
- 1組のデータ: 1組の平均(18)におきかえ
- 2組のデータ: 2組の平均(11)におきかえ
- 3組のデータ: 3組の平均(17)におきかえ
をしてから、全体の平均(15)からのずれの2乗和を計算すれば、水準間平方和が求められます。
表. 以下の表内の各データの、全体平均(15)からのズレの2乗をすべて足せばOK
| 組 | 平均 (点) | 1人目 (点) | 2人目 (点) | 3人目 (点) | 4人目 (点) | 5人目 (点) |
|---|---|---|---|---|---|---|
| 1組 | 18 | 18 | 18 | 18 | 18 | - |
| 2組 | 11 | 11 | 11 | 11 | 11 | 11 |
| 3組 | 17 | 17 | 17 | 17 | 17 | - |
表. 各データ毎に、ズレの2乗を算出し、グループ単位で合計したもの

上の表の小計部分をすべて足した\[\begin{align*}
S_A & = 36 + 80 + 16
\\ & = 132
\end{align*}\]が、水準間平方和 \( S_A \) となります。
| 要因 | 平方和 | 自由度 | 平方平均 | \( F \) 値 |
|---|---|---|---|---|
| 水準間 [郡間] | 132 | |||
| 残差 [郡内] | − | |||
| 全体 | − | − |
なお、この計算は、各グループごとに、グループ平均と全体平均からのずれの2乗を、各グループの標本サイズで掛けて(重み付けして)から、すべて足したものと言い換えられます。
そのため、例題の場合、1組、2組、3組分の郡間誤差をすべて求め、求めたものを足すことで計算できます。
1組の分の小計(標本平均: 18、標本サイズ: 4)\[
4 \times ( \textcolor{magenta}{18} - \textcolor{deepskyblue}{15} )^2 = 4 \times 9 = 36
\]
2組の分の小計(標本平均: 11、標本サイズ: 5)\[
5 \times ( \textcolor{teal}{11} - \textcolor{deepskyblue}{15} )^2 = 5 \times 16 = 80
\]
3組の分の小計(標本平均: 17、標本サイズ: 4)\[
4 \times ( \textcolor{orange}{17} - \textcolor{deepskyblue}{15} )^2 = 4 \times 4 = 16
\]
あとは、3つの組の小計をすべて足したもの\[\begin{align*}
S_A & = 36 + 80 + 16
\\ & = 132
\end{align*}\]が水準間平方和 \( S_A \) です。
b) 残差平方和(群内平方和)[SSW]
残差平方和は、「グループ内のばらつき度合い」をすべて足したものです。水準間(グループ間)とは関係のないばらつきの平方和という意味で、残差平方和と名付けられています。群間平方和とも呼ばれます。
残差平方和は、各データ値ごとに、データ値が属するグループの平均とのズレの2乗を求め、すべて足すこと計算ができます。
今回の例題の場合は、つぎのようにデータ
- 1組の各データ: 1組の平均(18)とのズレ
- 2組の各データ: 2組の平均(11)とのズレ
- 3組の各データ: 3組の平均(17)とのズレ
を計算したものを、すべて足せば残差平方和 \( S_E \) が求められます。
表. 各データ
| 組 | 平均 (点) | 1人目 (点) | 2人目 (点) | 3人目 (点) | 4人目 (点) | 5人目 (点) |
|---|---|---|---|---|---|---|
| 1組 | 18 | 13 | 20 | 20 | 19 | - |
| 2組 | 11 | 7 | 17 | 11 | 12 | 8 |
| 3組 | 17 | 19 | 18 | 20 | 11 | - |
表. 各データ毎に、ズレの2乗を算出し、グループ単位で合計したもの

各組(郡、グループ)ごとの誤差の和を小計として出しておいて、最後に小計をすべて足す方法がおすすめです。
実際に計算してみると、1組の小計34、2組の小計80、3組の小計16をすべて足して\[\begin{align*}
S_E & = 34 + 62 + 50
\\ & = 146
\end{align*}\]が残差平方和 \( S_E \) となります。
| 要因 | 平方和 | 自由度 | 平方平均 | \( F \) 値 |
|---|---|---|---|---|
| 水準間 [郡間] | 132 | |||
| 残差 [郡内] | 146 | − | ||
| 全体 | − | − |
c) 全体平方和
全体平方和は、「データ全体のばらつき度合い」をすべて足したものです。
具体的に、各データ値ごとに、データ全体との平均とのズレの2乗を求め、すべて足すこと計算ができます。
今回の例題の場合は、各データごとに、データ値と全体の平均(15)とのズレの2乗和を計算すればOKです。

こちらも、各組(郡、グループ)ごとの誤差の和を小計として出しておいて、最後に小計をすべて足す方法がおすすめです。
実際に計算してみると、1組の小計70、2組の小計142、3組の小計66をすべて足して\[\begin{align*}
S_T & = 70 + 142 + 66
\\ & = 278
\end{align*}\]が全体平方和 \( S_T \) です。
| 要因 | 平方和 | 自由度 | 平方平均 | \( F \) 値 |
|---|---|---|---|---|
| 水準間 [郡間] | 132 | |||
| 残差 [郡内] | 146 | − | ||
| 全体 | 278 | − | − |
d) 水準間平方和、残差平方和、全体平方和に成り立つ関係
全体平方和は、必ず「水準間平方和」と「残差平方和平方和」の和と等しくなります。つまり、
全体平方和(SST) = 水準間平方和(SSB) + 残差平方和(SSW)
が成り立ちます。(三平方の定理みたいですね。)
そのため、全体平方和、水準間平方和、残差平方和のうち、いずれか2つ求めることができれば、残りの1つが自動的に確定します。
実際に今回の例題を見ても、全体平方和(278) = 水準間平方和(132) + 残差平方和(146)の関係式が成り立っていますね。
| 要因 | 平方和 |
|---|---|
| 水準間 [郡間] | 132 |
| 残差 [郡内] | 146 |
| 合計 | 278 |
[ii] 自由度(郡間誤差、郡内誤差、全体誤差)
つぎに、郡間誤差、郡内誤差、全体誤差に対する自由度を求めていきましょう。
分散分析表の、(d)〜(f)を埋める操作に相当します。
| 要因 | 平方和 | 自由度 | 平方平均 | \( F \) 値 |
|---|---|---|---|---|
| 水準間 [郡間] | 132 | (d) \( \phi_A \) | ||
| 残差 [郡内] | 146 | (e) \( \phi_E \) | − | |
| 全体 | 278 | (f) \( \phi_T \) | − | − |
(d) 水準間 (群間) に対する自由度
水準間平方和(群間平方和) \( S_A \) は、グループ(郡)毎に、グループ内の標本平均 \( \overline{X}_i \) と、データ全体の標本平均 \( \overline{X} \) のずれを計算しています。\[
S_A = \sum^{k}_{i = 1} n_i \left( \overline{X}_i - \overline{X}\right)^{2}
\]
このとき、各グループの標本平均を計算するために、グループの数だけ独立した情報が必要だと思うかもしれません。
しかし、実際には、1つのグループを除く他のグループの標本平均がすべてわかっていれば、データ全体の標本平均を使って、残り1つのグループの標本平均を求めることができます。
そのため、水準間の自由度(=情報量)\( \phi_A \) としては、グループ数 \( k \) から1を引いた \( k = 1 \) なります。\[
\phi_A = k - 1
\]
今回の例題の場合、グループ数は、1組、2組、3組の3つなので \( k = 3 \) です。
| 組 | 平均 (点) | 1人目 (点) | 2人目 (点) | 3人目 (点) | 4人目 (点) | 5人目 (点) |
|---|---|---|---|---|---|---|
| 1組 | 18 | 13 | 20 | 20 | 19 | - |
| 2組 | 11 | 7 | 17 | 11 | 12 | 8 |
| 3組 | 17 | 19 | 18 | 20 | 11 | - |
そのため、水準間平方和に対する自由度は 3 - 1 = 2 となります。
| 要因 | 平方和 | 自由度 | 平方平均 | \( F \) 値 |
|---|---|---|---|---|
| 水準間 [郡間] | 132 | 2 | ||
| 残差 [郡内] | 146 | − | ||
| 全体 | 278 | − | − |
(e) 残差 (群内) に対する自由度
残差平方和(群内平方和)\( S_E \) は、あるグループ(\( i \) 番目)に着目したときの、標本平均 \( \overline{X}_i \) と、データ全体の標本平均 \( \overline{X} \) のズレを計算することで求めています。\[
S_E = \sum^{k}_{i = 1} n_i \left( \overline{X}_i - \overline{X}\right)^{2}
\]
ここで、ある \( i \) 番目のグループ内のズレを計算する際の情報量を考えてみましょう。
ズレを計算するには、グループ内にあるすべてのデータが必要です。しかし、1つを除くデータ点がわかっていれば、そのグループの標本平均から、残り1つの未知のデータ点の値を復元できるため、実際のデータ数よりも1つ少ない情報量でズレを計算できます。
この操作をすべてのグループで行うため、各グループのデータ数から1を引いた数を、グループの数 \( k \) 回合計します。
結果として、自由度(=情報量)\( \phi_E \)としては、データ数 \( N \) からグループ数 \( k \) を引いた \( N - k \) となります。\[
\phi_E = N - k
\]
今回の例題の場合、グループ数は、1組、2組、3組の3つなので \( k = 3 \)、データ数は全部で13個なので \( N = 13 \) ですね。
| 組 | 平均 (点) | 1人目 (点) | 2人目 (点) | 3人目 (点) | 4人目 (点) | 5人目 (点) |
|---|---|---|---|---|---|---|
| 1組 | 18 | 13 | 20 | 20 | 19 | - |
| 2組 | 11 | 7 | 17 | 11 | 12 | 8 |
| 3組 | 17 | 19 | 18 | 20 | 11 | - |
そのため、残差に対する自由度は 13 - 3 = 10 となります。
| 要因 | 平方和 | 自由度 | 平方平均 | \( F \) 値 |
|---|---|---|---|---|
| 水準間 [郡間] | 132 | 2 | ||
| 残差 [郡内] | 146 | 10 | − | |
| 全体 | 278 | − | − |
(f) 全体の自由度
全体平方和 \( S_T \) は、各データ値ごとに、データ全体の平均からのズレを計算して求めます。\[
S_T = \sum^{k}_{i = 1} \sum^{ n_i }_{ j = 1 } \left( X_{ij} - \overline{X} \right)^2
\]
このズレを計算するには、データ全体に含まれる \( N \) 個のデータが必要です。しかし、仮に1つのデータがわからなかったとしても、他のデータとデータ全体の標本平均から、その1つのデータを復元することが可能です。
したがって、実際のデータ数よりも1つ少ない情報量で全体誤差を求めることができます。 そのため、自由度(=情報量)\( \phi_T \) としては、データ数 \( N \) から1を引いた \( N - 1 \) となります。\[
\phi_T = N - 1
\]
今回の例題の場合、データ数は全部で13個なので \( N = 13 \) ですね。
| 組 | 平均 (点) | 1人目 (点) | 2人目 (点) | 3人目 (点) | 4人目 (点) | 5人目 (点) |
|---|---|---|---|---|---|---|
| 1組 | 18 | 13 | 20 | 20 | 19 | - |
| 2組 | 11 | 7 | 17 | 11 | 12 | 8 |
| 3組 | 17 | 19 | 18 | 20 | 11 | - |
そのため、全体の自由度は 13 - 1 = 12 となります。
| 要因 | 平方和 | 自由度 | 平方平均 | \( F \) 値 |
|---|---|---|---|---|
| 組 [郡間] | 132 | 2 | ||
| 誤差 [郡内] | 146 | 10 | − | |
| 全体 | 278 | 12 | − | − |
水準間に対する自由度、残差に対する自由度、全体の自由度に成り立つ関係
全体の自由度は、「水準間に対する自由度」と「残差に対する自由度」に分解して考えることができます。つまり、つぎのような関係が成立します[3]実際に、全体の自由度 \( N - 1 \)、水準間に対する自由度 \( k-1 \)、残差に対する自由度 \( N - k \) … Continue reading。
全体の自由度 = 水準間に対する自由度 + 残差に対する自由度
平方和(ズレの度合いの合計)だけでなく、自由度も分解ができると頭に入れておきましょう!
[iii] 水準間平方平均・残差平方平均(群間平方平均・残差平方平均)
つぎに、「グループ内のばらつき」と「グループ外のばらつき」を公平に比べるために、水準間平方平均 \( V_A \) 、残差平方平均 \( V_E \) の平方平均を求めます。
- \( V_A \) … 1自由度あたりの水準間平方和
- \( V_E \) … 1自由度あたりの残差平方和
分散分析表の、(g)〜(h)を埋める操作に相当します。
| 要因 | 平方和 | 自由度 | 平方平均 | \( F \) 値 |
|---|---|---|---|---|
| 水準間 [郡間] | 132 | 2 | (g) \( V_A \) | |
| 残差 [郡内] | 146 | 10 | (h) \( V_E \) | − |
| 全体 | 278 | 12 | − | − |
平方平均は1自由度あたりの平方和を表しているため、求め方としては、それぞれの平方和 \( S_A \), \( S_E \) を自由度 \( \phi_A = k-1 \), \( \phi_E = N - k \) で割ればOKです。
(g) 水準間平方平均 [MSB]\[\begin{align*}
V_A & = \frac{S_A}{ \phi_A }
\\ & = \frac{ S_A }{ k - 1}
\\ & = \frac{132}{2}
\\ & = 66.0
\end{align*}\]
(h) 残差平方平均 [MSW]\[\begin{align*}
V_E & = \frac{S_E}{ \phi_E }
\\ & = \frac{ S_E }{ N-k }
\\ & = \frac{146}{10}
\\ & = 14.6
\end{align*}\]
要因 平方和 自由度 平方平均 \( F \) 値 水準間
[郡間]132 2 66.0 残差
[郡内]146 10 14.6 − 全体 278 12 − −
なお、全体平方平均は、一元配置分散分析では使わないため、通常求めません。
なぜ平方平均でズレの度合いを比べるか?
水準間平方和、残差平方和は、ともに各グループ、各データごとにずれの度合いを累積して求める値です。
そのため、ばらつきの度合いに関係なく、データ数やグループ数が増えれば増えるほど平方和も増えてしまいます。これでは、グループ間の誤差とグループ内の誤差を公平に比べることができませんよね[4] … Continue reading。
そこで、「グループ内のばらつき」と「グループ外のばらつき」の比率をフェアに比べるために、一元配置分散分析では、平方和を自由度で割ることで、ばらつきをグループ数やデータ数に対して調整します[5] … Continue reading。
この調整により、水準間(グループ間)と残差(グループ内)のばらつきを標準化し、同じ基準で「グループ内のばらつき」と「グループ間のばらつき」の比率を求めることで、グループ間の誤差とグループ内の誤差を公平に比べられるようになります。
[iv] F値(F統計量)
F値は、水準間平方平均(群間平方平均) \( V_A \) が 残差平方平均(群内平方平均) \( V_E \) の何倍かを示すパラメータです。
\[
F = \frac{ V_A }{ V_E }
\]
簡単に言うと、F値は「グループ内のばらつき」に対して「グループ外のばらつき」がどれだけ大きいかを示す指標です。具体的には、「1自由度あたりのグループ内のばらつき」に対する「1自由度あたりのグループ外のばらつき」の比率として表されます。
今回の例題の場合、郡間誤差の平方平均は、\( V_A = 66.0 \)、郡内誤差の平方平均は、\( V_E = 14.6 \) でしたね。
そのため、F値は\[\begin{align*}
F & = \frac{ V_A }{ V_E }
\\ & = \frac{66.0}{14.6}
\\ & \fallingdotseq 4.521
\end{align*}\]となります。
| 要因 | 平方和 | 自由度 | 平方平均 | \( F \) 値 |
|---|---|---|---|---|
| 水準間 [郡間] | 132 | 2 | 66.0 | 4.521 |
| 残差 [郡内] | 146 | 10 | 14.6 | − |
| 全体 | 278 | 12 | − | − |
一元配置分散分析のF値と、F分布の関係
一元配置分散分析では、「グループ内のばらつき」と「グループ外のばらつき」のばらつき度合いの比率を基準に、仮説の採択/棄却を設定します。
では、この「2つのばらつきの比率」を表す分布といえば、どの分布が思い浮かびますか?
そう、F分布です。
F分布は、2つの標本のばらつき度合い \( \chi_1^2 \), \( \chi_2^2 \) を、それぞれの自由度 \( k_1 \), \( k_2 \) で正規化した比率を表します。\[
F = \frac{ \frac{ \chi_1^2 }{k_1 } }{ \frac{ \chi_2^2 }{k_2 } }
\]※上の値 \( F \) が自由度 \( (k_1,k_2) \) のF分布に従う。
この性質を利用して、一元配置分散分析では、次のようにF分布を使った仮説検定が行われます。
- \( \chi_1^2 \): グループ間のばらつき(水準間平方和 \( S_A \) )
- \( \chi_2^2 \): グループ内のばらつき(残差平方和 \( S_E \) )
- \( k_1 \): グループ間に対する自由度(水準間に対する自由度 \( \phi_A \) )
- \( k_2 \): グループ内に対する自由度(残差に対する自由度 \( \phi_E \) )
計算式にすると、以下のようになります。\[\begin{align*}
F & = \frac{ \frac{ S_A }{ \phi_A } }{ \frac{ S_E }{ \phi_E } }
\\ & = \frac{ V_A }{ V_E }
\end{align*}\]※ \( V_A \) は水準間平方平均、\( V_E \) は残差平方平均を表します。
この計算で得られたF値は、自由度 \( (\phi_A, \phi_E) \) のF分布に従います。そのため、F分布表から有意水準と対応する自由度 ( (\phi_A, \phi_E) ) の値を読み取り、計算したF値と比較することで仮説の採択または棄却を判断することができるのです。
(4) F分布表の読み取り:臨界値(採択/棄却の境界値)の確認
つぎに、有意水準5%で検定を行う際の臨界値をF分布表から読み取っていきましょう。
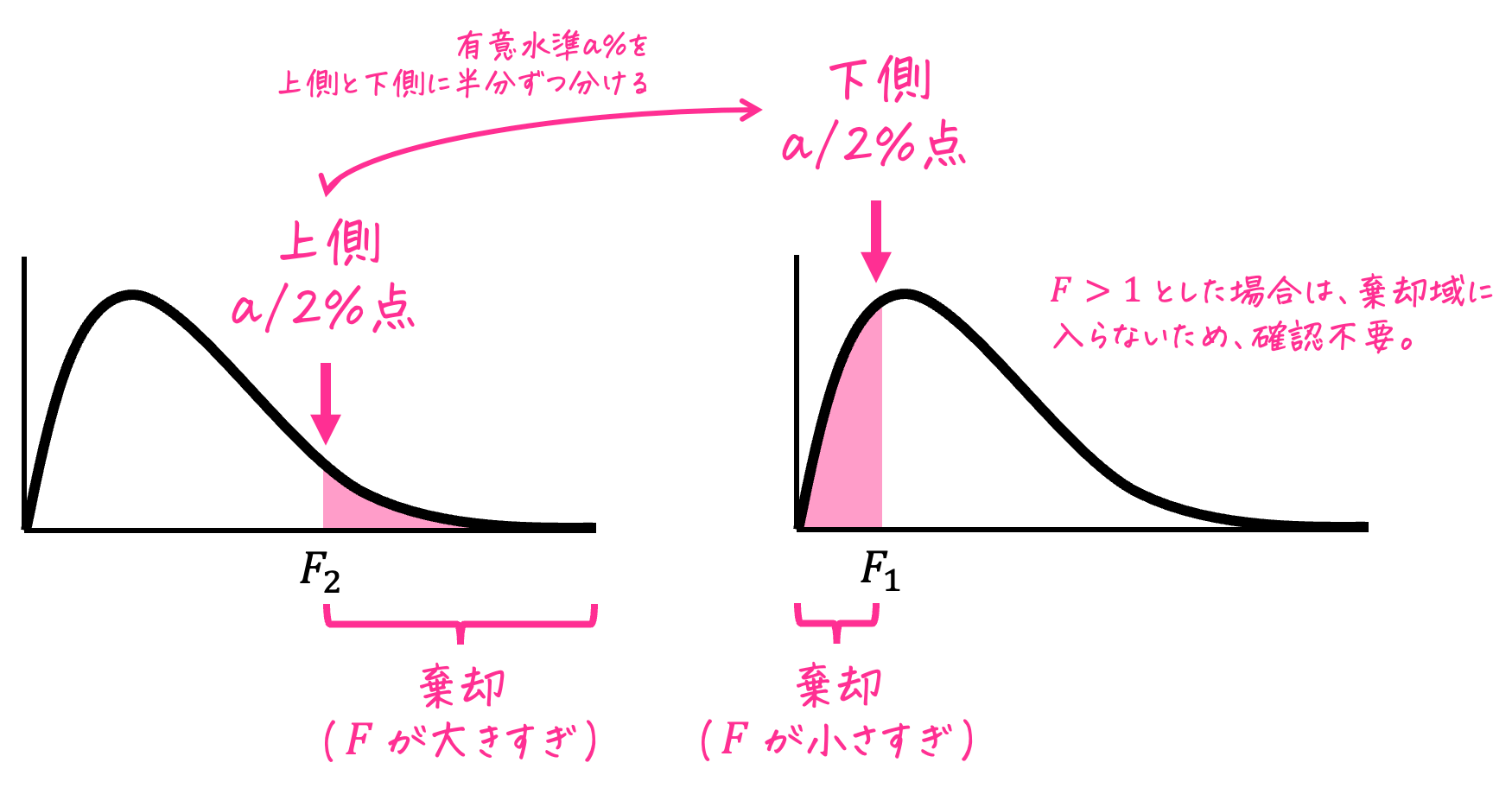
一元配置分散分析では、必ず片側検定を行う点に注意が必要です。
その理由は、一元配置分散分析において、「グループ間のばらつき」が「グループ内のばらつき」に対して大きい場合にのみ仮説が誤りであると判断され、少なくとも1つの母平均が異なると言えるからです。
つまり、「グループ間のばらつき」が「グループ内のばらつき」に対して小さい場合は問題がなく、ばらつきが大きい場合のみ問題があると解釈されます。

このため、一元配置分散分析では片側検定が実施されるのです。
今回は有意水準5%、自由度は\[\begin{align*}
(\phi_A, \phi_E) = (2,10)
\end{align*}\]なので、有意水準 \( \alpha = 0.05 \) [5%]、自由度 (2,10) に相当するF値を、F分布表から読み取ります。
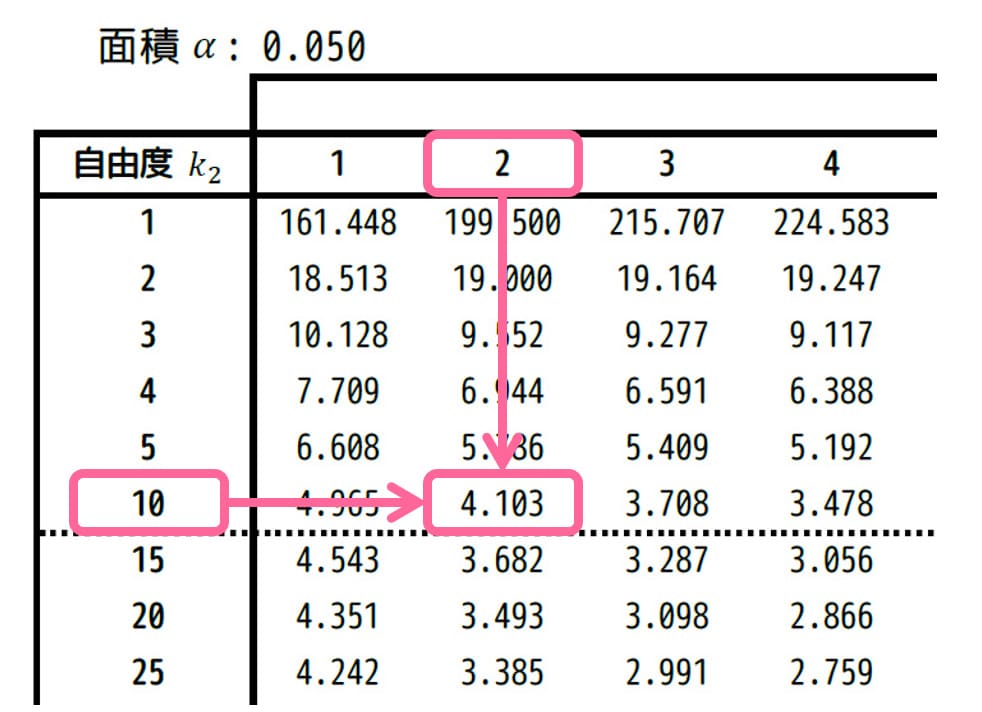
すると、4.103と読み取れます。\( F_0 = 4.103 \) とおきましょう。
(5) 結果の判定
あとは、(3)で計算したF値\[\begin{align*}
F & = \frac{ V_A }{ V_E }
\\ & = 4.521
\end{align*}\]および、(4)でF分布表から得た臨界値 \( F_0 = 4.103 \) から結論を出します。
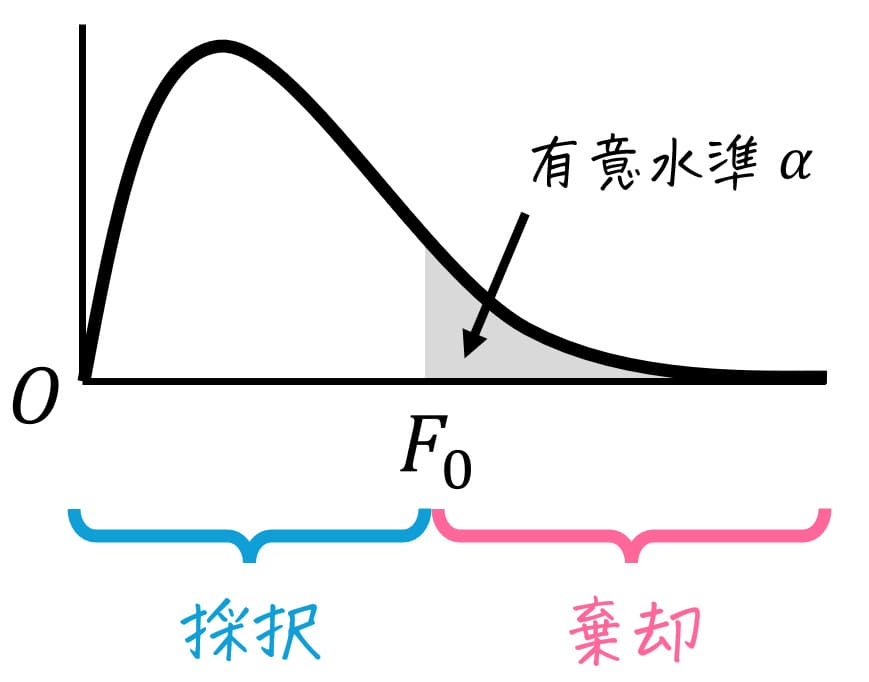
【結論の出し方】
- \( F \) が \( F_0 \) 以下のとき、つまり \( F \leqq F_0 \)
→ 仮説は採択:少なくとも1つのグループの母平均が他のグループと有意に異なるとは言えない。(各グループの母平均に有意な差はない。) - \( F \) が \( F_0 \) より大きいとき、つまり \( F > F_0 \)
→ 仮説は棄却:少なくとも1つのグループの母平均が他のグループと有意に異なるといえる。
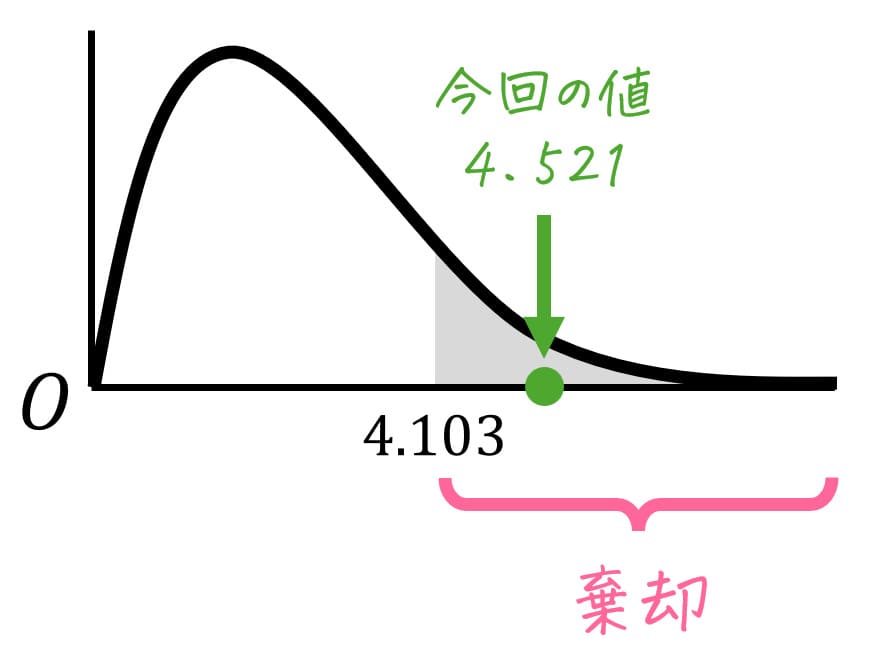
今回の場合は、\( F = 4.521 \)、F分布表から得た臨界値 \( \chi^2_0 = 4.103 \) より、\[
F = 4.521 > 4.103 = F_0
\]となります。
よって、仮説は棄却され、1組、2組、3組の小テストの点数の母平均のうち、少なくとも1つの母平均が異なると言えます。
\( k \) 個の水準(グループ/郡)からなるデータセットが、以下の表で与えられているとする。
| 要因 | 郡サイズ (データ数) | 郡平均 | データ1 | データ2 | … |
|---|---|---|---|---|---|
| 郡1 (水準1) | \( n_1 \) | \( \overline{X}_1 \) | \( X_{11} \) | \( X_{12} \) | … |
| 郡2 (水準2) | \( n_2 \) | \( \overline{X}_2 \) | \( X_{21} \) | \( X_{22} \) | … |
| ︙ | ︙ | ︙ | ︙ | ︙ | ⋱ |
| 郡k (水準k) | \( n_k \) | \( \overline{X}_k \) | \( X_{k1} \) | \( X_{k2} \) | … |
【変数の意味】
- \( n_i \) … 郡 \( i \) 内のデータサイズ(データ数)
- \( \overline{X} \) … 全データセット内の標本平均
- \( \overline{X}_i \) … 郡 \( i \) 内の標本平均
- \( X_{ij} \) … 郡 \( i \) 内のデータ \( j \)(\( j \)番目)のデータ値
このとき、以下のStep1〜Step5の流れで一元配置分散分析が可能である。
Step1. 帰無仮説と対立仮説の設定をする
帰無仮説 \( H_0 \): 仮説検定をするための「仮定」
各グループ(各水準)の母平均 \( \mu_1 \), \( \mu_2 \), …, \( \mu_k \) に有意な差はない。つまり、\( \mu_1 = \mu_2 = \cdots = \mu_k \)
対立仮説 \( H_1 \): 仮説検定を否定することで示したいもの
少なくとも1つのグループの母平均が他のグループと有意に異なるといえる。
Step2. 全体の標本平均、各郡の標本平均を求める
全体の標本平均 \( \overline{X} \)\[
\overline{X} = \frac{1}{N} \sum^{k}_{i = 1} \sum^{n_i}_{j = 1} X_{ij}
\]
郡 \( i \) の標本平均 \( \overline{X}_i \)\[
\overline{X}_i = \frac{1}{ n_i } \sum^{n_i}_{j = 1} X_{ij}
\]
Step3. 分散分析表を埋める
表. 分散分析表
| 要因 | 平方和 | 自由度 | 平方平均 | \( F \) 値 |
|---|---|---|---|---|
| 水準間 [群間] | (a) \( S_A \) | \( \phi_A = k - 1 \) | \( V_A = \frac{ S_A }{ \phi_A } \) | \( \frac{ V_A }{ V_E } \) |
| 残差 [郡内] | (b) \( S_E \) | \( \phi_E = N - k \) | \( V_E = \frac{ S_E }{ \phi_E } \) | − |
| 全体 | (c) \( S_T \) | \( \phi_T = N - 1 \) | − | − |
ここで、(a) 水準間平方和 \( S_A \)、(b) 残差平方和 \( S_E \)、(c) 全体平方和 \( S_T \) は以下の計算式で計算できる。
(a) 水準間平方和 (郡間平方和) \(S_A \) [SSB … Sum of Squares Between groups]
各郡ごとに、ある群 \( i \) に着目したときの、郡 \( i \) 内の標本平均 \( \overline{X}_i \) と、データ全体の標本平均 \( \overline{X} \) のずれを2乗したものを、各群毎のデータサイズ \( n_i \) で掛けた(重み付けした)ものを、すべて足したもの。\[
S_A = \textcolor{teal}{ \sum^{k}_{i = 1} } \textcolor{purple}{n_i} \left( \textcolor{red}{ \overline{X}_i - \overline{X} } \right)^{\textcolor{blue}{2}}
\]※ 全体誤差の公式の \( X_{ij} \) を、\( \overline{X}_i \) に書き換えて、\[\begin{align*}
\mathrm{SSB} & = \sum^{k}_{i = 1} \textcolor{purple}{\sum^{ n_i }_{ j = 1 } } \left( \overline{X}_i - \overline{X} \right)^2
\\ & = \sum^{k}_{i = 1} \textcolor{purple}{n_i} \left( \overline{X}_i - \overline{X} \right)^2
\end{align*}\]と変形したものと頭に入れておいてください。
(b) 残差平方和 (群内平方和) \( S_E \) [SSW … Sum of Squares Within groups]
すべてのデータに対して、ある郡 \( i \) に着目したときの、データ値 \( X_{ij} \) と郡 \( i \) 内の標本平均 \( \overline{X}_i \) のずれを2乗したものを計算し、すべて足したもの。\[
S_E = \textcolor{teal}{ \sum^{k}_{i = 1} \sum^{ n_i }_{ j = 1 } } \left( \textcolor{red}{ X_{ij} - \overline{X}_i } \right)^{\textcolor{blue}{2}}
\]※ 全体誤差の公式の \( \overline{X} \) を、\( \overline{X}_i \) に書き換えたもの、と頭に入れておいてください。
(c) 全体平方和 \( S_T \) [SST … Total Sum of Squares]
すべてのデータに対して、ある郡 \( i \) に着目したときの、データ値 \( X_{ij} \) とデータ全体の標本平均 \( \overline{X} \) のずれを2乗したものを計算し、すべて足したもの。\[
S_T = \textcolor{teal}{ \sum^{k}_{i = 1} \sum^{ n_i }_{ j = 1 } } \left( \textcolor{red}{ X_{ij} - \overline{X} } \right)^{\textcolor{blue}{2}}
\]
水準間平方和、残差平方和、全体誤差に成り立つ関係
全体平方和 \( S_T \) = 水準間平方和 \( S_A \) + 残差平方和 \( S_E \)
※ 全体平方和、水準間平方和、 残差平方和のうち、いずれか2つ求めることができれば、残りの1つを上の関係式から計算できる。
Step4. F分布表を読み取る
有意水準 \( \alpha \)、自由度 \( (k_1, k_2) = ( \phi_A, \phi_E \) のときのF値を、F分布表から読み取る。ただし、\( \phi_A = k-1 \)、\( \phi_E = N - k \)。
Step5. 採択/棄却の判定
Step3で求めた \( F \) と、Step4でF分布表から読み取った \( F_0 \) を比較して、採択/棄却の結論を出す。
- \( F \) が \( F_0 \) 以下のとき、つまり \( F \leqq F_0 \)
→ 仮説は採択:少なくとも1つのグループの母平均が他のグループと有意に異なるとは言えない。つまり、各グループの母平均に有意な差はない。 - \( F \) が \( F_0 \) より大きいとき、つまり \( F > F_0 \)
→ 仮説は棄却:少なくとも1つのグループの母平均が他のグループと有意に異なるといえる。

4. 残差(群内)平方平均を用いた母平均の区間推定
一元配置分散分析において、「残差平方平均(群内平方平均) \( V_E \)」は各グループ内の分散を表しており、グループ全体で共有される「誤差」を示しています。この誤差をもとにして、各グループごとに標本平均のばらつきを推定し、これを用いて母平均の信頼区間を計算することができます。
ここで、突然ですが問題です。
母分散が分からないときに、母平均を推定する際に使える分布と言えば、何だったでしょうか?
そう、t分布です。
母平均推定の際には、以下の4つの要素が必要です。
- 標本サイズ \( n \)
- 標本平均 \( \overline{X} \)
- 不偏分散 \( s^2 \)
- 信頼度、自由度 \( n-1 \) に相当するF分布表から読み取った値 \( t_0 \)
この4つの要素から、母平均 \( \mu \) の信頼区間を次のように推定することが出来ます。\[
\overline{X} - \frac{ t_0 s }{ \sqrt{n} } \leqq \mu \leqq \overline{X} + \frac{ t_0 s }{ \sqrt{n} }
\]
※ t分布を使って母平均の信頼区間を推定する方法がいまいちよく分からなかったという人は、以下の記事で復習しましょう。
一元配置分散分析では、上の信頼区間の不偏分散 \( s^2 \) の代わりに、残差平方平均 \( V_E \) を使用します[6]\( s^2 = V_E \) なので、\( s = \sqrt{ V_E } \) となる。。
これにより、一元配置信頼区間の結果から、次のように母平均 \( \mu \) を区間推定を実現できます。
一元配置分散分析で得られた残差平方平均 \( V_E \) から、各グループ(各郡)の母平均 \( \mu_i \) を、以下のように区間推定出来る。
\[
\overline{X}_i - \frac{ t_0 \sqrt{ V_E } }{ \sqrt{n_i} } \leqq \mu \leqq \overline{X}_i + \frac{ t_0 \sqrt{ V_E } }{ \sqrt{n_i} }
\]※ \( i \) は、i番目のグループを表す。
- \( \overline{X}_i \) … \( i \) 番目のグループの標本平均
- \( n_i \) … \( i \) 番目のグループの標本サイズ
- \( t_0 \) … 信頼度、および残差の自由度 \( \phi_E = N - k \) に相当するt分布表から読み取った値
では、先ほどの例題1のデータを使って、各グループ(各郡)の母平均をそれぞれ求めてみましょう。
桃山高校の1年生を対象とし、1組、2組、3組で数学の小テストを実施した。
ここで、3つの異なるクラスの成績を比較するために、1組、2組、3組の中から数人(4〜5人程度)のテスト結果を確認したところ、以下の結果が得られた。
| 組 | 1人目 (点) | 2人目 (点) | 3人目 (点) | 4人目 (点) | 5人目 (点) |
|---|---|---|---|---|---|
| 1組 | 13 | 20 | 20 | 19 | - |
| 2組 | 7 | 17 | 11 | 12 | 8 |
| 3組 | 19 | 18 | 20 | 11 | - |
※ 表内の "−" は、該当するデータが存在しないことを表す。言い換えると、1組、3組からは4人、2組からは5人のデータを抽出している。
この結果をもとに、1組、2組、3組の平均点(母平均)を等しいとみなしてよいかを確認するために、つぎの[1], [2]の計算を行った。
[1] 1組~3組、および全体の標本平均は、つぎの表の通りになった。表1. 1組、2組、3組の標本平均
| 組 | 標本平均 (点) |
|---|---|
| 1組 | 18 |
| 2組 | 11 |
| 3組 | 17 |
| 全体 | 15 |
表2. 分散分析表
| 要因 | 平方和 | 自由度 | 平方平均 | \( F \) 値 |
|---|---|---|---|---|
| 水準間 [郡間] | 132 | 2 | 66.0 | 4.521 |
| 残差 [郡内] | 146 | 10 | 14.6 | − |
| 全体 | 278 | 12 | − | − |
この[1], [2]から、1組、2組、3組それぞれの数学の小テストの点数の母平均を信頼度95%で区間推定しなさい。小数第2位まで求めること。
※ 必要であれば、こちらから片側t分布表をダウンロードできます。
※ 必要であれば、こちらから両側t分布表をダウンロードできます。
例題2の解説.
群内の誤差の平方平均は、\( V_E = 14.6 \) ですね。
このデータをもとに、1組、2組、3組の点数の母平均を信頼度95%で推定してみましょう。
[i] 1組の母平均 \( \mu_1 \)
1組の標本に対する標本平均は、\( \overline{X}_1 = 18 \)、標本サイズは \( n_1 = 4 \) ですね。
まず、信頼度95%、残差の自由度10に対応する値 \( t_0 \) をt分布表から読み取ります。
★ 両側t分布表から読み取る場合
\( \alpha = 0.050 \)、自由度 \( k = 10 \) に対応する \( t \) の値は、両側t分布表のつぎの箇所を読み取ればOKです。
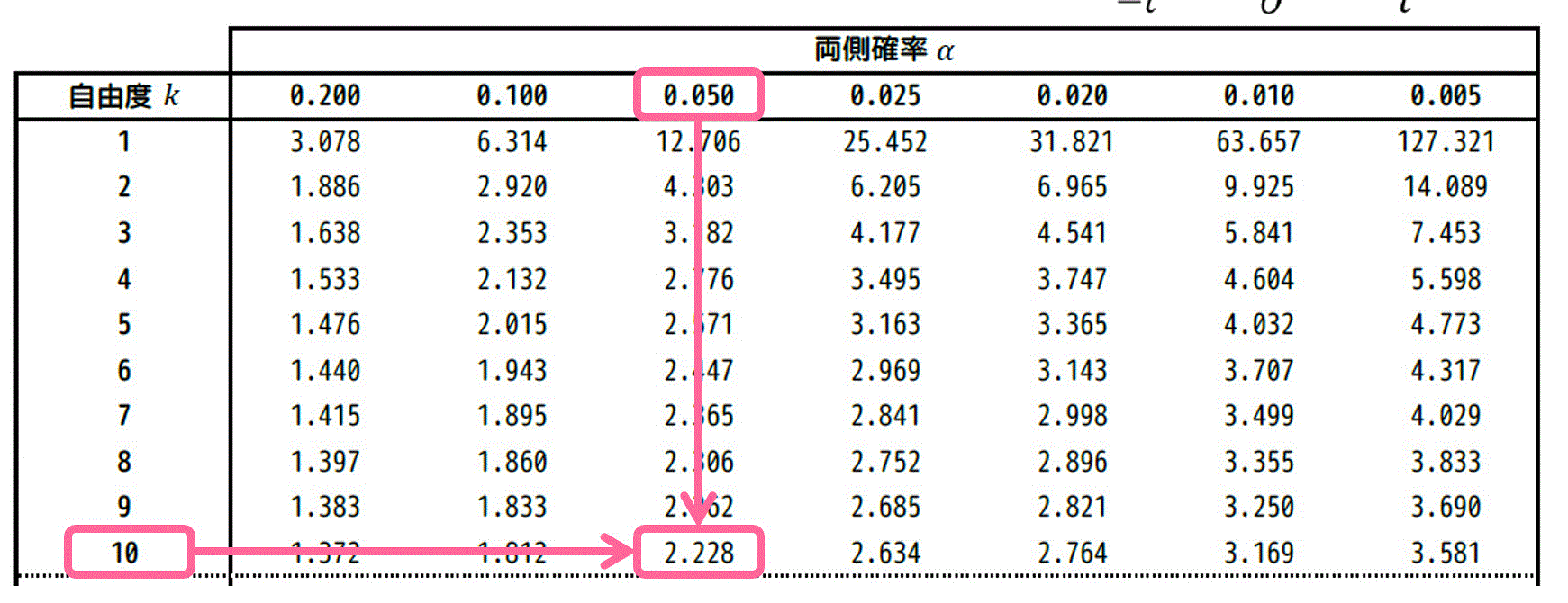
結果、2.228と読み取れます。そのため、\( t_0 = 2.228 \) ですね。
★ 片側t分布表から読み取る場合
\( \alpha = 0.025 \)、自由度 \( k = 10 \) に対応する \( t \) の値は、片側t分布表のつぎの箇所を読み取ればOKです。
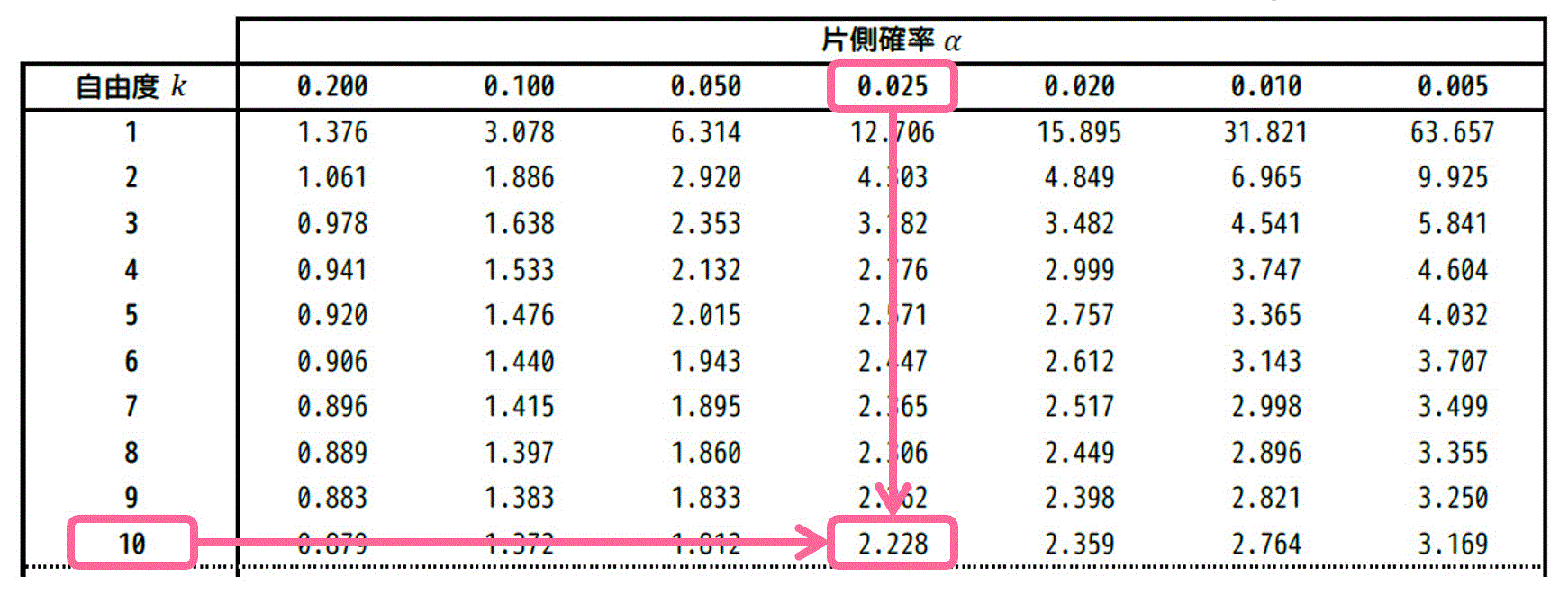
結果、2.228と読み取れます。そのため、\( t_0 = 2.228 \) ですね。
あとは、母平均の区間推定式\[
\overline{X}_1 - \frac{ t_0 \sqrt{ V_E } }{ \sqrt{n_1} } \leqq \mu_1 \leqq \overline{X}_1 + \frac{ t_0 \sqrt{ V_E} }{ \sqrt{n_1} }
\]に代入すれば結果が求められます。
代入すると、\[
18 - \frac{ 2.228 \cdot \sqrt{ 14.6 } }{ \sqrt{4} } \leqq \mu_1 \leqq 18 + \frac{ 2.228 \cdot \sqrt{ 14.6 } }{ \sqrt{4} }
\]\[
18 - 2.228 \cdot \sqrt{ \frac{14.6}{4} } \leqq \mu_1 \leqq 18 + 2.228 \cdot \sqrt{ \frac{14.6}{4} }
\]\[
13.743 \leqq \mu_1 \leqq 22.257
\]となります。(ルートの計算は電卓を使いましょう。)
よって、1組の母平均 \( \mu_1 \) 信頼区間は \( 13.74 \leqq \mu_1 \leqq 22.26 \) となります。
[ii] 2組の母平均 \( \mu_2 \)
1組の標本に対する標本平均は、\( \overline{X}_2 = 11 \)、標本サイズは \( n_2 = 5 \) ですね。
信頼度95%、自由度10に対応する値 \( t_0 \) は、[i]の計算時に \( t_0 = 2.228 \) と求めているので、この値を母平均の区間推定式\[
\overline{X}_2 - \frac{ t_0 \sqrt{ V_E } }{ \sqrt{n_2} } \leqq \mu_2 \leqq \overline{X}_2 + \frac{ t_0 \sqrt{ V_E} }{ \sqrt{n_2} }
\]に代入すれば結果が求められます。
代入すると、\[
11 - \frac{ 2.228 \cdot \sqrt{ 14.6 } }{ \sqrt{5} } \leqq \mu_2 \leqq 11 + \frac{ 2.228 \cdot \sqrt{ 14.6 } }{ \sqrt{5} }
\]\[
11 - 2.228 \cdot \sqrt{ \frac{14.6}{5} } \leqq \mu_2 \leqq 11 + 2.228 \cdot \sqrt{ \frac{14.6}{5} }
\]\[
7.193 \leqq \mu_2 \leqq 14.807
\]となります。
よって、2組の母平均 \( \mu_2 \) 信頼区間は \( 7.19 \leqq \mu_2 \leqq 14.81 \) となります。
[iii] 3組の母平均 \( \mu_3 \)
3組の標本に対する標本平均は、\( \overline{X}_3 = 17 \)、標本サイズは \( n_3 = 4 \) ですね。
信頼度95%、自由度10に対応する値 \( t_0 \) は、[i]の計算時に \( t_0 = 2.228 \) と求めているので、この値を母平均の区間推定式\[
\overline{X}_3 - \frac{ t_0 \sqrt{ V_E } }{ \sqrt{n}_3 } \leqq \mu \leqq \overline{X}_3 + \frac{ t_0 \sqrt{ V_E} }{ \sqrt{n}_3 }
\]に代入すればOKです。
代入すると、\[
17 - \frac{ 2.228 \cdot \sqrt{ 14.6 } }{ \sqrt{4} } \leqq \mu \leqq 17 + \frac{ 2.228 \cdot \sqrt{ 14.6 } }{ \sqrt{4} }
\]\[
17 - 2.228 \cdot \sqrt{ \frac{14.6}{4} } \leqq \mu \leqq 17 + 2.228 \cdot \sqrt{ \frac{14.6}{4} }
\]\[
12.743 \leqq \mu_3 \leqq 21.257
\]となります。
よって、3組の母平均 \( \mu_3 \) 信頼区間は \( 12.74 \leqq \mu_3 \leqq 21.26 \) となります。
5. 練習問題にチャレンジ!
桃山工場では、4つの異なる生産ラインでお菓子を製造している。ある日、それぞれの生産ラインで製造されたお菓子の重量に差があるかどうかを調べるために、生産された製品の中からいくつかを取り出して その重量を測定した。その結果を、以下の表1に記す。
表1. 各生産ラインごとの重量測定結果
| グループ(群) | 標本サイズ | 標本平均[g] |
|---|---|---|
| ライン1 | 9 | 105 |
| ライン2 | 5 | 91 |
| ライン3 | 4 | 94 |
| ライン4 | 6 | 98 |
この結果を用いて一元配置分散分析を行ったところ、以下の結果を得た。しかし、結果の一部が虫食いになって値が分からなくなってしまった。
表2. 分散分析の結果
| 要因 | 平方和 | 自由度 | 平方平均 | \( F \) 値 |
|---|---|---|---|---|
| 水準間 [郡間] | 36 | |||
| 残差 [郡内] | − | |||
| 全体 | 116 | − | − |
つぎの(1)~(5)の問いに答えなさい。
(1) 帰無仮説と対立仮説を述べなさい。
(2) 全体の標本平均を \( \overline{X} \)、ライン \( i \) の標本サイズ、標本平均をそれぞれ \( n_i \), \( \overline{X}_i \)、ライン \( i \) の \( j \) 番目のデータを \( X_{ij} \) とする。このとき、水準間(群間)平方和 \( S_A \)、残差(群内)平方和 \( S_E \) を求める式をそれぞれ立式しなさい。
(3) 虫食いになった一元配置分散分析表を埋めなさい。ただし、" - " の部分は埋めなくてよい。
(4) 有意水準5%で検定を行い、結論を示しなさい。
(5) 表1, 表2から、ライン1とライン3で生産された製品の重量を、信頼度95%で求めなさい。
※ 必要であれば、こちらからF分布表をダウンロードできます。
※ 必要であれば、こちらから片側t分布表をダウンロードできます。
※ 必要であれば、こちらから両側t分布表をダウンロードできます。
6. 練習問題の答え
(1) 帰無仮説と対立仮説の設定
帰無仮説 \( H_0 \): 仮説検定をするための「仮定」
ライン1~ライン4で生産されたお菓子の重量の母平均 \( \mu_1 \), \( \mu_2 \), \( \mu_3 \), \( \mu_4 \) はすべて等しい。つまり \( \mu_1 = \mu_2 = \mu_3 = \mu_4 \)。
(各グループの母平均に有意な差はない。)
対立仮説 \( H_1 \): 仮説検定を否定することで示したいもの
ライン1~ライン4で生産されたお菓子の重量の母平均 \( \mu_1 \), \( \mu_2 \), \( \mu_3 \), \( \mu_4 \) のうち、少なくとも1つのグループの母平均が他と異なる。つまり \( \mu_1 = \mu_2 = \mu_3 = \mu_4 \) とは言えない。
(少なくとも1つのグループの母平均が他のグループと有意に異なる。)
(2) 水準間平方和 \( S_A \)・残差平均和 \( S_E \) の立式
水準間平方和(群内平方和) \( S_A \)
各郡ごとに、ある群 \( i \) に着目したときの、郡 \( i \) 内の標本平均 \( \overline{X}_i \) と、データ全体の標本平均 \( \overline{X} \) のずれを2乗したものを、各群毎のデータサイズ \( n_i \) で掛けた(重み付けした)ものを、すべて足したもの。\[
S_A = \textcolor{teal}{ \sum^{k}_{i = 1} } \textcolor{purple}{n_i} \left( \textcolor{red}{ \overline{X}_i - \overline{X} } \right)^{\textcolor{blue}{2}}
\]
(残差平方和 (郡内平方和) \( S_E \)
全データに対して、ある郡 \( i \) に着目したときの、データ値 \( X_{ij} \) と郡 \( i \) 内の標本平均 \( \overline{X}_i \) のずれを2乗したものを計算し、すべて足したもの。\[
S_E = \textcolor{teal}{ \sum^{k}_{i = 1} \sum^{ n_i }_{ j = 1 } } \left( \textcolor{red}{ X_{ij} - \overline{X}_i } \right)^{\textcolor{blue}{2}}
\]
(3) 一元配置分散分析表の穴埋め
[i] 残差平方和の穴埋め
「全体平方和 = 水準間平方和 + 残差平方和」の公式を使います。つまり、
全体平方和 (116) = 水準間平方和 (36) + 残差平方和 (?)
に当てはまる ? の値を入れればOKです。116 - 36 = 80 で計算できます。
| 要因 | 平方和 | 自由度 | 平方平均 | \( F \) 値 |
|---|---|---|---|---|
| 水準間 [郡間] | 36 | |||
| 残差 [郡内] | 80 | − | ||
| 全体 | 116 | − | − |
[ii] 自由度の穴埋め
全データ数 \( N \)、群数 \( k \) を用いて自由度は以下のように穴埋めが出来ます。
| 要因 | 平方和 | 自由度 | 平方平均 | \( F \) 値 |
|---|---|---|---|---|
| 水準間 [郡間] | 36 | \( k - 1 \) | ||
| 残差 [郡内] | 80 | \( N - k \) | − | |
| 全体 | 116 | \( N - 1 \) | − | − |
今回は、全データ数 \( N \) は、ライン1の標本サイズ9、ライン2の標本サイズ5、ライン3の標本サイズ4、ライン4の標本サイズ6より、\[\begin{align*}
N & = 9+ 5 + 4 + 6
\\ & = 24
\end{align*}\]と求められます。
また、群数(グループ数)は4なので、\( k = 4 \) です。
よって、水準間に対する自由度は \( k-1 = 3 \)、残差に対する自由度は \( N-k = 20 \)、全体の自由度は \( N-1 = 23 \) と求められます。
| 要因 | 平方和 | 自由度 | 平方平均 | \( F \) 値 |
|---|---|---|---|---|
| 水準間 [郡間] | 36 | 3 | ||
| 残差 [郡内] | 80 | 20 | − | |
| 全体 | 116 | 23 | − | − |
[iii] 平方平均の穴埋め
平方平均は、平方和÷自由度で計算ができます。
今回の場合、水準間平方平均 \( V_A \) は、\[\begin{align*}
V_A & = \frac{ S_A }{ k - 1}
\\ & = \frac{36}{3}
\\ & = 12
\end{align*}\]と計算できます。
同様に、残差平方平均 \( V_E \) は\[\begin{align*}
V_A & = \frac{ V_A }{ N - k }
\\ & = \frac{80}{20}
\\ & = 4
\end{align*}\]と計算できます。
| 要因 | 平方和 | 自由度 | 平方平均 | \( F \) 値 |
|---|---|---|---|---|
| 水準間 [郡間] | 36 | 3 | 12 | |
| 残差 [郡内] | 80 | 20 | 4 | − |
| 全体 | 116 | 23 | − | − |
[iv] F値の穴埋め
F値は、水準間平方平均÷残差平方平均で計算ができます。
今回の場合、F値 \( F \) \[\begin{align*}
F & = \frac{ V_A }{ V_E }
\\ & = \frac{12}{4}
\\ & = 3
\end{align*}\]となります。
| 要因 | 平方和 | 自由度 | 平方平均 | \( F \) 値 |
|---|---|---|---|---|
| 水準間 [郡間] | 36 | 3 | 12 | 3 |
| 残差 [郡内] | 80 | 20 | 4 | − |
| 全体 | 116 | 23 | − | − |
(4) 検定の実施
[i] F分布表の読み取り
今回は、水準間自由度が3、残差自由度が20ですね。
なので、有意水準 \( \alpha = 0.05 \) [5%]、自由度 (3,20) に相当するF値を、F分布表から読み取ります。
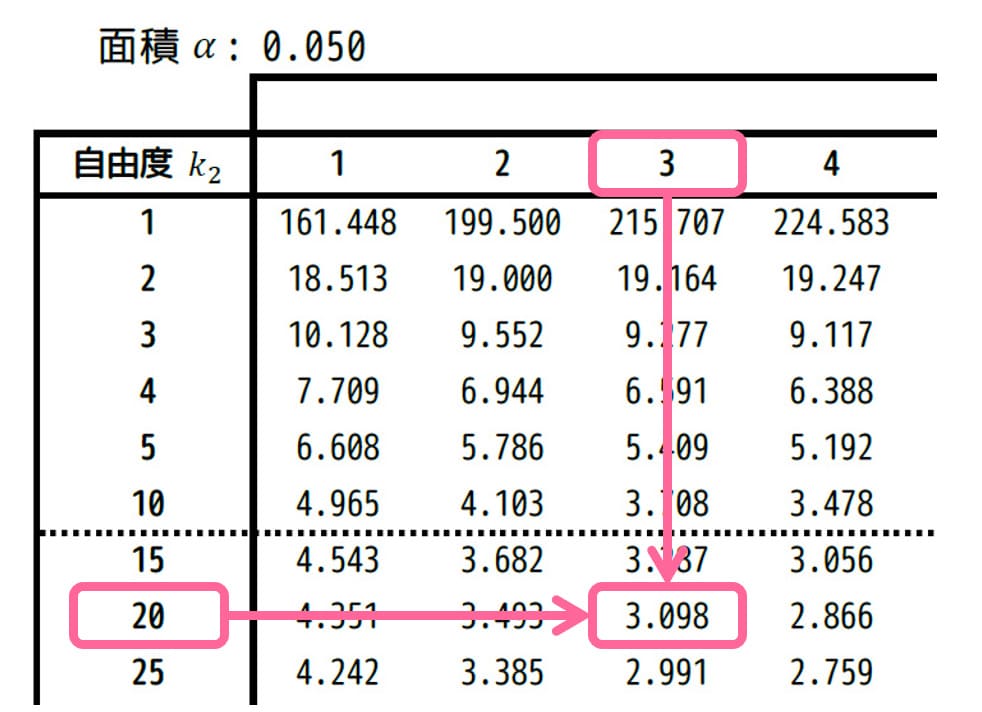
すると、3.098と読み取れます。\( F_0 = 3.098 \) とおきましょう。
[ii] 採択/棄却の判定
一元配置分散分析表の穴埋め時に求めたF値\[\begin{align*}
F & = \frac{ V_A }{ V_E }
\\ & = 3
\end{align*}\]および、(4)[i]でF分布表から得た臨界値 \( F_0 = 3.098 \) から結論を出します。
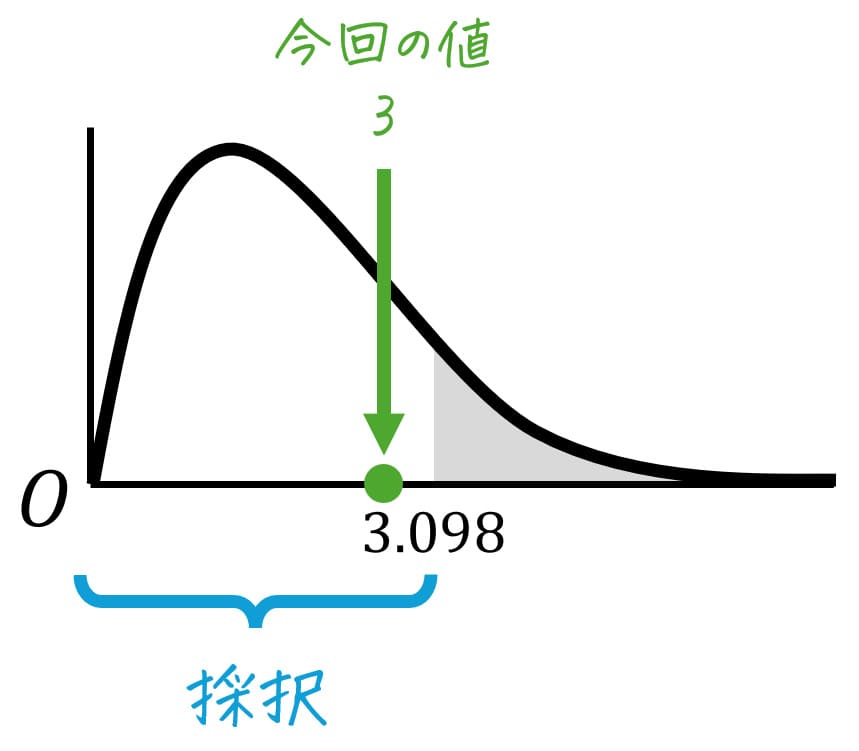
今回は、\( F = 3 \)、F分布表から得た臨界値 \( F_0 = 3.098 \) より、\[
F = 3 \leqq 3.098 = F_0
\]となります。
よって、仮説は採択され、ライン1~ライン4で生産されたお菓子の重量の母平均 \( \mu_1 \), \( \mu_2 \), \( \mu_3 \), \( \mu_4 \) のうち、少なくとも1つのグループの母平均が他と異なるとは言えません。(少なくとも1つのグループの母平均が他のグループと有意に異なるとは言えない。)
(5) 残差(群内)平方平均を用いた母平均の区間推定
(3)で求めた残差平方平均 \( V_E = 4 \) を用いて、母平均の区間推定を実施します。
[i] ライン1で生産された製品の重量の母平均 \( \mu \)
ライン1の群の標本サイズは \( n_1 = 9 \)、標本平均は \( \overline{X}_1 = 105 \) です。
また、残差の自由度20、信頼度95%に対応する \( t_0 \) は、t分布表から \( t_0 = 2.086 \) と読み取れます。
★ 両側t分布表から読み取る場合
\( \alpha = 0.050 \)、自由度 \( k = 20 \) に対応する \( t \) の値は、両側t分布表のつぎの箇所を読み取ればOKです。
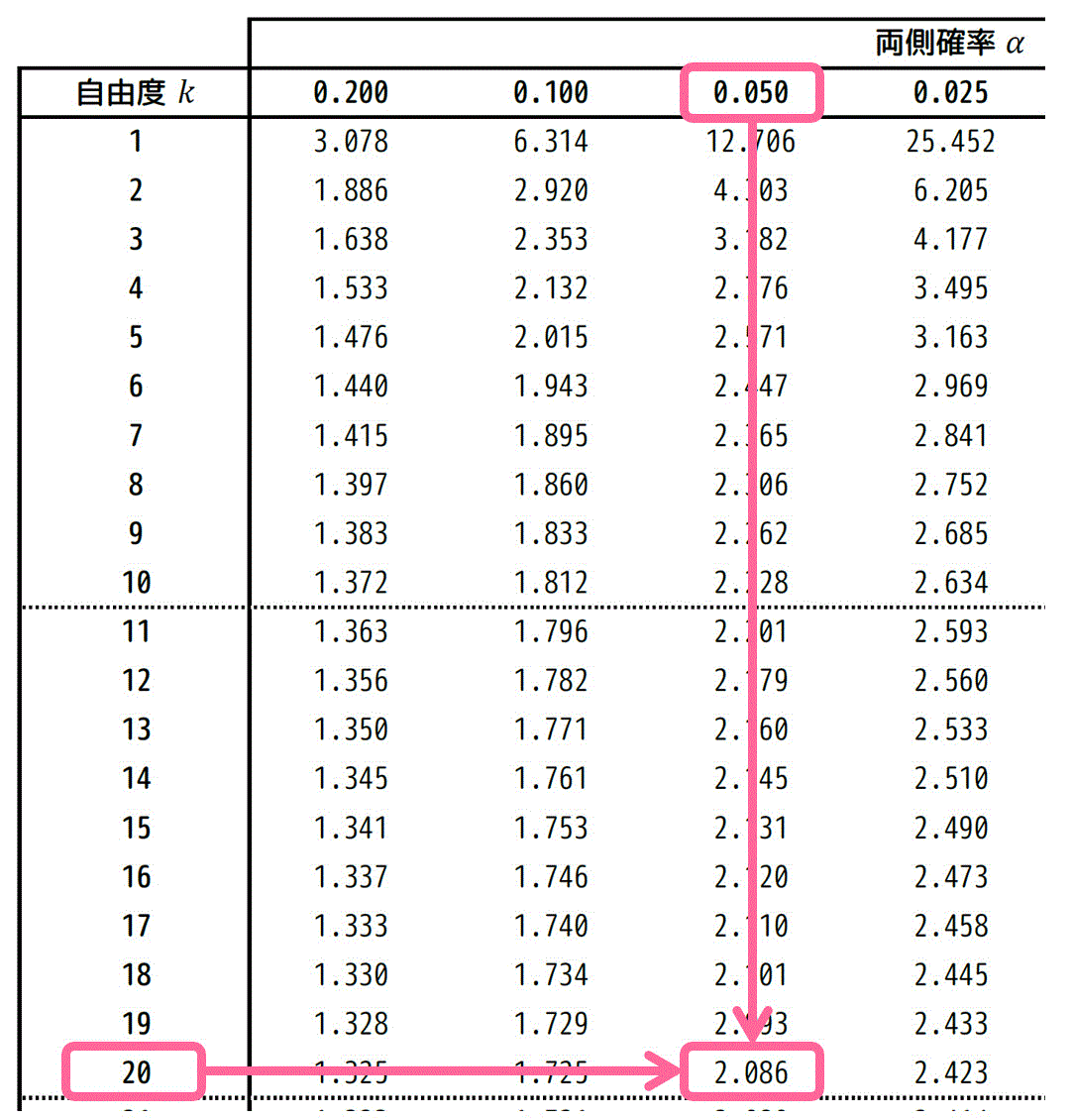
★ 片側t分布表から読み取る場合
\( \alpha = 0.025 \)、自由度 \( k = 20 \) に対応する \( t \) の値は、片側t分布表のつぎの箇所を読み取ればOKです。
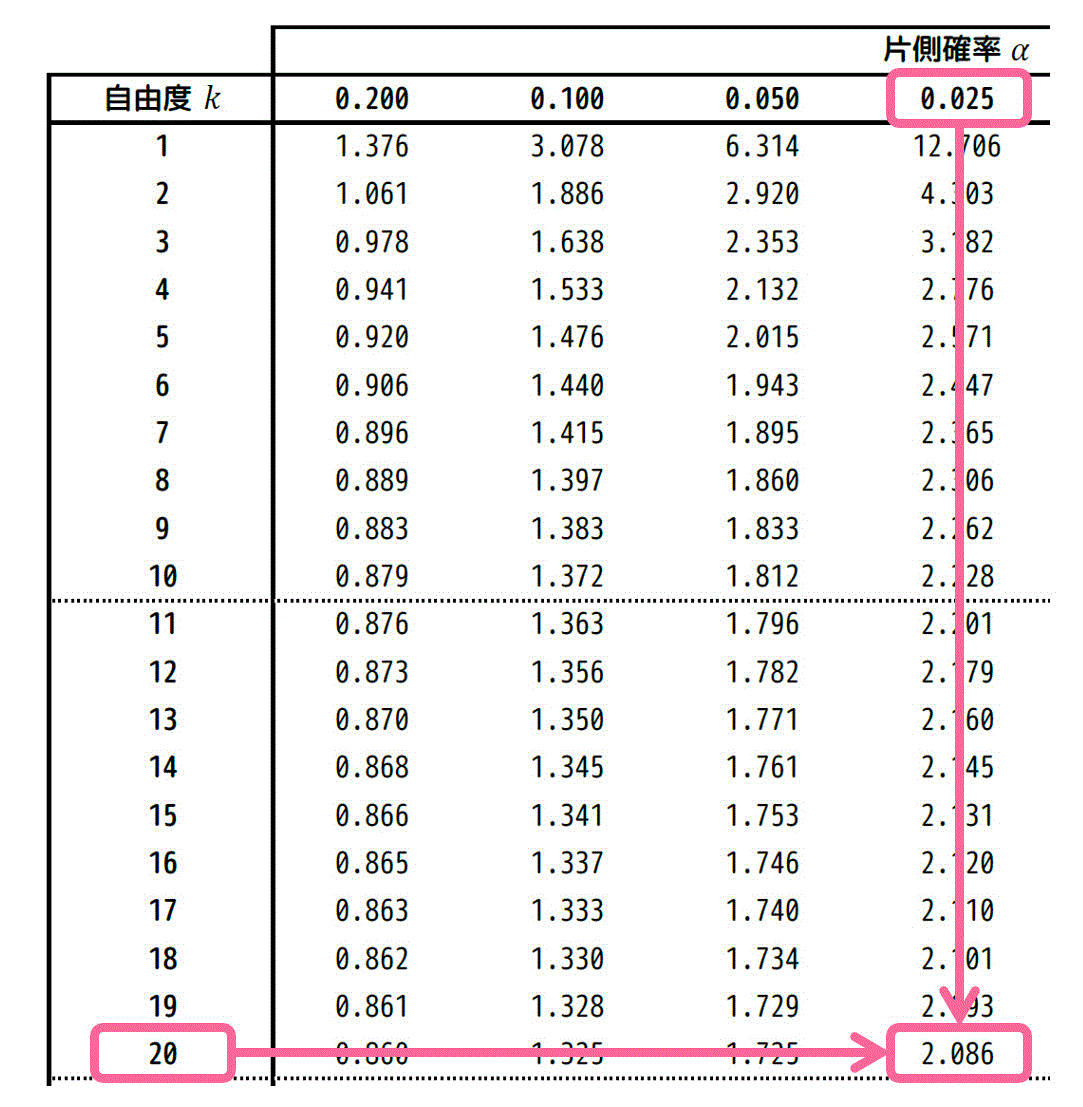
あとは、値を母平均の区間推定式\[
\overline{X}_1 - \frac{ t_0 \sqrt{ V_E } }{ \sqrt{n_1} } \leqq \mu_1 \leqq \overline{X}_2 + \frac{ t_0 \sqrt{ V_E} }{ \sqrt{n_1} }
\]に代入すれば結果が求められます。
代入すると、\[
105 - \frac{ 2.086 \cdot \sqrt{ 4 } }{ \sqrt{9} } \leqq \mu_1 \leqq 105 + \frac{ 2.086 \cdot \sqrt{ 4 } }{ \sqrt{9} }
\]\[
105 - 2.086 \cdot \frac{2}{3} \leqq \mu_1 \leqq 105 + 2.086 \cdot \frac{2}{3}
\]\[
103.609 \leqq \mu_1 \leqq 106.391
\]となります。
よって、ライン1で生産された製品の重量[g]の母平均 \( \mu_1 \) 信頼区間は \( 103.61 \leqq \mu_1 \leqq 106.39 \) となります。
[ii] ライン3で生産された製品の重量の母平均 \( \mu \)
ライン3の群の標本サイズは \( n_3 = 4 \)、標本平均は \( \overline{X}_3 = 94 \) です。
また、残差の自由度20、信頼度95%に対応する \( t_0 \) は、[i] ですでに \( t_0 = 2.086 \) と読み取っています。
あとは、値を母平均の区間推定式\[
\overline{X}_3 - \frac{ t_0 \sqrt{ V_E } }{ \sqrt{n_3} } \leqq \mu_3 \leqq \overline{X}_2 + \frac{ t_0 \sqrt{ V_E } }{ \sqrt{n_3} }
\]に代入すれば結果が求められます。
代入すると、\[
94 - \frac{ 2.086 \cdot \sqrt{ 4 } }{ \sqrt{4} } \leqq \mu_3 \leqq 94 + \frac{ 2.086 \cdot \sqrt{ 4} }{ \sqrt{4} }
\]\[
94 - 2.086 \leqq \mu_3 \leqq 94 + 2.086
\]\[
91.914 \leqq \mu_3 \leqq 96.086
\]となります。
よって、ライン1で生産された製品の重量[g]の母平均 \( \mu_3 \) 信頼区間は \( 91.91 \leqq \mu_1 \leqq 96.09 \) となります。
注釈
| ↑1 | データの値に変化を与える要素のことを「要因」、要因の中でも分析対象のものを「因子」と区別して言葉を使い分けることもあります。本記事では、要因と因子は同じものだと思っていただけたらOKです。 |
|---|---|
| ↑2 | 対立仮説を、「出てくるすべてのグループ(郡)の母平均が異なること」としないように注意! 例えば、3つのグループの場合、帰無仮説に相当するすべての母平均 \( \mu_1 \), \( \mu_2 \), \( \mu_3 \) が等しい、つまり \( \mu_1 = \mu_2 = \mu_3 \) を仮定しましょう。この仮定を満たさない例には、\( \mu_1 = \mu_2 = 3 \), \( \mu_3 = 4 \) がありますが、この例はすべてのグループ(郡)の母平均が異なるとは言えませんよね。 |
| ↑3 | 実際に、全体の自由度 \( N - 1 \)、水準間に対する自由度 \( k-1 \)、残差に対する自由度 \( N - k \) を代入すれば、関係が成立することがわかると思います。 |
| ↑4 | 例えば、2つの飲食店の価格を比べることを考えてみましょう。飲食店Aは「3人で3,000円のお店」、飲食店Bは「10人で7,500円のお店」だとします。このとき、「飲食店Bは、飲食店Aの2.5倍の合計金額だから、飲食店Bのほうが高い」と比較するのはナンセンスですよね。 |
| ↑5 | 先ほどの飲食店の例の場合、1人あたりの価格に揃えて考えてみると、「1人あたり1,000円の飲食店A」と「1人あたり750円の飲食店B」となります。この状態で、「飲食店Bは、飲食店Aよりも25%安いから、飲食店Bのほうが安い」と正確に比較することができますよね。 |
| ↑6 | \( s^2 = V_E \) なので、\( s = \sqrt{ V_E } \) となる。 |
関連広告・スポンサードリンク