スポンサードリンク
こんにちは、ももやまです。
母集団の平均(母平均)を推定する際には正規分布を使う方法が有効です。
しかし、正規分布を使うためには母集団の情報として母分散が必要になってきます。
仮に母分散が分からなくても、標本内のデータ数(標本のサイズ)が大きければ標本の分散を代わりに使うことが出来ます。しかし、データ数が少ないときは母分散=標本分散の近似も使えません。
そこで、今回は標本サイズが小さく、なおかつ母分散も分からないときの母平均の推定に使えるt分布の紹介と、実際にt分布を使って母平均を推定する方法について学習していきましょう。
目次
スポンサードリンク
1. t分布で出来ること
t分布は、標本から計算できる平均、分散から母平均(母集団の平均)を推定、仮説検定するために使います。
母集団の情報なしに母平均を推定できるところが、正規分布との違いです[1]正規分布で母平均を推定する際には、母分散が必要になってきます。。
特に、標本のサイズが小さい(標本のデータ数が少ない)場合[2]標本のデータ数が多ければ、"母分散=標本分散" … Continue readingに母平均を推定、仮説検定したい場合にt分布は強みを発揮します。
不偏分散とは
標本の分散 \( S^2 \) を求める際には、\[
S^2 = \frac{1}{n-1} \sum^{n}_{k = 1} \left( x_k - \overline{X} \right)^2
\]のように、"各データ \( x_1 \), \( x_2 \), … の値と標本平均 \( \overline{X} \) の差を2乗したもの" の総和を、標本サイズで割って求めることができるのでした。
しかし、推定や仮説検定の際には、最後に割る数を \( n \) ではなく \( n - 1 \) とした分散\[\begin{align*}
s^2 = \frac{1}{\textcolor{red}{n-1}} \sum^{n}_{k = 1} \left( x_k - \overline{X} \right)^2
\end{align*}\]の方が、より母分散に比べて近い推定値になるため、推定や仮説検定ではこの分散 \( s^2 \) が基本的に使われます。
この分散 \( s^2 \) は不偏分散と呼ばれますが、参考書によっては不偏分散を標本分散と呼ぶものもあります。
標本から標本平均、不偏分散から母平均の推定、仮説検定をする際に、t分布を使うことが出来る。
特に、標本のサイズが小さく、母分散=不偏分散の近似が難しいために正規分布が使えないときにt分布は強みを発揮する。
表. t分布と正規分布の比較
| t分布 | 正規分布 | |
|---|---|---|
| 必要な情報 | 標本平均・不偏分散 | 標本平均・母分散 |
| 推定できるもの | 母平均 | 母平均 |
| 使い分け | 標本のデータ数が少ないときに使用 | 標本のデータ数が多いときに使用 |
スポンサードリンク
2. t分布を使って母平均が推定できる仕組み
ここでは、t分布を使って母平均が推定出来る仕組みを、見てきましょう。
(1) 正規分布での母平均推定
まずは、正規分布表を使って母平均を推定する流れを途中まで振り返りましょう。
まず、母平均 \( \mu \)、母分散 \( \sigma^2 \) の母集団から大きさ \( n \) の標本を選び、その標本平均を \( \overline{X} \) とします。
すると、中心極限定理により、標本平均 \( \overline{X} \) の期待値 \( E( \overline{X} ) \)、分散 \( V ( \overline{X} ) \) は\[
E( \overline{X} ) = \mu , \ \ \ V ( \overline{X} ) = \frac{ \sigma^2 }{ n }
\]となり、標本平均 \( \overline{X} \) は正規分布 \( N ( \mu , \frac{ \sigma^2 }{ n } ) \) に従います。
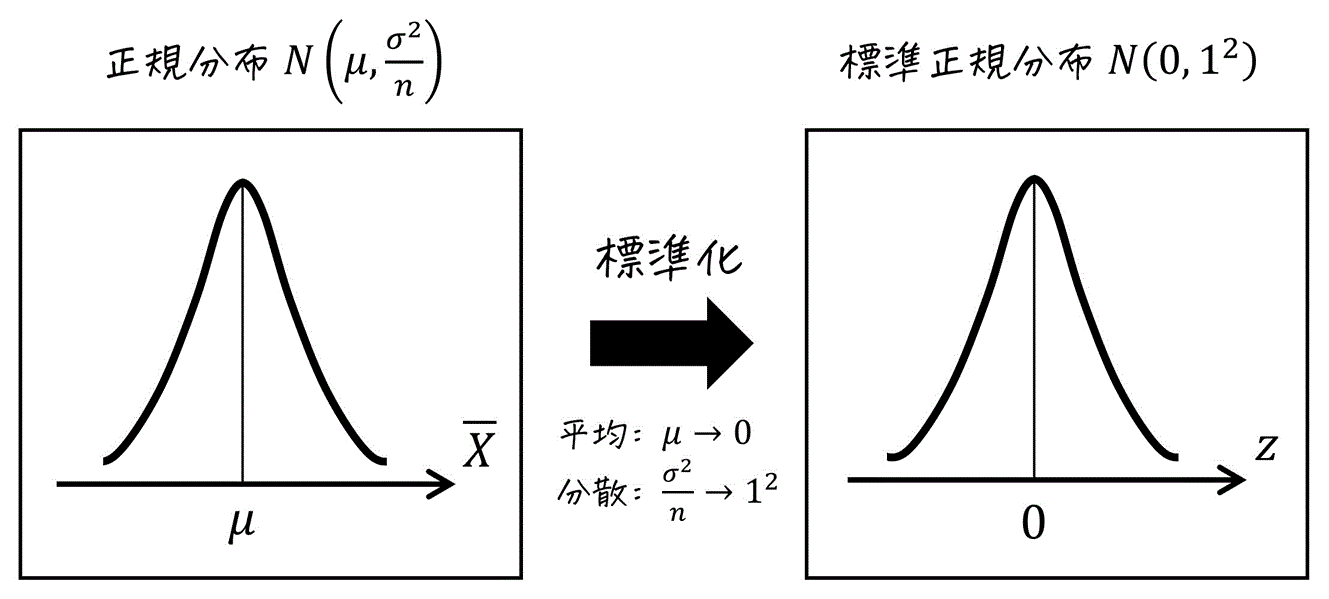
しかし、試験で与えられる正規分布表は、標準正規分布、つまり平均 \( 0 \)、分散 \( 1^2 \) の正規分布 \( N (0, 1^2) \) です。
そのため、標準正規分布表を使うためには、以下の図のような標準化を行い、標本平均 \( \overline{X} \) をzスコア\[
z = \frac{ \overline{X} - \mu }{ \frac{ \sigma }{ \sqrt{n} } }
\]の形にしてあげる必要があります。
(2) 正規分布からt分布へ
ここからは、母分散 \( \sigma^2 \) が分からないときの場合を考えていきましょう。
母分散 \( \sigma^2 \) が不明なので、先ほど正規分布の説明で出てきた変換式\[
\frac{ \overline{X} - \mu }{ \frac{ \sigma }{ \sqrt{n} } }
\]の母分散 \( \sigma^2 \) の代わりに、不偏分散 \( s^2 \) に置き換えた変換\[
t = \frac{ \overline{X} - \mu }{ \frac{ \textcolor{red}{s} }{ \sqrt{n} } }
\]を考えます。
しかし、不偏分散 \( s^2 \) に置き換えているため、上の式の \( t \) は標準正規分布には従いません。
そこで、不偏分散 \( s^2 \) を使って推定が出来るように生まれたのがt分布です。
(3) t分布と自由度
t分布には、正規分布には出てこなかった要素である、"自由度" があります。
[i] 自由度の概念
最初に、自由度の概念を理解しましょう。
まず、不偏分散 \( s^2 \) の推定精度は、標本のサイズ(標本のデータ数)に依存しますね。標本サイズが多ければ情報量は多くなるので、精度高く不偏分散が求まります。一方標本のサイズが小さければそれだけ情報量が少なくなるので、精度は低くなってしまいます。
そこで、標本の情報量を「何個分のデータの情報量を持っているか」で表したものを、統計の世界で自由度と呼びます。t分布を含む一部の分布では、標本の情報量の大小によって分布の形が変わるように作られています。
[ii] 何故自由度は標本サイズ-1なのか
つぎに、自由度がどのようになるか確認をしましょう。
単一の標本に対して、母平均を推定する場合は、自由度については以下のことを頭に入れておけばOKです。
単一の標本(母分散不明)について、母平均を推定する場合の自由度は次の通りである。
(自由度) = (標本のサイズ) - 1
ここで、「なぜ自由度は、標本のサイズから1減るの?」と気になる人も多いと思います。
そこで、ここから自由度が1減る仕組みについて説明いたします。
まず、不偏分散 \( s^2 \) は、\[\begin{align*}
s^2 = \frac{1}{n-1} \sum^{n}_{k = 1} \left( \textcolor{red}{x_k - \overline{X}} \right)^2
\end{align*}\]のように、各データ \( x_1 \), \( x_2 \), … の値と標本平均 \( \overline{X} \) の差を求めて、2乗してから "標本サイズ - 1" で割って求めるのでしたね。
ここで、不偏分散を求める際に出てくる「各データと標本平均の差」を求めるという部分に着目しましょう。
「各データと標本平均の差」を全てのデータごとに足していくと、その総和は必ず0になります。数式で書くと、\[\begin{align*}
\sum^{n}_{k = 1} \left( x_k - \overline{X} \right) & = \sum^{n}_{k = 1} x_k - \sum^{n}_{k = 1} \overline{X}
\\ & = n \overline{X} - n \overline{X}
\\ & = 0
\end{align*}\]となります。
例えば、データの値が 20, 40, 50, 70, 70(標本平均: 50)の場合の標本平均との差は次のように求められますね。
| \( x_1 \) | \( x_2 \) | \( x_3 \) | \( x_4 \) | \( x_5 \) | |
| 値 | 20 | 40 | 50 | 70 | 70 |
| 標本平均との差 | -30 | -10 | 0 | +20 | +20 |
実際にデータ毎の「各データと標本平均の差」の総和を計算すると、\[
-30 - 10 + 0 +20 + 20 = 0
\]となるので、0になります。
ここで、ある1つのデータが分からなくなったとします。
| \( x_1 \) | \( x_2 \) | \( x_3 \) | \( x_4 \) | \( x_5 \) | |
| 値 | 20 | ? | 50 | 70 | 70 |
| 標本平均との差 | -30 | ? | 0 | +20 | +20 |
この状況でも、標本平均が分かっていれば、標本平均から残り1つのデータを\[
50 \times 5 - 20 - 50 - 70 - 70 = 40
\]と推定することが出来ますね。
つまり、標本平均が分かっている状況では「元の標本の情報」と「元の標本1つデータを失った状態の情報」は全く同じ情報量と考えることができます。
言い換えると、標本サイズ \( n \) において、不偏分散 \( s^2 \) の計算時に使用している情報量は、実際の標本サイズ \( n \) ではなく、1つ少ない \( n-1 \) であると言えます。
そのため、 t分布を使う場合の自由度は、元の標本サイズ \( n \) から1減った \(n-1\) となるのです。
[iii] t分布のグラフ
ここでは、t分布のグラフの特徴を確認しておきましょう。
まず、t分布のグラフは正規分布と同じく \( t = 0 \) で左右対称になっています。
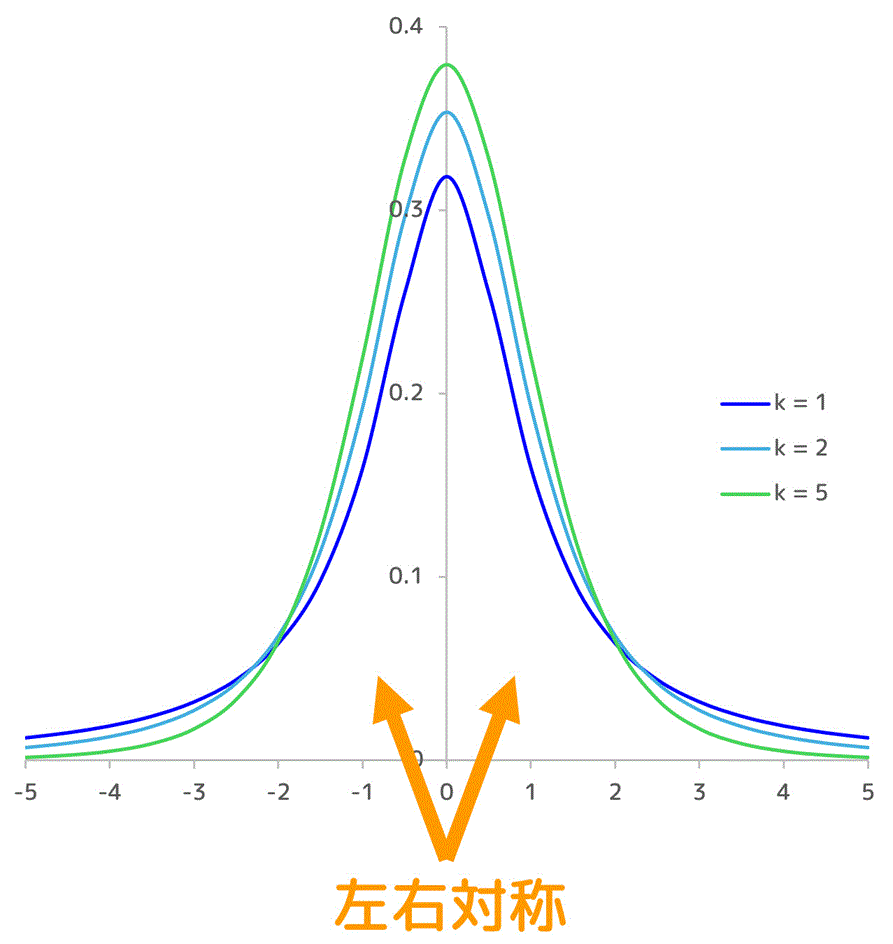
正規分布のグラフと比べてみましょう。
比べてみると、t分布の方が背が低いグラフになっていることが分かりますね。
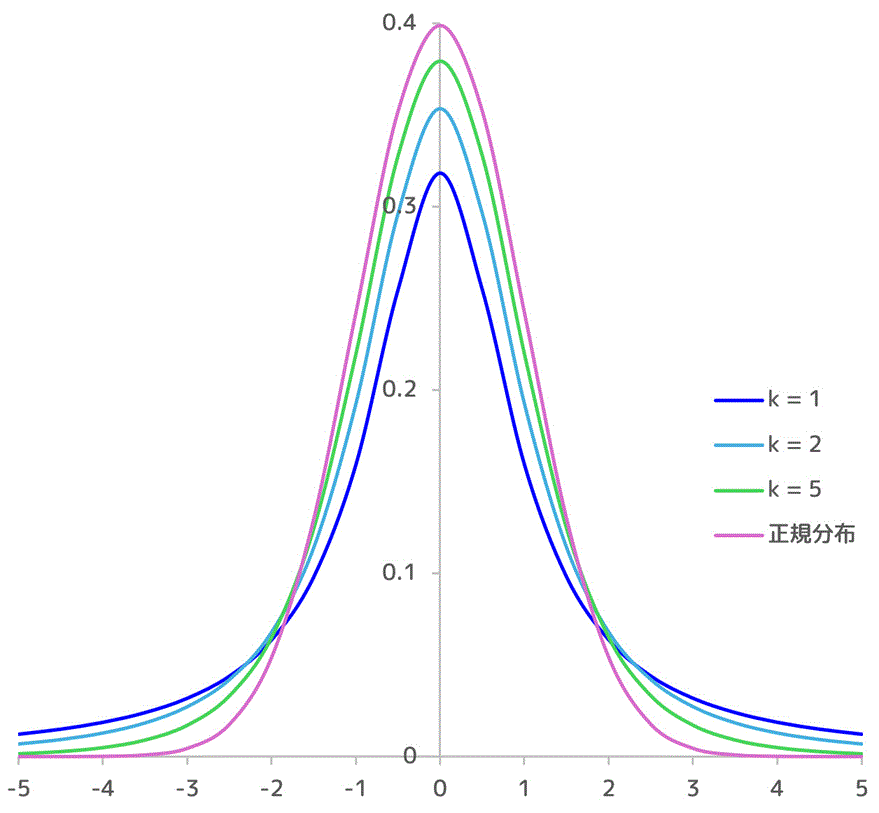
また、自由度 \( k \) を増やせば増やすほど、t分布のグラフは正規分布に近づきます。
自由度を30にすると、かなり正規分布に近づきますね[3]標本のサイズが30以上であれば、母分散を不偏分散と近似して正規分布をしても、精度よく母平均の推定が出来ると言われます。。
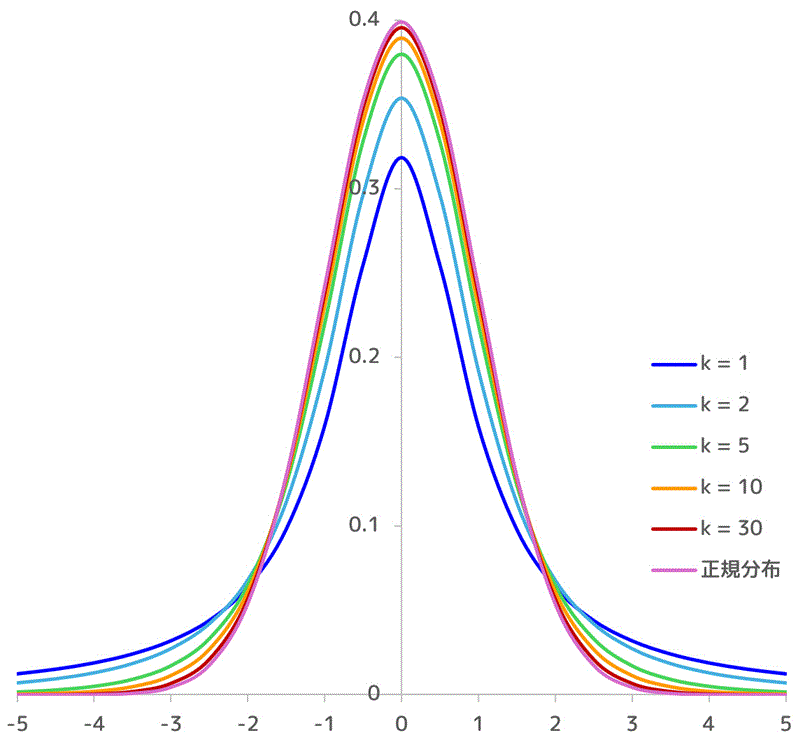
(4) t分布表の見方
t分布を使って母平均を推定する際には、t分布表と呼ばれる専用の表を使います。
試験の際にも必ずt分布表は与えられるため、t分布表の中身を暗記する必要がありません。t分布表が使えればOKです。
ただし、t分布表には両側t分布表と片側t分布表の2つがあり、それぞれで値の読み取り方が少しだけ違います。なので、両方のt分布表の使い方を確認しましょう。この記事では、両側t分布表と片側t分布表両方の使い方を紹介していきます。
例題、練習問題を解く際にお使いください。
※ 使っている参考書や授業に合わせて、両側t分布表、片側t分布表を選択することをおすすめします。なお、統計検定の場合、与えられる表は片側t分布表です。
[i] 両側t分布表の場合
両側t分布表は、グラフの右端部分と左端部分の面積の和 \( \alpha \) と自由度 \( k \) に対応する \( t \) の値が列挙されています。
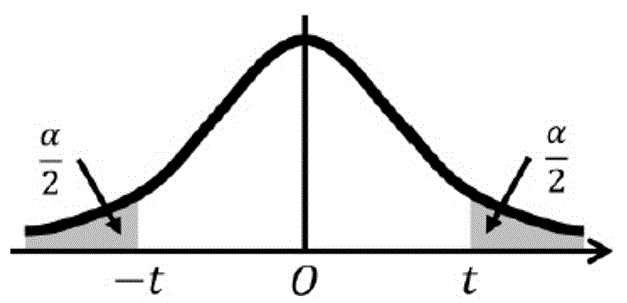
例えば、母分散が分からない標本サイズが10のデータを、信頼度95%で母平均を推定する場合を考えましょう。
信頼度95%で推定するためは、矢印部分の確率(白色部分の面積)が95% = 0.95 となるときの \( t \) の値を求める必要があります。
ここで、確率の和は1なので、灰色部分の面積 \( \alpha \) は 1 - 0.95 = 0.05 となります。
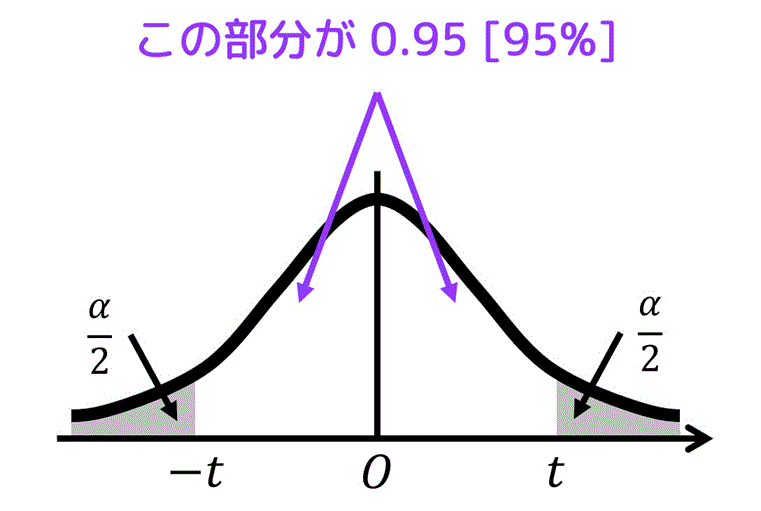
また、自由度は "標本サイズ - 1" より、10 - 1 = 9 となります。
あとは、\( \alpha = 0.05 \)、自由度 \( k = 9 \) に対応する \( t \) の値を両側t分布表から探せばOKです。
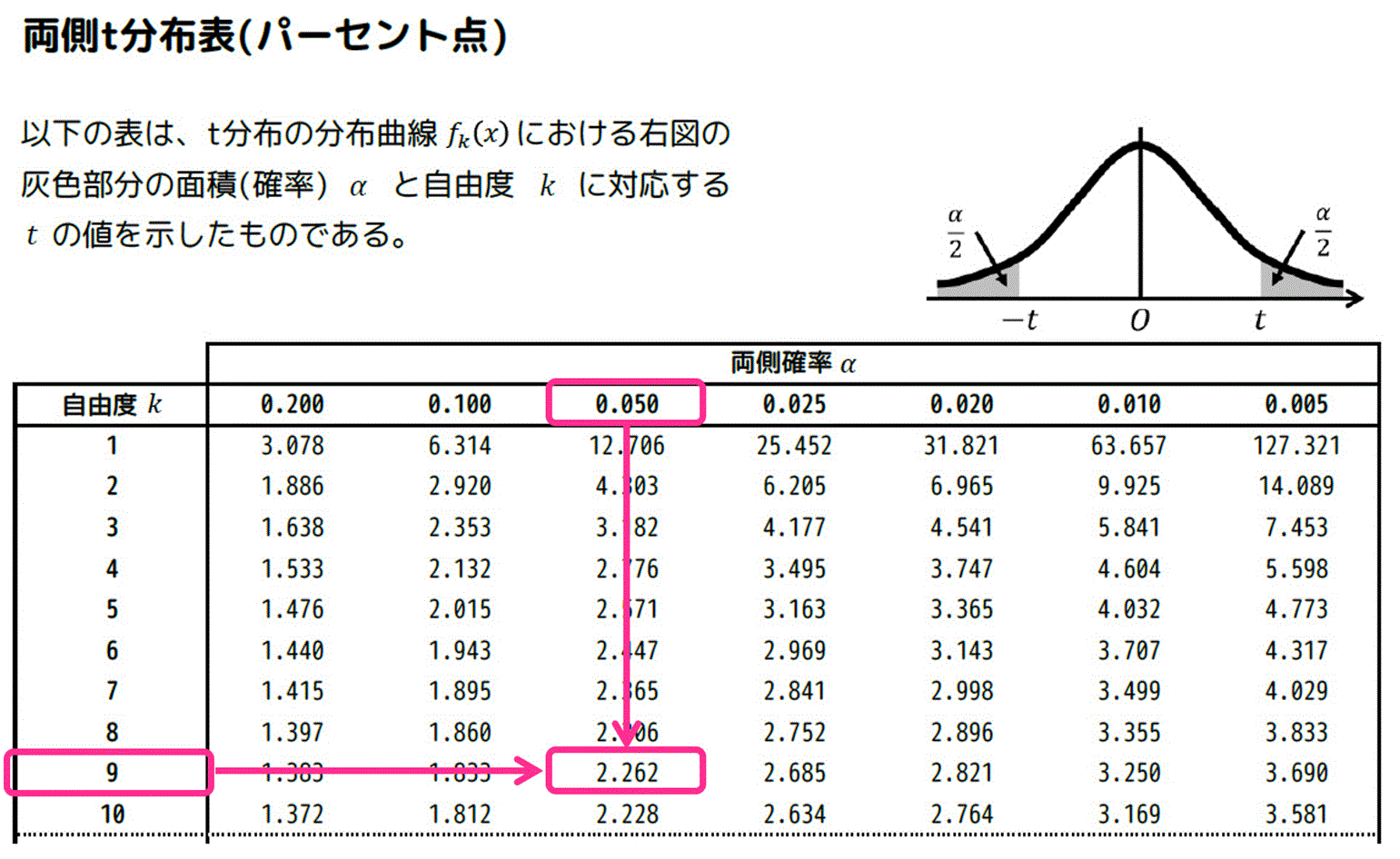
すると、対応する \( t \) の値は \( t = 2.262 \) と分かります。
[ii] 片側t分布表の場合
片側t分布表は、グラフの右端部分の面積の和 \( \alpha \) と自由度 \( k \) に対応する \( t \) の値が列挙されています。
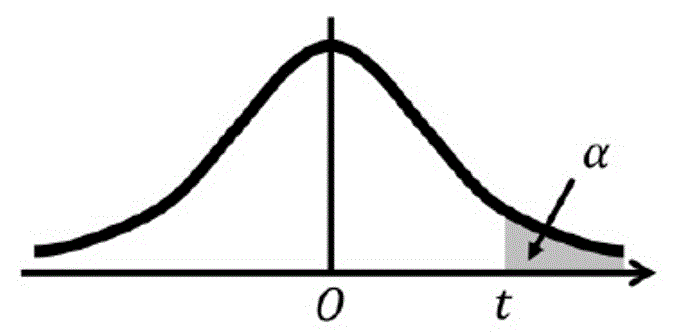
先ほどと同じく、母分散が分からない標本サイズが10のデータを、信頼度95%で母平均を推定する場合を考えましょう。
信頼度95%なので、矢印部分の確率(白色部分の面積)が95% = 0.95 となるときの \( t \) の値を片側t分布表から求めます。
まず、片側t分布表を使うために、青色部分の確率 \( \alpha \) を求めます。
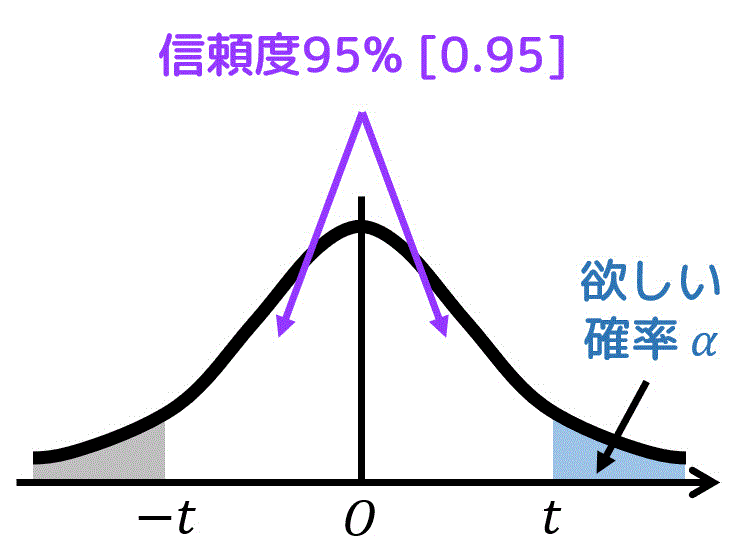
ここで、t分布のグラフは \( t = 0 \) で左右対称になっているため、各部分の面積(確率)をつぎのように求めることが出来ます。
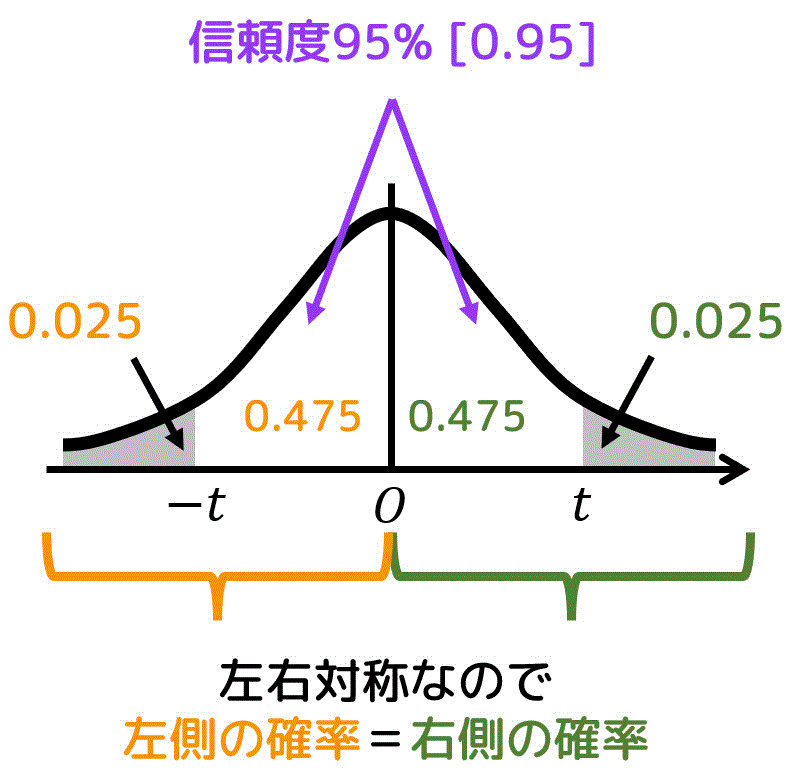
そのため、\( \alpha = 0.025 \) となります。
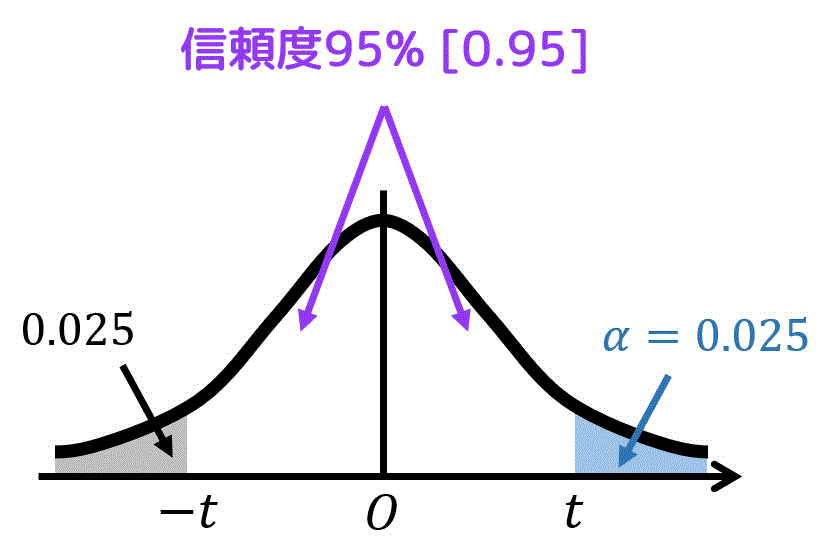
あとは、\( \alpha = 0.025 \)、自由度 \( k = 9 \) に対応する \( t \) の値を片側t分布表から探せばOKです。
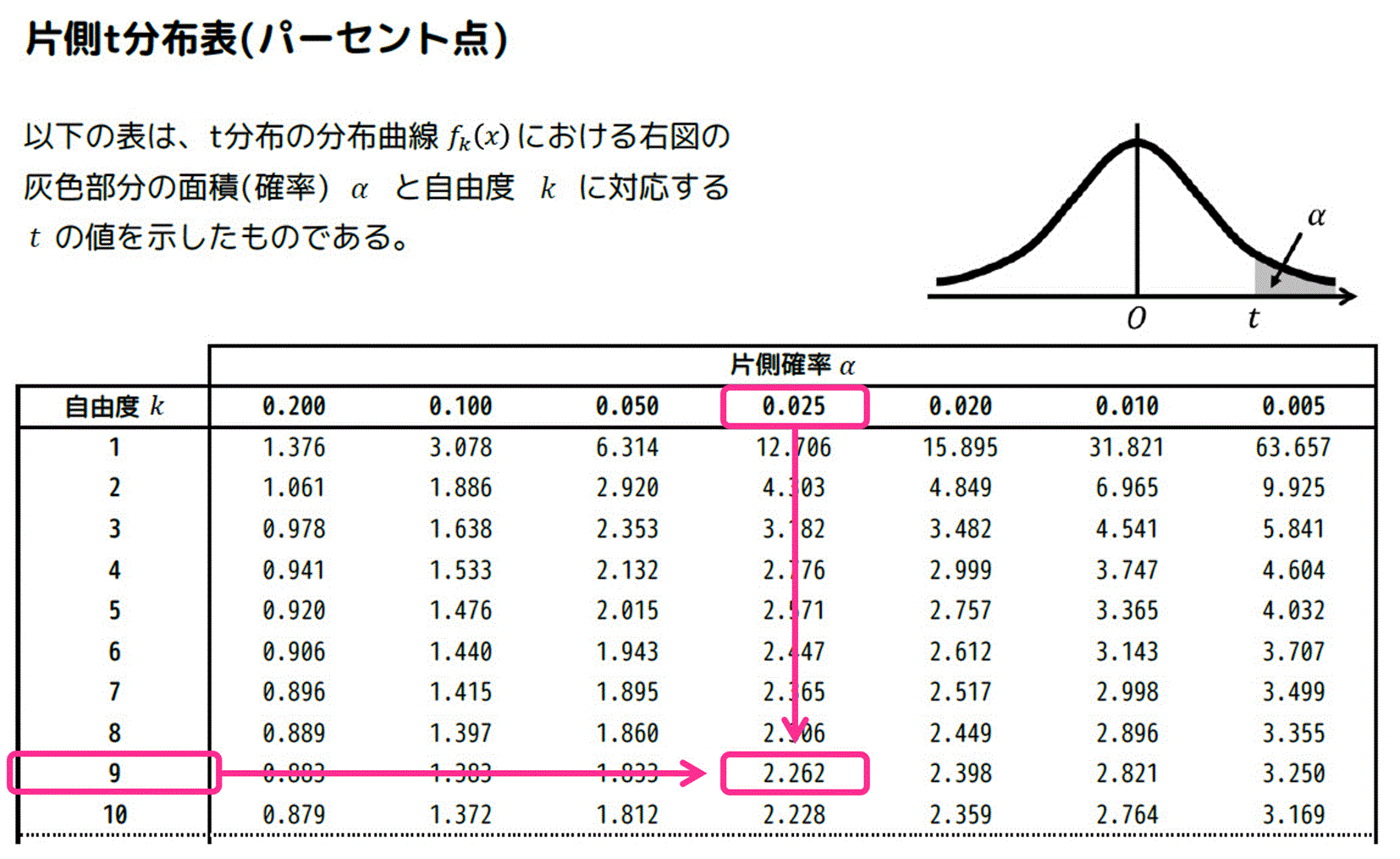
よって、対応する \( t \) の値は \( t = 2.262 \) と分かります。
スポンサードリンク
3. 例題で理解! t分布を用いた母平均の推定
ここからは、実際にt分布を用いて母平均を推定する方法を、例題を通じて学習していきましょう。
ある農家で取れたのニンジンの重さを調査をするために、ランダムに選んだ9個のニンジンの重さを測定ところ、重さの平均は200g、重さの不偏分散は64g2だった。この結果をもとに、ニンジンの重量の母平均を推定したい。つぎの(1), (2)の問いに答えなさい。
(1) 重さの区間推定を行うために必要な分布、および自由度として最も適切なものを、①〜④の中から1つ選びなさい。
① 正規分布
② 自由度8のt分布
③ 自由度9のt分布
④ 自由度10のt分布
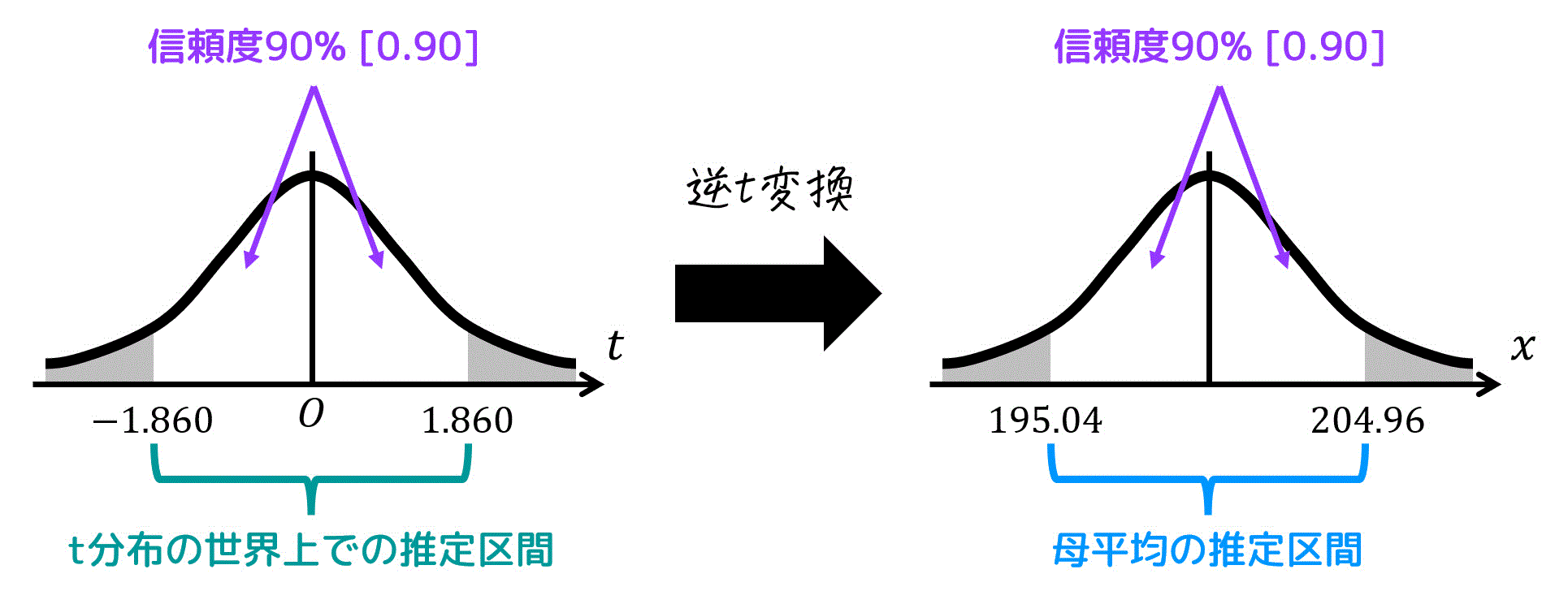
(2) 信頼度90%で母平均の区間推定を行い、結果を小数第2位まで求めなさい。
解説
(1)
まず、問題文からわかっていること、および求めたいものがなにかを確認します。
- 推定したいもの:母平均
- 母分散:不明
- 標本サイズ: 8
今回は、母分散が未知(かつ標本サイズが小さい)状態で、母平均を推定したいため、t分布を使用します。
つぎに、自由度を確認しましょう。
今回与えられた標本サイズ(データ数)は9のため、自由度は 9 - 1 = 8 となり、答えは②となります。
(2)
Step1. 推定に使う \( t \) の値を読み取る
まず、信頼度90%に相当する \( t \) の値をt分布表から読み取ります。
両側t分布表から読み取る場合
信頼度が90%なので、グラフの白色部分の面積が0.9となる。言い換えると、灰色部分 \( \alpha \)は0.1となる[4]確率(面積)の和が1、-t〜tの部分(信頼度部分)が0.9なので、残りの灰色部分の面積は 1 - 0.9 = 0.1。。
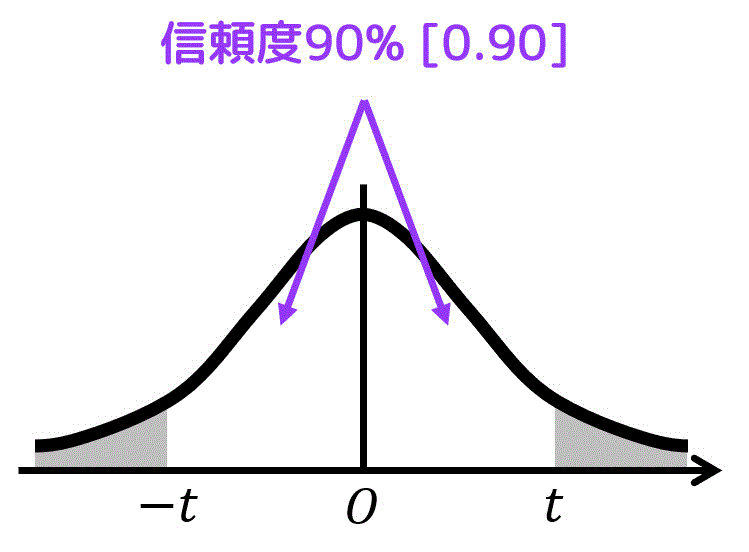
よって、\( \alpha = 0.1 \)、自由度 \( k = 8 \) のときの \( t \) の値を表から探せばOK。
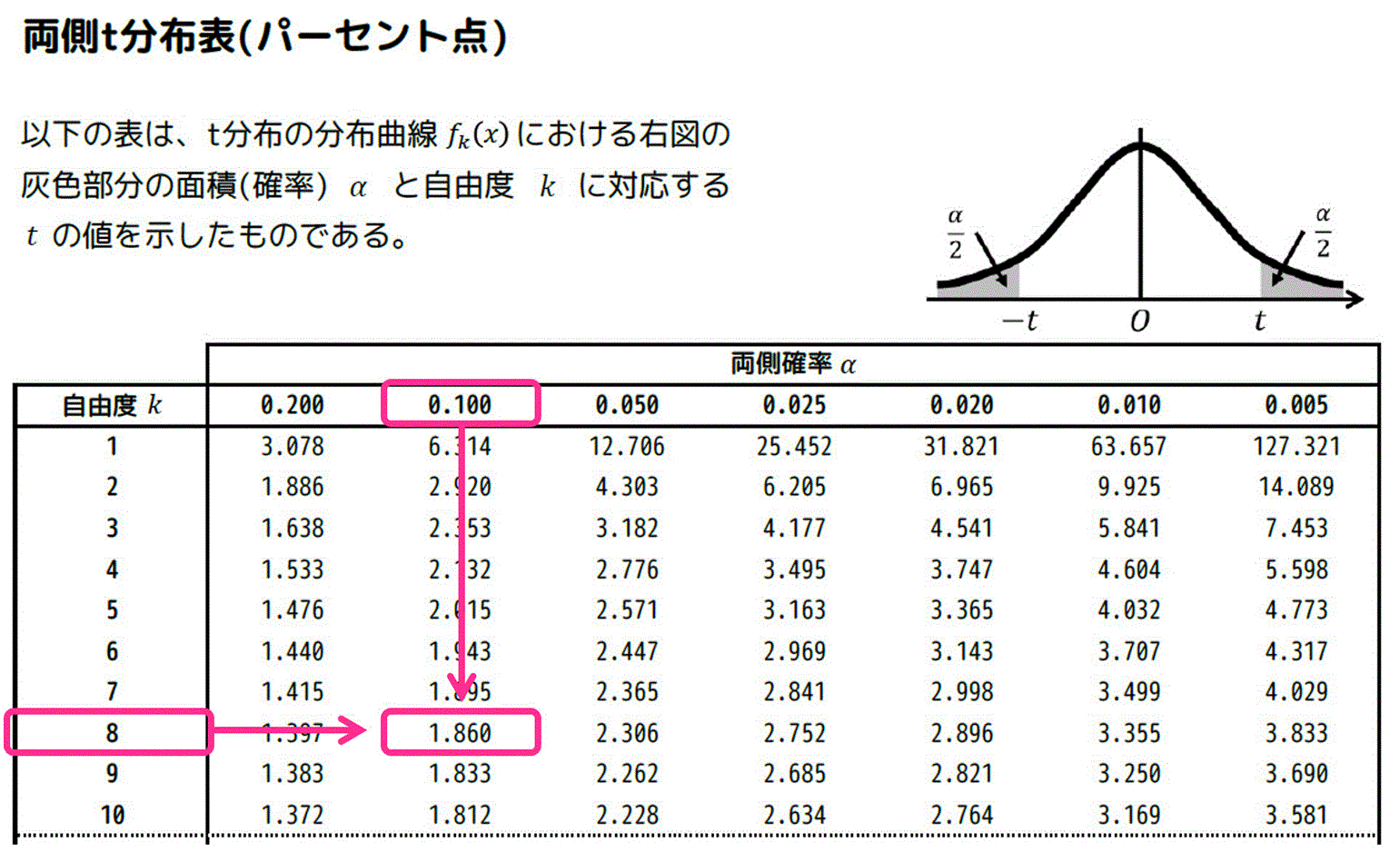
結果、\( t = 1.860 \) と読み取れる。
片側t分布表から読み取る場合
信頼度が90%なので、t分布の白色部分の面積が0.9となる。ここで、片側t分布で使う \( \alpha \) は下の図の青色部分の面積である。
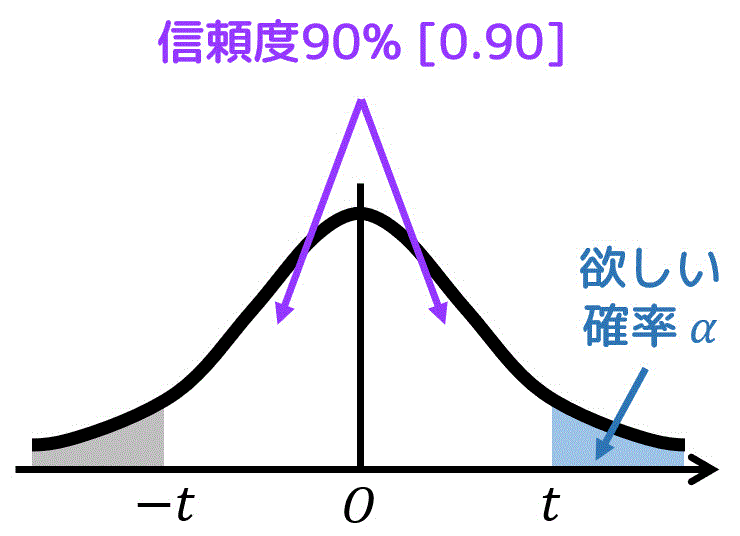
灰色部分の面積と青色部分の面積は等しいので、青色部分の面積 \( \alpha \) は、\[\begin{align*}
\alpha & = (1 - 0.1) \div 2 \\ & = 0.05
\end{align*}\]となる。
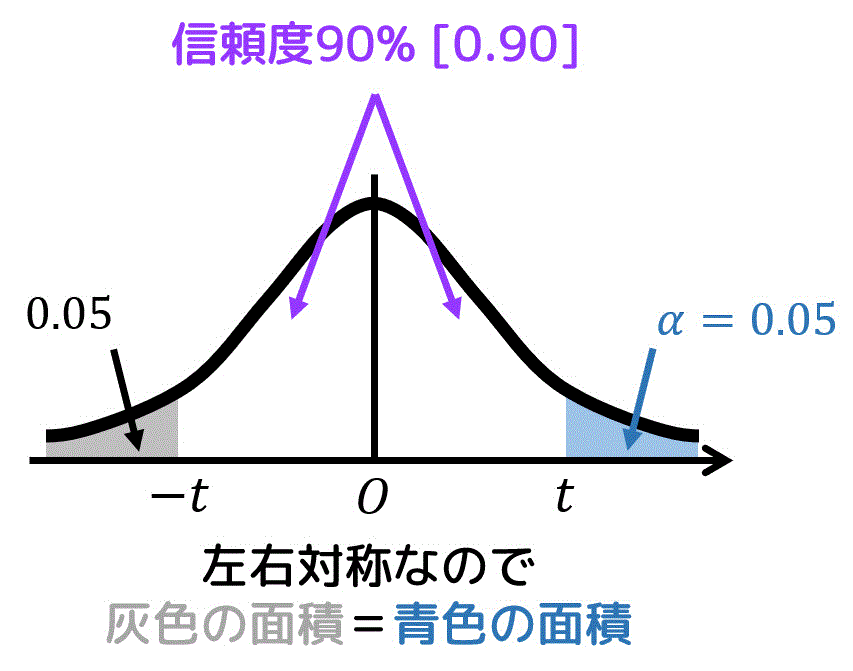
よって、\( \alpha = 0.05 \)、自由度 \( k = 8 \) のときの \( t \) の値を表から探せばOK。
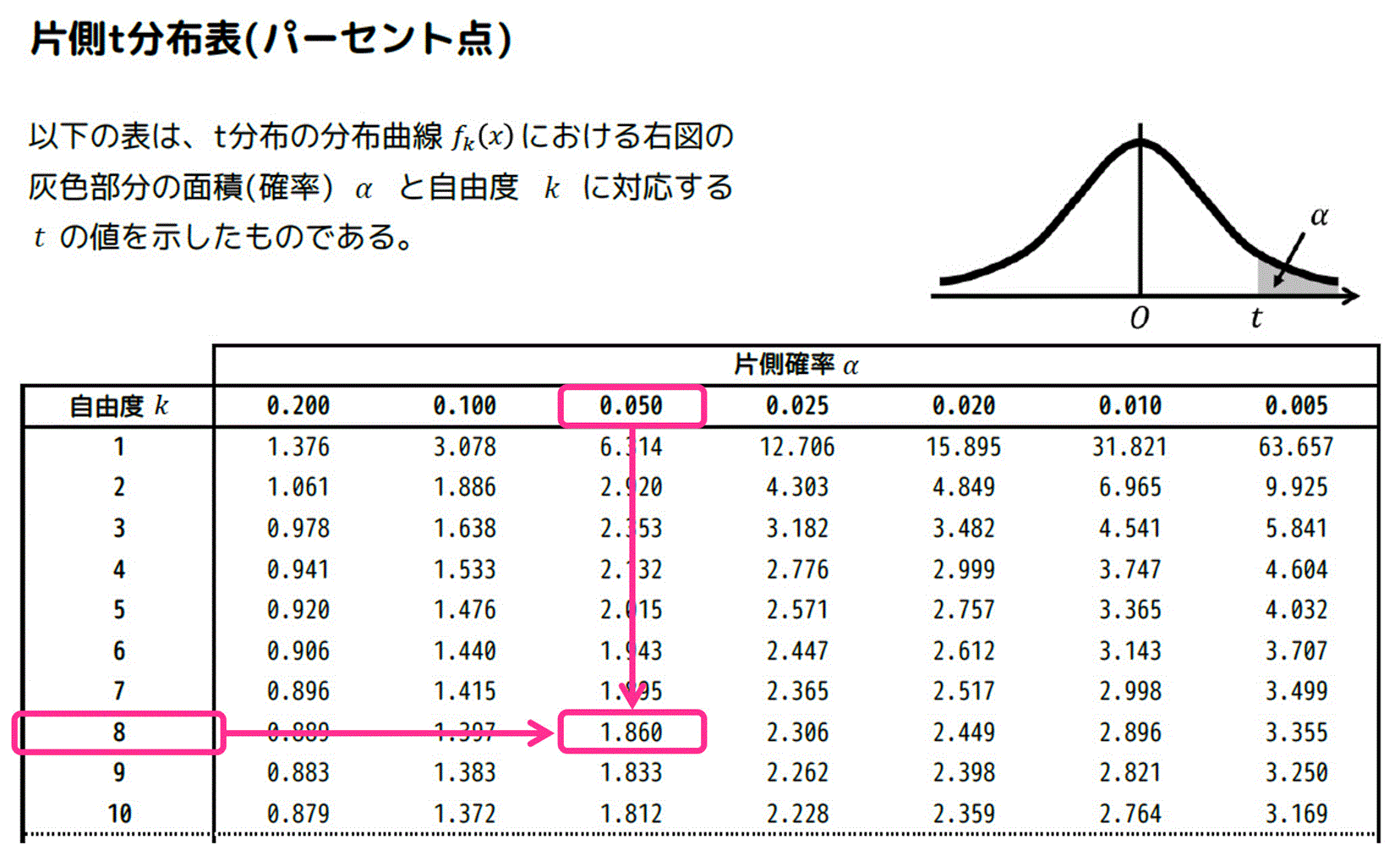
結果、\( t = 1.860 \) と読み取れる。
Step2. 推定に使う \( t \) の値を読み取る
信頼度に対応する \( t \) の値を読み取ったので、ここからは母平均を推定していきます。
母平均の推定公式の公式はあるのですが、せっかくなのでt分布の変換式\[
t = \frac{ \overline{X} - \mu }{ \frac{ s }{ \sqrt{n} } }
\]から母平均の推定公式を導出してみましょう。
t分布で登場するtの値と、母平均 \( \mu \)、標本サイズ \( n \)、標本平均 \( \overline{X} \)、不偏分散 \( s^2 \) には以下の式\[
t = \frac{ \overline{X} - \mu }{ \frac{ s }{ \sqrt{n} } } \tag{1}
\]が成り立つ。
ここで、ある信頼度、自由度に対応するt分布表から読み取った値が \( t = t_0 \) とする。すると、t分布の世界上の推定区間は\[
- t_0 \leqq t \leqq t_0 \tag{2}
\]となる。
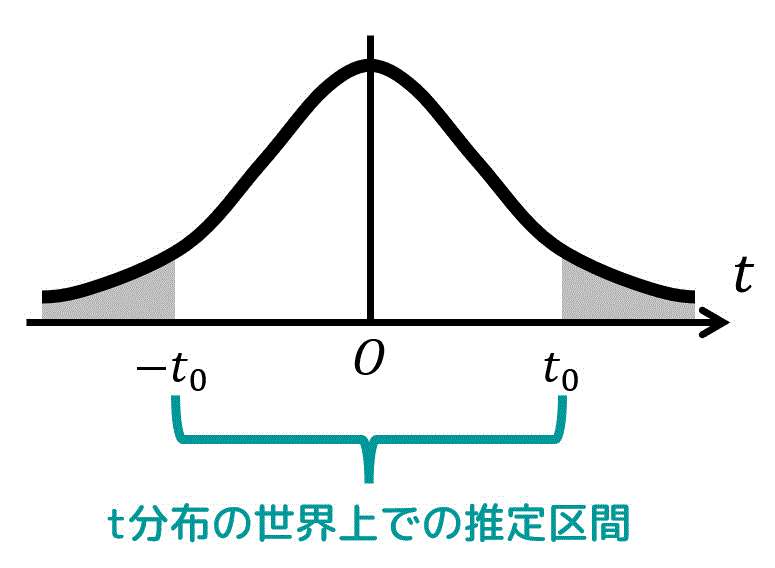
式(2)に、式(1)の \( t \) の値を代入すると\[
- t_0 \leqq \frac{ \overline{X} - \mu }{ \frac{ s }{ \sqrt{n} } } \leqq t_0 \tag{3}
\]となる。
次に、式(3)の両辺に \( \frac{ s }{ \sqrt{n} } \) を掛けると\[
- \frac{ t_0 s }{ \sqrt{n} } \leqq \overline{X} - \mu \leqq \frac{ t_0 s }{ \sqrt{n} } \tag {4}
\]となる。
さらに、式(4)の両辺から \( \overline{X} \) を引くと、\[
- \overline{X} - \frac{ t_0 s }{ \sqrt{n} } \leqq - \mu \leqq - \overline{X} + \frac{ t_0 s }{ \sqrt{n} } \tag{5}
\]となる。
最後に、式(5)の両辺を-1倍して\[
\overline{X} - \frac{ t_0 s }{ \sqrt{n} } \leqq \mu \leqq \overline{X} + \frac{ t_0 s }{ \sqrt{n} } \tag{6}
\]とすれば母平均の推定公式の導出完了。
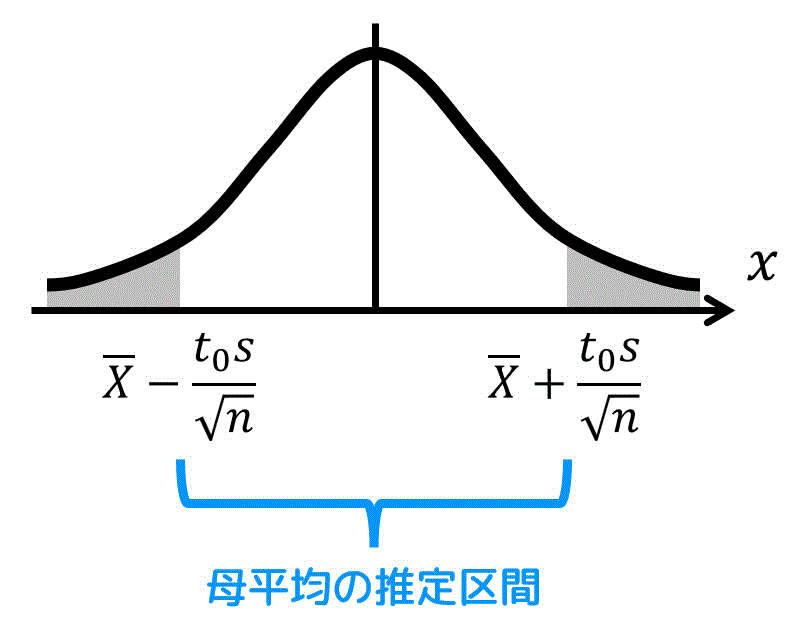
公式を図で表すと、以下のような感じに書けますね。
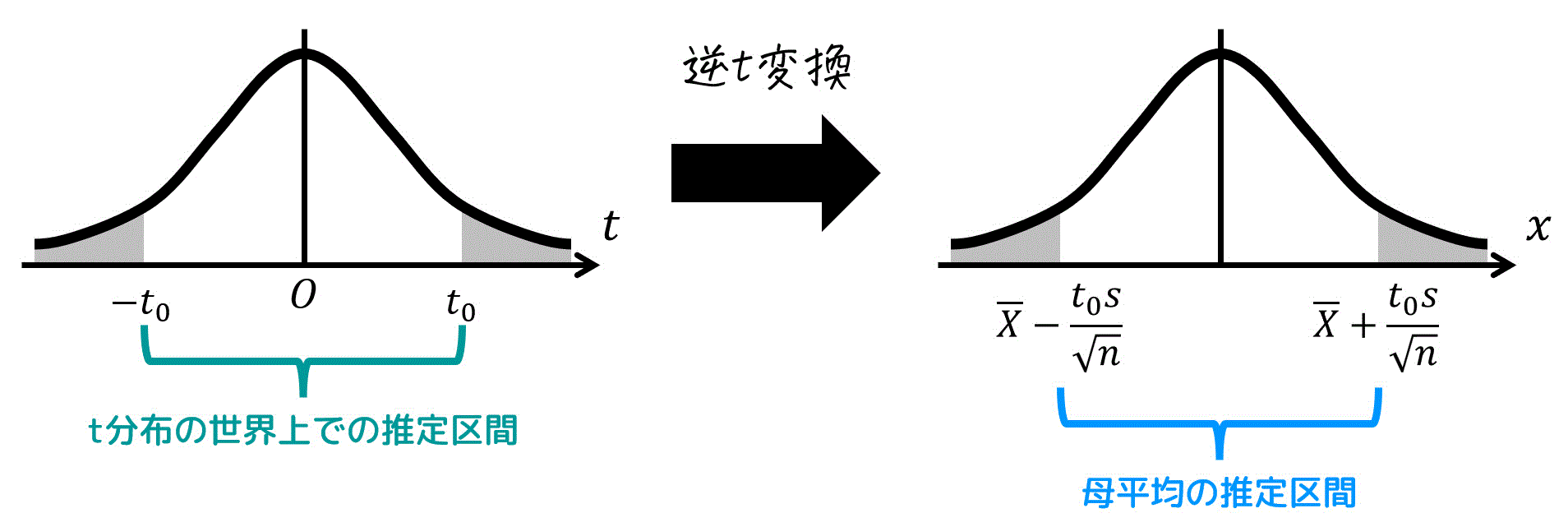
ではここからは、実際に公式を適用してみましょう。
まず、信頼度90%に対応する \( t \) の値は、(1)より \( t = 1.860 \) でしたね。
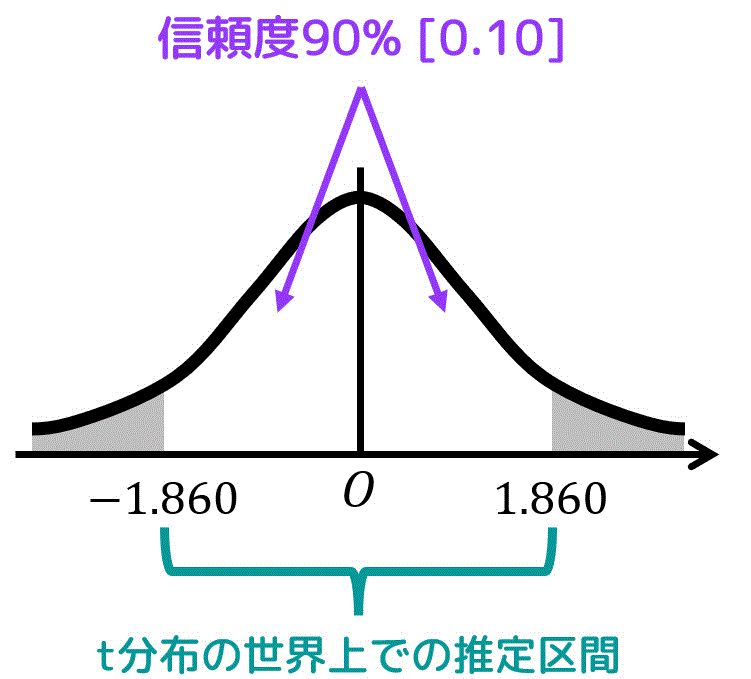
この数値と、標本のデータ数 \( n = 9 \)、標本平均 \( \overline{X} = 200 \)、不偏分散 \( s^2 = 64 \) (不偏標準偏差 \( s = 8 \))を公式\[
\overline{X} - \frac{ t_0 s }{ \sqrt{n} } \leqq \mu \leqq \overline{X} + \frac{ t_0 s }{ \sqrt{n} }
\]に代入しましょう。
実際に代入すると、\[
200 - \frac{ 1.860 \cdot 8 }{ \sqrt{9} } \leqq \mu \leqq 200 \cdot \frac{ 1.860 \cdot 8 }{ \sqrt{9} }
\]\[
200 - 4.96 \leqq \mu \leqq 200 + 4.96
\]と変形でき、信頼度90%での母平均推定結果を\[
195.04 \leqq \mu \leqq 204.96
\]と求められます。

※ 推定結果を \( [ 195.04, 204.96 ] \) のように [ ] を使って書いてもOK。
標本のサイズを \( n \)、標本平均が \( \overline{X} \)、不偏分散が \( s^2 \) (不偏標準偏差が \( s \) の標本を使って、
母集団の母分散が未知で、かつ標本サイズが小さい(目安: 30未満)のときの母平均 \( \mu \) の区間推定は、次のステップで行う。
※ 標本のデータ
- 標本のサイズ: \( n \)
- 標本平均: \( \overline{X} \)
- 不偏分散: \( s^2 \)(不偏標準偏差: \( s \))
Step1. 信頼度に対応する \( t \) の値を読み取る
自由度 \( n - 1 \)、信頼度に対応する \( \alpha \) の値から、信頼度に対応する \( t \) の値を読み取る。
ただし、\( \alpha \) の値は両側t分布表か片側t分布表かによって変わるので注意。
- 両側t分布表の場合
→ \( \alpha \) の値: 1 - 信頼度
→ 例: 信頼度95%であれば、\( \alpha = 1 - 0.95 = 0.05 \) - 片側t分布表の場合
→ \( \alpha \) の値: (1 - 信頼度) ÷ 2
→ 例: 信頼度95%であれば、\( \alpha = (1 - 0.95) \div 2 = 0.025 \)
ここで読み取った \( t \) の値を \( t_0 \) とする。
Step2. 読み取った値 \( t_0 \) から、信頼区間は次のように計算できる
\[
\overline{X} - \frac{ t_0 s }{ \sqrt{n} } \leqq \mu \leqq \overline{X} + \frac{ t_0 s }{ \sqrt{n} }
\]括弧表記を用いて\[
\left[ \overline{X} - \frac{ t_0 s }{ \sqrt{n} } , \overline{X} + \frac{ t_0 s }{ \sqrt{n} } \right]
\]と書いてもOK。
おまけ. 標本分散 \( S^2 \) が与えられた場合の不偏推定式
不偏分散 \( s^2 \) の代わりに標本分散\[
S^2 = \frac{1}{n} \sum^{n}_{k = 1} ( x_k - \overline{X} )
\]が与えられた場合は、信頼区間は\[
\overline{X} - \frac{ t_0 S }{ \sqrt{n-1} } \leqq \mu \leqq \overline{X} + \frac{ t_0 S }{ \sqrt{n-1} }
\]と求められる。括弧表記の場合は\[
\left[ \overline{X} - \frac{ t_0 S }{ \sqrt{n-1} } , \overline{X} + \frac{ t_0 S }{ \sqrt{n-1} } \right]
\]となる。
4. 練習問題
では、t分布を使って区間推定や仮説検定をする問題について、練習問題で理解できているか確認しましょう。
ある中学生の1年生全体が対象の、数学の期末テストが行われた。その中で、特定の塾に通っている4人(佐藤くん、西尾くん、池田さん、竹本さん)の期末テストの点数は、次の通りだった。
| 佐藤くん | 西尾くん | 池田さん | 竹本さん | |
|---|---|---|---|---|
| 期末テストの点数 | 72 | 60 | 84 | 76 |
この4人のテスト結果から、信頼度95%にて1年生全体の数学の平均点を推定したい。次の(1)~(3)の問いに答えなさい。必要であればt分布表を用いてもよい。
(1) 4人のテスト結果の平均点、および不偏分散を求めなさい。
(2) 母平均の区間推定を行うために、必要な分布を答えなさい。自由度がある分布については、自由度も答えなさい。
(3) 母平均の区間推定を行い、結果を小数第2位まで求めなさい。
5. 練習問題の答え
(1)
解答: 標本平均: 73 [点] 不偏分散: 100 [点2]
標本の平均\[\begin{align*}
\overline{X} & = \frac{1}{4} (72 + 60 + 84 + 76)
\\ & = 73
\end{align*}\]
計算ミスを減らすテクニックとして、いったん \( a = 70 \) とおいて、\[\begin{align*}
\overline{X} & = \frac{1}{4} \left\{ (a+2) + (a-10) + (a+14) + (a+6) \right\}
\\ & = \frac{1}{4} (4a + 12)
\\ & = a + 3
\\ & = 73
\end{align*}\]のように計算すると計算ミスを減らせる。
不偏分散
\[\begin{align*}
s^2 & = \frac{1}{4-1} \left\{ (73-72)^2 + (73-60)^2 + (73-84)^2 + (73-76)^2 \right\}
\\ & = \frac{1}{3} \left\{ 1^2 + 13^2 + (-11)^2 + (-3)^2 \right\}
\\ & = \frac{1}{3} \cdot 300
\\ & = 100
\end{align*}\]※ 不偏分散は割る数が \( n \) ではなく \( n-1 \) なので注意!
(2)
今回は、
- 母分散: 未知(かつ標本サイズ小さい)
- 推定したいもの: 母平均
なので推定に使う分布はt分布です。
また、今回与えられた標本サイズ(データ数)は4のため、自由度は 4 - 1 = 3 となります。
(3)
Step1. 推定に使う \( t \) の値を読み取る
まず、信頼度95%に相当する \( t \) の値をt分布表から読み取ります。
両側t分布表から読み取る場合
信頼度が95%なので、グラフの白色部分の面積が0.95。なので、\( \alpha \) の面積は 1 - 0.95 = 0.05。
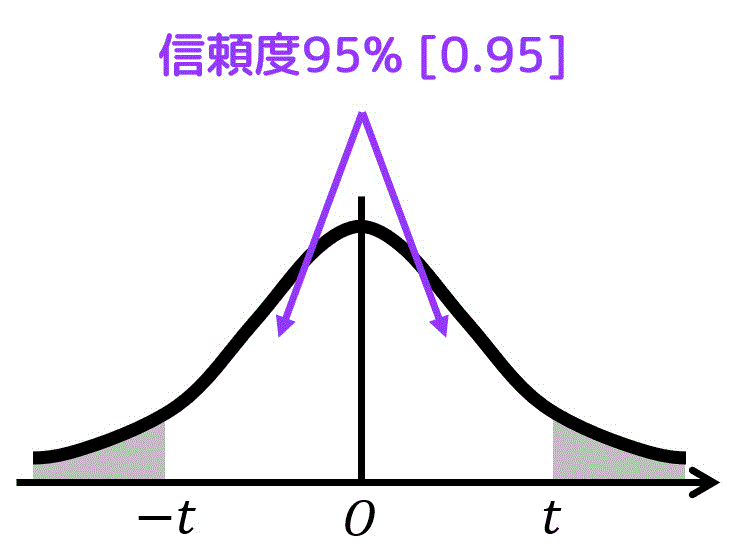
あとは、\( \alpha = 0.05 \)、自由度 \( k = 3 \) のときの \( t \) の値を表から探せばOK。

結果、\( t = 3.182 \) と読み取れる。
片側t分布表から読み取る場合
信頼度が95%なので、t分布の白色部分の面積が0.95となる。ここで、片側t分布で使う \( \alpha \) は下の図の青色部分の面積である。
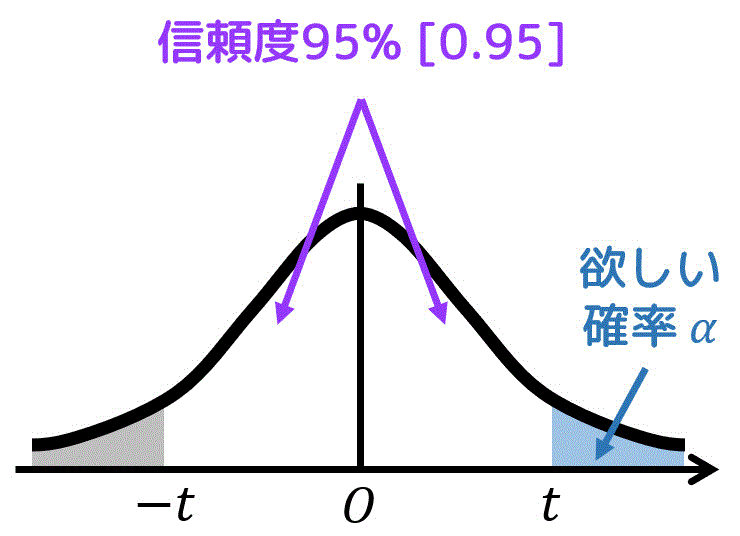
灰色部分の面積と青色部分の面積は等しいので、青色部分の面積 \( \alpha \) は、\[\begin{align*}
\alpha & = (1 - 0.95) \div 2 \\ & = 0.025
\end{align*}\]となる。
あとは、\( \alpha = 0.025 \)、自由度 \( k = 3 \) のときの \( t \) の値を表から探せばOK。

結果、\( t = 3.182 \) と読み取れる。
Step2. 読み取った値 \( t_0 \) から、信頼区間は次のように計算できる
Step1で読み取った \( t \) の値 3.182 を \( t_0 \) とする。
あとは、公式に\[
\overline{X} - \frac{ t_0 s }{ \sqrt{n} } \leqq \mu \leqq \overline{X} + \frac{ t_0 s }{ \sqrt{n} }
\]標本サイズ \( n = 4 \)、標本平均 \( \overline{X} = 73 \)、不偏分散 \( s^2 = 100 \)(不偏標準偏差 \( s = 10 \))を代入して母平均 \( \mu \) をすればOK。
計算すると、\[
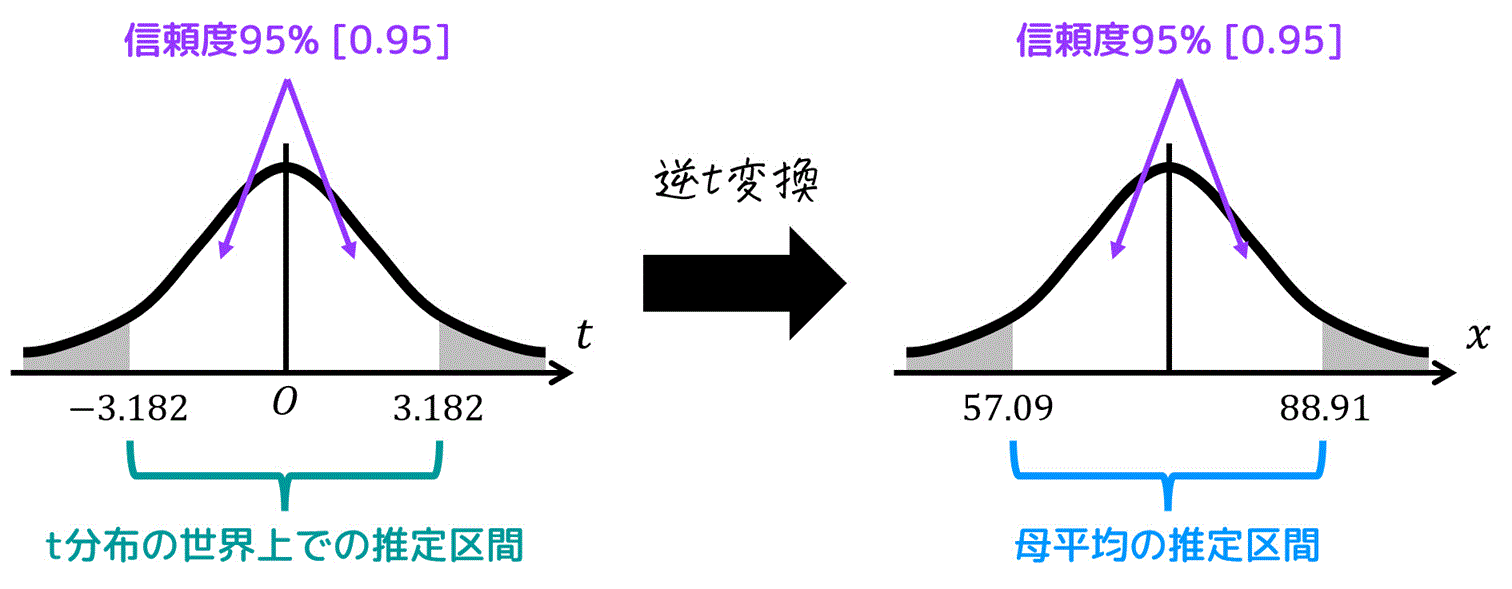
73 - \frac{3.182 \cdot 10}{ \sqrt{4} } \leqq \mu \leqq 73 + \frac{3.182 \cdot 10}{ \sqrt{4} }
\]\[
57.09 \leqq \mu \leqq 88.91
\]と母平均の信頼度95%推定結果を求めることができる。
※ \( \left[ 57.09 , 88.91 \right] \) と表記するのもOK。
関連広告・スポンサードリンク