スポンサードリンク
こんにちは、ももやまです。
「1年前期の離散数学の試験まであと1日しかない、あきらめよう。」って思ってる人、諦めないでください!!
そこで、試験前日でも3時間あれば総復習ができるように8題の練習問題を作成しました!
- 90分間で問題を解く。答えを回答フォームに入力する。
- 答えを送信後、間違った箇所を確認し、解説を見てどこで間違えたのか(理解ができていないのか)を確認する。
- 間違えた箇所を参考書や記事などで練習する。
- 時間があれば、合っている箇所も確認する。(青色と赤色の枠部分)
- 寝る。
時間がある人はじっくり、時間がない人は素早くこの記事にて1年前期の離散数学の復習をしましょう!
それぞれの練習問題の解説では、
- 試験で必要な知識:青色の枠
- 試験で必要な解き方:赤色の枠
で要点をまとめています。
スポンサードリンク
問題1. 論理式
次の \( A_1 \), \( A_2 \), \( A_3 \), \( A_4 \) の論理式\[\begin{align*}
A_1 & = (p \to q) \to r
\\ A_2 & = p \land (q \to r)
\\ A_3 & = (p \to q) \to (p \land r)
\\ A_4 & = (p \lor r ) \land (q \to r)
\end{align*}\]からなる論理式の集合を \( L = \{ A_1 , A_2, A_3, A_4 \} \) とする。
このときの論理的同値関係 \( \equiv \) による \( L \) の分割 \( L / \equiv \) として正しいものを1つ選びなさい。
★ [ 1 ] の選択肢★
- \( \left\{ \{ A_1 , A_2 \} , \{ A_3 , A_4 \} \right\} \)
- \( \left\{ \{ A_1 , A_3 \} , \{ A_2 , A_4 \} \right\} \)
- \( \left\{ \{ A_1 , A_4 \} , \{ A_2 , A_3 \} \right\} \)
- \( \left\{ \{ A_1 \} , \{ A_2 , A_3 , A_4 \} \right\} \)
- \( \left\{ \{ A_2 \} , \{ A_1 , A_3 , A_4 \} \right\} \)
- \( \left\{ \{ A_3 \} , \{ A_1 , A_2 , A_4 \} \right\} \)
- \( \left\{ \{ A_4 \} , \{ A_1 , A_2 , A_3 \} \right\} \)
- 上記以外
集合 \( L \) を何かしらの同値関係 \( \sim \) で分類することを \( L \) の分割と呼び、\( L / \sim \) と書く。また、\( L / \sim \) のことを商集合と呼ぶ。
例えば、集合 \( L = \{ 1, 5, 9, 16, 26, 36 \} \) を3で割ったあまりが等しい要素 \( \sim \) で分類すると、商集合 \( L / \sim \) は\[
L / \sim = \{ \{ 1, 16 \}, \{ 5, 26 \} , \{ 9, 36 \} \}
\]と求められる。
今回の問題では、論理的同値関係 \( \equiv \) による分割 \( 集合 \( L / \equiv \) をすればいいので、集合 \( L \) の論理式を同値な論理式ごとに分類すればOKです。
同値な方法を調べる方法には、以下の2つの方法があります。
- 4つの論理式を式変形により同値になるかを確かめる
- 4つの論理式の真理値表を書くことで、同値かどうかを調べる。
しかし、同値かどうかすらわからない4つの論理式をいちいち式変形で証明するのは非常に時間がかかります。
\( A_1 \), \( A_2 \), \( A_3 \), \( A_4 \) それぞれがどの論理式と同値かを調べるために真理値表を書きましょう。
\( A_1 \) の真理値表
| \( p \) | \( q \) | \( r \) | \( p \to q \) | \( (p \to q) \to r \) |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
\( A_2 \) の真理値表
| \( p \) | \( q \) | \( r \) | \( q \to r \) | \( p \land (q \to r) \) |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
\( A_3 \) の真理値表
| \( p \) | \( q \) | \( r \) | \( p \to q \) | \( p \land r \) | \( (p \to q) \to (p \land r) \) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
\( A_4 \) の真理値表
| \( p \) | \( q \) | \( r \) | \( p \lor r \) | \( q \to r \) | \( (p \lor r ) \land (q \to r) \) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
よって、\( A_1 \), \( A_2 \), \( A_3 \), \( A_4 \) の真理値表をまとめると以下のようになる。この中で、真理値が全く同じ論理式同士が同値である。
| \( p \) | \( q \) | \( r \) | \( A_1 \) | \( A_2 \) | \( A_3 \) | \( A_4 \) |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
上より、\( A_1 \) と \( A_4 \)、\( A_2 \) と \( A_3 \) がそれぞれ同値関係であることがわかる。
よって、\( L \) の分割 \( L / \equiv \) は\[
\left\{ \{ A_1 , A_4 \} , \{ A_2 , A_3 \} \right\}
\]となり、答えは3。
同値かどうかわからない論理式がたくさんあった場合でも、すべてのパターンの結果を確認する(それぞれの変数のときに結果がどうなるのかをもれなく調べる)ことで、式変形なしにどの論理式が同値であるのかを判断することができる。
このように、すべてのパターンの結果を確認する際に使われる表のことを真理値表と呼び、下のような表で表される。
真理値表の0, 1が完全一致している論理式は同値である。例えば、下の表であれば \( A_1 \) と \( A_4 \), \( A_2 \) と \( A_3 \) は同値である。
| \( p \) | \( q \) | \( r \) | \( A_1 \) | \( A_2 \) | \( A_3 \) | \( A_4 \) |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
※ ちなみに真理値表は0, 1ではなくF, Tを使って書くことも可能である。
論理式などについての詳しい内容はこちらをご覧ください。
真理値表を書き間違えないために、以下のやり方で0, 1を埋めていくのがおすすめ。
- \( p \land q \): \( p = 0 \) のところに0を埋める、\( q = 0 \) のところに0を埋める、余った箇所に1を埋める
- \( p \lor q \): \( p = 1 \) のところに1を埋める、\( q = 1 \) のところに1を埋める、余った箇所に1を埋める
- \( p \to q \): \( p = 0 \) のところに1を埋める、\( q = 1 \) のところに1を埋める、余った箇所に0を埋める
No.01 3 [7点]
スポンサードリンク
問題2. 集合の基礎
集合 \( S \) を \( S = \left\{ 1, \{ \phi , 2 \} \right\} \) とする。
次の(1)〜(7)の集合に対する関係が成り立つのであれば1を、成り立たないのであれば2をそれぞれ括弧番号と同じ回答番号に入力しなさい。例えば(2)の問題は [ 2 ] に回答すること。
(2) \( 1 \in S \)
(3) \( \phi \subseteq S \)
(4) \( \{ \phi , 2 \} \in S \)
(5) \( \{ \phi , 2 \} \in 2^S \)
(6) \( \left\{ \phi , \{ 1 \} \right\} \subseteq 2^S \)
(7) \( \left\{ 1 \right\} \subseteq 2^S \)
(8) \( \left\{ \{ 1 \} \right\} \in 2^S \)
[解説]
まずは、\( \in \) と \( \subseteq \) の意味をおさらいしましょう。
記号 \( x \in X \) :ある1つの要素 \( x \) が集合 \( X \) に含まれていることを表す。
[例]\( \{ a, b \} \in X \) → \( \{ a, b \} \) という要素が集合 \( X \) の中に含まれている
記号 \( S \subseteq X \) :集合 \( S \) に含まれているすべての要素 \( S \) が集合 \( X \) に含まれていることを表す。
[例]\( \{ a, b \} \subseteq S \) → 集合 \( \{ a, b \} \) のすべての要素が要素 \( S \) の中に入っている
今回のように、集合の中に集合が入ってるときは、1回集合の要素をすべて書き出すことをおすすめします。
今回の問題の場合、\[
S = \left\{ 1, \{ \phi , 2 \} \right\}
\]なので、集合 \( S \) の要素は \( 1 \) と \( \{ \phi , 2 \} \) の2つですね。
これを踏まえて(2)〜(4)まで答えていきましょう。
(2) \( 1 \in S \)
→ 要素 \( 1 \) が集合 \( S \) には含まれる。
集合 \( S \) には \( 1 \), \( \{ \phi , 2 \} \) の2つの要素があるため、要素 \( 1 \) は含まれている。よって、この式は成り立つ。答えは1。
(3) \( \phi \subseteq S \)
→ 集合 \( \phi \) のすべての要素が集合 \( S \)に含まれる。
空集合 \( \phi \) は何の要素も含まれていない。そのため \( \phi \) にある要素の中で、集合 \( S \) に含まれていない要素は存在しない。(だってそもそも \( \phi \) に要素なんてないんだから)
よって、この式も成り立つ。答えは1。
(4) \( \{ \phi , 2 \} \in S \)
→ 要素 \( \{ \phi , 2 \} \) が集合 \( S \) には含まれる。
集合 \( S \) には \( 1 \), \( \{ \phi , 2 \} \) の2つの要素があるため、要素 \( \{ \phi , 2 \} \) は含まれている。よって、この式は成り立つ。答えは1。
(5)〜(8)は、べき集合 \( 2^S \) に関する問題なので、べき集合の要素を書き出しましょう。
べき集合 \( 2^S \) の要素は、\( X \subseteq S \) を満たす \( X \) を全て書き出したものなので、\[
\phi , \ \{ 1 \} , \ \{ \{ \phi , 2 \} \} , \ \{ 1 , \{ \phi , 2 \} \}
\]の4つとなる。(べき集合 \( 2^S \) の要素数は、元の集合 \( S \) の要素数の2乗になる)
(5) \( \{ \phi , 2 \} \in 2^S \)
→ 要素 \( \{ \phi , 2 \} \) が集合 \( 2^S \) には含まれる。
集合 \( 2^S \) には要素 \( \{ \{ \phi , 2 \} \} \) は含まれているものの、要素 \( \{ \phi , 2 \} \) は含まれていない。よって、この式は成り立たない。答えは2。
(6) \( \left\{ \phi , \{ 1 \} \right\} \subseteq 2^S \)
→ 集合 \( \left\{ \phi , \{ 1 \} \right\} \) のすべての要素が集合 \( 2^S \) には含まれる。
集合 \( \left\{ \phi , \{ 1 \} \right\} \) には、\( \phi \) と \( \{ 1 \} \) の2つの要素が含まれている。集合 \( 2^S \) には、この2つの要素がすべて含まれているため、この式は成り立つ。答えは1。
(7) \( \left\{ 1 \right\} \subseteq 2^S \)
→ 集合 \( \left\{ 1 \right\} \) のすべての要素が集合 \( 2^S \) には含まれる。
集合 \( \left\{ 1 \right\} \) には、\( 1 \) の要素が含まれている。集合 \( 2^S \) には、要素 \( \{ 1 \} \) は含まれているが、要素 \( 1 \) は含まれていない。よってこの式は成り立たず、答えは2。
(8) \( \left\{ \{ 1 \} \right\} \in 2^S \)
→ 要素 \( \left\{ \{ 1 \} \right\} \) が集合 \( 2^S \) には含まれる。
集合 \( 2^S \) には要素 \( \{ \{ 1 \} \) は含まれているが、要素 \( \left\{ \{ 1 \} \right\} \) は含まれていない。よって、この式は成り立たない。答えは2。
[解答]No.02 1 [1点]
No.03 1 [1点]
No.04 1 [1点]
No.05 2 [1点]
No.06 1 [1点]
No.07 2 [1点]
No.08 2 [1点]
スポンサードリンク
問題3. 二項関係
2項関係 \( R_1 \), \( R_2 \) が次のように定義されている。(ただし自然数 \( \mathbb{N} \) は0を含むとする)\[
x R_1 y \ \Leftrightarrow \ 2x = y
\]\[
x R_2 y \ \Leftrightarrow \ \exists n \in \mathbb{N} \ \ \mathrm{s.t.} \ \ 2x + y = 3n
\]
このとき、\( R_1 \), \( R_2 \) が反射性、対称性、反対称性、推移性の各性質を満たすのであれば1を、満たさないのであれば2を対応する回答欄 [ 9 ] 〜 [ 16 ] に入力しなさい。
| 関係 | 反射性 | 対称性 | 反対称性 | 推移性 |
|---|---|---|---|---|
| \( R_1 \) | [ 9 ] | [ 10 ] | [ 11 ] | [ 12 ] |
| \( R_2 \) | [ 13 ] | [ 14 ] | [ 15 ] | [ 16 ] |
[解説]
まず、反射性、対称性、反対称性、推移性の4つの性質を復習しましょう。
ある集合 \( A \) 上の二項関係 \( R \) に対して、以下の4つの重要な性質はテストに頻出なので覚えておきましょう!
(1) 反射性(反射律): \( \forall \textcolor{deepskyblue}{x} \in A, \ \ \textcolor{deepskyblue}{x} R \textcolor{deepskyblue}{x} \)
→ ペア内の値が同じときは常に関係が成り立つ。
(2) 対称性(対称律): \( \forall \textcolor{deepskyblue}{x} \in A \ \ \forall \textcolor{magenta}{y} \in A , \ \ \forall \textcolor{deepskyblue}{x} R \textcolor{magenta}{y}\to \textcolor{magenta}{y} R \textcolor{deepskyblue}{x} \)
→ 関係 \( \textcolor{deepskyblue}{x} R y \) が成り立つとき、ペア内の変数 \( \textcolor{deepskyblue}{x} \), \( \textcolor{magenta}{y} \) を入れ替えて \( \textcolor{magenta}{y} R \textcolor{deepskyblue}{x} \) としても常に関係が成り立つ。
(3) 反対称性: \( \forall \textcolor{deepskyblue}{x} \in A \ \ \forall \textcolor{magenta}{y} \in A , \ \ \textcolor{deepskyblue}{x} R \textcolor{magenta}{y} \land \textcolor{magenta}{y} R \textcolor{deepskyblue}{x} \to \textcolor{deepskyblue}{x} = \textcolor{magenta}{y} \)
→ 2つの変数 \( \textcolor{deepskyblue}{x} \), \( \textcolor{magenta}{y} \) を入れ替えても常に関係が成り立つとき、その2つの変数 \( \textcolor{deepskyblue}{x} \), \(\textcolor{magenta}{y} \) の値は常に同じである。
(4) 推移性(推移律): \( \forall \textcolor{deepskyblue}{x} \in A \ \forall \textcolor{magenta}{y} \in A \ \forall \textcolor{limegreen}{z} \in A , \ \ \textcolor{deepskyblue}{x} R \textcolor{magenta}{y} \land \textcolor{magenta}{y} R \textcolor{limegreen}{z} \to \textcolor{deepskyblue}{x} R \textcolor{limegreen}{z} \)
→ \( \textcolor{deepskyblue}{x} \) と \( \textcolor{magenta}{y} \) の関係が成り立ち、\( \textcolor{magenta}{y} \) と \(\textcolor{limegreen}{z} \) の関係が成り立てば、三段論法のように \( \textcolor{deepskyblue}{x} \) と \(\textcolor{limegreen}{z} \) の関係が成り立つ。
(1)
関係 \( R_1 \): \( y \) は \( x \) の値を2倍したものになる関係
(i) 反射性: \( 2x = y \) なので、どう見ても \( x \) と \( y \) が等しいときに関係が成り立ちそうには見えない。例えば、\( x = 1 \), \( y = 1 \) のとき、\( 2 = 1 \) という地球ではありえない等式が成り立ってしまう。よって、答えは2。(反例: \( 1 \not R_1 1 \))
(ii) 対称性: 例えば、\( x = 1 \)、\( y = 2 \) とすると \( 2 = 2 \) で数式が成立するが、ひっくり返して \( x = 2 \)、\( y = 1 \) とすると \( 4 = 1 \) という地球上でありえない数式が誕生する。よって、対称性は成り立たない。よって、答えは2。(反例: \( 1 R_1 2 \) であるが \( 2 \not R_1 1 \))
(iii) 反対称性: 数式 \( 2x = y \) を入れ替えると \( 2y = x \) となる。この2つを連立させると、\[
4x = 2y = x
\]となり、\( 4x = x \) を満たすときのみ \( x \), \( y \) を入れ替えても関係が成り立つことがわかる。
ここで、\( 4x = x \) を満たす \( x \) は \( x = 0 \) のみ、さらに \( x = 0 \) のとき、\( y = 0 \) なので反対称性を満たす。よって答えは1。
(iv) 推移性: 関係 \( x R_1 y \) に対応する式は \( 2x = y \)、関係 \( y R_1 z \) に対応する式は \( 2y = z \) となるので、この2式を連立させると、\[
4x = 2y = z
\]という関係が成り立つ。この式を成立させるような \( x , z \) は例えば、\( (x,z) = (1,4) \) がある。ここで、関係 \( x R_1 z \) に対応する式 \( 2x = z \) に代入すると、\( 2 = 4 \) とやはりおかしな式になってしまう。よって、推移性も成り立たない。よって、答えは2。(反例: \( 1 R_1 2 \) かつ \( 2R_1 4 \) であるが \( 1 \not R_1 4 \))
No.09 2 [3点]
No.10 2 [3点]
No.11 1 [3点]
No.12 2 [3点]
(2)
関係 \( R_2 \): \( 2x+y \) の和が必ず3の倍数になる関係
\( \mathrm{s.t.} \) は such that の略です。つまり、\[
\exists n \in \mathbb{N} \ \ \mathrm{s.t.} \ \ 2x + y = 3n
\]を日本語で書くと、「\( 2x + y = 3n \) となるようなある(1つ以上の)整数 \( n \) が存在する。」となります。
(i) 反射性: 試しに、\( x = y = 1 \) を入れると3に、\( x = y = 2 \) を入れると6となり、\( x = y = 3 \) を入れると9になるっていうのを何個か試すと、\( x = y \) のときは反射性を満たしそうだなって気づくと思います。
ここで、\( x = y = a \) ( \( a \) は整数)を代入すると、\( 2a + a = 3a \) となり、\( x = y \) のときは必ず3の倍数になることがわかる。よって、反射性は満たすため、答えは1。
(ii) 対称性: まずは反例がないか探してみましょう。例えば、\( x = 1 \), \( y = 4 \) だと \( 2x+y = 6 \) を満たすので、入れ替えて \( x = 4 \), \( y = 1 \) とすると、\( 2x + y = 9 \) となり、「あれれ… 反例が見つからない…?」と思ってしまいます。
ここで、「成り立ちそうだな… 証明しなくてもいいし、答えは1だ!」って選ぶのもありでしょう。それも素晴らしい直感です。ただ、直感以外の方法で確認する方法を見ていきましょう。
まずは、\( x \) と \( y \) の余りで、\( 2x + y \) のあまりがどうなるかを確認してみましょう。
あまりによる場合分け
| \( x \) | \( y \) | \( 2x + y \) | \( 2y + x \) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | |
| 0 | 2 | 2 | |
| 1 | 0 | 2 | |
| 1 | 1 | 0 | 0 |
| 1 | 2 | 1 | |
| 2 | 0 | 1 | |
| 2 | 1 | 2 | |
| 2 | 2 | 0 | 0 |
確かに、\( 2x + y \) のあまりが0のとき、関係 \( R_2 \) の \( x \), \( y \) を入れ替えても、あまりが0になるため入れ替えても必ず3の倍数ですね。なので、対称性は満たされ、答えは1となります。
(iii) 反対称性: 対称性が成立するので、反対称性が成立しないことをまず疑う。
例えば、\( (x,y) = (1,4) \) のとき、\( 2x + y = 6 \) で、入れ替えて \( (x,y) = (4,1) \) としても \( 8 + 1 = 9 \) で3の倍数となり、成立するが、当然 \( 1 = 4 \) ではありませんよね。なので、反対称性は成り立たない。(
例えば、\( (x,y) = (1,4) \) のとき、\( 2x + y = 6 \) で、入れ替えて \( (x,y) = (4,1) \) としても \( 8 + 1 = 9 \) で3の倍数となり、成立するが、当然 \( 1 = 4 \) ではありませんよね。なので、反対称性は成り立たない。(反例: \( 1 R_2 4 \) かつ \( 4 R_2 1 \) であるが \( 1 \not = 4 \)
(iv) 推移性: この大問の中では一番難しいかも
(ii) 対称性を求めるときに、下のように \( x \), \( y \) のあまりに注目して場合分けを行いましたね。
| \( x \) | \( y \) | \( 2x + y \) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 2 | 2 |
| 1 | 0 | 2 |
| 1 | 1 | 0 |
| 1 | 2 | 1 |
| 2 | 0 | 1 |
| 2 | 1 | 2 |
| 2 | 2 | 0 |
ここで、関係 \( x R_2 y \) と \( y R_2 z \) が同時に成り立つということは、\( x \) と \( y \) のあまりが等しく、\( y \) と \( z \) のあまりも等しいということになります。ということは、当然 \( x \) と \( z \) のあまりも等しくなるため、\( x R_2 z \) の関係も成立しますね。なので、推移性が成り立ち、答えは1となります。
[解答]No.13 1 [3点]
No.14 1 [3点]
No.15 2 [3点]
No.16 1 [3点]
※ 二項関係がイマイチだなと思った人はこちらで復習しましょう。
今回のような反射性、対称性、反対称性、推移性が成り立つかどうかを考える際には、証明を考える前にまず身近な例で反例が見つからないかを調べる。特に0が許容されている場合には、0を代入することで反例が見つかることも多い。
関係 \( xRy \) の反例は、下のようにして探すのがよい。
- 反射性: \( x = y \) 以外のときに反例が見つかるかどうか
- 対称性: \( x \), \( y \) を入れ替えたときの値の変化を見る
- 反対称性: 対称性が成り立つ場合で、\( x \not = y \) となるような \( x, y \) を探す
- 推移性: \( xRy \) と \( yRz \) が成り立つのに \( xRz \) で成り立たないものを調べる。反射性が成り立たない場合は、\( xRy \) と \( yRx \) で成り立つのに \( xRx \) となるようなものを探すのもあり。
問題4. 述語論理
領域 \( S_1 \), \( S_2 \), \( S_3 \) が次のように定義されている。\[\begin{align*}
S_1 & = \{ 1, 2, 3, 4 \} \\
S_2 & = \mathbb{N} - \{ 0 \} \ \ \ ( 0以外の自然数 ) \\
S_3 & = \mathbb{Z} - \{ 0 \} \ \ \ ( 0 以外の整数 )
\end{align*} \]
さらに、\( S_1 \times S_1 \), \( S_2 \times S_2 \), \( S_3 \times S_3 \) 上の2項関係 \( \sqsubseteq \), \( \sqsubset \) を以下のように定義する。\[\begin{align*}
(x,y) \sqsubseteq (z,w) \ \Leftrightarrow \ \frac{x}{y} \leqq \frac{z}{w} \\
(x,y) \sqsubset (z,w) \ \Leftrightarrow \ \frac{x}{y} < \frac{z}{w} \\
\end{align*}\]このとき、領域 \( S_1 \), \( S_2 \), \( S_3 \) それぞれに対し、次の論理式 \( A_1 \), \(A_2 \), \( A_3 \), \( A_4 \) が真になる場合は1を、偽になる場合は2を対応する回答番号 [ 17 ] ~ [ 28 ] に入力しなさい。
\[\begin{align*}
A_1 & = \forall x \forall y \exists z \exists w \ \left( (x,y) \sqsubseteq (z,w) \right) \\
A_2 & = \forall x \forall y \exists z \exists w \ \left( (x,y) \sqsubset (z,w) \right) \\
A_3 & = \exists x \exists y \forall z \forall w \ \left( (x,y) \sqsubseteq (z,w) \right) \\
A_4 & = \exists x \exists y \forall z \forall w \ \left( (x,y) \sqsubset (z,w) \right)
\end{align*} \]
論理式 \( S_1 \) \( S_2 \) \( S_3 \) \( A_1 \) [ 17 ] [ 18 ] [ 19 ] \( A_2 \) [ 20 ] [ 21 ] [ 22 ] \( A_3 \) [ 23 ] [ 24 ] [ 25 ] \( A_4 \) [ 26 ] [ 27 ] [ 28 ]
[解説]
まずは、述語論理の読み方、読む順序について確認しましょう。
\( \forall a \) … すべての \( a \) に対して
→ \( a \) が (範囲内であれば) どんな値であっても成り立つときに使用
→ (範囲内のうち) 1つでも成り立たないものを見つければ偽となる
\( \exists a \) … ある \( a \) に対して
→ (\( a \) が (範囲内であればなんでもいいので) 1つ以上の \( a \) であっても成り立つときに使用
→ (範囲内のうち) 1つでも成り立つものを見つければ真となる
述語論理は、読む順番が非常に大切である。
(1) \( \textcolor{blue}{\forall m} \textcolor{red}{\exists w} \ \ \ CP(m,w) \)
→ [日本語的意味]: すべての男性 \( m \) は(1人以上の)女性 \( w \) とカップル関係である。
→ 男性は全員彼女持ちリア充。
(2) \( \textcolor{deepskyblue}{\exists m} \textcolor{magenta}{\forall w} \ \ \ CP(m,w) \)
→ [日本語的意味]: (ある1人以上の)男性 \( m \) はすべての女性 \( w \) とカップル関係である。
→ 1人(以上)だけ超超ハーレム状態。
(1)と(2)は見た目同じ関係に見えるが、\( \forall \) と \( \exists \) を入れ替えるだけで大きく意味が変わってしまうのだ。
※ \( CP(m,w) \) を 「男性 \( m \) と女性 \( w \) はカップルである。 」とする。
では、説明が終わったので解いていこう。
(1)\[
A_1 = \forall x \forall y \exists z \exists w \ \left( (x,y) \sqsubseteq (z,w) \right) \ \Leftrightarrow \ \forall x \forall y \exists z \exists w \left( \frac{x}{y} \leqq \frac{z}{w} \right)
\]
(1)では、まず最初に \( \forall x \forall y \) (すべての \( x \), \( y \))を決めてから、\( \exists z \exists w \) (ある \( z \), \( w \))を決めるパターンである。これからは、最初に決める方を [先攻]、あとに決める方を [後攻] としよう。つまり、
[先攻]: 範囲内のすべての \( x \), \( y \)
[後攻]: [先攻] に対し、ある1つの \( z \), \( w \) を満たせばOK
となる。今回の場合 \( x/y \leqq z/w \) なので、両辺が等しい(反射性が成り立つ)ときに常に条件が成り立つ。つまり、[先攻] すべての \( x \), \( y \) に対して、[後攻] ある1つの \( z \), \( w \) を \( z = x \), \( w = y \) とすることで、領域に関係なしに条件を満たすことができる。
よって、No.17~No.19の答えは真となる。
[★解答★]領域 \( S_1 \) : 真(No.17の答え1) [1点]
領域 \( S_2 \) : 真(No.18の答え1) [1点]
領域 \( S_3 \) : 真(No.19の答え1) [1点]
(2)\[
A_2 = \forall x \forall y \exists z \exists w \ \left( (x,y) \sqsubset (z,w) \right) \ \Leftrightarrow \ \forall x \forall y \exists z \exists w \left( \frac{x}{y} < \frac{z}{w} \right)
\]
(2)も(1)と同じく
[先攻]: 範囲内のすべての \( x \), \( y \)
[後攻]: [先攻] に対し、ある1つの \( z \), \( w \) を満たせばOK
のパターンである。しかし今回の場合 \( x/y < z/w \) なので、(1)のようには答えは見つからない。
ここで、問題文を少し読み替えてみよう。\[
\frac{x}{y} < \frac{z}{w}
\]ということは、
[先攻]: どんなに \( x/y \) を大きくしても
[後攻]: [先攻] よりも大きい \( z/w \) が1つ以上見つかる
この2つを満たせばOKとなる。(解析学の \( \varepsilon - \delta \) 論法に似た感じがしますね)
(i) 領域 \( S_1 \) の場合は、\( S_1 = \{ 1, 2, 3, 4 \} \) となっているため、\( x/y \) を最も大きくできるのは \( x = 4 \), \( y = 1 \) となる。しかし、[先攻] が \( x/y = 4/1 \) で来てしまうと、[後攻] 側は \( x/y = 4/1 \) より大きくなるような \( z/w \) を用意することができない。よって、領域 \( S_1 \) は満たすことができない。
(ii), (iii) 一方 \( S_2 \), \( S_3 \) であれば、正の方向についていくらでも大きな値を取ることができる。つまり、[先攻] がどんなに大きい \( x/y \) でやってきても、[後攻] は、[先攻] よりも必ず大きな値で応戦することができる。
- [先攻] \( x/y = 10^{10} / 1 \) → [後攻] \( z/w = 10^{11} / 1 \)
- [先攻] \( x/y = 10^{100} / 1 \) → [後攻] \( z/w = 10^{101} / 1 \)
- [先攻] \( x/y = 10^{100} / 1 \) → [後攻] \( z/w = 10^{1001} / 1 \)
よって、\( S_2 \), \( S_3 \) においては満たすため、偽となる。
[★ \( A_2 \) に対する解答★]領域 \( S_1 \) : 偽(No.20の答え2) [1点]
領域 \( S_2 \) : 真(No.21の答え1) [1点]
領域 \( S_3 \) : 真(No.22の答え1) [1点]
(3)\[
A_3 = \exists x \exists y \forall z \forall w \ \left( (x,y) \sqsubseteq (z,w) \right) \ \Leftrightarrow \ \exists x \exists y \forall z \forall w \left( \frac{x}{y} \leqq \frac{z}{w} \right)
\]
(3), (4) では攻守が交代する。つまり、
[先攻]: (範囲内のうちの)ある1つ以上の \( x \), \( y \)
[後攻]: [先攻] に対し、(範囲内)すべての \( z \), \( w \) を満たせばOK
→ [先攻] に対し、1つでも満たさない \( z \), \( w \) があればNG
となる。(1), (2)と違うのは、[先攻] 側1つに対し、[後攻] 側は範囲内すべての \( z/w \) を満たす必要があるという点である。
(i) 領域 \( S_1 \) の場合は、\( S_1 = \{ 1, 2, 3, 4 \} \) となっているため、\( x/y \) を最も小さくできるのは \( x = 1 \), \( y = 4 \) となる。[先攻] が \( x/y = 1/4 \) を与えることができれば、[後攻] 側の \( z/w \) は必ず \( z/w \) を \( 1/4 \) 以上にすることができる。よって、領域 \( S_1 \) は満たすため、真となる。
(ii), (iii) 一方 \( S_2 \), \( S_3 \) であれば、[先攻] がどんなに小さい \( x/y \) でやってきても、[後攻] は、分母 \( w \) の値を大きくすることで、[先攻] よりも必ず値を作ることができてしまう。よって、ある \( x/y \) に対し、\[
\frac{x}{y} \leqq \frac{z}{w}
\]を満たさないような \( z/w \) を1つ以上作れるため(反例)、\( S_2 \), \( S_3 \) は偽となる。
領域 \( S_1 \) : 真(No.23の答え1) [1点]
領域 \( S_2 \) : 偽(No.24の答え2) [1点]
領域 \( S_3 \) : 偽(No.25の答え2) [1点]
(4)\[
A_4 = \exists x \exists y \forall z \forall w \ \left( (x,y) \sqsubset (z,w) \right) \ \Leftrightarrow \ \exists x \exists y \forall z \forall w \left( \frac{x}{y} < \frac{z}{w} \right)
\]
攻守は(3)と同じく、
[先攻]: (範囲内のうちの)ある1つ以上の \( x \), \( y \)
[後攻]: [先攻] に対し、(範囲内)すべての \( z \), \( w \) を満たせばOK
→ [先攻] に対し、1つでも満たさない \( z \), \( w \) があればNG
となる。
(i) (3)と違い、\( x/y \) を最も小さくできる \( x = 1 \), \( y = 4 \) の場合であっても、\( z = 1 \), \( w = 4 \) とすることで、\[
\frac{x}{y} < \frac{z}{w}
\]\[
\frac{1}{4} < \frac{1}{4}
\]と成り立たない \( z/w \) を1つ用意(反例)することができるため、\( S_1 \) では満たさない。
(ii), (iii) (3)と同じく \( S_2 \), \( S_3 \) の場合、[先攻] がどんなに小さい \( x/y \) でやってきても、[後攻] は、分母 \( w \) の値を大きくすることで、[先攻] よりも必ず値を作ることができてしまう。
[★ \( A_4 \) に対する解答★]領域 \( S_1 \) : 偽(No.26の答え2) [1点]
領域 \( S_2 \) : 偽(No.27の答え2) [1点]
領域 \( S_3 \) : 偽(No.28の答え2) [1点]
今回のように、領域ごとに真偽を聞いてくる場合、正(もしくは負)の方向に無限大に続く領域かどうかを考える。
今回の問題の領域 \( S_1 \), \( S_2 \), \( S_3 \) だと無限大に続くかどうかは下のようになる。
- \( S_1 = \{ 1, 2, 3, 4 \} \) : 正の方向は4までなので無限大には続かない、負の方向に対しても1までと無限大には続かない
- \( S_2 = \mathbb{N} - \{ 0 \} \) : 正の方向は無限大に続くが、負の方向に対しては1までしか続かない(負の方向に対しては無限大には続かない)
- \( S_3 = \mathbb{Z} - \{ 0 \} \) : 正の方向は無限大に続くし、負の方向に対しても無限大に続く
| 領域 | 正の方向における上限 | 負の方向における上限 |
|---|---|---|
| \( S_1 \) | 4 | 1 |
| \( S_2 \) | ∞ | 1 |
| \( S_3 \) | ∞ | -∞ |
述語論理についてもっと復習をしたい人は、こちらの記事や動画をご覧ください。
(2023年5月に記事リニューアル & 動画作成しました!)
[記事]
[動画]
問題5. 半順序関係とハッセ図
次の図1のハッセ図で表される半順序集合 \( X = \{ a,b,c,d,e,f,g,h \} \) および \( X \) の部分集合 \( S = \{ b, c, e, h \} \) が存在する。このとき、次の(29)~(36)に当てはまる要素を選択肢の中からすべて選び、カッコ内の番号と同じ回答番号に入力しなさい。ただし、存在しない場合は「9. なし」のみを選択しなさい。
(29) 上界
(30) 下界
(31) 極大元
(32) 極小元
(33) 最大元
(34) 最小元
(35) 上限
(36) 下限
★ [ 29 ] ~ [ 36 ] の選択肢★
- \( a \)
- \( b \)
- \( c \)
- \( d \)
- \( e \)
- \( f \)
- \( g \)
- \( h \)
- なし
[例2] 存在しないと答える場合 → "なし"を選択
[解説]
まずは、ハッセ図の読み方を復習しましょう。
ハッセ図で表された半順序関係の大小は次のように考える。
- ある点 \( x \) からある点 \( y \) まで上方向に一方通行で(下方向に戻らず)辿れるとき、\( x \) は \( y \) 以上(よりも大きい or 同じ)であると呼び、\( x \preceq y \) と書く。
- ある点 \( x \) からある点 \( y \) まで下方向に一方通行で(上方向に戻らず)辿れるとき、\( x \) は \( y \) 以下(よりも大きい or 同じ)であると呼び、\( y \preceq x \) と書く。
- ある点 \( x \) からある点 \( y \) まで一方通行で辿れないとき、つまり上方向と下方向の両方の移動をしないと辿れないとき、比較不能であるといい、\( x \) と \( y \) の大小は比べられない。
※ 一方通行で辿れるというのは、1回も辿らない場合でも成り立つと考える。例えば、ある点 \( x \) からある点 \( x \) までは上方向にも下方向にも一方通行で辿れると考える。つまり、\( x \preceq x \) である。日本語だと、「\( x \) は \( x \) 以上であり、\( x \) 以下でもある。」となる。
次に半順序集合(ハッセ図)で重要な8つの用語を復習しましょう。
(1) 上界 [定義: \( X \) の部分集合 \( S \) すべての \( y \) に対し、\( y \preceq x \) であるような \( x \in X \)]
→ \( X \) の要素の中で、\( S \) のどの要素よりも大きい or 同じ要素が上界
(2) 下界 [定義: \( X \) の部分集合 \( S \) すべての \( y \) に対し、\( x \preceq y \) であるような \( x \in X \)]
→ \( X \) の要素の中で、\( S \) のどの要素よりも小さい or 同じ要素が下界
(3) 最大元 [定義: \( X \) の部分集合 \( S \) すべての \( y \) に対し、\( y \preceq x \) であるような \( x \in S \)]
→ 部分集合 \( S \) の要素の中で、他のどの \( S \) の要素よりも大きい要素
(※存在する場合は1つのみ)
(4) 最小元 [定義: \( X \) の部分集合 \( S \) すべての \( y \) に対し、\( x \preceq y \) であるような \( x \in S \)]
→ 部分集合 \( S \) の要素の中で、他のどの \( S \) の要素よりも小さい要素
(※存在する場合は1つのみ)
(5) 極大元 [定義: \( X \) の部分集合 \( S \) すべての \( y \) に対し、\( x \preceq y \) ならば \( x = y \) を満たすような \( x \in S \)]
→ 部分集合 \( S \) の要素の中で、他のどの \( S \) の要素よりも小さくない要素
→ ある部分集合 \( S \) の要素 \( a \) に比べ、\( a \) より大きい要素がなければOK
(6) 極小元 [定義: \( X \) の部分集合 \( S \) すべての \( y \) に対し、\( y \preceq x \) ならば \( x = y \) を満たすような \( x \in S \)]
→ 部分集合 \( S \) の要素の中で、他のどの \( S \) の要素よりも大きくない要素
→ ある部分集合 \( S \) の要素 \( a \) に比べ、\( a \) より小さい要素がなければOK
(7) 上限(最小上界) [定義: \( S \) のすべての上界 \( y \in S \) に対し、\( x \preceq y \) を満たすような \( x \in S \)]
→ 上界に含まれる要素の中で、他のどの上界の要素よりも小さい要素
(※存在する場合は1つのみ)
(8) 下限(最大上界) [定義: \( S \) のすべての下界 \( y \in S \) に対し、\( y \preceq x \) を満たすような \( x \in S \) ]
→ 下界に含まれる要素の中で、他のどの下界の要素よりも大きい要素
(※存在する場合は1つのみ)
定義を振り返ったところで1つずつ見ていきましょう。
(29) 上界
\( S = \{ b, c, e, h \} \) なので、この4つの要素よりも大きい(or 同じ)といえる要素が上界となりますね。
今回の場合は、\( a \) は \( S \) の要素である \( b \), \( c \), \( e \), \( h \) よりも大きいといえるので、\( a \) は上界と言えますね。
よって上界は \( a \) のみとなり、答えは1。
(\( b \) や \( c \ ) を選んでしまった人は、比較できない要素が含まれている点に注意しましょう。例えば、\( b \) と \( c \) は、一方通行では(上に行って下に行かないと)辿れないため、比較ができません。)
(30) 下界
\( S = \{ b, c, e, h \} \) なので、この4つの要素よりも小さい(or 同じ)といえる要素が下界となりますね。
今回の場合は、\( h \) は \( S \) の要素である \( b \), \( c \), \( e \), \( h \) よりも小さい(or 同じ)といえるので、\( h \) は上界と言えますね。
よって下界は \( h \) のみとなり、答えは8。
(31) 極大元
\( S = \{ b, c, e, h \} \) の4つの要素に対し、他のどの要素よりも小さくない要素はどれかを答えればOKです。
今回の場合は、\( b \) より大きい \( S \) の要素は存在しませんね。また、\( c \) より大きい \( S \) の要素も存在しませんね。
よって極大元は \( b,c \) となり、答えは2, 3。
(32) 極小元
\( S = \{ b, c, e, h \} \) の4つの要素に対し、他のどの要素よりも大きく要素はどれかを答えればOKです。
今回の場合は、\( h \) より小さい\( S \) の要素は存在しませんね。
よって極大元は \( h \) となり、答えは8。
(33) 最大元
\( S = \{ b, c, e, h \} \) の4つの要素に対し、他のどの要素よりも大きいといえる要素はどれかを答えればOKです。
今回の場合は、極大元である(他の要素よりも小さくない) \( b, c \) が候補になりますね。
しかし、\( b \) と \( c \) は大きさが比較できないため、他のどの要素よりも大きいとは言うことができません。
よって最大元は存在せず、答えは9。
(34) 最小元
\( S = \{ b, c, e, h \} \) の4つの要素に対し、他のどの要素よりも小さいといえる要素はどれかを答えればOKです。
今回の場合は、極小元である(他の要素よりも大きくない) \( h \) が候補になりますね。
\( h \) を見てみると、他のどの \( S \) 要素 \( b \), \( c \), \( e \) と比べても、\( h \) のほうが小さいと言えますね。
そのため、最小限は \( h \) となり、答えは8。
(35) 上限(最小上界)
今回の場合は、上界である \( a \) の1つの要素に対し、他のどの上界の要素よりも小さいといえる要素はどれかを答えればOKです。
ただし、上界が \( a \) のみなので、当然他のどの上界の要素に比べても \( a \) が小さいと言えますね。
(※ 小ささランキング1個中1位みたいな感覚です)
よって、上限の答えは \( a \) となり、答えは1となります。
(35) 上限(最小上界)
今回の場合は、上界である \( a \) に対し、他のどの上界の要素よりも小さいといえる要素はどれかを答えればOKです。(つまり上界の中の最下元を求めるイメージ)
ただし、上界が \( a \) のみなので、当然他のどの上界の要素に比べても \( a \) が小さいと言えますね。
(※ 小ささランキング1個中1位みたいな感覚です)
よって、上限の答えは \( a \) となり、答えは1となります。
(36) 下限(最大下界)
今回の場合は、下界である \( h \) に対し、他のどの下界の要素よりも大きいといえる要素はどれかを答えればOKです。(つまり下界の中の最大元を求めるイメージ)
ただし、下界が \( h \) のみなので、当然他のどの下界の要素に比べても \( h \) が大きいと言えますね。
(※ 大きさランキング1個中1位みたいな感覚です)
よって、下限の答えは \( h \) となり、答えは8となります。
[★ 解答★] [2点×8=16点 (各問は完答)]No.29 1
No.30 8
No.31 2, 3
No.32 8
No.33 9
No.34 8
No.35 1
No.36 8
問題6. 数え上げ
集合 \( A \) を \( A = \{ 1,2,3,4 \} \)、集合 \( B \) を \( B = \{ a, b, c \} \) とする。このとき、次の(37)~(42)で指示された数を数え上げ、その数カッコ内の番号と同じ回答番号に入力しなさい。必要であれば \( 2^8 = 256 \), \( 2^9 = 512 \), \( 2^{10} = 1024 \) を用いてもよい。(配点 6)
(37) 集合 \( A \) のべき集合 \( 2^A \) の要素数
(38) \( \{ 3,4 \} \subseteq X \subseteq A \) を満たす集合 \( X \) の個数
(39) 直積集合 \( B \times B \) の要素数
(40) 集合 \( B \) の二項関係の総数
(41) 集合 \( A \) から集合 \( B \) の全域関数で相異なるもの
(42) 集合 \( A \) から集合 \( A \) への全域関数で1対1対応(全単射)であるものはの個数
[解説]
(37) べき集合は、\( A \) の部分集合から作られる集合の組み合わせをすべて集めた集合のこと。
例えば、今回の場合だと、
- 要素数0の \( A \) の部分集合:\( \phi \)
- 要素数1の \( A \) の部分集合:\( \{ 1 \} \), \( \{ 2 \} \), \( \{ 3 \} \), \( \{ 4 \} \)
- 要素数2の \( A \) の部分集合:\( \{ 1, 2 \} \), \( \{ 1, 3 \} \), \( \{ 1, 4 \} \), \( \{ 2, 3 \} \), \( \{ 2, 4 \} \), \( \{ 3, 4 \} \)
- 要素数3の \( A \) の部分集合:\( \{ 1,2,3 \} \), \( \{ 1,2,4 \} \), \( \{ 1,3,4 \} \), \( \{ 2,3,4 \} \)
- 要素数4の \( A \) の部分集合:\( \{ 1,2,3,4 \} \)
のすべてを要素とした集合となります。よって、要素数は\[
1 + 4 + 6 + 4 + 1 = 16
\]と普通に数えてもいいのですが、それだと少し時間がかかってしまうので、もう少し早く数える方法を考えてみましょう。
今回の場合、\( A = \{ 1,2,3,4 \} \) のように、4つの要素を持った集合のべき集合の要素数を求めればOKですね。
部分集合を作る組み合わせとしては、それぞれの要素1, 2, 3, 4の4つに対して、選ぶか選ばないかの2通りの組み合わせがありますね。よって、\( 2^4 = 16 \) 個と答えを計算することができます。
(38) \[
\{ 3,4 \} \subseteq X \subseteq A
\]を満たす集合 \( X \) ということは、3, 4を固定した上で1, 2の2つの要素を選ぶか選ばないかの2通りの組み合わせができますね。つまり、\( 2^2 = 4 \) 個と答えを出すことができます。
(39) 直積集合は、ある集合の要素を並べて、\( (a,b) \) とペアにしたものを表します。
今回の場合、\( B = \{ a,b,c \} \) なため、直積集合は下のように \( 3 \times 3 = 9 \) 個の要素を持った集合となります。
| (a,a) | (a,b) | (a,c) |
| (b,a) | (b,b) | (b,c) |
| (c,a) | (c,b) | (c,c) |
※ 直積集合の場合、互いに入れ替えたもの(例えば \( (a,b) \) と \( (b,a) \) )を別にカウントするため、直積集合 \( A \times B \) の要素数は、[\( A \) 要素数]×[\( B \) の要素数] で計算を行うことができます。
(40) 集合の \( B \) の二項関係は、直積集合 \( B \times B \) からいくつか要素を選び、集合にしたものを表す。(→ 直積集合 \( B \times B \) のべき集合が2項関係となる)
つまり二項関係の選び方としては、直積集合 \( B \times B \) の要素数9個の中から、要素を選ぶか選ばないかの2通りの組み合わせだけ存在する。よって、二項関係の総数は \( 2^9 = 512 \) 個存在する。
(41) 全域関数というのは、関係の元(今回の問題の場合は集合 \( A \))に対して、必ず対応先の関係(今回の場合は集合 \( B \))が1つのみである関数のことを表します。
今回の問題の場合、
- 集合 \( A \) の要素 \( 1 \) → 集合 \( B \) の \( a \), \( b \), \( c \) いずれかに対応
- 集合 \( A \) の要素 \( 2 \) → 集合 \( B \) の \( a \), \( b \), \( c \) いずれかに対応
- 集合 \( A \) の要素 \( 3 \) → 集合 \( B \) の \( a \), \( b \), \( c \) いずれかに対応
- 集合 \( A \) の要素 \( 4 \) → 集合 \( B \) の \( a \), \( b \), \( c \) いずれかに対応
と、集合 \( A \) の4つの要素に対して、3通りの対応の方法がありますね。つまり、個数としては\[
3 \times 3 \times 3 \times 3 = 81
\]存在します。
(42) 1対1対応、関係の元(今回の問題の場合は集合 \( A \))に対して、必ず対応先の関係(今回の場合は集合 \( B \))が1つのみで、さらに対応先の関係 \( B \) に対し、対応元の関係 \( A \) が1通りしかない関係を表します。(恋愛でいうと一途な関係って感じですね。)
今回の問題の場合、
- 集合 \( A \) の要素 \( 1 \) → 集合 \( A \) の要素4通りの中の1つに対応
- 集合 \( A \) の要素 \( 2 \) → 集合 \( A \) でまだ対応していない3通りの中の1つに対応
- 集合 \( A \) の要素 \( 3 \) → 集合 \( A \) でまだ対応していない2通りの中の1つに対応
- 集合 \( A \) の要素 \( 4 \) → 集合 \( A \) の残りもの1つに対応
となるため、個数としては\[
4 \times 3 \times 2 \times 1 = 24
\]存在します。
No.37 16 [1点]
No.38 4 [1点]
No.39 9 [1点]
No.40 512 [1点]
No.41 81 [1点]
No.42 24 [1点]
集合 \( A \) の要素数が \( n \) 個、集合 \( B \) の要素数が \( m \) 個のときの数え上げは以下のようになる。具体値だけでなく、文字の場合でもできるようにしておくこと。
(1) 集合 \( A \) のべき集合 \( 2^A \) は、\( n \) 個の集合の要素それぞれに対して、場合と入れない場合の2つの選び方を考えるため、要素数は \( 2^n \) 個となる。
(2) \( \{ 3,4 \} \subseteq X \subseteq A \) を満たすものと聞かれたら、要素を固定し、それ以外の要素に対して、選ぶか選ばないかの2つの選び方があることを考えればよい。今回の場合、3, 4という2通りの要素を除いた残りの \( n - 2 \) 通りに対して、選ぶか選ばないかの2つの選び方があるため、答えは \( 2^{n-2} \) 通り。
(3) 集合 \( A \) の直積集合 \( A \times A \) の要素は、 \( (2,3 ) \) のように直積元と直積先の要素で構成される。よって、直積集合 \( A \times A \) の要素数は直積元 \( n \) × 直積先 \( n \) 個、合計 \( n^2 \) 個となる。なお、下のように表で考えるのもおすすめ。
| (1,1) | (1,2) | (1,3) | … | (1,n) |
| (2,1) | (2,2) | (2,3) | … | (2,n) |
| (3,1) | (3,2) | (3,3) | … | (3,n) |
| ︙ | ︙ | ︙ | ⋱ | ︙ |
| (n,1) | (n,2) | (n,3) | … | (n,n) |
(4) 集合 \( A \) の二項関係の総数は、直積集合 \( A \times A \) それぞれの \( n^2 \) 個の要素に対し、選ぶか選ばないかの2通りだけある。よって、\( 2^{n^2} \) 個存在する。
(5) 集合 \( A \) から集合 \( B \) の全域関数で相異なるものは、集合 \( A \) の \( n \) 個の要素それぞれに対し、集合 \( B \) の全域関数の要素の数の選び方、つまり \( m \) 通りの選び方が存在する。よって \( m \) 通りを \( n \) 回掛けただけ、つまり \( m^n \) 通りの選び方が存在する。
(6) 集合 \( A \) から集合 \( A \) への全域関数で1対1対応(全単射)であるものは、1要素目に対して \( n \) 通り、2要素目に対して残りの \( n - 1 \) 通り、3要素目に対して残りの \( n - 2 \) 通りとなるため、選び方としては、\[
n \times (n-1) \times (n-2) \times \cdots \times 2 \times 1
\]だけ存在する。これを簡単に表すと \( n! \) 通りとなる。
問題7. 数学的帰納法
次の命題を数学的帰納法を用いて証明したい。
\( n \geqq 5 \) のとき、\( 2^n > n^2 \) が常に成り立つ
回答番号 [ 46 ]・[ 47 ]・[ 48 ]・[ 52 ]については下の選択肢から最も適切な式、ごくを選び、番号で回答し、それ以外の回答番号については当てはまる整数を回答欄に直接入力することで証明を完成させなさい。
[証明](左辺) > (右辺) を示すためには、(左辺) - (右辺) > [ 43 ] であることを示せばよい。ここで、次の(1), (2)を考える。
(1) \( n = \left[ \ \ 44 \ \ \right] \) のとき\[
(左辺) - (右辺) = \left[ \ \ 45 \ \ \right] > \left[ \ \ 43 \ \ \right]
\]より、(1)において成立する。
(2) \( n \geqq 5 \) に対し、\( n = k \) のとき命題が成立すると仮定する。
ここで、\( n = \left[ \ \ 46 \ \ \right] \) のとき\[\begin{align*}
(左辺) - (右辺) & = 2^{ \left[ \ \ 46 \ \ \right] } - ( \left[ \ \ 46 \ \ \right] )^2
\\ & = 2 \cdot 2^{ \left[ \ \ 47 \ \ \right] } - ( \left[ \ \ 46 \ \ \right] )^2
\\ & > 2 \cdot k^2 - ( \left[ \ \ 46 \ \ \right] )^2 \ \ \ \left( \because \ \left[ \ \ 48 \ \ \right] \right)
\\ & = \left( k - \left[ \ \ 49 \ \ \right] \right)^2 - \left[ \ \ 50 \ \ \right]
\\ & \geqq \left[ \ \ 51 \ \ \right] \ \ \ \left( \because \ \left[ \ \ 52 \ \ \right] \right)
\\ & > \left[ \ \ 43 \ \ \right]
\end{align*}\]より、(2)においても成立する。
※ \( \because \) はその式変形が行える理由を表す
(1), (2) より題意は満たされ、\( n \geqq 5 \) のとき、\( 2^n > n^2 \) が常に成り立つことが数学的帰納法により証明できた。
★ [ 46 ]・[ 47 ] の選択肢 ★
- \( k - 1 \)
- \( k \)
- \( k + 1 \)
- \( k + 2 \)
- \( k + 3 \)
- \( k + 4 \)
- \( k + 5 \)
- \( k + 6 \)
- \( k + 7 \)
★ [ 48 ]・[ 52 ] の選択肢 ★
- 背理法の仮定
- 弧度法の仮定
- 帰納法の仮定
- 勘
- \( n = 5 \)
- \( n \not = 5 \)
- \( n \geqq 5 \)
- \( n < 5 \)
[解説]
(左辺) > (右辺) となっている不等式を証明する場合は、(左辺) - (右辺) > 0 と移項するのが定石。よって、[ 43 ] の答えは0。
帰納法では、以下の2ステップにより証明を行う。
- \( n \) が最も小さいときに成立することを証明する
(例えば \( n \geqq 5 \) 以上で示すのれあれば \( n = 5 \) のときを示す - \( n = k \) で成立が成り立つと仮定したときに、\( n = k + 1 \) で成り立つことを帰納法の仮定を用いて示す
1, 2を両方とも示すことで、ドミノ倒しのように証明を行う。
今回は、\( n \geqq 5 \) の \( n \) に対して示すので、ドミノ倒しの起点は \( n = 5 \) である。
※ 勢いに乗って \( n = 1 \) としないように!
(1) \( n = 5 \) のとき、\[\begin{align*}
(左辺) - (右辺) & = 2^5 - 5^2
\\ & = 32 - 25
\\ & = 7
\\ & > 0
\end{align*}\]となるため、(1)のとき成立。
次に、\( n \geqq 5 \) において \( n = k \) で題意が成立すること、つまり \( 2^k > k^2 \) が成立することを仮定する。つまり、目標は以下の通りとなる。
\( \textcolor{red}{2^k} > \textcolor{blue}{k^2} \) であることを仮定し、\( 2^{k+1} > (k+1)^2 \) であることを示したい
では、上の証明を始めよう。
(2) \( n = k + 1 \) のとき、\[\begin{align*}
(左辺) - (右辺) & = 2^{k+1} - (k+1)^2
\\ & = 2 \cdot \textcolor{red}{2^k} - (k+1)^2
\\ & > 2 \cdot \textcolor{blue}{k^2} - (k+1)^2 \ \ \left( \because 帰納法の仮定 \right)
\\ & = 2 k^2 - (k^2 + 2k + 1)
\\ & = k^2 - 2k - 1
\\ & = (k-1)^2 - 2
\\ & \geqq 14 \ \ \left( \because n \geqq 5 \right)
\\ & > 0
\end{align*}\]
となるため、(2)のときも成り立つことがわかる。
よって、(1), (2)より題意は満たされた。
\( (k-1)^2 - 2 \geqq \left[ \ \ 51 \ \ \right] \) の部分で、[ 51 ] に14以外の値を入れても数式が成り立つのではないかという質問を複数いただきました。
今回の設問では、\( n \geqq 5 \) を理由に \( (k-1)^2 - 2 \) の最小値が [ 51 ] 以上である(つまり \( (k-1)^2 - 2 \geqq 14 \) ことを言及する必要があるため、[ 51 ] に14以外の値を入れた人については誤答としています。
しかし、指摘を受け、私自身も「\( (k-1)^2 - 2 \) の最小値は \( n = k \geqq 5 \) で [ 51 ] となる」のような文章による補足が不足しているとも思いました。この点につきましては次回からの問題作成時に誘導の説明が不足しないよう気をつけます。
No.43 0 [1点]
No.44 5 [1点]
No.45 7 [1点]
No.46 3 [1点]
No.47 2 [1点]
No.48 3 [1点]
No.49 1 [1点]
No.50 2 [1点]
No.51 14 [1点]
No.52 7 [1点]
問題8. 差分方程式(漸化式)
次の(1), (2)の問いに答えなさい。
(1) 差分方程式\[
f(n) - 4 f(n-1) + f(n-2) + 6 f(n-3) = 0
\]の一般解と特殊解を求めたい。
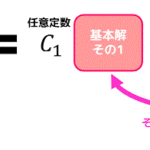
(i) 一般解は任意定数 \( C_1 \), \( C_2 \), \( C_3 \) を用いて\[
f(n) = C_1 ( \left[ \ \ 53 \ \ \right] )^n + C_2 ( \left[ \ \ 54 \ \ \right] )^n + C_3 ( \left[ \ \ 55 \ \ \right] )^n
\]と求めることができる。(ただし \( \left[ \ \ 53 \ \ \right] < \left[ \ \ 54 \ \ \right] < \left[ \ \ 55 \ \ \right] \))
(ii) \( f(0) = -1 \), \( f(1) = 3 \), \( f(2) = -3 \) とする。すると、\( C_1 = \left[ \ \ 56 \ \ \right] \), \( C_2 = \left[ \ \ 57 \ \ \right] \), \( C_3 = \left[ \ \ 58 \ \ \right] \) となり、特殊解を求めることができる。
(2) 差分方程式\[
f(n) - 5 f(n-1) + 6f(n-2) = 4n-6
\]の特殊解の1つは \( f(n) = an + b \) とおくことで\[
f(n) = \left[ \ \ 59 \ \ \right] n + \left[ \ \ 60 \ \ \right]
\]と求めることができる。
(1)
(i) 特性方程式は、\[\begin{align*}
t^3 - 4t^2 + t + 6 & = (t-2)(t^2 - 2t - 3)
\\ & = (t-2)(t-3)(t+1) = 0
\end{align*} \]を解けばよい。解は \( t = -1, 2, 3 \) となるため、一般解は\[
f(n) = C_1 ( -1 )^n + C_2 ( 2 )^n + C_3 ( 3 )^n
\]となる。
No.53 -1 [2点]
No.54 2 [2点]
No.55 3 [2点]
(ii) \( f(0) = -1 \), \( f(1) = 3 \), \( f(2) = -3 \) を代入すると、\[\begin{align*}
f(0) & = \ \ \ C_1 + \ \ C_2 + \ \ C_3 = -1 \\
f(1) & = - C_1 + 2 C_2 + 3 C_3 = \ \ \ 3 \\
f(2) & = \ \ \ C_1 + 4 C_2 + 9 C_3 = -3
\end{align*}\]となる。
あとは、この連立方程式を解けばよい。せっかくなので行列で解くと、\[
\left( \begin{array}{ccc} 1 & 1 & 1 \\ -1 & 2 & 3 \\ 1 & 4 & 9 \end{array} \right) \left( \begin{array}{ccc} C_1 \\ C_2 \\ C_3 \end{array} \right) = \left( \begin{array}{ccc} -1 \\ 3 \\ -3 \end{array} \right)
\]と \( A \vec{x} = \vec{b} \) の形になるので、
\[\begin{align*}
\left( \begin{array}{ccc} C_1 \\ C_2 \\ C_3 \end{array} \right) & =
\left( \begin{array}{ccc} 1 & 1 & 1 \\ -1 & 2 & 3 \\ 1 & 4 & 9 \end{array} \right)^{-1} \left( \begin{array}{ccc} -1 \\ 3 \\ -3 \end{array} \right)
\\ & = \frac{1}{12} \left( \begin{array}{ccc} 6 & -5 & 1 \\ 12 & 8 & -4 \\ -6 & -3 & 3 \end{array} \right) \left( \begin{array}{ccc} -1 \\ 3 \\ -3 \end{array} \right)
\\ & = \left( \begin{array}{ccc} -2 \\ 2 \\ -1 \end{array} \right)
\end{align*}\]と \( \vec{x} = A^{-1} \vec{b} \) にしてから解くこともできる。
※ ただ、普通は中学生で習う解き方のほうが圧倒的に早いです
よって、\( C_1 = -2 \), \( C_2 = 2 \), \( C_3 = -1 \) となるため、特殊解は\[
f(n) = -2 ( -1 )^n + 2 \cdot 2^n - \cdot 3^n
\]となる。
No.56 -2 [2点]
No.57 2 [2点]
No.58 -1 [2点]
※ 同次式の差分方程式がイマイチな人はこちらで復習しましょう。
(2) 問題文の通り \( f(n) = an + b \) とおく。すると、\[\begin{align*}
f(n) - 5 f(n-1) + 6f(n-2) & = an + b - 5( a(n-1) + b) + 6 ( a(n-2) + b)
\\ & = an + b - 5an + 5a - 5b + 6an - 12a + 6b
\\ & = 2an - 7a + 2b
\\ & = 4n - 6
2n + 4
\end{align*} \]となるので、\[ \left\{ \begin{array}{l}
2a = 4 \\ -7a + 2b = -6
\end{array} \right. \]を解けばよい。
すると、\( a = 2 \), \( b = 4 \) と求まる。よって、特殊解の1つは\[
f(n) = 2n + 4
\]となる。
No.59 2 [3点]
No.60 4 [3点]
※ 非同次式の差分方程式がイマイチな人はこちらで復習しましょう。
さいごに
今回の8個の大問は、以下の8個の題材から出題を行いました。
- 集合の基礎
- 論理式について
- 述語論理
- 二項関係
- 半順序関係とハッセ図
- 関数の数え上げ
- 数学的帰納法
- 差分方程式
実際に解いて見て、あまり出来ない箇所があれば、参考書や記事などを見ながら勉強してください。
関連広告・スポンサードリンク





![[基本情報・応用情報] うさぎでもわかる情報理論 第3羽 ハフマン符号化](https://www.momoyama-usagi.com/wp-content/uploads/joho3-2-3-150x150.jpg)