1週間で完成！ うさぎでもわかる確率分布と統計的な推測 3日目 確率密度関数

こんにちは、ももやまです。

今回は、数Bの「確率分布と統計的な推測」の分野の1つである「確率密度関数」について説明していきたいと思います。

※ 共通テストでは頻出する分野ではありませんが、次回解説する「正規分布」で少し「確率密度関数」の知識を使うので、時間があまりない人はざっと読んでおきましょう。

前回の「うさぎでもわかる確率分布と統計的な推測」2日目はこちら↓

www.momoyama-usagi.com

１．確率密度関数とヒストグラム

(1) ヒストグラムを細かく刻んでみよう

皆さんは、中1の「資料の整理」や数1の「データの分析」で、ヒストグラム*1を習いましたね。

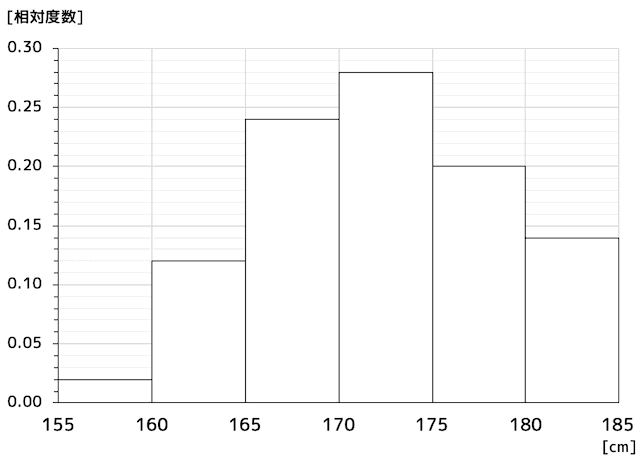
下の表は、大学1年生100人の身長を5cm単位で集計した表です。

	度数	相対度数
155〜160	2	0.02
160〜165	12	0.12
165〜170	24	0.24
170〜175	28	0.28
175〜180	20	0.20
180〜185	14	0.14
合計	100	1.00

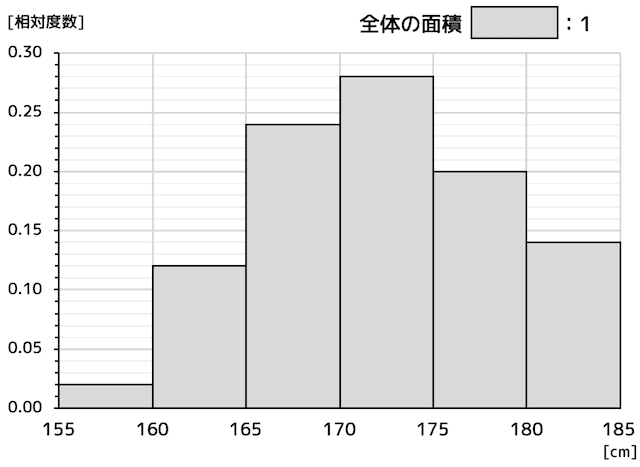
上の表の相対度数（全体の人数に対する割合）をヒストグラムにすると、下のようなグラフとなります。

さて、今は5cm単位でヒストグラムにしていましたが、1cm単位まで細かくしてみましょう。

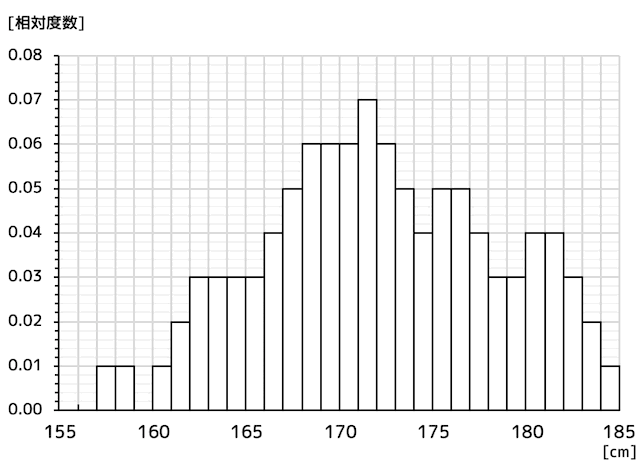
だいぶ細かくなりましたね。

さらに細かく細かく刻んでいき、横が微小の大きさになるまで刻んでいくと……

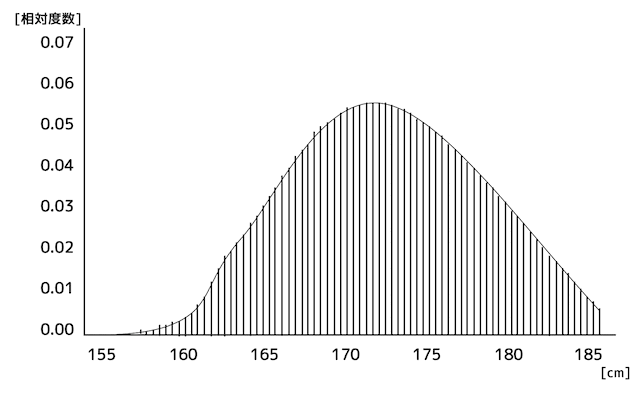
このようになめらかな曲線になりましたね。

ヒストグラムの区切り線を消しましょう。

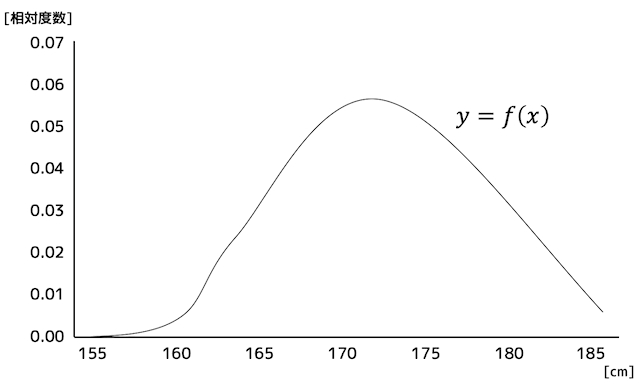
この曲線を、身長が のとき、相対度数が となる関数 と見ることができますね。

(2) 相対度数と確率

ところで、相対度数は、ある階級が全体の人数に対する割合を指していましたね。

再び大学1年生100人の身長測定結果の表を下に示します。

	度数	相対度数
155〜160	2	0.02
160〜165	12	0.12
165〜170	24	0.24
170〜175	28	0.28
175〜180	20	0.20
180〜185	14	0.14
合計	100	1.00

例えば、「身長が160cm以上165cm未満の人」は、100人中12人いるので、相対度数は「身長が160cm以上165cm未満の人」÷「全体（大学1年生100人）」より、0.12となります。

ここで、大学1年生100人から、無作為に1人選んだときに「身長が160cm以上165cm未満の人」である確率はどう計算できるか考えてみましょう。

確率は、「該当するすべてのパターン」÷「すべてのパターン」で求めることができますね。なので今回は、「身長が160cm以上165cm未満の人（12人）」÷「全体（大学1年生100人）」で確率を求められます。

つまり、相対度数というのは、無作為に1パターン選んだときに、ある階級に属する確率と言い換えることができますね。

(3) 確率密度関数ってなんだろう

すると、先程のグラフの [相対度数] の部分が [確率] に変わりますね（縦軸）。

ですが、ここで1つ問題が発生します。

(i) 確率密度とは・確率じゃだめなの？

先程のグラフは、ヒストグラムを細かく細かく刻んでしまっています。例えば、

• 身長が「170.0123141……cm」の人
• 身長が「160.0000000……cm」の人（全く狂いもなく160cmの人）

なんて人は絶対にいませんよね。そのため、細かく細かく刻んでしまうと、該当する階級の相対度数（確率）は0になってしまいます。このままだと、

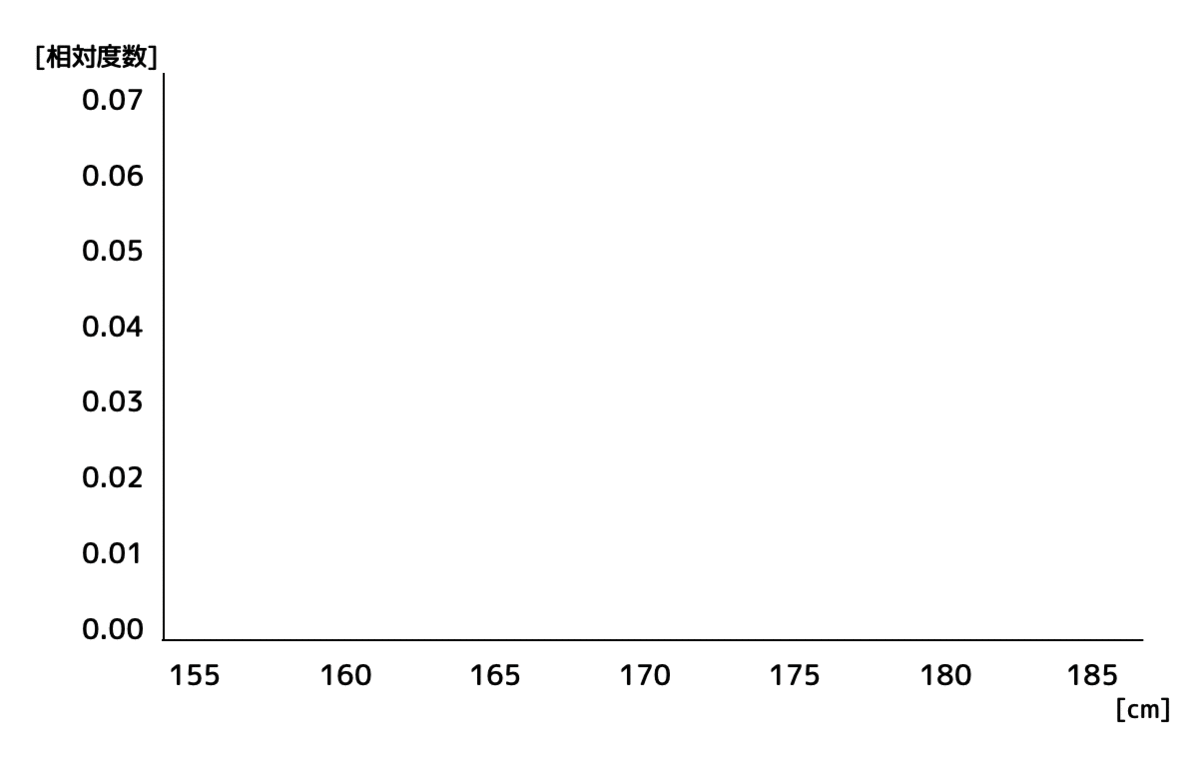
のようにどの階級の相対度数（つまり確率）も0になってしまいます。

そこで、細かく刻んだときの を確率ではなく、確率の密度とすることで、ピンポイントの値をしめしたときは確率0になっても、160cm〜165cmのようにある程度の範囲をしめしたときに確率が求められるようにするのです！

（具体的な求め方は次の章で説明します）

(ii) 確率密度関数をみてみよう

確率密度の話をしたので、いよいよ確率密度関数を見てみましょう。

下のグラフの関数 は、関数 は、ある確率変数 が の値となるときの確率密度 を示す関数となります。

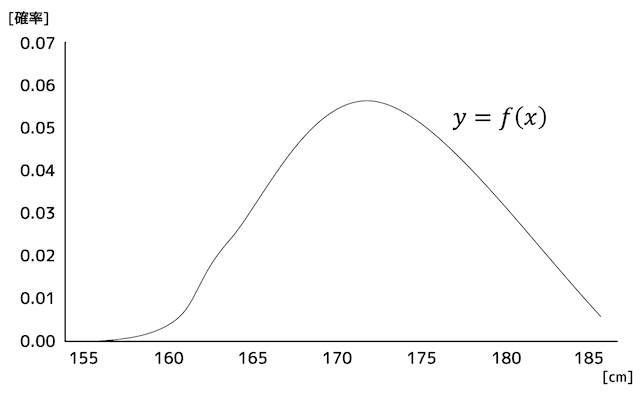
この関数をのことを確率密度関数と呼ぶのです！

なお、確率密度変数 で表される確率変数 は、連続的に値が変化する*2ため、連続的確率変数と呼ばれます。

つぎの章では、確率密度関数の定義の確認、そして確率密度関数から実際に確率を求める方法について説明していきましょう。

２．確率密度関数と面積

(1) 面積は確率だ！

またヒストグラムの話に戻りましょう。

	度数	相対度数
155〜160	2	0.02
160〜165	12	0.12
165〜170	24	0.24
170〜175	28	0.28
175〜180	20	0.20
180〜185	14	0.14
合計	100	1.00

当たり前ですが、（それぞれの階級の）相対度数をすべて足すと1になります。

そこで、ヒストグラム全体の面積（灰色部分）を1としましょう。

全体の面積を1とすると、例えば「160cm以上165cm未満」の部分を表している下のヒストグラムの灰色部分の面積は相対度数である0.12となりますね。

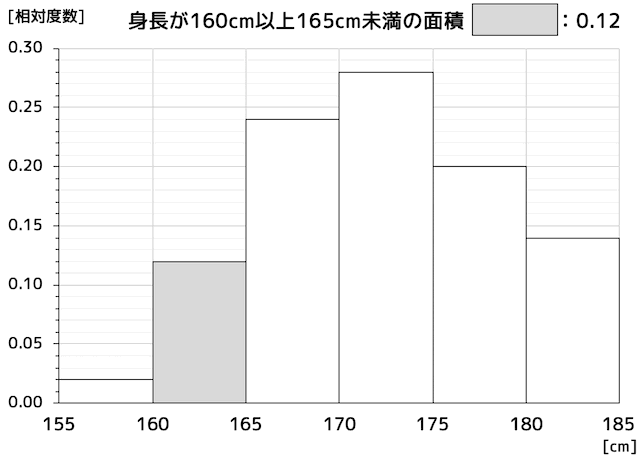
また、「第1章の(2)」で、ある階級Aの相対度数は「全体から無作為に1人選んだときに階級Aが選ばれる確率」と同じことを説明しましたね。

つまり、ヒストグラムの面積は、階級が選ばれる確率を表していることがわかりますね。

確率密度関数もヒストグラムと同じように面積がある範囲における確率を表しているのです！

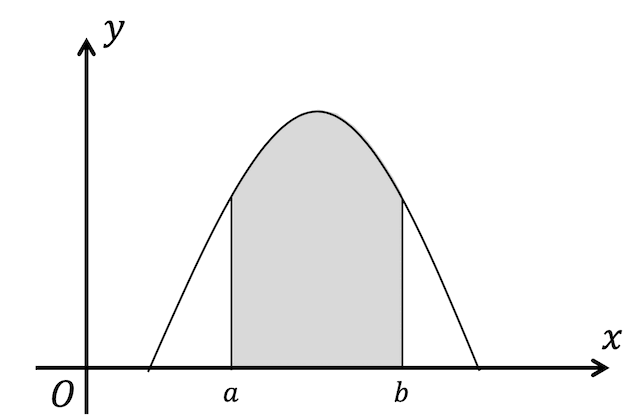
例えば下のグラフの灰色部分は、確率変数 が 以上 以下になる確率を表しています。

(2) 確率と積分

上のグラフで示される確率密度関数の灰色部分の面積、つまり が となる確率を考えてみましょう。

今回求めたい面積は、 にある 軸と関数 に囲まれた部分の面積ですね。

ここで、数2の「微分・積分」を思い出すと、ある関数 の , および 軸、関数 に囲まれた部分の面積は\[
\int^{b}_{a} f(x) \ dx
\]で求めることができますね。

つまり、確率変数 が確率密度関数で与えられるときの がある範囲となる確率は、積分で求めることができるのです！

３．確率密度関数で重要な4つのポイント

では、確率密度関数で抑えておくべき4つのポイントをまとめておきましょう。

確率密度関数で覚えておくべき4つの性質

確率密度関数 で与えられる確率変数 の取りうる値の範囲が とする。

このとき、

1. が となる確率は、積分\[
   \int^{b}_{a} f(x) \ dx
   \]で求めることができる。
2. 確率の和は当然1なので、 が （取りうる値全体）となる確率は当然1となる。数式で書くと、\[
   \int^{M}_{m} f(x) \ dx = 1
   \]である。
3. は、すべての実数 に対して となる。
   （確率の密度 は負にはなりえない。）
4. は、 となることもある。
   （ は確率ではなく、確率密度なので1を超えることがある。）

の重要な4つの性質がある。

たまに確率密度 が1を超えてるのを見て、「確率が1を超えてる！！」と言う人がいるのですが、上のポイントで抑えた通り、 は確率ではなく、確率密度なので1を超えることがある点を頭にいれておきましょう。

４．確率密度関数と平均・分散

(1) 確率が積分で求められる仕組み

第2章で「確率は積分で求められる」と説明しましたが、もう少し細かく積分で確率（つまり面積）が求まる仕組みをみていきましょう。

まず、 から の灰色部分を 方向が微小な大きさになるまで縦に刻むことを考えます。

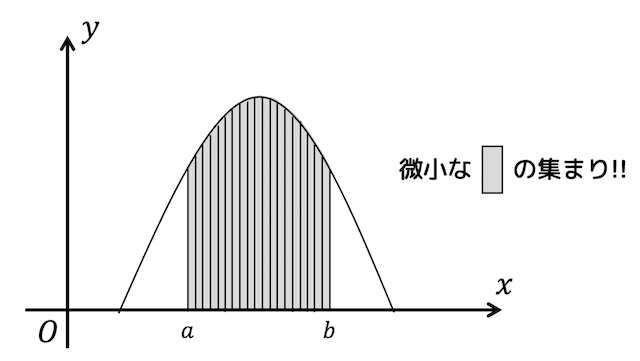
すると、灰色部分は、（横が）微小な長方形の集まりで表現することができますね。

この微小な長方形は「各階級におけるヒストグラムの棒の部分」だと思ってください。

数2の「微分・積分」で積分のイメージは、求めたい面積の部分を細かく刻んで、刻んだものをすべて足すと習いましたね。

先程、 が から の範囲にある、 にある 軸と関数 に囲まれた部分の面積は、\[
\int^{b}_{a} f(x) \ dx
\]で計算できると説明しました。

この数式\[
\int^{b}_{a} f(x) \ dx
\]の意味としては、 から の範囲にある「縦 、横 （微小に刻んだもの）の長方形の面積」を全部足したものとなります。

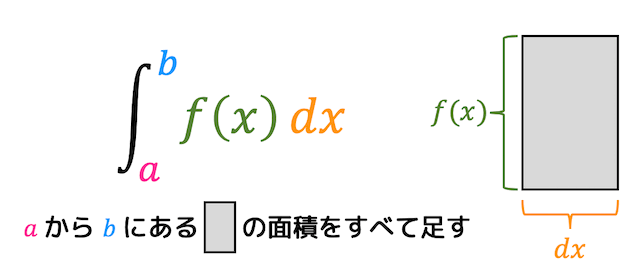
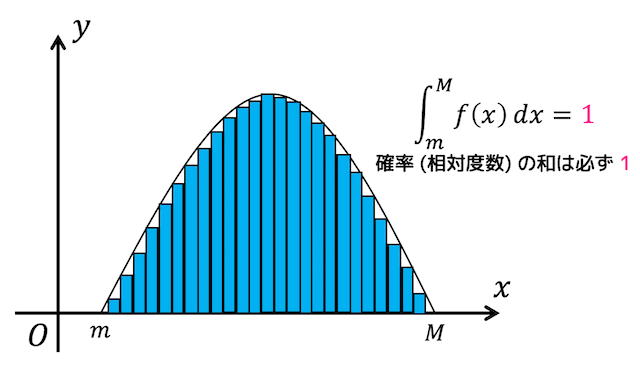
ところで、確率変数 の取りうる値の範囲が とするとき、\[
\int^{M}_{m} f(x) \ dx = 1
\]となることを「第3章」でまとめましたね。

これを図で表すと、「相対度数（確率）の和が1」が\[
\int^{M}_{m} f(x) \ dx = 1
\]に相当することがよりわかりやすくなるかと思います。

(2) 平均の求めかた

ある確率分布 の平均 は、「 のとりうる値 × となる確率」をすべて足したもので求めることができましたね。

確率密度関数 をもち、取りうる値の範囲が の連続型確率変数 が となる確率は、確率密度 を用いて と表せますね。

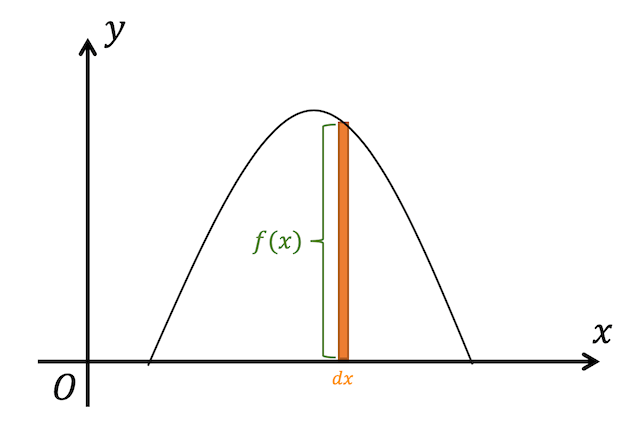
つまり、 となるときの確率が となるので、期待値 は、「 のとりうる値である と となる確率 の積」の和、つまり\[
\int^{M}_{m} x f(x) \ dx
\]を計算することで求められますね。

(3) 分散の求めかた

確率変数 の分散の求め方は2パターンありましたね。

1つは、「それぞれの の取りうる値と平均の差（偏差）を2乗したもの × となる確率」をすべて足したもの

もう1つは\[
V(X) = E ( X^2 ) - \left\{ E(X) \right\}^2 
\]で求めるパターン。

の2つがあります。

(i) 定義（偏差の2乗×それぞれの確率）で計算

確率密度関数では、 となるときの確率は確率密度 を用いて、 と表すことができましたね。

また、 のときの偏差の2乗は、平均 を用いて と表せますね。

なので、取りうる値の範囲が の確率変数 の分散 は、「偏差の2乗 と となる確率 の積」の和、つまり\[
\int^{M}_{m} (x - \mu )^2 f(x) \ dx
\]を計算することで求められますね。

しかし、こちらのパターンだと、 の因数分解がめんどくさいです。

そこで、「2乗平均 - 平均の2乗」で計算する方法にしましょう。

(ii) 2乗平均 - 平均の2乗で計算

確率密度関数では、 となるときの確率は確率密度 を用いて、 と表すことができましたね。

また、取りうる値の範囲が の2乗の平均 は、「 のとりうる値である と となる確率 の積」の和、つまり\[
E(X^2) = \int^{M}_{m} x^2 f(x) \ dx
\]で求められますね。

よって、分散 は、\[\begin{align*}
V(X) & = E ( X^2 ) - \left\{ E(X) \right\}^2
\\ & = \int^{M}_{m} x^2 f(x) \ dx - \left\{ E(X) \right\}^2
\end{align*}\]で求めることもできます。

基本的に「2乗平均 - 平均の2乗」で計算する方が計算時間が短くなるのでおすすめです。

５．練習問題

では、練習をしてみましょう！

なお、センター試験を想定しているため、穴埋め式としています。

（確率密度関数はどうしても積分計算が必要となってしまうため、確率密度関数の問題はそこまで出てきません。出しすぎると統計ではなく積分の問題になってしまうので……。）

練習1

取りうる値の範囲が  連続型確率変数 の確率密度関数 が\[
f(x) = kx(x-2)
\]で与えられている。

(1) このとき、 になる確率は、\[
\int^{2}_{0} f(x) \ dx = \left[ \ \ \ ア \ \ \ \right]
\]となるので、\[
k = \frac{ \left[ \ \ \ イウ \ \ \ \right] }{ \left[ \ \ \ エ \ \ \ \right] }
\]となる。

以下の問題では とする。

(2) さらに、 になる確率は、\[
\int^{1}_{0} f(x) \ dx = \frac{ \left[ \ \ \ オ \ \ \ \right] }{ \left[ \ \ \ カ \ \ \ \right] }
\]で求められ、 になる確率は、となる。

(3) 連続型確率変数 の平均 、分散 は、\[
E(X) = \left[ \ \ \ サ \ \ \ \right] , \ \ \ \ V(X) = \frac{ \left[ \ \ \ シ \ \ \ \right] }{ \left[ \ \ \ ス \ \ \ \right] }
\]となる。

(4) としたときの平均 、分散 は、\[
E(X) = \left[ \ \ \ セ \ \ \ \right] , \ \ \ \ V(X) = \frac{ \left[ \ \ \ ソ \ \ \ \right] }{ \left[ \ \ \ タ \ \ \ \right] }
\]となる。

練習2

取りうる値の範囲が  連続型確率変数 の確率密度関数 が\[
f(x) = \left\{ \begin{array}{l} \frac{1}{12} x \ \ \ ( 0 \leqq x \leqq 4) \\ - \frac{1}{6} (x-6) \ \ \ ( 4 \leqq x \leqq 6) \end{array}\right.
\]で与えられている。

(1) このとき、 になる確率は、、 になる確率は  、 になる確率は  である。

(2) 連続型確率変数 の平均 、標準偏差 はそれぞれ\[
E(X) = \frac{ \left[ \ \ \ カキ \ \ \ \right] }{ \left[ \ \ \ ク \ \ \ \right] }
\ \ \ \ \sigma (X) = \frac{ \sqrt{ \left[ \ \ \ ケコ \ \ \ \right] } }{ \left[ \ \ \ サ \ \ \ \right] }
\]となる。

６．練習問題の答え

解答1

(1)

は取りうる範囲全体なので当然確率は1となる。よって、\[
\int^{2}_{0} f(x) \ dx = 1
\]となる。（ア：1）

また、\[\begin{align*}
\int^{2}_{0} f(x) \ dx & = \int^{2}_{0} kx(x-2) \ dx
\\ & = \int^{2}_{0} kx^2 - 2kx \ dx
\\ & = \left[ \frac{1}{3} kx^3 - kx^2 \right]^{2}_{0}
\\ & =\frac{8}{3} k - 4k
\\ & = - \frac{4}{3} k
\end{align*}\]となるので、\[
- \frac{4}{3} k = 1 \\
k = \frac{-3}{4}
\]となる。（イウ：-3　エ：4）

(2)

となる確率は、\[\begin{align*}
\int^{1}_{0} f(x) \ dx & = \int^{1}_{0}  x(x-2)
\\ & = - \frac{3}{4} \int^{1}_{0}  x^2 - 2x
\\ & = - \frac{3}{4} \left[ \frac{1}{3} x^3 - x^2 \right]^{1}_{0}
\\ & = - \frac{3}{4} \left( \frac{1}{3} - 1 \right)
\\ & = - \frac{3}{4} \cdot \left( - \frac{2}{3} \right)
\\ & = \frac{1}{2}
\end{align*} \]となる。（オ：1　カ：2）

また、 となる確率は、\[\begin{align*}
\int^{\frac{3}{2}}_{\frac{1}{2}} f(x) \ dx & = \int^{\frac{3}{2}}_{\frac{1}{2}}  x(x-2)
\\ & = - \frac{3}{4} \int^{\frac{3}{2}}_{\frac{1}{2}} x^2 - 2x
\\ & = - \frac{3}{4} \left[ \frac{1}{3} x^3 - x^2 \right]^{\frac{3}{2}}_{\frac{1}{2}}
\\ & = - \frac{3}{4} \left( \left( \frac{1}{3} \cdot \frac{27}{8} - \frac{9}{4} \right) - \left( \frac{1}{3} \cdot \frac{1}{8} - \frac{1}{4} \right)   \right)
\\ & = - \frac{3}{4} \cdot \left( - \frac{9}{8} + \frac{5}{24} \right)
\\ & = - \frac{3}{4} \cdot \left( - \frac{22}{24} \right)
\\ & = \frac{11}{16}
\end{align*} \]となる。（キク：11　ケコ：16）

(3)

を取りうる連続型確率変数 の平均 は、\[\begin{align*}
E(X) & = \int^{2}_{0} x f(x) \ dx
\end{align*} \]で求められる。

よって、\[\begin{align*}
E(X) & = \int^{2}_{0}  x f(x) \ dx
\\ & = - \frac{3}{4} \int^{2}_{0} x^2 (x-2) \ dx
\\ & = - \frac{3}{4} \int^{2}_{0} x^3 - 2x^2 \ dx
\\ & = - \frac{3}{4} \left[ \frac{1}{4} x^4 - \frac{2}{3} x^3 \right]^{2}_{0}
\\ & = - \frac{3}{4} \left( 4 - \frac{16}{3} \right)
\\ & = - \frac{3}{4}\left(  - \frac{4}{3} \right)
\\ & = 1
\end{align*} \]となる。（サ：1）

また、 を取りうる連続型確率変数 の分散 は、\[\begin{align*}
V(X) & = E ( X^2 ) - \left\{ E(X) \right\}^2
\\ & = \int^{2}_{0} x^2 f(x) \ dx - \left\{ E(X) \right\}^2
\end{align*} \]で求められる。

ここで、2乗平均 は、\[\begin{align*}
E(X^2) & = \int^{2}_{0}  x^2 f(x) \ dx
\\ & = - \frac{3}{4} \int^{2}_{0} x^3 (x-2) \ dx
\\ & = - \frac{3}{4} \int^{2}_{0} x^4 - 2x^3 \ dx
\\ & = - \frac{3}{4} \left[ \frac{1}{5} x^5 - \frac{1}{2} x^4 \right]^{2}_{0}
\\ & = - \frac{3}{4} \left( \frac{32}{5} - 8 \right)
\\ & = - \frac{3}{4}\left(  - \frac{8}{5} \right)
\\ & = \frac{6}{5}
\end{align*} \]となるので分散 は、\[\begin{align*}
V(X) = E ( X^2 ) - \left\{ E(X) \right\}^2
\\ & = \int^{2}_{0} x^2 f(x) \ dx - \left\{ E(X) \right\}^2
\\ & = \frac{6}{5} - 1^2
\\ & = \frac{1}{5}
\end{align*} \]（シ：1　ス：5）

(4)

平均 、分散 はそれぞれ\[
E(X) = 1 , \ \ \ \ \ V(X) = \frac{1}{5}
\]なので、 としたときの平均 は、\[\begin{align*}
E(Y) & = E(2X+3)
\\ & = E(2X) + 3
\\ & = 2E(X) + 3
\\ & = 2 \cdot 1 + 3
\\ & = 5
\end{align*} \]となる。（セ：5）

また、分散 は、\[\begin{align*}
V(Y) & = V(2X+3)
\\ & = V(2X)
\\ & = 2^2 V(X) 
\\ & = 4 \cdot \frac{1}{5}
\\ & = \frac{4}{5}
\end{align*} \]となる。（ソ：4　タ：5）

解答2

(1)

は取りうる範囲全体なので当然確率は1となる。

（ア：1）

また、 となる確率は、\[\begin{align*}
\int^{3}_{0} f(x) \ dx & = \int^{3}_{0} \frac{1}{12} x \ dx
\\ & = \frac{1}{12} \int^{3}_{0} x \ dx
\\ & = \frac{1}{12} \left[ \frac{1}{2} x^2 \right]^{3}_{0}
\\ & = \frac{3}{8}
\end{align*} \]と計算できる。（イ：3　ウ：8）

[別解]

図示すると、下のような三角形の部分の面積を求めればOKなことがわかる。

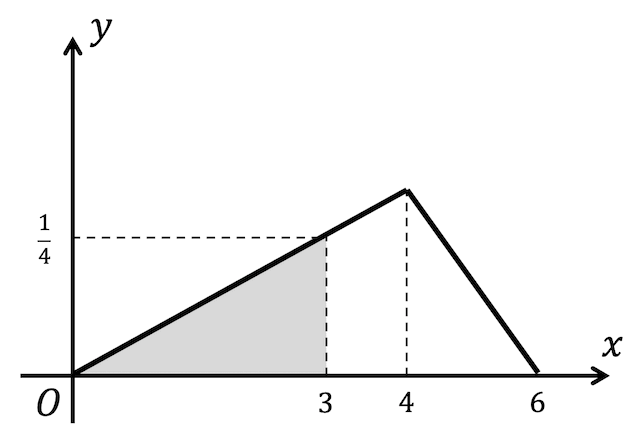
よって、\[
\frac{1}{2} \cdot 3 \cdot \frac{1}{4} = \frac{3}{8}
\]と求めてもOK。

さらに となる確率は、全体（）となる確率から、 となる確率を引くことで求められる。よって、\[
1 - \frac{3}{8} =  \frac{5}{8}
\]と計算できる。（エ：5　オ：8）

[別解]

真面目に計算すると、 となる部分は、\[\begin{align*}
\int^{6}_{3} f(x) \ dx & = \int^{4}_{3} \frac{1}{12} x \ dx + \int^{6}_{4} - \frac{1}{6} (x-6)
\\ & = \int^{4}_{3} \frac{1}{12} x \ dx - \int^{6}_{4} \frac{1}{6} (x-6)
\end{align*} \]で求められる。\[\begin{align*}
\int^{4}_{3} \frac{1}{12} x \ dx & = \left[ \frac{1}{24} x^2 \right]^{4}_{3}
\\ & = \frac{1}{24} ( 16 - 9 ) = \frac{7}{24}
\end{align*} \]\[\begin{align*}
\int^{6}_{4} \frac{1}{6} (x-6)\ dx & = \int^{6}_{4} \frac{1}{6} x - 1 \ dx
\\ & = \left[ \frac{1}{12} x^2 - x \right]^{6}_{4}
\\ & = 3 - 6 - \left( \frac{4}{3} - 4 \right)
\\ & = -3 + \frac{8}{3}
\\ & = - \frac{1}{3}
\end{align*} \]となるので、\[\begin{align*}
\int^{6}_{3} f(x) \ dx & = \int^{4}_{3} \frac{1}{12} x \ dx + \int^{6}_{4} - \frac{1}{6} (x-6)
\\ & = \frac{7}{24} + \frac{1}{3} \\ & = \frac{5}{8}
\end{align*} \]となる。

(2)

連続型確率変数 の期待値 は、\[\begin{align*}
\int^{6}_{0} x f(x) \ dx & = \int^{4}_{0} \frac{1}{12} x^2 \ dx + \int^{6}_{4} - \frac{1}{6} x(x-6)
\\ & = \int^{4}_{0} \frac{1}{12} x^2 \ dx - \int^{6}_{4} \frac{1}{6} x^2 - x \ dx
\end{align*} \]で求められる。

ここで、\[\begin{align*}
\int^{4}_{0} \frac{1}{12} x^2 \ dx & = \left[ \frac{1}{36} x^3 \right]^{4}_{0}
\\ & = \frac{1}{36} \cdot 64
\\ & = \frac{16}{9}
\end{align*} \]\[\begin{align*}
\int^{6}_{4} \frac{1}{6} x^2 - x \ dx & = \left[ \frac{1}{18} x^3 - \frac{1}{2} x^2 \right]^{6}_{4}
\\ & = 12 - 18 - \left( \frac{32}{9} - 8 \right)
\\ & = 2 - \frac{32}{9}
\\ & = - \frac{14}{9}
\end{align*} \]となるので、\[\begin{align*}
E(X) & = \int^{4}_{0} \frac{1}{12} x^2 \ dx - \int^{6}_{4} \frac{1}{6} x^2 - x \ dx
\\ & = \frac{16}{9} - \left( - \frac{14}{9} \right)
\\ & = \frac{10}{3}
\end{align*}\]となる。（カキ：10　ク：3）

また、標準偏差 は、\[
\sigma (X) = \sqrt{ V(X) }
\]で求められるので、まず分散 を求める。

連続型確率変数 の2乗平均 は、\[\begin{align*}
\int^{6}_{0} x^2 f(x) \ dx & = \int^{4}_{0} \frac{1}{12} x^3 \ dx + \int^{6}_{4} - \frac{1}{6} x^2 (x-6)
\\ & = \int^{4}_{0} \frac{1}{12} x^3 \ dx - \int^{6}_{4} \frac{1}{6} x^3 - x^2 \ dx
\end{align*} \]で求められる。

ここで、\[\begin{align*}
\int^{4}_{0} \frac{1}{12} x^3 \ dx & = \left[ \frac{1}{48} x^4 \right]^{4}_{0}
\\ & = \frac{1}{36} \cdot 64
\\ & = \frac{16}{3}
\end{align*} \]\[\begin{align*}
\int^{6}_{4} \frac{1}{6} x^3 - x^2 \ dx & = \left[ \frac{1}{24} x^4 - \frac{1}{3} x^3 \right]^{6}_{4}
\\ & = 54 - 72 - \left( \frac{32}{3} - \frac{64}{3} \right)
\\ & = - 18 + \frac{32}{3}
\\ & = - \frac{22}{3}
\end{align*} \]となるので、\[\begin{align*}
E(X^2) & = \int^{4}_{0} \frac{1}{12} x^3 \ dx - \int^{6}_{4} \frac{1}{6} x^3 - x^2 \ dx
\\ & = \frac{16}{3} + \frac{22}{3}
\\ & = \frac{38}{3}
\end{align*}\]となる。

よって、分散 は、\[\begin{align*}
V(X) & = E ( X^2 ) - \left\{ E(X) \right\}^2
\\ & = \int^{M}_{m} x^2 f(x) \ dx - \left\{ E(X) \right\}^2
\\ & = \frac{38}{3} - \left( \frac{10}{3} \right)^2
\\ & = \frac{14}{9}
\end{align*}\]となるので、標準偏差 は、\[\begin{align*}
\sigma (X) & = \sqrt{ V(X) }
\\ & = \frac{ \sqrt{14} }{3}
\end{align*} \]となります。（ケコ：14　サ：3）

おまけ　三角形の重心と平均

練習2の確率密度関数のグラフ と 軸で囲まれたグラフは、下の灰色部分のような三角形となりますね。

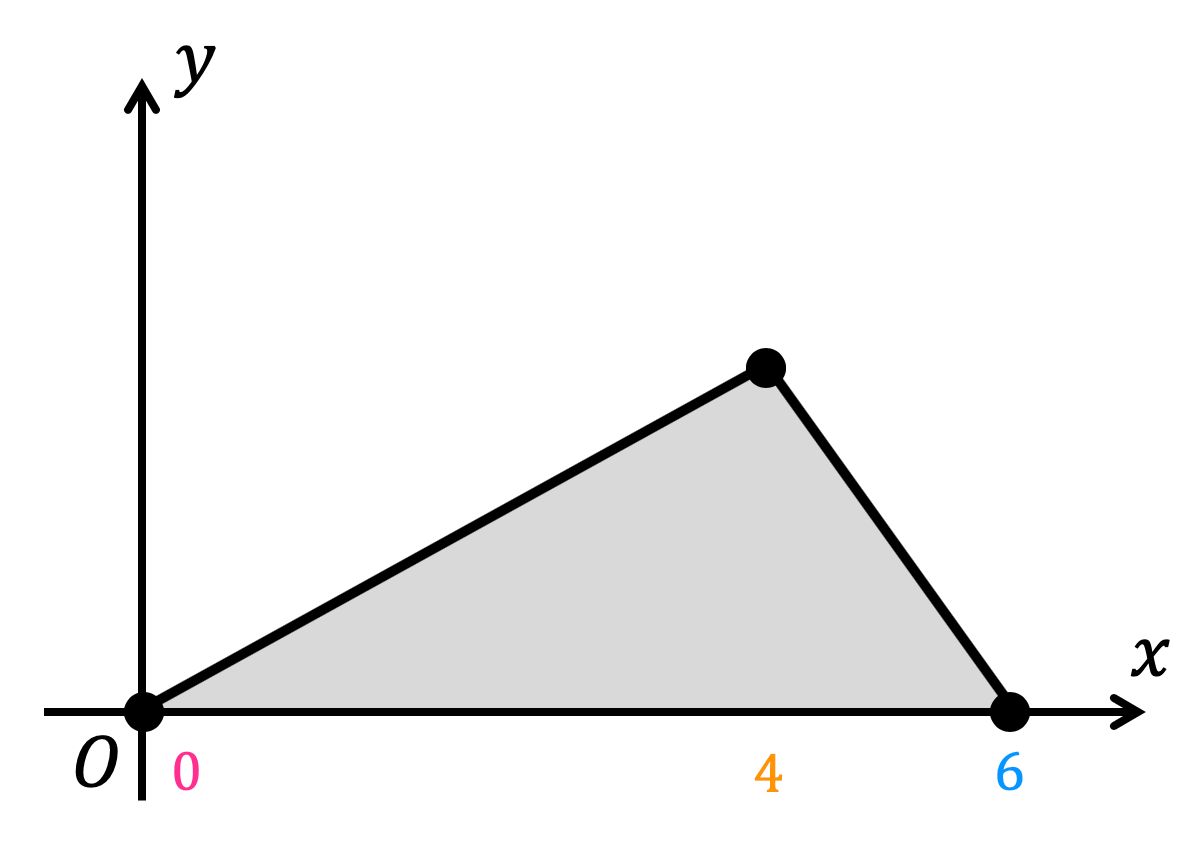
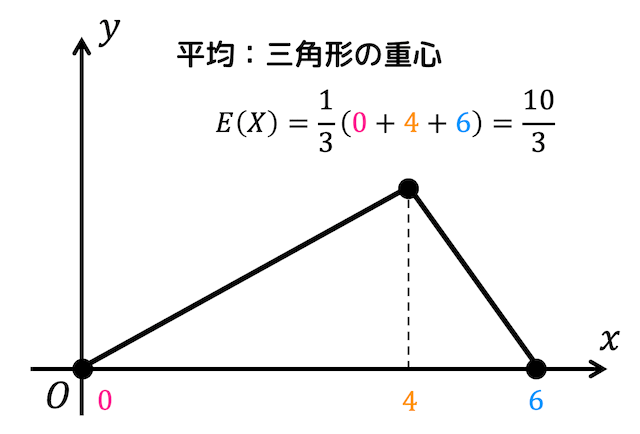
上の三角形の重心の 座標は、\[
\frac{1}{3} ( 0 + 4 + 6 ) = \frac{10}{3}
\]と計算できます。

あれ、先程求めた平均 と一致しましたね！

実は、連続型確率変数 の平均 の図形的意味は、, 、 軸、確率密度関数 で囲まれる図形の重心の 座標となるのです！

ですが、図形によっては重心を求めるために大学数学で習う積分（二重積分）を使う必要があり、かなり大変です。

ですが3点の 座標が , , の三角形の重心であれば\[
\frac{1}{3} ( x_1 + x_2 + x_3 )
\]と簡単に求められますね。

そのため、練習2のような囲まれる部分が三角形となる場合の平均 は、重心を使うことであっという間に求めることができるのです！

, 、 軸、確率密度関数 で囲まれる図形が三角形のときの平均 は三角形のそれぞれの頂点の 座標 , , を用いて\[
x = \frac{1}{3} ( x_1 + x_2 + x_3)
\]で求められる。

囲まれる部分が三角形のときの平均 E(X)

７．さいごに

今回は、「確率分布と統計的な推測」の分野に出てくる「確率密度関数」について説明しました。

実際に今回の練習問題のように積分を計算させるような問題はほとんど出てこないですが*3、「確率密度関数」がどんなものなのかは頭にいれておきましょう。

次回は、「確率分布と統計的な推測」の分野に出てくる最も大切な分布の1つである「正規分布」について説明していきたいと思います。

ということで、いつものように下にまとめを書いていきたいと思います。

まとめ

確率密度関数 のイメージは、ヒストグラムを細かく細かく刻んだもの。

を取りうる連続型確率変数 が確率密度関数 で与えられる

このとき、 となる確率は、積分\[
\int^{b}_{a} f(x) \ dx
\]で求めることができる。また、確率の総和は1なので\[
\int^{M}_{m} f(x) \ dx = 1
\]も成立する。

また、連続型確率変数の平均 は\[
E(X) = \int^{M}_{m} x f(x) \ dx
\]で求められ、分散 は\[
V(X) = \int^{M}_{m} x^2 f(x) \ dx - \left\{ E(X) \right\}^2
\]で求められる。

*1:長方形の柱で度数分布を表すグラフのことです。棒グラフに似ていますが、棒グラフとは少し異なります。

*2:今まで出てきた確率変数 は連続的に値が変化しません（離散型確率変数と呼ばれます。）。例えば、コインの表が出た回数を とする場合、 が2.5のように小数になることはありませんね。なので連続的に値は変化するとは言えませんね。

*3:統計ではなく積分の問題になっちゃうので