うさぎでもわかる解析　Part11　広義積分（広義積分の基本と注意点）・優関数の原理

こんにちは、ももやまです。
今回は広義積分のまとめをしたいと思います。

 

 

スポンサードリンク

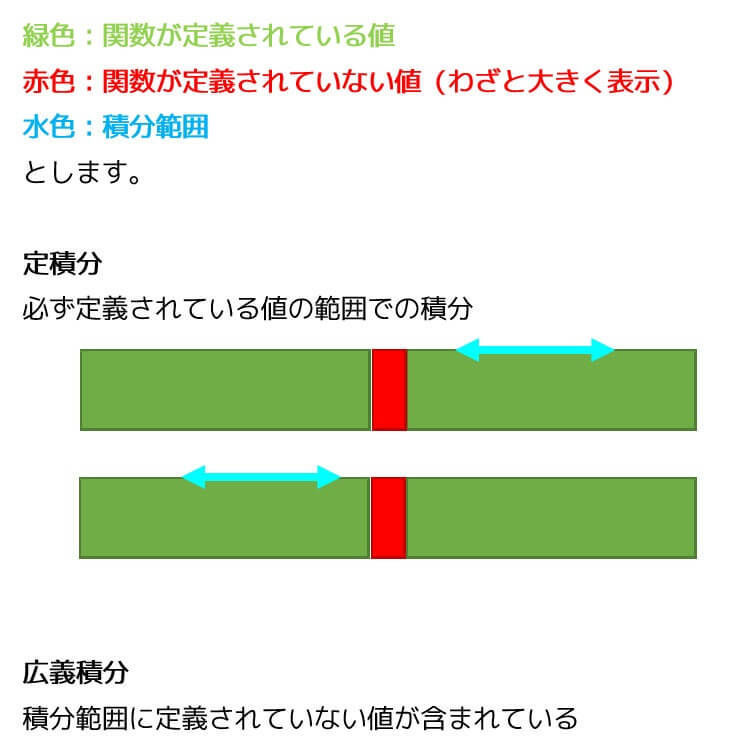
１．普通の定積分と広義積分の違い

定積分では積分範囲が定義されている値の範囲に必ず含まれていました。

積分範囲を直線状に図示すると下のようになります。

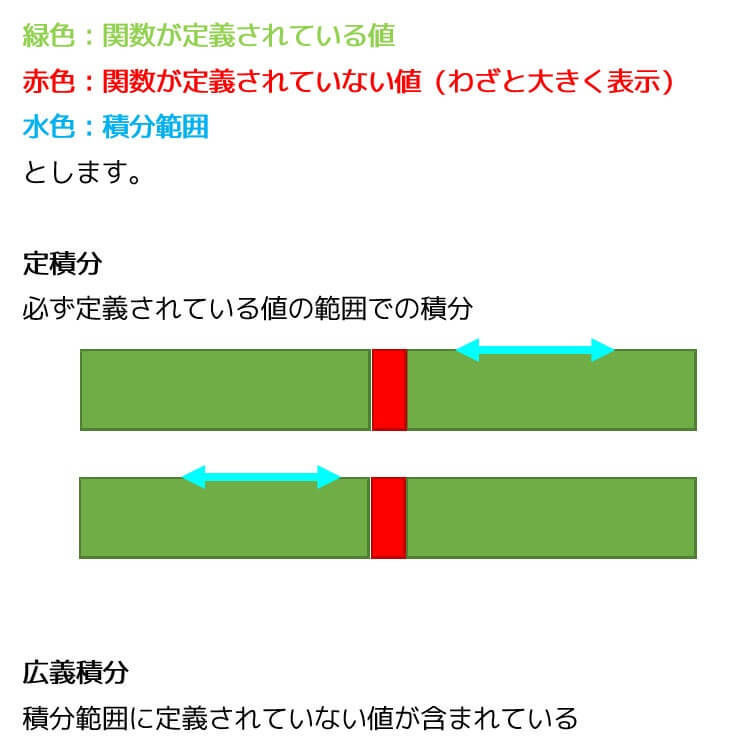
しかし広義積分では、積分範囲が積分をする関数（被積分関数）で定義されていない場合や、無限大方向での積分などが含まれます。

そのため、一旦定義されない部分を文字でおいてから極限を取ります。

流れとしては、

1. 定義されていない範囲を一旦文字でおく
2. 文字でおいた部分の極限をとる（ぎりぎり定義域を外れないように）

となります。

では、様々な広義積分の例を見てみましょう。

パターン1　積分範囲の端が定義されない値の場合

図で表すとこのような形となります。

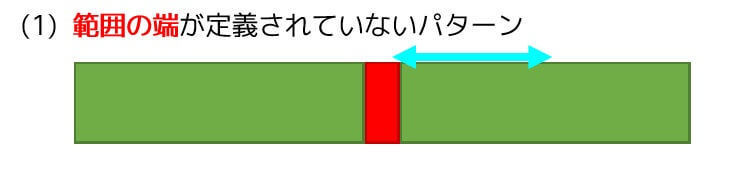
まずは、一番基本的なパターンを見ていきましょう。

例題1

広義積分\[ \int^{1}_0 \frac{1}{\sqrt{x}} \ \ dx \]を求めなさい。 

解説1

まずだめな答案を示します。\[\begin{align*} \int^{1}_0 \frac{1}{\sqrt{x}} \ \ dx & = \left[ 2 \sqrt{x} \right]^{1}_0
\\ & = 2 - 2 \sqrt{0} = 2 
\end{align*} \]皆さんは思うはずです。

別に何もおかしいところはないじゃん！！　と。

しかしよく見てください。\( x = 0 \) のとき、被積分関数の値は \( \frac{1}{0} \) というおかしな値になりますね。

なので、これは普通の積分ではなく、広義積分を使って解いてあげなければなりません。

 

では、正しい答えを示します。

積分される関数は、\( x = 0 \) では定義されていませんね。

この場合は、一旦0の部分を \( t \) （記号はなんでもいい）とし、あとで \( t \) を0に近づける極限を取ってあげればOKです。

（ちなみに一番使われる記号は微小な値を指し示す \(  \epsilon \) です。あまり使いたくないので勝手に \( t \) を使っています。）

 

\[\begin{align*} \int^{1}_t \frac{1}{\sqrt{x}} \ \ dx & = \left[ 2 \sqrt{x} \right]^{1}_t
\\ & = 2 - 2 \sqrt{t} 
\end{align*} \]となる。

 

あとは、\( t \) が含まれている数式部分の極限を求めます。\[ \lim_{t \to +0} \sqrt{t} = 0 \]となるので、 \[ \int^{1}_0 \frac{1}{\sqrt{x}} \ \ dx = 2 \]と求めることができます。

 

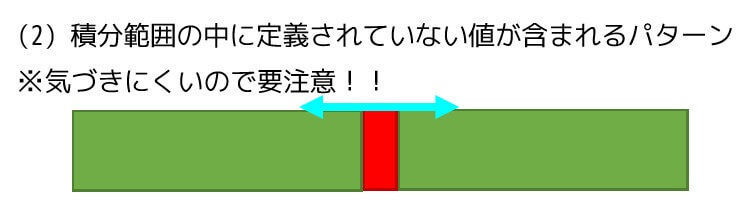
パターン2　積分範囲内に定義されない値が含まれている場合

ある程度学習した人でも気付きにくいパターンなので特に注意してください。

積分範囲の端は定義されているが、積分範囲内に定義されていない値が含まれているパターンです。

図にすると下のようになります。

例題2

広義積分\[ \int^{1}_{-1} \frac{1}{x^2} \ \ dx \]を求めなさい。 

解説2

×だめな答案例（要注意!!）

あ、これ簡単じゃーん。\[\begin{align*} \int^{1}_{-1} \frac{1}{x^2} \ \ dx & = \left[ - \frac{1}{x} \right]^{1}_{-1}
\\ & = -1 - 1 = -2
\end{align*} \]よく見てみましょう。その関数、\( x = 0 \) で定義されてませんよ。

 

○正解

この問題の場合は、定義されてない値が積分範囲の間に含まれていますね。
そのため、定義されている値を避けて積分をしなければなりません。

 

定義されている値を避けるには、

• 積分のはじめの値 → 定義されていない値よりもわずかに小さい値
• 定義されてない値よりもわずかに大きい値 → 積分の終わりの値

の２つにわけて定義域を外れないように積分をする必要があります。

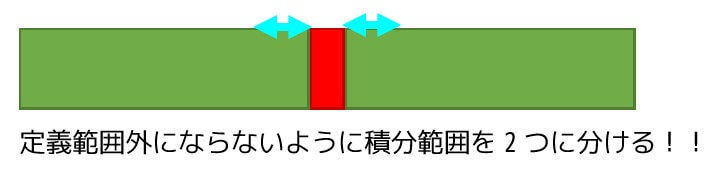
今回の場合、\( x = 0 \) が定義されていないので、\( x = -1 \) から、\( x = 0 \) よりほんの少しだけ小さい値と \( x = 0 \) よりほんの少し大きい値から \( x = 1 \) までの2つにわけて計算します。そのため、\[\begin{align*} \int^{1}_{-1} \frac{1}{x^2} \ \ dx & =\lim_{t \to +0} \int^{-t}_{-1} \frac{1}{x^2} \ dx + \lim_{t \to +0} \int^{1}_{t} \frac{1}{x^2} \ dx
\end{align*} \]の2つに分解されます。

実際に2つの積分を計算します。

１つ目\[\begin{align*} \int^{-t}_{-1} \frac{1}{x^2} \ \ dx & = \left[ - \frac{1}{x} \right]^{-t}_{-1}
\\ & = -1 + \frac{1}{t}
\end{align*} \] \[ \lim_{t \to +0} \frac{1}{t} = \infty \] となり、\[ \int^{-t}_{-1} \frac{1}{x^2} \ \ dx = \infty \]

 

\[\begin{align*} \int^{1}_{t} \frac{1}{x^2} \ \ dx & = \left[ - \frac{1}{x} \right]^{1}_{t}
\\ & = -1 + \frac{1}{t}
\end{align*} \] \[ \lim_{t \to +0} \frac{1}{t} = \infty \] となり、\[ \int^{1}_{t} \frac{1}{x^2} \ \ dx = \infty \]となり、2つの広義積分はともに無限大に発散するので、\[ \int^{1}_{-1} \frac{1}{x^2} \ \ dx = \infty \]となり、無限大に発散することがわかる。

（2つに分解した際に、どちらか片方でも広義積分が発散した場合、分解する前の極限も発散するので実はわざわざ2つとも調べる必要はありません。）

 

 

パターン3　積分範囲に無限大が含まれている場合

このパターンは積分範囲に無限大が入っているので広義積分かどうかが非常に判断しやすいです。

図にすると下のようになります。

例題3

広義積分\[ \int^{\infty}_{0} \frac{1}{(1+x)^4} \ \ dx \]を求めなさい。 

解説3

範囲に無限大があるので一旦 \( R \) と置く。

\[\begin{align*} & \int^{R}_{0} \frac{1}{(1+x)^4} \ dx 
\\ = &  \int^{R}_{0} (1+x)^{-4} \ dx
\\ = & \left[ - \frac{1}{3} (1+x)^{-3} \right]^{R}_{0}
\\ = & - \frac{1}{3} (1+R)^{-3} + \frac{1}{3}
\\ = &  \frac{1}{3} - \frac{1}{3(1+R)^3}
\end{align*} \]となる。

あとは、\( R \) を無限大に飛ばせばよい。\[ \lim_{R \to \infty} \frac{1}{3(1+R)^3} = 0 \]より、\[\begin{align*}  \int^{\infty}_{0} \frac{1}{(1+x)^4} \ \ dx 
 = \frac{1}{3}
\end{align*} \]となる。

スポンサードリンク

２．注意！　偶関数・奇関数の広義積分

皆さんは偶関数、奇関数のときは次の公式を習っていると思います。

 

しかし、広義積分のときはこの公式の適用には注意が必要です。

収束の可能性を判定してからでないと公式は適用できません。

奇関数の場合（要注意！！）

積分関数が奇関数の場合は特に注意が必要です。

例題4

次の広義積分を求めなさい。\[ \int^{\infty}_{- \infty}  x \cos x \ dx \]

 

解説4

×だめな答案例（要注意!!）

あ、ラッキー！！　積分関数は奇関数じゃん！！\[ \int^{\infty}_{- \infty}  x \cos x \ dx = 0\]典型的な間違いの例です。

その広義積分、本当に収束しますか？

 

○正解

範囲を

• 負の無限大 → 0
• 0 → 正の無限大

にわけてみましょう。

わけたあとは部分積分を使いましょう。

連鎖公式（ブンブン・瞬間部分積分）が使えます。\[\begin{align*}
& \int^{R}_{0} x  \cos x  \ dx
\\ = & \left[ x (\sin x) - 1 (- \cos x)    \right]^{R}_{0}
\\ = & R \sin R + \cos R - 1
\end{align*} \]と計算ができる。ここで極限をとる。\[ \lim_{R \to \infty} R \sin R + \cos R - 1 \]の計算は発散してしまい、計算することができない。

（この時点で問題の広義積分は発散することが確定するので、試験などのときはここで問題の広義積分が発散することを言ってもOK）

 

同様に\[\begin{align*}
& \int^{0}_{-R} x  \cos x  \ dx
\\ = & \left[ x (\sin x) - 1 (- \cos x)    \right]^{0}_{-R}
\\ = & - R \sin R - \cos R + 1
\end{align*} \]と計算できる。同様に極限を取ると発散をする。

 

なので、上記の広義積分は発散する。

偶関数の場合

偶関数の場合は、広義積分が収束する*1場合は、\[ \int^{a}_{-a} f(x) dx = 2 \int^{a}_{-a} f(x) dx \]が成立できるので偶関数の計算には使っても構いません。

例題5

次の広義積分を求めなさい。\[ \int^{\infty}_{- \infty}  \frac{1}{1+x^2} \ dx \]

 

解説5

偶関数であることを使わずに地道に解いた場合

\[ \begin{align*}
\int^{R}_{-R}  \frac{1}{1+x^2} \ dx
= & \left[ \tan^{-1} x \right]^{R}_{-R}
\\ = & \tan^{-1} R - \tan^{-1} \left( -R \right)
\end{align*} \]となる。ここで極限をとる。\[ \lim_{R \to \infty} \tan^{-1} R - \tan^{-1} \left( -R \right) = \frac{\pi}{2} + \frac{\pi}{2} = \pi \]と計算ができるので、\[ \int^{\infty}_{- \infty}  \frac{1}{1+x^2} \ dx = \pi \]となる。

偶関数であることを使った場合

\[ \begin{align*}
\int^{R}_{-R}  \frac{1}{1+x^2} \ dx
2 \int^{R}_{0}  \frac{1}{1+x^2} \ dx
= & \left[ \tan^{-1} x \right]^{R}_{0}
\\ = & \tan^{-1} R 
\end{align*} \]となる。ここで極限をとる。\[ \lim_{R \to \infty} \tan^{-1} R = \frac{\pi}{2} \]と計算ができるので、\[ \int^{\infty}_{- \infty}  \frac{1}{1+x^2} \ dx = \pi \]となる。

 

 

 

スポンサードリンク

３．優関数の原理

実際に広義積分が収束するのかを計算するのが難しい関数でも、より大きくて計算しやすい関数が同じ積分範囲内で収束することを示せば、計算するのが難しい関数でも収束することを示すことができます。

これを優関数の原理といいます。なお、この原理では、収束することは示せても、どの値に収束するのかはわかりません。

 

より詳細な定理を下に記述しました。 

 

 

例題6

広義積分\[ \int^{\infty}_{0} e^{-x} \sin^3 x \ dx \]が収束することを示しなさい。

 

解答6

（計算しなさいではなく、収束することを示しなさいの場合は優関数の原理を使うのが高いと思ってください。）

\( | \sin x | \leqq 1 \) を満たすので、\( | \sin^3 x | \leqq 1 \) も当然満たす。

なので、積分範囲内では常に \[ \left| e^{-x} \sin^3 x \right| \leqq e^{-x} \]となる。

なので、\[ \int^{\infty}_{0} e^{-x} \ dx \]が収束することを示せばよい。

 

ここで、\[\begin{align*}  \int^{R}_{0} e^{-x} \ dx 
= &  \left[ - e^{-x} \right]^R_{0}
\\ = & -e^{-R} + 1
\\ = & 1 - \frac{1}{e^R}
\end{align*} \]となる。ここで、\[ \lim_{R \to \infty} \frac{1}{e^R} = 0 \]より、\[ \begin{align*}  \int^{\infty}_{0} e^{-x}  \ dx 
 = 1
\end{align*} \]となり、収束する。

よって、\[ \int^{\infty}_{0} e^{-x} \sin^3 x \ dx \]も収束することが示された。

（実際に計算すると3/10となります。）

 

４．練習問題

では、実際に何問か広義積分の練習をしましょう。

練習1

つぎの広義積分の値を求めなさい。

(1) \[ \int^{1}_{0} \frac{1}{\sqrt{1-x^2}} \ dx \]

(2) \[ \int^{1}_{ -\frac{1}{2} } \frac{1}{\sqrt{2x + 1}} \ dx \]

(3) \[ \int^{\infty}_{1} x e^{-x} \ dx \]

(4) \[ \int^{3}_{0} \log x \ dx \]

 

練習2

つぎの問いに答えなさい。

(1)

つぎの広義積分

\[ \int^{\infty}_{0} x e^{-x^2} \ dx \]の値を求めなさい。

(2)

つぎの広義積分

 \[ \int^{\infty}_{0} e^{-x^2} \ dx \]が収束することを示しなさい。
（この数式はガウス積分と呼ばれます。）

 

練習3

次の広義積分、収束するか、しないか。

理由をつけて答えなさい。

(1) \[ \int^{\infty}_{0} \frac{ \cos x}{1+x^2} \ dx \]

(2) \[ \int^{1}_{-1} \frac{x}{x^2-1} \ dx \]

(3) \[ \int^{\infty}_{- \infty} \frac{1}{\sqrt{1+x^4}} \ dx \]

 

 

５．練習問題の答え

解答1

(1) 

被積分関数は \( x = 1 \) のとき定義されていない。

なので、1に少しだけ小さい値まで積分して最後に極限をとればよい。

まずは積分計算。1だけ少し小さい値は \( 1 - t \) とすればOK。\[\begin{align*}  \int^{1-t}_{0} \frac{1}{\sqrt{1-x^2}} \ dx 
 = &  \left[ \sin^{-1} x \right]^{1-t}_0
\\ = & \sin^{-1} \left(1-t \right)  - \sin^{-1} 0 
\\ = & \sin^{-1} \left(1-t \right)
\end{align*} \]となる。ここで、\[ \lim_{t \to +0} \sin^{-1} \left(1-t \right) = \frac{\pi}{2} \]より、\[ \begin{align*} \int^{1}_0 \frac{1}{\sqrt{1-x^2}} \ dx 
 = \frac{\pi}{2}
\end{align*} \]と計算できる。

 

(2)

被積分関数は積分開始地点である \( x = -1/2 \) のとき定義されていない。

なので、\( -1/2 \) より少し大きい値から積分をしてあげればよい。

\[\begin{align*}  \int^{1}_{-\frac{1}{2} + t} \frac{1}{\sqrt{2x + 1}} \ dx 
= & \frac{1}{2} \int^{1}_{-\frac{1}{2} + t} \frac{2}{\sqrt{2x + 1}} \ dx 
\\ = & \frac{1}{2} \left[ 2\sqrt{2x+1} \right]^{1}_{-\frac{1}{2} + t}
\\ = &  \sqrt{3} - \sqrt{2t}
\end{align*} \]となる。ここで、\[ \lim_{t \to +0} \sqrt{2t} = 0 \]より、\[ \begin{align*} \int^{1}_{-\frac{1}{2} + t} \frac{1}{\sqrt{2x + 1}} \ dx 
 = \sqrt{3}
\end{align*} \]と計算できる。

 

(3)

範囲に無限大が含まれたタイプの広義積分。

部分積分（ブンブン可）で求める。

\[\begin{align*} & \int^{R}_{1} x e^{-x} \ dx 
\\ = & \left[ x \left( -e^{-x} \right) - e^{-x} \right]^{R}_{1}
\\ = & \left[ -(x+1) e^{-x}  \right]^{R}_{1}
\\ = &  -e^{-R} (R+1) + 2 e^{-1}
\\ = &  \frac{2}{e} - \frac{R+1}{e^R}
\end{align*} \]となる。ここで、\[ \lim_{R \to \infty} \frac{R+1}{e^R} = 0 \]より、\[ \begin{align*} \int^{R}_{1} x e^{-x} \ dx 
 = \frac{2}{e}
\end{align*} \]と計算できる。

 

(4)

被積分関数は \( x = 0 \) のとき定義されていない。

なので、0に少しだけ大きい値まで積分して最後に極限をとればよい。\[\begin{align*}  \int^{3}_{t} \log x \ dx 
= &  \left[ x \log x - x \right]^{3}_{t}
\\ = &  3 \log 3 - 3 - \left( t \log t - t \right)
\end{align*} \]となる。ここで、\[\begin{align*} \lim_{t \to +0} t \log t - t & = \lim_{t \to +0} t ( \log t - 1 )  \\ & = \lim_{t \to +0} \frac{\log t - 1}{\frac{1}{t}} \\ & =
\lim_{t \to +0} \frac{ \frac{1}{t} }{- \frac{1}{t^2}}
\\ & = \lim_{t \to +0} -t = 0
\end{align*} \]より、\[ \begin{align*} \int^{3}_{t} \log x \ dx 
 = 3 \log 3 - 3
\end{align*} \]となる。

 

解答2

(1)

無限大が含まれる積分なので、一旦 \( R \) とおいてあとで無限大に極限を飛ばす。\[\begin{align*} & \int^{R}_{0} x e^{-x^2} \ dx 
\\ = & \left[ -\frac{1}{2} e^{-x^2}  \right]^{R}_{0}
\\ = & - \frac{1}{2} e^{-R^2} + \frac{1}{2}
\\ = & \frac{1}{2} - \frac{1}{2e^{R^2}}
\end{align*} \]となる。ここで、\[ \lim_{R \to \infty} \frac{1}{2e^{R^2}} = 0 \]より、\[ \begin{align*} \int^{\infty}_{0} x e^{-x^2} \ dx 
 = \frac{1}{2}
\end{align*} \]となる。

(2) \[ \int^{\infty}_{0} e^{-x^2} \ dx \]の広義積分を直接計算して収束することは難しいので、優関数の原理を用いる。

\( x \leqq 1 \) において、\( |e^{-x^2}| \leqq xe^{-x^2} \) が成立する。…(i)

さらに、\[ \begin{align*} & \int^{\infty}_{0} e^{-x^2} \ dx \\ = &
\int^{\infty}_{1} e^{-x^2} \ dx + \int^{1}_{0} e^{-x^2} \ dx
\end{align*}  \]と分解する。\[\int^{1}_{0} e^{-x^2} \ dx\]は広義積分ではないので当然収束する。なので、\[\int^{\infty}_{1} e^{-x^2} \ dx \]が収束することを示せばよい。

また、(1)より、\[ \begin{align*} \int^{\infty}_{0} x e^{-x^2} \ dx
\end{align*} \]は収束する（当然 1〜正の無限の範囲でも収束する）。…(ii)

よって、(i), (ii) より、題意の積分は収束することが示された。

 

解答3

(1)

解答：収束する

理由

\( | \cos x | \leqq 1 \) である。よって、

\[ \left| \frac{ \cos x}{1+x^2}  \right| \leqq \frac{1}{1+x^2} \ dx \]を常に満たす。

つぎに、\[ \int^{\infty}_{0} \frac{1}{1+x^2} \ dx \]が収束することを確かめる。（優関数の原理）。

 

ここで、\[ \begin{align*}
\int^{R}_{0}  \frac{1}{1+x^2} \ dx
\int^{R}_{0}  \frac{1}{1+x^2} \ dx
= & \left[ \tan^{-1} x \right]^{R}_{0}
\\ = & \tan^{-1} R 
\end{align*} \]となる。ここで極限をとる。\[ \lim_{R \to \infty} \tan^{-1} R = \frac{\pi}{2} \]と計算ができるので、\[ \int^{\infty}_{0}  \frac{1}{1+x^2} \ dx = \frac{\pi}{2} \]となり、収束する。

 

よって、\[ \int^{\infty}_{0} \frac{ \cos x}{1+x^2} \ dx \]も収束することがわかる。

 

(2)

解答：収束しない

理由

-1〜0、0〜1で積分をわける。

\[ \int^{1}_{-1} \frac{x}{x^2-1} \ dx = \int^{1}_{0} \frac{x}{x^2-1} \ dx + \int^{0}_{-1} \frac{x}{x^2-1} \ dx \]

前半の積分は \( x = 1 \) で定義されないので、1よりもわずかに少ない値で積分。\[ \begin{align*}
\int^{1-t}_{0} \frac{x}{x^2-1} \ dx & = \left[ \frac{1}{2} \log \left| x^2 - 1 \right| \right] 
\\ & = \frac{1}{2} \log \left| (1-t)^2 - 1 \right| 
\\ & = \frac{1}{2} \log \left| t^2 -2t \right|
\end{align*} \]となる。

 

(3)

解答：収束する

理由

 

被積分関数は偶関数。ここで、被積分関数が収束すると仮定する。

仮定より、\[\int^{\infty}_{- \infty} \frac{1}{\sqrt{1+x^4}} \ dx = 2 \int^{\infty}_{0} \frac{1}{\sqrt{1+x^4}} \ dx \]も収束する。

さらに、\[\begin{align*} \int^{\infty}_{0} \frac{1}{\sqrt{1+x^4}} \ dx =  \int^{\infty}_{1} \frac{1}{\sqrt{1+x^4}} \ dx + \int^{1}_{0} \frac{1}{\sqrt{1+x^4}} \ dx
\end{align*} \]と分解できるので、\[ \int^{\infty}_{1} \frac{1}{\sqrt{1+x^4}} \ dx \]の収束を示せばよい。

さらに、1以上の \( x \) に対し、\[ \left| \frac{1}{\sqrt{1+x^4}} \right| \leqq \frac{1}{\sqrt{x^4}} = \frac{1}{x^2}\]が成立する。

なので、\[ \int^{\infty}_{1} \frac{1}{x^2} \ dx \]の収束を調べればよい。[\begin{align*} & \int^{R}_{1} \frac{1}{x^2} \ dx 
\\ = & \left[ - \frac{1}{x}  \right]^{R}_{1}
\\ = & 1 - \frac{1}{R}
\end{align*} \]となる。\[ \lim_{R \to \infty} \frac{1}{R} = 0 \]なので、\[ \int^{\infty}_{1} \frac{1}{x^2} \ dx = 1 \]に収束する。

よって仮定は正しく、題意の積分は収束する。

 

６．さいごに

今回は、定積分に極限がセットになった広義積分についてのまとめを行いました。

広義積分は、今後習う二重積分などで突然不意打ちをしてくるので、これ広義積分だなっていうのを見分けられるようにして、不意打ちを回避できるようにしましょう。

次回からは、1変数関数ではなく、少し進化した2変数関数の話に入ります。