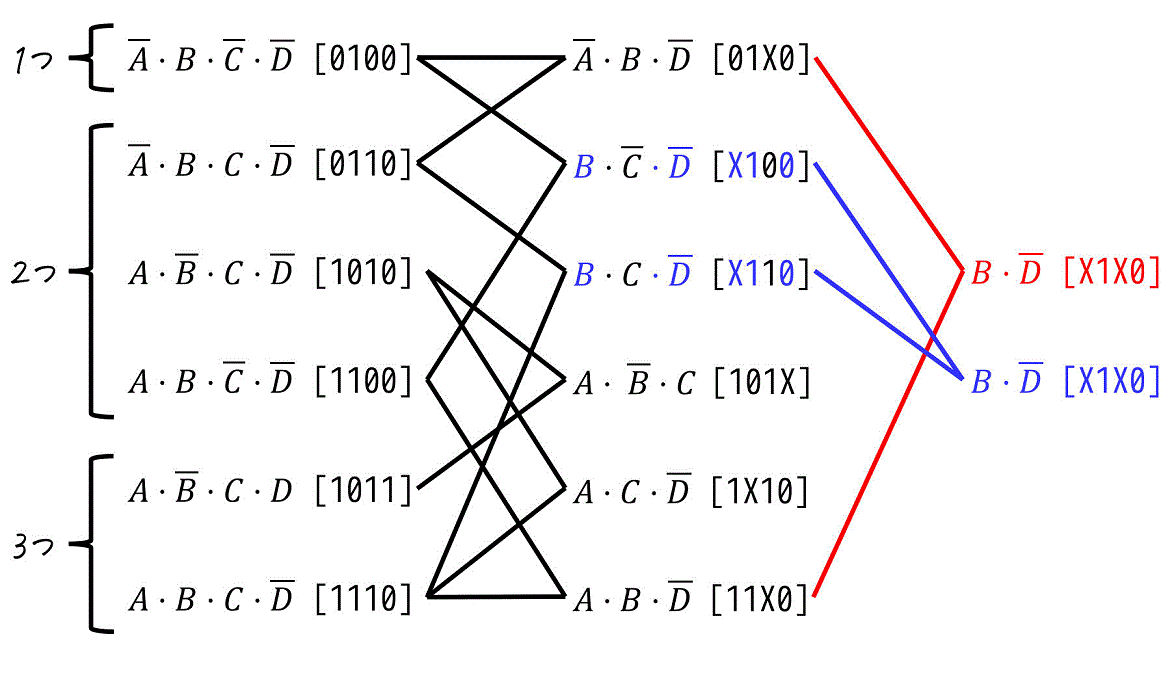
スポンサードリンク
こんにちは、ももやまです。
論理式(論理回路)を簡略化する方法の1つに、簡略化できる項を□や〇などで囲うことで見つけ出すカルノー図がありましたね。
この方法は、視覚的にわかりやすいため、(4変数までであれば)人間の目では分かりやすい一方、視覚的な認識が難しいコンピュータにはカルノー図による論理式の簡略化はできません[1]できたとしても非常に難易度が高いです。。
そこで、今回はコンピュータ上でも論理式を簡単化できるクワイン・マクラスキー法について見ていきましょう。
目次
スポンサードリンク
1. クワイン・マクラスキー法の使い方
具体例を出しながら説明したほうがわかりやすいと思うので、実際に、\[
X = \bar{A} B \bar{C} \bar{D} + AB \bar{D} + ABC \bar{D} + A \bar{B} C + \bar{A} B C \bar{D}
\]をクアリン・マクラスキー法を用いて簡略化する手順を見ていきましょう。
[下準備] 主加法標準形(選言標準形) へ変換
クワイン・マクラスキー法を適用する前に、まずは論理式 \( X \) を主加法標準形に変換しましょう。
変換の手順としては、まずは真理値表を書きましょう。
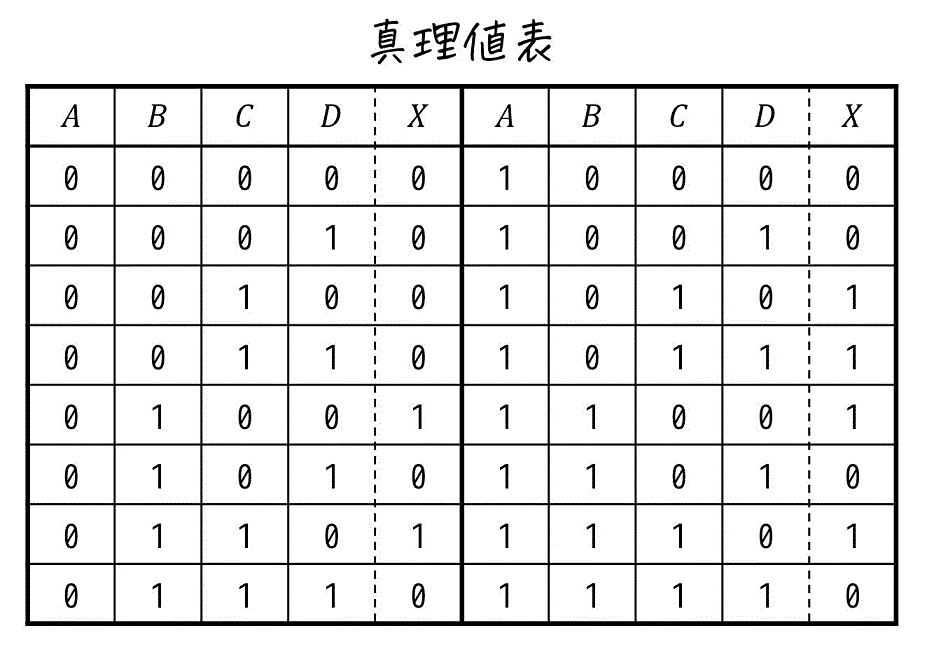
つぎに、\( X \) が1となる部分に着目します。
1となる部分をすべて足していった形が主加法標準形となります。
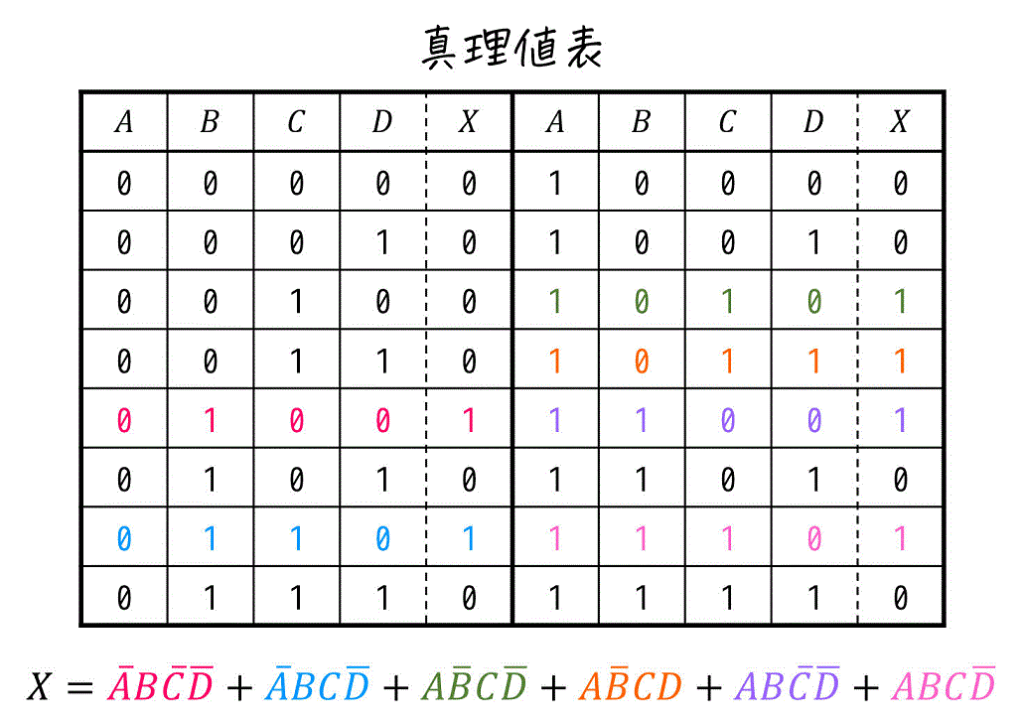
主加法標準形で求めたを和ごとに分解したもののことを最小項と呼びます。
今回の場合、論理式 \( X \) から出てくる最小項は \( \bar{A} B \bar{C} \bar{D} \), \( \bar{A} BC \bar{D} \), \( A \bar{B} C \bar{D} \), \( A \bar{B} CD \), \( AB \bar{C} \bar{D} \), \( ABC \bar{D} \) の7個ですね。
※ 上の説明でも「主加法標準形があまりよくわからないなぁ」や「もうちょっと主加法標準形の復習をしたい」思った人は、下の記事でより詳しい解説を載せているのでご覧ください。
Step1. 主項を求める
まずは、与えられた論理式 \( X \) の主項[2]主項とは、最も簡単化された論理式を和ごとに分解したそれぞれの項(部品)のことです。例えば、最も簡単化された論理式が\[Y = A + \bar{B} … Continue readingを求めましょう。
(1) まずは主加法標準形の項(最小項)を並べる
まずは、主加法標準形で求めた項(最小項)を縦に並べましょう。
ここで主項を求めやすくするために、「真理値表に変換した際の1の数」でそれぞれの最小項をグループ分けしましょう[3]例えば \( \bar{A} B C \bar{D} \) であれば、\( B \) と \( C \) が真理値表の1に対応するため、「真理値表に変換した際の1の数」は2となります。。
グループ分けしたあとに、グループごと(1の数が少ないグループごと)に主加法標準形で求めた項を縦に並べればOKです[4]今回の場合、「1つのグループ」、「2つのグループ」、「3つのグループ」の3種類となります。。
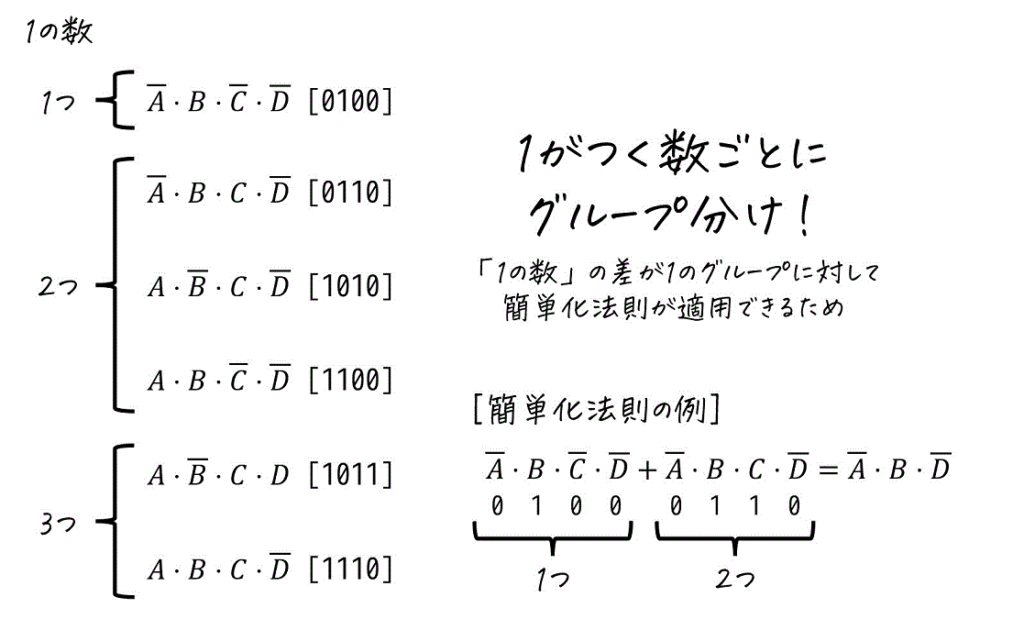
(2) 論理演算の簡単化法則を適用し、項をまとめる
つぎに、論理演算の簡単化法則\[\begin{align*}
A B + A \bar{B} & = A ( B + \bar{B} )
\\ & = A
\end{align*}\]を用いて、最小項をどんどんまとめていきます。

ここで項をまとめていく際のコツですが、まとめる2つの項は必ず\[
\underbrace{ \bar{A} B \bar{C} \bar{D} }_{1 \ \mathrm{が1つ}} + \underbrace{ \bar{A} B C \bar{D} }_{1 \ \mathrm{が2つ}} = \bar{A} B \bar{D}
\]のように、2つの項の「1の数」の差が1となります。
そのため、最小項をまとめる際には
- 「1の数が1つのグループ」の項と「1の数が2つのグループ」の項
- 「1の数が2つのグループ」の項と「1の数が3つのグループ」の項
のみに着目しながらまとめていくと、まとめ漏れを防ぐことができます[5]やみくもにすべての項を確認するよりも、「1の数」の差が1となる項だけを確認することで、確認すべきペアの数を減らせるので、ミスが減ります。。
同じように、残りの最小項に対してもまとめていきましょう。

すると、下のように6つの項が出てきたかと思います。
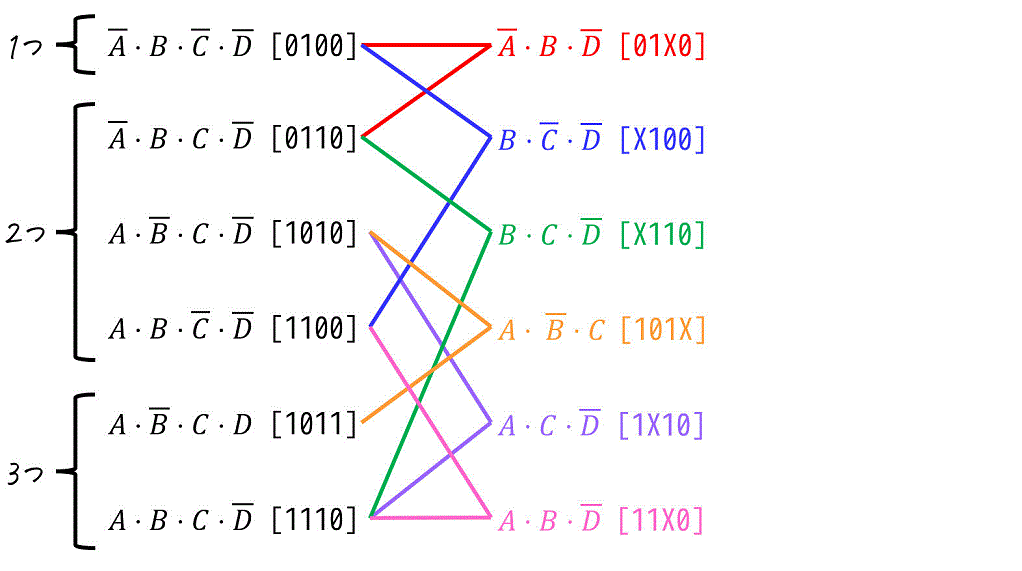
この6つの項に対しても、まとめられる項があればまとめていきます。
ここからは、「真理値表の1の数」に加えて真理値表の X (0でも1でもよい、Don’t Care)の位置に着目すると、まとめ漏れがなくせるのでおすすめです。
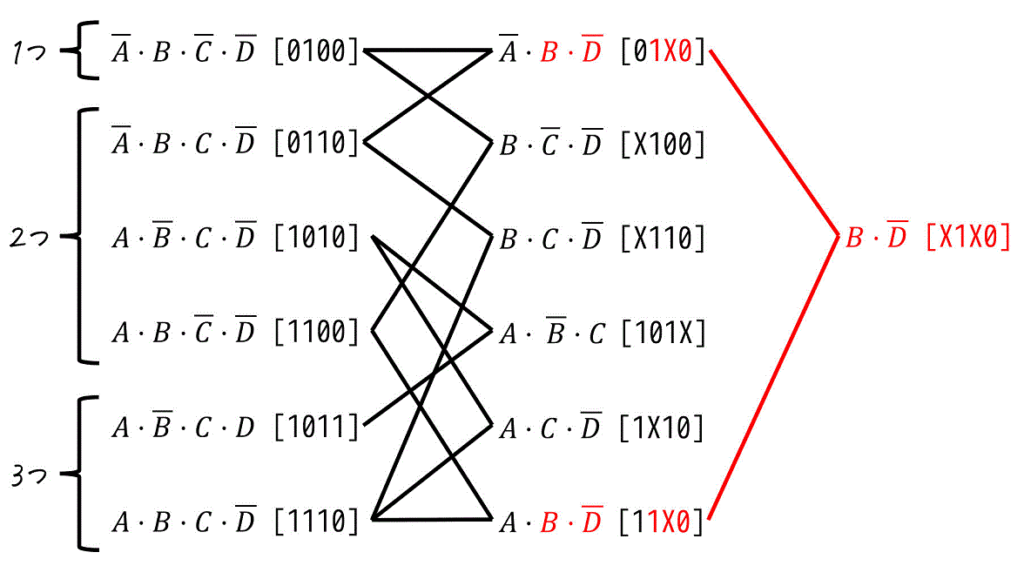
あと一息です。頑張りましょう。
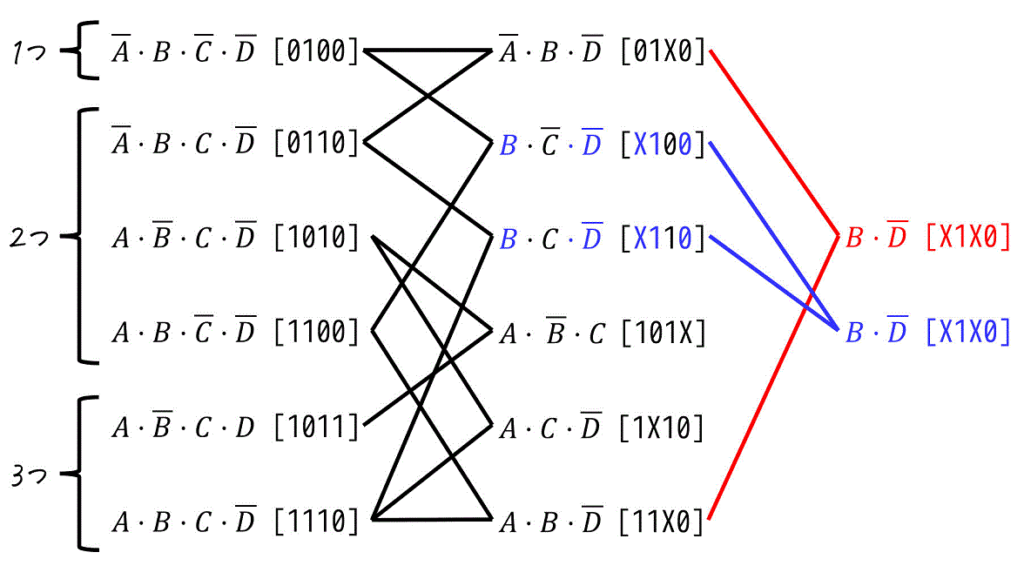
おつかれさまでした、これでもう「まとめられる項」はありません。
まとめられる項がなくなったら、「これ以上まとめられなかった項」を□や〇やらで囲ってください。これらの項が主項です。
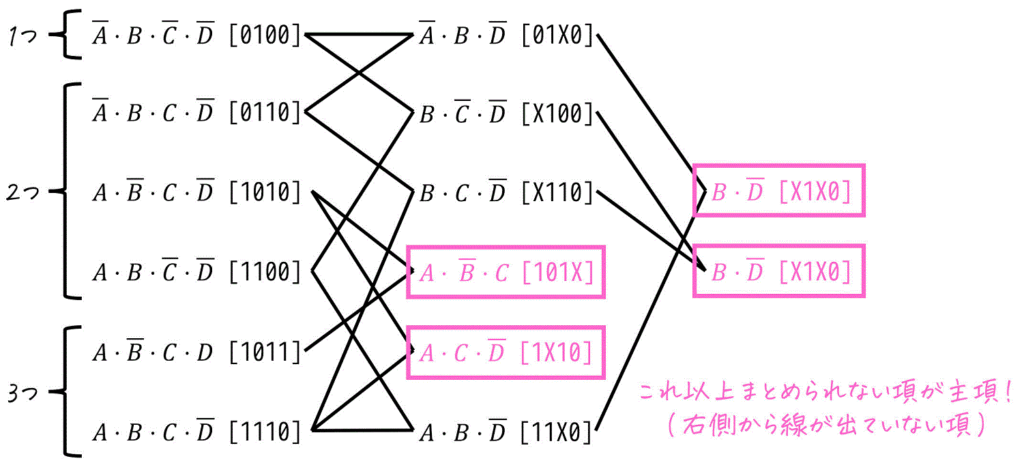
(この図のことは、圧縮図とか圧縮表などと呼ばれます)
よって今回の場合は、\( B \bar{D} \), \( A \bar{B} C \), \( A C \bar{D} \) の3つが主項になることがわかりますね。
※ \( B \bar{D} \) が2つ出てくるように、同じ項が重複して出てくることもありますが、特に気にする必要はありません。ダブルカウントしなければOKです。
Step2. 必須主項を求める
Step1で求めた主項の和を取るだけ、つまり\[
X = B \bar{D} + A \bar{B} C + AC \bar{D}
\]とするだけではまだ冗長な論理式になっている(最も簡単な論理式とはなっていない)ことがあります。
そこで、Step1で求めた主項の中でも「論理式を表すために必要な主項」である必須主項を求めていくことで、どの主項が冗長なのかを調べていくのがこのStep2です。
(1) 主項表(最小項がどの主項に含まれるか示した表)を書く
まずは、最小項が求めたどの主項に対応する(包含される)かを調べていくために、最小項がどの主項に対応したかを示す表を作ります。この表のことを主項表と呼びます。主項表を書くことによって、最小項が求めたどの主項に対応する(包含される)かを調べていくことができます。
書き方は、行か列のどちらかを最小項、もう片方を主項にした表を書いていき、主項に対応する部分に〇を付けていきます。
表の書き方は様々です。例えば、左下のように普通の表を書くこともあれば、右下のように簡略化した書き方をすることもあります。(今回は両方の表を書いていますが、どちらか片方でOKです)
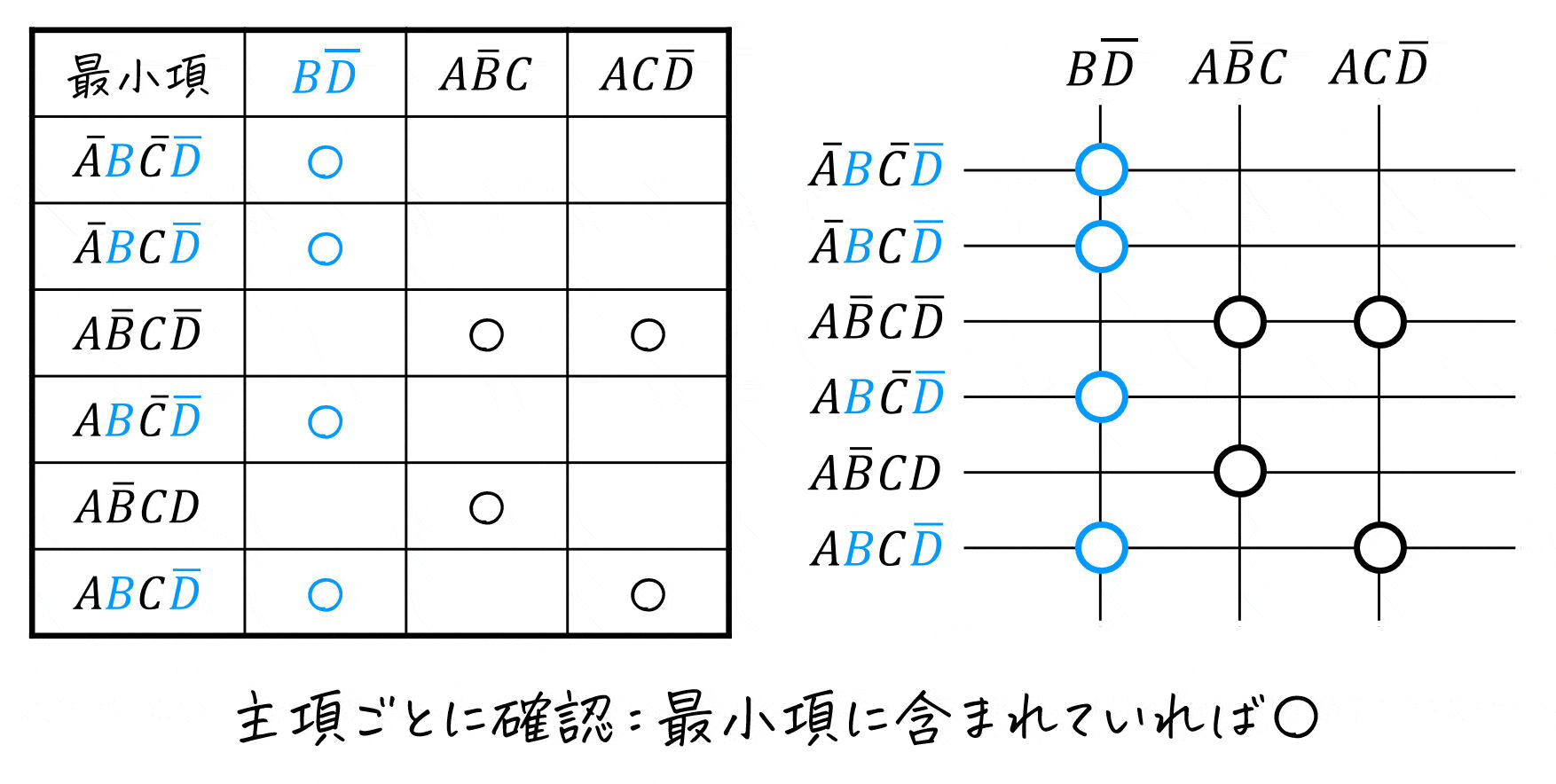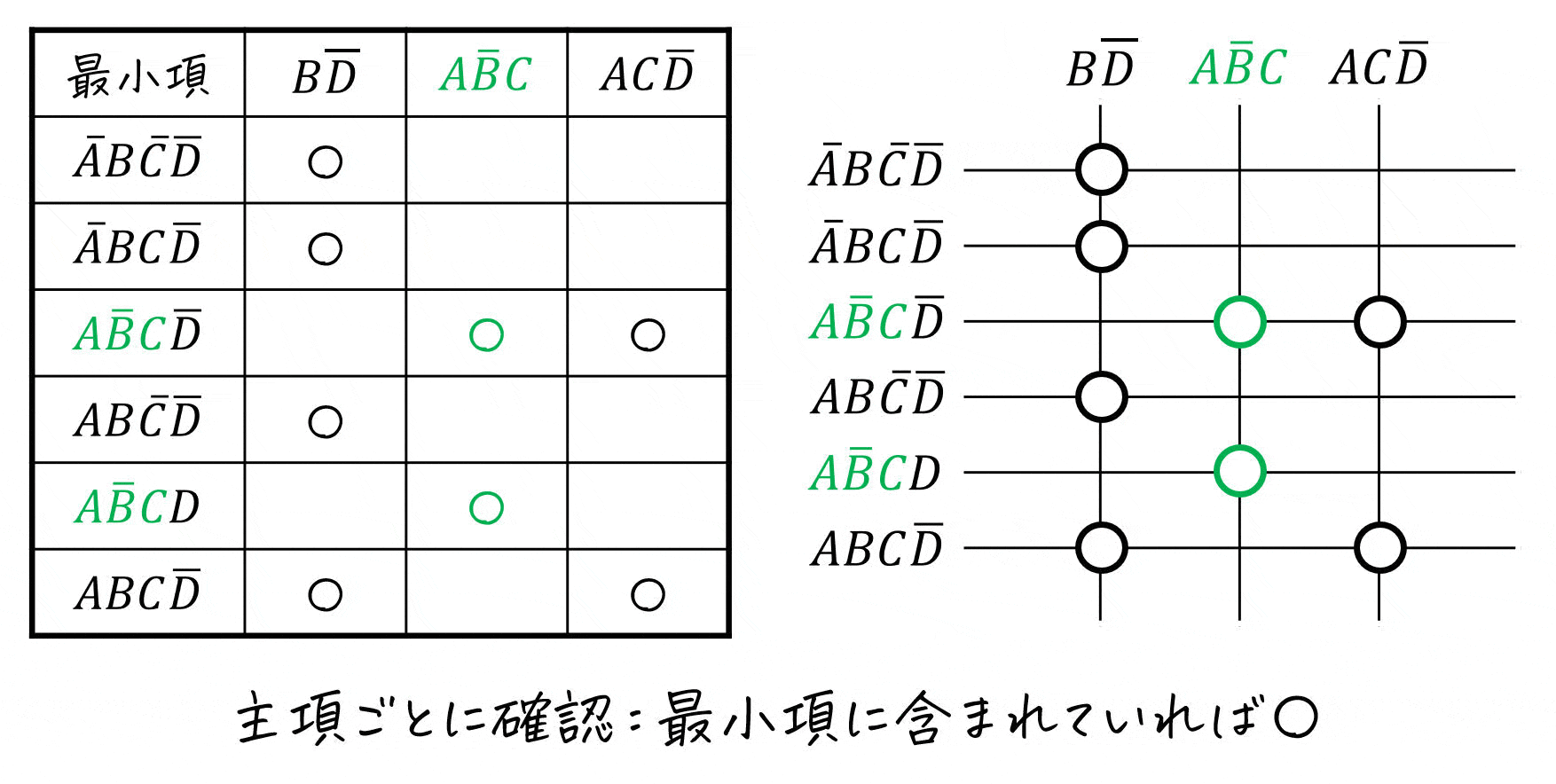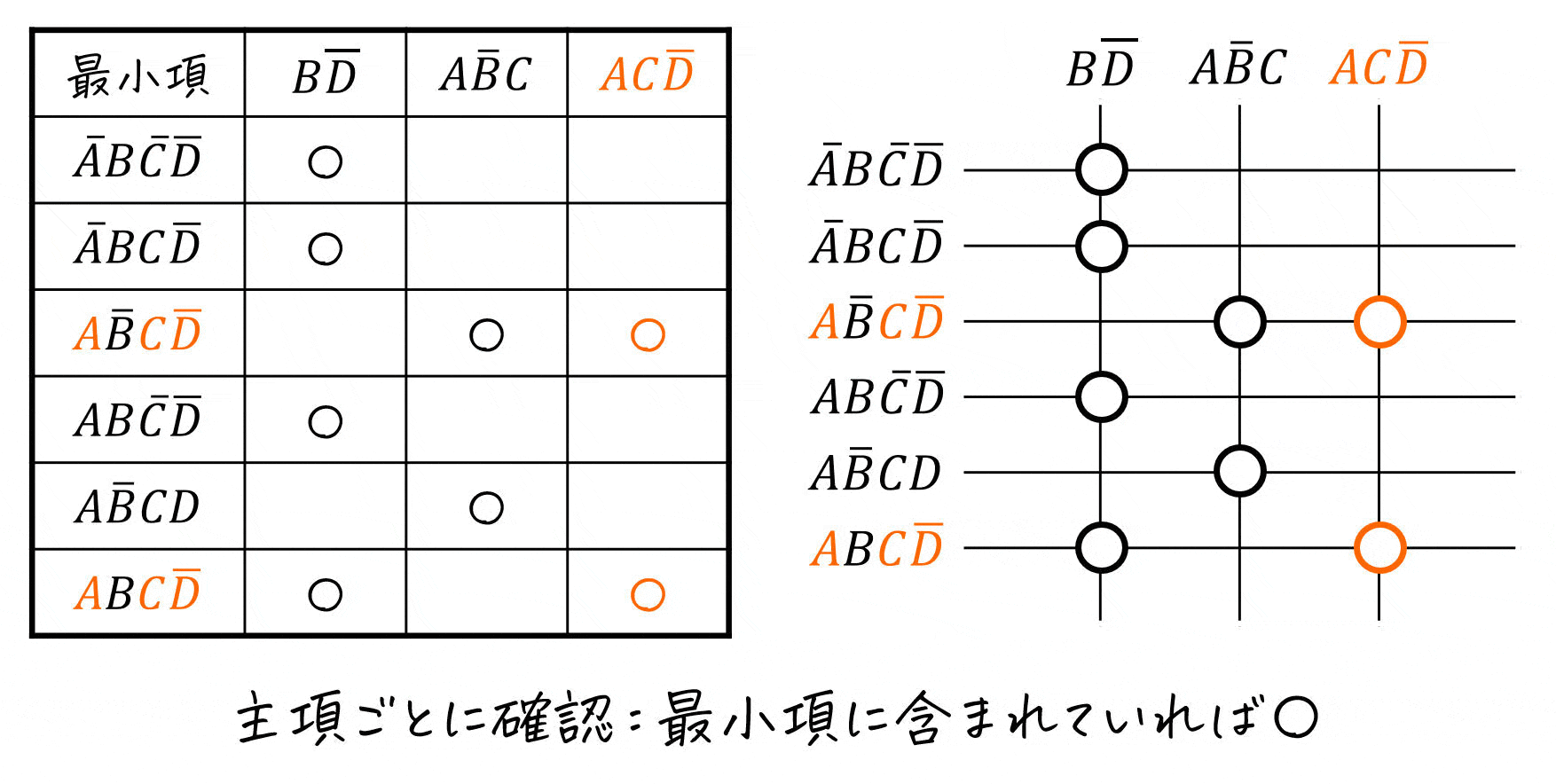
[ワンポイントアドバイス] 最小項を書く順番
主項表を書く際に最小項を並べて行きましたが、最小項を並べる順番は主項を求めるために書いた図(圧縮図・圧縮表)と同じ並びにすることをおすすめします。
2つの表で最小項を同じ並びにすることで、「それぞれの最小項が対応する主項の位置(○の位置)」と「主項から逆にたどれる最小項」が対応するため、検算に使うことができます。
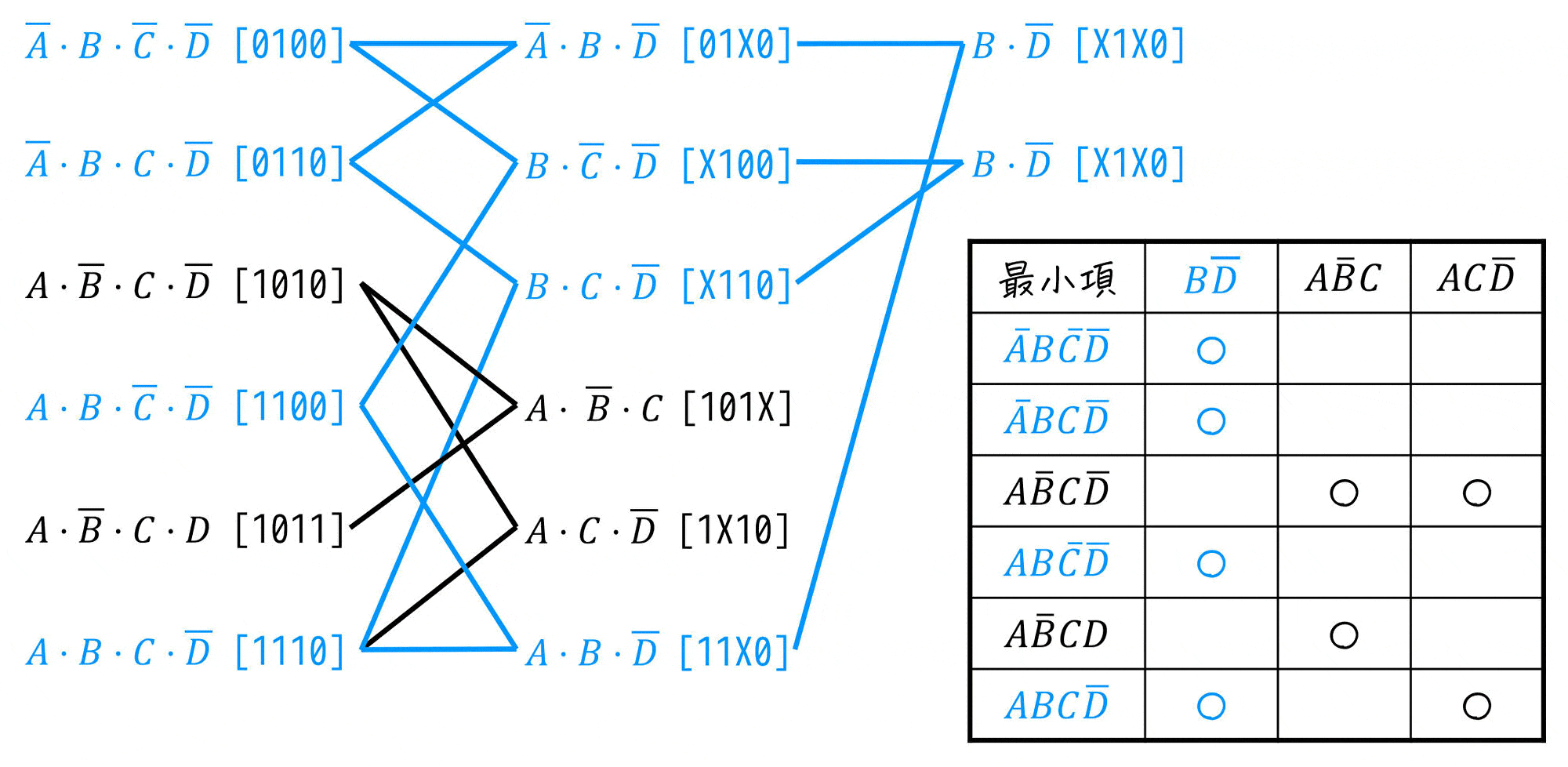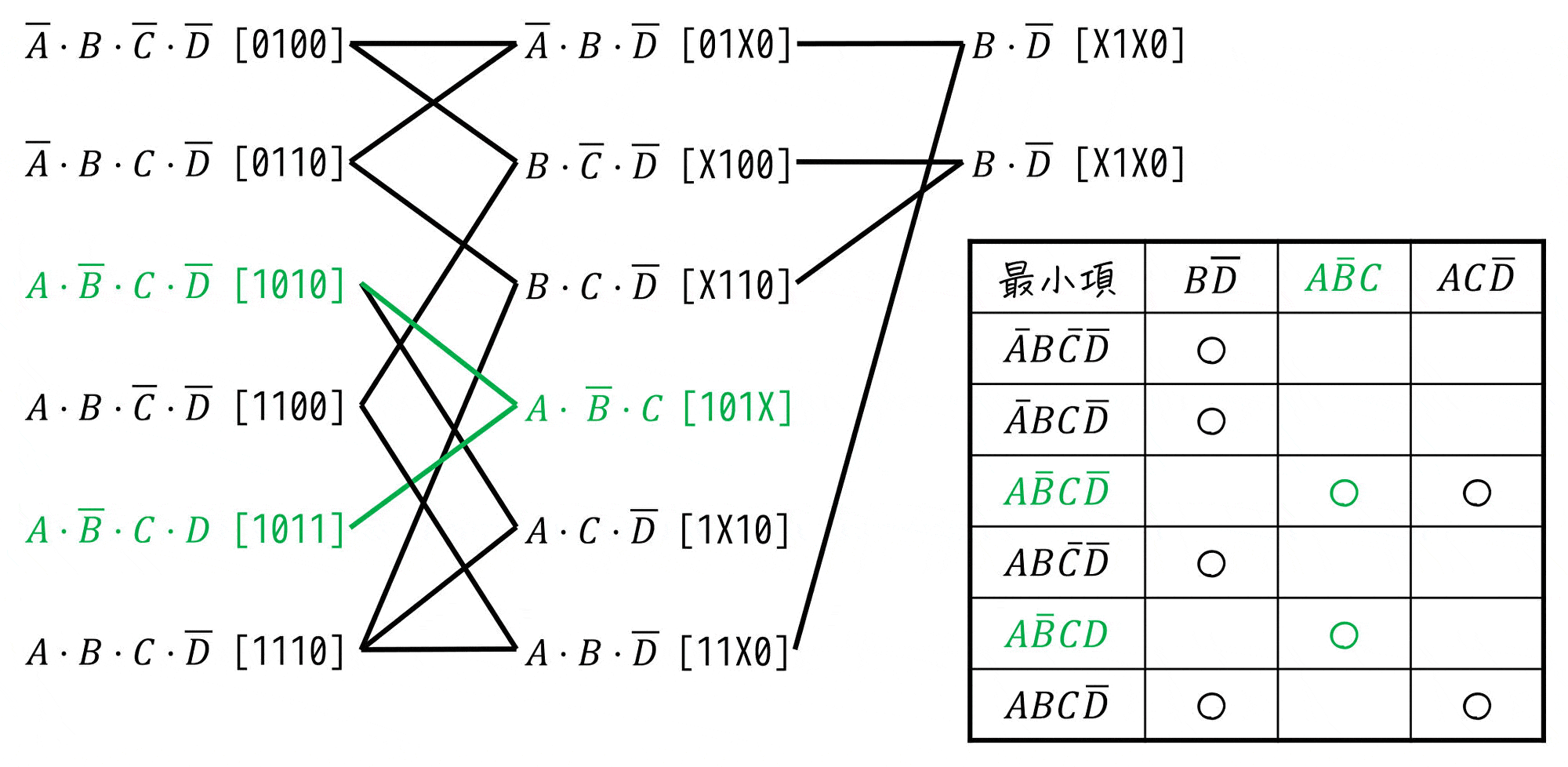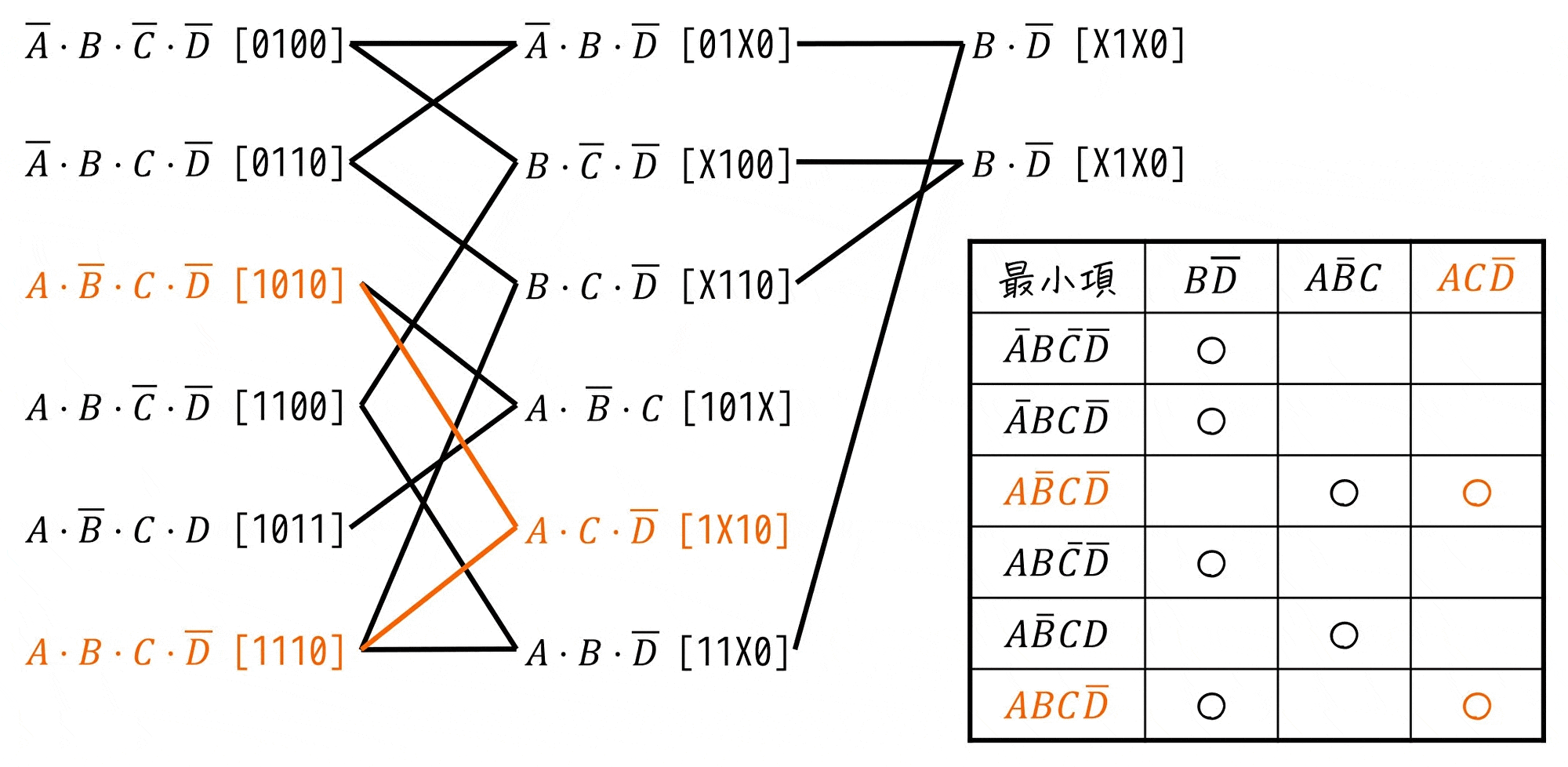
(線をたどることで○があっているかの検算が可能)
(2) 1つの最小項にしか対応しない主項をチェック
つぎに、最小項(今回の場合は表の行)ごとに、何個の主項に対応しているか(包含される)を確認していき、1つの主項にしか対応していない最小項をマークします。
マークの仕方はなんでもいいですが、今回は「1つの主項にしか対応されていない部分」の〇を黒く塗りつぶして●で表すことにします。
(さらにここでは分かりやすくするためにマークした最小項をピンク色にしています)
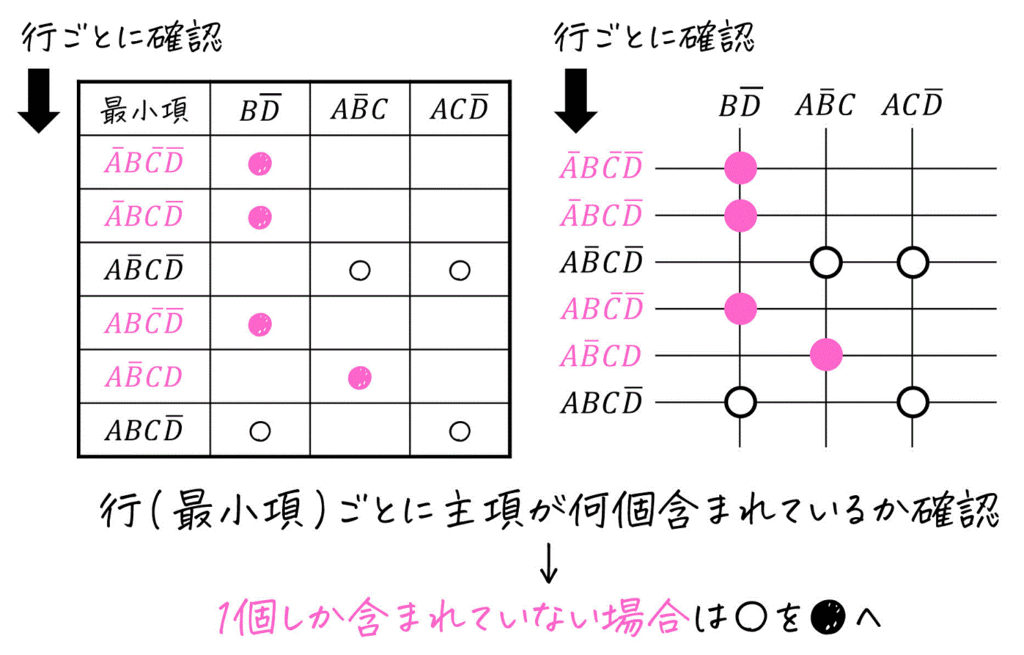
(3) ●が1つでもある主項が必須手項
さいごに、主項(今回は表の列)ごとに、1個でも●が含まれるような主項を選んでください。選んだ主項が必須主項となります[6]●がついている最小項は、対応する主項が1つであることを示しています。そのため、その(対応する1つの)主項を必ず選択しないと論理式 \( X \) … Continue reading。
今回の場合だと、\( B \bar{D} \), \( A \bar{B} C \) となります。
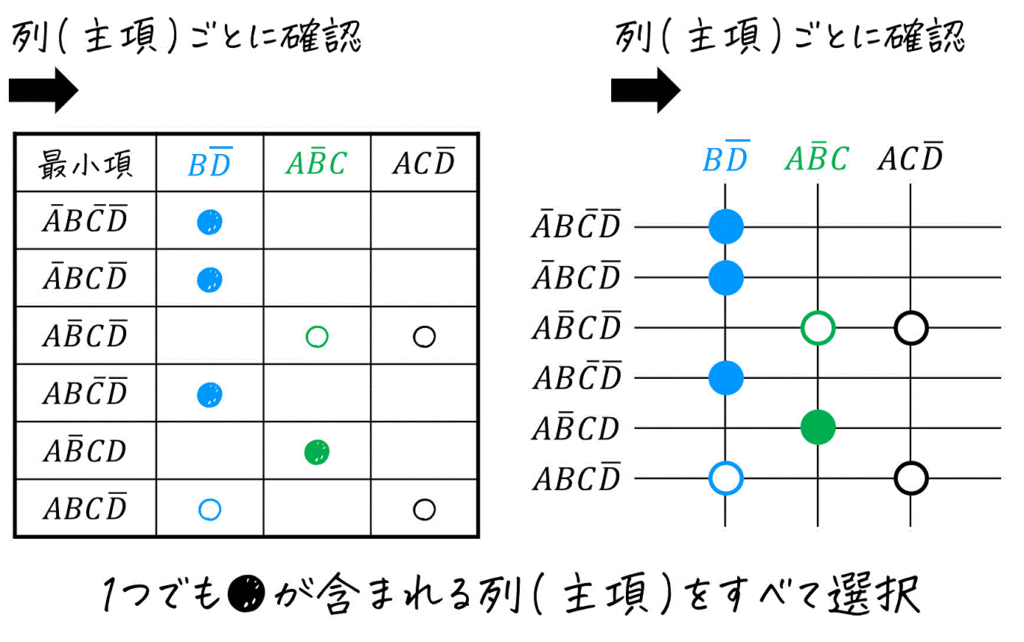
必須主項を選んだら、すべての最小項が含まれている(以降「カバーされていると」表記)かどうかを確認してください。
今回の例の場合、必須主項だけですべての最小項がカバー出来ていますね。このように、すべての最小項がカバーされていればStep3を飛ばして、Step4に飛んでください。
一方、カバーされていない最小項があれば、引き続きStep3へ行きます。
Step3. 残りの最小項を対応させるような主項を選択
必須主項だけですべての最小項を対応させることが出来ない場合は、残りの主項を「選んだ項にある「変数の数」の和ができるだけ少なくなるように」選択します[7]例えば、\( A \bar{B} \) と \( \bar{A} B C \) を選択した場合は、変数の数は2と3なので、和は5となります。。
今回の例の場合は必須主項だけでカバー出来てしまっているので、他の例を出してみます。
例えば、論理式\[
Y = \bar{A} B \bar{C} \bar{D} + \bar{A} B \bar{C} D + A \bar{B} C D + AB \bar{C} D + ABCD
\]にクワイン・マクラスキー法を適用していくと、論理式 \( Y \) をStep2までの結果が下の主項表で表すことができます。
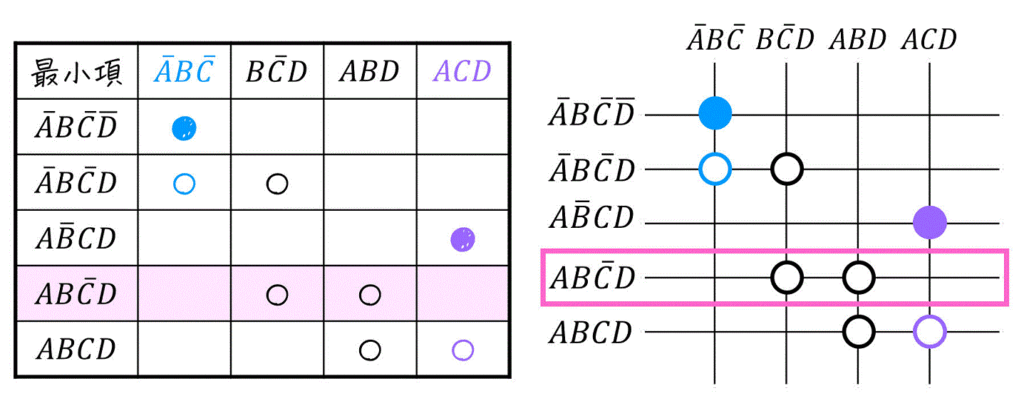
[上の主項表の詳細情報]
最小項: \( \bar{A} B \bar{C} \bar{D} \), \( \bar{A} B \bar{C} D \), \( A \bar{B} CD \), \( A B \bar{C} D \), \( ABCD \)
主項: \( \textcolor{deepskyblue}{ \bar{A} B \bar{C} } \), \( B \bar{C} D \), \( ABD \), \( \textcolor{purple}{ ACD } \)
※ 色がついている主項が必須主項
このとき、主項の \( \bar{A} B \bar{C} \), \( ACD \) だけでは最小項 \( AB \bar{C} D \) がカバーできていませんよね。
そのため、必須主項以外の主項 \( B \bar{C} D \), \( ABD \) を用いて最小項 \( AB \bar{C} D \) をカバーする必要があります。
今回の場合、\( B \bar{C} D \), \( ABD \) をどちらを選んでも \( AB \bar{C} D \) をカバーすることができます。さらに、変数の数はどちらも同じ3つなので、どちらを選んでもOKです。
(どちらを選んでも、最も簡単な論理式を作ることができます。)
Step4. 「必須主項」と「Step3で選んだ主項」を全て足す(和を取る)
最後に、「必須主項」および「Step3で選んだ主項」をすべて足せば(和を取れば)最も簡単な論理式(最簡形)の導出完了です。
今回の例の場合は、必須主項は \( B \bar{D} \), \( A \bar{B} D \) で、Step3では主項を選んでいない(必須主項だけですべての最小項をカバーできている)ため、最簡形は\[
X = B \bar{D} + A \bar{B} C
\]となります。
また、Step3で出した論理式の場合、必須主項は \( \bar{A} B \bar{C} \), \( ACD \) で、Step3では \( B \bar{C} D \), \( ABD \) のうちのどちらか1つを選べばOKなので、最簡形は\[\begin{align*}
Y & = \bar{A} B \bar{C} + ACD + B \bar{C} D \\
Y & = \bar{A} B \bar{C} + ACD + ABD
\end{align*}\]となります。
(最簡形が2つありますが、テストの際にはどちらか片方を答えればOKな場合がほとんどです。)
Step1. 主項(最簡形の部品)を求める
(論理演算の簡単化公式を連鎖させることで)
Step2. 主項の中から必須主項を選び出す
(主項表を書く)
Step3. 必須主項以外でカバーできない最小項を、必須主項以外の主項から選ぶ。
(選んだ項にある「変数の数」の和ができるだけ少なくなるように選ぶ)
Step4. Step2とStep3で選んだ項を全て足す。
スポンサードリンク
2. 練習問題
それでは、実際にクワイン・マクラスキー法を用いて論理式を最簡形に変形してみましょう。
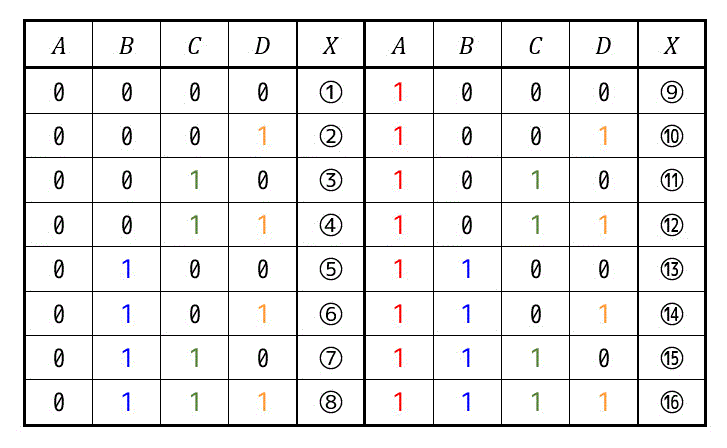
つぎの真理値表で表される論理式 \( X \) がある。次の(1), (2)の問いに答えなさい。
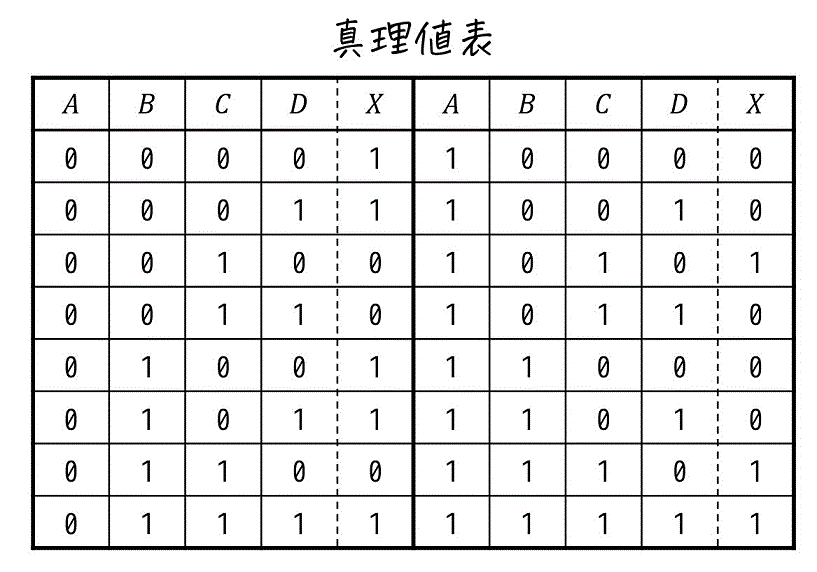
(1) 論理式 \( X \) の主加法標準形を求めなさい。
(2) (1)の論理式をクワイン・マクラスキー法によって簡略化したい。
(2-i) \( X \) の主項を求めなさい。
(2-ii) (2-i) の中から、必須主項を求めなさい。
(2-iii) \( X \) を最簡形に変形しなさい。
スポンサードリンク
3. 練習問題の答え
(1) 主加法標準形の導出
主加法標準形は、真理値表の1の部分に着目し、それらを全て足せばOKです。
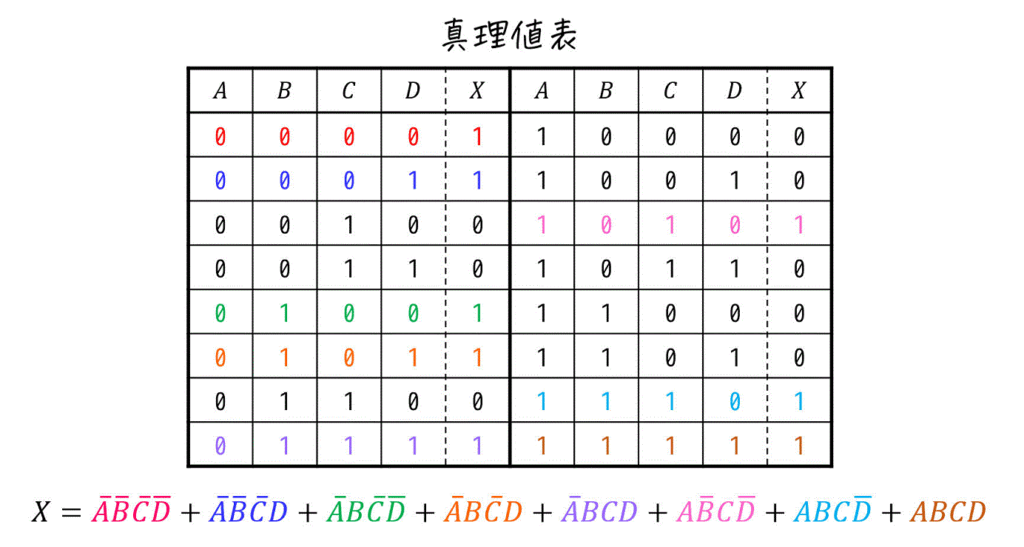
よって、\[
X = \bar{A} \bar{B} \bar{C} \bar{D} + \bar{A} \bar{B} \bar{C} D + \bar{A} B \bar{C} \bar{D} + \bar{A} B \bar{C} D + \bar{A} BCD + A \bar{B} C \bar{D} + ABC \bar{D} + ABCD
\]となります。
(2-i) 主項の導出
まずは、真理値表の1の数ごとにグループ分けをしましょう。
すると、
| 1の数 | 最小項 |
|---|---|
| 0個 | \( \bar{A} \bar{B} \bar{C} \bar{D} \) [0000] |
| 1個 | \( \bar{A} \bar{B} \bar{C} D \) [0001], \( \bar{A} B \bar{C} \bar{D} \) [0100] |
| 2個 | \( \bar{A} B \bar{C} D \) [0101], \( A \bar{B} C \bar{D} \) [1010] |
| 3個 | \( \bar{A} BCD \) [0111], \( ABC \bar{D} \) [1110] |
| 4個 | \( ABCD \) [1111] |
となります。
あとは、グループごと(1の数が少ないグループ順)に最小項を上から列挙していってから、どんどん項をまとめていきましょう。

まとめ終わったら、これ以上まとめられなかった項(右側に線がない項)をすべて列挙すれば主項が求まります。
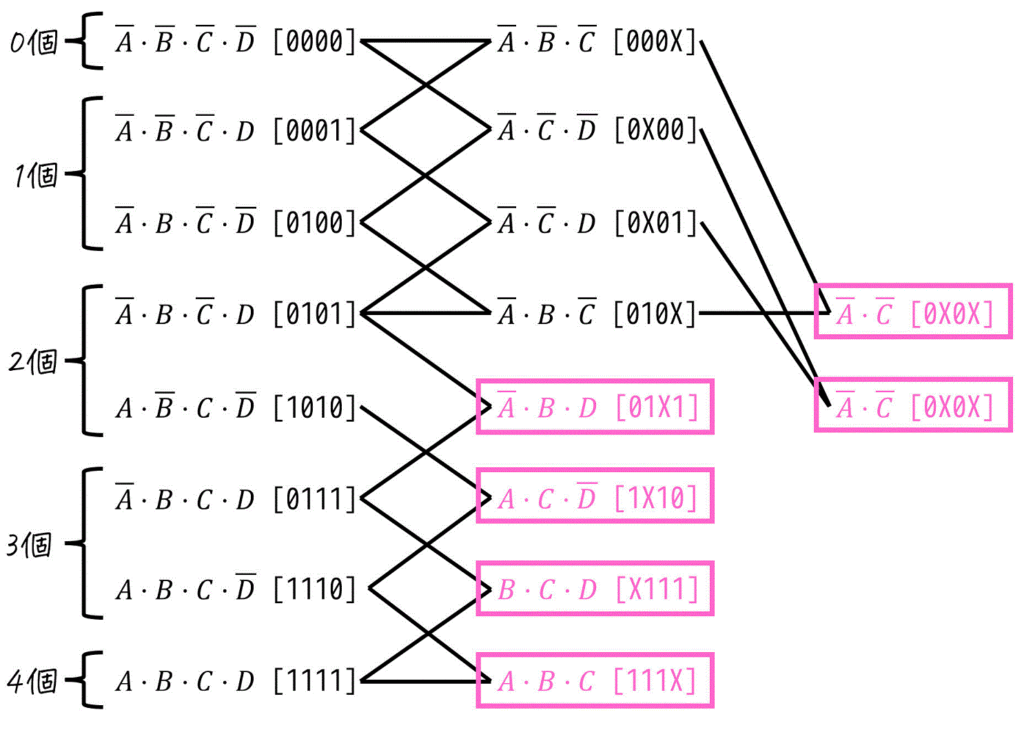
よって、主項は \( \bar{A} \bar{C} \), \( \bar{A} BD \), \( A C \bar{D} \), \( BCD \), \( ABC \) となります。(全部で5つ)
(2-ii) 必須主項の導出
つづいて、必須主項を求めていきます。
まずは、最小項と主項の対応表(主項表)を書きましょう。
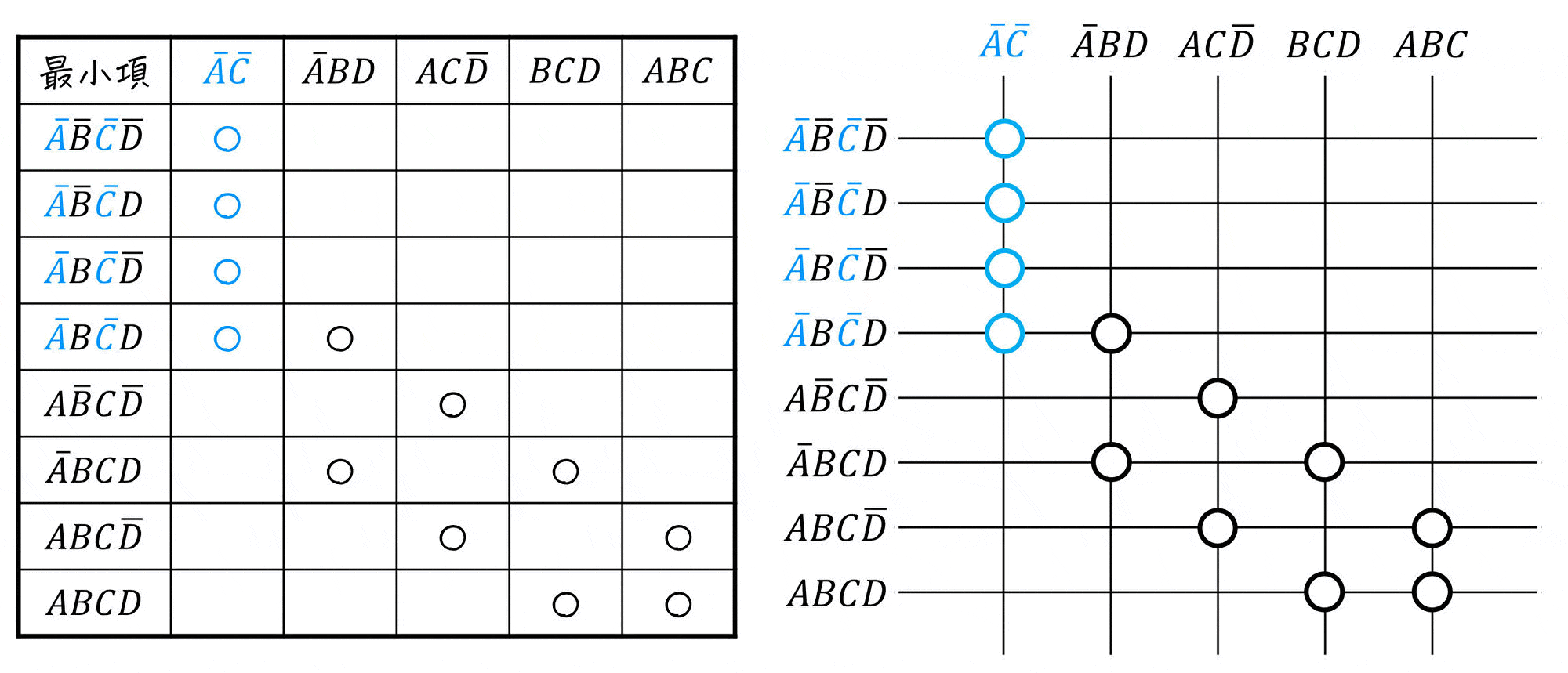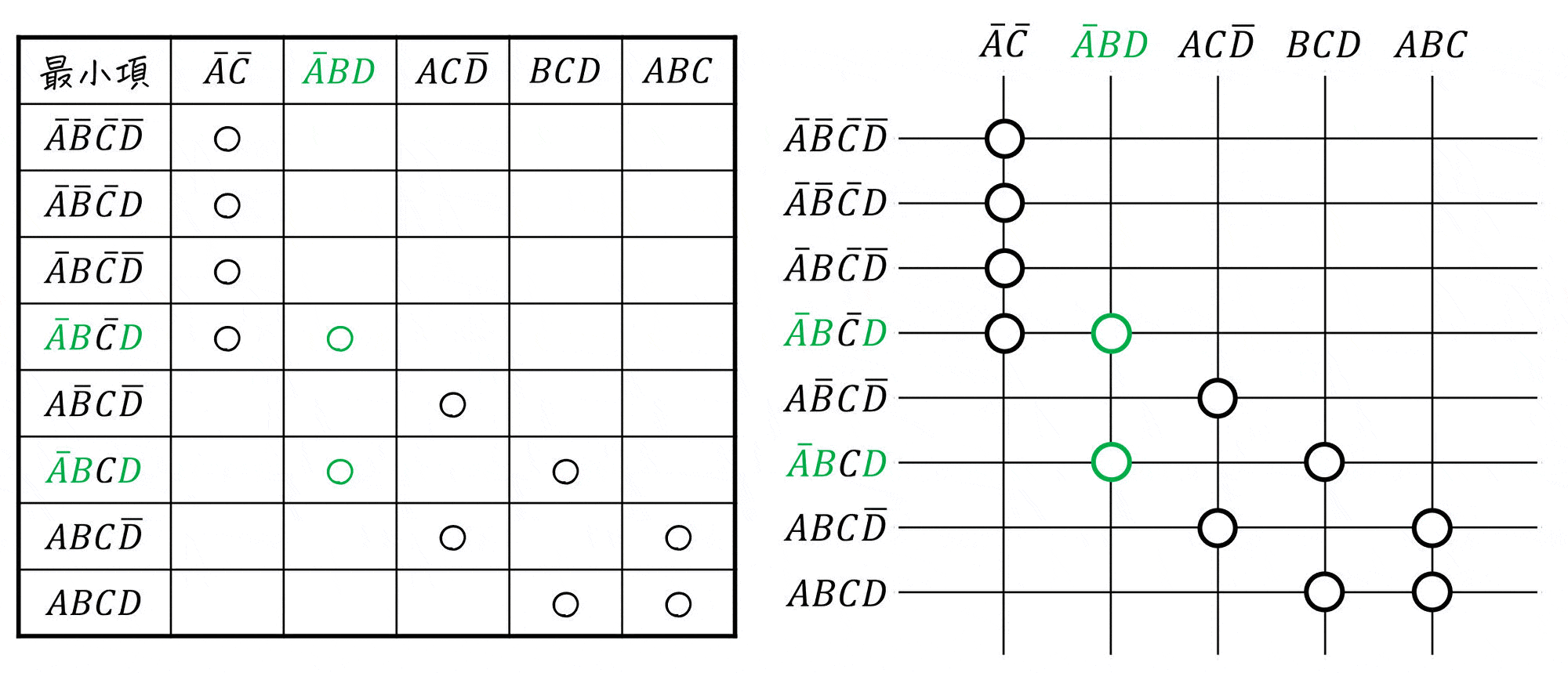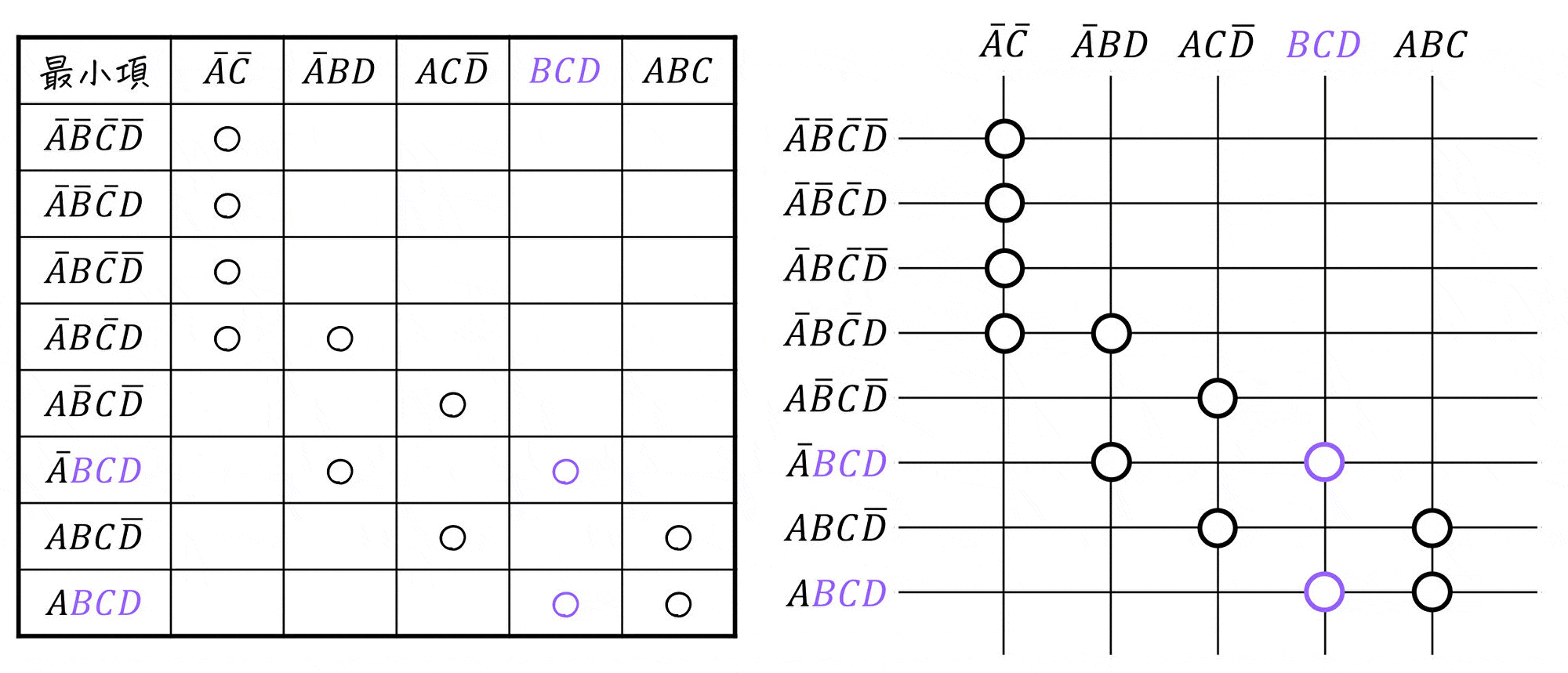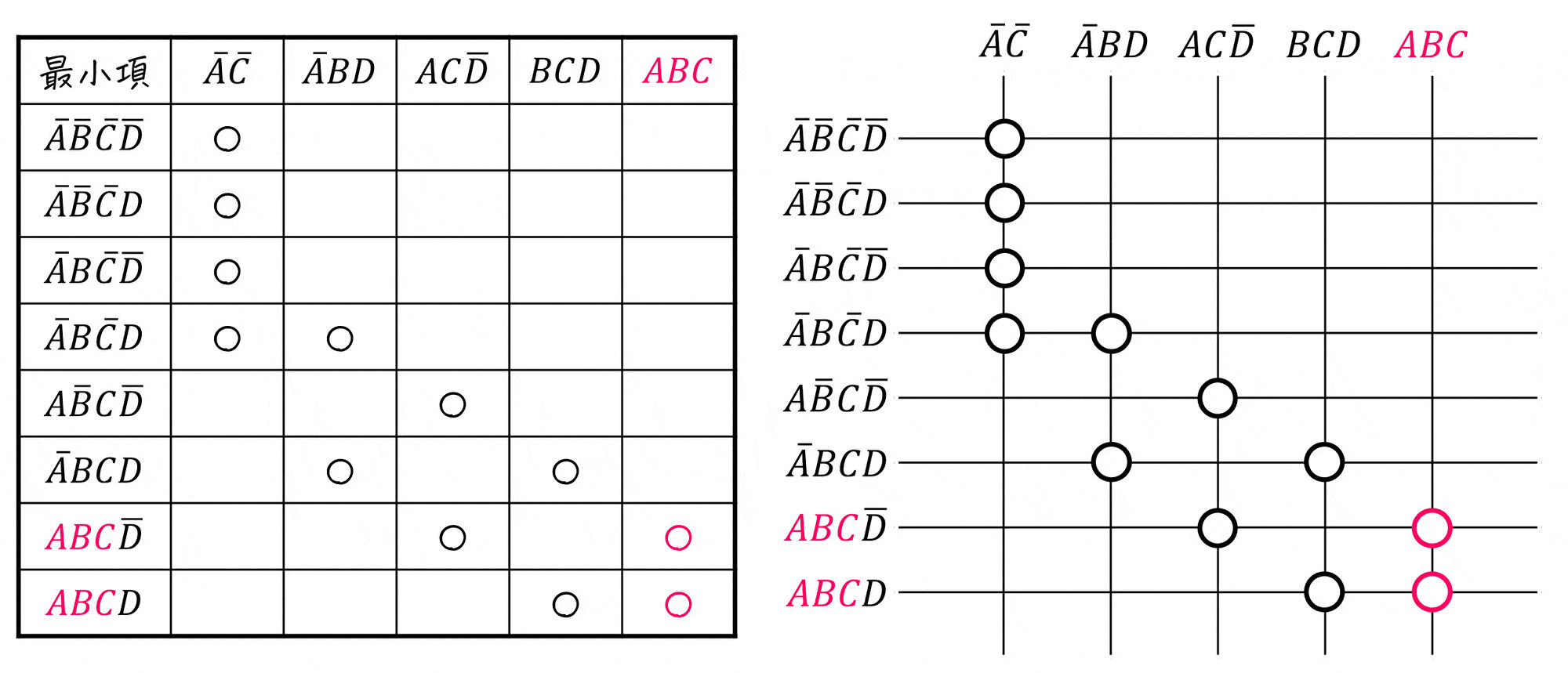
書き終わったら、(2-i)で作った表と照らし合わせをしておきましょう。
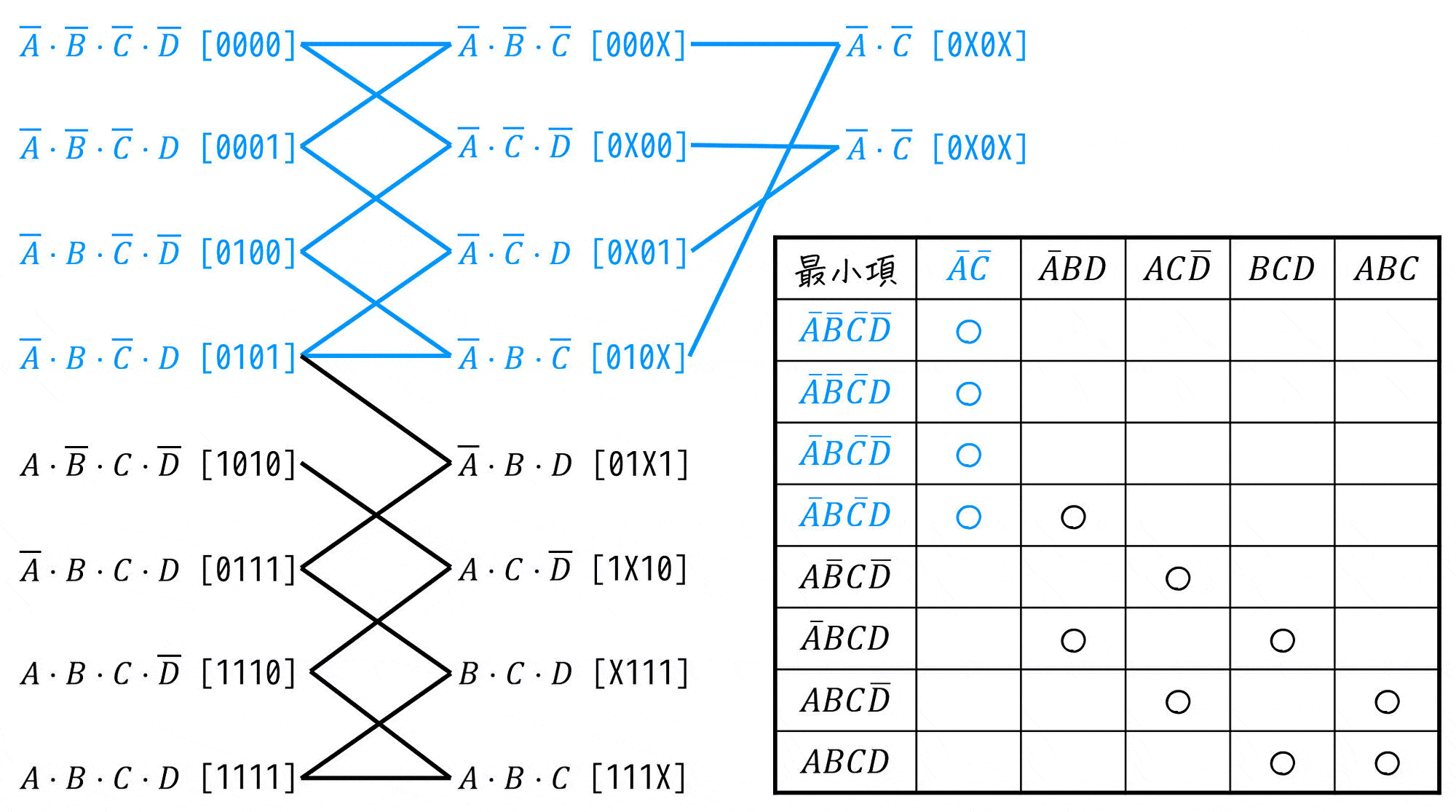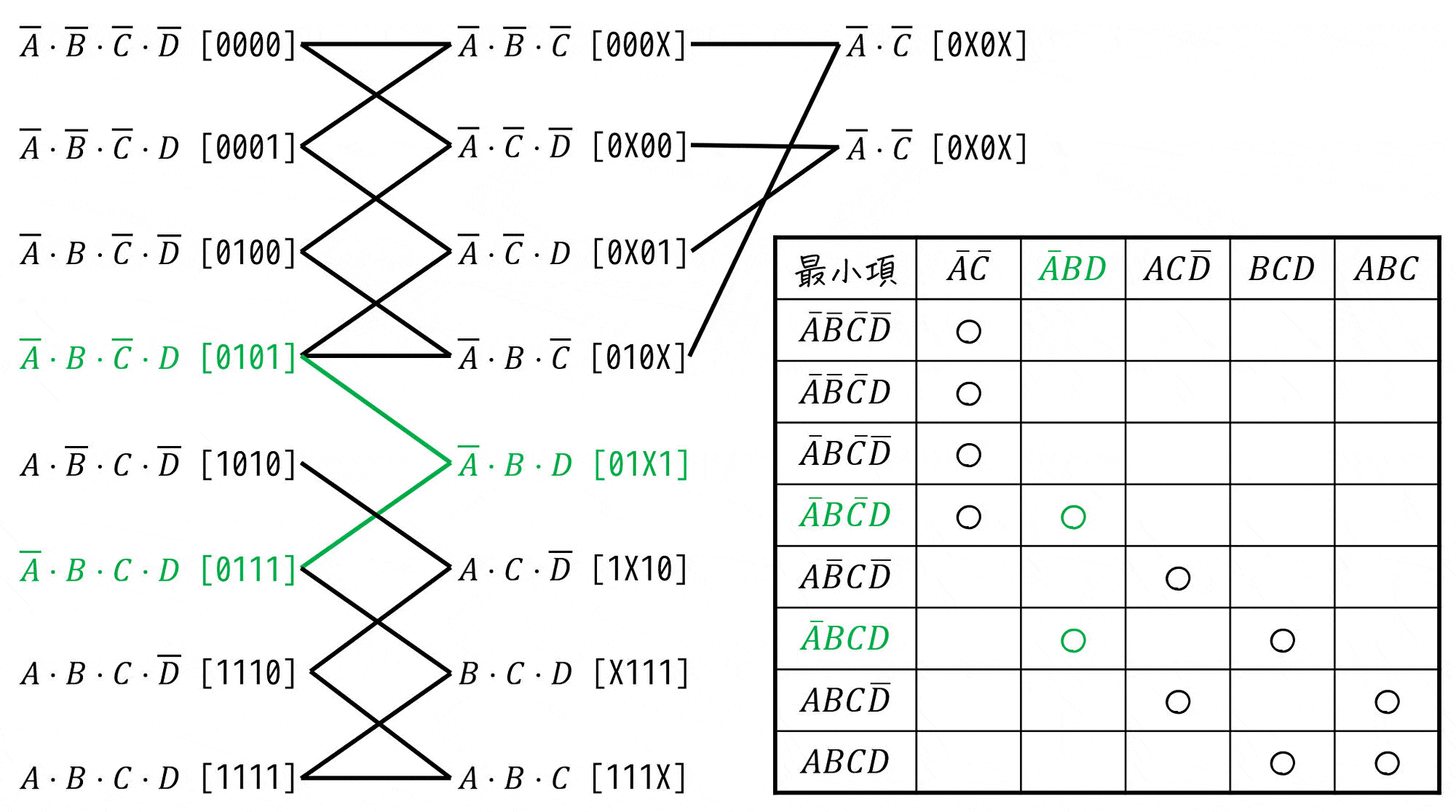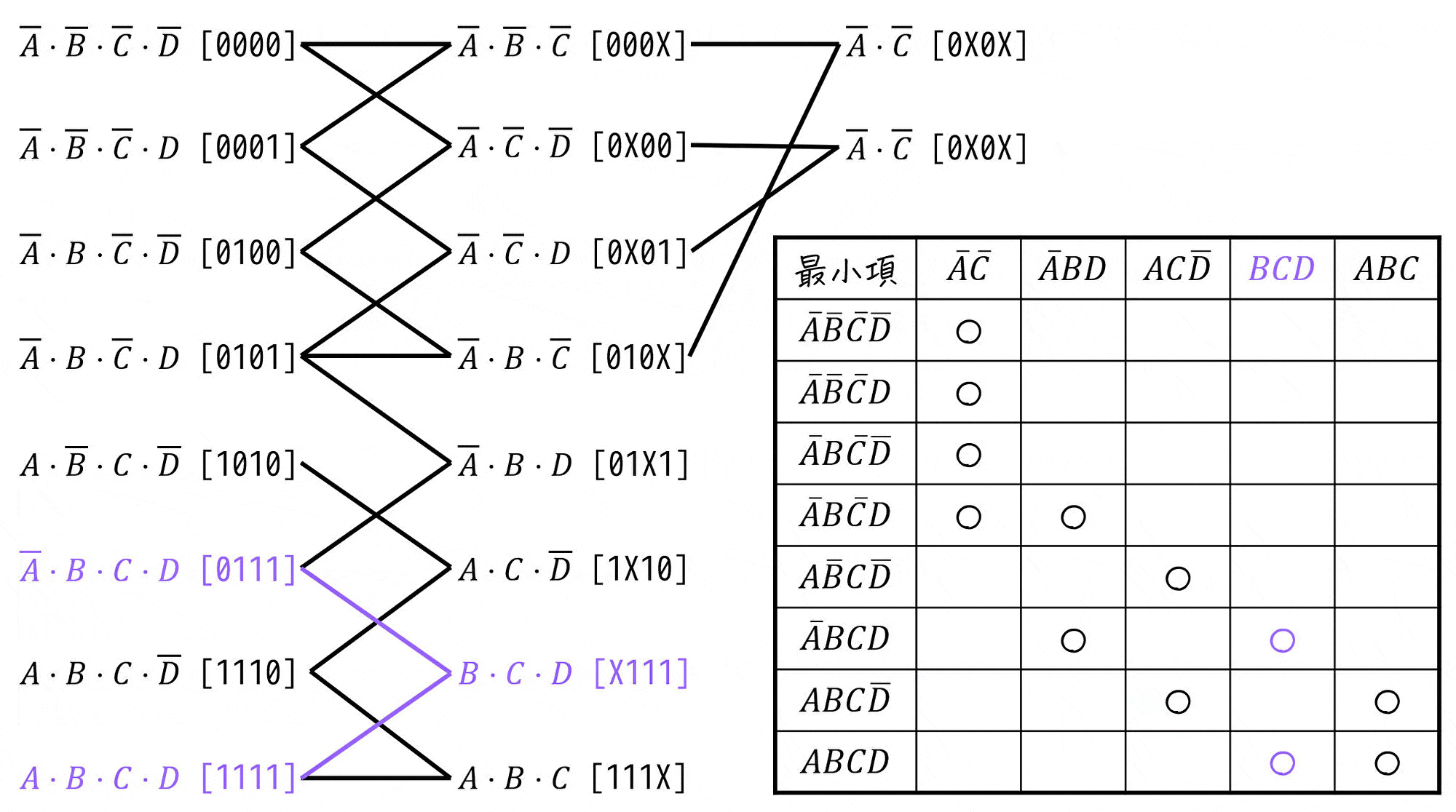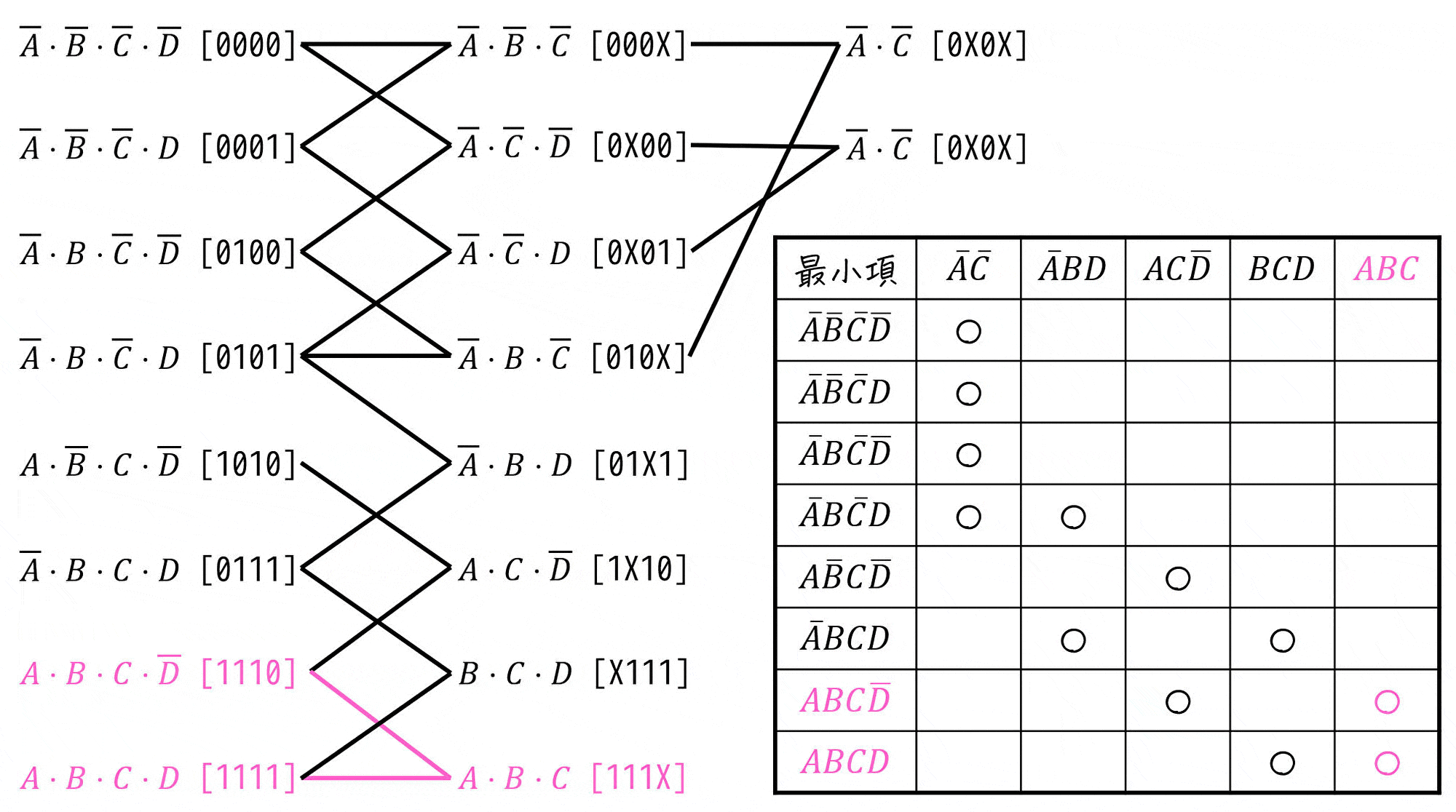
つぎに、最小項ごとに「1つの主項にしか対応していないかどうかを確認」し、該当する部分の○を●で書き換えます。
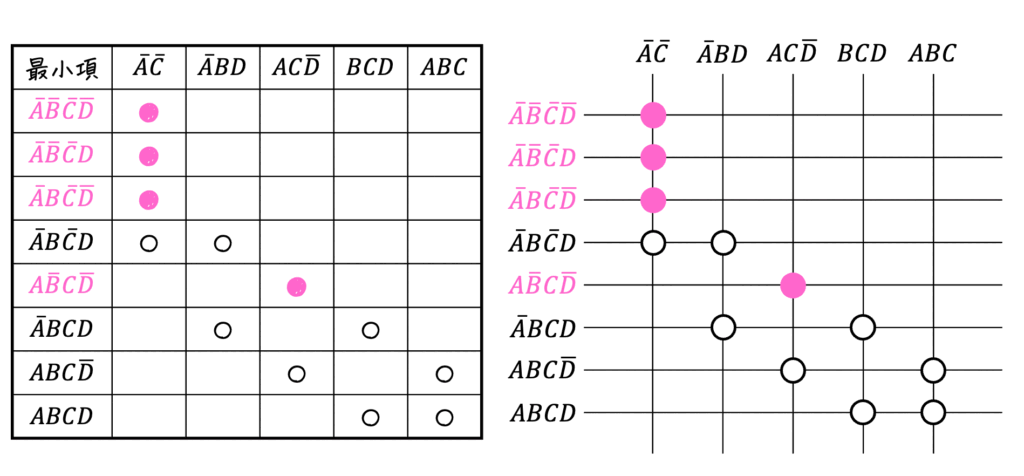
あとは、主項ごとに「1つでも●となっている主項」をすべて選べばOKです。
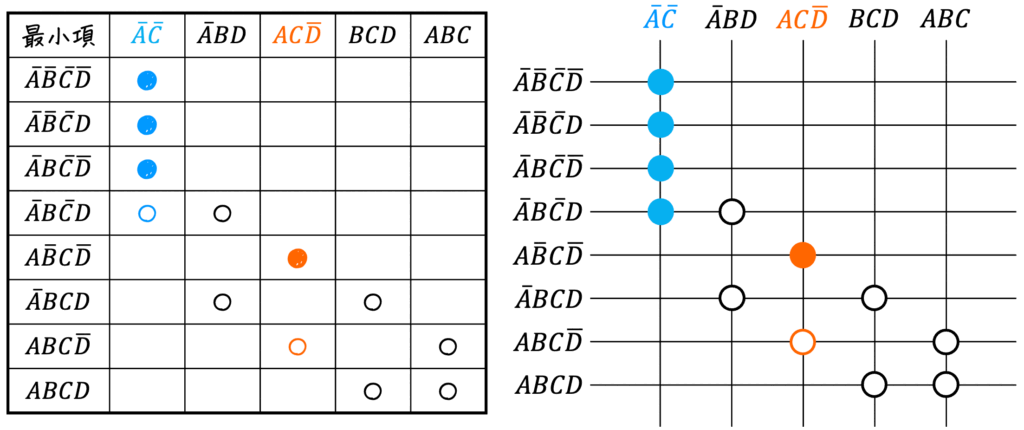
よって、必須主項は \( \textcolor{deepskyblue}{ \bar{A} \bar{C} } \), \( \textcolor{orange}{ AC \bar{D} } \) となります。(2つ)
(2-iii) 必須主項以外も考える
選んだ2つの必須主項だけですべての最小項をカバーできているかどうかを確認すると、まだ \( \bar{A} BCD \), \( ABCD \) の2つがカバーできていないことがわかります。
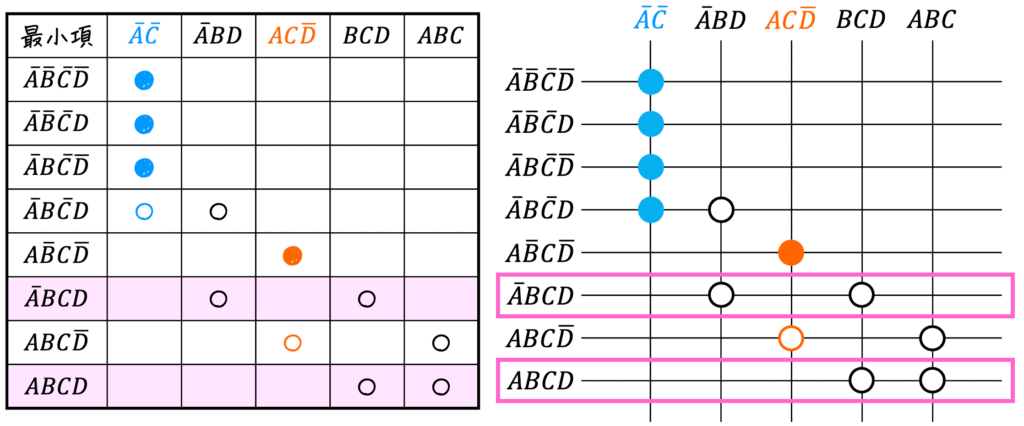
そこで、残りの3つの主項 \( \bar{A} B D \), \( BCD \), \( ABC \) から、できるだけ「選んだ主項の変数の数の和」が少なくなるように \( \bar{A} BCD \), \( ABCD \) をカバーすることを考えます。
今回の場合、\( BCD \) を選ぶことで残りの \( \bar{A} BCD \), \( ABCD \) がカバーでき、必須主項と合わせることで全ての最小項がカバーできることがわかります。
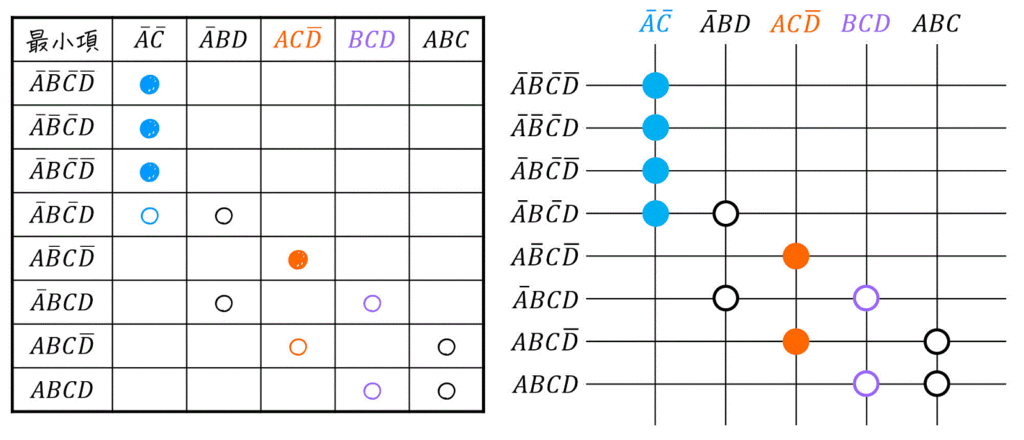
よって、必須主項 \( \bar{A} \bar{C} \), \( A C \bar{D} \)、および追加で選択した主項 \( BCD \) の和\[
X = \bar{A} \bar{C} + A C \bar{D} + BCD
\]が最簡形となります。
注釈
| ↑1 | できたとしても非常に難易度が高いです。 |
|---|---|
| ↑2 | 主項とは、最も簡単化された論理式を和ごとに分解したそれぞれの項(部品)のことです。例えば、最も簡単化された論理式が\[ Y = A + \bar{B} C \]であれば、主項は \( A \), \( \bar{B} C \) の2つとなります。 |
| ↑3 | 例えば \( \bar{A} B C \bar{D} \) であれば、\( B \) と \( C \) が真理値表の1に対応するため、「真理値表に変換した際の1の数」は2となります。 |
| ↑4 | 今回の場合、「1つのグループ」、「2つのグループ」、「3つのグループ」の3種類となります。 |
| ↑5 | やみくもにすべての項を確認するよりも、「1の数」の差が1となる項だけを確認することで、確認すべきペアの数を減らせるので、ミスが減ります。 |
| ↑6 | ●がついている最小項は、対応する主項が1つであることを示しています。そのため、その(対応する1つの)主項を必ず選択しないと論理式 \( X \) を表現することはできません。 |
| ↑7 | 例えば、\( A \bar{B} \) と \( \bar{A} B C \) を選択した場合は、変数の数は2と3なので、和は5となります。 |
関連広告・スポンサードリンク