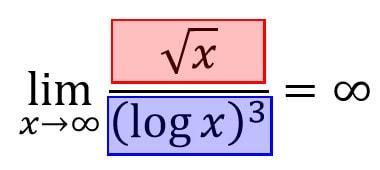
スポンサードリンク
こんにちは。ももやまです。
今回は少し短めですが、極限における関数の発散速度についてまとめてみました。
一応高校生の内容なのですが、計算するときにロピタルの定理を使ってしまっているので、まだロピタルの定理を習っていない人はおとなしく別の方法で計算をしてください。*1
グラフは、以下のサイトを使って描画しました。
注意:このサイトでは十分に大きい変数として、 \( n \) と \( x \) の両方を使っています。
発散速度とは、十分に \( n \) (もしくは \( x \) )が大きくなったときに \( n \) の値が増えていくにつれてどちらのほうがより無限大に早く近づくのかを表しています。例えば、\( \log x \), \( x^{2} \), \( e^{x} \) の3つの場合だと、どれが一番より早く無限大に近づくでしょうか?
試しにグラフを描いてみます
グラフを見てみると、\( e^{x} \) はやはり早いですね。つぎに \( x^{2} \) 、最後に \( \log x \) といったところでしょうか。
では他の関数だとどうなるでしょう? 結論を先に言います。\( a \lt 1 \lt b \lt c \) とするとき、
\[\begin{align*} 1 < & (\log n)^{a} < (\log n)^{b} < (\log n)^{c} \\ < & n^{a} < n^{b} < n^{c} < b^{n} < c^{n} < n! \end{align*} \]となります。( \( a^{n} \) は実は1より弱いことに注意)
簡単に言うと(対数関数 log) < (多項式 \( xb \)) < (指数関数 \( bx \) )となります。
今回は、より結果が大きくなる方を「項が強い」と表記します。
例えば、\( n^{2} \) と \( n^{3} \) の場合は \( n^{3} \) のほうが大きいことはわかりやすいと思います。
しかし、\( n^{2} \)、\( 2^{n} \) 、\( \log_2 x \) 、 \( n! \)、 \( n^{n} \) のようにパッと見ただけでは少しわかりにくいものもあるかもしれません。
ここでは、それぞれの強さを見比べていきましょう。
目次
スポンサードリンク
1.項の強さの判定方法
強さをみくらべる前に、2つの項の強さを判定する方法について説明したいと思います。
2つの項の強さを比べるには、それぞれの項を分子、分母のどちらかにおき、無限大へ飛ばします。
飛ばした結果は3パターンにわかれるので、3パターンそれぞれを説明していきたいとおもいます。
(1) 分子が強かった場合
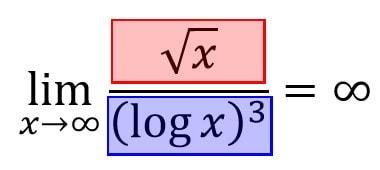
このように、分子のほうが分母よりも強い項であった場合、極限の計算結果は発散し、無限大になります。
(2) 分母が強かった場合
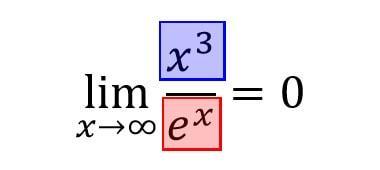
逆に分母のほうが分子よりも強い項であった場合、極限の計算結果は0に収束します。
(3) どちらとも同じ場合
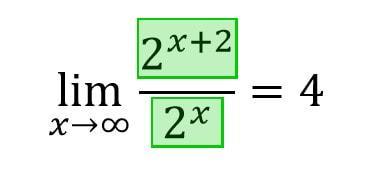
分子、分母ともに同じ強さの項であった場合、極限の計算結果は0以外に収束します。
また、極限の計算結果は分子が分母の何倍かを示します。(この場合は4倍)
スポンサードリンク
2.項の強さ比較
(1) logの底はいくらであっても強さは同じ
まずは、logについてです。logの場合は、底が2だろうが10だろうがe(自然対数)だろうが強さは変わりません。
うーんと思った人のために底の変換公式を使ってみます。\[ \log_{10} n = \frac{ \log_{2} n}{ \log_{2} 10} \]となり、\( \log _{10} n \) は \( \log_2 n \) と比べてたかが \( \frac{1}{ \log_{2} 10} \) 倍、つまり定数倍なので項の強さとしては同じことがわかりますね。 ついでにグラフも載せてみます。赤が\( \log_2 {x} \), 青が \( \log_e {x} \), 緑が \( \log_{10} {x} \) となります。
ちなみにオーダー表記する際には底の数値は関係ない(底に \( n \) があったら別)なので基本的に底の数値を省略して \( O(\log n) \) と表記します。
(2) logは何乗されてもnよりは弱い
例えば、\( \log_e n \) と \( n \) はどちらが強いでしょうかと聞かれたらすぐに答えられると思います。 \[ \lim_ {n \to \infty} \frac{\log_e n}{n} = 0 \]なので、\( \log_e n \)ですね(ロピタルの定理やはさみうちの定理から出せます)。グラフを見ても明らかですよね。(赤色:\( \log_e n \) 青色:\( n \))
ですが \( (\log n)^{a} \) と \( n \) は \( a \) の値がどんな値であっても \( n \) のほうが強いと思いますか?
と言うことで極限を取ってみましょう。途中ロピタルの定理を使っています。
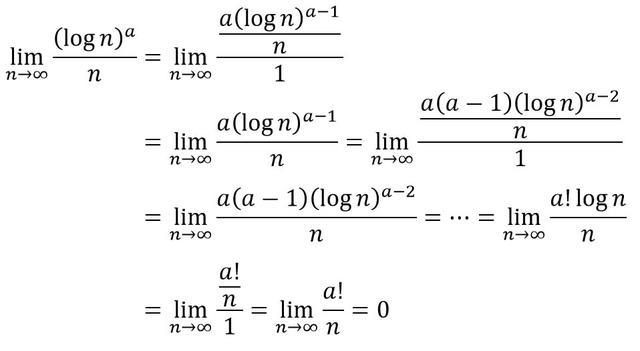
数式を見ればわかると思いますが、1回ロピタルを使うと分母の \( n \) がなくなりますね。しかし、分子の微分の結果 \( 1/n \) が発生し、また分母の \( n \) が復活します。なので、何回微分しても分母には \( n \) が残ってしまい最終的に結果が0となってしまうので、\( a \) の値がいくらであっても \( n \) のほうが強いことがわかりますね。(もちろん \( n^{0.1} \) など、指数部分が小さくなってもlogのほうが弱いことには変わりありません。)
(3) 指数関数は多項式 (na) よりも圧倒的に強い
指数関数、例えば \( 2^{n} \) や \( 3^{n} \) は、多項式である \( n^{2} \) や \( n^{3} \) よりも圧倒的に強いです。まずはグラフで比較してみましょう。赤色:\( x^{n} \) 青色:\( (1.1)^{n} \)
途中までは \( 2^{n} \) が勝っていたのですがさすが指数関数あとの追い上げがすごいです。
グラフから指数関数の速度がすごいことがわかっていただけたでしょうか。
今度は極限で比較してみましょう。\( n^{100} \) と \( 2^{n} \) を比べてみます。
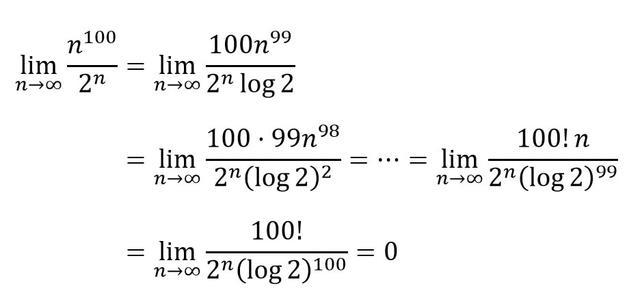
多項式側は、ロピタルの定理を適用し続ければいつかは定数項になるのですが、指数関数はロピタルの定理を使っても形が変化せず、 \( 2^{n} \) の形を保ち続けるので永久に消えず、\( 2^{n} \) 、つまり指数関数側のほうが強いことがわかりますね。
余談ですが、高校数学では指数関数の中でも \( e^{x} \) が出てくることが多いです。\( e^{x} \) の場合だと微分しても余計な残骸などは発生せず、ずっと \( e^{x} \) のままですね。
(4) 指数関数よりも強い階乗
なんと階乗、つまり \( n! \) は指数関数である \( 2^{n} \) よりも強いです。
今回も極限を使って階乗のほうが強いことを示したいのですが、今回はロピタルの定理が使えません。
ということではさみうちの定理を使って\[ \lim_ {n \to \infty} \frac{7^{n}}{n!} =0 \]を示してみます。
\[\begin{align*}
\frac{7!}{n!} & = \frac{7 \cdot 7 \cdots 7 \cdot 7}{n(n-1)(n-2) \cdots 2 \cdot 1}
\\ & = \underbrace{ \frac{7}{n} \cdot \frac{7}{n-1} \cdots \frac{7}{9} \cdot \frac{7}{8} }_{n-7 \ \mathrm{個} } \cdot \frac{7 \cdot 7 \cdots 7 \cdot 7}{7 \cdot 6 \cdots 2 \cdot 1}
\\ & \leqq \underbrace{ \frac{7}{8} \cdot \frac{7}{8} \cdots \frac{7}{8} \cdot \frac{7}{8} }_{n-7 \ \mathrm{個}} \cdot \frac{7^7}{7!}
\\ & = \left( \frac{7}{8} \right)^{n-7} \cdot \frac{7^7}{7!}
\end{align*}\]
ここで、\[
\lim_{n \to \infty} \left( \frac{7}{8} \right)^{n-7} \cdot \frac{7^7}{7!} = 0
\]は明らか。よってはさみうちの原理により、\[
\lim_{n \to \infty} \frac{7^n}{n!} = 0
\]となる。
よって \( n! \) のほうが \( a^{n} \) の指数関数よりも強いことがわかりますね。(今回は \( a = 7 \) でやっていますが…)
(5) 基本的に指数が後ろのほうに来ればくるほど強い
(a) \( n^{n} \) (b) \( 2^{2^{n}} \) (c) \( 2^{n^{2}} \) (d) \( n^{2^{2}} \)
この4つを強い順にに並び替えてみましょう。
わからなかったらロピタルと言いたいのですが、今回は指数が2つくっついていてめんどくさいので底が2の対数でlogをとっていきましょう。
(a) \( n \log_2 n \) (b) \( 2^{n} \log_2 2 \) (c) \( n^{2} \log_2 2 \) (d) \( 2^{2} \log_2 2 \)
となりますね。よって強さは (b) > (c) > (a) > (d) となりますね。 *2
ちなみに(d)以外はすべて階乗 \( n! \) よりも強い関数です。
\( n! = n(n-1)(n-2) \cdots 3 \cdot 2 \cdot 1 \)
\( n^{n} = n \cdot n \cdot n \cdot \cdots \cdot n \cdot n \cdot n \)
ほらね。明らかでしょ。
このように指数が2つ以上くっついててわけわからん状態になった場合はlogで外してあげることを覚えておきましょう。
スポンサードリンク
3.さいごに
今回は極限における発散速度の比較について説明しました。
項の強さ、つまり発散速度はアルゴリズムの良し悪しを評価する際にオーダー記法で使うことが多いので情報系のことを習っている人はぜひ発散速度については覚えておきましょう。
大学生でロピタルの定理を習っている場合はどっちの発散速度が早いかを忘れてもすぐに計算することができますね。
高校生の場合でも指数関数、多項式、対数関数の順に早く発散することを頭の片隅に入れておけば極限計算のときに役にたつかもしれません。
関連広告・スポンサードリンク





![うさぎでもわかる計算機システム Part01 2進数 [基本情報対応]](https://www.momoyama-usagi.com/wp-content/uploads/2021/05/20190612102246-1-150x150.gif)