スポンサードリンク
こんにちは、ももやまです。
前回に引き続き部分空間のお話です。
今回は部分空間の和空間、交空間について、図などを用いてわかりやすく説明していきたいと思います。
今回も例題や練習問題を用意しているのでぜひチャレンジしてみてください!
[注意]前回の部分空間その1の内容である解空間・生成系の部分空間の次元や基底を求め方を理解していることを前提に説明しているため、まだ解空間や生成系の部分空間の次元や基底の求め方があまりよくわかっていない人はこちらの記事をご覧になってからこの記事を見ることをおすすめします。
目次
スポンサードリンク
1.部分空間の組み合わせ
部分空間を組み合わせることで新たに部分空間を作成することができます。
今回は主な2つの組み合わせ方(和空間・交空間)について説明していきます。
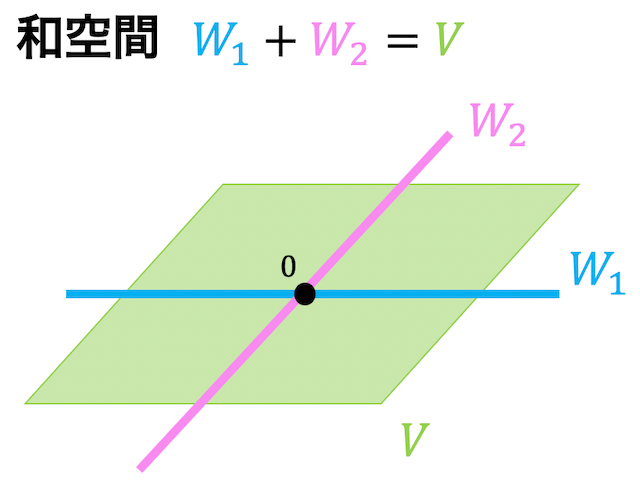
(1) 和空間 \( W_1 + W_2 \)
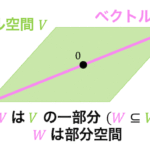
つぎの図のような部分空間 \( W_1 \), \( W_2 \) があるとします。
このとき、\( W_1 \) と \( W_2 \) はともに1次元の部分空間ですね。
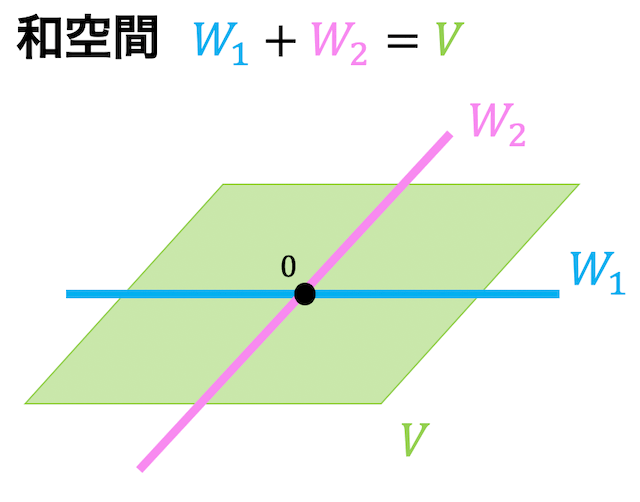
2つの部分空間内 \( W_1 \), \( W_2 \) にあるベクトルを合わせた部分空間 \( V \) を考えます。このとき部分空間 \( V \) は平面な(2次元)ベクトル空間となります。
これを和空間といい、\( W_1 + W_2 \) と表します。
(2) 交空間(共通部分) \( W_1 \cap W_2 \)
つぎに別の下図のような部分空間 \( W_1 \), \( W_2 \) があるとします。
このとき、\( W_1 \) と \( W_2 \) はともに2次元の部分空間ですね。
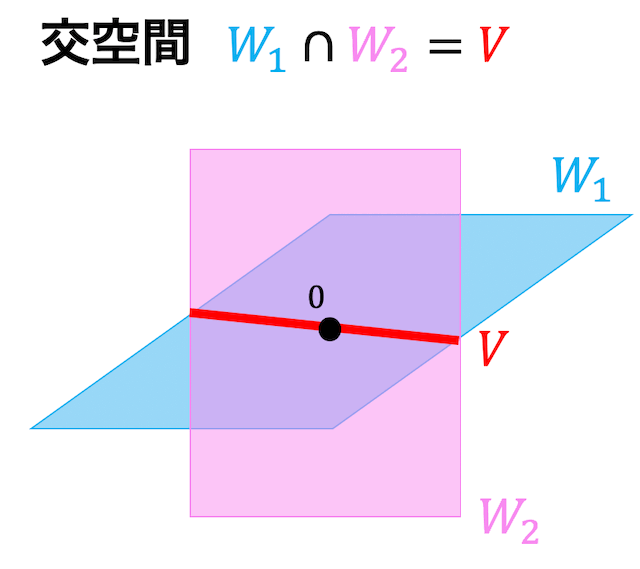
2つの部分空間内 \( W_1 \), \( W_2 \) に両方とも属している部分空間 \( V \) を考えます。このとき部分空間 \( V \) は原点を通る直線(1次元)ベクトル空間となります。
これを交空間といい、\( W_1 \cap W_2 \) で表します。
(交空間のことを共通部分という人もいます。)
\( W_1 \), \( W_2 \) がベクトル空間の部分空間であるとする。
このとき、\[
W_1 + W_2 = \left\{ \vec{x_1} + \vec{x_2} \ \middle| \ \vec{x_1} \in W_1 , \vec{x_2} \in W_2 \right\} \]\[
W_1 \cap W_2 = \left\{ \vec{x} \ \middle| \ \vec{x} \in W_1 かつ \vec{x} \in W_2 \right\}
\]はともに部分空間となり、\( W_1 + W_2 \) を和空間、\( W_1 \cap W_2 \) を交空間という。
和空間、交空間がともに部分空間となることを簡単に示したいと思います。
余裕があれば見てみましょう(余裕ない人はスキップしてOKです)。
和空間が部分空間となることの証明
\( W_1 \) 、\( W_2 \) が部分空間であると仮定すると、\[
W_1 + W_2 = \left\{ \vec{x_1} + \vec{x_2} \ \middle| \ \vec{x_1} \in W_1 , \vec{x_2} \in W_2 \right\}
\]が成立する。
ここで、\( W_1 + W_2 \) に属するベクトルを \( \vec{x} \), \( \vec{y} \) とすると、\[
\vec{x} = \vec{x_1} + \vec{x_2} \ \ \ \left( \vec{x_1} \in W_1, \vec{x_2} \in W_2 \right) \]\[
\vec{y} = \vec{y_1} + \vec{y_2} \ \ \ \left( \vec{y_1} \in W_1, \vec{y_2} \in W_2 \right)
\]が成立する。
(\( \vec{0} \in W_1 + W_2 \) は明らか)
(i) ベクトル空間に属するベクトルの和もベクトル空間かどうかの確認
\[
\vec{x} + \vec{y} = \left(\vec{x_1} + \vec{y_1} \right) + \left( \vec{x_2} + \vec{y_2} \right)
\]\[ \left( \vec{x_1} + \vec{y_1} \in W_1 + W_2, \vec{x_2} + \vec{y_2} \in W_1 + W_2 \right)
\]より(i)成立。
(ii) ベクトル空間に属するベクトルを定数倍してもベクトル空間かどうかの確認
\[ \begin{align*}
k \vec{x} = k \vec{x_1} + k \vec{x_2} \ \ \ \left( k \vec{x_1} \in W_1 , k \vec{x_2} \in W_2 \right)
\end{align*} \]より(ii)成立。
交空間が部分空間となることの証明
\( W_1 \) 、\( W_2 \) が部分空間であると仮定すると、\[
W_1 \cap W_2 =\left\{ \vec{x} \ \middle| \ \vec{x} \in W_1 \ かつ \ \vec{x} \in W_2 \right\}
\]が成立する。
ここで、\( W_1 \cap W_2 \) に属するベクトルを \( \vec{x} \), \( \vec{y} \) とすると、\[
\vec{x} , \vec{y} \in W_1 \ かつ \ \vec{x}, \vec{y} \in W_2
\]が成立する。
(\( \vec{0} \in W_1 \cap W_2 \) は明らか)
(i) ベクトル空間に属するベクトルの和もベクトル空間かどうかの確認
\[ \vec{x} + \vec{y} \in W_1 \ かつ \ \vec{x} + \vec{y} \in W_2 \] が成立するので、\[\vec{x} + \vec{y} \in W_1 \cap W_2 \]も成立し、(i)成立。
(ii) ベクトル空間に属するベクトルを定数倍してもベクトル空間かどうかの確認
\[ k\vec{x} \in W_1 \ かつ \ k \vec{x} \in W_2 \] が成立するので、\[ k \vec{x} \in W_1 \cap W_2 \]も成立し、(ii)成立。
スポンサードリンク
2.和空間・交空間の次元
和空間、交空間の次元には以下のような式が成り立ちます。
部分空間 \( W_1 \), \( W_2 \) と和空間 \( W_1 + W_2 \)、交空間 \( W_1 \cap W_2 \) の次元にはつぎのような関係が成り立つ。\[
\dim W_1 + \dim W_2 = \dim ( W_1 + W_2 ) + \dim ( W_1 \cap W_2)
\]
わかりやすく図で表してみました。
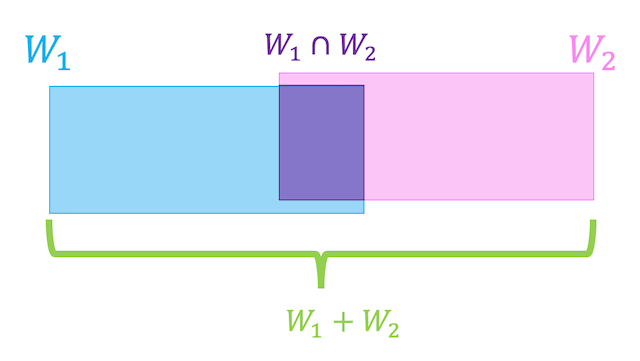
\( W_1 \cap W_2 \) はのりしろだと思ってください。
また、次のように、\( W_1 \cap W_2 \) の次元が0、つまり\[
W_1 \cap W_2 = \left\{ \vec{0} \right\} \]\[ \dim W_1 \cap W_2 = 0
\]を満たすとき、和空間 \( W_1 + W_2 \) を直和といい、\( W_1 \oplus W_2 \) で表します。
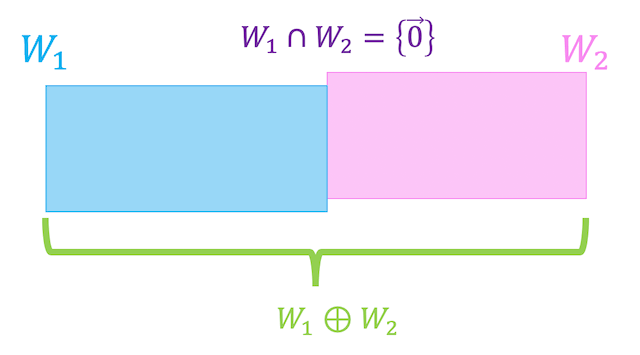
このとき、\( W_1 \cap W_2 \) の次元が0なため、\[
\dim W_1 \oplus W_2 = \dim W_1 + \dim W_2
\]が成立します。
では、1つ例題で和空間と交空間を出してみましょう。
例題では生成系の部分空間の和空間、交空間を実際に計算します。
例題
つぎの \( \mathbb{R}^n \) のベクトルの部分空間として、\[
W_1 = \left< \left( \begin{array}{ccc} 1 \\ 0 \\ 1 \\ 3 \end{array} \right) , \left( \begin{array}{ccc} 1 \\ 1 \\ 1 \\ 1 \end{array} \right), \left( \begin{array}{ccc} 1 \\ 2 \\ 0 \\ 1 \end{array} \right) \right> , \ W_2 = \left< \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \\ 0 \end{array} \right) , \left( \begin{array}{ccc} 2 \\ 2 \\ 2 \\ 2 \end{array} \right), \left( \begin{array}{ccc} 0 \\ 1 \\ 1 \\ 1 \end{array} \right) \right>
\]で生成される部分空間を考える。
(1) \( W_1 \), \( W_2 \) の次元を求めなさい。
(2) 和空間 \( W_1 + W_2 \) の次元と基底を求めなさい。
(3) 交空間 \( W_1 \cap W_2 \) の次元と基底を求めなさい。
解説
(1), (2)
\( W_1 \) に属するベクトルを\[
\vec{a_1} = \left( \begin{array}{ccc} 1 \\ 0 \\ 1 \\ 3 \end{array} \right) , \ \ \vec{a_2} = \left( \begin{array}{ccc} 1 \\ 1 \\ 1 \\ 1 \end{array} \right), \ \ \vec{a_3} = \left( \begin{array}{ccc} 1 \\ 2 \\ 0 \\ 1 \end{array} \right)
\]とし、\( W_2 \) に属するベクトルを\[
\vec{b_1} = \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \\ 0 \end{array} \right) , \ \ \vec{b_2} = \left( \begin{array}{ccc} 2 \\ 2 \\ 2 \\ 2 \end{array} \right), \ \ \vec{b_3} = \left( \begin{array}{ccc} 0 \\ 1 \\ 1 \\ 1 \end{array} \right)
\]とする。行列 \( C = (A|B) \) を \[
C = (A|B) = \left( \begin{array}{ccc|ccc} 1 & 1 & 1 & 1 & 2 & 0 \\ 0 & 1 & 2 & 0 & 2 & 1 \\ 1 & 1 & 0 & -1 & 2 & 1 \\ 3 & 1 & 1 & 0 & 2 & 1 \end{array} \right)
\]とする。\[
\begin{align*} &
\left( \begin{array}{ccc|ccc} 1 & 1 & 1 & 1 & 2 & 0 \\ 0 & 1 & 2 & 0 & 2 & 1 \\ 1_{-1} & 1_{-1} & 0_{-1} & -1_{-1} & 2_{-2} & 1 \\ 3_{-3} & 1_{-3} & 1_{-3} & 0_{-3} & 2_{-6} & 1 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc|ccc} 1 & 1_{-1} & 1_{-2} & 1 & 2_{-2} & 0_{-1} \\ 0 & 1 & 2 & 0 & 2 & 1 \\ 0 & 0 & -1 & -2 & 0 & 1 \\ 0 & -2_{+2} & -2_{+4} & -3 & -4_{+4} & 1_{+2} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc|ccc} 1 & 0 & -1_{+1} & 1_{+2} & 0 & -1_{-1} \\ 0 & 1 & 2_{-2} & 0_{-4} & 2 & 1_{+2} \\ 0 & 0 & -1 & -2 & 0 & 1 \\ 0 & 0 & 2_{-2} & -3_{-4} & 0 & 3_{+2} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc|ccc} 1_{\times 7} & 0_{\times 7} & 0_{\times 7} & 3_{\times 7} & 0_{\times 7} & -2_{\times 7} \\ 0_{\times 7} & 1_{\times 7} & 0_{\times 7} & -4_{\times 7} & 2_{\times 7} & 3_{\times 7} \\ 0_{\times 7} & 0_{\times 7} & -1_{\times 7} & -2_{\times 7} & 0_{\times 7} & 1_{\times 7} \\ 0 & 0 & 0 & -7 & 0 & 5 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc|ccc} 7 & 0 & 0 & 21_{-21} & 0 & -14_{+15} \\ 0 & 7 & 0 & -28_{+28} & 14 & 21_{-20} \\ 0 & 0 & -7 & -14_{+14} & 0 & 7_{-10} \\ 0 & 0 & 0 & -7 & 0 & 5 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc|ccc} 7 & 0 & 0 & 0 & 0 & 1 \\ 0 & 7 & 0 & 0 & 14 & 1 \\ 0 & 0 & -7 & 0 & 0 & -3 \\ 0 & 0 & 0 & -7 & 0 & 5 \end{array} \right)
\end{align*}
\]と変形できる。
(1)
変形より \( W_1 \), \( W_2 \) の次元はともに3。
(2)
\( W_1 + W_2 \) の次元は4となる。
1次独立なベクトルの最大組は行基本変形の結果より、\( \vec{a_1} \), \( \vec{a_2} \), \( \vec{a_3} \), \( \vec{b_1} \) となる。
よって基底は\[
\left\{ \ \vec{a_1}, \vec{a_2}, \vec{a_3}, \vec{a_4} \right\} \]\[
\left\{ \
\left( \begin{array}{ccc} 1 \\ 0 \\ 1 \\ 3 \end{array} \right) , \
\left( \begin{array}{ccc} 1 \\ 1 \\ 1 \\ 1 \end{array} \right) , \
\left( \begin{array}{ccc} 1 \\ 2 \\ 0 \\ 1 \end{array} \right) , \
\left( \begin{array}{ccc} 1 \\ 0 \\ -1 \\ 0 \end{array} \right) \
\right\}
\]となる。
(3)
まずは、共通部分 \( W_1 \cap W_2 \) の次元を求める。\[
\dim W_1 + \dim W_2 = \dim ( W_1 + W_2 ) + \dim ( W_1 \cap W_2)
\]より、\[\begin{align*}
\dim ( W_1 \cap W_2) & = \dim W_1 + \dim W_2 - \dim ( W_1 + W_2 )
\\ & = 3 + 3 - 4 = 2
\end{align*} \]となり、次元は2と求まる。
共通部分は、\( W_1 \) に属するベクトルの1次結合 = \( W_2 \) に属するベクトルの1次結合 を満たすものを求めればよい。
(2)の行基本変形より、\[
\vec{a_1} + \vec{a_2} + 3 \vec{a_3} - 5 \vec{b_1} = 7 \vec{b_3} \]\[
2 \vec{a_2} = \vec{b_2}
\]の関係式が成立する(行基本変形の前後で1次結合関係は変わらない)。
(ベクトルa) = (ベクトルb) の形になるように変形をすると、\[
\vec{a_1} + \vec{a_2} + 3 \vec{a_3} = 5 \vec{b_1} + 7 \vec{b_3} \]\[
2 \vec{a_2} = \vec{b_2} \
\]となる。
よって、共通部分 \( A \cap B \) の基底は、\[
\left\{ \
\vec{a_1} + \vec{a_2} + 3 \vec{a_3}, 2 \vec{a_2} \
\right\}
\]\[
\left\{ \
5 \vec{b_1} + 7 \vec{b_3} , \vec{b_2} \
\right\}
\]\[
\left\{ \
\left( \begin{array}{ccc} 5 \\ 7 \\ 2 \\ 7 \end{array} \right) , \
\left( \begin{array}{ccc} 2 \\ 2 \\ 2 \\ 2 \end{array} \right) \
\right\}
\]となる。
(ベクトルa, bどちらを使っても計算できますが、ベクトルbを使ったほうが早く計算ができます。ベクトルaは検算にどうぞ。)
スポンサードリンク
3.練習問題
では、2問ほど練習してみましょう。
例題では生成系の部分空間の和空間と交空間を求めましたが、練習問題では解空間の部分空間も載せているのでぜひチャレンジしてみてください。
練習1 生成系の和空間・交空間
つぎの \( \mathbb{R}^n \) のベクトルの部分空間として、\[
W_1 = \left< \left( \begin{array}{ccc} 1 \\ 0 \\ 1 \\ -1 \end{array} \right) , \left( \begin{array}{ccc} 1 \\ 1 \\ 2 \\ -3 \end{array} \right), \left( \begin{array}{ccc} 0 \\ 2 \\ -1 \\ 1 \end{array} \right) \right> , \ W_2 = \left< \left( \begin{array}{ccc} 5 \\ 3 \\ 5 \\ -6 \end{array} \right) , \left( \begin{array}{ccc} 3 \\ 1 \\ 4 \\ -5 \end{array} \right), \left( \begin{array}{ccc} 1 \\ -1 \\ 3 \\ -4 \end{array} \right) \right>
\]とする。このとき、次の部分空間 \( W_1 \), \( W_2 \) について、次の問いに答えなさい。
(1) \( W_1 \), \( W_2 \) の次元と基底を求めなさい。
(2) 和空間 \( W_1 + W_2 \) の次元と基底を求めなさい。
(3) 交空間 \( W_1 \cap W_2 \) の次元と基底を求めなさい。
練習2 解空間の和空間・交空間
行列 \( A,B \) を \[
A = \left( \begin{array}{ccc} 1 & -2 & -9 & 7 \\ 1 & 0 & 3 & 2
\end{array} \right) \]\[
B = \left( \begin{array}{ccc} 1 & -1 & -6 & 6 \\ -2 & 0 & 4 & -9
\end{array} \right)
\]とする。このとき、次の部分空間 \( W_1 \), \( W_2 \) について、次の問いに答えなさい。\[
W_1 = \left\{ \vec{x} \in \mathbb{R}^4 \ \middle| \ A \vec{x} = \vec{0} \right\} \]\[
W_2 = \left\{ \vec{x} \in \mathbb{R}^4 \ \middle| \ B \vec{x} = \vec{0} \right\}
\]
(1) \( W_1 \), \( W_2 \) の次元と基底を求めなさい。
(2) 和空間 \( W_1 + W_2 \) の次元と基底を求めなさい。
(3) 交空間 \( W_1 \cap W_2 \) の次元と基底を求めなさい。
4.練習問題の答え
解答1
\( W_1 \) に属するベクトルを\[
\vec{a_1} = \left( \begin{array}{ccc} 1 \\ 0 \\ 1 \\ -1 \end{array} \right) , \ \ \vec{a_2} = \left( \begin{array}{ccc} 1 \\ 1 \\ 2 \\ -3 \end{array} \right), \ \ \vec{a_3} = \left( \begin{array}{ccc} 0 \\ 2 \\ -1 \\ 1 \end{array} \right)
\]とし、\( W_2 \) に属するベクトルを\[
\vec{b_1} = \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \\ 0 \end{array} \right) , \ \ \vec{b_2} = \left( \begin{array}{ccc} 2 \\ 2 \\ 2 \\ 2 \end{array} \right), \ \ \vec{b_3} = \left( \begin{array}{ccc} 0 \\ 1 \\ 1 \\ 1 \end{array} \right)
\]とする。
行列 \( C = (A|B) \) を \[
C = (A|B) = ( \vec{a_1}, \vec{a_2}, \vec{a_3} | \vec{b_1}, \vec{b_2}, \vec{b_3} )
\]とする。 \[
C = (A|B) = \left( \begin{array}{ccc|ccc} 1 & 1 & 0 & 5 & 3 & 1 \\ 0 & 1 & 2 & 3 & 1 & -1 \\ 1 & 2 & -1 & 5 & 4 & 3 \\ -1 & -3 & 1 & -6 & -5 & -4 \end{array} \right)
\]とする。\[
\begin{align*} &
\left( \begin{array}{ccc|ccc} 1 & 1 & 0 & 5 & 3 & 1 \\ 0 & 1 & 2 & 3 & 1 & -1 \\ 1_{-1} & 2_{-1} & -1 & 5_{-5} & 4_{-3} & 3_{-1} \\ -1_{+1} & -3_{+1} & 1 & -6_{+5} & -5_{+3} & -4_{+1} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc|ccc} 1 & 1_{-1} & 0_{-2} & 5_{-3} & 3_{-1} & 1_{+1} \\ 0 & 1 & 2 & 3 & 1 & -1 \\ 0 & 1 & -1 & 0 & 1 & 2 \\ 0 & -2_{+2} & 1_{+4} & -1_{+6} & -2_{+2} & -3_{-2} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc|ccc} 1 & 0 & -2 & 2 & 2 & 2 \\ 0 & 1 & 2 & 3 & 1 & -1 \\ 0 & 1_{-1} & -1_{-2} & 0_{-3} & 1_{-1} & 2_{+1} \\ 0 & 0 & 5 & 5 & 0 & -5 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc|ccc} 1 & 0 & -2_{+2} & 2_{+2} & 2 & 2_{-2} \\ 0 & 1 & 2_{-2} & 3_{-2} & 1 & -1_{+2} \\ 0_{\div (-3)} & 0_{\div (-3)} & -3_{\div (-3)} & -3_{\div (-3)} & 0_{\div (-3)} & 3_{\div (-3)} \\ 0 & 0 & 5_{-5} & 5_{-5} & 0 & -5_{+5} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc|ccc} 1 & 0 & 0 & 4 & 2 & 0 \\ 0 & 1 & 0 & 1 & 1 & 1 \\ 0 & 0 & 1 & 1 & 0 & -1 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array} \right)
\end{align*}
\]と変形できる。
(1)
行基本変形の左側3列が \( W_1 \)、右側3列が \( W_2 \) である。
\( W_1 \) の次元は明らかに3。
\( W_2 \) の次元はまだわからないので右側3列だけを更に行基本変形する。\[
\begin{align*} &
\left( \begin{array}{ccc} 4_{-4} & 2_{-4} & 0_{-4} \\ 1 & 1 & 1 \\ 1_{-1} & 0_{-1} & -1_{-1} \\ 0 & 0 & 0 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 0 & -2_{+2} & -4_{+4} \\ 1 & 1 & 1 \\ 0 & -1 & -2 \\ 0 & 0 & 0 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 0 & 0 & 0 \\ 1 & 1_{-1} & 1_{-2} \\ 0 & -1 & -2 \\ 0 & 0 & 0 \end{array} \right)
\end{align*}
\]と変形できるので、\( W_2 \) の次元は2となる。
(2)
行列 \( C \) の階数が3なので、\( W_1 + W_2 \) の次数は3。
また、行列 \( C \) の行基本変形の結果より、\( \vec{a_1} \), \( \vec{a_2} \), \( \vec{a_3} \) が1次独立なベクトルの最大組。
よって基底は\[
\left\{ \ \vec{a_1}, \vec{a_2}, \vec{a_3} \right\} \]\[
\left\{ \
\left( \begin{array}{ccc} 1 \\ 0 \\ 1 \\ -1 \end{array} \right) , \
\left( \begin{array}{ccc} 1 \\ 1 \\ 2 \\ -3 \end{array} \right) , \
\left( \begin{array}{ccc} 0 \\ 2 \\ -1 \\ 1 \end{array} \right) , \
\right\}
\]となる。
(3)
まずは、共通部分 \( W_1 \cap W_2 \) の次元を求める。\[
\dim W_1 + \dim W_2 = \dim ( W_1 + W_2 ) + \dim ( W_1 \cap W_2)
\]より、\[\begin{align*}
\dim ( W_1 \cap W_2) & = \dim W_1 + \dim W_2 - \dim ( W_1 + W_2 )
\\ & = 3 + 2 - 3 = 2
\end{align*} \]となり、次元は2となる。
行基本変形より、\[
2\vec{a_1} + \vec{a_2} = \vec{b_2} \]\[
\vec{a_2} - \vec{a_3} = \vec{b_3}
\]の関係式が成立する(行基本変形の前後で1次結合関係は変わらない)。
(ベクトルa) = (ベクトルb) の形になっているので変形は不要。
また、\[
\begin{align*} B & = ( \vec{b_2} , \vec{b_3} ) \\ & =
\left( \begin{array}{ccc} 3_{-3} & 1_{+3} \\ 1 & -1 \\ 4_{-4} & 3_{+4} \\ -5_{+5} & -4_{-5} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 0 & 4_{\div 4} \\ 1 & -1_{+1} \\ 0 & 7_{-7} \\ 0 & -9_{+9} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 0 & 1 \\ 1 & 0 \\ 0 & 0 \\ 0 & 0 \end{array} \right)
\end{align*}
\]より、\( \vec{b_2} \), \( \vec{b_3} \) はともに1次独立である。
(行基本変形などで示しましょう。)
よって、共通部分 \( A \cap B \) の基底は、\[
\left\{ \
2\vec{a_1} + \vec{a_2}, \vec{a_2} - \vec{a_3}
\right\}
\]\[
\left\{ \
\vec{b_2} , \vec{b_3}
\right\}
\]\[
\left\{ \
\left( \begin{array}{ccc} 3 \\ 1 \\ 4 \\ -5 \end{array} \right) , \
\left( \begin{array}{ccc} 1 \\ -1 \\ 3 \\ -4 \end{array} \right)
\right\}
\]となる。
解答2
(1)
\( A \vec{x} = \vec{0} \), \( B \vec{x} = \vec{0} \) の解を求める。\[
\begin{align*} A = &
\left( \begin{array}{ccc} 1 & -2 & -9 & 7 \\ 1_{-1} & 0_{+2} & 3_{+9} & 2_{-7} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & -2_{+2} & -9_{+12} & 7_{-5} \\ 0 & 2 & 12 & -5 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 0 & 3 & 2 \\ 0 & 2 & 12 & -5 \end{array} \right)
\end{align*}
\]と行基本変形できるので、\[
\dim W_1 = n - \mathrm{Rank} \ A = 4 - 2 = 2
\]となる。
また、連立方程式の解は\[
\left\{ \begin{array}{l} x + 3z + 2w = 0 \\ 2y + 12z - 5w = 0 \end{array}\right.
\]を解くと求められる(自由度は2)。
ここで、\( z = s \), \( w = 2t \) とおくと、\( x = -3s - 4t \), \( y = -6s + 5t \) となるので、\[
\vec{x} =
\left( \begin{array}{ccc} x \\ y \\ z \\ w \end{array} \right)
= s \left( \begin{array}{ccc} -3 \\ -6 \\ 1 \\ 0 \end{array} \right)
+ t \left( \begin{array}{ccc} -4 \\ 5 \\ 0 \\ 2 \end{array} \right)
\]となり、\( V \) の基底は\[
V = \left\{\ \left( \begin{array}{ccc} -3 \\ -6 \\ 1 \\ 0 \end{array} \right), \left( \begin{array}{ccc} -4 \\ 5 \\ 0 \\ 2 \end{array} \right) \ \right\}
\]となります(基底は基本解の組み合わせ)。
\[
\begin{align*} B = &
\left( \begin{array}{ccc} 1 & -1 & -6 & 6 \\ -2_{+2} & 0_{-2} & 4_{-12} & -9_{+12} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1_{\times 2} & -1_{\times 2} & -6_{\times 2} & 6_{\times 2} \\ 0 & -2 & -8 & 3 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 2 & -2_{+2} & -12_{+8} & 12_{-3} \\ 0 & -2 & -8 & 3 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 2 & 0 & -4 & 9 \\ 0 & -2 & -8 & 3 \end{array} \right)
\end{align*}
\]
と行基本変形できるので、\[
\dim W_2 = n - \mathrm{Rank} \ A = 4 - 2 = 2
\]となる。
また、連立方程式の解は\[
\left\{ \begin{array}{l} 2x - 4z + 9w = 0 \\ -2y - 8z + 3w = 0 \end{array}\right.
\]を解くと求められる(自由度は2)。
ここで、\( z = s \), \( w = 2t \) とおくと、\( x = 2s - 9t \), \( y = -4s + 3t \) となるので、\[
\vec{x} =
\left( \begin{array}{ccc} x \\ y \\ z \\ w \end{array} \right)
= s \left( \begin{array}{ccc} 2 \\ -4 \\ 1 \\ 0 \end{array} \right)
+ t \left( \begin{array}{ccc} -9 \\ 3 \\ 0 \\ 2 \end{array} \right)
\]となり、\( V \) の基底は\[
V = \left\{\ \left( \begin{array}{ccc} 2 \\ -4 \\ 1 \\ 0 \end{array} \right), \left( \begin{array}{ccc} -9 \\ 3 \\ 0 \\ 2 \end{array} \right) \ \right\}
\]となります(基底は基本解の組み合わせ)。
(2)
和空間の基底 \( W_1 + W_2 \) は、(1)で求めた生成系の和空間\[
W_1 + W_2 = \left< \left( \begin{array}{ccc} -3 \\ -6 \\ 1 \\ 0 \end{array} \right), \left( \begin{array}{ccc} -4 \\ 5 \\ 0 \\ 2 \end{array} \right) , \left( \begin{array}{ccc} 2 \\ -4 \\ 1 \\ 0 \end{array} \right), \left( \begin{array}{ccc} -9 \\ 3 \\ 0 \\ 2 \end{array} \right) \right>
\]の基底を求めればよい。
\( W_1 + W_2 \) に属するベクトルを\[
\vec{a_1} = \left( \begin{array}{ccc} -3 \\ -6 \\ 1 \\ 0 \end{array} \right) , \ \ \vec{a_2} = \left( \begin{array}{ccc} -4 \\ 5 \\ 0 \\ 2 \end{array} \right), \ \ \vec{b_1} = \left( \begin{array}{ccc} 2 \\ -4 \\ 1 \\ 0 \end{array} \right), \ \ \vec{b_2} = \left( \begin{array}{ccc} -9 \\ 3 \\ 0 \\ 2 \end{array} \right)
\]とする。\[
\begin{align*} C = &
\left( \begin{array}{cc|cc} -3_{+3} & -4 & 2_{+3} & -9 \\ -6_{+6} & 5 & -4_{+6} & 3 \\ 1 & 0 & 1 & 0 \\ 0_{\div 2} & 2_{\div 2} & 0_{\div 2} & 2_{\div 2} \end{array} \right) \\ \to \ &
\left( \begin{array}{cc|cc} 0 & -4_{+4} & 5 & -9_{+4} \\ 0 & 5_{-5} & 2 & 3_{-5} \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \end{array} \right) \\ \to \ &
\left( \begin{array}{cc|cc} 0 & 0 & 5_{\div 5} & -5_{\div 5} \\ 0 & 0 & 2_{-2} & -2_{+2} \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \end{array} \right) \\ \to \ &
\left( \begin{array}{cc|cc} 0 & 0 & 1 & -1 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \end{array} \right) \\ \to \ &
\left( \begin{array}{cc|cc} 1 & 0 & 1_{-1} & 0_{+1} \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & -1 \\ 0 & 0 & 0 & 0 \end{array} \right) \\ \to \ &
\left( \begin{array}{cc|cc} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & -1 \\ 0 & 0 & 0 & 0 \end{array} \right)
\end{align*}
\]となるので、行基本変形の結果より、\( \vec{a_1} \), \( \vec{a_2} \), \( \vec{a_3} \) が1次独立なベクトルの最大組。
よって基底は\[
\left\{ \ \vec{a_1}, \vec{a_2}, \vec{a_3} \right\} \]\[
\left\{ \
\left( \begin{array}{ccc} -3 \\ -6 \\ 1 \\ 0 \end{array} \right) , \
\left( \begin{array}{ccc} -4 \\ 5 \\ 0 \\ 2 \end{array} \right) , \
\left( \begin{array}{ccc} 2 \\ -4 \\ 1 \\ 0 \end{array} \right) , \
\right\}
\]となる。
(3)
共通部分 \( W_1 \cap W_2 \) の次元を求める。\[
\dim W_1 + \dim W_2 = \dim ( W_1 + W_2 ) + \dim ( W_1 \cap W_2)
\]より、\[\begin{align*}
\dim ( W_1 \cap W_2) & = \dim W_1 + \dim W_2 - \dim ( W_1 + W_2 )
\\ & = 2 + 2 - 3 = 1
\end{align*} \]となり、次元は1となる。
また、(2)の行基本変形より、\[
\vec{a_1} + \vec{a_2} - \vec{b_1} = \vec{b_2}
\]の関係式が成立する(行基本変形の前後で1次結合関係は変わらない)。
(ベクトルa) = (ベクトルb) の形になるように変形をすると、\[
\vec{a_1} + \vec{a_2} = \vec{b_1} + \vec{b_2}
\]となる。
よって、共通部分 \( A \cap B \) の基底は、\[
\left\{ \
\vec{a_1} + \vec{a_2}
\right\}
\]\[
\left\{ \
\vec{b_1} + \vec{b_2}
\right\}
\]\[
\left\{ \
\left( \begin{array}{ccc} -7 \\ -1 \\ 1 \\ 2 \end{array} \right) \
\right\}
\]となる。
直接 \( W_1 \cap W_2 \) を求める方法もある。
\( W_1 \) の方程式と \( W_2 \) の方程式の両方を満たすものが交空間の基底となる。
行列 \( C \) を \[
C = \left( \begin{array}{ccc} 1 & -2 & -9 & 7 \\ 1 & 0 & 3 & 2 \\ 1 & -1 & -6 & 6 \\ -2 & 0 & 4 & -9 \end{array} \right)
\]とすると\[
W_1 \cap W_2 = \left\{ \vec{x} \in \mathbb{R}^4 \ \middle| \ C \vec{x} = \vec{0} \right\}
\]を求めればよい。
\( C \vec{x} = \vec{0} \) の解を求める。\[
\begin{align*} C = &
\left( \begin{array}{ccc} 1 & -2 & -9 & 7 \\ 1_{-1} & 0_{+2} & 3_{+9} & 2_{-7} \\ 1_{-1} & -1_{+2} & -6_{+9} & 6_{-7} \\ -2_{+2} & 0_{-4} & 4_{-18} & -9_{+14} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & -2_{+2} & -9_{+6} & 7_{-2} \\ 0 & 2_{-2} & 12_{-6} & -5_{+2} \\ 0 & 1 & 3 & -1 \\ 0 & -4_{+4} & -14_{+12} & 5_{-4} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 0 & -3 & 5 \\ 0 & 0 & 6_{-6} & -3_{+3} \\ 0 & 1 & 3_{-2} & -1_{+1} \\ 0 & 0 & -2 & 1 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 0 & -3 & 5 \\ 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & -2 & 1 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 0 & -3 & 5 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & -2 & 1 \\ 0 & 0 & 0 & 0 \end{array} \right)
\end{align*}
\]と行基本変形できるので、\[
\dim W_1 \cap W_2 = n - \mathrm{Rank} \ A = 4 - 3 = 1
\]となる。
また、連立方程式の解は\[
\left\{ \begin{array}{l} x - 3z + 5w = 0 \\ y + z = 0 \\ -2z + w = 0 \end{array}\right.
\]を解くと求められる(自由度は1)。
ここで、\( z = t \) とおくと、\( w = 2t \), \( y = -t \), \( x = -7t \)となるので、\[
\vec{x} =
\left( \begin{array}{ccc} x \\ y \\ z \\ w \end{array} \right)
= t \left( \begin{array}{ccc} -7 \\ -1 \\ 1 \\ 2 \end{array} \right)
\]となり、\( V \) の基底は\[
V = \left\{\ \left( \begin{array}{ccc} -7 \\ -1 \\ 1 \\ 2 \end{array} \right) \ \right\}
\]となります(基底は基本解の組み合わせ)。
5.さいごに
今回は部分空間の和空間と交空間の基底と次元についてのまとめを行いました。
和空間と交空間の次元の定理\[
\dim W_1 + \dim W_2 = \dim ( W_1 + W_2 ) + \dim ( W_1 \cap W_2)
\]は交空間を求める際に大変便利なのでぜひ利用しましょう。
また、和空間、交空間を求める際には少し大きめな行列を行基本変形する必要があるため、計算量が多くなってしまいます。なので特に注意して行基本変形を行いましょう。
関連広告・スポンサードリンク