確率統計分野で頻出な確率分布　離散型確率分布編

2020年5月6日 2024年8月23日 28分22秒

ももうさ

スポンサードリンク

こんにちは、ももやまです。

今回は、大学の「確率・統計」や統計検定、院試などで出てくる確率分布のうち、離散型型確率分布、具体的には

（離散）一様分布
ベルヌーイ試行
二項分布
ポアソン分布
多項分布
幾何分布
超幾何分布

がどんなものなのかについて説明していきたいと思います。

また、特に重要な分布については数式や例題や別記事などで補足しております。

なお、確率変数、確率分布、平均（期待値）、分散などの基本的な用語がよくわからない人 or 忘れてしまった人は、下の記事で復習してからこちらの記事をご覧になることをおすすめします。

www.momoyama-usagi.com

スポンサードリンク

０．離散型確率分布・連続型確率分布の違い

離散型確率分布について説明する前に、まずは離散型確率分布と連続型確率分布の違いについて説明していきたいと思います。

(1) 離散型確率分布

例えば、サイコロを1回振った時に出てきた目を確率変数 $X$ とします。

サイコロを1回振ったときに出てくる目は「1, 2, 3, 4, 5, 6」の6つですね。

なので、 $X$ も 1, 2, 3, 4, 5, 6 の6つの値しかとりませんよね。

（例えば $X = 5.5$ や $X = 3.5$ のような値にはなりませんね）

このように、とぎれとぎれの値を持つような確率変数 $X$ が従う分布のことを離散型確率分布（離散確率分布）と呼びます。

言い換えると、それぞれの $X$ が取りうる値の確率を列挙することができるような分布のことを離散型確率分布と言います。

例えば1個のサイコロを振ったときに出てくる値の目を $X$ とした場合、

X	確率
1	$\frac{1}{6}$
2	$\frac{1}{6}$
3	$\frac{1}{6}$
4	$\frac{1}{6}$
5	$\frac{1}{6}$
6	$\frac{1}{6}$

のように6通りすべてを列挙できます。

(2) 連続型確率分布

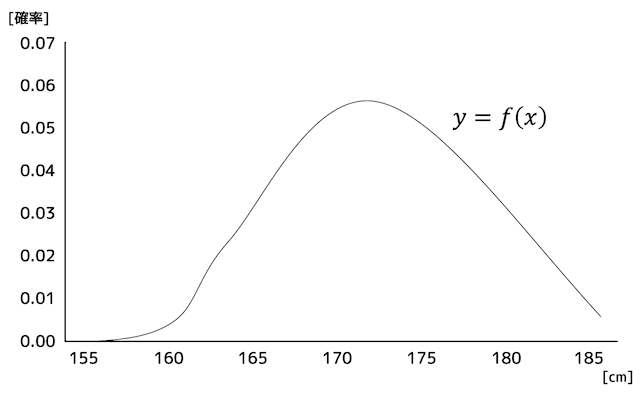
例えば、ある大学の男子学生から1人選んだときの身長を $X$ cm とします。

ところが、世の中には身長が「163.000000… [cm]」や「166.000000… [cm]」のように、ちょうどぴったり163[cm]や166[cm]の人はいませんね。

つまり、 $X = 163$ , $X = 166$ となる確率は0ですね。

（ $X$ を他の数字にしても同じです。175だろうが156.7だろうが確率は0です）

このように、 $X$ が連続（値がとぎれとぎれにならない）な確率変数 $X$ が従う分布のことを連続型確率分布（連続確率分布）と呼びます。

言い換えると、それぞれの $X$ が取りうる値の確率を列挙することができないような確率分布が連続型確率分布です。

連続型確率分布では、それぞれの $X$ が取りうる値の確率を列挙することができないため、下のように $X$ を一定範囲ごとに区切って、範囲内となる確率（相対度数）を調べることで列挙を行います。

	度数	相対度数
155〜160	2	0.02
160〜165	12	0.12
165〜170	24	0.24
170〜175	28	0.28
175〜180	20	0.20
180〜185	14	0.14
合計	100	1.00

区切る一定範囲を細かく細かく刻んでいくと、下のようにヒストグラムを関数 $y = f (x)$ とみなすことができます。

このような関数のことを確率密度関数と呼びます。

（確率密度関数に関する詳しいお話はこちらをご覧ください。）

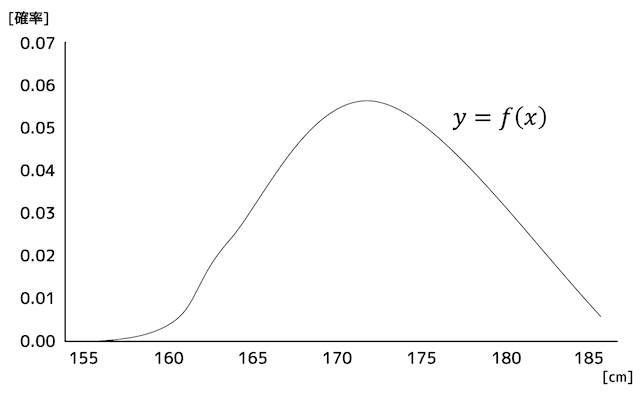
関数 $y = f (x)$ は、ある確率変数 $X$ が $x$ の値となるときの確率密度 $y$ を示しています。

なお、身長に限らず、実験などで「長さ」や「時間」や「重さ」などを測定したときの測定値はすべて連続型の確率変数となります。

ということで、ここからは離散型の確率分布で重要なものをいくつか紹介し、特に重要なものは例題などを含めて説明していきましょう。

スポンサードリンク

１．（離散）一様分布

ある確率変数 $X$ がとりうる値がすべて等しい確率となるような分布のことを離散一様分布と呼びます。

数Aで確率を習ったときに出てきた「同様に確からしい」事象がまさに一様分布に従う事象となります。

例えば、1回サイコロを振って出た目を $X$ としましょう。

サイコロの目の中で1, 2, 3, 4, 5, 6どの目も出る確率は全く同じ（1/6）ですよね。

なので、サイコロの出目 $X$ は一様分布に従うことがわかりますね。

スポンサードリンク

２．ベルヌーイ分布

(1) ベルヌーイ分布とは

ベルヌーイ分布を説明する前に、ベルヌーイ試行について説明しましょう。

ベルヌーイ試行とは、

試行結果が2通り（成功 or 失敗）しかない
試行を繰り返した際に、それぞれの試行が独立である
（前や後の試行が一切影響しない）
試行を繰り返した際に、成功（失敗）確率が変化しない

試行のことを表します。例えば、

（コイントスで）表が出る or 裏が出る
（サイコロで）1の目が出る or 出ない
（トランプで）1のカードを引く or 引かない

のような試行がベルヌーイ試行となります。

ベルヌーイ分布とは、ある確率変数 $X$ がベルヌーイ試行の結果となっているもの、つまり確率変数が2通りの値（基本的には0か1）しかとらないような分布のことを表します。

(2) ベルヌーイ分布の期待値・分散

では、ある確率分布 $X$ が確率 $p$ で $X = 1$ （成功）となり、 $1 - p$ で $X = 0$ （失敗）となるようなベルヌーイ分布であるときの期待値 $E (X)$ と分散 $V (X)$ を求めてみましょう。

X	確率
1	p
0	1-p

期待値 $E (X)$ 、分散 $V (X)$ はそれぞれ $\begin{aligned} E (X) & = 1 \cdot p + 0 \cdot (1 - p) \\ = p \end{aligned}$ $\begin{aligned} V (X) & = 1^{2} \cdot p + 0^{2} \cdot (1 - p) - {E (X)}^{2} \\ = p - p^{2} \\ = p (1 - p) \end{aligned}$ と計算することができます。

３．二項分布

ベルヌーイ試行（結果が2通りしかないような試行）を $n$ 回繰り返したとき、事象が起こる回数 $X$ が従う分布のことを二項分布のことを呼びます。

二項分布の代表例としては、

同じコインを100回コイントスしたときに表が出る回数
サイコロを180回振ったときに1の目が出る回数
じゃんけんを100回したときに勝つ回数

があります。

二項分布は、離散型確率分布の中でも特に重要なので、別の記事で詳しく説明しています。

詳しい説明については、下の記事をご覧ください。

www.momoyama-usagi.com

二項分布の平均・分散ある確率変数

X

が二項分布に従うときの平均

E (X)

、分散

V (X)

は、

E (X) = n p V (X) = E (X) \cdot (1 - p) = n p (1 - p)

で求められる。

（ただし $p$ は事象が起こる確率、 $n$ は試行回数）

二項分布は超重要なので、例題で確認していきましょう。

（ついでに確率の復習もしておきましょう。）

例題1

赤玉が3個、白玉が2個が入った箱がある。

この箱の中から、玉を1つ取り出し、取り出した玉の色を記録してから元に戻す操作（復元抽出）を繰り返す。赤玉が出た回数を $X$ とするとき、次の(1)～(3)の問いに答えなさい。

(1) 操作を1回行ったとき、赤玉が出る確率を求めなさい。
(2) 操作を2回行ったとき、赤玉が1回出る確率を求めなさい。
(3) 操作を150回行ったとき、赤玉が出る回数の平均 $E (X)$ と分散 $V (X)$ を求めなさい。

解説1

(1)

5つの玉には、赤玉が3つあるので、確率は $\frac{3}{5}$ となる。

(2)

操作を行ったときに、赤玉が1回出るパターンとしては、

1回目：赤　2回目：白
1回目：白　2回目：赤

の2パターンがある。よって、確率は $2 \cdot \frac{3}{5} \cdot \frac{2}{5} = \frac{12}{25}$ となる。

(3)

いよいよ二項分布の公式を使う問題です。

箱から玉を出したときに出てくる玉は

赤玉（確率3/5）
赤玉以外 [白玉] （確率2/5）

の2つですね。さらに、それぞれの操作は独立（他の回の操作に影響されない）なので、赤玉が出る回数 $X$ は二項分布に従うといえますね。

よって、平均 $E (X)$ と分散 $V (X)$ は、 $\begin{aligned} E (X) & = 150 \cdot \frac{3}{5} \\ = 90 \end{aligned}$ $\begin{aligned} V (X) & = E (X) \cdot (1 - \frac{3}{5}) \\ = 90 \cdot \frac{2}{5} \\ = 36 \end{aligned}$ と求めることができます。

４．ポアソン分布

(1) ポアソン分布とは

先程出てきた二項分布の平均を $μ$ と固定します。

すると、 $μ = n p$ となりますね。

ここで、二項分布の試行回数 $n$ を十分に大きくすることを考えます。

すると、平均が固定されているため、 $p$ は十分に小さくなりますね。

このように、二項分布の $n$ を大きく（ $p$ を小さく）した分布のことをポアソン分布と呼びます。

（二項分布の確率 $p$ が小さくなったバージョンがポアソン分布）

(2) ポアソン分布を用いた確率の求め方

ポアソン分布に従う試行を $n$ 回行ったときに事象が $k$ 回発生する確率 $f (n, k)$ を求めてみましょう。

確率 $p$ で事象が発生する試行を $n$ 回起こったとき、事象が $k$ 回起こる確率 $f (n, k)$ は、 $f (n, k) =_{n} C_{k} p^{k} (1 - p)^{n - k}$ で求めることができますね。

ここで、上の式を展開すると、 $\begin{aligned} f (n, k) & =_{n} C_{k} p^{k} (1 - p)^{n - k} \\ = \frac{n!}{k! (n - k)!} p^{k} (1 - p)^{n - k} \\ = \frac{n (n - 1) (n - 2) \dots (n - (k - 2)) (n - (k - 1))}{k!} p^{k} (1 - p)^{n - k} \\ = {n (n - 1) (n - 2) \dots (n - (k - 2)) (n - (k - 1)) p^{k}} \cdot \frac{1}{k!} \cdot (1 - p)^{n - k} \end{aligned}$ と3つの部分に分けることができます。

それぞれに対し、 $n \to \infty$ とすると、 $\begin{aligned} lim_{n \to \infty} n (n - 1) (n - 2) \dots (n - (k - 2)) (n - (k - 1)) p^{k} \\ = & lim_{n \to \infty} (\frac{n}{n} \cdot \frac{n - 1}{n} \dots \frac{n - (k - 1)}{n}) n^{k} p^{k} \\ = & lim_{n \to \infty} 1 (1 - \frac{1}{n}) (1 - \frac{2}{n}) \dots (1 - \frac{k - 1}{n}) (n p)^{k} \\ = & μ^{k} (∵ μ = n p) \end{aligned}$

$\begin{array}{r} lim_{n \to \infty} \frac{1}{k!} = \frac{1}{k!} \end{array}$

$\begin{aligned} lim_{n \to \infty} (1 - p)^{n - k} \\ = & lim_{n \to \infty} {(1 - \frac{μ}{n})}^{n - k} (∵ μ = n p) \\ = & lim_{n \to \infty} {(1 - \frac{μ}{n})}^{n} {(1 - \frac{μ}{n})}^{- k} \\ = & e^{- μ} \cdot 1 \\ = & e^{- μ} \end{aligned}$

と計算できるので、 $n \to \infty$ のときの確率 $f (n, k)$ は $\begin{aligned} f (n, k) & =_{n} C_{k} p^{k} (1 - p)^{n - k} \\ = {n (n - 1) (n - 2) \dots (n - (k - 2)) (n - (k - 1)) p^{k}} \cdot \frac{1}{k!} \cdot (1 - p)^{n - k} \\ = μ^{k} \cdot \frac{1}{k!} \cdot e^{- μ} \\ = \frac{μ^{k}}{k!} e^{- μ} \end{aligned}$ と求められます。

上で導出した式がポアソン分布の公式となります！

つまり、ある一定期間内に事象が平均 $μ = n p$ 回発生するとき、同じ一定期間内に事象が $k$ 回発生する確率が $\frac{μ^{k}}{k!} e^{- μ}$ で求められることを表しています。

（ただし、 $p$ が小さいことが条件）

ポアソン分布ある一定期間内に平均

μ

回事象が発生するとき、同じ一定期間内で事象が

k

回発生する確率はポアソン分布に従い、その確率は

\frac{μ^{k}}{k!} e^{- μ}

で求めることができる。

(3) ポアソン分布の平均・分散

ある確率変数 $X$ がポアソン分布に従うときの平均 $E (X)$ 、分散 $V (X)$ は簡単に求めることができます。

平均は、 $E (X) = μ = n p$ と仮定しているので計算の必要すらありませんね。

分散は、二項分布の分散 $V (X) = n p (1 - p)$ の $n$ を $n \to \infty$ とすることで求められます。

実際に計算すると、 $\begin{aligned} V (X) & = lim_{n \to \infty} n p (1 - p) \\ = lim_{n \to \infty} μ (1 - p) \\ = lim_{n \to \infty} μ (1 - \frac{μ}{n}) \\ = μ \end{aligned}$ となり、 $V (X) = μ$ と求められます。

平均 $E (X)$ と分散 $V (X)$ が等しくなるなんて不思議ですね。

(4) ポアソン分布を用いた例題

では、実際にポアソン分布を使った問題を解いていきましょう。

期末試験や数検でもたまに出てきますよ。

例題2

※ 必要であれば $e = 2.71$ , $\frac{1}{e} = 0.37$ を用いてもよい。

(1)

（このお話はあくまでも仮定です）

コナンくんが住んでいる街「米花町」では、1週間に平均1回殺人事件が発生する。

殺人事件の発生回数がポアソン分布に従うと仮定したとき、1週間に3回殺人事件が発生する確率を小数第2位まで求めなさい。

(2)

あるソーシャルゲームのガチャでは、最高レアを1%の確率で引くことができる。

100連ガチャを回したとき、つまり100回ガチャを引く試行を行ったとき、最高レアが1回も出ない確率、1回だけ出る確率、2回だけ出る確率をそれぞれ求めなさい。

解答2

ある一定期間内で平均 $μ$ 回発生する事象が $k$ 回発生する確率 $p (μ, k)$ は、 $p (μ, k) = \frac{μ^{k}}{k!} e^{- μ}$ で計算できる。

(1)

今回は、ある期間内に1回殺人事件が発生するので $μ = 1$ 、求めたい確率は3回発生するときなので、 $k = 3$ となる。

よって、確率は、 $\begin{array}{r} \frac{1^{3}}{3!} e^{- 1} = \frac{1}{6} \cdot 0.37 ≒ 0.06 \end{array}$ となる。

(2)

100回ガチャを引く試行を行ったとき、確率0.01で出てくる最高レアを引く回数の平均 $μ$ は二項分布に従う*1ので $μ = 100 \cdot 0.01 = 1$ となり、平均 $μ = 1$ と求められる。

また、確率 $p = 0.01$ と小さいため、最高レアを引く回数はポアソン分布に従うと仮定できる。

よって、1回も最高レアを引けない確率は $k = 0$ のときのポアソン分布なので、 $\frac{1^{0}}{0!} e^{- 1} = 0.37$ で計算できる。

また、1回だけ最高レアを引く確率は $k = 1$ のときのポアソン分布なので、 $\frac{1^{1}}{1!} e^{- 1} = 0.37$ で計算でき、2回だけ最高レアを引く確率（ $k = 2$ のときのポアソン分布）は $\frac{1^{2}}{2!} e^{- 1} = 0.19$ と計算できる。

（二項分布の場合）

0回、1回、2回最高レアが出る確率は $_{100} C_{0} \cdot {(\frac{1}{100})}^{0} {(\frac{99}{100})}^{100} = 0.37$ $_{100} C_{1} \cdot {(\frac{1}{100})}^{1} {(\frac{99}{100})}^{99} = 0.37$ $_{100} C_{0} \cdot {(\frac{1}{100})}^{2} {(\frac{99}{100})}^{98} = 0.18$ で計算できる。

（ $1 / e = 0.37$ と近似してるため、2回最高レアが出る確率が0.18ではなく0.19となってしまっていますがまぁ誤差です）

５．多項分布

(1) 多項分布とは

二項分布は、1回の試行で起こりえる結果が2通り（出る or 出ない）の試行を何回か繰り返したときに事象が起こる回数 $X$ が従う分布でしたね。

この2通りの部分を $m$ 通り（3通り以上）に拡張したものが多項分布となります。

(2) 多項分布の平均と分散

$i$ 番目の事象が発生する回数 $X_{i}$ が多項分布に従うときの平均 $E (X_{i})$ と分散 $V (X_{i})$ は簡単に求められます。

二項分布の式の $p$ の部分を、 $i$ 番目の事象が起こる確率 $p_{i}$ に書き換えることで、 $E (X_{i}) = n p_{i} V (X_{i}) = E (X_{i}) \cdot (1 - p_{i}) = n p_{i} (1 - p_{i})$ と導出できます。

（ $i$ 番目の事象が起こる確率 $p_{i}$ と起こらない確率 $1 - p_{i}$ と考えると二項分布と同じように考えられます！）

６．幾何分布

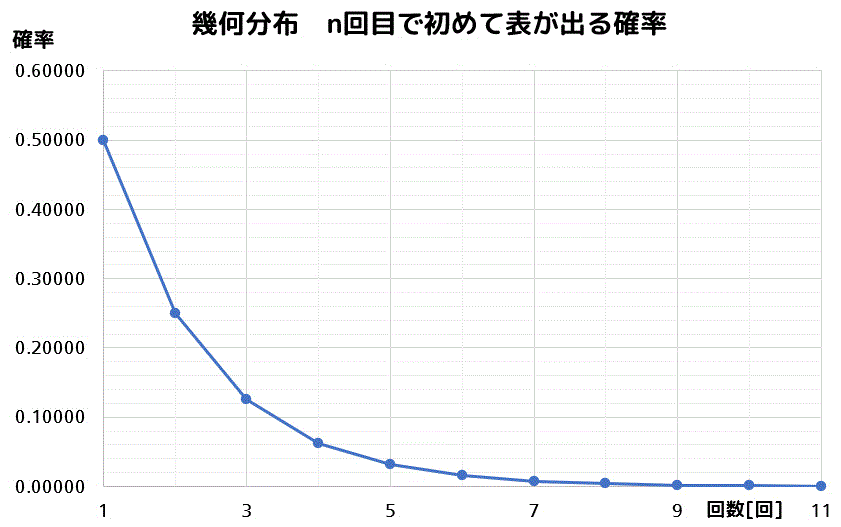
確率 $p$ で発生するベルヌーイ試行を繰り返したときに、事象が初めて発生するまでの試行回数 $X$ が従う分布のことを幾何分布と呼びます。

例えばコイントスで、表が初めて出る確率を考えてみましょう。

1回目で初めて表が出る確率は、言うまでもなく1/2です。

2回目で初めて表が出る確率は、1回目で裏が出て、2回目で表が出ればいいので、 $\frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4}$ と計算できます。

3回目、4回目…と計算していき、表にしていくと下のように0に収束するようなグラフを得ることができます。

もう1つ例を考えてみましょう。

サイコロを振ったときに $n$ 回目で初めて1の目が出る確率を表にしてみると……

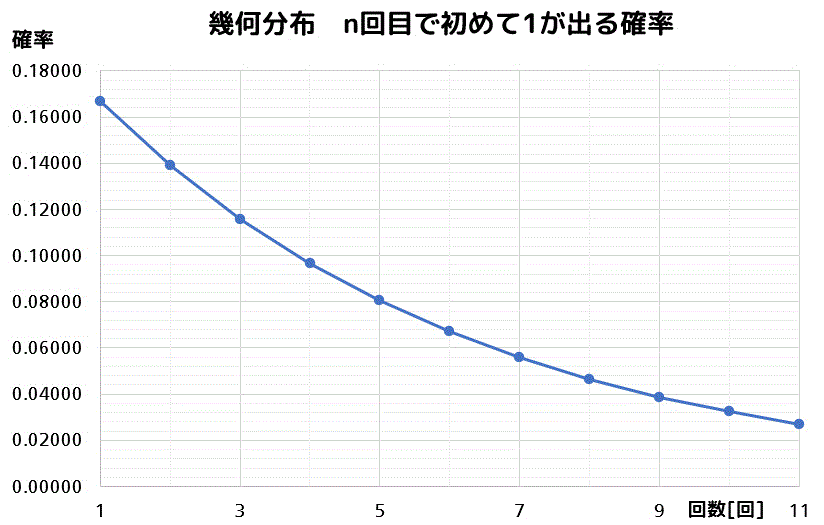
少し緩やかになりましたが、回数を増やすにつれて0に収束するようなグラフとなりましたね。

（上のような回数を増やすにつれて0に収束していくグラフが幾何分布の特徴！）

７．超幾何分布

ある2つの集団（あたりの集団 or はずれの集団）があるとします。

この集団から、何回か復元抽出を行ったときにあたりを引ける回数 $X$ が従う分布は二項分布となることを先程学習しました。

（具体例：赤玉5個、白玉5個入った箱から、無作為に1つ選び、選んだものを記録してからもとに戻す操作（復元抽出）を4回繰り返したとき、赤玉が出る回数 $X$ は二項分布に従う。）

上の復元抽出を非復元抽出、つまり選んだものを元に戻さずそのまま試行を繰り返したものが超幾何分布となります。

（具体例：赤玉5個、白玉5個入った箱から、無作為に1つ選び、選んだものを戻さずに操作を4回繰り返したとき、赤玉が出る回数 $X$ は超幾何分布に従う。）

超幾何分布についてもう少し理解を深めるために例題を解いてみましょう。

例題3

(1)

赤玉が3個、白玉が2個が入った箱がある。この箱の中から、同時に2つ取り出す（非復元抽出）。

このとき、赤玉が1回出る確率 $P_{1}$ を求めなさい。

（ちなみに復元抽出の場合の確率：12/25）

(2)

$n$ 個のボールが入った箱に $m$ 個赤玉が入っている。

この中から同時に $k$ 個取り出したときに赤玉が $i$ 個入っている確率 $P_{2}$ を求めなさい。

解説3

(1)

5個の箱の中から、同時に2つ取り出す取り出し方は $_{5} C_{2} = 10$ で計算でき、10通りとなる。

また、取り出した2つの玉のうち、赤が1個、白が1個ずつ選ばれる総数は、

赤玉が3個中1個選ばれる確率
→ $_{3} C_{1} = 3$ 通り
白玉が2個中1個
→ $_{2} C_{1} = 2$ 通り

の積で決まるので、6通りとなる。

よって、確率 $P_{1}$ は、 $\begin{aligned} P_{1} & = \frac{_{3} C_{1} \cdot_{2} C_{1}}{_{5} C_{2}} \\ = \frac{6}{10} \\ = \frac{3}{5} \end{aligned}$ と求めることができる。