スポンサードリンク
こんにちは、ももやまです。
またまた数3(解析学)の記事の紹介です。
今回は、倍角の公式・和積の公式を用いた三角関数の積分テクニックについてまとめました。
目次
スポンサードリンク
1.三角関数の加法定理
皆さんは三角関数の加法定理を覚えていますか。
覚えてない人はすぐ思い出しましょう!!
積分で使う三角関数の加法定理はこの4つ!!
符号に気をつけよう!!(とくに \( \cos \) の加法定理)
\[ \sin( \alpha + \beta ) = \sin \alpha \cos \beta + \cos \alpha \sin \beta \]\[ \sin( \alpha - \beta ) = \sin \alpha \cos \beta - \cos \alpha \sin \beta \]\[ \cos( \alpha + \beta ) = \cos \alpha \cos \beta - \sin \alpha \sin \beta \]\[ \cos( \alpha - \beta ) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \]となる。
この公式は、他の三角関数の公式を導く上で必要なものとなるので必ず覚えて置きましょう。
(語呂合わせとかで覚える人が多いです。「幸子小林小林幸子……」のように…)
![]()
スポンサードリンク
2.倍角の公式を用いた積分
\( \cos \) の倍角の公式を使うことで、\( \sin \) や \( \cos \) の2乗(3乗)を外してあげることができます。
倍角の公式を忘れてしまった場合は、\( \cos( \alpha + \beta ) \) の加法定理の \( \alpha \), \( \beta \) それぞれに \( x \) を代入し、導きましょう。
導いた後は、\( \cos^2 x - \sin^2 x \) から、不要なほうを \( \sin^2 x + \cos^2 x = 1 \) を用いて消去し、変形を行いましょう。
例えば、\( \sin^2 x \) がほしければ、
\[ \begin{align*} & \cos^2 x - \sin^2 x - ( \sin^2 x + \cos^2 x - 1)
\\ = & 1 - 2 \sin^2 x \end{align*} \]と変形すれば導出ができます。
\( \cos^2 x \) がほしければ、
\[ \begin{align*} & \cos^2 x - \sin^2 x + ( \sin^2 x + \cos^2 x - 1)
\\ = & 2 \cos^2 x - 1 \end{align*} \]と変形すれば導出ができます。
\( \cos \) の倍角の公式は、
\[\begin{align*} \cos 2x & = \cos^2 x - \sin^2 x
\\ & = 2 \cos^2 x - 1
\\ & = 1 - 2 \sin^2 x
\end{align*}\]となるので、変形して\[ \sin^2 x = \frac{1}{2} \left( 1 - \cos 2x \right) \\ \cos^2 x = \frac{1}{2} \left( 1 + \cos 2x \right) \]となる。
例題1
不定積分\[ \int \sin^2 x \ dx \] を求めなさい。
解説1
\( \sin^2 x \) の2乗が邪魔なので倍角の公式を適応する。
すると、\[\begin{align*} & \int \sin^2 x \ dx
\\ = & \frac{1}{2} \int 1 - \cos 2x \ dx
\\ = & \frac{1}{2} \left( x - \frac{1}{2} \sin 2x \right) + C
\\ = & \frac{1}{4} \left( 2x - \sin 2x \right) + C
\end{align*} \]と計算できます。
同様に \( \cos x \) の場合も練習してみましょう。
今回は練習問題を間に挟んでいくスタイルでやってみます。
スポンサードリンク
3.積和の公式を用いた積分
積分では、和の形のものは簡単に分解することができますが、積の形のものは簡単に分解することができません(部分積分が必要)。
そこで、三角関数が積で表された積分については、積和の公式で和の形にしてあげることで簡単に計算をすることができます。
積和の公式はあまり使用頻度が高くないので忘れてしまっているかもしれません。
できれば覚えてほしいですが、最低限導出過程だけは頭に入れておきましょう。
導出過程を下に示します。
積和公式の導出過程
\( \sin \alpha \sin \beta \) から和へ
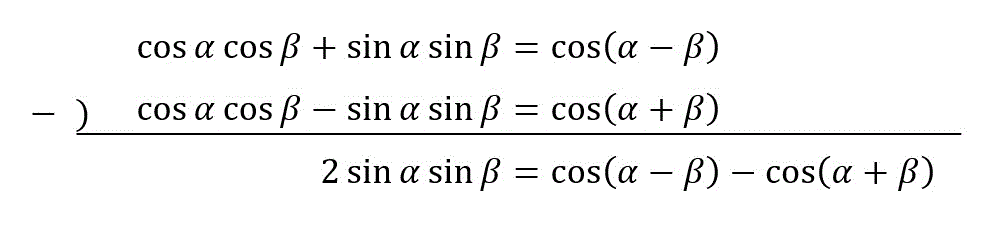
\( \sin \alpha \cos \beta \) から和へ
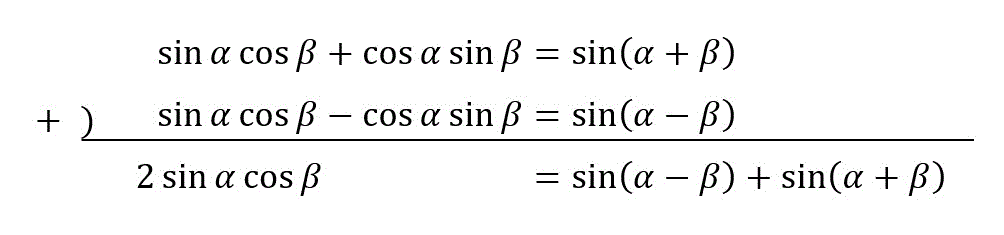
\( \cos \alpha \cos \beta \) から和へ
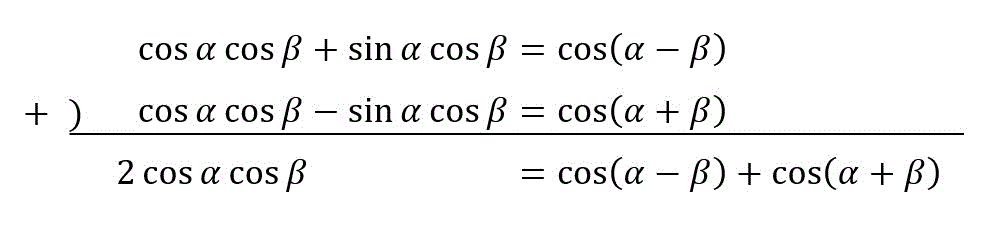
それぞれの積和の公式は、\[\begin{align*} \sin \alpha \sin \beta & = \frac{1}{2} \left( \cos ( \alpha - \beta) \right) - \left( \cos ( \alpha + \beta) \right) \\
\cos \alpha \cos \beta & = \frac{1}{2} \left( \cos ( \alpha - \beta) \right) + \left( \cos ( \alpha + \beta) \right) \\
\sin \alpha \cos \beta & = \frac{1}{2} \left( \sin ( \alpha - \beta) \right) + \left( \sin ( \alpha + \beta) \right) \end{align*} \]となる。
\( \sin \) 同士、\( \cos \) 同士の積和の公式では \( \alpha \gt \beta \) にしておいたほうが中身がマイナスにならないので少しいいかも。
例題2
不定積分\[ \int \sin 5x \cos 3x \ dx \] を求めなさい。
解説2
三角関数の積の形を和の形にしてあげるために積和の公式を適用する。\[\begin{align*} & \int \sin 5x \cos 3x \ dx
\\ = & \frac{1}{2} \int \sin(5x - 3x) + \sin (5x + 3x) \ dx
\\ = & \frac{1}{2} \int \sin 2x + \sin 8x \ dx
\\ = & \frac{1}{2} \left(\frac{1}{2} (- \cos 2x) + \frac{1}{8} ( - \cos 8x) \right) + C
\\ = & - \frac{1}{4} \cos 2x - \frac{1}{16} \cos 8x + C
\end{align*} \]となる。
4.練習問題
では練習してみましょう!
練習1
不定積分\[ \int \cos^2 x \ dx \] を求めなさい。
練習2
不定積分\[ \int \sin 3x \sin 2x \ dx \] を求めなさい。
練習3
不定積分\[ \int \cos 2x \cos 5x \ dx \] を求めなさい。
練習4
不定積分\[ \int \sin^3 x \ dx \] を求めたい。
(1) \( \sin^3 x \) を、\( \sin x \), \( \sin 3x \) を用いて表しなさい。
(2) 不定積分を計算しなさい。
練習5
不定積分\[ \int \cos^3 x \ dx \] を求めたい。
(1) \( \cos^3 x \) を、\( \cos x \), \( \cos 3x \) を用いて表しなさい。
(2) 不定積分を計算しなさい。
5.練習問題の答え
解答1
\( \cos^2 x \) の2乗が邪魔なので例題1と同じように倍角の公式を適応する。
すると、\[\begin{align*} & \int \cos^2 x \ dx
\\ = & \frac{1}{2} \int 1 + \cos 2x \ dx
\\ = & \frac{1}{2} \left( x + \frac{1}{2} \sin 2x \right) + C
\\ = & \frac{1}{4} \left( 2x + \sin 2x \right) + C
\end{align*} \]と計算できます。
解答2
和積の公式で和に直す。\[\begin{align*} & \int \sin 3x \sin 2x \ dx
\\ = & \int \frac{1}{2} \left( \cos(3x - 2x) - \cos (3x + 2x) \right) \ dx
\\ = & \int \frac{1}{2} \left( \cos x - \cos 5x \right) \ dx
\\ = & \frac{1}{2} \left(\sin x - \frac{1}{5} \sin 5x \right) + C
\\ = & \frac{1}{2} \sin x - \frac{1}{10} \sin 5x + C
\end{align*} \]
解説3
和積の公式で和に直すが、このままだと \( \cos \) の中身が負になるので、前後を入れ替えてあげるとややこしい計算がなくなる。
\[\begin{align*} & \int \cos 2x \cos 5x \ dx
\\ = & \int \cos 5x \cos 2x \ dx
\\ = & \frac{1}{2} \int \cos(5x - 2x) + \cos (5x + 2x) \ dx
\\ = & \frac{1}{2} \int \cos 3x + \cos 7x \ dx
\\ = & \frac{1}{2} \left(\frac{1}{3} \sin 3x + \frac{1}{7} \sin 7x \right) + C
\\ = & \frac{1}{6} \sin 3x + \frac{1}{14} \sin 7x + C
\end{align*} \]
解説4
(1)
3倍角の公式は2倍角の公式と加法定理から示すことができる。\[\begin{align*}
\sin 3x & = \sin (2x + x)
\\ & = \sin 2x \cos x + \cos 2x \sin x
\\ & = 2 \sin x \cos x \cdot \cos x + \left(1 - 2 \sin^2 x \right) ) \sin x
\\ & = 2 \sin x \cos^2 x + \sin x - 2 \sin^3 x
\\ & = 2 \sin x (1 - \sin^2 x) + \sin x - 2 \sin^3 x
\\ & = 2 \sin x - \sin^3 x + \sin x - 2 \sin^3 x
\\ & = 3 \sin x - 4 \sin^3 x
\end{align*} \]より、\[ \sin^3 x = \frac{1}{4} \left(3 \sin x - \sin 3x \right) \]となる。
(2)
(1)の計算結果を使って計算をする。\[\begin{align*} & \int \sin^3 x \ dx
\\ = & \frac{1}{4} \int 3 \sin x - \sin 3x \ dx
\\ = & \frac{1}{4} \left( - 3 \cos x + \frac{1}{3} \cos 3x \right) + C
\\ = & - \frac{3}{4} \cos x + \frac{1}{12} \cos 3x + C
\end{align*} \]
(2)の別解(完全誘導無視)
\[\begin{align*} & \int \sin^3 x \ dx
\\ = & \int \sin^2 x \sin x \ dx
\\ = & \int \left(1 - \cos^2 x \right) \sin x \ dx
\end{align*} \]としてから、\( \cos x = t \) とおく。すると、\( - \sin x dx = dt \) より、\( dx = - \frac{1}{\sin x} dt \) となる。\[\begin{align*} & \int \left(1 - \cos^2 x \right) \sin x \ dx
\\ = & \left( 1 - t^2 \right) \sin x \cdot \left(- \frac{1}{\sin x} \right) \ dt
\\ = & t^2 - 1 \ dt
\\ = & \frac{1}{3} t^3 - t + C
\\ = & \frac{1}{3} \cos^3 x - \cos x + C
\end{align*} \]と計算できる(形が全然違うけど実は同じ答え)。
解説5
(1)
加法定理と倍角の定理を使って計算をすればよい。\[\begin{align*}
\cos 3x & = \cos (2x + x)
\\ & = \cos 2x \cos x + \sin 2x \sin x
\\ & = \left( 2 \cos^2 x - 1 \right) \cos x - 2 \sin x \cos x \cdot \sin x
\\ & = 2 \cos^3 x - \cos x - 2 \sin^2 x \cos x
\\ & = 2 \cos^3 x - \cos x - 2 \left(1 - cos^2 x\right) \cos x
\\ & = 2 \cos^3 x - \cos x + 2 \cos^3 x - 2 \cos x
\\ & = 4 \cos^3 x - 3 \cos x
\end{align*} \]より、\[ \cos^3 x = \frac{1}{4} \left(3 \cos x + \cos 3x \right) \]となる。
(2)
(1)の計算結果を使って計算をする。\[\begin{align*} & \int \cos^3 x \ dx
\\ = & \frac{1}{4} \int 3 \cos x + \cos 3x \ dx
\\ = & \frac{1}{4} \left( 3 \sin x + \frac{1}{3} \sin 3x \right) + C
\\ = & \frac{3}{4} \sin x + \frac{1}{12} \sin 3x + C
\end{align*} \]となる。
(2)の別解(完全誘導無視)
\[\begin{align*} & \int \cos^3 x \ dx
\\ = & \int \cos^2 x \cos x \ dx
\\ = & \int \left(1 - \sin^2 x \right) \cos x \ dx
\end{align*} \]としてから、\( \sin x = t \) とおく。すると、\( \cos x dx = dt \) より、\( dx = \frac{1}{\cos x} dt \) となる。\[\begin{align*} & \int \left(1 - \sin^2 x \right) \cos x \ dx
\\ = & \left( 1 - t^2 \right) \cos x \cdot \left(\frac{1}{\cos x} \right) \ dt
\\ = & 1 - t^2 \ dt
\\ = & t - \frac{1}{3} t^3 + C
\\ = & \sin x - \frac{1}{3} \sin^3 x + C
\end{align*} \]と計算できる(やはり形が全然違うけど実は同じ答え)。
3倍角の公式も下にまとめておきます。
\( \sin 3x \), \( \cos 3x \) それぞれの3倍角の公式は、\[ \sin 3x = 3 \sin x - 4 \sin^3 x \\ \cos 3x = 4 \cos^3 x - 3 \cos x \]となる。
変形をすると、\[\sin^3 x = \frac{1}{4} \left(3 \sin x - \sin 3x \right) \\ \cos^3 x = \frac{1}{4} \left(3 \cos x + \cos 3x \right) \]となる。
6.さいごに
今回は倍角の公式・積和の公式を用いた三角関数の積分テクニックについてまとめました。
加法定理を忘れてしまっている人は頭の中に必ず叩き込んでおきましょう。
また、倍角の公式・積和の公式の導出過程もちゃんと理解しておきましょう!!
主にこの積分は数3ではもちろんのこと、解析学でもよく使われます。
関連広告・スポンサードリンク