![うさぎでもわかる計算機システム Part02 2の補数表現 [基本情報対応]](https://www.momoyama-usagi.com/wp-content/uploads/2021/05/20190615204157-1.gif)
スポンサードリンク
こんにちは! ももやまです!
今回は、前回に加えて「負の数」も表せる2の補数表現についてまとめていきたいと思います!
前回の2進数の絶対値表現(負の数なし)のお話しはこちらから。
目次
スポンサードリンク
1.負の数の表し方
計算機上は、0と1という2つの数でしか表現されていません。
なので、「マイナス」などの記号を使って負の数を使うことができません。
なので、一番上の桁が0か1かどうかで正負を判断します。
たとえば、0110の場合だと一番上の位は0なので正となります。
1110のように一番上の位が1だと負の数となりますね。

残りの3bitは数値を表します。ですが、この数字の表し方にも様々な表現法があります。
符号+絶対値表現
皆さんが簡単に思い浮かぶものとしては、最上位ビットを符号、残りの3bitを値の絶対値としてみるやり方です。
たとえば、上の0110の場合は、符号が0で+、110は10進数に直すと6なので0110を符号+絶対値表現すると+6になります。
下の1110の場合は、符号部分が1なので-、絶対値部分は110なので6となり、-6を表します。
確かにこのやり方は人間からみると簡単かもしれませんが、計算機上で考えたときに、足し算や引き算の処理が複雑になり、計算機自体が複雑になってしまいます。
また、0000bと1000bは+0と-0になってしまい、0の表現方法が2つできてしまい、大変ややこしいです。
なので、計算機上で正負の数を表す際には、下で説明する2の補数が使われています。
スポンサードリンク
2.2の補数表現とは
1で説明した「符号+絶対値表現」だと人間が理解できても計算機上でめんどくさいことになるので、計算機上で負の数を扱え、かつ簡単に正負にかかわらず計算を実現できるようにしたのが2の補数表現です。
では、2の補数表現とはどのようなものかを見ていきましょう。
2の補数表現では、表したい数が正の数の場合は0よりどれだけ大きいのか、負の数の場合は0よりどれだけ小さいのかで考えます。
また、計算機が扱える桁の中も一番上位の位を正の数か負の数かを判定する桁とします。この桁が0の場合は正の数(もしくは0)、1の場合は負の数とします。
今回は、4bitの場合を考えてみましょう。このとき、一番上のビットが正負を表す記号、残り3つが数(絶対値)を表します。
たとえば、-2という数を考えてみてください。
-2は、0から2を引いた値ですね。
ここで-2をどうやって2進数で表現するか少し迷いますね。
2の補数は、図のように全部0の2進数と全部1の2進数が隣同士にくっつけてしまい、輪のような形で表現します。
例えば、4bitの場合、0000bは10進数の0なので、1111bが10進数の-1となります。
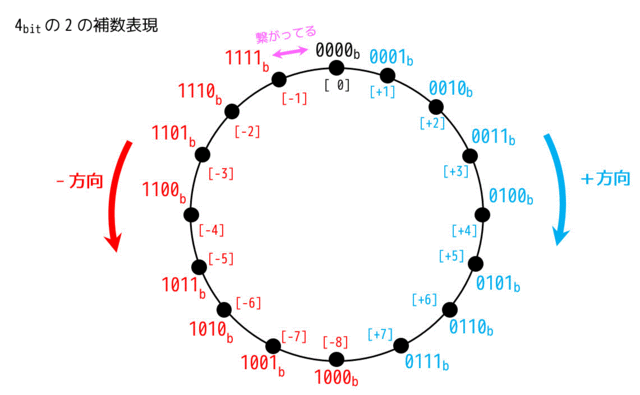
こうすることで、時計回りはプラスの方向、反時計回りはマイナスの方向となり、0よりどれだけ大きい/小さいというのを考えやすくなります。
先程の例に戻りましょう。-2は0から2を引いた値ですね。
なので、0から2つマイナス方向(左方向)に行った1110bが2の補数表現における-2となります。
0000~1111のすべての2進数と10進数の対応を表にしてみました。
| 2進 | 10進 | 2進 | 10進 |
| 0000 | 0 | 1000 | -8 |
| 0001 | 1 | 1001 | -7 |
| 0010 | 2 | 1010 | -6 |
| 0011 | 3 | 1011 | -5 |
| 0100 | 4 | 1100 | -4 |
| 0101 | 5 | 1101 | -3 |
| 0110 | 6 | 1110 | -2 |
| 0111 | 7 | 1111 | -1 |
4ビットの場合は、-8から+7までの10進数を扱うことができますね。
では、\( n \) ビットの場合に扱える10進数の範囲はどうなるでしょうか。
\( n \) ビットのときの扱える数の通り数はそれぞれを選ぶか選ばないかの2通りなので、\( 2^n \) 通りありますね。
\( 2^n \) 通りのうちの半数を負の数、もう半分を0と正の数で使いますね。
なので、負の数は \( - 2^{n-1} \) まで、正の数は0を表すための1個を引いて \( 2^{n-1} - 1 \) まで扱うことができます。
よって、\( n \) ビットのときの2の補数表現で表すことができる数の範囲は、整数 \( x \) として、\[ -2^{n-1} \leqq x \leqq 2^{n-1} - 1\]となります。例えば、6ビットの場合は\[-32 \leqq x \leqq 31 \]となります。
スポンサードリンク
3.2の補数の作成方法
では、2の補数(10進数の正負を入れ替えたもの)の作り方を説明します。2パターンあるのでそれぞれのパターンの説明をしていきます。
主に、2の補数表現で表された負の数の絶対値を求めるときに使います。
(2の補数表現で表された負の数はそのままだと数字を読み取るが大変なので2の補数を作ってそこから数値を読み取る。)
(1) 1の補数を作って1を足す
まずは多くの人が紹介する、1の補数を作り1を加算するやり方を紹介します。
1の補数とは、2進数の0と1を入れ替えたものを表します。
例えば、0110bなら1001b、1110bなら0001bとなります。
つぎに、入れ替えた数に1を足しこみます。
これを2の補数と呼びます。
1001bに1を足し込むと1010b、0001bに1を足し込むと0010bとなります。
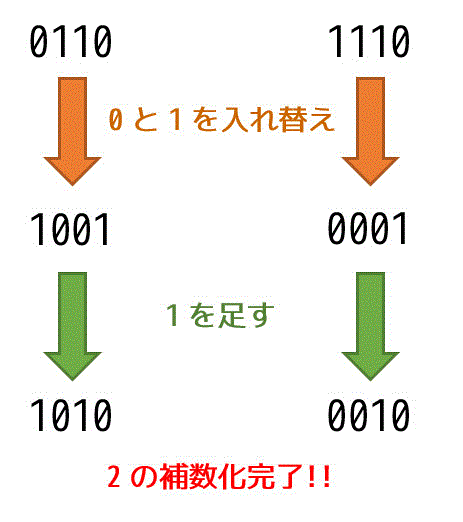
これで2の補数の完成です。試しに上の表で正しく正負が入れ替わっているかを確認しましょう。
0110bの2の補数は1010bでしたね。0110bは6、1010bは-6と正しく正負が入れ替わっています。
同様に1110bの2の補数は0010bでしたね。1110bは-2、0010bは2とこちらも正しく正負が入れ替わっていますね。
このように、「2進数の0と1を入れ替えて1を加算する」ことで2の補数表現のときに正負を入れ替えることが可能となります。
(2) 100…0 から減算
すべてのビットが1の2進数に1を足して、100…0 の形にしたものから減算して2の補数を出す方法もあります。
たとえば、4bitの場合は10000b、8bitの場合は 1 0000 0000bからもとの数を引くと2の補数を求めることができます。
0110b, 1110bの2の補数は以下のように求めることができます。
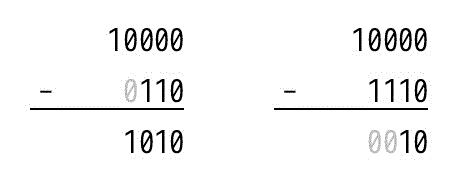
確かに2の補数が求まっていますね。
4.2の補数同士の足し算
2の補数同士の足し算は、正負に関係なく同様の方法で足し算をすることができます。
試しに4つほど例を出してみましょう。

このように、正の数、負の数にかかわらず、足し算が正しく行われていることがわかりますね。
しかし、つぎのように正しく計算が行われないこともあります。

正の数同士の数を足して負の数になることや、負の数同士を足して正の数になることは普通の足し算ではありえませんよね。これは、計算結果が2の補数表現で表せる限度を超えてしまったために発生します。
オーバーフローによって計算結果が正しくなくなるのは、
- 正の数+正の数で範囲をオーバーして負の数になる
- 負の数+負の数で範囲をオーバーして正の数になる
この2つが考えられます。いずれも2の補数表現で表せる限界を突破した際に起こります。
5.int型の上限
C、Javaなどではint型を使いますね、それらの型には表せる数の上限があります。
int型は、4バイト(32bit)までの数を扱うことができます。32bitの2の補数表現で表せる数の範囲は、\( -2^{31} \sim 2^{31} -1 \) 、べき乗を展開して -2147483648~2147483647 まで表すことができます。
実際にプログラムを書いて上限を突破する瞬間をみてみましょう。
プログラム
#include<stdio.h> int main(){ for(int i = 2147483640; i < 2147483650; i += 1) { printf("%d\n",i); } return 0; }
実行結果
2147483640 2147483641 2147483642 2147483643 2147483644 2147483645 2147483646 2147483647 -2147483648 -2147483647 (以降無限ループ)
このように \( 2^{31} -1 \) の範囲を超えてしまうと、オーバーフローにより、負の数になってしまっていますね。2147483650を超えることもないため、永久に無限ループします。
このように、型の上限を超えないようにプログラムを書く際には意識をする必要があります。
おまけ 負の数を考えない宣言法もあります。int の前に unsigned を付けることで、負の範囲をなくし、代わりに正の範囲を約2倍にすることができます。(範囲が \( 0 \sim 2^{32} -1 \) となる)
#include<stdio.h> int main(){ for(unsigned int i = 2147483640; i < 2147483650; i += 1) { printf("%u\n",i); // %dではなく %u に注意 } return 0; }
実行結果
2147483640 2147483641 2147483642 2147483643 2147483644 2147483645 2147483646 2147483647 2147483648 2147483649
この場合は上限を超えないのできっちり10回だけ実行されます。
6.練習問題
では早速練習していきましょう!
今回も基本情報、ITパスポート、応用情報からの過去問を用意しています。
練習1
負の整数を2の補数で表現するとき, 8桁の2進数で表現できる数値の範囲を10進数で表したものはどれか。
[ITパスポート平成24年春期 問52]
ア:-256~255
イ:-255~256
ウ:-128~127
エ:-127~128
練習2
2進数 10110101 の8けたの2の補数はどれか。
[平成12年度春季 基本情報]
ア:01001010
イ:01001011
ウ:10110100
エ:10110110
練習3
つぎの1~5の中から正しい文章を選びなさい。
- 5bitの2の補数表現で0を表す方法は00000bと10000bの2通りがある。
- 5bitの2の補数表現で-16は表せない。
- 5bitの2の補数表現で18は10010bと表される。
- 5bitの2の補数表現で10100bは-4を表している。
- 5bitの2の補数表現で-7は11001bと表される。
練習4
負数を2の補数で表す8ビットの数値がある。この値を10進数で表現すると-100である。この値を符号なしの数値として解釈すると,10進数で幾らか。
[基本情報技術者平成17年春期 午前問3]
ア:28
イ:100
ウ:156
エ:228
練習5
つぎの(1)~(4)の足し算を4bitの2の補数表現で行い、結果を10進数と2進数で答えなさい。さらにオーバーフローなどにより、10進数の計算結果と異なる結果が出たものに×をつけなさい。過程も示すこと。
(1) 2 + 7
(2) 2 + (-7)
(3) -2 + 7
(4) -2 - (-7)
練習6
負数を2の補数で表現する符号付き16ビットの2進数を16進法で表示したもののうち,4倍するとあふれが生じるものはどれか。
[基本情報技術者平成19年春期 午前問3]
ア:1FFF
イ:DFFF
ウ:E000
エ:FFFF
練習7
2進数の表現で,2の補数を使用する理由はどれか。
[応用情報技術者平成21年秋期 午前問1]
ア:値が1のビットを数えることでビット誤りを検出できる。
イ:減算を、負数の作成と加算処理で行うことができる。
ウ:除算を、減算の組合せで行うことができる。
エ:ビットの反転だけで、負数を求めることができる。
練習8
5月に実施されたうさぎ大学よる線形代数の試験では、95人の受験者がいた。線
試験は100点満点とし、この線形代数の試験の平均点を求めるために全員の点数の合計を算出したい。このとき、次の問いに答えなさい。
ただし、必要ならば \( 2^{10} = 1024 \) は用いてもよい。
(1) 合計点を2の補数表現で確実に表すためには、最低何bit必要ですか。
(2) (1)のbit数の場合、あと受験者が何人増えても合計点を正しく計算できますか。
練習9
負の整数を表現する代表的な方法として、次の3種類がある。
- 1の補数による表現
- 2の補数による表現
- 絶対値に符号を付けた表現(左端ビットが0の場合は正,1の場合は負)
4ビットのパターン1101bを 1~3 の方法で表現したものと解釈したとき、値が小さい順になるように3つの方法を並べたものはどれか。
[応用情報技術者平成25年秋期 午前問3]
ア:1 < 3 < 2
イ:2 < 1 < 3
ウ:2 < 3 < 1
エ:3 < 2 < 1
練習10
\( n \) ビットの2の補数表現で表せる数の範囲を \( n \) を用いて答えなさい。
7.練習問題の解答
解答1
正解:ウ
8ビットのうちの半分を負の数、0と正の数をもう半分が使う。
なので、負の数は \( -2^7 = -32 \cdot 4 = -128 \) まで、正の数は、0が含まれるため1個引いて \( 2^7 - 1 = 127 \) まで表現が可能。よって答えはウの「-128~127」
\( n \) ビットの場合でも答えられるようになっておきましょう。
解答2
正解:イ
2の補数にするためにまずは 10110101b の0と1を入れかえましょう。
すると、01001010b となります。あとは1を足すだけ。
よって答えは 01001011b となる。
解答3
正解:5
それぞれの選択肢を見ていこう。
- 誤り。0が00000bと10000bで表されるのは符号+絶対値表現の表し方
- 誤り。5bitの2の補数表現で表すことができるのは -16~15 なのでギリギリ-16は表せる。
- 誤り。10010bはそもそも最上位ビットが1なので負の数。一応いくらなのかを求めると、補数を取って1を足せば絶対値がわかるので、10010b → 01101b → 01110b より絶対値は-14、よって -14 であることがわかる。
- 誤り。負の数なので補数を取って1を足す。10100b → 01011b → 01100b より絶対値は12より、-12であることがわかる。
- 正しい。-7は負の数なので、正の数の7の2の補数を取る。7は00111bなので、2の補数を取ると11000b、さらに1を足すと11001bとなる。
解答4
正解:ウ
まずは、-100を2の補数に直します。
100を8ビットの2の補数で表すと0110 0100bとなります。
つぎに2の補数に直します。まずは0と1を入れ替えます。
すると、1001 1011b となります。さらに1を加算するので 1001 1100b となります。
あとはこれを補数を使わない絶対値表現にすればよい。\[ 2^7 + 2^4 + 2^3 + 2^2 = 128 + 16 + 8 + 4 = 156\]となるので答えはウの156。
解答5
オーバーフローで計算結果がおかしくなるのは
- 正の数同士を足して負の数になるとき
- 負の数同士を足して正の数になるとき
である。下に(1)~(4)の計算結果を記す。

解答6
正解:イ
まずは、それぞれの16進数を2進数に直す。
ア:1FFF → 0001 1111 1111 1111(最上位ビットが0→正)
イ:DFFF → 1101 1111 1111 1111(最上位ビットが1→負)
ウ:E000 → 1110 0000 0000 0000(最上位ビットが1→負)
エ:FFFF → 1111 1111 1111 1111(最上位ビットが1→負)
あとはそれぞれを4倍にする。2進数の場合、4倍にする処理は、2ビット左にシフトする処理をすればよい。それぞれの進数を2ビット左にシフトさせると、
ア:0111 1111 1111 1100(最上位ビットが0→正)
イ:0111 1111 1111 1100(最上位ビットが0→正)
ウ:1000 0000 0000 0000(最上位ビットが1→負)
エ:1111 1111 1111 1100(最上位ビットが1→負)
となる。
あふれの条件としては、4倍の処理(正の倍数処理をしても正負は入れ替わらない)をしているにも関わらず、正の数が負になっているもしくは負の数が正の数になっているものである。
ア、ウ、エの3つは計算結果後も正負は入れ替わっていないので正しく計算できている。
一方イは負の数が正の数になっているので桁あふれが発生している。
よって答えはイのDFFF。
解答7
解答:イ
2の補数表現を使うと、引き算(負の数の足し算)を足し算と同じように実行できる。その選択肢に合致するのはイ。ちなみに
ア:パリティビットの説明(誤り検出、情報理論で学びます。)
ウ:文章は正しいのですが2の補数表現には関係ありません
エ:1の補数の説明です。2の補数にするためには、ビットを反転して1を加算する必要があります。
解答8
解答:(1) 15bit (2) 68人
(1) 点数が最大になる場合を考える。全員が満点(100点)をとった場合なので、合計点は \( 95 \times 100 = 9500 \) となる。
つぎに9500より大きくて、もっとも小さい \( 2^n \) の \( n \) の値を考える。
\( 2^{13} = 8192 \)、\( 2^{14} = 16384 \) なので、\[2^{13} \leqq 9500 < 2^{14}\] となる。よって \( n = 14 \)
ここで注意したいのは2の補数表現で表すということだ。
つまり、正負を表す1bitがさらに必要となる。
よって答えは最低15bit必要。
(2)
(1)の答えの場合、合計が16384未満であれば正しく総和が計算できる。
まずは、あと何点増えても(1)のbit数のままで計算ができるかを求める。
現在の想定される最大の合計点は9500なので、増えてもいい点数は \( 16383 - 9500 = 6884 \) と計算できる。
各個人の点数の最大値は100点なので、あと68人受験者が増えても合計点が正しく計算できることがわかる(69人になると6884をオーバーするので1bit増やす必要がある)。
練習9
解答:エ
1~3の場合の2進数1101bの10進数の値を求める。
最上位ビットが1なので、負なのは確定。それぞれの表記法では絶対値が異なるのでそれぞれの絶対値を求める。
- 1の補数の場合、値の絶対値は0と1を反転する。1101b → 0010b より絶対値は2
- 2の補数の場合、1の補数に1を加算した値が絶対値。 2 + 1 より 3。
- 絶対値に符号をつけた表現の場合、最上位ビット以外の値をそのまま読み取ったのが絶対値。よって5。
よって小さい順に -5, -3, -2 となる。よって 3 < 2 < 1 の順となり、答えはエとなる。
練習10
解答:\( -2^{n-1} \sim 2^{n-1} - 1 \)
7.さいごに
今回は計算機上で負の数を表現する方法、とくに2の補数表現についてまとめました。
\( n \) ビットの2の補数表現で表せる値の範囲は意味を理解してから覚えましょう。
次回は小数の表現法である浮動小数点表記についてのまとめを行いたいと思います。
関連広告・スポンサードリンク