スポンサードリンク
こんにちは、ももやまです。
久しぶりに離散数学の内容を書いてみようかと思います。
今回からしばらくは離散数学の中でもグラフ理論のお話になります。
グラフ理論の参考書もかなり難しい言葉で書いているものが多かったのでこの記事ではうさぎでもわかるようにかみ砕いた言葉でなるべく説明しています。
目次
スポンサードリンク
1.グラフ理論のグラフってなに?
皆さんはグラフと言うと下のようなグラフを思い浮かぶと思います。

しかし、グラフ理論で使うグラフは上のようなグラフではありません!
グラフ理論で使うようなグラフは下のようなやつです。
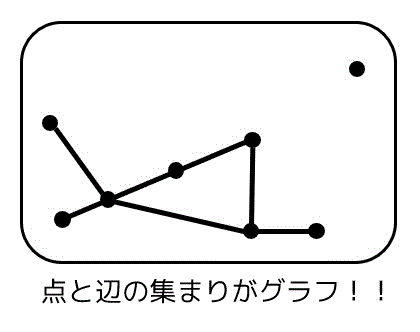
多くの人がこう思うと思います。
「こんな点と辺の集まりについて勉強して何が楽しいん? いいことあるん?」
ということでもっとわかりやすい例をもってきました。
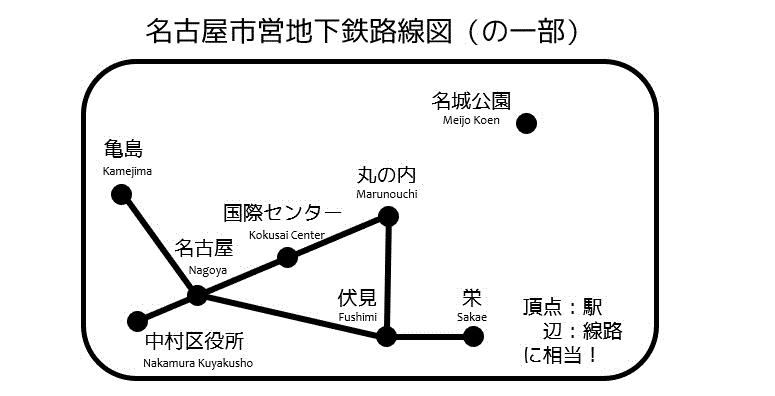
この図はとある名古屋の地下鉄の路線図の一部分なのですが、先程紹介したグラフと同じですよね。
実はグラフ理論の点は路線図でいう駅、辺は路線図でいう線路に相当するのです!
これならなじみがありますよね!
(他にもグラフ理論のグラフに相当するものはネットワーク、化学構造などたくさんあります!)
スポンサードリンク
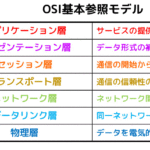
2.グラフ理論の基本用語紹介
では、これから3回にわけてグラフ理論で使われる基本用語について説明していきたいと思います。
(1) グラフとは(再確認)
先ほどグラフは点と辺の集まりと説明しましたね。
グラフとはなにかを定義っぽく書いてみましょう。
点集合 \( V \)、辺集合 \( E \) の順序対(ペア) \( G = (V,E) \) をグラフという。
また、点集合 \( V \) の各要素 \( v_1 \), \( v_2 \), … のことを点、頂点、節点などと呼び、辺集合 \( E \) の各要素 \( e_1 \), \( e_2 \), … のことを辺、枝などと呼ぶ。
人によってはグラフ \( G \) の点集合のことを \( V(G) \)、辺集合のことを \( E(G) \) と表記することもあります。
集合ってなんだっけと思った人はこちらをご覧ください。
(後ほど部分集合などの集合用語も出てくるのでわからなくなったら下の記事から復習しましょう。)
(2) 点集合と辺集合
早速ですがグラフ \( G \) の点集合 \( V \) と辺集合 \( E \) をみていきましょう。

点集合 \( V \) にはグラフ \( G \) にどんな点があるかが格納されていますね。今回の場合だと、\( a \), \( b \), \( c \), \( d \), \( e \), \( f \), \( g \), \( h \) の8つですね。
同様に辺集合 \( E \) にはグラフ \( G \) にどんな辺があるかが格納されていますね。今回の場合だと、\( (a,c) \), \( (b,c) \), \( (c,d) \), \( (c,f) \), \( (d,e) \), \( (e,f) \), \( (f,g) \) の7つありますね。
辺集合の要素は辺の名前よりもどことどこの点を結んでいるかで表されることが多いです*1。
例えば、\( (a,c) \) だと点 \( a \) と点 \( c \) を結んでいる辺、\( (c,f) \) だと点 \( c \) と点 \( f \) を結んでいる辺を表しています*2。
ちなみに先程紹介した路線図バージョンだと下のようになります。

(3) 有向グラフ・無向グラフ
グラフには向きを考えない(順不同)な無向グラフと向きを考える有向グラフがあります。
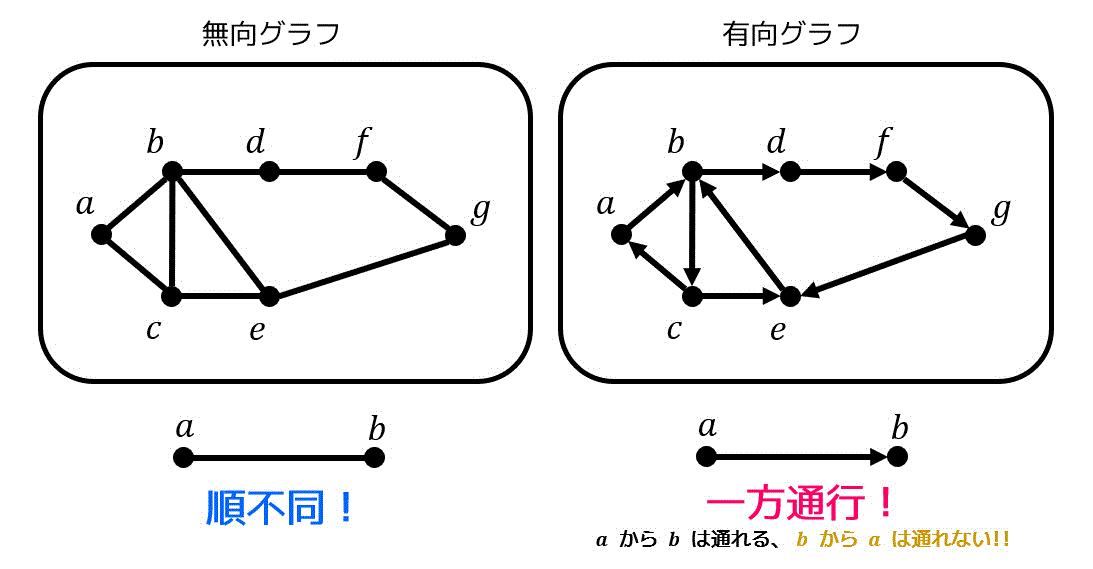
無向グラフ
今まで紹介してきたグラフは無向グラフとなります。
無向グラフの場合、辺の向きが関係ないので、辺 \( (a,b) \) と辺 \( (b,a) \) も同じ意味となります*3。
有向グラフ
一方向きを考えるグラフのことを有向グラフと呼びます。イメージとしては一方通行の道路を思ってください*4。
有向グラフの場合、辺の向きが関係あるので、辺 \( (a,b) \) と辺 \( (b,a) \) の意味が変わってきます。
(4) 点の数・辺の数
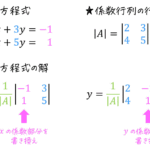
点集合 \( V \) の要素数 \( |V| \) はグラフの点の個数を表し、辺集合 \( E \) の要素数 \( |E| \) はグラフの辺の個数を表します。
(2)の図の例でいくと、\( |V| = 8 \), \( |E| = 7 \) となりますね。
グラフ理論においては、グラフの点の個数を \( n \), 辺の個数を \( m \) で表します。つまり、\[
|V| = n = 8, \ \ \ |E| = m = 7
\]となりますね。
(5) 有限グラフ・無限グラフ
点の数 \( n \) および辺の数 \( m \) がともに有限のグラフのことを有限グラフと呼びます。
一方、点の数 \( n \) 、辺の数 \( m \) のどちらか片方でも無限のグラフのことを無限グラフと呼びます*5。
今後更新していく記事においては、グラフと書いてあったら有限グラフを表していると考えてOKです。
(6) 次数
無向グラフの場合
各点につながっている辺の本数のことを次数と呼びます。
(言い換えると隣接している(隣り合っている)点の数を表します。)
さらに次数が0の(どの辺ともつながっていない)点のことを孤立点と呼びます。
試しに最初に出したグラフの次数をみていきましょう。
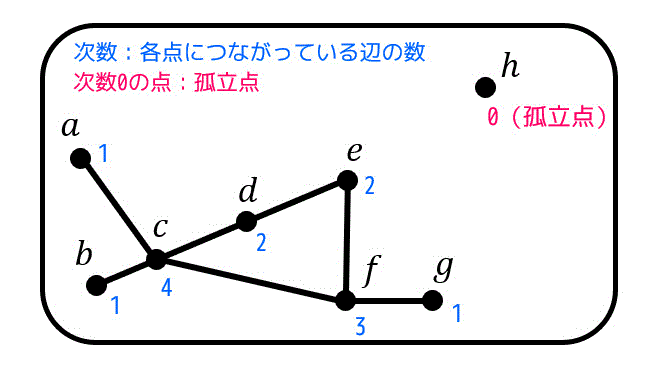
点 \( v \) の次数のことを \( d(v) \) と書きます。
例えば点 \( c \) は点 \( a \), \( b \), \( d \), \( f \) に隣接していますね。なので次数は4となっていますね。なので \( d(c) = 4 \) です。
また、点 \( h \) はどの点とも隣接していませんね。なので次数が0の孤立点となっています。記号で表すと \( d(h) = 0 \) です。
さらに次数が偶数の点のことを偶点、奇数の点のことを奇点と呼びます。
上のグラフの場合、偶点は \( c \), \( d \), \( e \), \( h \)、奇点は \( a \), \( b \), \( f \), \( g \) となります。
また、あるグラフ \( G \) の次数の最大値のことを最大次数 \( \Delta (G) \)、最小値のことを最小次数 \( \delta (G) \) と呼びます。
有向グラフの場合(入次数・出次数とは)
有向グラフの場合はある点に入ってくる辺の数を表す入次数、ある点から出ていく辺の数を表す出次数の2つにわけて次数を表します。
ある点 \( v \) における入次数のことを記号で \( d^- (v) \)、出次数のことを記号で \( d^+ (v) \) と表します。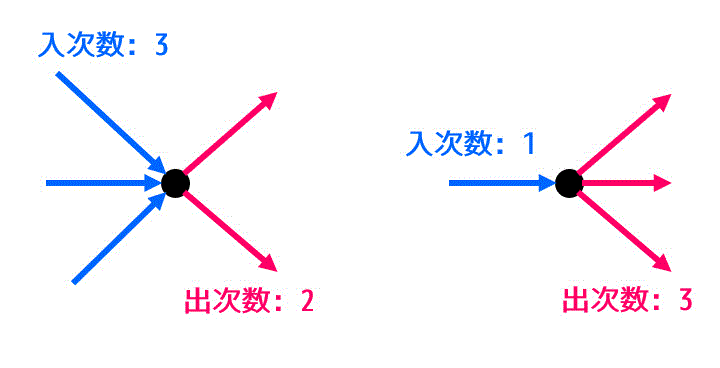
(7) 多重辺・ループ
多重辺
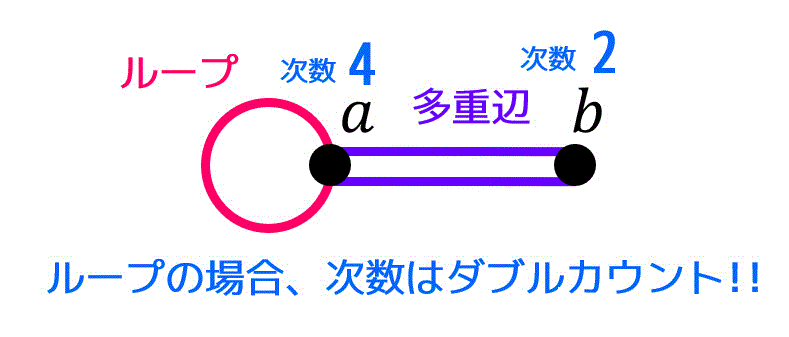
下の紫の辺のように、それぞれの点同士の間に2つ以上の辺が結ばれているような辺のことを多重辺と呼びます。
多重辺の場合でも次数は辺の数だけカウントされます。例えば \( b \) の次数 \( d(b) \) は2となります。
ループ
下の赤の辺のように、全く同じ点同士を結んでいるような辺のことをループと呼びます。
ループの場合、次数をダブルカウントします。例えば、点 \( a \) の次数は多重辺の2本の辺とループが1つあるため、2+2で次数 \( d(a) \) は4となります。
(8) 単純グラフ・多重グラフ
ループと多重辺をともに持たないようなグラフのことを単純グラフと呼びます。
一方ループ・多重辺のうちのどちらか片方でも持つようなグラフのことを多重グラフと呼びます*6。
(9) 次数の和と握手定理
実はどのようなグラフにおいても次数の和は必ず辺の数の2倍となるのです! これを握手定理と呼びます。
どのようなグラフであっても次数の和はグラフの辺の数の2倍に等しい。
(つまり必ず次数の総和は偶数)
数式で書くと、グラフ \( G \) の辺集合 \( E \) が\[
E = \{ v_1, v_2, v_3, \cdots, v_n \}
\]で与えられるとき、\[
\sum^{n}_{i = 1} d(v_i) = 2m
\]となる。これを握手定理と呼ぶ。
まず辺が1本のときを考えましょう。このときの次数の総和は明らかに2ですね。
さらに(次数の和がグラフの辺の数の2倍になっている)あるグラフに辺を1本増やすことを考えましょう。
この辺が点 \( (u,v) \) を結んでいるとすると、左側の \( u \) で次数が+1、\( v \) が次数が+1され、1つ辺を追加するとどんな辺であっても必ず次数は+2されますね*7。
なので、次数の総和はグラフの辺の数の2倍に等しくなることがわかると思います。
例えばさきほど次数を計算したこちらのグラフの次数の総和を計算すると、\[
1 + 1 + 4 + 2 + 2 + 3 + 1 + 0 = 14
\]となりますね。辺の数は7本なので、確かにグラフの次数の総和が辺の数の2倍になっていることがわかりますね!

さらに握手定理を応用することでこんな定理を示すこともできちゃいます。
次数が奇数である点の個数は必ず偶数個である。
握手定理の応用
次数が奇数である点の個数が奇数個であると仮定する。
すると、次数が奇数である点の次数の総和は(奇数)×(奇数)=(奇数)となる。
また、次数が偶数である点の次数の総和は必ず偶数*8となる。
よって次数の総和*9は必ず奇数となってしまう。よって仮定が矛盾する。
よって、次数が奇数である点の個数は必ず偶数個となる。
さらに、有向グラフの場合、入次数と出次数には下のような関係があります。
どのような有向グラフであっても入次数と出次数の総和は等しくなる。
(入次数の総和も出次数の総和も辺の数と同じになる)
辺を1本追加すると入次数と出次数もそれぞれ同じ数(1つ)ずつ増えるので辺が何本であっても入次数と出次数の数はグラフの辺の数のままだからです。
(10) 計算機上でのグラフの表現方法
人間の頭の中では路線図などのグラフを図で理解できますが、計算機(コンピューター)上では図のままでは理解することができませんね…。
ここではどうやって計算機上でグラフを表現するのかを下の2つのグラフを例に説明していきましょう。

計算機上で表現する方法には主に2つがあり、1つはリストを用いた方法、もう1つは行列を用いた方法です。
無向グラフの場合
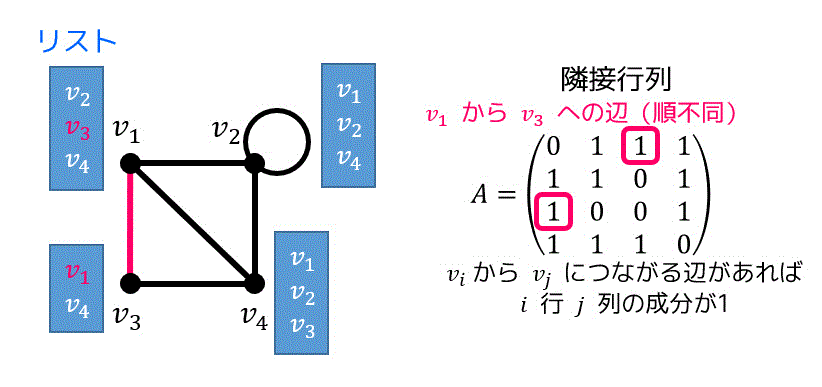
リストを用いて表現する場合、それぞれの頂点においてどの頂点と接続されているかを下のようにリストに格納します。
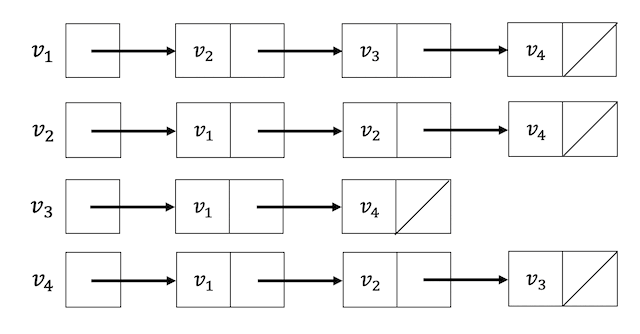
上の例の場合、点 \( v_1 \) と接続している点は \( v_2 \), \( v_3 \) ,\( v_4 \) の3つなのでリストには \( v_2 \), \( v_3 \), \( v_4 \) の3つの点が入っています*10。
一方行列を用いて格納する場合、辺が \( v_i \) と \( v_j \) でつながっていれば \( i \) 行 \( j \) 列に格納されている要素が1、つながっていなければ0を格納します。この行列のことを隣接行列と呼びます。
上の図の例の場合、\( v_1 \) から \( v_3 \) をつないでいるような辺は存在しますよね。なので、1行3列の要素は1になっています。
また、無向グラフには順番がないので、\( v_1 \) から \( v_3 \) をつないでいるような辺は、\( v_3 \) から \( v_1 \) をつないでいるような辺と言い換えられるので3行1列の要素も同様に1となっています。
一方、\( v_2 \) から \( v_3 \) をつないでいるような辺はありませんよね。なので2行3列の要素は0になっていますね。
無向グラフの場合、\( i \) 行 \( j \) 列の要素、\( j \) 行 \( i \) 列の要素は必ず同じになるので*11、元の隣接行列 \( A \) とその転置 \( {}^t\! A \) が必ず等しくなります。なので、隣接行列 \( A \) は必ず対称行列となります。
有向グラフの場合
有向グラフの場合も無向グラフと同様にグラフの表し方が2通りあります。
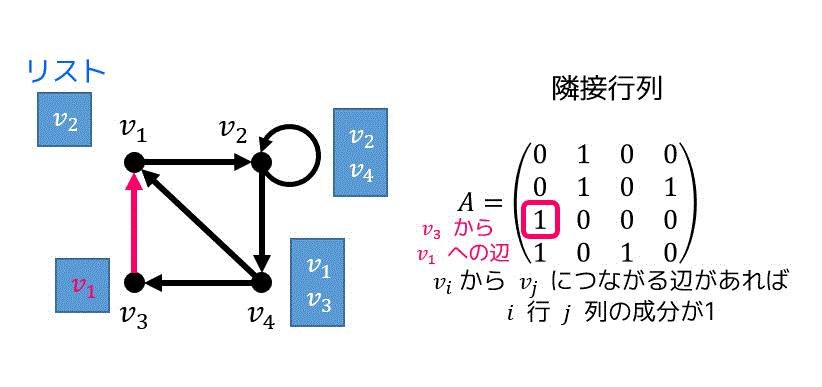
リストの場合はそれぞれの頂点においてどの頂点と接続されているかをリストに格納します。
リストを図示すると下のようになります。
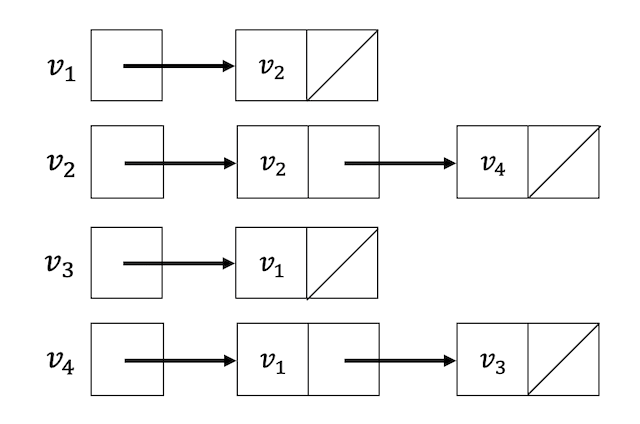
ただし、有向グラフなので逆方向の辺はリストに入れられていないところに注意してください。
例えば、\( v_1 \) と接続している点は \( v_2 \) だけしかありません。\( v_3 \), \( v_4 \) は向きが異なるためリストには入れられていません。
同様に隣接行列の場合、\( v_3 \) から \( v_1 \) をつないでいるような辺は存在するので3行1列成分は1となっていますが逆方向の1行3列は向きが反対なので0になっていますね。
(11) 部分グラフ・全域部分グラフ・誘導部分グラフ
部分グラフ
あるグラフの頂点や辺の一部分をとってきたようなグラフを部分グラフと呼びます。
部分集合のグラフバージョンだと思ってもらってOKです。
定義で書くと下のようになります。
点集合 \( V \) および辺集合 \( E \) からなるグラフ \( G(V,E) \) において、\( V' \subseteq V \) かつ \( E' \subseteq E \) が成り立つとき、グラフ \( G' = (V', E') \) は \( G \) の部分グラフという。
(点集合 \( V \) 、辺集合 \( E \) それぞれの部分集合からなるグラフと思ってください。)
もとのグラフに対しての部分グラフの例*12を下に示しました。
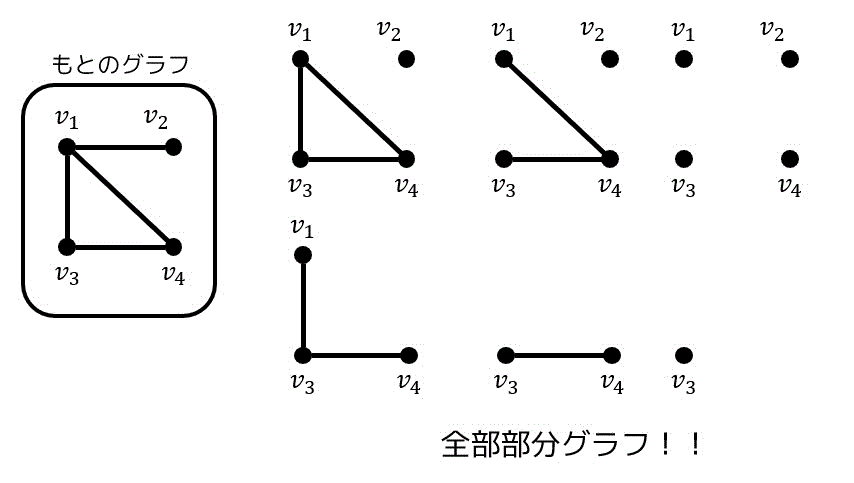
全域部分グラフ
部分グラフの中でも、元の頂点と全く同じ頂点を使っているようなグラフのことを全域部分グラフといいます。ただし、元の辺と全く同じ辺を使う必要はありません。
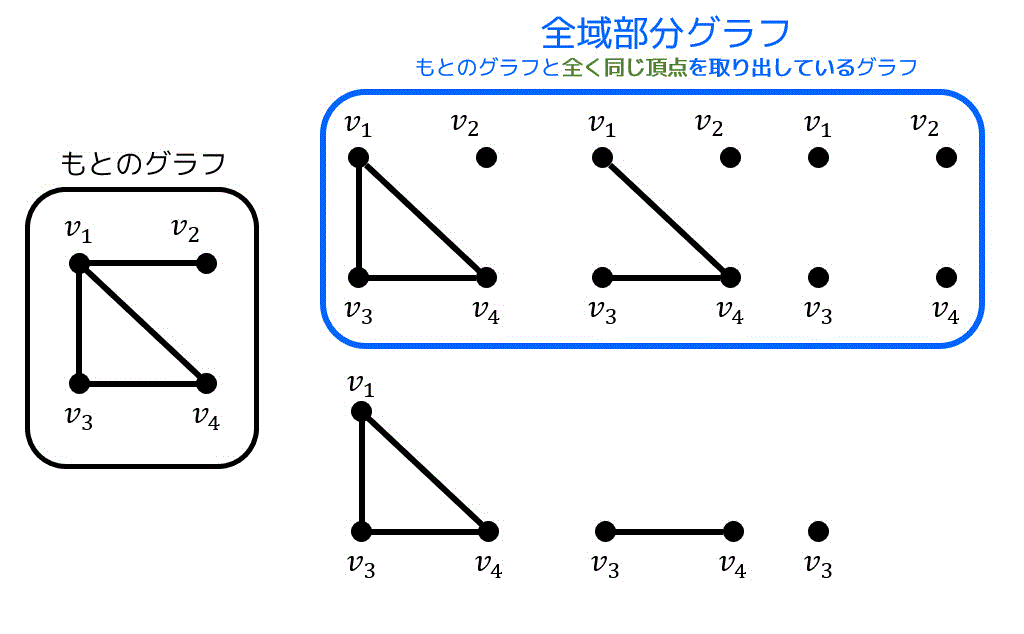
上の図のようなグラフの場合、\( v_1 \), \( v_2 \), \( v_3 \), \( v_4 \) すべてを使っているような部分グラフが全域部分グラフとなります。
誘導部分グラフ
部分グラフの中でも、元のグラフからいくつか頂点を取り出し、取り出した頂点間の辺の有無がもとのグラフと一致するものを誘導部分グラフと呼びます*13。
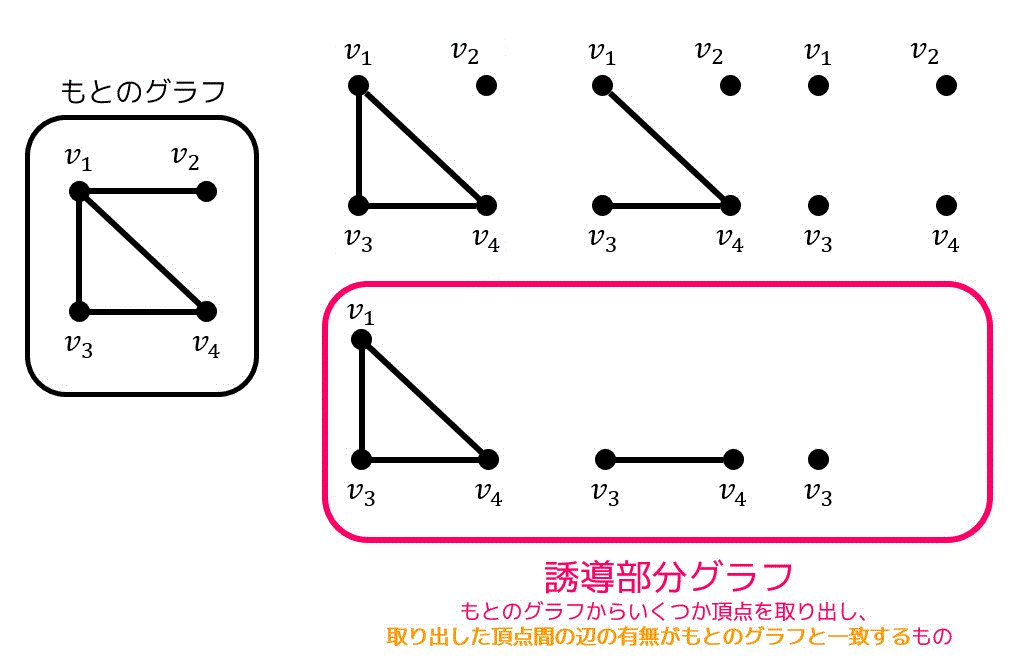
上の図のようなグラフの場合、もとのグラフには \( (v_1, v_2) \), \( (v_1,v_3) \), \( (v_1, v_4) \), \( (v_3,v_4) \) の4箇所に辺がありますね。
例えば、\( v_1 \), \( v_3 \), \( v_4 \) の3つの点を取り出した場合、3つの点の間に接続されているような辺は \( (v_1,v_3) \), \( (v_1, v_4) \), \( (v_3,v_4) \) の3本なので、この3本が接続されているようなグラフが誘導部分グラフとなります。
ちなみに誘導部分グラフは、それぞれの頂点の取り出し方に対して必ず1通りとなります。
スポンサードリンク
3.練習問題
では、少しだけ練習をしてみましょう。
練習
グラフ \( G \) の点集合 \( V \)、辺集合 \( E \) をそれぞれ\[
V = \{ v_1, v_2, v_3, v_4, v_5 \} \\
E = \{ (v_1, v_2), (v_2, v_3), (v_2, v_4), (v_2 , v_5), ( v_3 , v_5), (v_4, v_5) \}
\]とする。このとき、次の問いに書きなさい。
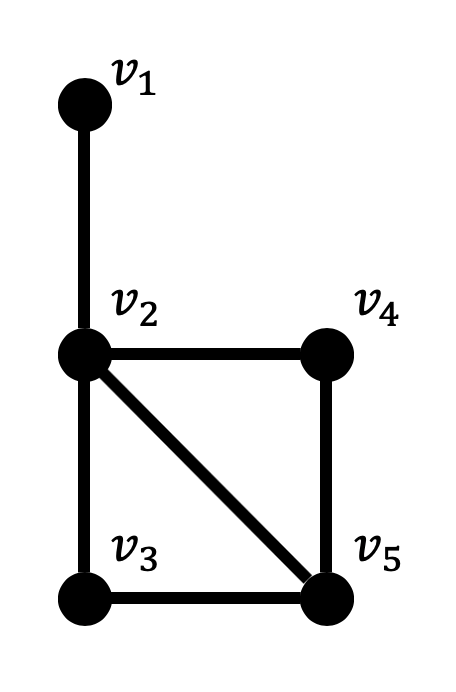
(1) グラフ \( G \) を図示しなさい。
(2) グラフ \( G \) の点の数と辺の数を答えなさい。
(3) それぞれの点における次数 \( d(v_1) \), \( d(v_2) \), \( d(v_3) \), \( d(v_4) \), \( d(v_5) \) を答え、さらに最大次数、最小次数を答えなさい。
(4) グラフ \( G \) の隣接リスト、隣接行列を答えなさい。
(5) グラフ \( G \) の全域部分グラフではあるが、誘導部分グラフではないグラフを1つ答えなさい。
(6) グラフ \( G \) の全域部分グラフの中で、辺の数が5本であるものをすべて答えなさい。
(7) グラフ \( G \) の誘導部分グラフの中で、点の数が4個であるものをすべて答えなさい。
4.練習問題の答え
(1)
左側が答え、右側が各点における次数を書いたもの
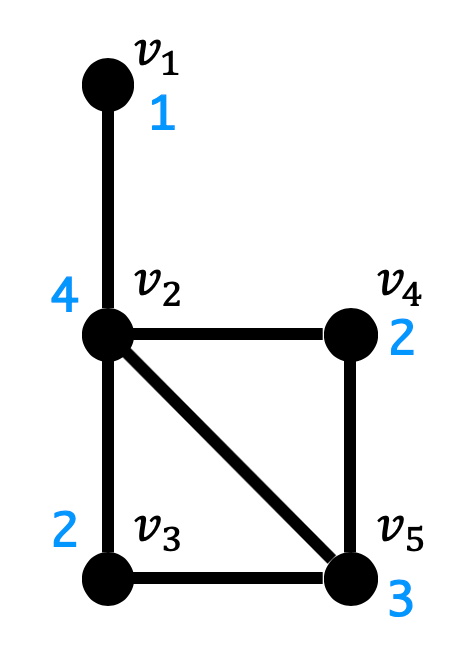
(2)
点の数:5 辺の数:6
数えるだけです()
(3)
それぞれの次数は、\[
d(v_1) = 1, \ \ \ d(v_2) = 4, \ \ \ d(v_3) = 2 \\
d(v_4) = 2 , \ \ \ d(v_5) = 3
\]となる。
よって最高次数は4、最低次数は1である。
(4)
隣接リスト(左側の図は隣接している点を示している)
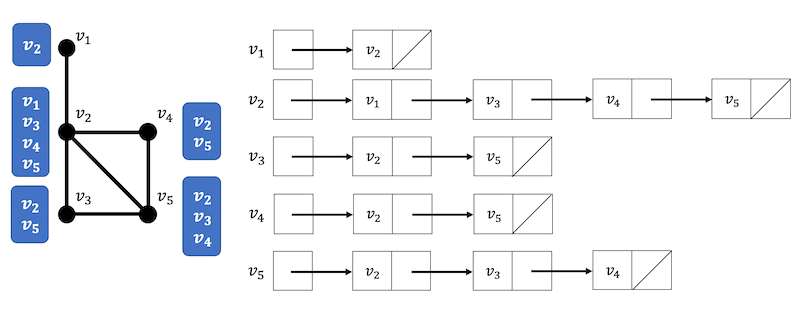
隣接行列\[
\left( \begin{array}{ccc} 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 1 & 0 \end{array} \right)
\]
(5)
全域部分グラフではあるが、誘導部分グラフではないグラフなので、すべての頂点を使っていて、かつもとのグラフから辺をいくつか抜いたようなグラフを1つ書けばよい。
例えば下のようなグラフが該当する。
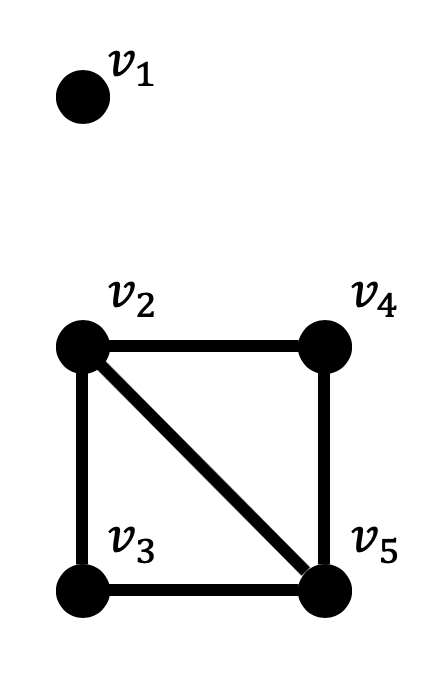
(6)
全域部分グラフなので、頂点は \( v_1 \), \( v_2 \), \( v_3 \), \( v_4 \), \( v_5 \) のすべてを使わなければならない。
すべての頂点を使ったもののうち、辺の数が5本であるものをすべて列挙すればよい。
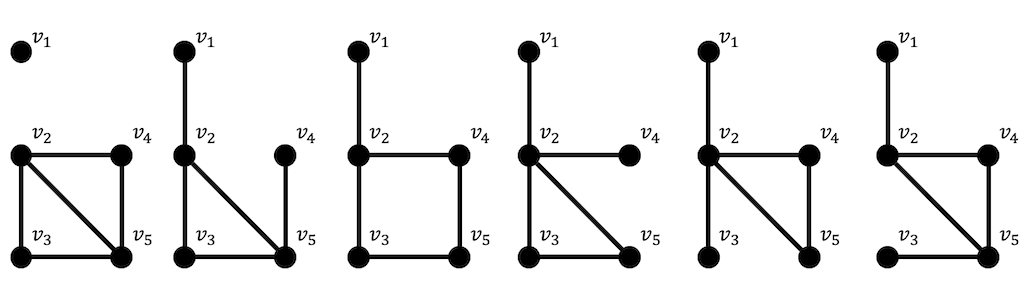
ちなみにもとの数の辺は6本、今回答える辺の数は5本なので辺を選ぶ組み合わせは\[
{}_6 \mathrm{C} _5 = 6
\]となり、6通りであることが明らかとなる。
計算しておけば列挙漏れを防ぐことが可能なのでぜひ計算することをおすすめする*14。
(7)
4頂点の誘導部分グラフなので、取り出したそれぞれの4頂点間の辺の有無がもとのグラフと一致するものを書いていけばよい。
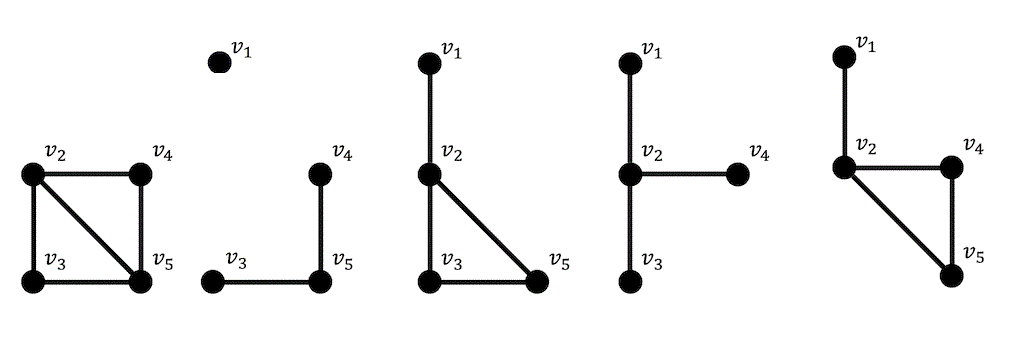
ちなみにもとのグラフの点の数は5本、今回求める誘導部分グラフの点の数は4本なので頂点を選ぶ組み合わせは\[
{}_5 \mathrm{C} _4 = 5
\]となり、5通りである。
それぞれの頂点の取り出し方に対して必ず1通りなので4つの頂点からなる誘導部分グラフは全部で5通りあることがわかる。
こちらも計算しておけば列挙漏れが防ぐことが可能なのでこちらも計算することをおすすめします。
5.さいごに
今回は離散数学のグラフ理論部分のグラフの基本用語の一部をわかりやすくまとめてみました。
グラフ理論はとにかく用語がたくさんあるのでまずはその用語の意味を理解するところからがスタートです。
次回もグラフ理論の基本用語についてまとめていきたいと思うのでそちらもぜひご覧ください!
*1:参考書によっては結んでいる表現の他に
- 辺 \( (a,b) \) は \( a \) と \( b \) に接続している。
- \( a \) および \( b \) は辺 \( (a,b) \) の端点である。
- 点 \( b \) は点 \( a \) に隣接している。(辺を使わずに表現)
と書かれていることもあります。
*2:正確には \( \{a,c \} \) や \( \{c,f\} \) などと { } を用いて書くべきですが、グラフ理論においては、普通のかっこ ( ) で書かれることが多いです。
*3:基本的には順番どおり書くことが多い。
*4:例えば \( (a,b) \) であれば \( a \) から \( b \) にはいけるけど \( b \) から \( a \) にはいけない。
*5:有限グラフではないグラフは無限グラフと思っていただいてOKです。
*6:ループ、多重辺をともにもたないグラフを単純グラフと呼ぶ方だけ覚えて単純グラフじゃないグラフは多重グラフと覚えておいてもOKです。
*7:ちなみにループの場合はダブルカウントされるのでループであっても次数は必ず+2されます。
*8:偶数になにをかけても偶数なので。
*9:次数が奇数である点の次数の総和 + 次数が偶数である点の次数の総和で求められる。
*10:順不同ですが基本的には番号順やら \( a \) ,\( b \), \( c \) 順に格納されています。
*11:\( v_i \) から \( v_j \) に辺があれば必ず \( v_j \) から \( v_i \) にも辺はあるため
*12:あくまでも例なので他にも部分グラフはたくさんあります。
*13:少し言い換えると、取り出してきた頂点の中で、もとのグラフに辺が接続されていた場所すべてに辺が接続されているようなグラフです。
*14:6本の中からいずれか1本を抜くと考えて \( {}_6 \mathrm{C} _1 \) と考えてもOK。
関連広告・スポンサードリンク