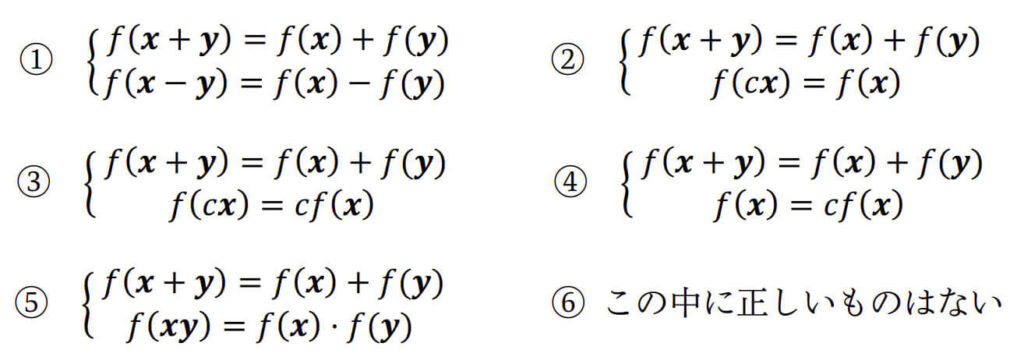4時間で復習！　1年後期線形代数総まとめ　後編

2021年11月24日 2021年11月28日 116分58秒

ももうさ

スポンサードリンク

こんにちは、ももやまです。

「1年後期の線形代数の試験まであと1日しかない、あきらめよう。」って思ってる人、諦めないでください！！

そこで、試験前日でも4時間あれば総復習ができるように11題の練習問題を作成しました！

※ 問題8～問題11は選択問題です。大学のテスト範囲などに合わせて1問を選択してください。

練習の仕方

90分間で問題を解く。答えを回答フォームに入力する。
答えを送信後、間違った箇所を確認し、解説を見てどこで間違えたのか（理解ができていないのか）を確認する。
間違えた箇所を参考書や記事などで練習する。
時間があれば、合っている箇所も確認する。（青色と赤色の枠部分）
寝る。

問題ダウンロードはこちら！！

回答フォームはこちら！！

時間がある人はじっくり、時間がない人は素早くこの記事にて1年後期の線形代数の復習をしましょう！

本記事では、練習問題の解説を載せております。さらに、要点を

試験で必要な知識：青色の枠
試験で必要な解き方：赤色の枠
試験で使える豆知識：オレンジ色の枠
ワンポイントアドバイス：紫色の枠

などでまとめております。

※ この記事は記述式問題である、問題6～問題11の解説を載せております。問題1～問題5の記述式問題の解説は、下のリンクを御覧ください。

問題6. 記述小問集合
問題7. 対角化（誘導少なめ）
問題8. 直交行列による対角化
問題9. 2次形式と2次曲線
問題10. 行列の \( n \) 乗
問題11. ジョルダン標準形

スポンサードリンク

問題6. 記述小問集合

次の(1)～(3)の問いに答えなさい。

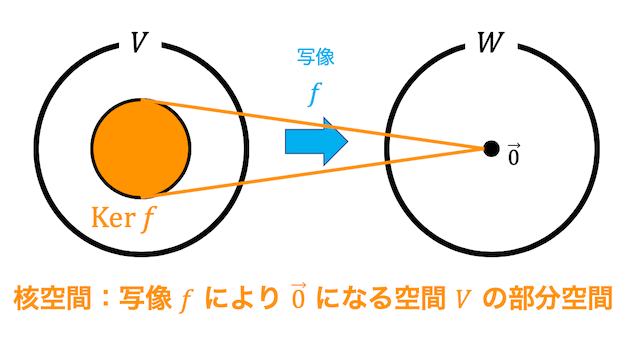
(1) 核と像

問題6-(1)

つぎの行列 \( A \) から定まる線形写像 \( f \) がある。\[
A = \left( \begin{array}{ccc} 1 & -1 & 2 & 1 \\ 2 & -1 & 1 & -2 \\ 3 & -2 & 3 & -1 \end{array} \right)
\]

(i) 核 \( \mathrm{Ker} \ f \) の次元と基底1組を求めなさい。
(ii) 像 \( \mathrm{Im} \ f \) の次元と基底1組を求めなさい。

この分野に該当するうさぎ塾の記事はこちら ↓↓

まずは、核空間と像空間についての求め方の確認をしましょう。

線形写像の核空間と像空間

\( \mathbb{R}^n \to \mathbb{R}^m \) への線形写像 \( f \) の表現行列を \( A \) とする。このとき、核空間 \( \mathrm{Ker} \ f \)、像空間 \( \mathrm{Im} \ f \) の次元と基底は以下のように求められる。

(1) 核空間 \( \mathrm{Ker} \ f \)

次元: \( n - \mathrm{Rank} \ A \)
基底: 連立方程式 \( A \boldsymbol{x} = \boldsymbol{0} \) の解空間

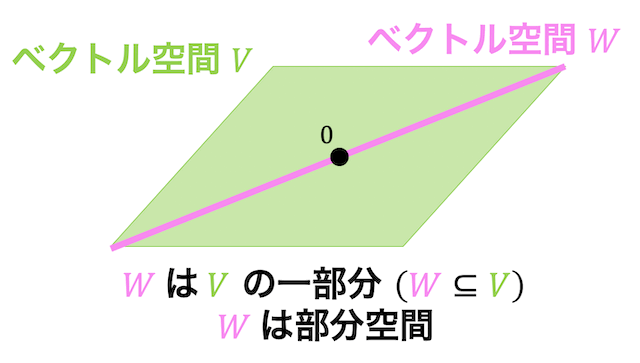
(2) 像空間 \( \mathrm{Im} \ f \)

次元: \( \mathrm{Rank} \ A \)
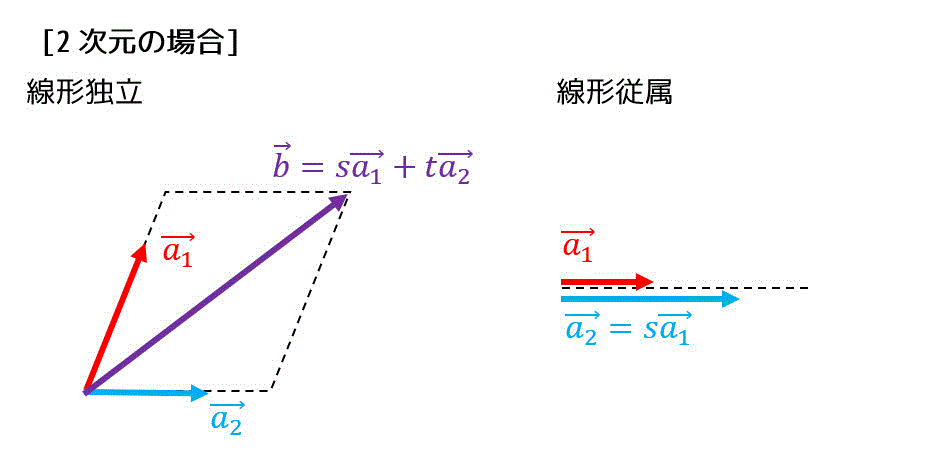
基底: \( A = ( \boldsymbol{a}_1, \boldsymbol{a}_2, \cdots, \boldsymbol{a}_n ) \) としたときの、ベクトルが生成する部分空間^[1]\( \boldsymbol{a}_1, \boldsymbol{a}_2, \cdots, \boldsymbol{a}_n \) から選べる線形独立（1次独立）なベクトルの最大組。

核空間、像空間ともに行列 \( A \) を行基本変形する必要があるので、まずは変形していきましょう。\[\begin{align*}
A & = \left( \begin{array}{ccc} 1 & -1 & 2 & 1 \\ 2 & -1 & 1 & -2 \\ 3 & -2 & 3 & -1 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & -1 & 2 & 1 \\ 0 & 1 & -3 & -4 \\ 0 & 1 & -3 & -4 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & -1 & 2 & 1 \\ 2 & -1 & 1 & -2 \\ 3 & -2 & 3 & -1 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 0 & -1 & -3 \\ 0 & 1 & -3 & -4 \\ 0 & 0 & 0 & 0 \end{array} \right)
\end{align*}\]

となるので、行列 \( A \) の階数は \( \mathrm{Rank} \ A = 2 \) となる。

(i) 核空間 [次元2点＋基底3点＝5点]

核空間の次元は、\[\begin{align*}
\dim \mathrm{Ker} \ f & = n - \mathrm{Rank} \ A
\\ & = 4 - 2
\\ & = 2
\end{align*}\]より、2となる。（結果のみでOKだが、途中式が間違えていれば（例えば \( n - \mathrm{Rank} \ A \) を \( \mathrm{Rank} \ A \) と間違えている）点数なし）

また、核空間の基底は、連立方程式 \( A \boldsymbol{x} = \boldsymbol{0} \) の解空間の集合である。

ここで、\[
\boldsymbol{x} = \left( \begin{array}{ccc} x \\ y \\ z \\ w \end{array} \right)
\]とすると連立方程式の解は、行基本変形の結果より\[
\left( \begin{array}{ccc} 1 & 0 & -1 & -3 \\ 0 & 1 & -3 & -4 \\ 0 & 0 & 0 & 0 \end{array} \right) \left( \begin{array}{ccc} x \\ y \\ z \\ w \end{array} \right) = \left( \begin{array}{ccc} 0 \\ 0 \\ 0 \\ 0 \end{array} \right)
\]\[
\left\{ \begin{array}{l} x - z - 3w = 0 \\ y - 3z - 4w = 0 \end{array} \right.
\]の結果に等しい。

ここで、未知数4つの方程式に対し、行列の階数は2なので、解を表現するためには 4 - 2 = 2 個の任意定数が必要である。任意定数を \( s, t \) とすると、連立方程式の解は\[
\left( \begin{array}{ccc} x \\ y \\ z \\ w \end{array} \right) =
s \left( \begin{array}{ccc} 1 \\ 3 \\ 1 \\ 0 \end{array} \right) +
t \left( \begin{array}{ccc} 3 \\ 4 \\ 0 \\ 1 \end{array} \right)
\]となる。

よって線形写像 \( f \) の核空間 \( \mathrm{Ker} \ f \) は、\[
\mathrm{Ker} \ f = \left\{ \left( \begin{array}{ccc} 1 \\ 3 \\ 1 \\ 0 \end{array} \right), \left( \begin{array}{ccc} 3 \\ 4 \\ 0 \\ 1 \end{array} \right) \right\}
\]となる。

(ii) 像空間 [次元2点＋基底3点＝5点]

像空間の次元は、\[\begin{align*}
\dim \mathrm{Im} \ f & = \mathrm{Rank} \ A
\\ & = 2
\end{align*}\]より、2となる。（(i)と同じく答えのみでOKだが、途中式に誤りがあれば点数を与えない）

また、像空間の基底は \( A = ( \boldsymbol{a}_1, \boldsymbol{a}_2, \boldsymbol{a}_3, \boldsymbol{a}_4 )\) として見たときの、4本から生成される部分空間の基底、つまり4本の中から線形独立なベクトルを次元の数（今回は2本）選んで組にしたものと同じ。

ここで、行基本変形後の行列を \( B \) とし、\[\begin{align*}
B & = \left( \begin{array}{ccc} \textcolor{red}{1} & \textcolor{blue}{0} & -1 & -3 \\ \textcolor{red}{0} & \textcolor{blue}{1} & -3 & -4 \\ \textcolor{red}{0} & \textcolor{blue}{0} & 0 & 0 \end{array} \right)
\\ & = \left( \textcolor{red}{ \boldsymbol{b}_1 } , \textcolor{blue}{ \boldsymbol{b}_2 } , \boldsymbol{b}_3, \boldsymbol{b}_4 \right)
\end{align*}\]とする。

ここで、\( \textcolor{red}{ \boldsymbol{b}_1 } \), \( \textcolor{blue}{ \boldsymbol{b}_2 } \) は明らかに線形独立な2組となる。

さらに、行基本変形の前後でベクトル間の関係は変化しないので、\( \boldsymbol{a}_1, \boldsymbol{a}_2 \) も線形独立な2組である。

よって、像 \( \mathrm{Im} \ f \) の基底は\[
\mathrm{Im} \ f = \left\{ \left( \begin{array}{ccc} 1 \\ 2 \\ 3 \end{array} \right), \left( \begin{array}{ccc} -1 \\ -1 \\ -2 \end{array} \right) \right\}
\]となる。

※ \( \{ \boldsymbol{a}_1, \boldsymbol{a}_2 \} \) でなくても、線形独立な組が2つ選べていたらOK。例えば、 \( \{ \boldsymbol{a}_1, \boldsymbol{a}_3 \} \) なども正解。

(2) ベクトルと線形結合

問題6-(2)

つぎのベクトル \( \boldsymbol{a}_1 \), \( \boldsymbol{a}_2 \), \( \boldsymbol{a}_3 \), \( \boldsymbol{a}_4 \) がある。(i), (ii)の問いに答えなさい。\[
\boldsymbol{a}_1 = \left( \begin{array}{ccc} 1 \\ 2 \\ 1 \end{array} \right) , \ \
\boldsymbol{a}_2 = \left( \begin{array}{ccc} -3 \\ 4 \\ -5 \end{array} \right) , \ \
\boldsymbol{a}_3 = \left( \begin{array}{ccc} 4 \\ -7 \\ 7 \end{array} \right) , \ \
\boldsymbol{a}_4 = \left( \begin{array}{ccc} 2 \\ -1 \\ 3 \end{array} \right)
\]

(i) \( \boldsymbol{a}_1 \), \( \boldsymbol{a}_2 \), \( \boldsymbol{a}_3 \), \( \boldsymbol{a}_4 \) が生成する \( \mathbb{R}^3 \) の部分空間の基底を求めなさい。
(ii) \( \boldsymbol{a}_1 \), \( \boldsymbol{a}_2 \), \( \boldsymbol{a}_3 \), \( \boldsymbol{a}_4 \) のうち、部分空間の基底に含まれないベクトルすべてを(i)で求めた基底の線形結合（1次結合）で表しなさい。

この分野に該当するうさぎ塾の記事はこちら ↓↓

(i) [6点]

生成系の部分空間の基底は、ベクトル内から選べる線形独立な最大組となる。

ここで、行列 \( A \) を\[\begin{align*}
A & = ( \boldsymbol{a}_1 , \boldsymbol{a}_2 , \boldsymbol{a}_3 , \boldsymbol{a}_4 )
\\ & = \left( \begin{array}{ccc} 1 & -3 & 4 & 2 \\ 2 & 4 & -7 & -1 \\ 1 & -5 & 7 & 3 \end{array} \right)
\end{align*}\]とおき、行基本変形を行う。\[\begin{align*}
A & = \left( \begin{array}{ccc} 1 & -3 & 4 & 2 \\ 2 & 4 & -7 & -1 \\ 1 & -5 & 7 & 3 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & -3 & 4 & 2 \\ 0 & 10 & -15 & -5 \\ 0 & -2 & 3 & 1 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 1 & -2 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & -2 & 3 & 1 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 1 & -2 & 0 \\ 0 & -2 & 3 & 1 \\ 0 & 0 & 0 & 0 \end{array} \right)
\end{align*}\]

さらに、行基本変形後の行列を \( B \) とし、\[\begin{align*}
B & = \left( \begin{array}{ccc} \textcolor{red}{1} & 1 & -2 & \textcolor{blue}{0} \\ \textcolor{red}{0} & -2 & 3 & \textcolor{blue}{1} \\ \textcolor{red}{0} & 0 & 0 & \textcolor{blue}{0} \end{array} \right)
\\ & = \left( \textcolor{red}{ \boldsymbol{b}_1 } , \boldsymbol{b}_2 , \boldsymbol{b}_3, \textcolor{blue}{ \boldsymbol{b}_4 } \right)
\end{align*}\]とする。

ここで、\( \textcolor{red}{ \boldsymbol{b}_1 } \), \( \textcolor{blue}{ \boldsymbol{b}_4 } \) は明らかに線形独立な2組となる。

さらに、行基本変形の前後でベクトル間の関係は変化しないので、\( \boldsymbol{a}_1, \boldsymbol{a}_4 \) も線形独立な2組である。

よって、 \( \boldsymbol{a}_1 \), \( \boldsymbol{a}_2 \), \( \boldsymbol{a}_3 \), \( \boldsymbol{a}_4 \) が生成する \( \mathbb{R}^3 \) の部分空間の基底は\[
\{ \boldsymbol{a}_1, \boldsymbol{a}_4 \} = \left\{ \left( \begin{array}{ccc} 1 \\ 2 \\ 1 \end{array} \right) , \left( \begin{array}{ccc} 2 \\ -1 \\ 3 \end{array} \right) \right\}
\]となる。（6点。誤っていれば基底の次元が正しければ3点。）

※ \( \{ \boldsymbol{a}_1, \boldsymbol{a}_4 \} \) でなくても、線形独立な組が2つ選べていたらOK。例えば、 \( \{ \boldsymbol{a}_1, \boldsymbol{a}_2 \} \) なども正解。

(ii) [4点]

部分空間に含まれないベクトル \( \boldsymbol{a}_2 \), \( \boldsymbol{a}_3 \) を基底 \( \{ \boldsymbol{a}_1, \boldsymbol{a}_4 \} \) で表せばOK。

ここで、ベクトル\[
\boldsymbol{b}_1 = \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right) , \ \
\boldsymbol{b}_2 = \left( \begin{array}{ccc} 1 \\ -2 \\ 0 \end{array} \right) , \ \
\boldsymbol{b}_3 = \left( \begin{array}{ccc} -2 \\ 3 \\ 7 \end{array} \right) , \ \
\boldsymbol{b}_4 = \left( \begin{array}{ccc} 0 \\ 1 \\ 0 \end{array} \right)
\]より、\( \boldsymbol{b}_2 \), \( \boldsymbol{b}_3 \) は\[
\begin{array}{l} \boldsymbol{b}_2 = \boldsymbol{b}_1 - 2 \boldsymbol{b}_4 \\ \boldsymbol{b}_3 = -2 \boldsymbol{b}_1 + 3 \boldsymbol{b}_4 \end{array}
\]と表すことができる。

さらに、行基本変形の前後でベクトル間の関係は変化しないので、\[
\begin{array}{l} \boldsymbol{a}_2 = \boldsymbol{a}_1 - 2 \boldsymbol{a}_4 \\ \boldsymbol{a}_3 = -2 \boldsymbol{a}_1 + 3 \boldsymbol{a}_4 \end{array}
\]の関係式が成り立つ。（2点×2＝4点）

ワンポイントアドバイス

関係式を求めた後に、問題文のベクトルを与えることで本当に関係式が成立しているかを確かめることを強くおすすめします。

今回の場合だと、\[
\boldsymbol{a}_1 - 2 \boldsymbol{a}_4 = \left( \begin{array}{ccc} -3 \\ 4 \\ -5 \end{array} \right)
\]\[
-2 \boldsymbol{a}_1 + 3 \boldsymbol{a}_4 = \left( \begin{array}{ccc} 2 \\ -1 \\ 3 \end{array} \right)
\]を確認すればOKです。

(3) 線形写像

問題6-(3)

写像\[
f : \ \mathbb{R}^2 \to \mathbb{R}^2 , \ \ \ f \left( \begin{array}{ccc} x_1 \\ x_2 \end{array} \right) = \left( \begin{array}{ccc} 2x_1 - x_2 \\ x_1 + 3x_2 \end{array} \right)
\]は線形写像か。線形写像であればその証明を、線形写像でなければ反例を1つ挙げなさい。

解答：線形写像である。[2点]

証明 [8点]

任意のベクトル \( \boldsymbol{x}, \boldsymbol{y} \)、および任意の実数 \( k \) において、\[
\begin{array}{l} f ( \boldsymbol{x} + \boldsymbol{y} ) & = f ( \boldsymbol{x} ) + f ( \boldsymbol{y} ) \\
f (k \boldsymbol{x} ) & = k f ( \boldsymbol{x} ) \end{array}
\]が成立することを示す。

ここで、行列 \( A \)、ベクトル \( \boldsymbol{x} \) を\[
A = \left( \begin{array}{ccc} 2 & -1 \\ 1 & 3 \end{array} \right) , \ \ \
\boldsymbol{x} = \left( \begin{array}{ccc} x \\ y \end{array} \right)
\]とおく。すると、\[\begin{align*}
f \left( \begin{array}{ccc} x_1 \\ x_2 \end{array} \right) & = \left( \begin{array}{ccc} 2x_1 - x_2 \\ x_1 + 3x_2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 2 & -1 \\ 1 & 3 \end{array} \right) \left( \begin{array}{ccc} x_1 \\ x_2 \end{array} \right)
\\ & = A \boldsymbol{x}
\end{align*}\]となり、\( f ( \boldsymbol{x} ) = A \boldsymbol{x} \) と表せる。

(i) \( f ( \boldsymbol{x} + \boldsymbol{y} ) = f ( \boldsymbol{x} ) + f ( \boldsymbol{y} ) \) の証明

\[\begin{align*}
f ( \boldsymbol{x} + \boldsymbol{y} ) & = A ( \boldsymbol{x} + \boldsymbol{y} )
\\ & = A \boldsymbol{x} + A \boldsymbol{y}
\\ & = f( \boldsymbol{x} ) + f ( \boldsymbol{y} )
\end{align*}\]

より、(i)成立。

(ii) \( f (k \boldsymbol{x} ) = k f ( \boldsymbol{x} ) \) の証明

\[\begin{align*}
f ( k \boldsymbol{x} ) & = A ( k \boldsymbol{x} )
\\ & = k A \boldsymbol{x}
\\ & =k f( \boldsymbol{x} )
\end{align*}\]

より、(ii)成立。

(i), (ii) より、\( f \) が線形写像であることが示された。

（配点：(i), (ii)の証明に各4点）

線形写像の定義

ある写像 \( f \) が次の1, 2を満たすとき、線形写像となる。

(1) 足し算の分離が可能\[
f( \boldsymbol{x} + \boldsymbol{y} ) = f( \boldsymbol{x} ) + f ( \boldsymbol{y} )
\]

(2) 定数倍の分離が可能\[
f( k \boldsymbol{x}) = k f ( \boldsymbol{x} )
\]

※ \( \boldsymbol{x} \), \( \boldsymbol{y} \) はn次元ベクトル、\( k \) は実数
※ 証明の際は、行列 \( A \) をおき、行列の計算法則を使うと簡単に証明できます。

スポンサードリンク

問題7. 対角化（誘導少なめ）

問題7

行列\[
A = \left( \begin{array}{ccc} 4 & 3 & 4 \\ 0 & 1 & 0 \\ -2 & -3 & -2 \end{array} \right)
\]を対角化したい。

(1) 行列 \( A \) の固有値をすべて求めなさい。
(2) それぞれの固有値に属する固有ベクトルを求めなさい。固有ベクトルの代わりに固有空間を求めてもよい。
(3) 行列 \( A \) は対角化可能か。可能であれば正則行列 \( P \) を用いて \( A \) を対角化しなさい。不可能であれば、対角化ができない理由を書きなさい。

この分野に該当するうさぎ塾の記事はこちら ↓↓

(1) [各固有値ごとに3点×3＝9点]

行列 \( A \) の固有値を \( t \) とする^[2]前編では \( \lambda \) とおいていたのですが、\( \lambda \) の入力が少しめんどくさいので \( t \) とおかせてください。。

すると、固有値は\[\begin{align*}
|A - tE| & = \left| \begin{array}{ccc} 4-t & 3 & 4 \\ 0 & 1-t & 0 \\ -2 & -3 & -2-t \end{array} \right|
\\ & = (1-t) \left| \begin{array}{ccc} 4-t & 4 \\ -2 & -2-t \end{array} \right|
\\ & = (1-t) \left\{ (4-t)(-2-t)-(-8) \right\}
\\ & = (1-t) \left\{ (t-4)(t+2)+8 \right\}
\\ & = (1-t) ( t^2 - 2t - 8 + 8 )
\\ & = t(1-t)(t-2) = 0
\end{align*}\]より、固有値は0, 1, 2となる。

※ 問題分量がかなり多いので、余因子展開が簡単にできるようにすることで、問題難易度をちょっと易しめにしています。

ワンポイントアドバイス

固有値の総和は行列の対角成分の和に一致しているので、検算に大変便利です。

今回の場合は、対角成分の和は\[
\left( \begin{array}{ccc} \textcolor{red}{4} & 3 & 4 \\ 0 & \textcolor{red}{1} & 0 \\ -2 & -3 & \textcolor{red}{-2} \end{array} \right)
\]は、4 + 1 - 2 = 3 ですね。

固有値の和は 0 + 1 + 2 = 3 と比べると、確かに一致していますね！
（重解の場合は重解の数だけカウントしてください）

(2) [各固有ベクトルごとに3点×3＝9点]

※ (1)の固有値が誤っている場合、その固有値に対する固有ベクトルへの点数は与えない

固有ベクトル \( \boldsymbol{p} \) は、固有値ごとに連立方程式 \( (A - tE) \boldsymbol{p} = \boldsymbol{0} \) を解けばOK。

(i) 固有値0に対する固有ベクトル \( \boldsymbol{p}_1 \)

連立方程式 \( (A - 0E) \boldsymbol{p} = \boldsymbol{0} \) を解く。

\[\begin{align*}
A & = \left( \begin{array}{ccc} 4 & 3 & 4 \\ 0 & 1 & 0 \\ -2 & -3 & -2 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 4 & 0 & 4 \\ 0 & 1 & 0 \\ -2 & 0 & -2 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array} \right)
\end{align*}\]

よって、\( A - 0E \) の階数は2なので、固有ベクトルは3 - 2 = 1本存在する。

ここで、行基本変形より、連立方程式 \( ( A - 0E) \boldsymbol{p} = \boldsymbol{0} \) の解は\[
\left\{ \begin{array}{l} x+ z = 0 \\ y = 0 \end{array} \right.
\]の解と同じ。任意定数を \( k \) とおくと、解は\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \end{array} \right)
\]と表せる。

この解の \( k = 1 \) を固有ベクトル \( \boldsymbol{p}_1 \) とする。\[
\boldsymbol{p}_1 = \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \end{array} \right)
\]

なお、固有空間は、\[
V(0) = \left\{ \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \end{array} \right) \right\}
\]となる。

(ii) 固有値1に対する固有ベクトル \( \boldsymbol{p}_2 \)

連立方程式 \( (A - 1E) \boldsymbol{p} = \boldsymbol{0} \) を解く。

\[\begin{align*}
A-E & = \left( \begin{array}{ccc} 3 & 3 & 4 \\ 0 & 0 & 0 \\ -2 & -3 & -3 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 3 & 3 & 4 \\ 0 & 0 & 0 \\ 1 & 0 & 1 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 0 & 3 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & 1 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 0 & 1 \\ 0 & 3 & 1 \\ 0 & 0 & 0 \end{array} \right)
\end{align*}\]

よって、\( A - E \) の階数は2なので、固有ベクトルは3 - 2 = 1本存在する。

ここで、行基本変形より、連立方程式 \( ( A - 1E) \boldsymbol{p} = \boldsymbol{0} \) の解は\[
\left\{ \begin{array}{l} x+ z = 0 \\ 3y+z = 0 \end{array} \right.
\]の解と同じ。任意定数を \( k \) とおくと、解は\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = k \left( \begin{array}{ccc} 3 \\ 1 \\ -3 \end{array} \right)
\]と表せる。

この解の \( k = 1 \) を固有ベクトル \( \boldsymbol{p}_2 \) とする。\[
\boldsymbol{p}_2 = \left( \begin{array}{ccc} 3 \\ 1 \\ -3 \end{array} \right)
\]

なお、固有空間は、\[
V(1) = \left\{ \left( \begin{array}{ccc} 3 \\ 1 \\ -3 \end{array} \right) \right\}
\]となる。

(iii) 固有値2に対する固有ベクトル \( \boldsymbol{p}_3 \)

連立方程式 \( (A - 2E) \boldsymbol{p} = \boldsymbol{0} \) を解く。

\[\begin{align*}
A-2E & = \left( \begin{array}{ccc} 2 & 3 & 4 \\ 0 & -1 & 0 \\ -2 & -3 & -4 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 2 & 0 & 4 \\ 0 & -1 & 0 \\ -2 & 0 & -4 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 2 & 0 & 4 \\ 0 & -1 & 0 \\ 0 & 0 & 0 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 0 & 2 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array} \right)
\end{align*}\]

よって、\( A - 2E \) の階数は2なので、固有ベクトルは3 - 2 = 1本存在する。

ここで、行基本変形より、連立方程式 \( ( A - 2E) \boldsymbol{p} = \boldsymbol{0} \) の解は\[
\left\{ \begin{array}{l} x+ 2z = 0 \\ y = 0 \end{array} \right.
\]の解と同じ。任意定数を \( k \) とおくと、解は\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = k \left( \begin{array}{ccc} 2 \\ 0 \\ -1 \end{array} \right)
\]と表せる。

この解の \( k = 1 \) を固有ベクトル \( \boldsymbol{p}_3 \) とする。\[
\boldsymbol{p}_3 = \left( \begin{array}{ccc} 2 \\ 0 \\ -1 \end{array} \right)
\]

なお、固有空間は、\[
V(2) = \left\{ \left( \begin{array}{ccc} 2 \\ 0 \\ -1 \end{array} \right) \right\}
\]となる。

(3) [2点]

行列 \( P \) を\[\begin{align*}
P & = ( \boldsymbol{p}_1, \boldsymbol{p}_2, \boldsymbol{p}_3 )
\\ & = \left( \begin{array}{ccc} 1 & 3 & 2 \\ 0 & 1 & 0 \\ -1 & -3 & -1 \end{array} \right)
\end{align*}\]とすると、\[\begin{align*}
AP & = A ( \boldsymbol{p}_1, \boldsymbol{p}_2, \boldsymbol{p}_3 )
\\ & = (A \boldsymbol{p}_1,A \boldsymbol{p}_2,A \boldsymbol{p}_3 )
\\ & = (0 \boldsymbol{p}_1, 1 \boldsymbol{p}_2, 2 \boldsymbol{p}_3 )
\\ & = ( \boldsymbol{p}_1, \boldsymbol{p}_2, \boldsymbol{p}_3 ) \left( \begin{array}{ccc} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{array} \right)
\\ & = P \left( \begin{array}{ccc} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{array} \right)
\\ & = PD
\end{align*}\]となるので、\( AP = PD \) が成り立つ。さらに、両辺に左側から \( P^{-1} \) を掛けることで、\[
P^{-1} AP = D = \left( \begin{array}{ccc} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{array} \right)
\]と対角化を行うことができる。

対角化の流れ

3次正方行列 ( A ) の対角化の流れは以下の通り。
※ 3次以外でも基本的な流れは同じ

Step1. \( |A-tE|=0 \) と解いて固有値 \( t_1 \), \( t_2 \), \( t_3 \) を求める
※ 重解が含まれることもある
※ 計算後に \( t_1 + t_2 + t_3 = \) [行列の対角成分の和] を確認！

Step2. 各固有値ごとに固有ベクトル \( \boldsymbol{p}_1 \), \( \boldsymbol{p}_2 \), \( \boldsymbol{p}_3 \) を求める
※ 固有ベクトルが3本なければ対角化できない^[3]固有空間でいうと、\[ \dim V(t_1) + \dim V(t_2) + \dim V(t_3) = 3 \]を満たしていれば対角化OK

Step3. 正則行列 \( P \) を用いて、以下のように \( P^{-1} AP = D \) を対角化する。\[
P = ( \textcolor{red}{\boldsymbol{p}_1}, \textcolor{blue}{\boldsymbol{p}_2}, \textcolor{green}{\boldsymbol{p}_3} ) , \ \ \ D = \left( \begin{array}{ccc} \textcolor{red}{t_1} & \textcolor{blue}{0} & \textcolor{green}{0} \\ \textcolor{red}{0} & \textcolor{blue}{t_2} & \textcolor{green}{0} \\ \textcolor{red}{0} & \textcolor{blue}{0} & \textcolor{green}{t_3} \end{array} \right)
\]※ 各列に対して、固有値と固有ベクトルが組になっているのがポイント

ワンポイントアドバイス

もし時間があれば \( AP = PD \) が一致することを確認して検算するのもありです。

今回の場合、\[
AP = PD = \left( \begin{array}{ccc} 0 & 3 & 4 \\ 0 & 1 & 0 \\ 0 & -3 & -2 \end{array} \right)
\]となります。

スポンサードリンク

問題8. 直交行列による対角化

問題8

(1) 実対称行列\[
A = \left( \begin{array}{ccc} 3 & 1 & 1 \\ 1 & 3 & 1 \\ 1 & 1 & 3 \end{array} \right)
\]を直交行列 \( P \) を用いて対角化しなさい。

(2) 2次形式\[
q( x_1, x_2, x_3) = 3x_1^2 + 3x_2^2 + 3x_3^2 + 2 x_1 x_2 + 2 x_1 x_3 + 2x_2 x_3
\]の標準形、および標準形にする直交変数変換の式を1つ求めなさい。

この分野に該当するうさぎ塾の記事はこちら ↓↓

(1) [15点]

Step1. 固有値を求める

行列 \( A \) の固有値を \( t \) とする。

すると、固有値は\[\begin{align*}
|A - tE| & = \left| \begin{array}{ccc} 3-t & 1 & 1 \\ 1 & 3-t & 1 \\ 1 & 1 & 3-t \end{array} \right|
\\ & = \left| \begin{array}{ccc} 5-t & 5-t & 5-t \\ 1 & 3-t & 1 \\ 1 & 1 & 3-t \end{array} \right|
\\ & = (5-t) \left| \begin{array}{ccc} 1 & 1 & 1 \\ 1 & 3-t & 1 \\ 1 & 1 & 3-t \end{array} \right|
\\ & = (5-t) \left| \begin{array}{ccc} 1 & 1 & 1 \\ 0 & 2-t & 0 \\ 0 & 0 & 2-t \end{array} \right|
\\ & = (5-t) \left| \begin{array}{ccc} 2-t & 0 \\ 0 & 2-t \end{array} \right|
\\ & = (5-t)(2-t)^2 = 0
\end{align*}\]より、固有値は5, 2（2重解）となる。 [固有値5に2点、2重解の固有値2に3点]

[検算] (固有値の総和) = (対角成分の和) = 9 を確認

Step2. \( p_1 \), \( p_2 \), \( p_3 \) が互いに正規直交基底となるような固有ベクトルを求める

(i) 固有値が2のとき

連立方程式 \( (A - 2E) \boldsymbol{p} = \boldsymbol{0} \) を解く。

\[\begin{align*}
A - 2E & = \left( \begin{array}{ccc} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 1 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right)
\end{align*}\]

よって、\( A - 2E \) の階数は1なので、連立方程式 \( x + y + z = 0 \) の解の表現には任意定数が2つ必要。任意定数を \( s, t \) とすると、\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = s \left( \begin{array}{ccc} 1 \\ -1 \\ 0 \end{array} \right) + t \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \end{array} \right)
\]となる。

ここで、\[
\boldsymbol{a}_1 = \left( \begin{array}{ccc} 1 \\ -1 \\ 0 \end{array} \right) , \ \ \
\boldsymbol{a}_2 = \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \end{array} \right)
\]は固有ベクトルだが、大きさが1ではなく、互いに直交化していない。

そこで、グラム・シュミットの直交化法を用いて2つのベクトルを直交化する。\[\begin{align*}
\boldsymbol{a}_1 & = \frac{\boldsymbol{a}_1}{ | \boldsymbol{a}_1| }
\\ & = \frac{1}{ \sqrt{2} } \left( \begin{array}{ccc} 1 \\ -1 \\ 0 \end{array} \right)
\end{align*}\]

\[\begin{align*}
\boldsymbol{b}_2 & = \boldsymbol{a}_2 - ( \boldsymbol{a}_2 \cdot \boldsymbol{p}_1 )
\\ & = \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \end{array} \right) - \frac{1}{\sqrt{2}} \cdot \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 \\ -1 \\ 0 \end{array} \right)
\\ & = \frac{1}{2} \left( \begin{array}{ccc} 2 \\ 0 \\ -2 \end{array} \right) - \frac{1}{2} \left( \begin{array}{ccc} 1 \\ -1 \\ 0 \end{array} \right)
\\ & = \frac{1}{2} \left( \begin{array}{ccc} 1 \\ 1 \\ -2 \end{array} \right)
\end{align*}\]となる。

あとは \( \boldsymbol{p}_2 \) を正規化するだけ。\[\begin{align*}
\boldsymbol{p}_2 & = \frac{ \boldsymbol{b}_2 }{ | \boldsymbol{b}_2 | }
\\ & = \frac{1}{\sqrt{6}} \left( \begin{array}{ccc} 1 \\ 1 \\ -2 \end{array} \right)
\end{align*}\]

よって、正規直交化された固有ベクトルは\[
\boldsymbol{p}_1 = \frac{1}{ \sqrt{2} } \left( \begin{array}{ccc} 1 \\ -1 \\ 0 \end{array} \right) , \ \ \
\boldsymbol{p}_2 = \frac{1}{ \sqrt{6} } \left( \begin{array}{ccc} 1 \\ 1 \\ -2 \end{array} \right)
\]となる。[6点（固有ベクトルは正しいが直交化出来ていない場合は2点）]

ワンポイントアドバイス

\( \boldsymbol{b}_2 \) を出した段階で、 \( \boldsymbol{p}_1 \cdot \boldsymbol{b}_2 = 0 \) を確かめましょう。

また、正規化する際には分数部分を一旦無視してから正規化すると少し計算スピードが上がります。例えば、今回であれば赤色のベクトルを青色のベクトルとみなしてから正規化をします。\[
\textcolor{red}{ \frac{1}{2} \left( \begin{array}{ccc} 1 \\ 1 \\ -2 \end{array} \right) } \to \textcolor{blue}{ \left( \begin{array}{ccc} 1 \\ 1 \\ -2 \end{array} \right) }
\]※ 正規化をするとどうせ大きさが1になるので、向きさえ変えなければ正規化前に大きさを変えてもOK。

(ii) 固有値が5のとき

連立方程式 \( (A - 5E) \boldsymbol{p} = \boldsymbol{0} \) を解く。

\[\begin{align*}
A - 2E & = \left( \begin{array}{ccc} -2 & 1 & 1 \\ 1 & -2 & 1 \\ 1 & 1 & -2 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 0 & 3 & -3 \\ 0 & -3 & 3 \\ 1 & 1 & -2 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 0 & 1 & -1 \\ 0 & 0 & 0 \\ 1 & 0 & -1 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 0 & -1 \\ 0 & 1 & -1 \\ 0 & 0 & 0 \end{array} \right)
\end{align*}\]

ここで、\[
\left\{ \begin{array}{l} x - z = 0 \\ y-z = 0 \end{array} \right.
\]を解くと、解は任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 1 \\ 1 \end{array} \right)
\]と表せる。

よって、大きさ1に正規化した固有ベクトル \( \boldsymbol{p}_3 \) は\[
\boldsymbol{p}_3 = \frac{1}{ \sqrt{3} } \left( \begin{array}{ccc} 1 \\ 1 \\ 1 \end{array} \right)
\]となる。[3点]

Step3. 固有値と正規直交基底をなす固有ベクトルを用いて対角化

\( \boldsymbol{p}_1 \), \( \boldsymbol{p}_2 \), \( \boldsymbol{p}_3 \) は互いに直交行列となるので、以下のような直交行列\[\begin{align*}
P & = ( \boldsymbol{p}_1 , \boldsymbol{p}_2 , \boldsymbol{p}_3 )
\\ & = \frac{1}{ \sqrt{6} } \left( \begin{array}{ccc} \sqrt{3} & 1 & \sqrt{2} \\ - \sqrt{3} & 1 & \sqrt{2} \\ 0 & -2 & \sqrt{2} \end{array} \right)
\end{align*}\]を用いて、\[
P^{-1} AP = \left( \begin{array}{ccc} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 5 \end{array} \right)
\]と対角化できる^[4]直交行列の場合、\( P^{-1} = {}^t P \) が成立するため、\( P^{-1} AP \) を \( {}^t PAP \) と表記することもあります。。[結論に1点（正規直交基底・および固有値に誤りがあれば与えない）]

ワンポイントアドバイス

\[
AP = PD = \frac{1}{ \sqrt{6} } \left( \begin{array}{ccc} 2 \sqrt{3} & 2 & 5 \sqrt{2} \\ - 2 \sqrt{3} & 2 & 5 \sqrt{2} \\ 0 & -4 & 5 \sqrt{2} \end{array} \right)
\]

※ 検算時は \( \frac{1}{ \sqrt{6} } \) を無視してから検算することをおすすめします

(2) [5点]

(1)で求めた \( P \) を用いて \( y_1 \), \( y_2 \), \( y_3 \) を\[\begin{align*}
\left( \begin{array}{ccc} y_1 \\ y_2 \\ y_3 \end{array} \right) & = {}^t P \left( \begin{array}{ccc} x_1 \\ x_2 \\ x_3 \end{array} \right)
\\ \left( \begin{array}{ccc} x_1 \\ x_2 \\ x_3 \end{array} \right) & = P \left( \begin{array}{ccc} y_1 \\ y_2 \\ y_3 \end{array} \right)
\end{align*}\]とおく。（この式に2点：どちらか片方のみでOK）

すると、標準形は\[
2y_1^2 + 2y_2^2 + 5y_3^2
\]となる。（3点・上の2点がない場合は与えない）

直交行列による対角化＋2次形式の流れ

3次実正方行列\[
A = \left( \begin{array}{ccc} a & p & q \\ p & b & r \\ q & r & c \end{array} \right)
\]を直交行列 \( P \) により対角化する流れは下の通り
※ 3次以外でも基本的な流れは同じ

Step1. \( |A-tE|=0 \) と解いて固有値 \( \alpha \), \( \beta \), \( \gamma \) を求める
※ ここまでは通常の対角化と同じ
※ 重解が含まれることもある
※ 計算後に \( \alpha + \beta + \gamma = \) [行列の対角成分の和] を確認！

Step2. 各固有値ごとに大きさが1の固有ベクトル \( \boldsymbol{p}_1 \), \( \boldsymbol{p}_2 \), \( \boldsymbol{p}_3 \) を求める。

ただし、重解となる固有値に対する固有ベクトルの組は、そのままでは正規直交基底にはならないので、グラム・シュミットの直交化法により正規直交基底になるようにする。

※ 異なる固有値に対する固有ベクトルは、正規化さえしていれば勝手に正規直交基底になるので、固有値が重解でなければ正規化だけをすればOK。

Step3. 直交行列 \( P \) を用いて、以下のように \( P^{-1} AP \) を対角化する。\[
P = ( \textcolor{red}{\boldsymbol{p}_1}, \textcolor{blue}{\boldsymbol{p}_2}, \textcolor{green}{\boldsymbol{p}_3} ) , \ \ \ D = \left( \begin{array}{ccc} \textcolor{red}{\alpha} & \textcolor{blue}{0} & \textcolor{green}{0} \\ \textcolor{red}{0} & \textcolor{blue}{\beta} & \textcolor{green}{0} \\ \textcolor{red}{0} & \textcolor{blue}{0} & \textcolor{green}{\gamma} \end{array} \right)
\]※ 各列に対して、固有値と固有ベクトルが組になっているのがポイント

Step4. \[
\boldsymbol{x} = \left( \begin{array}{ccc} x_1 \\ x_2 \\ x_3 \end{array} \right), \ \ \ \boldsymbol{y} = \left( \begin{array}{ccc} y_1 \\ y_2 \\ y_3 \end{array} \right)
\]とし、2次形式を\[
a x_1^2 + b x_2^2 + c x_3^2 + 2p x_1 x_2 + 2q x_1 x_3 + 2r x_2 x_3 = {}^t \boldsymbol{x} A \boldsymbol{x}
\]と行列を用いて表す。

Step5. 変換法則 \( \boldsymbol{y} = {}^t P \boldsymbol{x} \) もしくは \( \boldsymbol{x} = P \boldsymbol{y} \) を用いて、\[
a x_1^2 + b x_2^2 + c x_3^2 + 2p x_1 x_2 + 2q x_1 x_3 + 2r x_2 x_3 = \textcolor{red}{\alpha} y_1^2 + \textcolor{blue}{\beta} y_2^2 + \textcolor{green}{\gamma} y_3^2
\]と標準形にする。

問題9. 2次形式と2次曲線

問題9

(1) 2次形式 \( 5x^2 - 2xy + 5y^2 \) の標準形を求めなさい。
(2) 2次形式 \( 5x^2 - 2xy + 5y^2 + 10x - 2y -7 = 0 \) の標準形を求めなさい。
(3) 2次曲線 \( 5x^2 - 2xy + 5y^2 + 10x - 2y - 7 = 0 \) のグラフを書きなさい。

この分野に該当するうさぎ塾の記事はこちら ↓↓

(1) [7点]

Step1. 主要部分 \( 5x^2 - 2xy + 5y^2 \) を行列表記する

行列 \( A \)、ベクトル \( \boldsymbol{x} \) を\[
A = \left( \begin{array}{ccc} 5 & -1 \\ -1 & 5 \end{array} \right), \ \ \
\boldsymbol{x} = \left( \begin{array}{ccc} x \\ y \end{array} \right)
\]とおく。すると、主要部分は\[
5x^2 - 2xy + 5y^2 = {}^t \! \boldsymbol{x} A \boldsymbol{x}
\]と表せる。[1点]

Step2. 行列 \( A \) を直交行列で対角化

次に行列 \( A \) を直交行列で対角化しましょう。

早速固有値 \( t \) を求めます。

\[\begin{align*}
|A-tE| & = \left| \begin{array}{ccc} 5-t & -1 \\ -1 & 5-t \end{array} \right|
\\ & = (5-t)^2 - 1
\\ & = t^2 - 10t + 24
\\ & = (t-4)(t-6) = 0
\end{align*}\]より、固有値は4, 6となる。[1点×2]

[検算] (固有値の総和) = (対角成分の和) = 10 を確認

(i) 固有値4に対する固有ベクトル \( \boldsymbol{p}_1 \)

連立方程式 \( (A - 4E) \boldsymbol{p} = \boldsymbol{0} \) を解く。

\[\begin{align*}
A - 4E & = \left( \begin{array}{ccc} 1 & -1 \\ -1 & 1 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & -1 \\ 0 & 0 \end{array} \right)
\end{align*}\]

ここで、\( A - 4E \) の階数は1なので、連立方程式 \( x - y = 0 \) の解の表現には任意定数が1つ必要。任意定数を \( k \) とすると、\[
\left( \begin{array}{ccc} x \\ y \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)
\]となる。

よって、大きさ1に正規化した固有ベクトル \( \boldsymbol{p}_1 \) は\[
\boldsymbol{p}_1 = \frac{1}{ \sqrt{2} } \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)
\]となる。

(ii) 固有値6に対する固有ベクトル \( \boldsymbol{p}_2 \)

連立方程式 \( (A - 6E) \boldsymbol{p} = \boldsymbol{0} \) を解く。

\[\begin{align*}
A - 6E & = \left( \begin{array}{ccc} -1 & -1 \\ -1 & -1 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 1 \\ 0 & 0 \end{array} \right)
\end{align*}\]

ここで、\( A - 6E \) の階数は1なので、連立方程式 \( x + y = 0 \) の解の表現には任意定数が1つ必要。任意定数を \( k \) とすると、\[
\left( \begin{array}{ccc} x \\ y \end{array} \right) = k \left( \begin{array}{ccc} -1 \\ 1 \end{array} \right)
\]となる。

よって、大きさ1に正規化した固有ベクトル \( \boldsymbol{p}_2 \) は\[
\boldsymbol{p}_1 = \frac{1}{ \sqrt{2} } \left( \begin{array}{ccc} -1 \\ 1 \end{array} \right)
\]となる。

\( \boldsymbol{p}_1 \), \( \boldsymbol{p}_2 \) は正規直交基底になる^[5]\( A \) は実対象行列なので異なる固有値に対する固有ベクトルは、大きさが1であれば必ず直交します。ので、直交行列\[
P = ( \textcolor{red}{\boldsymbol{p}_1}, \textcolor{blue}{\boldsymbol{p}_2} ) = \frac{1}{ \sqrt{2} } \left( \begin{array}{ccc} 1 & -1 \\ 1 & 1 \end{array} \right)
\]を用いて\[\begin{align*}
P^{-1} AP = \frac{1}{ \sqrt{2} } \left( \begin{array}{ccc} \textcolor{red}{4} & 0 \\ 0 & \textcolor{blue}{6} \end{array} \right)
\end{align*}\]と対角化できる。 [各固有ベクトルに1点×2・対角化の結果に1点]

ワンポイントアドバイス

直交行列 \( P \) が\[
P = \left( \begin{array}{ccc} \textcolor{magenta}{\cos \theta} & - \textcolor{deepskyblue}{\sin \theta} \\ \textcolor{deepskyblue}{\sin \theta} & \textcolor{magenta}{\cos \theta} \end{array} \right)
\]の形になるように固有ベクトルを定めることをおすすめします。
（ \( \cos \theta \) の値を揃えると自然と回転行列になります）

\[
AP = PD = \frac{1}{ \sqrt{2} } \left( \begin{array}{ccc} 4 & -6 \\ 4 & 6 \end{array} \right)
\]

※ 検算時は \( \frac{1}{ \sqrt{2} } \) を無視してから検算することをおすすめします

Step3. 行列 \( P \) を用いて標準形を求める

ここで、\( X \), \( Y \) をベクトル \( \boldsymbol{y} \) を用いてつぎのようにおく。\[
\boldsymbol{y} = \left( \begin{array}{ccc} X \\ Y \end{array} \right)
\]

さらに \( \boldsymbol{x} = P \boldsymbol{y} \) の関係式が成り立つので、主要部分は\[
5x^2 - 2xy + 5y^2 = 4X^2 + 6Y^2
\]となる。[結果に1点]

(2) [5点]

Step4. 2次曲線の標準形を求める

\( \boldsymbol{x} = P \boldsymbol{y} \) の関係式より、\[\begin{align*}
\left( \begin{array}{ccc} x \\ y \end{array} \right) & = P \left( \begin{array}{ccc} X \\ Y \end{array} \right)
\\ & = \frac{1}{ \sqrt{2} } \left( \begin{array}{ccc} 1 & -1 \\ 1 & 1 \end{array} \right) \left( \begin{array}{ccc} X \\ Y \end{array} \right)
\\ & = \frac{1}{ \sqrt{2} } \left( \begin{array}{ccc} X-Y \\ X+Y \end{array} \right)
\end{align*}\]

となるので、\[
x = \frac{ \sqrt{2} }{2} ( X-Y) , \ \ \ y = \frac{ \sqrt{2} }{2} (X+Y)
\]となる。

ここで、\[\begin{align*}
\textcolor{deepskyblue}{5x^2 - 2xy + 5y^2} + 10x - 2y - 7 & = \textcolor{deepskyblue}{4X^2 + 6Y^2} + 10 \cdot \frac{ \sqrt{2} }{2} ( X-Y) - 2 \cdot \frac{ \sqrt{2} }{2} (X+Y) - 7
\\ & = 4 X^2 + 6 Y^2 + 5 \sqrt{2} (X-Y) - \sqrt{2} (X+Y) - 7
\\ & = 4 X^2 + 6 Y^2 + 4 \sqrt{2} X - 6 \sqrt{2} Y - 7
\\ & = 4 \left( X + \frac{ \sqrt{2} }{2} \right)^2 + 6 \left( Y - \frac{ \sqrt{2} }{2} \right)^2 - 12
\end{align*}\]と変形ができる。[3点]

さらに、\[
4 \left( X + \frac{ \sqrt{2} }{2} \right)^2 + 6 \left( Y - \frac{ \sqrt{2} }{2} \right)^2 - 12 = 0
\]\[
4 \left( X + \frac{ \sqrt{2} }{2} \right)^2 + 6 \left( Y - \frac{ \sqrt{2} }{2} \right)^2 = 12
\]と変換できるので、標準形は\[
\frac{ \left( X + \frac{ \sqrt{2} }{2} \right)^2 }{3} + \frac{ \left( Y - \frac{ \sqrt{2} }{2} \right)^2 }{2} = 1
\]となる。[2点]

(3) [8点]

Step5. 標準形がどのような図形なのかを考える

標準形\[
\frac{ \left( X + \frac{ \sqrt{2} }{2} \right)^2 }{(\sqrt{3})^2} + \frac{ \left( Y - \frac{ \sqrt{2} }{2} \right)^2 }{ (\sqrt{2})^2 } = 1
\]は、\( X \) 軸の長さ \( 2 \times \sqrt{3} \)、\( Y \) 軸の長さ \( 2 \times \sqrt{2} \)、中心 \( \left( - \frac{ \sqrt{2}}{2}, \frac{ \sqrt{2} }{2} \right) \) の楕円となる。[2点]

Step6. 回転行列 \( P \) の関係を見る

ここで、標準形 \( X , Y \) からもとの変数 \( x, y \) に変換するための変換行列 \( P \) は図形的にどのような変換をしているかを考える。行列 \( P \) は、\[\begin{align*}
P & = \frac{1}{ \sqrt{2} } \left( \begin{array}{ccc} 1 & -1 \\ 1 & 1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} \textcolor{magenta}{\frac{1}{ \sqrt{2} }} & - \textcolor{deepskyblue}{\frac{1}{ \sqrt{2} }} \\ \textcolor{deepskyblue}{\frac{1}{ \sqrt{2} }} & \textcolor{magenta}{\frac{1}{ \sqrt{2} }} \end{array} \right)
\\ & = \left( \begin{array}{ccc} \textcolor{magenta}{\cos \theta} & - \textcolor{deepskyblue}{\sin \theta} \\ \textcolor{deepskyblue}{\sin \theta} & \textcolor{magenta}{\cos \theta} \end{array} \right)
\end{align*}\]

と回転行列の形になっている。そのため、\[\begin{align*}
\tan \theta & = \frac{ \textcolor{deepskyblue}{ \sin \theta} }{ \textcolor{magenta}{ \cos \theta} }
\\ & = \frac{ \frac{1}{ \sqrt{2} } }{ \frac{1}{ \sqrt{2} } }
\\ & = 1
\end{align*}\]となるため、\( \tan \theta = 1 \)、つまり \( \theta = 45^{\circ} \) となる。

つまり、\( P \) は原点中心に反時計回りに45°回転する変換を表している。 [2点]

また、変換後の楕円の中心座標は\[
\frac{1}{ \sqrt{2} } \left( \begin{array}{ccc} 1 & -1 \\ 1 & 1 \end{array} \right) \cdot \frac{ \sqrt{2} }{2} \left( \begin{array}{ccc} -1 \\ 1 \end{array} \right) = \left( \begin{array}{ccc} -1 \\ 0 \end{array} \right)
\]より、(1,0)となることがわかる。 [2点（グラフで認識出来たらOK）]

Step7. グラフを描く

よって、グラフは下のようになる。 [2点]

※ 緑色の線は傾き \( \tan \theta = 1 \) の曲線を表す。

2次曲線のグラフを書く流れ

2次曲線\[
a x^2 + 2p xy + b y^2 + 2qx + 2ry + c = 0
\]のグラフを書く手順は以下の通り。

※ 3次以外でも基本的な流れは同じ

Step1. 主要部分 \( ax^2 + 2p xy + b^2 \) を行列 \( A \)、ベクトル \( \boldsymbol{x} \) で表す。\[
A = \left( \begin{array}{ccc} a & p \\ p & b \end{array} \right) , \ \ \
\boldsymbol{x} = \left( \begin{array}{ccc} x \\ y \end{array} \right)
\]で

Step2. 行列 \( A \) を直交行列 \( P \) になるように \( P^{-1} AP \) を対角化する。\[
P^{-1} AP = \left( \begin{array}{ccc} \alpha & 0 \\ 0 & \beta \end{array} \right)
\]その際に \( P \) が回転行列\[
P = \left( \begin{array}{ccc} \textcolor{magenta}{\cos \theta} & - \textcolor{deepskyblue}{\sin \theta} \\ \textcolor{deepskyblue}{\sin \theta} & \textcolor{magenta}{\cos \theta} \end{array} \right)
\]になるようにする。

※ 2×2の行列の場合、固有値に重解は発生しないため、グラム・シュミットの直交化を使うことは基本ない^[6]異なる固有値に対する固有ベクトルは、正規化さえしていれば勝手に正規直交基底になるので、固有値が重解でなければ正規化だけをすればOK。。

Step3. \( P \boldsymbol{y} = \boldsymbol{x} \) を用いて、以下のように主要部分を標準形にする。\[
ax^2 + 2p xy + b^2 = \alpha X^2 + \beta Y^2
\]

Step4. \( \boldsymbol{x} = P \boldsymbol{y} \) の関係式から、主要部分以外も \( X \), \( Y \) を用いて表す。

さらに、\[
\textcolor{red}{\frac{(X-a')^2}{p^2} + \frac{(Y-a')^2}{q^2} = 1} \ \ \
\textcolor{blue}{\frac{(X-a')^2}{p^2} - \frac{(Y-a')^2}{q^2} = 1}
\]の形にする。（前者は楕円、後者は双曲線となる。）

Step5. 標準形から、図形の意味を考える。

Step6. 回転行列 \( P \) はどのように回転しているのかを調べ、さらに中心点を回転させる。

Step7. グラフを書く

問題10. 行列の \( n \) 乗

問題10

行列\[
A = \left( \begin{array}{ccc} -1 & -6 \\ 2 & 6 \end{array} \right)
\]のべき乗 \( A^n \) を求めなさい。

この分野に該当するうさぎ塾の記事はこちら ↓↓

Step1. 行列 \( A \) の固有値を求める

行列 \( A \) の固有値を \( t \) とする。

すると、固有値は\[\begin{align*}
|A - tE| & = \left| \begin{array}{ccc} -1 & -6 \\ 2 & 6 \end{array} \right|
\\ & = \left| \begin{array}{ccc} -1-t & -6 \\ 2 & 6-t \end{array} \right|
\\ & = (-1-t)(6-t) - (-12)
\\ & = (t+1)(t-6) + 12
\\ & = t^2 - 5t + 6
\\ & = (t-2)(t-3) = 0
\end{align*}\]より、固有値は2, 3となる。

[検算] (固有値の総和) = (対角成分の和) = 5 を確認

Step2. 行列 \( A \) の固有ベクトルを求め、対角化

(1) 固有値2に対する固有ベクトル \( \boldsymbol{p}_1 \)

連立方程式 \( (A-2E) \boldsymbol{p} = \boldsymbol{0} \) を解く

\[\begin{align*}
A - 2E & = \left( \begin{array}{ccc} -3 & -6 \\ 2 & 4 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 2 \\ 0 & 0 \end{array} \right)
\end{align*}\]

ここで、\( A - 2E \) の階数は1なので、連立方程式 \( x+2y = 0 \) の解の表現には任意定数が1つ必要。任意定数を \( k \) とすると、\[
\left( \begin{array}{ccc} x \\ y \end{array} \right) = k \left( \begin{array}{ccc} 2 \\ -1 \end{array} \right)
\]となる。

\ この解の \( k = 1 \) を固有ベクトル \( \boldsymbol{p}_1 \) とする。\[
\boldsymbol{p}_1 = \left( \begin{array}{ccc} 2 \\ -1 \end{array} \right)
\]

(2) 固有値3に対する固有ベクトル \( \boldsymbol{p}_2 \)

連立方程式 \( (A-3E) \boldsymbol{p} = \boldsymbol{0} \) を解く

\[\begin{align*}
A - 3E & = \left( \begin{array}{ccc} -4 & -6 \\ 2 & 3 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 2 & 3 \\ 0 & 0 \end{array} \right)
\end{align*}\]

ここで、\( A - 3E \) の階数は1なので、連立方程式 \( 2x+3y = 0 \) の解の表現には任意定数が1つ必要。任意定数を \( k \) とすると、\[
\left( \begin{array}{ccc} x \\ y \end{array} \right) = k \left( \begin{array}{ccc} 3 \\ -2 \end{array} \right)
\]となる。

\ この解の \( k = 1 \) を固有ベクトル \( \boldsymbol{p}_2 \) とする。\[
\boldsymbol{p}_1 = \left( \begin{array}{ccc} 3 \\ -2 \end{array} \right)
\]

よって、(1), (2)より、正則行列 \( P \) を用いて、行列 \( A \) を下のように対角化できる。\[\begin{align*}
P & = ( \textcolor{red}{ \boldsymbol{p}_1 }, \textcolor{blue}{ \boldsymbol{p}_2 } )
\\ & = \left( \begin{array}{ccc} 2 & 3 \\ -1 & -2 \end{array} \right)
\end{align*}\]\[
P^{-1} AP = \left( \begin{array}{ccc} \textcolor{red}{2} & 0 \\ 0 & \textcolor{blue}{3} \end{array} \right) = D
\]

ワンポイントアドバイス (検算)

\[
AP = PD = \left( \begin{array}{ccc} 4 & 9 \\ -2 & -6 \end{array} \right)
\]

Step3. \( A^n = P D^n P^{-1} \) の導出

ここで、\( P^{-1} AP = D \) より、両辺の左から \( P \)、右から \( P^{-1} \) を掛けると \( A = P D P^{-1} \) の関係式が導出できる。

さらに、\[\begin{align*}
A^n & = \underbrace{A A \cdot \cdots A}_{ n \ \mathrm{個} }
\\ & = \underbrace{ (PDP^{-1}) (PDP^{-1}) \cdots (PDP^{-1}) }_ { n \ \mathrm{個} }
\\ & = P D \underbrace{(P^{-1} P)}_{E} D \underbrace{(P^{-1} P)}_{E} \cdots D P^{-1}
\\ & = P \underbrace{ DD \cdots D }_{ n \ \mathrm{個}} P^{-1}
\\ & = P D^n P^{-1}
\end{align*}\]となる。

Step4. \( D^n \) と \( P^{-1} \) を求める

こで、対角行列\( D \) のべき乗は\[\begin{align*}
D^n = \left( \begin{array}{ccc} 2^n & 0 \\ 0 & 3^n \end{array} \right)
\end{align*}\]となる。

ここで、\( P^{-1} \) は、\[\begin{align*}
P^{-1} & = \frac{1}{|P|} \left( \begin{array}{ccc} -2 & -3 \\ 1 & 2 \end{array} \right)
\\ & = \frac{1}{-1} \left( \begin{array}{ccc} -2 & -3 \\ 1 & 2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 2 & 3 \\ -1 & -2 \end{array} \right)
\end{align*}\]と計算できる。

よって、\[\begin{align*}
A^n & = P D^n P^{-1}
\\ & = \left( \begin{array}{ccc} 2 & 3 \\ -1 & -2 \end{array} \right) \left( \begin{array}{ccc} 2^n & 0 \\ 0 & 3^n \end{array} \right) \left( \begin{array}{ccc} 2 & 3 \\ -1 & -2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 2^{n+1} & 3^{n+1} \\ -2^n & -2 \cdot 3^n \end{array} \right) \left( \begin{array}{ccc} 2 & 3 \\ -1 & -2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 2 \cdot 2^{n+1} - 3^{n+1} & 3 \cdot 2^{n+1} - 2 \cdot 3^{n+1} \\ -2 \cdot 2^n + 2 \cdot 3^n & -3 \cdot 2^n + 4 \cdot 3^n \end{array} \right)
\\ & = \left( \begin{array}{ccc} 2^{n+2} - 3^{n+1} & 6( 2^n - 3^n) \\ 2( 3^n - 2^n) & -3 \cdot 2^n + 4 \cdot 3^n \end{array} \right)
\end{align*}\]と計算できる。

ワンポイントアドバイス (検算)

時間に余裕があれば \( n = 0 \), \( n = 1 \) を入れて検算してみよう。

ちなみに、\[
A^0 = E = \left( \begin{array}{ccc} 1 & 0 \\ 0 & 1 \end{array} \right) \]\[
A^1 = A = \left( \begin{array}{ccc} -1 & -6 \\ 2 & 6 \end{array} \right)
\]です。

対角化を用いた行列のn乗の求め方

行列 \( A \) のべき乗 \( A^n \) を求める手順

Step1. 行列 \( A \) の固有値を求める

Step2. 固有値に対応する固有ベクトルを求め、正則行列 \( P \) を用いて \( P^{-1} AP = D \) を対角化する。

Step3. \( P^{-1} AP = D \) から \( A^n = P D^n P^{-1} \) を導く。

Step4. \( D^n \) と \( P \) の逆行列を求める。

Step5. あとは計算あるのみ

問題11. ジョルダン標準形

問題11

行列\[
A = \left( \begin{array}{ccc} 2 & -7 & 6 \\ 1 & -2 & 2 \\ 1 & -5 & 5 \end{array} \right)
\]を、正則行列 \( P \) を用いてジョルダン標準形 \( J = P^{-1} AP \) を求めなさい。

この分野に該当するうさぎ塾の記事はこちら ↓↓

Step1. 行列 \( A \) の固有値を求める

行列 \( A \) の固有値を \( t \) とする。

すると、固有値は\[\begin{align*}
|A - tE| & = \left| \begin{array}{ccc} 2-t & -7 & 6 \\ 1 & -2-t & 2 \\ 1 & -5 & 5-t \end{array} \right|
\\ & = \left| \begin{array}{ccc} 2-t & -7 & 6 \\ 1 & -2-t & 2 \\ 0 & -3+t & 3-t \end{array} \right|
\\ & = (3-t) \left| \begin{array}{ccc} 2-t & -7 & 6 \\ 1 & -2-t & 2 \\ 0 & -1 & 1 \end{array} \right|
\\ & = (3-t) \left| \begin{array}{ccc} 2-t & -1 & 0 \\ 1 & -t & 0 \\ 0 & -1 & 1 \end{array} \right|
\\ & = (3-t) \left| \begin{array}{ccc} 2-t & -1 \\ 1 & -t \end{array} \right|
\\ & = (3-t) \left\{ (2-t)(-t) - (-1) \right\}
\\ & = (3-t) \left\{ t(t-2) + 1 \right\}
\\ & = (3-t)(t^2 - 2t+1)
\\ & = (3-t)(t-1)^2 = 0
\end{align*}\]より、固有値は3, 1 (2重解となる)となる。

[検算] (固有値の総和) = (対角成分の和) = 5 を確認

Step2. 行列 \( A \) の広義固有ベクトルを求めていく。

(i) 固有値1について

連立方程式 \( (A-1E) \boldsymbol{p} = \boldsymbol{0} \) を解く

\[\begin{align*}
A - 1E & = \left( \begin{array}{ccc} 1 & -7 & 6 \\ 1 & -3 & 2 \\ 1 & -5 & 4 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & -7 & 6 \\ 0 & 4 & -4 \\ 0 & 2 & -2 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & -1 & 0 \\ 0 & 1 & -1 \\ 0 & 0 & 0 \end{array} \right)
\end{align*}\]

ここで、\( A - E \) の階数は2なので、連立方程式\[
\left\{ \begin{array}{l} x - y = 0 \\ y - z = 0 \end{array} \right.
\]の解の表現には任意定数が1つ必要。任意定数を \( k \) とすると、\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 1 \\ 1 \end{array} \right)
\]となる。

この解の \( k = 1 \) を固有ベクトル \( \boldsymbol{p}_1 \) とする。\[
\boldsymbol{p}_1 = \left( \begin{array}{ccc} 1 \\ 1 \\ 1 \end{array} \right)
\]

ここで、固有値1は2重解だが固有ベクトルが1つしかない。

そこで、連立方程式 \( (A - E) \boldsymbol{p}_2 = \boldsymbol{p}_1 \) を満たすようなベクトルを求める。

\[\begin{align*}
(A - 1E | \boldsymbol{p}_1) & = \left( \begin{array}{ccc|c} 1 & -7 & 6 & 1 \\ 1 & -3 & 2 & 1 \\ 1 & -5 & 4 & 1 \end{array} \right)
\\ & \to \left( \begin{array}{ccc|c} 1 & -7 & 6 & 1\\ 0 & 4 & -4 & 0 \\ 0 & 2 & -2 & 0 \end{array} \right)
\\ & \to \left( \begin{array}{ccc|c} 1 & -1 & 0 & 1 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 0 & 0 \end{array} \right)
\end{align*}\]となる。

連立方程式\[
\left\{ \begin{array}{l} x - y = 1 \\ y - z = 0 \end{array} \right.
\]を満たすような \( \boldsymbol{0} \) 以外かつ \( \boldsymbol{p}_1 \) と線形従属にならないような解として\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right)
\]がある。よって、\( \boldsymbol{p}_2 \) を\[
\boldsymbol{p}_2 = \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right)
\]とする。

(ii) 固有値3について

連立方程式 \( (A-3E) \boldsymbol{p} = \boldsymbol{0} \) を解く

\[\begin{align*}
A - 3E & = \left( \begin{array}{ccc} -1 & -7 & 6 \\ 1 & -5 & 2 \\ 1 & -5 & 2 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 0 & -12 & 8 \\ 1 & -5 & 2 \\ 0 & 0 & 0 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & -5 & 2 \\ 0 & -12 & 8 \\ 0 & 0 & 0 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & -5 & 2 \\ 0 & 3 & -2 \\ 0 & 0 & 0 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & -2 & 0 \\ 0 & 3 & -2 \\ 0 & 0 & 0 \end{array} \right)
\end{align*}\]

ここで、\( A - 3E \) の階数は2なので、連立方程式\[
\left\{ \begin{array}{l} x-2y=0 \\ 3y - 2z = 0 \end{array} \right.
\]の解の表現には任意定数が1つ必要。任意定数を \( k \) とすると、\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = k \left( \begin{array}{ccc} 4 \\ 2 \\ 3 \end{array} \right)
\]となる。

この解の \( k = 1 \) を固有ベクトル \( \boldsymbol{p}_1 \) とする。\[
\boldsymbol{p}_3 = \left( \begin{array}{ccc} 4 \\ 2 \\ 3 \end{array} \right)
\]

ここで、\( \boldsymbol{p}_1 \) は固有値1に属する固有ベクトル、\( \boldsymbol{p}_3 \) は固有値3に属する固有ベクトルなので、\[
\begin{array}{l} A \boldsymbol{p}_1 = \boldsymbol{p}_1 \\ A \boldsymbol{p}_3 = 3 \boldsymbol{p}_3 \end{array}
\]が成立する。

また、\( (A - E) \boldsymbol{p}_2 = \boldsymbol{p}_1 \) より、\[\begin{align*}
(A - E) \boldsymbol{p}_2 & = A \boldsymbol{p}_2 - E \boldsymbol{p}_2
\\ & = A \boldsymbol{p}_2 - \boldsymbol{p}_2 = \boldsymbol{p}_1
\end{align*}\]\[
A \boldsymbol{p}_2 = \boldsymbol{p}_1 + \boldsymbol{p}_2
\]の関係式も成り立つ。

よって、正則行列 \( P \) を\[\begin{align*}
P & = ( \boldsymbol{p}_1, \boldsymbol{p}_2, \boldsymbol{p}_3 )
\\ & = \left( \begin{array}{ccc} 1 & 1 & 4 \\ 1 & 0 & 2 \\ 1 & 0 & 3 \end{array} \right)
\end{align*}\]とすると、\[\begin{align*}
AP & = A ( \boldsymbol{p}_1, \boldsymbol{p}_2, \boldsymbol{p}_3 )
\\ & = (A \boldsymbol{p}_1, A \boldsymbol{p}_2, A \boldsymbol{p}_3 )
\\ & = (\boldsymbol{p}_1, \boldsymbol{p}_1 + \boldsymbol{p}_2, 3 \boldsymbol{p}_3 )
\\ & = ( \boldsymbol{p}_1, \boldsymbol{p}_2, \boldsymbol{p}_3 ) \left( \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 3 \end{array} \right)
\\ & = P \left( \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 3 \end{array} \right)
\end{align*}\]となる。

ここで、\[
J = \left( \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 3 \end{array} \right)
\]とすると、\( AP = PJ \) となり、両辺の左から \( P^{-1} \) を掛けると、\[\begin{align*}
P^{-1} AP = J = \left( \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 3 \end{array} \right)
\end{align*}\]となり、ジョルダン標準形が求められた。

ワンポイントアドバイス (検算)

\[
AP = PJ = \left( \begin{array}{ccc} 1 & 2 & 12 \\ 1 & 1 & 6 \\ 1 & 1 & 9 \end{array} \right)
\]

注釈[+]

注釈
↑1	\( \boldsymbol{a}_1, \boldsymbol{a}_2, \cdots, \boldsymbol{a}_n \) から選べる線形独立（1次独立）なベクトルの最大組。
↑2	前編では \( \lambda \) とおいていたのですが、\( \lambda \) の入力が少しめんどくさいので \( t \) とおかせてください。
↑3	固有空間でいうと、\[ \dim V(t_1) + \dim V(t_2) + \dim V(t_3) = 3 \]を満たしていれば対角化OK
↑4	直交行列の場合、\( P^{-1} = {}^t P \) が成立するため、\( P^{-1} AP \) を \( {}^t PAP \) と表記することもあります。
↑5	\( A \) は実対象行列なので異なる固有値に対する固有ベクトルは、大きさが1であれば必ず直交します。
↑6	異なる固有値に対する固有ベクトルは、正規化さえしていれば勝手に正規直交基底になるので、固有値が重解でなければ正規化だけをすればOK。