スポンサードリンク
こんにちは、ももやまです。
前回は決定性オートマトン(DFA)について説明しました。
今回は決定性ではないオートマトン、非決定性オートマトン(NFA)についてまとめていきたいと思います。
前回の決定性オートマトン(第01羽)についての記事はこちらから!
目次
スポンサードリンク
1.非決定性オートマトン(NFA)と決定性オートマトン(DFA)の2つの違い
非決定性オートマトンは、決定性オートマトンと違う点を2つ持っています。
その1 状態遷移が1本道でなくてもOK
決定性オートマトンは、状態遷移図のたどり方が必ず1本道でしたね。
一方、非決定性オートマトンでは、状態遷移図のたどり方が1本道ではなくてもOKです!
その2 初期状態が2つ以上あってもOK
前回の決定性オートマトンの説明で、初期状態(スタート地点)は必ず1つと説明しましたね。
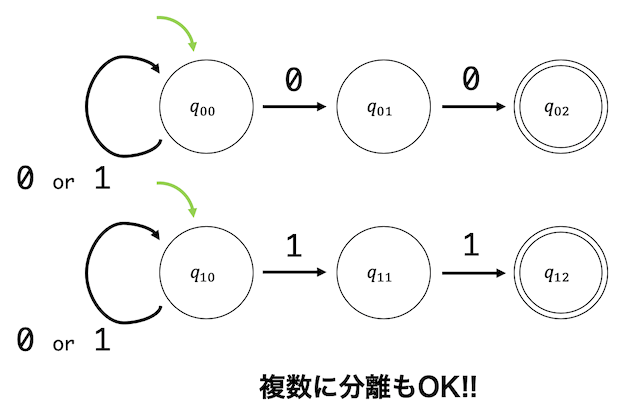
一方、非決定性オートマトンでは、初期状態が2つ以上設定することもOKです!
なので、このように状態遷移図を2つに分けることもできます!
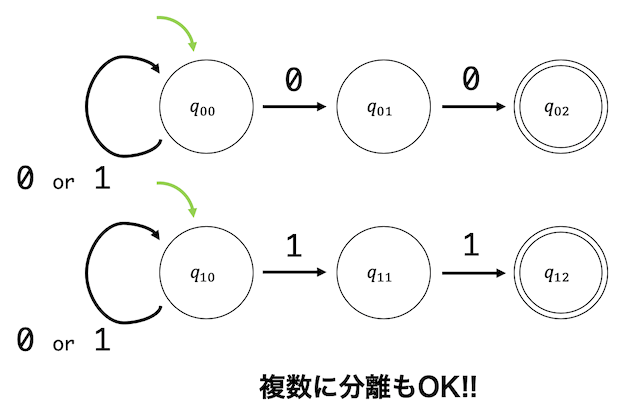
以上の2つの違いから、非決定性オートマトンは決定性オートマトンに比べてより直感的なオートマトンの記述が可能です!
スポンサードリンク
2.非決定性オートマトンを書いてみよう
では、非決定性オートマトンを書く練習をすることで、より直感的にオートマトンを記述できることを体感してもらいましょう。
例題1
つぎの(1), (2)の条件を満たすような文字列を受理するような非決定性オートマトンの状態遷移図を書きなさい。
(1) 00で始まる文字列を受理するもの。
(2) 2文字以上の文字列で、文字列の始点と終点が異なるような文字列を受理するもの。
(受理例:00111→始点は0、終点は1なので受理 1000→始点は1、終点は0なので受理)
(非受理例:1→2文字以上ないため拒否 01010→始点が0、終点が0なので拒否)
解説1
(1)
00で始まる文字列ということは、最初の2文字が0,0であれば残りはどんな文字であっても受理するようなオートマトンとなる。
つまり、
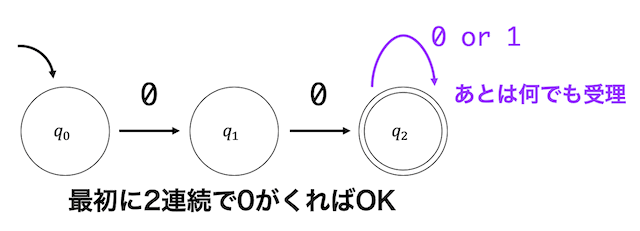
となる。
(2)
文字列の始点と終点が異なるようなものを受理するためには、0で始まって1で終わるも文字列もしくは1で始まって0で終わる文字列を受理させればよい。
つまり、「0で始まって1で終わるものを受理する非決定性オートマトン」と「1で始まって0で終わるものを受理する非決定性オートマトン」を2つセットで書けばよい。
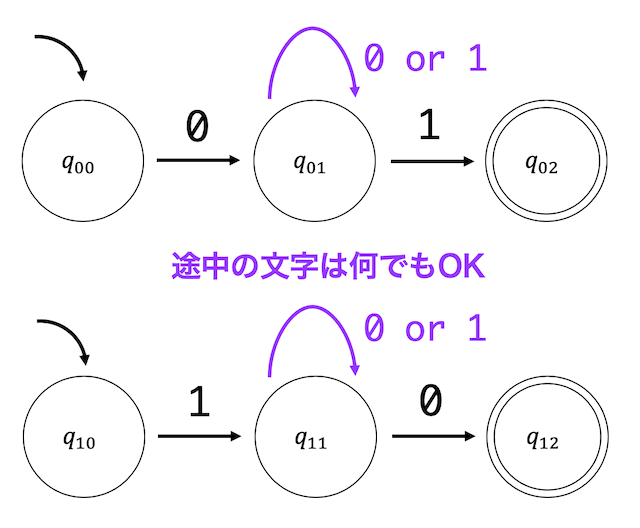
と書ける。
もちろん1つにまとめて
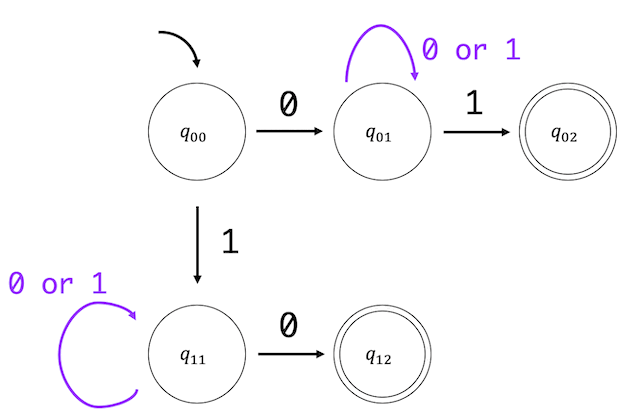
と書いてもOK。
スポンサードリンク
3.非決定性オートマトンの状態遷移表
決定性オートマトンと異なり、非決定性オートマトンの場合は遷移先が2つ以上になったり、1つもないことがあります。そのため、状態遷移を把握するのが決定性に比べて少しめんどくさいです。
そのため、状態遷移表を書くことで状態遷移を把握しやすくします。
では、非決定性オートマトンの状態遷移表の書き方について例題を2つほど踏まえながら説明していきましょう。
例題2
つぎの(1), (2)の状態遷移図で表される非決定性オートマトンの状態遷移表を書きなさい。
(1)
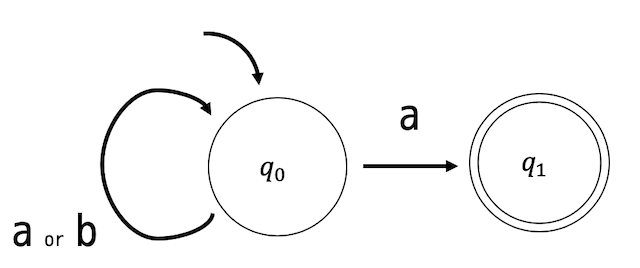
(2)
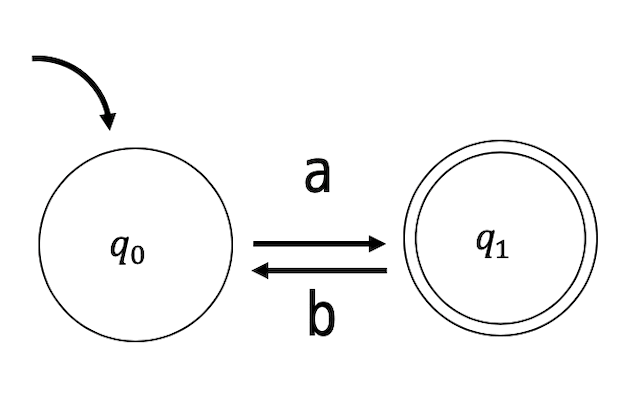
解説2
(1)
初期状態は \( q_0 \) ですね。
まずは、初期状態から遷移可能な場所を \( a \) のとき、 \( b \) のときに場合分けして考えましょう。
\( a \) のとき:\( q_0 \), \( q_1 \) の2箇所に遷移可能
\( b \) のとき:\( q_0 \) に遷移可能
\( a \), \( b \) それぞれの動き(遷移可能場所)がわかったので \( q_0 \) のときの動きを状態遷移図に記録します。
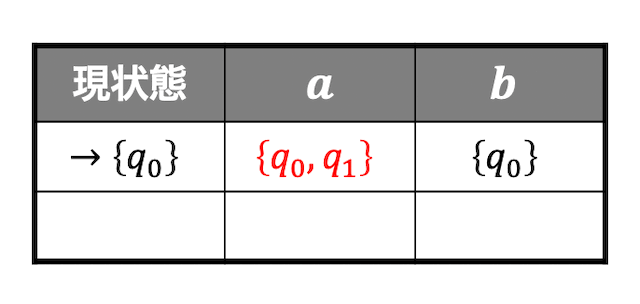
ここで新たに生成された \( q_0 \) と \( q_1 \) の2状態が含まれた状態 \( \{ q_0,q_1 \} \) について考えましょう。
\( \{q_0, q_1\} \) には、受理状態である \( q_1 \) が含まれていますね。このように、複数状態含まれた中に1状態でも受理状態が含まれる場合、複数状態をもつ状態も受理状態となります。
なので、\( \{q_0, q_1\} \) も受理状態となります。赤色などの別の色に着色するか、○印などの記号をつけておきましょう。
今度は状態 \( \{ q_0,q_1 \} \) が遷移できる場所を \( a \) のとき \( b \) のときで場合分けしましょう。
複数状態の場合、それぞれの状態から遷移可能なすべての状態を考えます。
\( a \) のとき:\( q_0 \) からは\( q_0 \), \( q_1 \) の2箇所に遷移可能、\( q_1 \) からはどこも遷移できない。よって \( q_0 \) ,\( q_1 \) の2箇所に遷移可能。
\( b \) のとき:\( q_0 \) からは \( q_0 \) に遷移可能。\( q_1 \) からはどこも遷移できない。よって \( q_0 \) から遷移可能。
\( a \), \( b \) のときの遷移先がわかったので \( \{ q_0,q_1 \} \) のときの動きを状態遷移図に記録します。
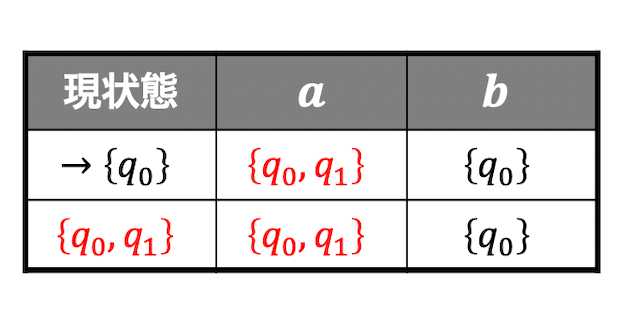
これですべての状態を調べおわりましたね。状態遷移表の完成です!
今回は2状態でしたが、実際は未知の状態が出てこなくなるまで調べる必要があるため、かなりの状態数となってしまうこともあります。
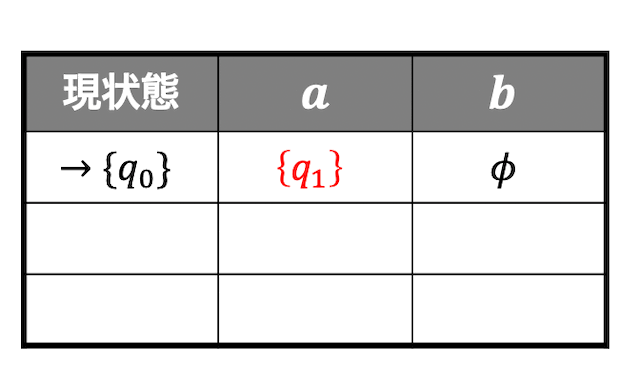
(2)

初期状態は \( q_0 \) ですね。
(1)と同じように初期状態から遷移可能な場所を \( a \) のとき、 \( b \) のときに場合分けして考えましょう。
\( a \) のとき:\( q_1 \) に遷移可能
\( b \) のとき:どこにも遷移できない
\( b \) のときの遷移先がないため、空の状態 \( \phi \) となります。、空状態も1つの状態として考えてください。
ここで、\( q_1 \) と \( \phi \) という未知の遷移が2つ出てきましたね。
この2つの遷移先を調べてみましょう。
\( q_1 \) の遷移先
\( a \) のとき:どこにも遷移できない
\( b \) のとき:\( q_0 \) に遷移可能
こちらも \( a \) のときはどこにも遷移できず、空状態 \( \phi \) となってしまいます。
\( q_1 \) の状態遷移を表に記録すると、

となります。
最後に空状態ですが、空状態にどんな文字を入れてもどの状態にもいけません。なので、空状態 \( \phi \) からは \( a \), \( b \) どちらの文字を入れても空状態 \( \phi \) となります。よって、
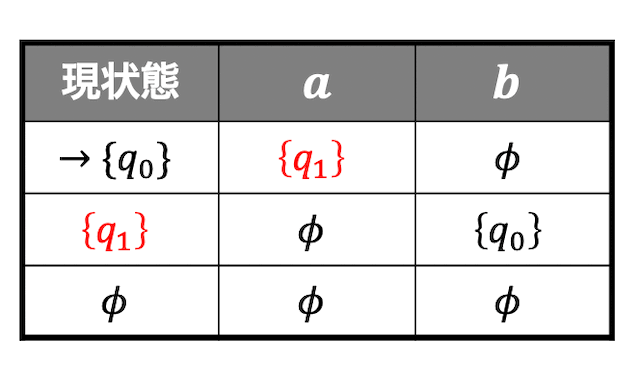
となります。
このように複数先の遷移をする状態やどこにも遷移しない空の状態も1つの状態として考えることにより、それぞれの状態と文字による遷移先を明確に表すことができます。
4.非決定性オートマトン(NFA)から決定性オートマトン(DFA)の変換
先ほど非決定性オートマトンを状態遷移表にする練習をしましたね。
実は、状態遷移表にすることで、それぞれの状態と次の文字に対する遷移先が1つに表すことができます。
すべての非決定性オートマトンで状態遷移表を書くことができるので、非決定性オートマトンで表すことができるオートマトンは、決定性オートマトンでも表すことができます!*1
例題2(1)の非決定性オートマトンを思い出して見ましょう。

この非決定性オートマトンを状態遷移表にし、変数名を簡単にする*2と……
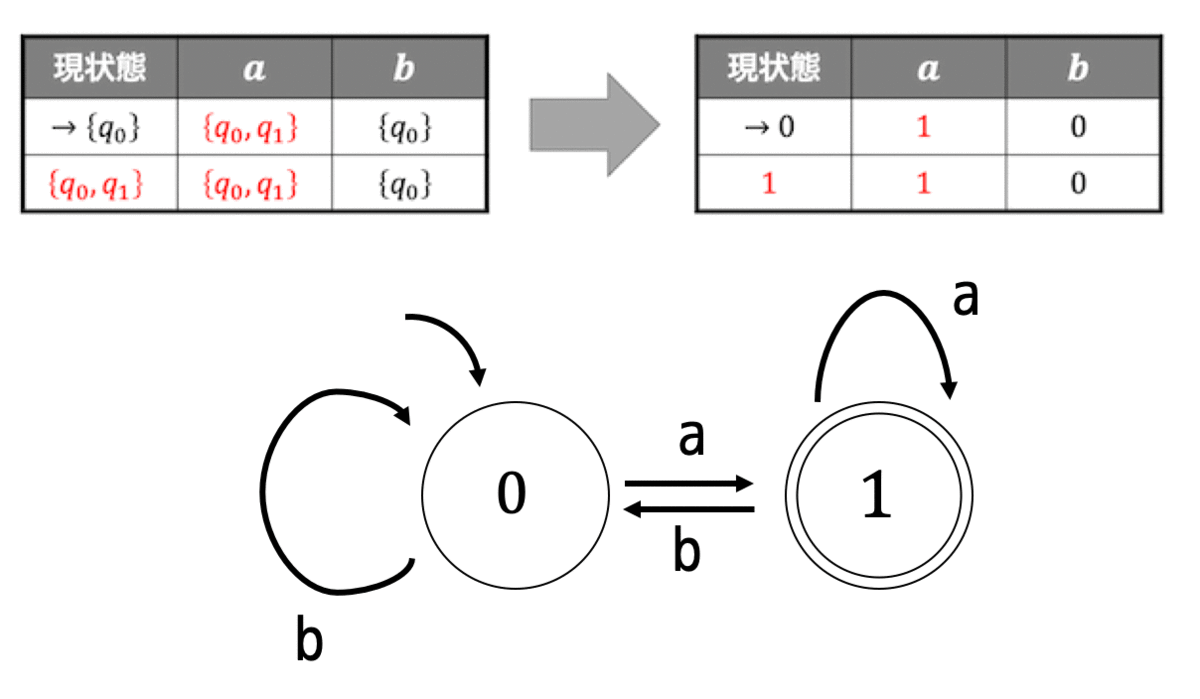
[2021/04/20 訂正]
状態遷移図の遷移先(矢印)が誤ったものになっていたため、訂正を行いました。申し訳ございません。
このように、決定性オートマトンに変換することができます!
(状態遷移表→状態遷移図は表を見ながらミスせずに矢印を書くだけなので解説省略します。)
例題2(2)の非決定性オートマトンも……
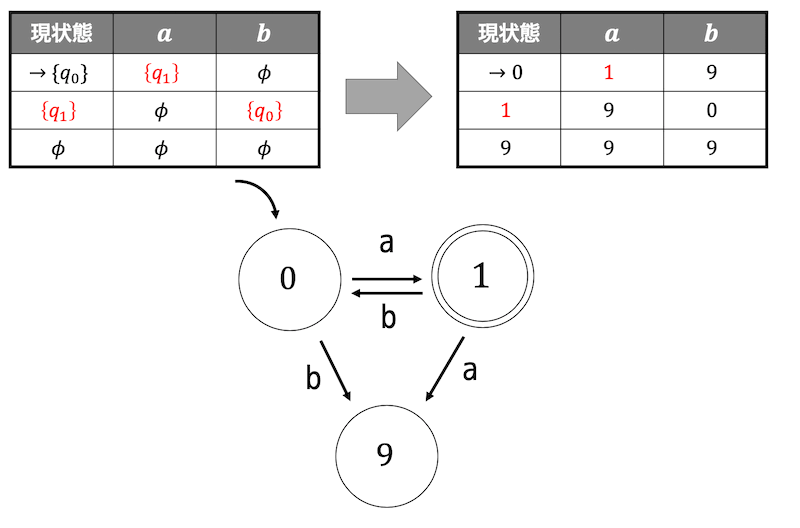
このように非決定性の状態遷移表を記述することで簡単に決定性オートマトンに変換することができます!
※ 空状態 \( \phi \) は現状態からどこにもいけないようなときのみ使用することをおすすめします。
例えば現状態が \( \{ 1,2 \} \) で状態1からは3に遷移できるけど状態2からはどこにも遷移できないとき、\( \{ 3, \phi \} \) ではなく \( \{3 \} \) としましょう。(状態数が増えてしまうので…)
5.練習問題
では、少しだけですが練習をしてみましょう。
練習1
\( \Sigma = \{a,b\} \) とする。
\( a \) が1文字以上続いたあとに \( b \) が1文字以上続くような文字列を受理するような言語 \( L \) 、\[
L = \left\{ a^i b^j \ \middle| \ i \geqq 1, j \geqq 1 \right\}
\]について次の(1), (2)の問いに答えなさい。
(1) \( L \) を受理する非決定性オートマトンを求めなさい。
(2) (1)の状態遷移表を書くことにより、\( L \) を受理する決定性オートマトンを求めなさい。
練習2
\( \Sigma = \{0,1\} \) とする。
つぎの(1), (2)で表されている非決定性オートマトンを決定性オートマトンに直しなさい。
(1)
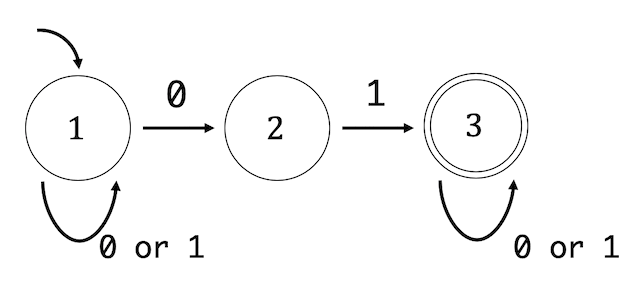
(2)
6.練習問題の答え
解答1
(1)
\( a \) が1回続いてから、\( b \) が1回以上続くような非決定性オートマトンは、下のように書ける。
(最初に \( b \) が来たり、abbbabのように \( b \) のあとに \( a \) が来るような文字列は受理しないことに注意)
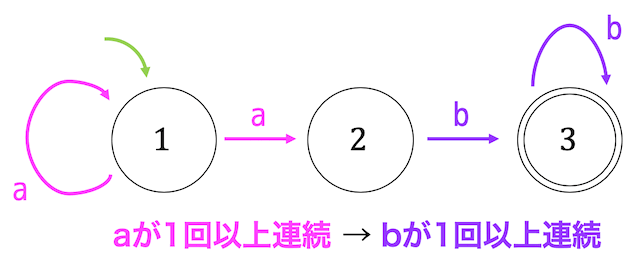
(2)
(1)で書いたオートマトンの状態遷移表を書き、変数名を簡単にする。受理状態が3、初期状態が1であることを忘れずに。
(現状態にかかれている2桁の数、12は状態1、状態2が両方含まれる状態を指す。カッコを書くのがめんどくさいため、省略した。また、状態9は空の状態、Dead state、あり地獄を表す。)
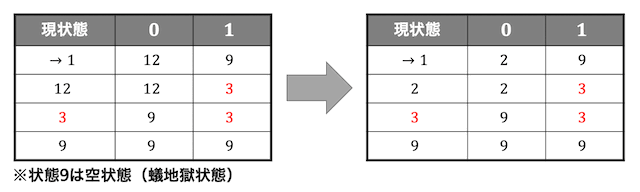
あとは作成した状態遷移表をもとに状態遷移図を書けばよい。
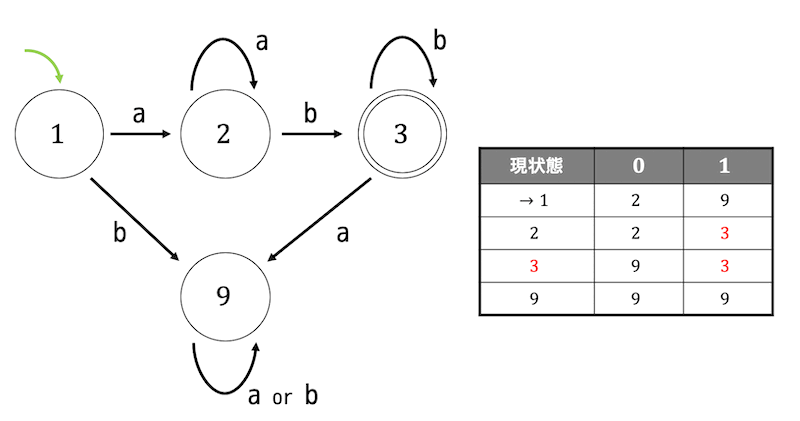
となる。
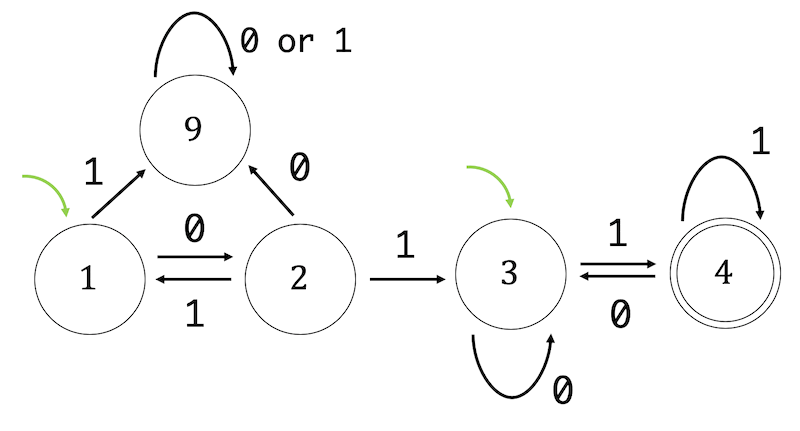
解答2
(1)
下のように状態遷移表を書いてから状態遷移図に変形すればいい。
(図の12は状態1と状態2が両方含まれる状態、123は状態1、状態2、状態3がすべて含まれる状態を表す。)
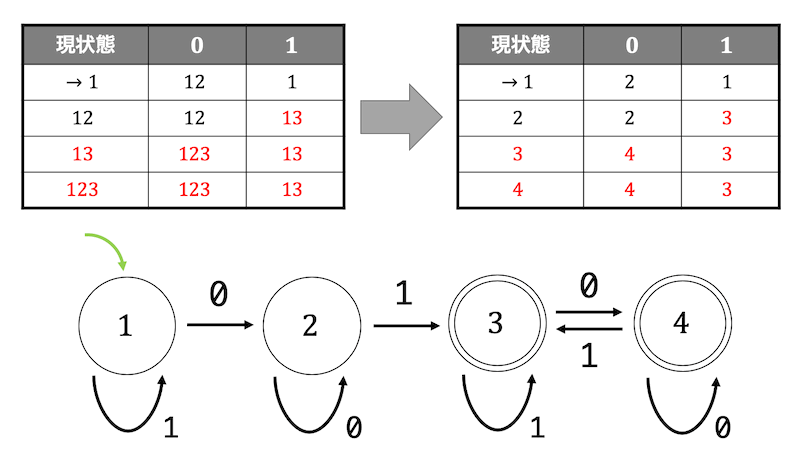
実は、状態3と状態4はとある方法を使うと1つにまとめることもできますが、まとめる方法はまた別の機会に紹介します。
(2)
状態が増えてきたら、それぞれの状態から各文字における遷移先を下のようにメモしておくとミスが減らせるかもしれません。
1 → 0: 2 1: 9
2 → 0: 9 1: 13
3 → 0: 3 1: 4
4 → 0: 3 1: 4
9 → 0: 9 1: 9
初期値が2つあることに注意してください。
(1)と同じように2桁以上の数字で表された状態は、複数の状態を表しています。)
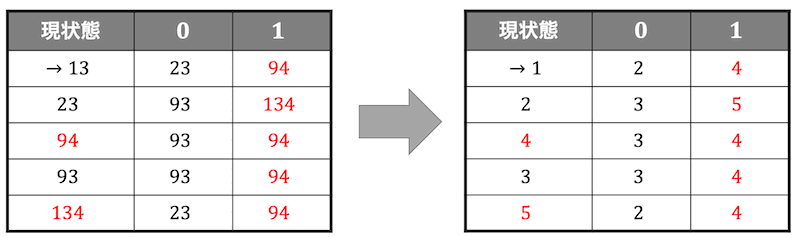
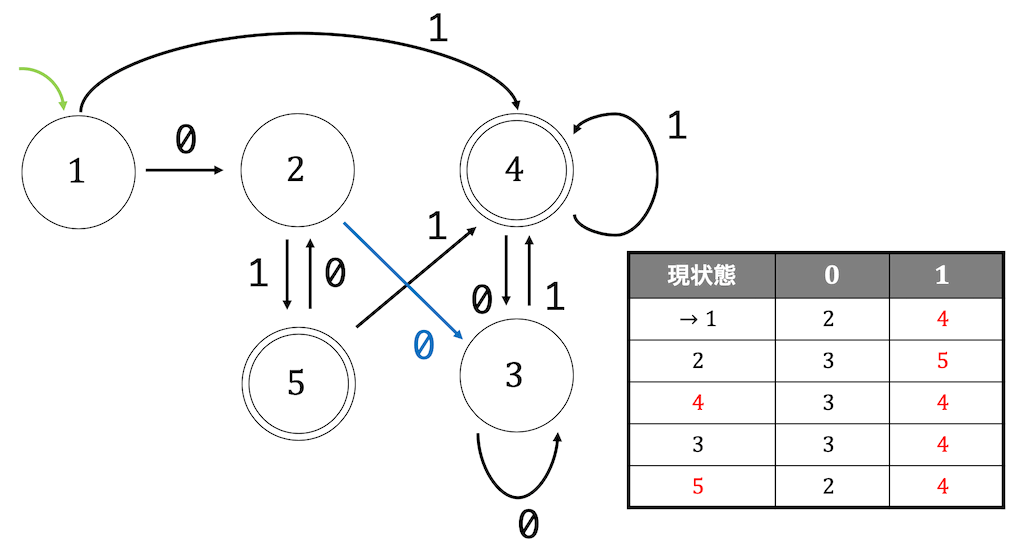
状態遷移表より、状態遷移図は以下のようになる。
(色はわかりやすくするためにつけているだけです)
7.さいごに
今回は、非決定性オートマトン(NFA)の書き方、非決定性オートマトン(NFA)を決定性オートマトン(DFA)に変換する方法についてまとめました。
非決定性オートマトンで表すことのできるものは必ず決定性オートマトンに直すことができるので、決定性オートマトンが書くのが難しいなと思った人は、最初に直感的に書きやすい非決定性オートマトンを求めてから決定性オートマトンに変換するのをおすすめします。
Next「第03羽」はこちら!↓
関連広告・スポンサードリンク