スポンサードリンク
こんにちは、ももやまです。
今回からオートマトンについてのまとめも少しずつしていこうと思います。
※注意
わかりやすく噛み砕いて説明しているため、厳密な定義と若干異なることを書いている可能性があります。ご了承ください。
目次
スポンサードリンク
1.決定性オートマトンの状態遷移図はすごろくや!
決定性オートマトンと言われると皆さん少し難しいなと思ってしまうかもしれません。
なので、今回はすごろくでオートマトンを例えることにしましょう!
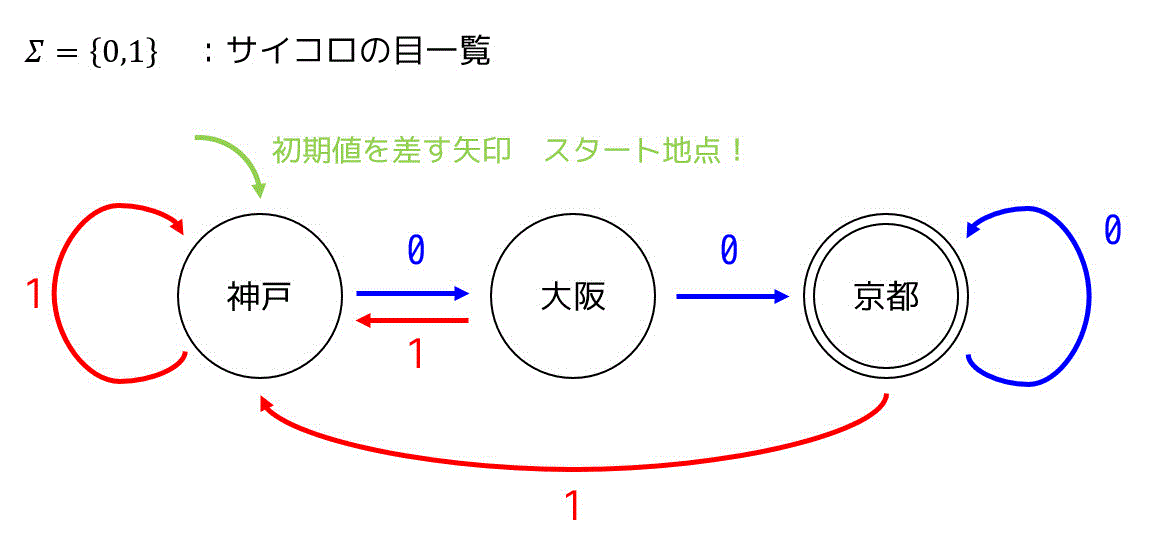
例えばこんなすごろくのマップがあるとします。
(オートマトンの世界ではこれを状態遷移図と呼びます。)
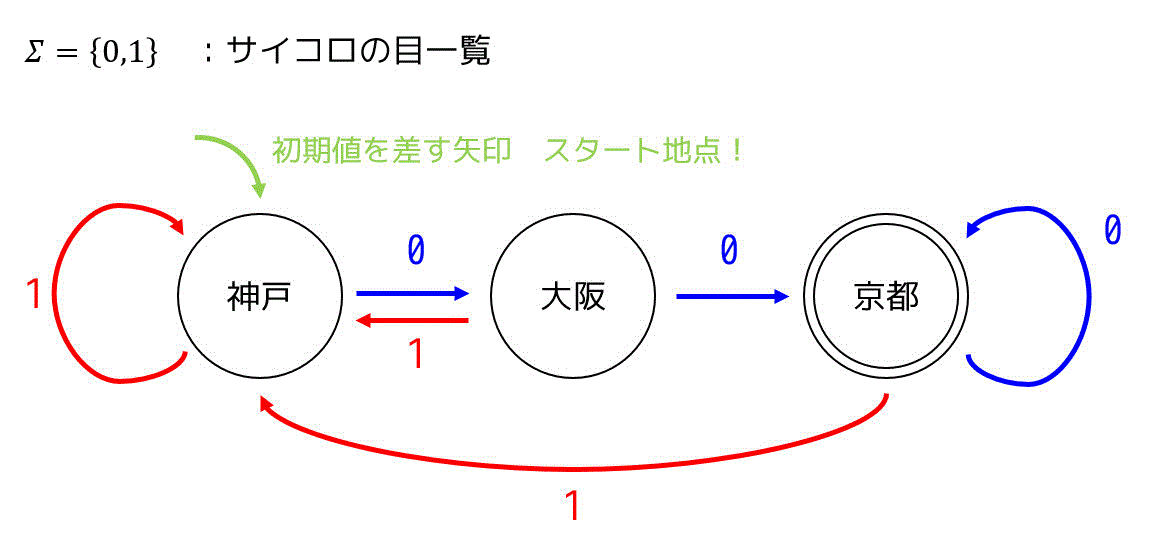
まず最初に \( \Sigma \) という謎の記号がありますね。これは、このすごろくで使うサイコロの出目の種類の一覧を表しています。今回は {0,1} なので、0の目と1の目だけが書かれているサイコロを使います。
(実際のオートマトンでは出目ではなく、入力された文字列の受理非受理を判定できる文字の種類を表しています。)
次に、このマップには◎で書かれたマス(京都)と○で書かれたマス(大阪・神戸)がありますね。◎のマスはゴールのマスを表し、○のマスはゴール以外のマスを表します。
(実際のオートマトンではこのマスのことを状態と呼びます。)
また、神戸に数字がかかれていない緑色の矢印がついていますね。これはスタート地点を表します。
つまり、このすごろくのスタート地点は神戸、ゴール地点は京都にあるものだと思ってください。
(実際のオートマトンでもスタート地点はスタート地点ですが、初期状態と正式には呼びます。)
さらにマスからは0の矢印、1の矢印の2つの矢印が出ていますね。これは、出目が0だったときの行き先、出目が1だったときの行き先を表しています。
例えば、「神戸」にいるときに1を出すと「大阪」、「大阪」にいるときに1を出すと「神戸」に戻ります。
(実際のオートマトンでは、行き先のことを遷移先と呼びます。)
では、少しだけこの(オートマトンちっくな)すごろくを読む練習をしてみましょう。
例題0(オートマトンわかっている人は飛ばしてOKです)
つぎのようなすごろく(上の例と同じ)があるとする。(1),(2)の問いに答えなさい。
※1回ゴールした後もサイコロを降ることができるが、最終的にゴール地点にいないとゴールしたことにはならないため注意すること

(1) つぎのすごろくで、Aさんの出目が「1→0→1→0→0」、Bさんの出目が「0→0→1→0→1」だったとき、2人はそれぞれのどのようにマスを動くかを考えましょう。また、2人はゴールしているかしていないかも判定しなさい。
(2) このすごろくでゴールするためにはどのような出目が出ればいいかを自由に考えてみましょう。
解説0
(1)
スタート地点は2人とも「神戸」
Aさん
1ターン目:出目1:神戸→神戸
2ターン目:出目0:神戸→大阪
3ターン目:出目1:大阪→神戸
4ターン目:出目0:神戸→大阪
5ターン目:出目0:大阪→京都
よって最終的にゴール地点「京都」にいるため、ゴールしている。
Bさん
1ターン目:出目0:神戸→大阪
2ターン目:出目0:大阪→京都
(ゴール地点だがなぜかBさんはサイコロを振り続ける)
3ターン目:出目1:京都→神戸
4ターン目:出目0:神戸→大阪
5ターン目:出目1:大阪→神戸
よって最終的にゴール地点「京都」にはいないため、ゴールしてない。
(2)
すごろくのマップをよく見てみましょう。
0が出た場合は、神戸→大阪、大阪→京都とすすめるのですが、1が出た場合、強制的に神戸に戻されますね。
つまり、このすごろくは「2連続で出目0を出す」のがゴールの条件となります。
スポンサードリンク
2.決定性オートマトンを読んでみよう
(有限)オートマトンとは、文字列を識別する機械です。与えられた文字列が条件に一致する(受理する)かしないか(受理しない、拒否する)を判定します。
今回はオートマトンの一部である決定性オートマトン(Deterministic Finite Automaton, DFA)の説明をしていきましょう!
(以後オートマトンはこの記事においては決定性オートマトンのことを表すと思ってOKです)
(1) 決定性オートマトンに必要な5つの要素
決定性オートマトンは、下で説明する5つの要素で構成されています。5つの要素を式で表現することもできますがかなりわかりにくいので実際に決定性オートマトンを表現する際には下のような図で表現することが多いです。
(問題も図で与えられていることがほとんどです。)
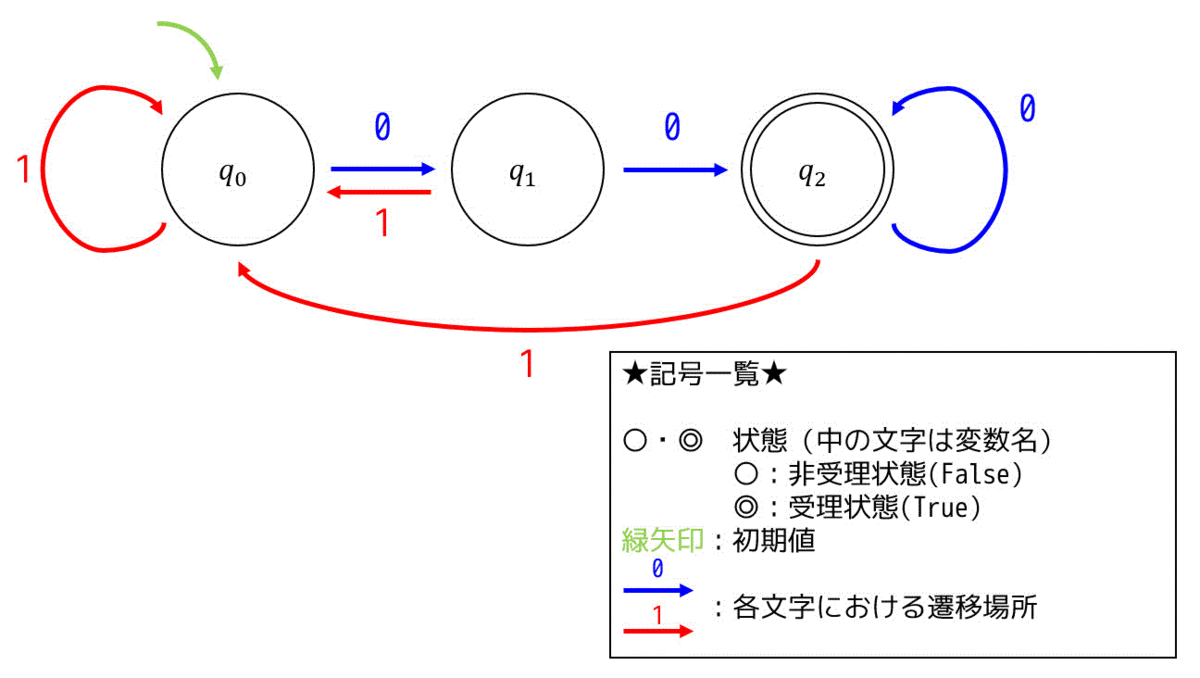
この図は、さきほど説明したすごろくとほぼ同じ(名前以外一緒)状態遷移図となっています。
では、決定性オートマトンに必要な5つの要素を状態遷移図の説明をしながら書いていこうと思います。
状態(State) \( Q \)
すごろくでいうマス目と同じです。○、◎の中に書かれているのは変数名で、作成者は自由に名前をつけてあげることができます。
○が非受理状態(False)を表し、◎が受理状態(True)を表します。
(受理状態と非受理状態の数に制限はないので、受理状態が2つ以上になったり受理状態がなくてもOKです。return 文を複数箇所に書いてもOKみたいなもんですね。)
入力記号 \( \Sigma \)
オートマトンが入力、受理状態(True/False)かどうかを判定できる記号を表しています。
例えば、\( \Sigma = \{0,1 \} \) だと、0,1で構成される文字列、\( \Sigma = \{a,b\} \) だとa,bで構成される文字列の受理非受理の判定ができます。
先程のすごろくでいうと、サイコロの出目の種類となります。
遷移先
現在の状態とつぎの文字によって遷移先を表す関数です。
下でも紹介しますが、決定性オートマトンの場合、現在の状態とつぎの文字における遷移先は必ず1通りとなります。
遷移先の書き方としては、\[
\delta(現在の状態,つぎの文字) = つぎの状態 \\
\delta(q_0, 0) = q_0 , \ \ \delta(q_0,1) = q_1
\]のように書いていきます。
しかし、いちいち関数を記述するのは面倒くさいため、図や表(後ほど説明します)を使って遷移先を表します。
表(状態遷移表)の場合、それぞれの状態(マス目)から、0の矢印、1の矢印が出ています。これは、それぞれ文字が0のときの移動先、文字が1のときの移動先を表しています。
すごろくで表現すると、それぞれのマスとつぎの出目における移動先を表すものとなります。
初期状態(初期値) \( q_0 \)
文字列を読み始めたときの初期状態を表します。
下にある状態遷移図の場合、\( q_0 \) の部分に数字が書かれていない矢印がありますね。
これを初期値と呼ばれます。すごろくでいうスタート地点だと思ってください。
(当然ですが初期値は1つのみです)
最終状態 \( F \)
文字列を読み終わったときに止まると受理される箇所を表しています。
状態遷移図の場合、◎で表されます。
先程説明しましたが、最終状態は必ず1つである必要はなく、2つ以上あっても、あるいは1つもなくてもOKなことに注意してください(大事なことなので2回言いましたよ~)。
この5つを用いると、オートマトンを表現することができます。この5つをまとめて、オートマトン \( M \) を\[
M = ( Q, \Sigma, \delta,q_0, F)
\]と書くことができます。
しかし、上のような式だとわかりにくいので実際には図を使ったり表を使うことでオートマトンを視覚的にわかりやすく表現します。
オートマトンを図で表したものを状態遷移図、表で表したものを状態遷移表と呼びます。
(2) 状態遷移図の読み方
では、実際に1つ状態遷移図を見てみましょう。
(色はわかりやすくするためにつけているので実際にはついていません。)

上の状態遷移図を例にして、1つ文字が受理されるかの判定をしてみましょう!
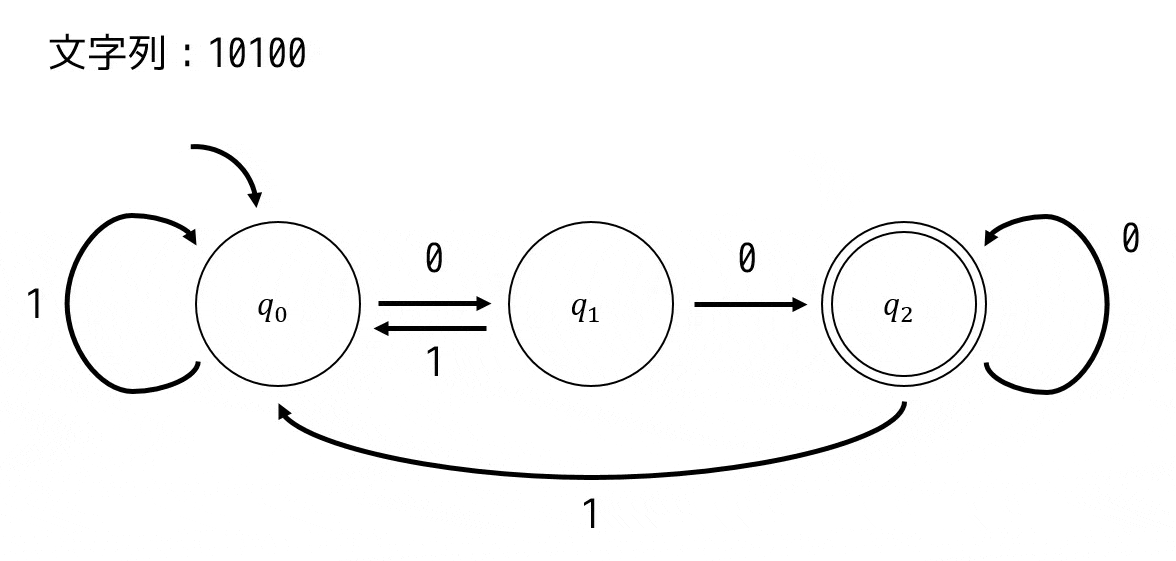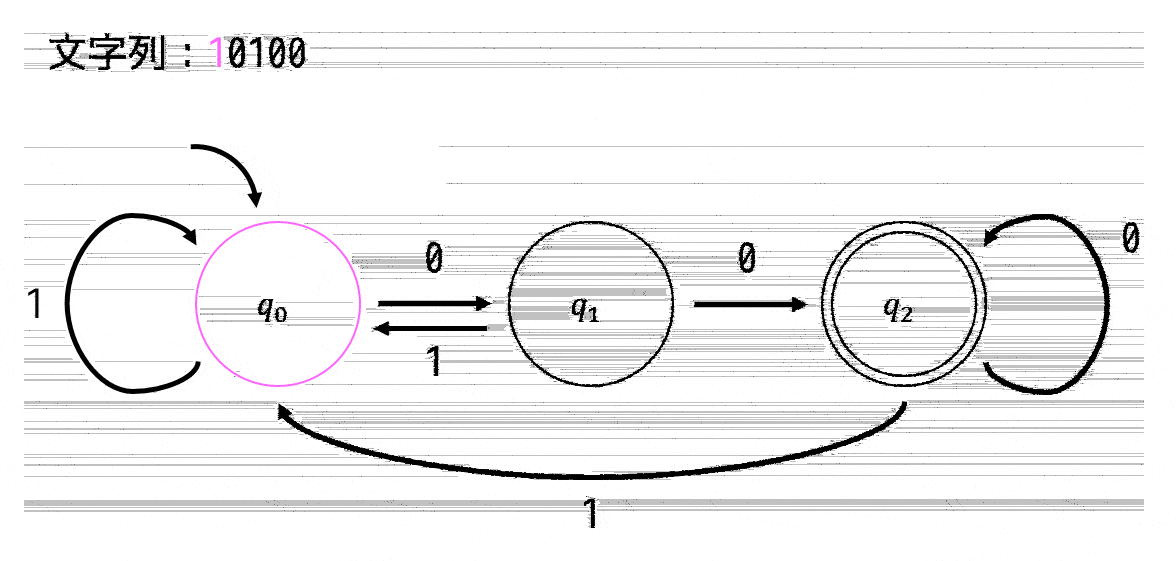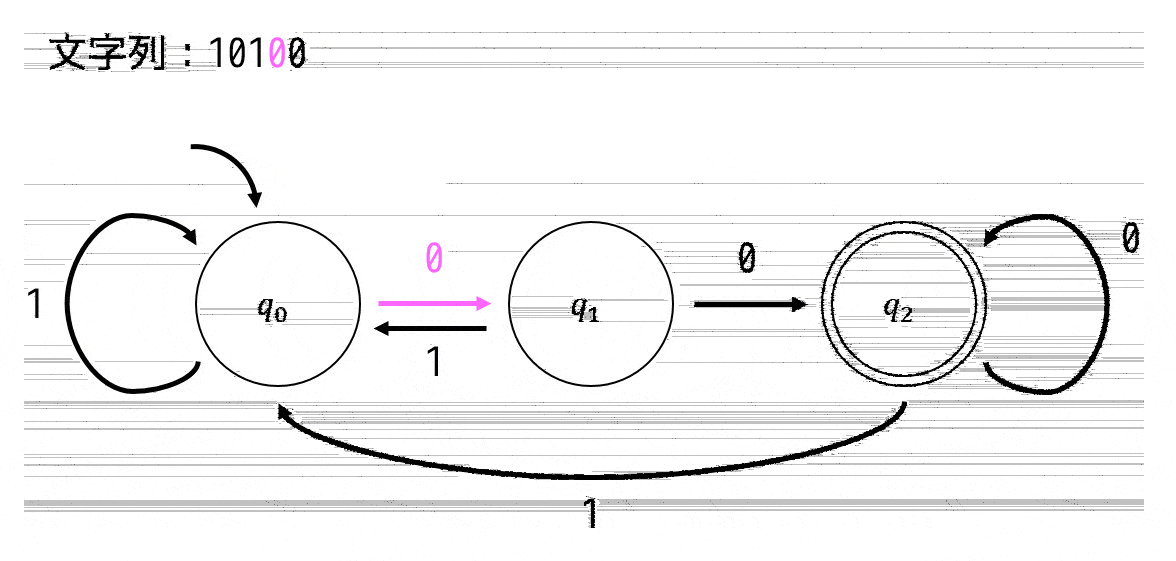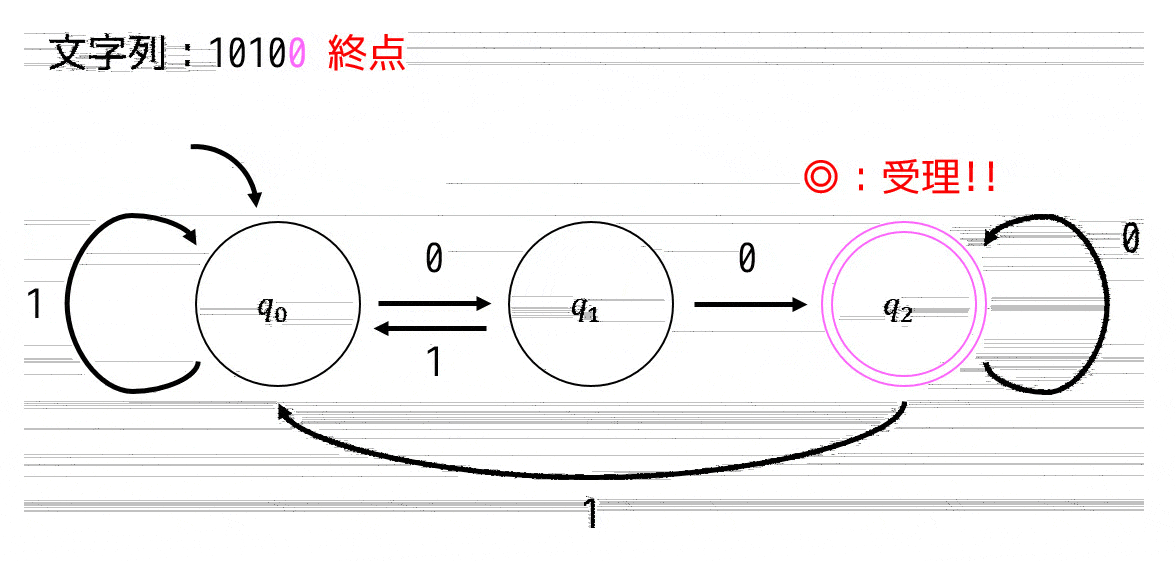
例として、文字列:10100 が入力された場合の状態遷移図のたどり方を説明します。
まず、初期値の矢印が \( q_0 \) にあるため、スタート地点は \( q_0 \) となります。
つぎに、1文字ずつ順番に文字に沿って状態遷移図をたどっていきます。
1文字目:1 \( q_0 \to q_0 \)
2文字目:0 \( q_0 \to q_1 \)
3文字目:1 \( q_1 \to q_0 \)
4文字目:0 \( q_0 \to q_1 \)
5文字目:0 \( q_1 \to q_2 \)
とたどっていけますね。最後の文字をたどったときに \( q_2 \) となっているので10100は受理されることがわかりますね。
(◎である \( q_2 \) にいれば受理、そうでなければ受理しない)
10100が受理されるかどうかの判定の様子をアニメーションでも表現してみました。
もう1つ状態遷移図をたどる練習をしてみましょう。
「文字列:00101」が受理されるかを状態遷移図をたどることで判定してみましょう。
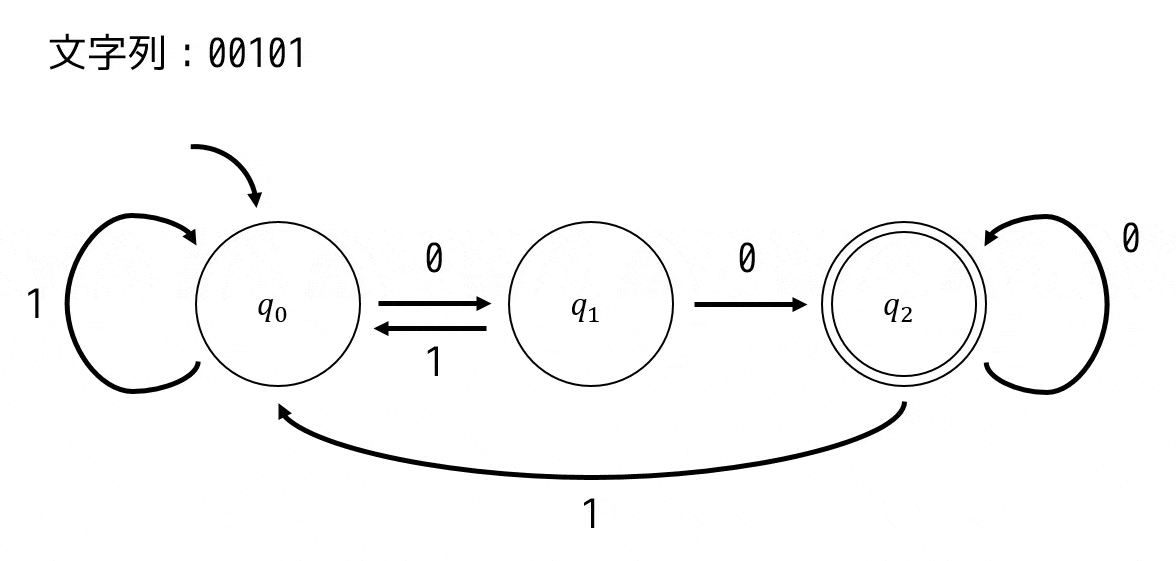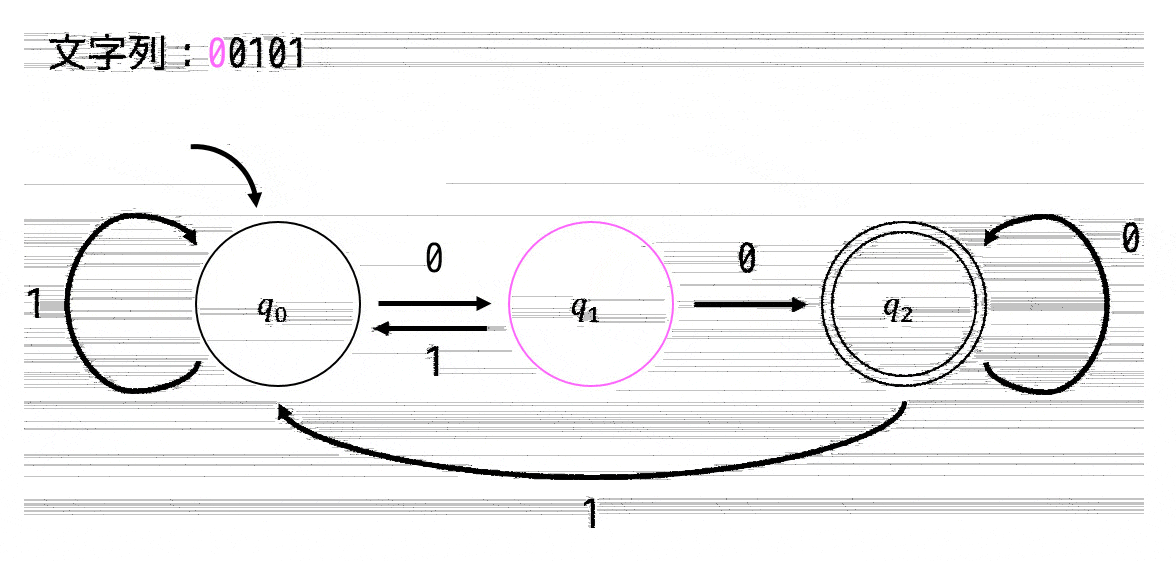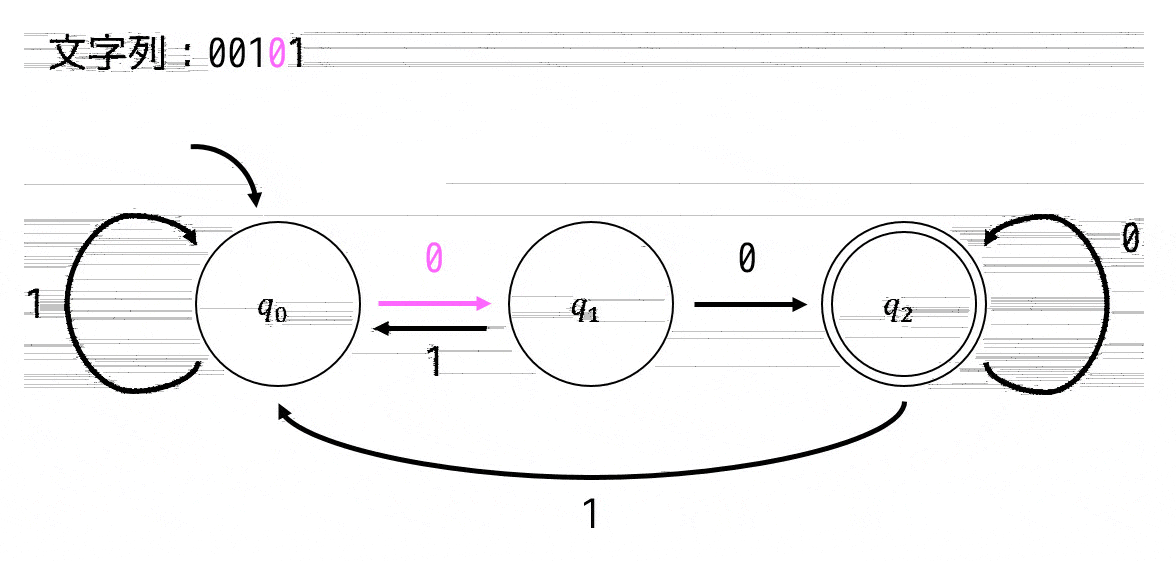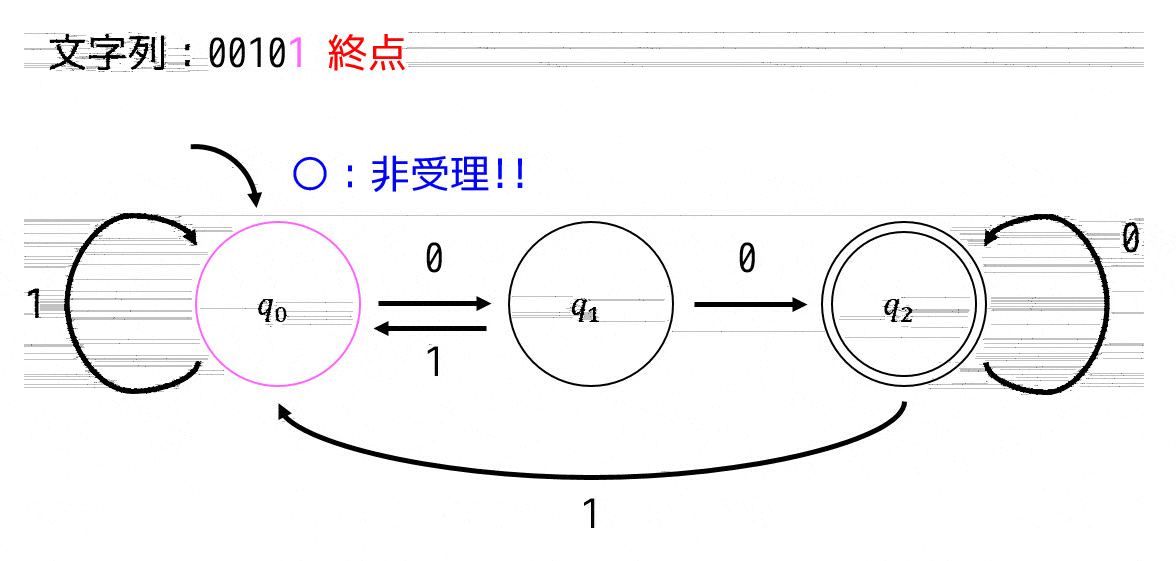
この場合は、\[
q_0 \xrightarrow{0} q_1 \xrightarrow{0} q_2 \xrightarrow{1} q_0 \xrightarrow{0} q_1 \xrightarrow{1} q_0
\]とたどれます。最後の文字をたどったときに \( q_0 \) となっているので受理しないことがわかります。
(3) 状態遷移表の読み方
それぞれの状態において、どの文字が入力されたらどの状態に移動するかを表で表す書き方もあります。上の状態遷移図で表されるオートマトンを状態遷移図にすると、以下のようになります。
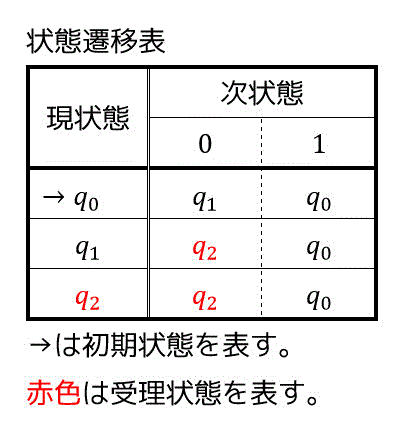
例えば、\( q_1 \) のときに0が来ると \( q_2 \) へ、1が来ると \( q_0 \) になることが表からすぐに読み取れますね。
受理状態は赤色にしたり○をつけたりしておくとわかりやすいのでおすすめです。
スポンサードリンク
3.決定性オートマトン(DFA)と非決定性オートマトン(NFA)の違い
有限オートマトンには、決定性オートマトン(Deterministic Finite Automaton, DFA)と非決定性オートマトン(Nondeterministic Finite Automaton)の2つがあります。
この2つの違いは、状態遷移図のたどり方が1本道かどうかということです。
たどり方が1本道かどうかというのを言い換えると、それぞれの状態と入力される文字によってつぎに遷移される状態は一意に決まるか、といえます。
先ほど出てきたこの状態遷移図で表されるオートマトンは、\( q_0 \), \( q_1 \), \( q_2 \) どこをみても0のときの遷移先(矢印)、1のときの遷移先が1本ずつ書かれていますね。
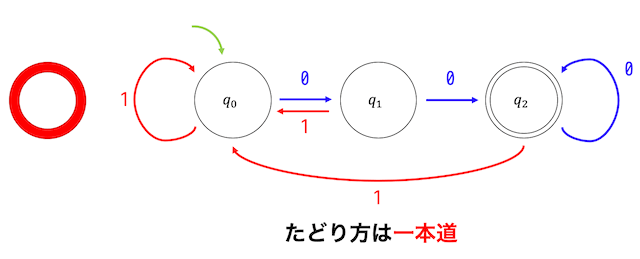
なのでこのオートマトンは決定性オートマトン(DFA)ということができます。
しかし、下の状態遷移図で表されるオートマトンはどうでしょうか。
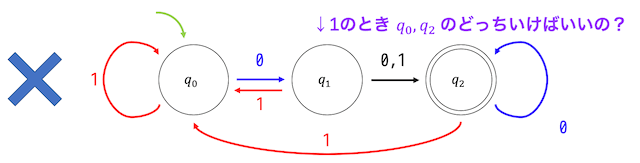
\( q_1 \) の1の遷移先が \( q_0 \), \( q_2 \) の2通りありますね。このように、それぞれの状態とつぎの文字に対しての遷移先が2つ以上あるもの、つまり途中で分かれ道をしてしまうようなものは決定性オートマトンとは言えません。非決定性オートマトンとなってしまいます。
もう1つ決定性オートマトンではないものを紹介しましょう。このオートマトンが決定性オートマトン理由を考えてみましょう。
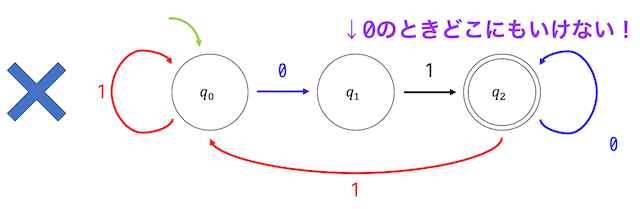
\( q_1 \) の0のときの遷移先がありませんね。このように、それぞれの状態と次の文字に対しての遷移先が存在しないものがある場合、つまり途中で道が切れてしまうようなものも決定性オートマトンとは言えません。
では、 まずは決定性オートマトンを読む練習をしてみましょう!
例題1
\( \Sigma = \{0,1\} \) とする。次の状態遷移図で表現される決定性オートマトンで受理される文字列はどれか。ここで、ビット列は左から順に読み込まれるものとする。
[基本情報技術者平成28年春期 午前問2]
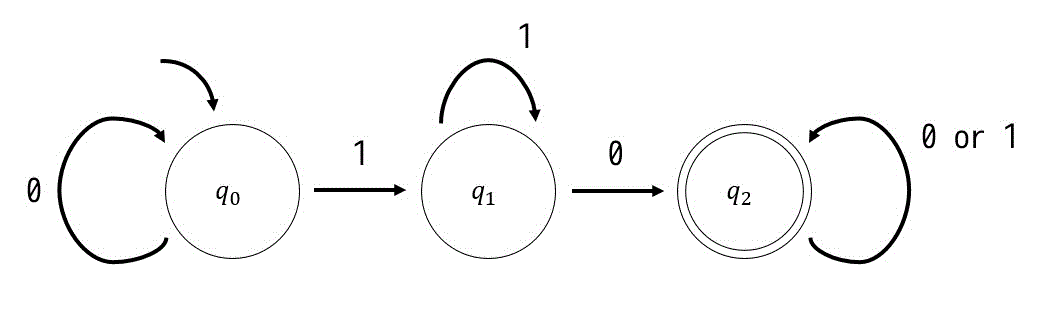
ア:0000
イ:0111
ウ:1010
エ:1111
おまけ:この決定性オートマトンはどんな文字列を受理するか。日本語で答えなさい。
解説1
解答:ウ
ア~エの文字をすべてたどっていきましょう。\[
ア \ \ q_0 \xrightarrow{0} q_0 \xrightarrow{0} q_0 \xrightarrow{0} q_0 \xrightarrow{0} q_0 \\
イ \ \ q_0 \xrightarrow{0} q_0 \xrightarrow{1} q_1 \xrightarrow{1} q_1 \xrightarrow{0} q_1 \\
ウ \ \ q_0 \xrightarrow{1} q_1 \xrightarrow{0} q_2 \xrightarrow{1} q_2 \xrightarrow{0} q_2 \\
エ \ \ q_0 \xrightarrow{1} q_1 \xrightarrow{1} q_1 \xrightarrow{1} q_1 \xrightarrow{1} q_1 \\
\]となる。
この中で受理するのは、文字列をたどり終わったときに受理状態である \( q_2 \) にいるウだけである。
4.決定性オートマトンの書き方
では、いよいよ決定性オートマトンを書く練習をしてみましょう!
試しに例題で紹介する2つのオートマトンを書いてみましょう。
※決定性オートマトンを書く際の注意点
- 初期値の矢印を忘れないこと!
- 各状態からそれぞれの入力(0,1やa,bが多い)における遷移先(矢印)がすべて書かれている(or複数書いていない)ことを確認すること!
例題2
\( \Sigma = \{0,1\} \) とする。
つぎの(1), (2)の条件を満たすような文字列を受理するような決定性オートマトンの状態遷移図を書きなさい。
(1) 11で終わる文字列を受理するもの。
(2) 1で始まる文字列を2進数とみたとき、2のべき乗(1,2,4,8,16…)となっている文字を受理するもの。
解説2
(1)
実は、上で紹介したオートマトンをちょっと変えるだけで作ることができます。
まず、11で終わるということは、下のように、1が2連続以上で来たら受理という形がつくれますね。
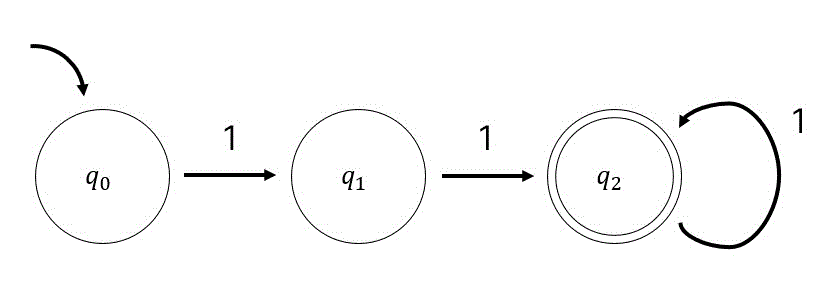
この \( q_0 \) は「1が0回連続で来た状態」、\( q_1 \) は「1が1回連続で来た状態」、\( q_2 \) は「1が2回以上連続で来た状態」を表すと思ってください。
つぎに、0が来た場合の処理を考えましょう。0が来るということは、1が来た回数の連続、コンボが途切れてしまいますね。なので0が来たときは \( q_0 \), \( q_1 \), \( q_2 \) どの状態にいても振り出しの \( q_0 \) に戻ると考えられますね。
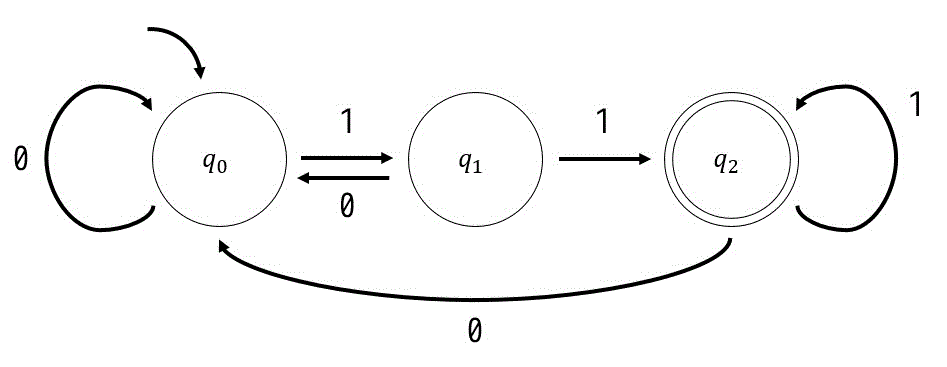
よって、上のような状態遷移図が完成します。
(2)
入力された文字を2進数とすることで、数にに
1→1
2→10
4→100
8→1000
16→10000
と調べていくと、最初に1が来て、残りはずっと0になるような文字列を受理するようなオートマトンを作ればよいことがわかります。
最初に1が来て、残りが0になるということは、
- 最初に1が来た場合は受理状態へ(0の場合は永久に受理しない)
- 受理状態では0が続いている間は受理のまま(1回でも1が来た時点で永久に受理しない)
といえますね。つまり、状態遷移図の基本形として、
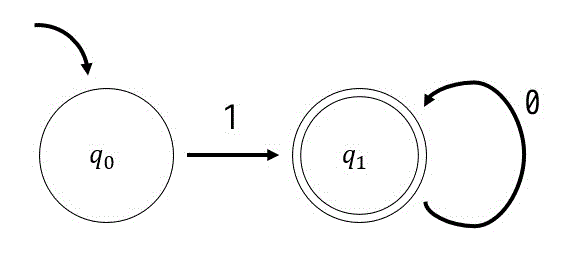
が完成しますね。
あとは、永久に受理しない状態を表現するだけですね。永久に受理しない状態は、下のような状態遷移にすることで、永久に受理しない状態を表現することができます。
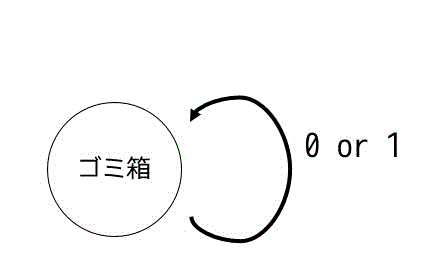
このような状態のことを私はDead State、ゴミ箱、あり地獄と呼んでいます。
つまり、(2)の状態遷移図は、
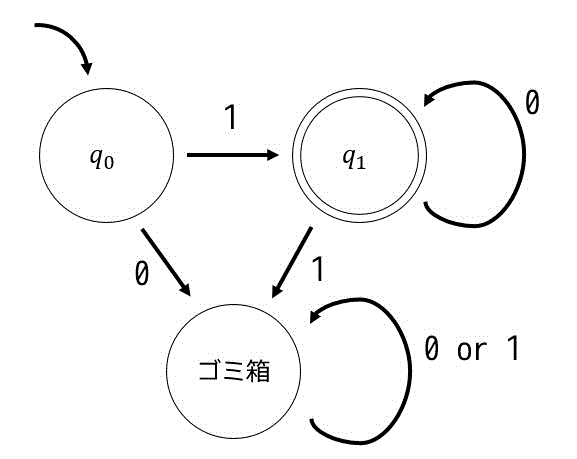
となります。
5.練習問題
では、練習をしてみましょう。
練習1がオートマトンを読む練習、練習2がオートマトンを書く練習となっております。
練習1
\( \Sigma = \{0,1\} \) とする。次の状態遷移図で表現される決定性オートマトンで受理される文字列はどれか。
[応用情報技術者平成21年春期 午前問3]
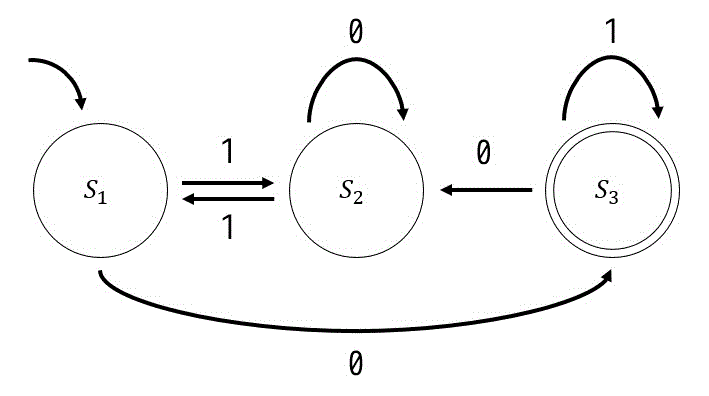
ア:1011
イ:1100
ウ:1101
エ:1110
練習2
\( \Sigma = \{0,1\} \) とする。
つぎの(1), (2)の条件を満たすような文字列を受理するような決定性オートマトンの状態遷移図を書きなさい。
(1) 文字列内の文字数が3の倍数のときに受理するもの。
(0文字、空文字は3の倍数とする。)
(2) 1で始まる文字列を2進数とみたとき、3の倍数となっているものを受理するもの。
6.練習問題の答え
解答1
解答:ウ
ア~エの文字をすべてたどっていきましょう。\[
ア \ \ S_1 \xrightarrow{1} S_2 \xrightarrow{0} S_2 \xrightarrow{1} S_1 \xrightarrow{1} S_1
\\
イ \ \ S_1 \xrightarrow{1} S_2 \xrightarrow{1} S_1 \xrightarrow{0} S_3 \xrightarrow{0} S_2 \\
ウ \ \ S_1 \xrightarrow{1} S_2 \xrightarrow{1} S_1 \xrightarrow{0} S_3 \xrightarrow{1} S_3 \\
エ \ \ S_1 \xrightarrow{1} S_2 \xrightarrow{1} S_1 \xrightarrow{1} S_2 \xrightarrow{0} S_2 \\
\]となる。
この中で受理するのは、文字列をたどり終わったときに受理状態である \( S_3 \) にいるウだけである。
解答2
(1)
必要な状態は、
- 文字数を3で割ったときのあまりが0の状態
- 文字数を3で割ったときのあまりが1の状態
- 文字数を3で割ったときのあまりが2の状態
の3つである。また、文字数は入力が 0,1 に関わらず1文字増えると入力が1増えていく。よって状態遷移図は
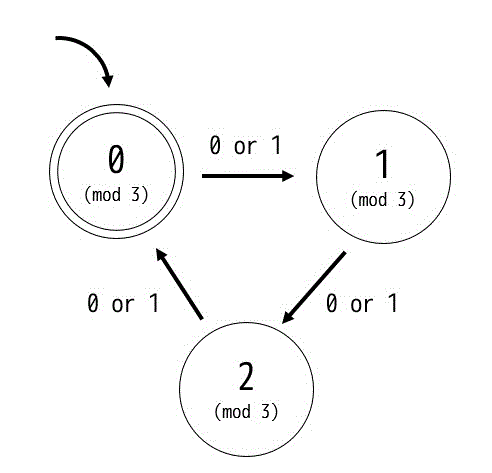
となる。
(2)
とある2進数を3で割ったあまりが0のとき、1のとき、2のときの3つに場合分けをする。
それぞれのときに0を加えたとき、1を加えたときに3で割ったあまりがどうなるかを考える。
ある2進数の右端に0を加えると、その2進数の値は2倍に、1を加えると2倍+1される。
(2進数を1ビット左にシフトさせることを考えています。わからなければこちらの記事で確認しましょう。)
(i) ある2進数を3で割ったときのあまりが0のとき
2進数は \( 3k \) と書ける(\( k \) は1以上の自然数)。
0を加える:値は2倍\[ 2 \times 3k = 6k \equiv 0 \bmod 3\]
1を加える:値は2倍+1\[ 2 \times 3k + 1 = 6k + 1 \equiv 0 \bmod 3\]
(ii) ある2進数を3で割ったときのあまりが1のとき
2進数は \( 3k+1 \) と書ける(\( k \) は1以上の自然数)。
0を加える:値は2倍\[ 2(3k+1) = 6k + 2 \equiv 0 \bmod 3\]
1を加える:値は2倍+1\[ 2(3k+1) + 1 = 6k + 3 \equiv 0 \bmod 3\]
(iii) ある2進数を3で割ったときのあまりが2のとき
2進数は \( 3k+2 \) と書ける(\( k \) は1以上の自然数)。
0を加える:値は2倍\[ 2(3k+2) = 6k + 4 \equiv 1 \bmod 3\]
1を加える:値は2倍+1\[ 2(3k+2) + 1 = 6k + 5 \equiv 2 \bmod 3\]
となる。よって、それぞれの2進数のあまりが0,1,2のときに0を加えたとき、1を加えたときのあまりを表にすると以下の通りになる。
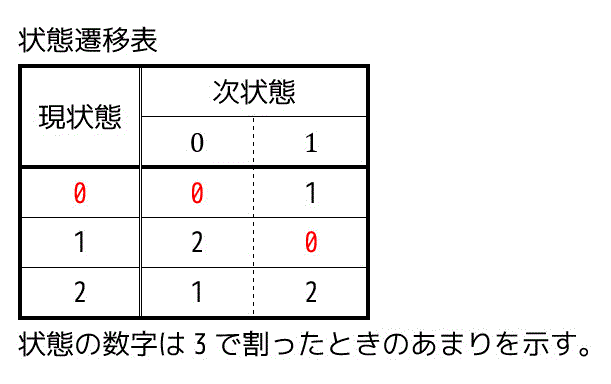
よって、あまりの処理の部分だけの状態遷移図は、表から下のようにかける。
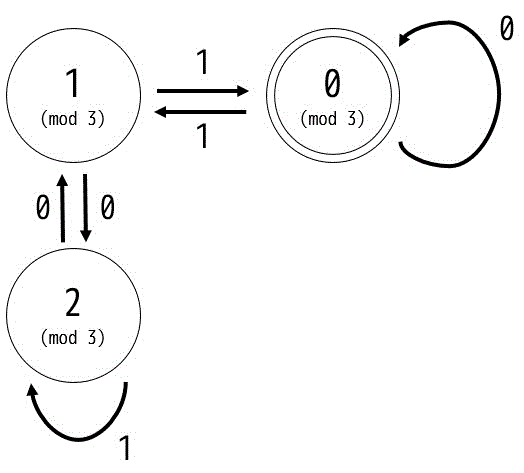
あとは、最初の文字が0のとき、1のときで場合分けすればよい。
0のときはそもそも受理されたらアウトなので0のときは蟻地獄へ、1のときは「2進数の1bのあまりは1」なのであまりが1の状態へ遷移させればよい。
よって(2)の状態遷移図は、
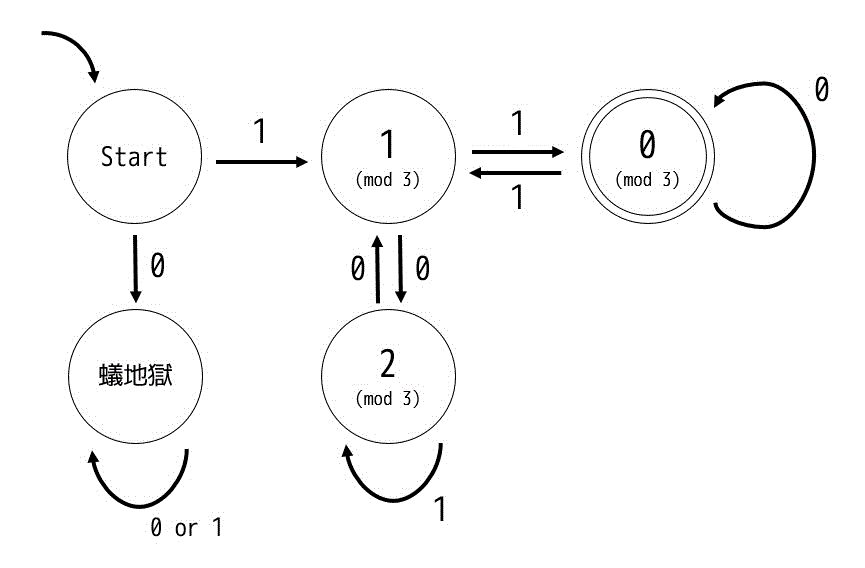
となる。
7.さいごに
今回はオートマトンの状態遷移図をすごろくに例えて説明し、動きがわかったところで決定性オートマトンの用語、特徴、読み方、書き方について説明しました。
オートマトンを書くのは、プログラミングと同じように最初は慣れが必要です。最初は少し時間がかかるかもしれませんが、書いていくうちにコツがつかめていくと思います。
次回はより直感的にオートマトンを記述することができる非決定性オートマトンについて説明していきたいと思います。
Next「第02羽」はこちら!↓
関連広告・スポンサードリンク