論理プログラム(Prolog)のコツ

2019年5月31日 2022年7月31日 21分48秒

ももうさ

スポンサードリンク

こんにちは！　ももやまです！
今回も論理プログラム(Prolog)についての記事です。

Prologのプログラムの記述は他のプログラムと異なり、独特な記述法で少しむずかしいですよね。
今回は、そんな独特な記述法をする論理プログラム(Prolog)を記述するちょっとしたコツをまとめていきます。

１．Prologのリスト処理は再帰処理！
２．Prolog独特の記号・関数
３．プログラムの例
- (1) 解は1つの場合
- 解がたくさん出てくる場合
４．練習問題
５．さいごに

スポンサードリンク

１．Prologのリスト処理は再帰処理！

再帰処理が苦手な人には大変申し訳無いのですが、Prologで出てくるプログラムには、リスト処理のときに必ず再帰処理が組み込まれています。

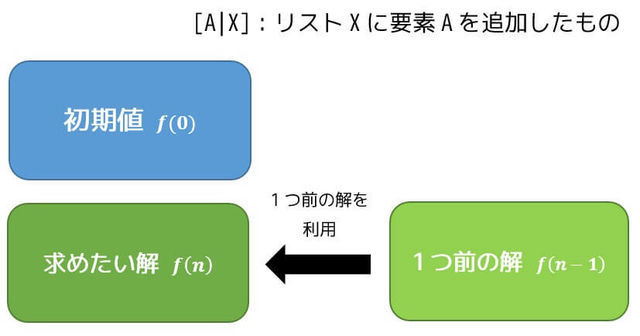
再帰処理とは、

1. 初期値（最も簡単なときの値）を求めるステップを記述
2. 1つ前の答えを使って答えを求めるステップを記述

の2つのステップを使う処理のことをいいます。

図でも見てみましょう。

f:id:momoyama1192:20190608222920j:plain

例えば次のようなプログラムを考えましょう。

第1パラメータ X に任意のデータ（変数除く）を要素とするとき、X の要素をそれぞれ重複させたリストを第2パラメータ Y に求めるPrologプログラム dupl(X,Y) を作成せよ。

例えば、dupl([a],Y)の実行結果は Y = [a] , dupl([a,b],Y) の実行結果は Y = [a,a,b,b] となる。

まずは初期値を考えます。この場合、初期値は X が空のリストのときですね。
X が空であれば当然 Yも空です。なので、dupl([],[]). が最も簡単な解ですね。

つぎに1つ前の答えを使って答えをつくるステップ（漸化式）を組み立てます。

この際確実に [X|Y] （リスト Y の先頭に要素 X を追加）を使います。

X の要素を重複させたリストが Y になるのであれば、X にある要素 A を1回連結したリストは Y のリストはある要素 A を2回連結させたリストになりますね。

これで漸化式の成立です。

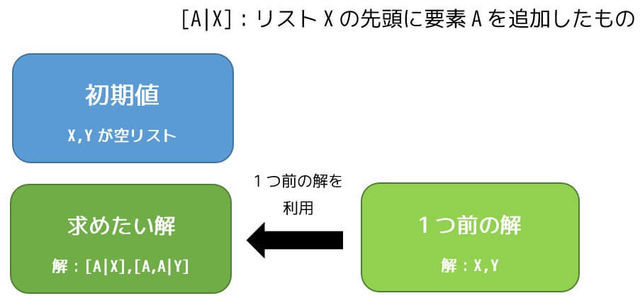
これをPrologで表記すると、 dupl([A|X],[A,A|Y]) :- dupl(X,Y). と表記できますね。
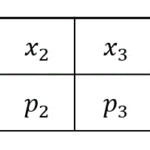
うーんちょっとわからない…、と思った人は、次のように四角などで囲ってあげるとわかりやすくなりかるかもしれません。

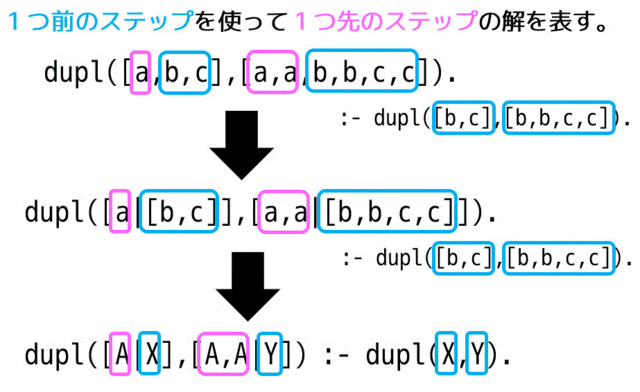
漸化式やほかの言語の再帰関数と違って = ではなく、:- を使うところにも注意してください。
:- を数学記号であらわすと \( \gets \) となります。向きが \( \to \) の反対なので注意してください。
数学っぽく表現すると、\( {\tt dupl}( [ w | x ] ,[w,w|y ]) \gets {\tt dupl}(x,y) \) *1となります。

よって、このプログラムは、

dupl([],[]).
dupl([A|X],[A,A|Y]) :- dupl(X,Y)

と表せます。

スポンサードリンク

２．Prolog独特の記号・関数

その1：数式

Prologでは、他のプログラミング言語と同じように + （足し算）, -（引き算）, *（掛け算）,/（割り算）をすることができます。計算順序も、他のプログラミング言語*2と同じ順序なんですが、１つだけ注意する点があります。

それは、

Ans = 1 + 2 + 3.

のように普通に計算式を入れるだけでは、

Ans = 1+2+3 ?

と表示されてしまい、計算結果の 6 を出してくれません。
計算結果を出してほしい場合は、= の代わりにisを使います。今回の例でいくと、

Ans is 1 + 2 + 3.

と入れて実行すれば、

Ans = 6 ? ;

となり、正しい答えを出してくれます。

余談ですが、次のようなプログラムはエラーになってしまいます。

1 + 2 + 3 is Ans.  % (変数 is 数式)の順番でないとだめ
Ans is Ans + 1.    % a = a + 1 [a += 1]のような書き方はだめ

また、数式比較として、以下の記号が使えます。

以下の記号 =< がProlog独特の記号なので注意してください。
（ <= ではないので注意）。

演算子	数学記号	例	意味
==	\( = \)	A == B	AはBと等しい
\=	\( \not = \)	A \= B	AとBは等しくない
<	\( \lt \)	A < B	AはBよりより小さい
=<	\( \leqq \)	A =< B	AはB以下
>	\( \gt \)	A > B	AはBよりも大きい
>=	\( \geqq \)	A >= B	AはB以上

その2：ライブラリ関数

つぎは、Prologでよく使うライブラリ関数を2つ紹介します。

(1) member

まずはmember関数です。 member(X,Y).は、リストYに要素Xがあるか判定してくれます。

いくつか実行例を紹介します。

| ?- member(a,[a,b,c,d]).
yes % リスト[a,b,c,d]の中に要素aがあるのでyes
| ?- member(e,[a,b,c,d]).
no % リスト [a,b,c,d] の中に要素eはないのでno
| ?- member(a,[[a,b],c,d]).
no % リスト [[a,b],c,d]]の中に要素[a,b]はあるがaはないのでno
| ?-

また、次のように実行してあげることで、リスト内の要素をすべて調べてあげることができます。

| ?- member(X,[1,2,[3,4],5]).
X = 1 ? ;
X = 2 ? ;
X = [3,4] ? ;
X = 5 ? ;
no

(2) append

つぎにappend関数です。 append(X,Y,Z).は、リストXにリストYを結合して、リストZを作成します。

いくつか実行例を紹介します。

| ?- append([a,b],[c,d],[a,b,c,d]).
yes % [a,b]に[c,d]を結合すると[a,b,c,d]なのでyes
| ?- append([a,b],[c,d],[c,d,a,b]).
no % [c,d,a,b]ではなく、[a,b,c,d]なのでno
| ?- append([1,2],[3,4],X).
X = [1,2,3,4] ?
yes % [1,2] と [3,4] を結合すると [1,2,3,4]
| ?- append([1,2],[1,2,[3,4]],X).
X = [1,2,1,2,[3,4]] ?
yes % [1,2]と[1,2,[3,4]]を結合すると [1,2,1,2,[3,4]]

次のように実行してあげると、リストの結合パターンをすべて表示してくれます。

| ?- append(X,Y,[a,b,c,d]).
X = [],
Y = [a,b,c,d] ? ;
X = [a],
Y = [b,c,d] ? ;
X = [a,b],
Y = [c,d] ? ;
X = [a,b,c],
Y = [d] ? ;
X = [a,b,c,d],
Y = [] ? ;
% 全部で5パターン

その3：カットオペレーター

Prolog独特の表記としてカットオペレーター ( ! )があります。

カットオペレーターについては、こちらの記事にまとめているのでご覧ください！

www.momoyama-usagi.com

その4：無名変数

Prolog独特の表記の1つとして、無名変数 _ があります。
無名変数は、余計な変数を宣言しないために使われます。
他の言語でも宣言している変数を使う*3なんてことはしませんよね。

例えば、このプログラムを見てください。

% delete(X,Y,Z) → リストXから要素Yをすべて除いたものがリストZ
delete([],_,[]). % 初期値：ここで無名変数を使っている
delete([Y|X],Y,Z) :- delete(X,Y,Z),!.  % 変数Yを代入しているので_にしたらだめ
delete([A|X],Y,[A|Z]) :- delete(X,Y,Z).  % 変数Yを代入しているので_にしたらだめ

このプログラムの初期値は、リストXが空リストのときですね。リストXが空なら当然リストZも空ですね。

このとき、要素Yは一切関係がありませんね。だから、delete([],Y,[]).と書いちゃえばいいのですが、要素Yは他の要素に代入とかもしていませんよね（他の2つは代入している）。

なので、無駄に変数宣言してる感じになりますね。なので、要素Yは無名変数_とします。

その5：各節の大文字の変数はすべて独立

他の言語の場合、一度宣言した変数は他の行でも同じ意味を持ちます。例えば、

p(x,y)
p(y,x)

は、x,yに代入されている変数が違うので、この２つの結果はそれぞれ違う結果となります。しか

Prologの場合、

p1(X,Y) :- q(X,Z),q(Z,Y). % 1節目
p2(Y,X) :- q(Y,Z),q(Z,X). % 2節目

1節目と2節目では違う変数名を使っていますが、:-の右側をよく見ると同じ操作をしているのがわかるでしょうか（p1とp2は同じ処理内容）。

このようにPrologでは、それぞれの節で変数は独立している^[1]それぞれの節ごとに変数がリセットされる、例えば1節目の変数Xと2節目の変数Xは全く関係がない。ことに注意が必要です。

スポンサードリンク

３．プログラムの例

Prologプログラムは大きくわけて2つに分類することができます。

(1) 解は1つの場合

まずは、解が1つしかないパターンです。
1つしか解がないので、バックトラックしても解は出ません。

試しに例題と2で説明したisを使って1つプログラムを書いてみましょう。

[例題1]

第1パラメータ X のリスト内の数字の要素の和を第2パラメータ Y に求めるPrologプログラム su,(X,Y) を作成せよ。ただし、リスト X 内に数字以外の要素はないものとしてよい。

例えば、sum([1,2],Y)の実行結果は Y = 3 , sum([3,3,4],Y) の実行結果は Y = 10 となる。

このように、解が1つしかないパターンの場合は、初期値の多くの入力は「空リスト」となります。なので、空リストの場合を定義します。

この問題の場合、空リストの場合のリストの要素の和はもちろん0ですよね。なので、「空リストのときは0」を書きます。これをPrologで書くとsum([],0).となります。

つぎに1つ前の答えを使って答えをつくるステップ（漸化式）を組み立てます。

1つ前のステップが sum(X,Sum). とします。リスト X の合計が Subsum のとき、リスト X に要素 A を追加したときのリスト [A|X] の合計 Sum は、Subsum + A で表せますね。

なので、sum([A|X],Sum) :- sum(X,Subsum),Sum is Subsum + A.で記述することができます。

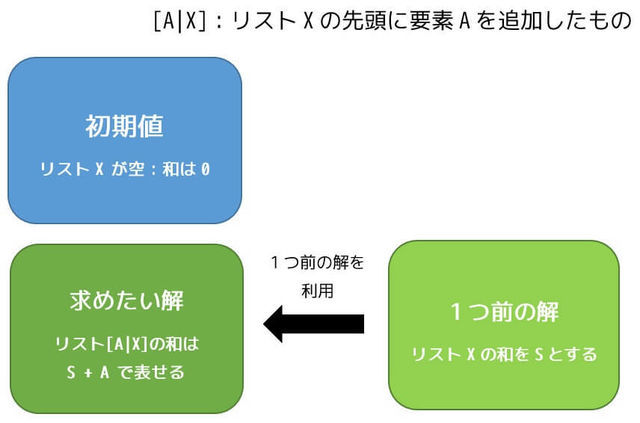
よって、このプログラムは、

sum([],0).
sum([A|X],Sum) :- sum(X,Subsum),Sum is Subsum + A.

と書けます。

中には、初期値が「空リスト」ではないものもあります。次のプログラムを考えてみましょう。

[例題2]

第1パラメータ X に長さ1以上のリストを要素とするとき、、X の要素間と両端に * を追加したリストを第2パラメータ Y に求めるPrologプログラム insertkome(X,Y) を作成せよ。
例えば、insertkome([a,b],Y)の実行結果は Y = [*,a,*,b,*] , insertkome([a,b,c],Y) の実行結果は Y = [*,a,*,b,*,c,*] となる。

この問題の場合、長さ1以上という制限がかかっているため、初期値は「空リスト」ではないことに注意してください。

長さ1の場合、つまりリストの中に要素 X のみが入っているときはinsertkome([X],[*,X,*]).で表すことができます。

1つ前のステップが insertkome(X,Y). とします。X にある要素 A を1回連結したリストは Y リストはある2つの要素 *,A を先頭に連結したリストになりますね。これをプログラムで書くと、insertkome([A|X],[*,A|Y]) :- insertkome(X,Y). となります。

以上の2ステップをまとめると、以下のようなプログラムが完成します。

insertkome([X],[*,X,*]). % 初期値、長さ1以上に注意
insertkome([A|X],[*,A|Y]) :- insertkome(X,Y). % 漸化式部分

漸化式部分の式が書けないなと思った人は、次のように色を付けたり囲ったりするのがおすすめです。

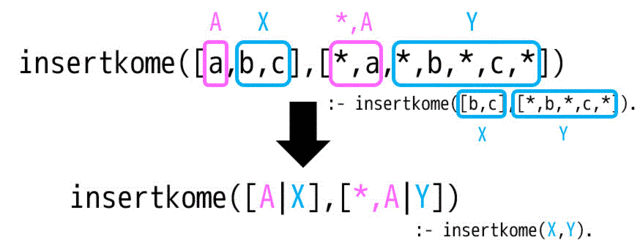
つぎに漸化式部分が少し特殊なプログラムも見てみましょう。

[例題3]

第1パラメータ X の要素を反転したものに第2パラメータ Y の要素を第3パラメータZに連結したPrologプログラム rev(X,Y,Z) を作成せよ。
例えば、rev([a,b],[c,d],Z).の実行結果は Z = [b,a,c,d] , rev([1,2,3],[a,b],Z). の実行結果は Z = [3,2,1,a,b] となる。

この問題の初期値は少し迷いどころですが、Xが空リストのときにしましょう。
すると、リストYをリストZに代入するだけなので、初期値状態は rev([],Y,Y).と書けます。

あとは、「X の要素を反転しながら Y に追加するという操作」を再起に落とし込みましょう。
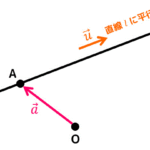
落とし込む際には、下のように具体的な例を使いながら操作をするのがおすすめです。

すると、

第1パラメータ X の先頭要素 A を抜く
抜いた要素 A を第2パラメータ Y の先頭に挿入する

という操作を X が空になるまで追加すればOKなことが分かりますね。ここで、再起の最中はリストZは変化しない点に注意が必要です。*4

よってこれをプログラム化すると rev([A|X],Y,Z) :- rev(X,[A|Y],Z).となります。

答えは

rev([],X,X).
rev([A|X],Y,Z) :- rev(X,[A|Y],Z).

となります。

初期値や漸化式部分は1行とは限らず2行以上になることもあるので注意してください。練習問題では2行以上になるパターンを用意しています。

解がたくさん出てくる場合

Prologでは、バックトラックを複数回行うことで、該当する解を複数出してあげることができます。

例えば、次のようなプログラムを考えてみましょう。

[例題4]

第1パラメータをリスト L とする。、第2パタメータXの要素に一致するリストL中の要素の1つ前の要素を第3パラメータ Back に、1つ後の要素を第4パラメーターNextに求めるプログラム findpf(L,X,Back,Next). を作成すること。

ただし、要素Xが複数ある場合は、該当する解をすべて求めること。ただし、リストの先頭と最後の要素は無視してよい。

例えば、findpf([a,b,a,c,b,d,a,f],a,Back,Next)の実行結果は以下の通りである。

| ?- findpf([a,b,a,c,b,d,a,f],a,Back,Next).
Back = b,
Next = c ? ;
Back = d,
Next = f ? ;
no

この場合はプログラムの書き方が「答えが1通りの場合」と異なってきます。

まず、解となる場合の条件を書きます。この問題の場合、解となるためには

リスト内の要素が X に等しい
先頭か最後尾ではない（前後にリストがある）

の2つの条件が必要となります。これをPrologで記述すると、findpf([Back,X,Next|W],X,Back,Next).となります。

しかし、Wは他にどこにも使われていない余分な宣言をしている変数ですね。なので、Wの代わりに無名変数_を使い、findpf([Back,X,Next|_],X,Back,Next).とします。

つぎに、漸化式部分を書きます。

複数個解をもつようなプログラムの場合は、「解をもつための条件」を上で記述しているため、ここでは「調べるリストを1つ進める動作」を記述します。

今回は調べるリストは Xですね。

リストを1つすすめるためには、findpf([_|R],X,Back,Next) :- findpf(R,X,Back,Next).とすればリストをすすめることができます。よってこのプログラムは

findpf([Back,X,Next|_],X,Back,Next). % 解の条件
findpf([_|R],X,Back,Next) :- findpf(R,X,Back,Next). % リストXを進める操作

と書くことができます。

リスト処理のときのポイント

解が1つのとき
１．初期値（空リストが多い）を書く
２．漸化式を書く

解が複数のとき
１．解となる条件を書く
２．調べるリストを進める操作を書く

では2つのパターンの練習をしてみましょう！

４．練習問題

では、2問練習してみましょう！

(1) 練習1

第1パラメータをリスト L とする。、第2パタメータXに、Lの要素と、要素が偶数番目なら0、奇数番目なら1をリストにしたPrologプログラムoddeven(L,X)を作成しなさい。バックトラックするごとに要素を1つ順番に出るようにすること。

例えば、oddeven([a,b,c,d,e],X)の実行結果は以下の通りである。

| ?- oddeven([a,b,c,d,e],X).
X = [a,1] ? ;
X = [b,0] ? ;
X = [c,1] ? ;
X = [d,0] ? ;
X = [e,1] ? ;
no

練習2

第1パラメータ X リストを与えたときに、同じ要素が2つ以上あった場合、1つだけ残し、それ以外をすべて削除したリストを第2パラメータ Y に求めるPrologプログラムunique(X,Y)を作成しなさい。

ただし、バックトラックにより、誤った解が出ないようにしなさい。

解答1

oddeven([A|_],[A,1]). % リストが1つなら奇数
oddeven([_,A|_],[A,0]). % リストが2つなら偶数
oddeven([_,_|Y],X) :- oddeven(Y,X). % 2つずつ進めるのに注意

解の条件を偶数と奇数の2つにわける。

条件を2つに分けているので、3行目の解を進める部分の記述に要注意。2つずつリストLを進めないと同じ解が2回表示されてしまう。

解答2

unique([],[]). % 初期値
unique([A|X],Y) :- unique(X,Y),member(A,X),!. % 重複している場合は X は追加し Y はそのまま
unique([A|X],[A|Y]) :- unique(X,Y). % 重複してない場合は両方のリストに追加

初期値は問題ない。
問題は2行目と3行目である。

2行目に重複している場合、3行目に重複していない場合を記述した。

すでにリスト内に要素 A が入っているかどうかはmember関数を使って判別することができる。
また、カットオペレーターの位置にも要注意。必ず member(A,X) よりも右側にカットオペレーターは書くこと。*5