スポンサードリンク
こんにちは、ももやまです。
第3羽~第5羽はノルムについてお勉強しましょう!
目次
スポンサードリンク
1. 高校数学までのノルム
高校数学では、下の例題のような感じにベクトルの大きさを「始点から終点までの長さ(距離)」として計算していましたね。
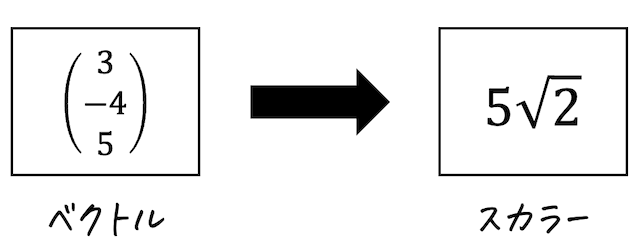
次のベクトル \( \vec{a} \) の長さ(大きさ)\( | \vec{a} | \) を答えなさい。\[
\vec{a} = \left( \begin{array}{ccc} 4 \\ -3 \\ 5 \end{array} \right)
\]
\[\begin{align*}
| \vec{a} | & = \sqrt{ 4^2 + (-3)^2 + 5^2 }
\\ & = \sqrt{50}
\\ & = 5 \sqrt{2}
\end{align*}\]
今回はこの高校数学で習った「ベクトルの大きさ」の概念をより一般化した「ノルム」について見ていきましょう。
スポンサードリンク
2. ノルムとは
ベクトルは、そのままの状態だと大小を比べられません。
例えば、2つのベクトル\[
\vec{a} = \left( \begin{array}{ccc} 1 \\ 2 \\ - 1 \end{array} \right) , \ \ \ \vec{b} = \left( \begin{array}{ccc} 2 \\ -3 \\ -0 \end{array} \right)
\]に対して、\( \vec{a} < \vec{b} \) みたいなことは出来ないということです。
ただし、これをスカラー(1つの数字)にすれば比べることができますね。そこで、ベクトルをスカラーに変換するための変換式(関数)を考えましょう。
この変換式のことをノルムと呼び、\( \| \vec{a} \| \) や \( | \vec{a} | \) などの記号で表されます。
ベクトル \( \vec{a} \) をスカラーに対応させる関数をノルムと呼び、\( \| \vec{a} \| \) と表記する。
ただし、ノルムと呼ぶためには次の1~4を必ず満たすように対応させる必要がある。
- \( \| \vec{a} \| \geqq 0 \)
(ノルムは必ず0以上) - \( \| \vec{a} \| = 0 \Leftrightarrow \vec{a} = \vec{0} \)
(ゼロベクトルのノルムは必ず0、ノルムが0のベクトルは必ずゼロベクトル) - \( \| c \vec{a} \| = |c| \cdot \| \vec{a} \| \)
(定数倍をノルムの外に出すことが可能) - \( \| \vec{a} + \vec{b} \| \leqq \| \vec{a} \| + \| \vec{b} \| \)
(三角不等式)
※1 \( | \vec{a} | \) と表記することもあるが、絶対値とごちゃごちゃになるため、大学数学では \( \| \vec{a} \| \) のように縦線2本での表記を行うことが多い。
※2 \( c \) は実数。外に出す際には絶対値をつけ忘れないように注意。
※3 高校数学で習ったベクトルの長さ \( | \vec{a} | \) は代表的なノルムの一種。
上の条件さえ満たしてしまえば、好きな方法でノルム(ベクトルの大きさ)を定義してあげることができます!!
なお、皆さんが高校時代に習ったベクトルの大きさは、「ベクトルの始点から終点までの最短距離(ユークリッド距離)」と呼ばれるノルムの中でも最もメジャーなものです。
大学数学でも、ユークリッド距離を使う場面は多いですが、問題によっては「ユークリッド距離以外の大きさの測り方」をする必要がある場面が出てきます。
そこで、3章以降は大学数学でよく出てくる \( L_p \) ノルムを紹介します。
スポンサードリンク
3. pノルム(\( L^p \) ノルム)
\( p \) ノルム(\( L^p \) ノルム)の定義式を確認しましょう。
\( n \) 次元ベクトル\[
\vec{a} = \left( \begin{array}{ccc} a_1 \\ a_2 \\ \vdots \\ a_n \end{array} \right)
\]がある。
このとき、ベクトルの \( p \) ノルム(\( L^p \) ノルムは次のように定義、計算でき、\( \| \vec{a} \|_p \) と表記される。\[\begin{align*}
\| \vec{a} \|_p & = \sqrt[p]{ | a_1 |^p + | a_2 |^p + \cdots + | a_n |^p }
\\ & = \sqrt[p]{ \sum^{n}_{k = 1} | a_k |^p }
\end{align*}\]
※ \( p \) の範囲は \( p \geqq 1 \) である[1]\( p < 1 \) のときは、ノルムの条件4(三角不等式)を満たさないため、定義されない。。
例えば\[
\vec{a} = \left( \begin{array}{ccc} -5 \\ 1 \\ 6 \\ -1 \end{array} \right)
\]のときの3ノルム(\( L^3 \) ノルム)は、\[\begin{align*}
\| \vec{a} \|_3 & = \sqrt[3]{ |-5|^3 + |1|^3+ |6|^3 + |-1|^3 }
\\ & = \sqrt[3]{ 125 + 1 + 216 + 1 }
\\ & = \sqrt[3]{343}
\\ & = \sqrt[3]{7^3}
\\ & = 7
\end{align*}\]と計算できます。
4. 1ノルム・2ノルム・∞ノルム
この章では、ノルムの中でも頻出の1ノルム・2ノルム・∞ノルム(\( L^1 \), \( L^2 \), \( L^{\infty} \) ノルム)の定義と計算例を見てみましょう。
(1) 1ノルム ( \( L^1 \) ノルム )・絶対値ノルム
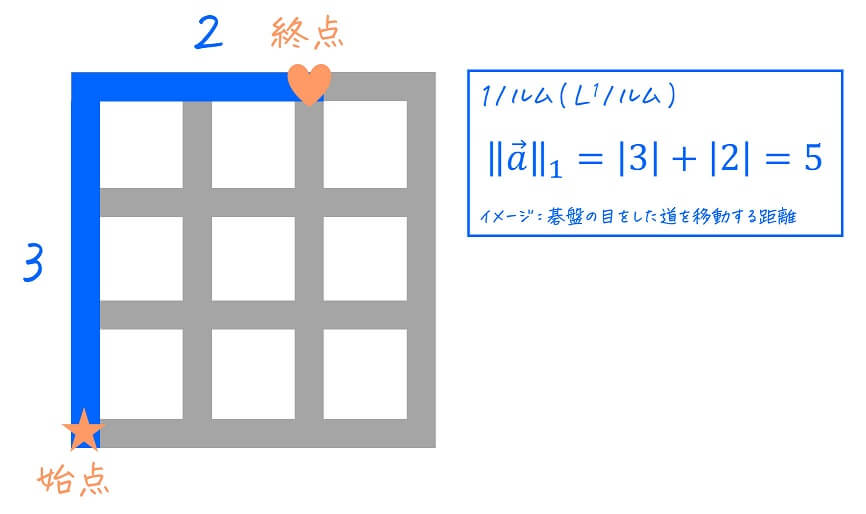
1ノルム(\( L^1 \) ノルム)ではベクトルの各成分の要素の絶対値の和をノルムとします。
\( n \) 次元ベクトル\[
\vec{a} = \left( \begin{array}{ccc} a_1 \\ a_2 \\ \vdots \\ a_n \end{array} \right)
\]の1ノルム(\( L^1 \) ノルム)は次のように計算でき、\( \| \vec{a} \|_1 \) で表される。
\[\begin{align*}
\| \vec{a} \|_1 & = |a_1| + |a_2| + \cdots + |a_n|
\\ & = \sum^{n}_{k = 1} | a_k |
\end{align*}\]
イメージとしては、碁盤の目の町をした道を移動する場合の最短距離(マンハッタン距離)です。
1つ計算例を見てみましょう。
次のベクトル \( \vec{a} \) の1ノルム(\( L^1 \) ノルム)を求めなさい。\[
\vec{a} = \left( \begin{array}{ccc} 4 \\ -1 \\ 8 \\ -2 \\ -6 \end{array} \right)
\]
\[\begin{align*}
\| \vec{a} \|_1 &= |4| + |-1| + |8| + |-2| + |-6|
\\ &= 21
\end{align*}\]
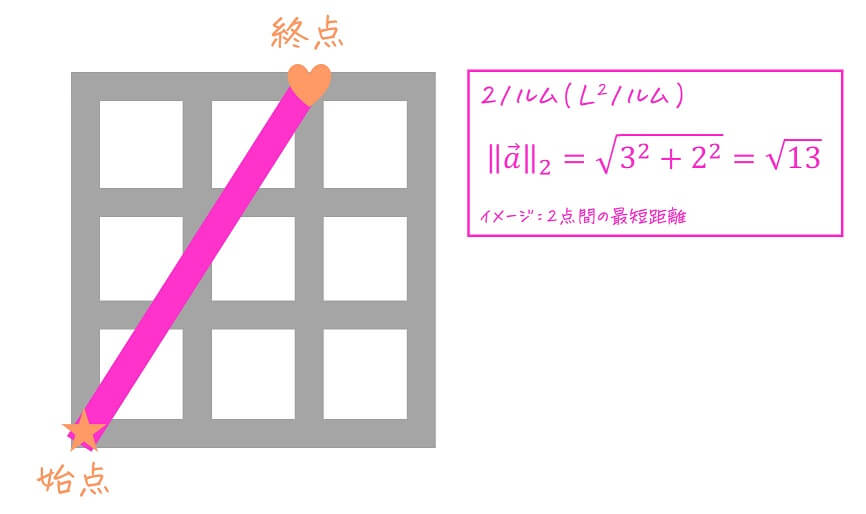
(2) 2ノルム ( \( L^2 \) ノルム )・ユークリッド距離
2ノルム(\( L^2 \) ノルムは、皆さんお馴染みのユークリッド距離です。
\( n \) 次元ベクトル\[
\vec{a} = \left( \begin{array}{ccc} a_1 \\ a_2 \\ \vdots \\ a_n \end{array} \right)
\]の2ノルム(\( L^2 \) ノルム)は次のように計算でき、\( \| \vec{a} \|_2 \) もしくは \( \| \vec{a} \| \) で表される。
\[\begin{align*}
\| \vec{a} \|_2 & = \sqrt{ a_1^2 + a_2^2 + \cdots + a_n^2}
\\ & = \sqrt{ \sum^{n}_{k = 1} a_k^2 }
\end{align*}\]
※ \( a_k^2 = | a_k^2 | \) なので絶対値を取った。
単に「ノルム」といった場合、この2ノルム(\( L^2 \) ノルム)を指していると思っていただけたらOKです。
再び計算例を見てみましょう。
次のベクトル \( \vec{a} \) の2ノルム(\( L^2 \) ノルム)を求めなさい。\[
\vec{a} = \left( \begin{array}{ccc} 4 \\ -1 \\ 8 \\ -2 \\ -6 \end{array} \right)
\]
\[\begin{align*}
\| \vec{a} \|_2 &= \sqrt{ 4^2 + (-1)^2 + (8)^2 + (-2)^2 + (-6)^2 }
\\ & = \sqrt{ 16 + 1 + 64 + 4 + 36}
\\ & = \sqrt{121}
\\ &= 11
\end{align*}\]
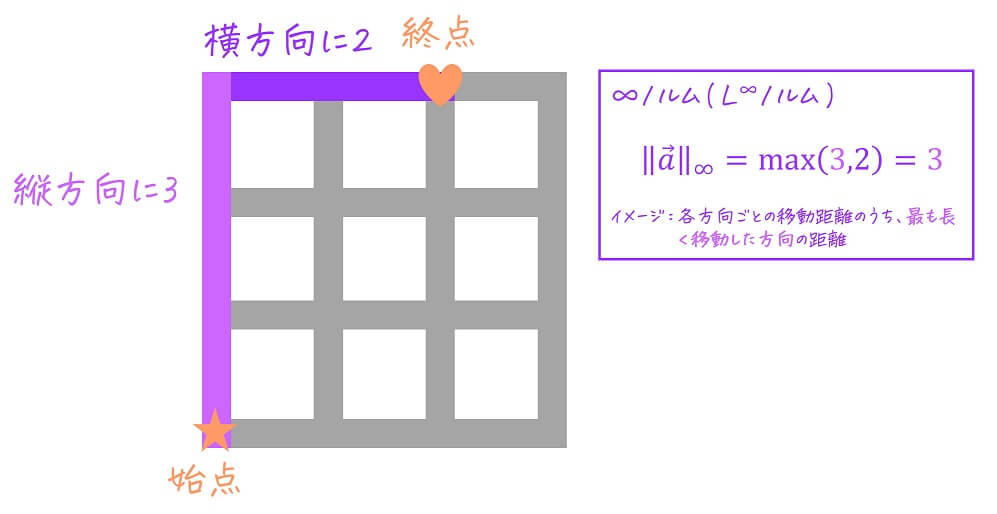
(3) ∞ノルム ( \( L^{\infty} \) ノルム )・最大値ノルム
ノルムで大小を比べる際には、\( p \to \infty \)、つまり∞ノルム(\( L^{\infty} \) ノルム)も使われます。
具体的に \( p \to \infty \) とすると、\[\begin{align*}
\lim_{p \to \infty} \| \vec{a} \|_p & = \sqrt[p]{ | a_1 |^p + | a_2 |^p + \cdots + | a_n |^p }
\\ & = \max ( |a_1| , |a_2| , \cdots , |a_n| )
\\ & = \max_{1 \leqq k \leqq n} | a_k |
\end{align*}\]となり、「各成分の絶対値」の最大値が∞ノルムの値となります[2]最も絶対値大きい成分以外は微小な値として考える。。
\( n \) 次元ベクトル\[
\vec{a} = \left( \begin{array}{ccc} a_1 \\ a_2 \\ \vdots \\ a_n \end{array} \right)
\]の∞ノルム(\( L^{\infty} \) ノルム)は次のように計算でき、\( \| \vec{a} \|_{\infty} \) で表される。
\[\begin{align*}
\| \vec{a} \|_\infty & = \max \left( |a_1|, |a_2|, \cdots , | a_n | \right)
\\ & = \max_{1 \leqq k \leqq n} | a_k |
\end{align*}\]
※ ベクトルの成分の絶対値が最も大きいものが \( \| \vec{a} \|_{\infty} \) となる。
イメージとしては、碁盤の目をした道を始点から終点までたどるときに「最も長く移動した方向の距離」が∞ノルムです。
計算例を見てみましょう。
次のベクトル \( \vec{a} \) の∞ノルム(\( L^{\infty} \) ノルム)を求めなさい。\[
\vec{a} = \left( \begin{array}{ccc} 4 \\ -1 \\ 8 \\ -2 \\ -6 \end{array} \right)
\]
\[\begin{align*}
\| \vec{a} \|_{\infty} &= \max ( |4|, |-1|, |8|, |-2|, |-6| )
\\ & = 8
\end{align*}\]
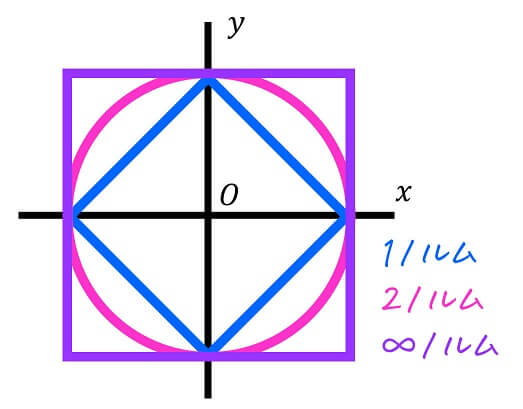
pノルム (p = 1, 2,∞) : ノルムが1のときの領域
\( \| \vec{a} \|_p = 1 \) のときの領域を \( p = 1, 2, \infty \) のときに分けて2次元の座標系に図示すると、下のようになります。

\( p = 1 \) のときはひし形、\( p = 2 \) のときは単位円となり、さらに \( p \) が大きくなると正方形に近づいていきます。
5. 練習問題
それでは、1問計算練習をしてみましょう。
次のベクトル \( \vec{a} \) の1ノルム、2ノルム、∞ノルム(\( L^{1} \), \( L^{2} \) , \( L^{\infty} \) ノルム)を求めなさい。\[
\vec{a} = \left( \begin{array}{ccc} 1 \\ -7 \\ -5 \\ -3 \\ 4 \end{array} \right)
\]
[解答]
(1) 1ノルム(\( L^1 \) ノルム)
\[\begin{align*}
\| \vec{a} \|_1 & = |1| + |-7| + |-5| + |-3| + |4|
\\ & = 20
\end{align*}\]
(2) 2ノルム(\( L^2 \) ノルム)
\[\begin{align*}
\| \vec{a} \|_2 & = \sqrt{ 1^2 + (-7)^2 + (-5)^2 + (-3)^2 + 4^2 }
\\ & = \sqrt{ 1 + 49 + 25 + 9 + 16 }
\\ & = \sqrt{100}
\\ & = 10
\end{align*}\]
(3) ∞ノルム(\( L^{\infty} \) ノルム)
\[\begin{align*}
\| \vec{a} \|_{\infty} & = \max ( |1|, |-7|, |-5|, |-3|, |4| )
\\ & = 7
\end{align*}\]
6. さいごに
今回は、ベクトルの大きさを比べるための道具である「ノルム」として、代表的な1ノルム、2ノルム、∞ノルムを見ていきました。
次回は、行列のノルムを見ていきましょう。
関連広告・スポンサードリンク