スポンサードリンク
こんにちは、ももやまです。
(3回中)2回目では、双曲線関数の中でも微分、積分、極限およびマクローリン展開に関する内容について説明していきます。
- 双曲線関数ってなに?
- 双曲線関数のグラフ
- 双曲線関数の基本変形公式
- 双曲線関数の加法定理
- 双曲線関数の2倍角・3倍角公式
- 双曲線関数の積和公式
- 双曲線関数の微分
- 双曲線関数の積分
- 双曲線関数の極限
- 双曲線関数のマクローリン展開
- 双曲線関数の逆関数
※ 下の赤い部分について解説をしていきます
↓↓ 1回目(双曲線関数のいろは)についての記事はこちら!↓↓
目次
スポンサードリンク
[復習] 双曲線関数の定義式
まずは、今回の内容で使う双曲線関数の定義式や基本公式を復習しましょう。
\[\begin{align*}
\sinh x & = \frac{ e^{x} - e^{-x} }{2} \\
\cosh x & = \frac{ e^{x} + e^{-x} }{2} \\
\tanh x & = \frac{ \sinh x }{ \cosh x }
\\ & = \frac{ e^{x} - e^{-x} }{ e^{x} + e^{-x} }
\end{align*}\]
\[
\cosh^2 x \textcolor{red}{-} \sinh^2 x = 1
\]\[
\tanh x = \frac{\sinh x }{\cosh x}
\]\[
1 \textcolor{red}{-} \tanh^2 x = \frac{1}{ \cosh^2 x }
\]
スポンサードリンク
1. 双曲線関数の微分
(1) 公式一覧
まずは、双曲線関数の微分公式を見てみましょう。
教科書では \( \sinh x \), \( \cosh x \), \( \tanh x \) の形で表示されていることが多いですが、計算速度を早めるために \( \sinh ax \), \( \cosh ax \), \( \tanh ax \) の形で覚えましょう。
★ 基本パターン\[\begin{align*}
\frac{d}{dx} \sinh x & = \cosh x \\
\frac{d}{dx} \cosh x & = \sinh x \\
\frac{d}{dx} \tanh x & = \frac{1}{\cosh^2 x}
\end{align*}\]
★ 公式拡張Ver\[\begin{align*}
\frac{d}{dx} \sinh f(x) & = f'(x) \cosh f(x) \\
\frac{d}{dx} \cosh f(x) & = f'(x) \sinh f(x) \\
\frac{d}{dx} \tanh f(x) & = \frac{f'(x)}{\cosh^2 f(x)}
\end{align*}\]
※ \( \cosh f(x) \) の微分でマイナスがつかないので注意!
★ 基本パターン\[\begin{align*}
\frac{d}{dx} \sin x & = \cos x \\
\frac{d}{dx} \cos x & = \textcolor{red}{-} \sin x \\
\frac{d}{dx} \tan x & = \frac{1}{\cos^2 x}
\end{align*}\]
★ 公式拡張Ver\[\begin{align*}
\frac{d}{dx} \sin f(x) & = f'(x) \cos f(x) \\
\frac{d}{dx} \cos f(x) & = \textcolor{red}{-} f'(x) \sin f(x) \\
\frac{d}{dx} \tan f(x) & = \frac{f'(x)}{\cos^2 f(x)}
\end{align*}\]
(2) 公式の導出
[1] \( \sinh f(x) \) の微分まずは、\( \sinh x \) の微分を求める。
\[\begin{align*}
\frac{d}{dx} \sinh x & = \frac{d}{dx} \frac{1}{2} ( e^{x} - e^{-x} )
\\ & = \frac{1}{2} \frac{d}{dx} ( e^{x} - e^{-x} )
\\ & = \frac{1}{2} \cdot ( e^{x} + e^{-x} )
\\ & = \frac{e^{x} + e^{-x}}{2}
\\ & = \cosh x
\end{align*}\]
つぎに、\( \sinh f(x) \) の微分を求めるために、\( y = \sinh t \), \( t = f(x) \) とおく。
すると、\( y = \sinh t \) となり、\[
\frac{dy}{dt} = \cosh t , \ \ \ \frac{dt}{dx} = f'(x)
\]となる。
よって、\[\begin{align*}
\frac{d}{dx} \sinh f(x) & = \frac{dy}{dt} \cdot \frac{dt}{dx}
\\ & = \cosh t \cdot f'(x)
\\ & = f'(x) \cosh f(x)
\end{align*}\]と求められる。
\frac{d}{dx} \cosh x & = \frac{d}{dx} \frac{1}{2} ( e^{x} + e^{-x} )
\\ & = \frac{1}{2} \frac{d}{dx} ( e^{x} + e^{-x} )
\\ & = \frac{1}{2} \cdot ( e^{x} - e^{-x} )
\\ & = \frac{e^{x} - e^{-x}}{2}
\\ & = \sinh x
\end{align*}\]
つぎに、\( \cosh f(x) \) の微分を求めるために、\( y = \cosh t \), \( t = f(x) \) とおく。
すると、\( y = \cosh t \) となり、\[
\frac{dy}{dt} = \sinh t , \ \ \ \frac{dt}{dx} = f'(x)
\]となる。
よって、\[\begin{align*}
\frac{d}{dx} \cosh f(x) & = \frac{dy}{dt} \cdot \frac{dt}{dx}
\\ & = \sinh t \cdot f'(x)
\\ & = f'(x) \sinh f(x)
\end{align*}\]と求められる。
\frac{d}{dx} \tanh ax & = \frac{d}{dx} \frac{ e^{x} - e^{-x} }{ e^{x} + e^{-x} }
\\ & = \frac{ (e^{x} - e^{-x})' (e^{x} + e^{-x}) - (e^{x} - e^{-x}) (e^{x} + e^{-x})' }{ (e^{x} + e^{-x})^2 }
\\ & = \frac{ ( e^{x} + e^{-x} ) (e^{ax} + e^{-ax}) - (e^{x} - e^{-x}) (e^{x} - e^{-x} ) }{ (e^{x} + e^{-x})^2 }
\\ & = \frac{ ( e^{x} + e^{-x} )^2 - (e^{x} - e^{-x})^2 }{ (e^{x} + e^{-x})^2 }
\\ & = \frac{ ( e^{2x} + 2 + e^{-2x} ) - ( e^{2x} - 2 + e^{-2x} ) }{ (e^{x} + e^{-x})^2 }
\\ & = \frac{ 4 }{ (e^{x} + e^{-x})^2 }
\\ & = \frac{ \frac{1}{4} \cdot 4 }{ \frac{1}{4} (e^{x} + e^{-x})^2 }
\\ & = \frac{ 1 }{ (\frac{e^{x} + e^{-x}}{2})^2 }
\\ & = \frac{ 1 }{ \cosh^2 x}
\end{align*}\]
つぎに、\( \tanh f(x) \) の微分を求めるために、\( y = \tanh t \), \( t = f(x) \) とおく。
すると、\( y = \tanh t \) となり、\[
\frac{dy}{dt} = \frac{1}{ \cosh^2 t} , \ \ \ \frac{dt}{dx} = f'(x)
\]となる。
よって、\[\begin{align*}
\frac{d}{dx} \tanh f(x) & = \frac{dy}{dt} \cdot \frac{dt}{dx}
\\ & = \frac{1}{ \cosh^2 t} \cdot f'(x)
\\ & = \frac{f'(x)}{ \cosh^2 t}
\end{align*}\]と求められる。
\[\begin{align*}
\frac{d}{dx} \tanh f(x) & = \frac{d}{dx} \frac{ \sinh f(x) }{ \cosh f(x) }
\\ & = \frac{ (\sinh f(x))' \cosh f(x) - \sinh f(x) ( \cosh f(x) )' }{ \cosh^2 f(x) }
\\ & = \frac{ f'(x) \cosh^2 f(x) - f'(x) \sinh^2 f(x) }{ \cosh^2 f(x) }
\\ & = \frac{ f'(x) \left\{ \cosh^2 f(x) - \sinh^2 f(x) \right\} }{ \cosh^2 f(x) }
\\ & = \frac{ f'(x) }{ \cosh^2 f(x) }
\end{align*}\]
(3) 例題で計算練習
次の関数 \( f(x) \) を微分することで、導関数 \( f'(x) \) を求めなさい。
(1)\[
f(x) = \tanh 3x
\]
(2)\[
f(x) = \sinh (x^2-3x+1)
\]
(3)\[
f(x) = \cosh^5 x
\]
(4)\[
f(x) = \sinh x \cosh x
\]
[解説1]
(1)
公式\[
\frac{d}{dx} \tanh g(x) = \frac{g'(x)}{\cosh^2 g(x)}
\]に \( g(x) = 3x \) を代入すればOK。
(問題に \( f(x) \) が出てくるので、紛らわしくないように公式の方は \( g(x) \) にしています)
よって、\[
f'(x) = \frac{3}{ \cosh^2 3x }
\]となる。
(2) 公式\[
\frac{d}{dx} \sinh g(x) = f'(x) \cosh g(x)
\]に \( g(x) = x^2 -3x + 1 \) を代入すればOK。
((1)と同じく、問題に \( f(x) \) が出てくるので、紛らわしくないように公式の方は \( g(x) \) にしています)
よって、\[
f'(x) = (2x - 3) \cosh (x^2-3x+1)
\]となる。
(3)
\( t = \cosh^5 x \) とおいてから合成関数の微分公式を使う。
すると、\( f(t) = t^5 \) となる。
\[\begin{align*}
\frac{df}{dx} & = \frac{df}{dt} \cdot \frac{dt}{dx}
\\ & = 5t^4 \cdot \sinh x
\\ & = 5 \cosh^4 x \sinh x
\end{align*}\]
よって、\[
f'(x) = 5 \cosh^4 x \sinh x
\]となる。
(4)
[解法1] 素直に計算
\[\begin{align*}
f'(x) & = (\sinh x)' \cosh x + \sinh x ( \cosh x )'
\\ & = \cosh x \cdot \cosh x + \sinh x \cdot \sinh x
\\ & = \cosh^2 x + \sinh^2 x
\end{align*}\]
[解法2] 倍角の公式を使ってから計算
\[
\sinh x \cosh x = \frac{1}{2} \sinh 2x
\]なので、\[\begin{align*}
f'(x) & = \frac{1}{2} \cdot 2 \cosh 2x
\\ & = \cosh 2x ( = \cosh^2 x + \sinh^2 x )
\end{align*}\]と計算してもOK。
スポンサードリンク
2. 双曲線関数の積分
(1) 公式一覧
まずは公式を見ていきましょう。微分のときと同じく、\( \sinh ax \), \( \cosh ax \), \( \tanh ax \) と定数 \( a \) を付けたバージョンで表示しています。
★ 基本パターン\[\begin{align*}
\int \sinh x \ dx& = \cosh x + C \\
\int \cosh x \ dx & = \sinh x + C \\
\int \tanh x \ dx & = \log ( \cosh x ) + C \\
\int \frac{1 }{ \cosh^2 x } \ dx & = \tanh x + C
\end{align*}\]
★ 公式拡張Ver\[\begin{align*}
\int \sinh (ax+b) \ dx& = \frac{1}{a} \cosh (ax+b) + C \\
\int \cosh (ax+b) \ dx & = \frac{1}{a} \sinh (ax+b) + C \\
\int \tanh (ax+b) \ dx & = \frac{1}{a} \log \left\{ \cosh (ax+b) \right\} + C \\
\int \frac{1 }{ \cosh^2 (ax+b) } \ dx & = \frac{1}{a} \tanh (ax+b) + C
\end{align*}\]※ \( a \), \( b \) は定数。ただし、\( a \not = 0 \)。
※ \( C \) は積分定数
※ \( \sinh (ax+b) \) の積分でマイナスがつかないので注意!
★ 基本パターン\[\begin{align*}
\int \sin x \ dx& = \textcolor{red}{-} \cos x + C \\
\int \cos x \ dx & = \sin x + C \\
\int \tan x \ dx & = \textcolor{red}{-} \log ( \cos x ) + C \\
\int \frac{1 }{ \cos^2 x } \ dx & = \tan x + C
\end{align*}\]
★ 公式拡張Ver\[\begin{align*}
\int \sin (ax+b) \ dx& = \textcolor{red}{-} \frac{1}{a} \cos (ax+b) + C \\
\int \cos (ax+b) \ dx & = \frac{1}{a} \sin (ax+b) + C \\
\int \tan (ax+b) \ dx & = \textcolor{red}{-} \frac{1}{a} \log \left\{ \cos (ax+b) \right\} + C \\
\int \frac{1 }{ \cos^2 (ax+b) } \ dx & = \frac{1}{a} \tan (ax+b) + C
\end{align*}\]※ \( a \), \( b \) は定数。ただし、\( a \not = 0 \)。
※ \( C \) は積分定数
(2) 公式の導出
3番目の\[
\int \tanh (ax+b) \ dx = \frac{1}{a} \log \left\{ \cosh (ax+b) \right\} + C
\]以外は、1-(1)の「三角関数の微分公式」に \( f(x) = ax + b \) を代入してから逆に適用する(微分したものを元に戻す)だけで導出できます。
3番目の公式だけは、導出をしておきましょう。
\[\begin{align*}
\int \tanh (ax+b) \ dx & = \int \frac{ \sinh (ax+b) }{ \cosh (ax+b) } \ dx
\\ & = \frac{1}{a} \int \frac{ a \sinh (ax+b) }{ \cosh (ax+b) } \ dx
\\ & = \frac{1}{a} \int \frac{ (\left\{ \cosh (ax+b) \right\}' }{ \cosh (ax+b) } \ dx
\\ & = \frac{1}{a} \log \left\{ \cosh (ax+b) \right\} + C
\end{align*}\]
(3) 例題で計算練習
公式を頭に入れるために、実際に計算練習をしましょう。
次の(1), (2)の計算(不定積分)をしなさい。
(1)\[
\int \sinh 2x \ dx
\]
(2)\[
\int x^2 \sinh x \ dx
\]
(3)\[
\int \sinh 4x \cosh 6x \ dx
\]
[解説2]
(1)
公式\[
\int \sinh ax \ dx = \frac{1}{a} \cosh ax + C
\]に \( a = 2 \) を代入すればOK。
よって、積分定数 \( C \) を用いることで\[\begin{align*}
\int \sinh 2x \ dx & = \frac{1}{2} \cosh 2x
\end{align*}\]と計算できる。
(2)
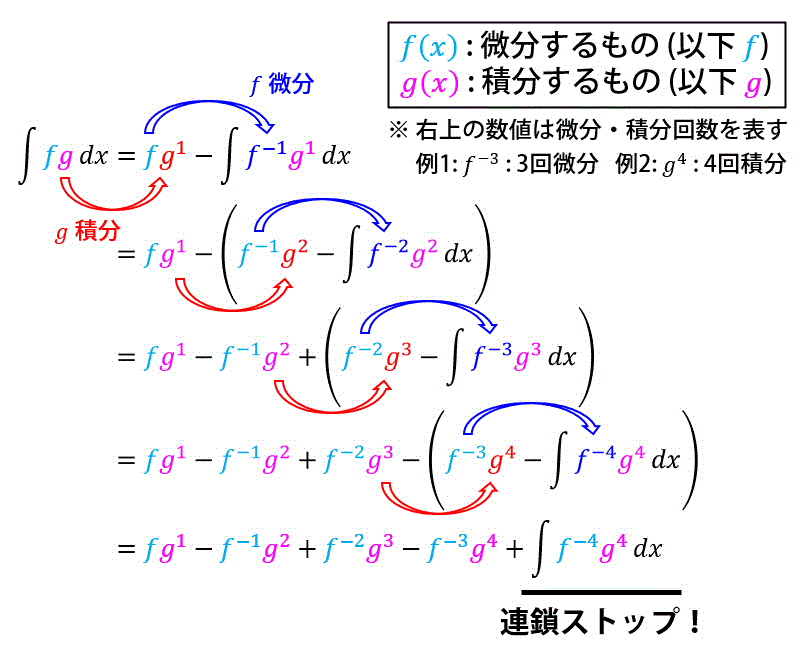
多項式 ( \( x^a \) ) × 双曲線関数 ( \( \sinh x \), \( \cosh x \) ) の形を見かけたら部分積分をすることを考えましょう[1]\( x^2 \sin x \) … Continue reading。
\[\begin{align*}
\int x^2 \sinh x & = x^2 \cosh x - 2x \sinh x + 2 \cosh + C
\\ & = (x^2 - 2 ) \cosh x - 2 x \sinh x + C
\end{align*}\]
※ 部分積分は連鎖公式(ブンブン積分・瞬間部分積分)を使うのがおすすめです。詳しくは下の記事から。
(3)
今回のように \( \sinh ax \) もしくは \( \cosh ax \) が2つ掛け合わされたような形の関数を積分する場合は、逆双曲線関数の積和の公式が非常に便利です。
まずは、積和の公式を確認しましょう。
(積和の公式の導出手順はこちらで確認できます。)
\[\begin{align*}
\sinh \alpha \cosh \beta & = \frac{1}{2} \left\{ \sinh ( \alpha + \beta ) + \sinh ( \alpha - \beta ) \right\} \\
\cosh \alpha \sinh \beta & = \frac{1}{2} \left\{ \sinh ( \alpha + \beta ) - \sinh ( \alpha - \beta ) \right\} \\
\cosh \alpha \cosh \beta & = \frac{1}{2} \left\{ \cosh ( \alpha + \beta ) + \cosh ( \alpha - \beta ) \right\} \\
\sinh \alpha \sinh \beta & = \frac{1}{2} \left\{ \cosh ( \alpha + \beta ) - \cosh ( \alpha - \beta ) \right\}
\end{align*}\]
今回は、\[
\sinh \alpha \cosh \beta = \frac{1}{2} \left\{ \sinh ( \alpha + \beta ) + \sinh ( \alpha - \beta ) \right\}
\]に、\( \alpha = 4x \), \( \beta = 6x \) を代入することで2つの双曲線関数の和に分解することができます。
よって、\[\begin{align*}
\int \sinh 4x \cosh 6x \ dx & = \int \frac{1}{2} \left\{ \sinh ( 4x + 6x ) + \sinh ( 4x - 6x ) \right\} \ dx
\\ & = \frac{1}{2} \int \sinh 10x \ dx + \frac{1}{2} \sinh (-2x) \ dx
\\ & = \frac{1}{20} \cosh 10x - \frac{1}{4} \cosh (-2x) + C
\\ & = \frac{1}{20} \cosh 10x - \frac{1}{4} \cosh 2x + C
\end{align*}\]と計算できる。
3. 双曲線関数の極限
双曲線関数の極限ですが、極限のために覚えなければいけない公式は基本的にありません。
というのも、双曲線関数の極限は
- 定義式(\( e \) を使った形)に変形する
- ロピタルの公式を適用する
ことでなんとかなるからです。
ということで、この章では「例題による問題演習」で双曲線関数の極限を見ていきましょう。
(1) sinh x, cosh x, tanh x の極限
まずは、\( \sinh x \), \( \cosh x \), \( \tanh x \) の極限を見てみましょう。
※ グラフの形を頭に入れておけば自然に
\( \sinh x \) の極限
\[
\lim_{x \to \infty} \sinh x = \infty , \ \ \ \lim_{x \to - \infty} \sinh x = - \infty
\]
\( \cosh x \) の極限
\[
\lim_{x \to \infty} \cosh x = \infty , \ \ \ \lim_{x \to - \infty} \cosh x = \infty
\]
\( \tanh x \) の極限
\[
\lim_{x \to \infty} \tanh x = 1 , \ \ \ \lim_{x \to - \infty} \tanh x = -1
\]
※ グラフの形を頭に入れておけば意識して極限を覚えなくてもOK。
赤色 → \( y = \sinh x \) のグラフ(奇関数)
青色 → \( y = \cosh x \) のグラフ(偶関数)
緑色 → \( y = \tanh x \) のグラフ(奇関数)
[導出]
[ \( \sinh x \) の極限 ]\[\begin{align*}
\lim_{x \to \infty} \sinh x & = \lim_{x \to \infty} \frac{1}{2} ( \underbrace{ e^x }_{0} - \underbrace{ e^{-x} }_{ \infty } ) \\ & = \infty \\
\end{align*}\]
\[\begin{align*}
\lim_{x \to - \infty} \sinh x & = \lim_{x \to - \infty} \frac{1}{2} ( e^x + e^{-x} )
\\ & = \lim_{t \to \infty} \frac{1}{2} ( \underbrace{ e^{-t} }_{0} - \underbrace{ e^{t} }_{ \infty } ) \ \ \ ( x \to - t )
\\ & = - \infty
\end{align*}\]
\[\begin{align*}
\lim_{x \to \infty} \cosh x & = \lim_{x \to \infty} \frac{1}{2} ( \underbrace{ e^x }_{0} + \underbrace{ e^{-x} }_{ \infty } )
\\ & = \infty
\end{align*}\]
\[\begin{align*}
\lim_{x \to - \infty} \cosh x & = \lim_{x \to - \infty} \frac{1}{2} ( \underbrace{ e^x }_{0} + \underbrace{ e^{-x} }_{ \infty } )
\\ & = \lim_{t \to \infty} \frac{1}{2} ( \underbrace{ e^{-t} }_{0} + \underbrace{ e^{t} }_{ \infty } ) \ \ \ ( x \to - t )
\\ & = \infty
\end{align*}\]
\[\begin{align*}
\lim_{x \to \infty} \tanh x & = \lim_{x \to \infty} \frac{ \sinh x }{ \cosh x }
\\ & = \lim_{x \to \infty} \frac{ e^{x} - e^{-x} }{ e^{x} + e^{-x} }
\\ & = \lim_{x \to \infty} \frac{1 - \overbrace{ e^{-2x} }^{0} }{1 + \underbrace{ e^{-2x} }_{0} }
\\ & = 1
\end{align*}\]と4パターンの式に変形できることを思い出す。
\[\begin{align*}
\lim_{x \to - \infty} \tanh x & = \lim_{x \to - \infty} \frac{ \sinh x }{ \cosh x }
\\ & = \lim_{x \to - \infty} \frac{ e^{x} - e^{-x} }{ e^{x} + e^{-x} }
\\ & = \lim_{t \to \infty} \frac{ e^{-t} - e^{t} }{ e^{-t} + e^{t} } \ \ \ ( x \to -t )
\\ & = \lim_{t \to \infty} \frac{ \overbrace{ e^{-2t} }^0 - 1 }{ \underbrace{ e^{-2t} }_{0} + 1 }
\\ & = -1
\end{align*}\]
(2) 定義式に変形するパターン
まずは、定義式に変形するパターンを見てみましょう。
次の極限を計算しなさい。
\[
\lim_{x \to \infty} \frac{ \sinh x }{ e^x }
\]
[解説3]
\[\begin{align*}
\lim_{x \to \infty} \frac{ \sinh x }{ e^x } & = \frac{ \frac{ e^x + e^{-x} }{2} }{e^x}
\\ & = \lim_{x \to \infty} \frac{ e^x + e^{-x} }{ 2 e^x}
\\ & = \lim_{x \to \infty} \frac{1}{2} ( 1 + \underbrace{ e^{-2x} }_{0} )
\\ & = \frac{1}{2}
\end{align*}\]
(3) ロピタルの定理を使うパターン
ロピタルの定理を使って計算するパターンも見てみましょう。
次の(1)~(3)の極限を計算しなさい。
(1)\[
\lim_{x \to 0} \frac{ \sinh x }{ x }
\]
(2)\[
\lim_{x \to 0} \frac{ \tanh x }{ x }
\]
(3)\[
\lim_{x \to 0} \frac{ \cosh x - 1 }{ x^2 }
\]
[解説4]
(1)
与式の分子、分母がともに0に収束し、0/0の不定形となる。
ここで、\[\begin{align*}
\lim_{x \to 0} \frac{ \sinh x }{ x } & = \lim_{x \to 0} \frac{ \cosh x }{ 1 }
\\ & = 1
\end{align*}\]
よって、ロピタルの定理より、\[
\lim_{x \to 0} \frac{ \sinh x }{ x } = 1
\]と求められる。(1に収束する)
(2)
与式の分子、分母がともに0に収束し、0/0の不定形となる。
ここで、\[\begin{align*}
\lim_{x \to 0} \frac{ \tanh x }{ x } & = \lim_{x \to 0} \frac{ \frac{1}{ \cosh^2 x } }{ 1 }
\\ & = \lim_{x \to 0} \frac{1}{ \cosh^2 x }
\\ & = 1
\end{align*}\]
よって、ロピタルの定理より、\[
\lim_{x \to 0} \frac{ \tanh x }{ x } = 1
\]と求められる。(1に収束する)
(3)
与式の分子、分母がともに0に収束し、0/0の不定形となる。
ここで、\[\begin{align*}
\lim_{x \to 0} \frac{ \cosh x - 1 }{ x^2 } & = \lim_{x \to 0} \frac{ \sinh x }{ 2x }
\\ & = \lim_{x \to 0} \frac{ \cosh x }{ 2 }
\\ & = \frac{1}{2}
\end{align*}\]
よって、ロピタルの定理より、\[
\lim_{x \to 0} \frac{ \cosh x - 1 }{ x^2 } = \frac{1}{2}
\]と求められる。(1/2に収束する)
\[\begin{align*}
\lim_{x \to 0} \frac{ \sinh x }{ x } & = 1 \\
\lim_{x \to 0} \frac{ \tanh x }{ x } & = 1
\end{align*}\]
※ ロピタルの定理で簡単に導出できるので覚えなくてOK
4. 双曲線関数のマクローリン展開(x = 0のテイラー展開)
(1) 公式一覧
\[\begin{align*}
\sinh x & = x + \frac{1}{3!} x^3 + \frac{1}{5!} x^5 + \frac{1}{7} x^7 + \cdots \\
\cosh x & = 1 + \frac{1}{2!} x^2 + \frac{1}{4!} x^4 + \frac{1}{6!} x^6 + \cdots \\
\tanh x & = x - \frac{1}{3} x^3 + \frac{2}{15} x^5 + \cdots
\end{align*}\]
シグマを使った形で書くと、\[\begin{align*}
\sinh x & = \sum^{\infty}_{n = 0} \frac{ 1 }{(2n+1)!} x^{2n+1} \\
\cosh x & = \sum^{\infty}_{n = 0} \frac{ 1 }{(2n+1)!} x^{2n}
\end{align*}\]
\[\begin{align*}
\sin x & = x - \frac{1}{3!} x^3 + \frac{1}{5!} x^5 - \frac{1}{7} x^7 + \cdots \\
\cos x & = 1 - \frac{1}{2!} x^2 + \frac{1}{4!} x^4 - \frac{1}{6!} x^6 + \cdots \\
\tan x & = x + \frac{1}{3} x^3 + \frac{2}{15} x^5 + \cdots
\end{align*}\]
シグマを使った形で書くと、\[\begin{align*}
\sinh x & = \sum^{\infty}_{n = 0} \frac{ (-1)^n }{(2n+1)!} x^{2n+1} \\
\cosh x & = \sum^{\infty}_{n = 0} \frac{ (-1)^{n} }{(2n+1)!} x^{2n}
\end{align*}\]
(2) 公式の導出
ひたすら微分をし、微分をしたものに \( x = 0 \) を代入していけばOKです。
今回は、5次のマクローリン展開まで求めてみましょう。
[導出] sinh x のマクローリン展開
\( f(x) = \sinh x \) とする。
\[\begin{align*}
f(x) & = \sinh x , \ \ \ f(0) = 0 \\
f'(x) & = \cosh x , \ \ \ f'(0) = 1 \\
f''(x) & = \sinh x , \ \ \ f''(0) = 0 \\
f'''(x) & = \cosh x , \ \ \ f'''(0) = 1 \\
f^{(4)} (x) & = \sinh x , \ \ \ f^{(4)} (0) = 0 \\
f^{(5)} (x) & = \cosh x , \ \ \ f^{(5)} (0) = 1
\end{align*}\]
となるので、あとはマクローリン展開の公式に入れるだけ。
\[\begin{align*}
f(x) & \fallingdotseq f(0) + \frac{ f'(0) }{1!} x + \frac{ f''(0) }{2!} x^2 + \frac{ f'''(0) }{3!} x^3 + \frac{ f^{(4)} (0) }{4!} x^4 + \frac{ f^{(5)} (0) }{5!} x^5
\\ & = x + \frac{1}{3!} x^3 + \frac{1}{5!} x^5
\end{align*}\]
[導出] cosh x のマクローリン展開
\( f(x) = \cosh x \) とする。
\[\begin{align*}
f(x) & = \cosh x , \ \ \ f(0) = 1 \\
f'(x) & = \sinh x , \ \ \ f'(0) = 0 \\
f''(x) & = \cosh x , \ \ \ f''(0) = 1 \\
f'''(x) & = \sinh x , \ \ \ f'''(0) = 0 \\
f^{(4)} (x) & = \cosh x , \ \ \ f^{(4)} (0) = 1 \\
f^{(5)} (x) & = \sinh x , \ \ \ f^{(5)} (0) = 0
\end{align*}\]
となるので、あとはマクローリン展開の公式に入れるだけ。
\[\begin{align*}
f(x) & \fallingdotseq f(0) + \frac{ f'(0) }{1!} x + \frac{ f''(0) }{2!} x^2 + \frac{ f'''(0) }{3!} x^3 + \frac{ f^{(4)} (0) }{4!} x^4 + \frac{ f^{(5)} (0) }{5!} x^5
\\ & = 1 + \frac{1}{2!} x^2 + \frac{1}{4!} x^4
\end{align*}\]
[導出] tanh x のマクローリン展開
\( \frac{1}{ \cosh^2 x } \) を微分していくのは少しつらいので、\[
\frac{1}{ \cosh^2 x } = 1 - \tanh^2 x
\]の公式をうまく使おう。
\( f(x) = \tanh x \) とする。
\[\begin{align*}
f(x) & = \tanh x \\
f'(x) & = \frac{1}{ \cosh^2 x }
\\ & = 1 - \tanh^2 x \\
f''(x) & = - 2 \tanh x \cdot \frac{1}{ \cosh^2 x }
\\ & = -2 \tanh x ( 1 - \tanh^2 x )
\\ & = 2 \tanh^3 x - 2 \tanh x \\
f'''(x) & = 6 \tanh^2 x \cdot \frac{1}{ \cosh^2 x } - 2 \cdot \frac{1}{ \cosh^2 x }
\\ & = 6 \tanh^2 x ( 1 - \tanh^2 x ) - 2 ( 1 - \tanh^2 x )
\\ & = -6 \tanh^4 x + 8 \tanh^2 x - 2 \\
f^{(4)} & = - 24 \tanh^3 x \cdot \frac{1}{ \cosh^2 x } + 16 \tanh x \cdot \frac{1}{ \cosh^2 x }
\\ & = - 24 \tanh^3 x (1 - \tanh^2 x) + 16 \tanh x (1 - \tanh^2 x)
\\ & = 24 \tanh^5 - 40 \tanh^3 x + 16 \tanh x \\
f^{(5)} & = 120 \tanh^4 \cdot \frac{1}{ \cosh^2 x } - 120 \tanh^2 x \cdot \frac{1}{\cosh^2 x} + 16 \cdot \frac{1}{ \cosh^2 x}
\\ & = 120 \tanh^4 x (1 - \tanh^2 x) - 120 \tanh^2 x (1 - \tanh^2 x) + 16 (1 - \tanh^2x )
\\ & = - 120 \tanh^6 x + 240 \tanh^4 x - 136 \tanh^2 x + 16
\end{align*}\]
つぎに、\( x = 0 \) を代入する。
\[\begin{align*}
f(0) & = 0 \\
f'(0) & = 1 \\
f''(0) & = 0 \\
f'''(0) & = -2 \\
f^{(4)} & = 0 \\
f^{(5)} & = 16
\end{align*}\]
となるので、あとはマクローリン展開の公式に入れるだけ。
\[\begin{align*}
f(x) & \fallingdotseq f(0) + \frac{ f'(0) }{1!} x + \frac{ f''(0) }{2!} x^2 + \frac{ f'''(0) }{3!} x^3 + \frac{ f^{(4)} (0) }{4!} x^4 + \frac{ f^{(5)} (0) }{5!} x^5
\\ & = \frac{1}{1!} x - \frac{2}{3!} x^3 + \frac{16}{5!} x^5
\\ & = x - \frac{1}{3} x^3 + \frac{2}{15} x^5
\end{align*}\]
(3) 例題で計算練習
では、実際に例題で双曲線関数のマクローリン展開の問題を解いてみましょう。
つぎの関数のマクローリン展開を5次の項まで求めなさい。\[
f(x) = \sinh 2x
\]
[解説4-1] 解法1 … ごり押しで解く
\[\begin{align*}
f(x) & = \sinh 3x , \ \ \ f(0) = 0 \\
f'(x) & = 2 \cosh 3x , \ \ \ f'(0) = 2 \\
f''(x) & = 4 \sinh 3x , \ \ \ f''(0) = 0 \\
f'''(x) & = 8 \cosh 3x , \ \ \ f'''(0) = 8 \\
f^{(4)} (x) & 16 = \sinh 3x , \ \ \ f^{(4)} (0) = 0 \\
f^{(5)} (x) & 32 = \cosh 3x , \ \ \ f^{(5)} (0) = 32
\end{align*}\]
となるので、あとはマクローリン展開の公式に入れるだけ。
\[\begin{align*}
f(x) & \fallingdotseq f(0) + \frac{ f'(0) }{1!} x + \frac{ f''(0) }{2!} x^2 + \frac{ f'''(0) }{3!} x^3 + \frac{ f^{(4)} (0) }{4!} x^4 + \frac{ f^{(5)} (0) }{5!} x^5
\\ & = 2x + \frac{8}{3!} x^3 + \frac{32}{5!} x^5
\\ & = 2x + \frac{4}{3} x^3 + \frac{4}{15} x^5
\end{align*}\]
[解説4-2] 解法2 … sinh x の公式をうまく使う
\( \sinh x \) の5次までのマクローリン展開は\[
\sinh x \fallingdotseq x + \frac{1}{3!} x^3 + \frac{1}{5!} x^5
\]で計算できる。
この \( x \) を \( x \to 2x \) とすればOK。
よって、\[\begin{align*}
f(x) & = (2x) + \frac{1}{3!} (2x)^3 + \frac{1}{5!} (2x)^5
\\ & = 2x + \frac{4}{3} x^3 + \frac{4}{15} x^5
\end{align*}\]と \( f(x) \) の5次の項までのマクローリン展開を求められる。
5. さいごに
今回は、双曲線関数の中でも
- 微分・積分
- 極限
- マクローリン展開
など、微積に関わる分野を中心に解説をしていきました。
次回は、双曲線関数の逆関数についてみていきましょう。
(双曲線関数に関するラスト記事になる予定です)
注釈
| ↑1 | \( x^2 \sin x \) などの多項式×三角関数の積分と同じように、多項式は微分するといつか0になるため、多項式を部分積分の微分する側にすると、いつか連鎖がストップしてくれるため。 |
|---|
関連広告・スポンサードリンク