うさぎでもわかる離散数学　第1羽　集合編

こんにちは！
離散数学が難しすぎてわからないと言っている人が多かったので簡単にまとめたものを書いてみたいと思います！

初回である第1羽は「集合」についてまとめてみました。ぜひ見てください！

※注意

簡単にまとめているので、厳密的な定義とは若干違うことを書いているかもしれません。ご了承ください。

 

用語やら記号を解説する前に一部の集合を定義しておこうと思います。

全体集合 \( U \) を1以上10以下の自然数とする。つまり、\( U = \{1,2,3,4,5,6,7,8,9,10\} \) とする。また、集合 \( A,B,C \) をそれぞれ
\[ A = \{2,4,6,8,10\}, B = \{3,6,9\}, C = \{4,8\} \]としましょう。

スポンサードリンク

まずは高校で習う記号や用語の解説

01: 全体集合  \( U \)

考える対象の全体を表す集合を表す。英語で Universal Set と呼ばれるため、 \( U \) という記号で表されることが多い。

02: 空集合  \( \phi \)   \( \emptyset \) 

要素（集合の中身）を1つももたない集合のことである。厳密な空集合の記号は \( \emptyset \)  だが、参考書によっては \( \phi \) が使われることも多く、私も \( \phi \) の記号のほうが好きなため、本記事では空集合は \( \phi \) で表すことにする。

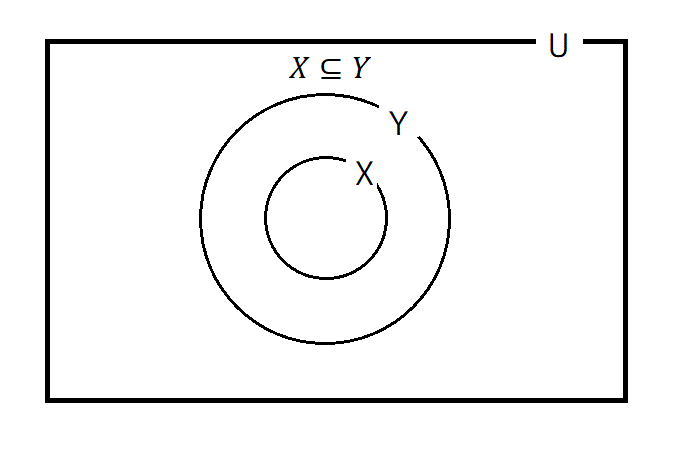
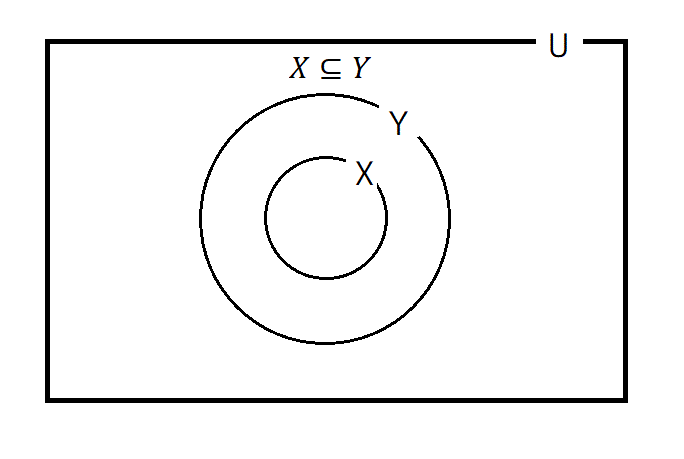
03: 部分集合

\( x\in X \) ならば常に \( x\in Y \) が成り立つとき、つまり\( X \) の要素全てが \( Y \) の中に含まれているとき、\( X \) は \( Y \) の部分集合といえ、 \( X\subseteq Y \) のように表せる。この場合、集合 \( X \) は集合 \( Y \) の部分集合であるという意味を持つ。

今回の例で言うと、\( \{2,8\}\subseteq A, C \subseteq A \) などが挙げられる。

※先生によって部分集合の記号は異なることがあるので注意。
 \( \subseteq \) のかわりに \( \subset \) や \( \subseteqq \) を部分集合とするところもある。（高校数学の場合は \( \subset \) が部分集合と習うはず。）

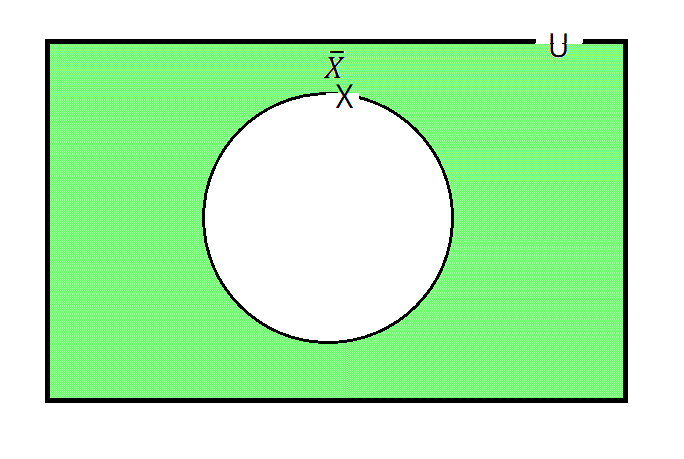
04: 補集合 \( \overline{X} \) , \( X^{c} \)

全体集合 \( U \) のうち、\( \overline{X} \) に属さない要素全体を表す。

今回の例の場合、\( \overline{A} = \{1,3,5,7,9\} \) , \( \overline{B} = \{1,2,4,5,7,8,10\} \) となる。 

05: \( a\in X \)

\( a \) は集合 \( X \) に属する。

今回の例で言うと、\( 2\in A, 6\in B \) などが挙げられる。

06: \( a\notin X \)

\( a \) は集合 \( X \) に属さない。

今回の例で言うと、\( 5\notin A, 7\notin B \) などが挙げられる。

 

07: \( X = Y \)

集合 \( X \) と集合 \( Y \) の要素は等しい、つまりすべての要素が等しい。
定義で言うと、 \( X \subseteq Y \) かつ \( Y \subseteq X \) が成り立つとき、 \( X = Y \) ということができる。

今回の例で言うと、\( \{3,6,9\} = B \) は成り立つが、\( \{2,8\} = A \) は成り立たない。

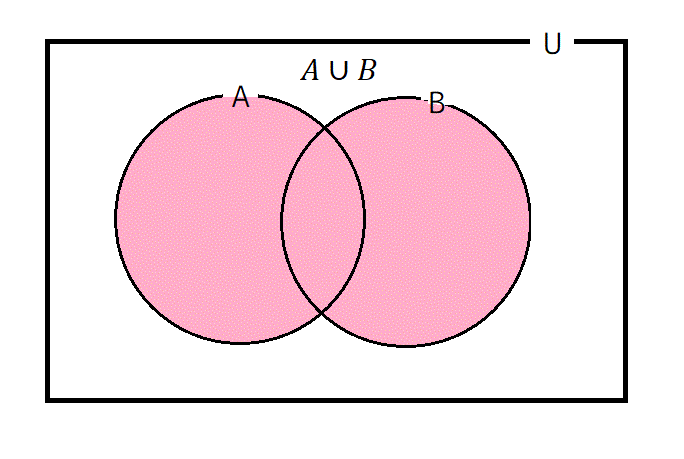
08: 和集合 \( X \cup Y \)

集合 \( X \) と集合 \( Y \) の和集合、つまり \( X,Y \) のうち少なくともどちらか一方に属する要素全体の集合である。記号の読み方としては、「和集合」、「かっぷ」、「ゆにおん」、「または」などがあります。（厳密な先生だと「または」って呼ぶと怒る先生もいるので注意）

今回の例で言うと、\( A \cup B = \{2,3,4,6,8,9,10\}, A \cup C = \{2,4,6,8,10\}, B \cup C = \{3,4,6,8,9\} \) となる。 

 09: 積集合（共通部分） \( X \cap Y \)

 

集合 \( X \) と集合 \( Y \) の積集合、つまり \( X,Y \) の両方に属する要素全体の集合である。読み方としては、「積集合」、「共通部分」、「ぎゃっぷ」、「いんたーせくしょん」、「かつ」などがあります。（「かつ」と読むと「または」のように怒る先生もいるので注意）

今回の例で言うと、\( A \cap B = \{6\}, A \cap C = \{4,8\}, B \cap C = \phi \) となる。

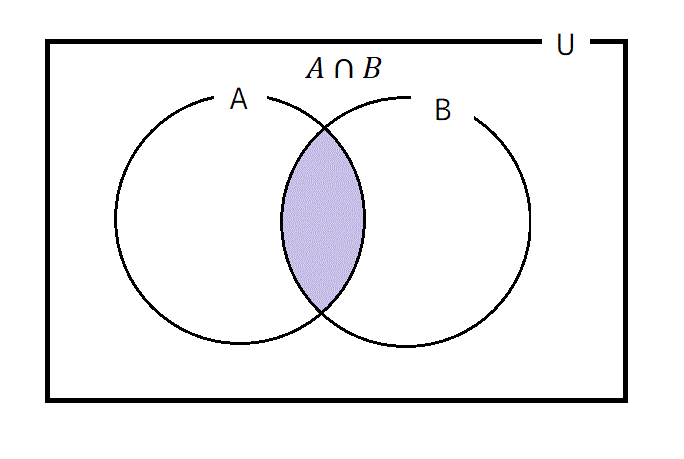
（修正：10月17日　積集合の説明の一部分が和集合になっていたミスを修正しました。）

[ここからが大学で習う範囲] 

先程と同じく、\( A = \{2,4,6,8,10\} \),  \( B = \{3,6,9\} \), \( C = \{4,8\} \) とします。

10: 差集合 \( X - Y \)

集合 \( X \) に含まれているが、集合 \( Y \) には含まれていない要素を除いた集合である。\( X \cap \overline{Y} \) と同じである。
今回の例の場合、\( A - B = \{2,4,8,10\} \) , \( A - C = \{2,6,10\} \) となる。

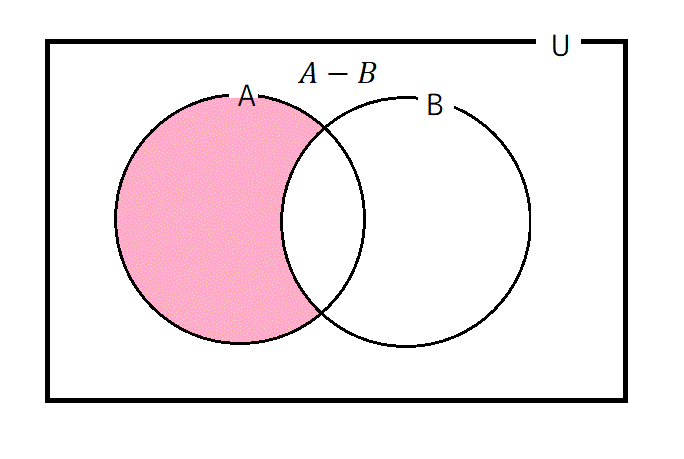
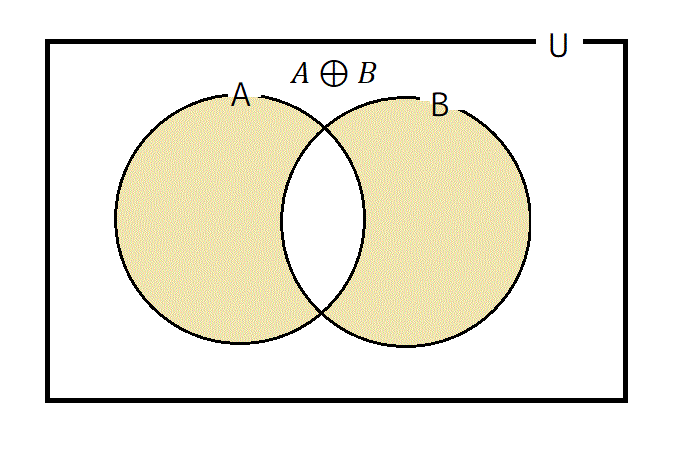
11: \( X \oplus Y \) , \( X \Delta Y \)

集合 \( X \) と集合 \( Y \) のうち、片方の集合のみにある要素を集めた集合である。
\( X \oplus Y = (X - Y) \cup (Y - X) = (X \cap \overline{Y}) \cup (Y \cap \overline{X}) \) と変形できる。 

今回の例の場合、\( A \oplus B = \{2,3,4,8,9,10\} \) , \( A \oplus C = \{2,6,10\} \) となる。

12: \( |X| \)

集合 \( X \) に含まれている要素の個数を表す。

今回の例の場合、\( |A| = 5 \) , \( |B| = 3 \) となる。

13: べき（冪）集合　\( 2^{X} \)

集合 \( X \) の部分集合から作られる集合をすべて集めたもの。なんと、集合の中に集合が入ってしまう。マトリョシカっぽいね。

例えば、\( S = \{1,2,3\} \) とする。まず、\( S \) から作成できる部分集合を要素数ごとに場合分けしてすべて列挙していく。

(1) 要素数が0のとき：\( \phi \) の1個 （個数計算式：\( {}_3 C _0  = 1 \) ）
(2) 要素数が1のとき：\( \{1\},\{2\},\{3\} \) の3個 （個数計算式：\( {}_3 C _1  = 3 \) ）
(3) 要素数が2のとき：\( \{1,2\},\{1,3\},\{2,3\} \) の3個 （個数計算式：\( {}_3 C _2  = 3 \) ）
(4) 要素数が3のとき：\( \{1,2,3\} \) の1個 （個数計算式：\( {}_3 C _3  = 1 \) ）

の合計8個となる。

べき集合はこれらの集合をすべて集めたものなので、\( S \) の冪集合 \( 2^{S} \) は、\( 2^{S} = \{\phi,\{1\},\{2\},\{3\},\{1,2\},\{1,3\},\{2,3\},\{1,2,3\}\} \) とすることができる。

 

ちなみに要素数が \( n \) 個の集合のべき集合の要素数は \( 2^{n} \) 個と求めることができる。これは、それぞれの要素に対して、選ぶか選ばないかの2つの可能性がある

\( n \) 個の要素に対して、選ぶか選ばないの2つの可能性があるだから、 要素数は \( 2^{n} \) 個になるからである。
（本当か？って人は \( n = 3,4 \) くらいで試して実験してみてください。）

14: 直積集合 \( X \times Y \)

集合 \( X \) と集合 \( Y \) に対して、それぞれの集合から1つずつ要素を取り出して組にしたものを表す。例えば、\( X = \{1,2,3\} \) , \( Y = \{a,b\} \) とすると、\( X \times Y = \{(1,a),(1,b),(2,a),(2,b),(3,a),(3,b)\} \) と表せる。

ちなみに集合 \( X \) の要素数を \( n \) 個、集合 \( Y \) の要素数を \( m \) 個とすると、直積集合 \( X \times Y \) の要素数は \( nm \) 個となる。

15: 商集合（分割） \( A/{\sim} \)

例えば、集合を \( \{a,b,c,d,e\} \) とします。これらの集合を \( \{\{a,b,e\},\{c,d\}\} \) とか、\( \{\{a,c\},\{b,e\},\{e\}\} \)  のように小さな集合に分割することを類別するといいます。類別するときには、もとのすべての集合の要素が、必ず小さな集合のどこかに入るようにしてください（２つ以上の小さな集合に入るのもだめ）。

 

集合\( A \) を同値類 \( \sim \) で類別したものを商集合 \( A /{\sim} \) で表します。

 

例えば 集合 \( A \) を \( A = \{2,9,12,19,23,25\} \) とし、同値類 \( \sim \) を「要素を5で割ったときのあまりが等しいもの」とします。すると、

\[ A /{\sim} = \{\{2,12\},\{9,19\},\{23\},\{25\}\} \] 

 

となります。ちなみに \( \sim \) の記号で同値類を定義することもOK。

例えば商集合 \( A /{\equiv} \) とすれば、集合 \( A \) に含まれてる論理式の中で、同値なものごとに類別するなんてことができちゃう！

 

用語の説明はここまで。高校までは集合の要素として、数字だけしか入っていなかったけど、大学範囲になると、数字以外にも文字が入ったりさらには集合の中に集合が入ったりするのだ！

 

集合の中に集合が入るのでマトリョシカ状態になり、記号の意味を正しく理解してないとわけわかめである。集合の中に集合が入るので、\( \{\phi,\{1,\phi\}\} \) のように、集合の中に空集合がたくさん入ってわけがわからなくなるのだ。

わけがわからなくなりそうなときは、集合の要素がなにかをすべて書き出していけばよい。下のように図を書いてみるといいかも。

 \( S \) の要素、つまり \( S \) の箱の中に入っているものは、\( \phi \) と、\( \{1,\phi\} \) の2つである。箱で例えると、空の箱と、1と空の箱が入った箱である。

もう1つ集合の中に集合が入っているものの例を挙げてみよう。\( S = \{1,\{2,3\}\} \) とする。同じく図示してみよう。

この集合の要素は\( 1 \)と\( \{2,3\} \)、つまり箱の中身は1と2と3が入った箱である。

 

つぎの4つの関係が成立するかどうかを少し考えてみよう。

(1) \( 1 \in \{1,\{2,3\}\} \)
(2) \( 2 \in \{1,\{2,3\}\} \)
(3) \( \{1,2\} \subseteq \{1,\{2,3\}\} \)
(4) \( \{2,3\} \subseteq \{1,\{2,3\}\} \)

この数式の(1),(2)を日本語、箱に置き換えると、

(1) 1は集合 \( S \) の要素である。（\( S \) の箱の中に1はある）
(2) 2は集合 \( S \) の要素である。（\( S \) の箱の中に2はある）

となる。(1)の場合は\( S \) の箱の中に1はあるので正しいことがわかる。

一方(2)の場合は\( S \) の箱の中に入っているのは2の単品ではなく、2と3が入った箱がある。2の単品がないため、この関係が正しいとは言えない。よって誤りなことがわかる。

 

また、部分集合である、というのは「左辺に入っている箱の中身はすべて右辺の箱に入っている」ということである。(3),(4)に出てくる \( \{1,2\} \) と \( \{2,3\} \) はそれぞれ1と2が入った箱と2と3が入った箱を表している。つまり、

(3) 1と2の要素が集合 \( S \) にある。（\( S \) の箱の中には1と2がある）
(4) 2と3の要素が集合 \( S \) にある。（\( S \) の箱の中に2と3がある）

と日本語では言える。この2つの日本語は正しいかを考えよう。(3)の場合、1の単品は \( S \) の中にあるが、2の単品はないため正しくないことがわかる。(4)の場合は2の単品どころか3の単品すらないためこちらも正しくない。

よって(3)と(4)はどちらも誤りである。

 

ちなみに(4)を正しい関係に変えるためには、「2と3が入った箱が\( S \) の中にある」とするか、「\( S \) の箱の中に1と2の箱がある」とする必要がある。これを数式にすると、\( \{2,3\} \in \{1,\{2,3\}\} \) もしくは \( \{\{2,3\}\} \subseteq \{1,\{2,3\}\} \) とすると正しい関係である、ということができるよ！

 

スポンサードリンク

例題などなど

ここからは、例題を交えて解説をしていきたいとおもいます。

例題1（レベル1）

\( \phi \in \phi \) と \( \phi \subseteq \phi \) 、成り立つのはどっち？

解答1（レベル1）

\(  \phi \) は空集合なので要素を1つも持たない。よって \(  \phi \) も要素に持たず、\( \phi \in \phi \) は誤りであることがわかる。
また、空集合はすべての要素の部分集合なので、\( \phi \subseteq \phi \) は成立する。
よって答えは \( \phi \subseteq \phi \) となる。

 

例題2（レベル2）

\( \{1,\phi\} \in \{1,\{1,\phi\}\} \) と \( \{1,\phi\} \subseteq \{1,\{1,\phi\}\} \) 、成り立つのはどっち？

解答2（レベル2）

このように複雑になるとわけが分からなくなってくるので左辺と右辺の集合の中身、つまり箱の中身はなにかを1つずつしらべていく。

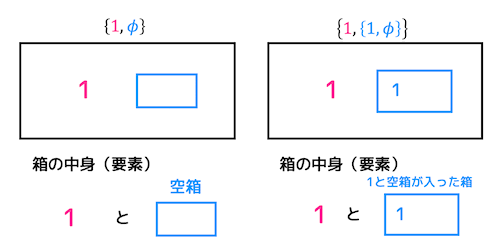
\( \{1,\phi\} \) の箱の中には1と空の箱が入っている。
\(  \{1,\{1,\phi\}\} \) の箱の中には1と1と空の箱が入った箱が入っている。

\( \{1,\phi\} \in \{1,\{1,\phi\}\} \) は、「1と1の空の箱が入った箱 \(  \{1,\{1,\phi\}\} \)  に1のと空の箱が入った箱 \( \{1,\phi\} \) はありますか？」という問題に変わる。実際見てみると1と空の箱が入った箱があるのでこれは正しいことがわかる。

 

一方 \( \{1,\phi\} \subseteq \{1,\{1,\phi\}\} \) というのは、左辺に入っている要素が右辺に全て入っていないと正しいと言えない。つまり、「1と1の空の箱が入った箱 \(  \{1,\{1,\phi\}\} \) の中には1と空の箱 \(  \{1,\{1,\phi\}\} \) はありますか？」という問題に変わる。この場合、右辺に1はあるが、空の箱は入っていない。よってこれは誤りだということがわかる。

よって答えは \( \{1,\phi\} \in \{1,\{1,\phi\}\} \) となる。

 

例題3（レベル2）

\( \phi \cup \{\phi\} \) と \( \{\phi\} \cap \{1,\phi,\{\phi\}\} \) を求めなさい。

解答3（レベル2）

\( \phi \) には要素は存在しない。（箱の中身：空）
\(   \{\phi\} \) の要素は空集合である。（箱の中身：空の箱）

よって、\( \phi \cup \{\phi\} = \{\phi\} \) となる。（中身：空の箱）

また、\(   \{1,\phi,\{\phi\}\} \) の要素は1と空集合と空集合からなる集合である。
（中身：1、空の箱、空の箱が入っている箱の3つ）

「空の箱」と「1、空の箱、空の箱が入っている箱」の共通している箱の中身は「空の箱」となる。

よって、 \( \{\phi\} \cap \{1,\phi,\{\phi\}\} = \{\phi\} \) となる。

例題4（レベル3）

集合 \( S \) を \( S = \{1,\{2,3\}\} \) とする。次の(1)～(3)の問いに答えなさい。
(1) 集合 \( S \) の部分集合を全て求めなさい。
(2) 集合 \( S \) のべき集合 \( 2^{S} \) を求めなさい。
(3) \( \{1\} \in 2^{S} \)、\( \{\{2,3\}\}\subseteq 2^{S} \) のうち、正しい関係はどちらか？

解答4

(1) 集合の要素数ごとに場合分けをすればよい。
(i) 要素数が0の部分集合：\( \phi \) の1つ
(ii) 要素数が1の部分集合：\( \{1\},\{\{2,3\}\} \) の2つ 
(iii) 要素数が2の部分集合：\( \{1,\{2,3\}\} \) の1つ
よって答えは \( \phi,\{1\},\{\{2,3\}\},\{1,\{2,3\}\} \) の4つとなる。
（箱に言い換えると空の箱、1が入った箱、2と3が入った箱に入った箱、1と2と3が入った箱に入った箱）

(2) \( S \) のべき集合は、\( S \) の部分集合から作られる集合をすべて集めたものである。(1)より、\( 2^{S} = \{\phi,\{1\},\{\{2,3\}\},\{1,\{2,3\}\}\} \) と求めることができる。

(3) 例題1のように要素（箱）を全部書いてから比較したほうがいいかも。
\( S \) のべき集合の中に \( \{1\} \) （1が入った箱）は入っているため、\( \{1\} \in 2^{S} \) は正しいといえる。

また、2と3が入った箱のべき集合 は\( S \) のべき集合の中には含まれていない（べき集合の中にあるのは2と3が入った箱 \( \{2,3\} \) ではなく、2と3がが入った箱が入っている箱 \( \{\{2,3\}\} \) なので微妙に違う）ので、\( \{\{2,3\}\}\subseteq 2^{S} \) は誤りなことがわかる。

よって \( \{1\} \in 2^{S} \) が正しい。

 

最後に演習問題のGoogleフォームを設置しました。
理解しているかのチェックに使ってみてください。
10分もあればできると思います。

forms.gle

スポンサードリンク

最後に

今回は離散数学では避けて通れないであろう集合分野について少しまとめてみました。
第2羽では、命題と真理値表（場合分けみたいなもん）について少し説明したいとおもいます。ではまた次回！

 

第2羽はこちらから！

www.momoyama-usagi.com