スポンサードリンク
こんにちは、ももやまです。
全射、単射、写像、難しくありませんか?
多くの教科書、およびネットでは難しい数式や専門用語がずらりと並べられて説明されていますよね。
今回は、あまり専門用語を使わずに簡単な言葉で関数・写像、および全射と単射についてまとめたいと思います。
おまけとして合成写像、逆写像、全域関数、部分関数をまとめていますがこちらは番外編なので見なくても大丈夫です。余裕があるって人は理解してみるといいと思います。
前回の第5羽はこちらから
半順序、ハッセ図についてまとめています。
☆注意☆
先生によって、写像の解釈が2パターンに分かれるので注意してください
(1) 写像は関数よりも広義、つまり写像の特殊なパターンが関数という扱い
(2) 写像と関数は名前だけ違ってて意味は全く同じ
この記事では「6.全域関数、部分関数」以外の説明では (1) として扱っていきます。一応 (2) の場合の注意もほんの少しですが行っています。
線形代数学における写像についてはこちらの3つの記事をご覧ください!
前編 基礎について
中編 線形写像における 合成写像・逆写像
後編 線形写像の核空間、像空間・線形写像における全射・単射・全単射
スポンサードリンク
1.関数ってなに?
中学、高校で関数というのを習いましたよね。例えば、
\( y = 2x + 1 \)
\( y = x \log x + x \)
\( y = \sin x + \cos x \)
とかがありますよね。つまり関数というのは入力した値 \( x \) によって何らかの処理がされて \( y \) として出力される仕組み、さらに簡単に言うと何かしらの値 \( x \) を入れたら、何らかの値 \( y \) が返ってくる魔法の箱となりますよね。
\( y \) のことを \( f(x) \) と書くことも多いですよね。これは「入力した値 \( x \) に関係 \( f \) を適用したもの」と言えるからです。
また、関数の入力 \( x \) が取りうる値の範囲を定義域といい、関数の出力 \( f(x) \) が取りうる値の範囲のことを値域と言います。
スポンサードリンク
2.写像
関数というのは、数字に関係がある写像のことを表します(高校までにならった関数はすべて数式で表されてましたよね)。つまり、関数は写像です。
写像は関数という概念をより広くした、つまり数字以外にも例えば文字などの対応付けにも対応したものなのです。*1
写像は集合 \( A \) の各要素にそれぞれの集合 \( B \) の要素がただ1つだけ関係している関係のことなのですが、日本語で説明されても難しいので図を使って説明したいと思います。
集合 \( A \) から集合 \( B \) への写像を \( f \) とします。これを記号で表すと、 \( f: A \to B \) となります。集合 \( A \) のある要素 \( a \) と \( b \) の対応付けを \( f(a) = b \) と表したり、\( f: a \mapsto b \) と表したりします。
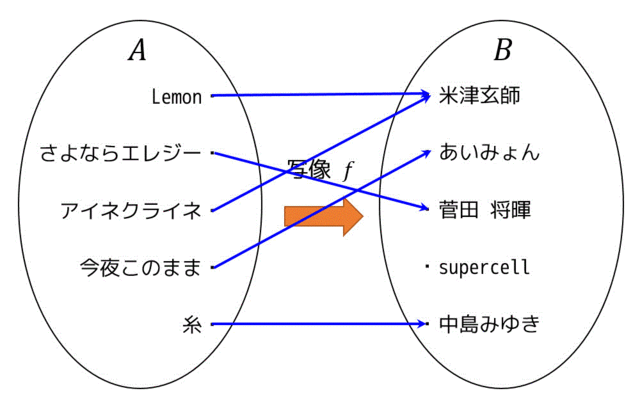
写像の例を1つ示したいと思います。集合 \( A \) を曲名の集合 A = {Lemon,さよならエレジー,アイネクライネ,今夜このまま,糸} とし、集合 \( B \) をアーティスト名の集合 B = {米津玄師,あいみょん,菅田 将暉,supercell,中島みゆき} とします。
写像の対応元の集合 \( A \) のことを始域、もしくは定義域と言い、対応先の集合 \( B \) のことを終域と言います。また、対応先の集合 \( B \) のうち、対応元 \( A \) から関係がある要素をすべて集めた集合、つまり \( \{f(a) | a \in A\} \) のことを値域と呼びます。
この写像を図で表すとこのようになります。青線は、集合 \( A \) と集合 \( B \) の対応付けを表しています。
この場合、
始域・定義域:{Lemon,さよならエレジー,アイネクライネ,今夜このまま,糸}
終域:{米津玄師,あいみょん,菅田 将暉,supercell,中島みゆき}
値域:{米津玄師,あいみょん,菅田 将暉,中島みゆき}
となります。
※supercellには集合 \( A \) からの関係がないので値域には含まれない
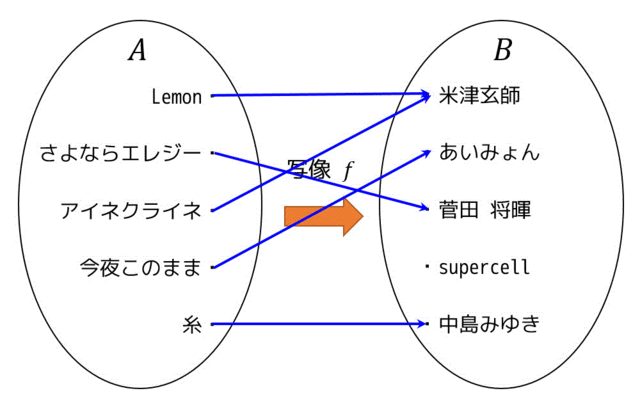
写像の条件を図で言い換えると、始点側 \( A \) の要素から1本だけの矢印が出ている関係と言うことができます。集合 \( A \) のことを定義域とも言うのですが、高校までに習った関数の場合だと、「定義域なのに値がない」とか、「\( x \) を代入したら2つ以上の解が出る」なんてことはないですよね。
写像とは言えない例を2つ示したいと思います。
例1:始点側が矢印がない要素が存在するパターン
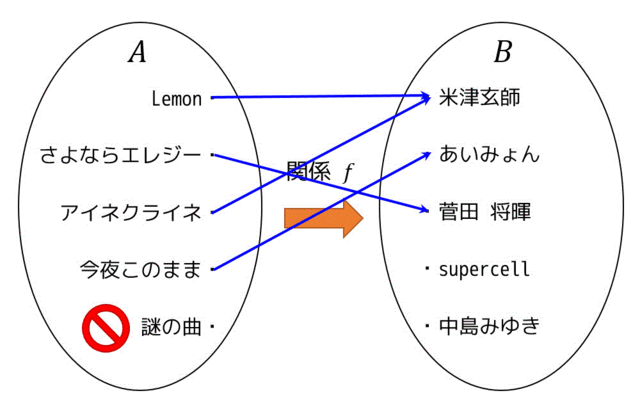
始点に矢印がない要素があるということは、関数に例えると \( x \) に定義域の範囲の値を入れても \( f(x) \) の値が出てこないという怖いことになります。
写像でも同じように始点に矢印がない要素があれば写像とは言えなくなります。
ちなみにこの場合、定義域には「謎の曲」は含まれません。
例2:始点側が2つ以上ある要素が存在するパターン
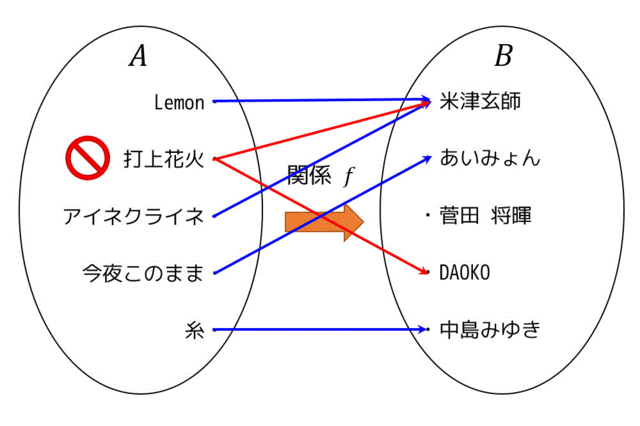
始点が2つ以上あるということは、関数に例えると \( x \) に定義域の範囲の値を入れると \( f(x) \) の値が2パターン以上出てくるというありえないことになります。
写像でも同じように始点が2つ以上あったら写像とは言えなくなります。
スポンサードリンク
3.全射・単射
(1) 全射
\( \forall b\in B,\,\exists a\in A \;\text{ s.t. }f(a)=b \)
集合 \( B \) の任意の要素 \( b \) に対して、\( f(a) = b \) を満たす \( b \in B \) を満たす \( a \in A \) が存在すること。
言い換えると、ゴール先の集合 \( B \) のどの要素も少なくとも1つは関係を持っているということです。
全射の具体例を1つ図で示してみます。これを図1とします。
この図の場合、\( B \) の要素は全て集合 \( A \) から矢印が刺されていますよね。よってこれは全射ということができます。
(2) 単射
\( (\forall a_1, a_2 \in A)\; a_1 \neq a_2 \ \Longrightarrow \ f(a_1) \neq f(a_2) \)
\( (\forall a_1, a_2 \in A)\; f(a_1)=f(a_2) \ \Longrightarrow \ a_1=a_2 \)
集合 \( A \) の要素 \( a_1, a_2 \) が異なれば \( f(a_1),f(a_2) \) の結果も必ず異なるということ。
さらに分かりやすくすると、スタート地点の集合 \( A \) が異なればゴール地点の集合 \( B \) も必ず異なるということです。
こちらも図で例を示したいと思います。
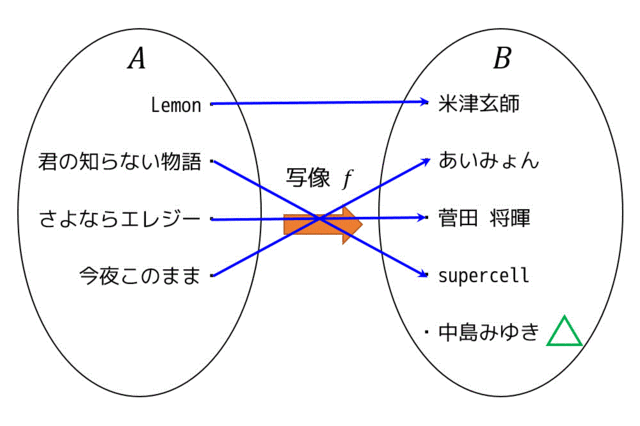
この図の場合、確かにスタート地点 \( A \) が異なれば、ゴール地点 \( B \) も異なることがわかりますよね。よって単射ということができます。
(3) 全単射
全射と単射の両方の条件を満たすものを全単射と言います。
図で全単射の例を示します。
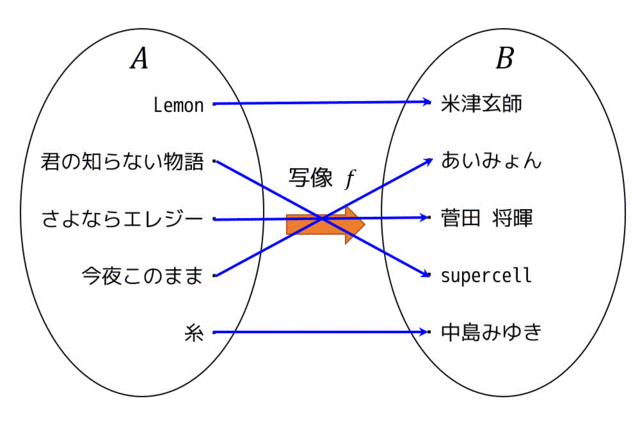
この図の場合、「\( B \) の要素は全て集合 \( A \) から矢印が刺されていて(全射であり)」、「スタート地点 \( A \) が異なれば、ゴール地点 \( B \) も異なる(単射である)」と言えますよね。
よって全射でも単射でもあるので全単射です。
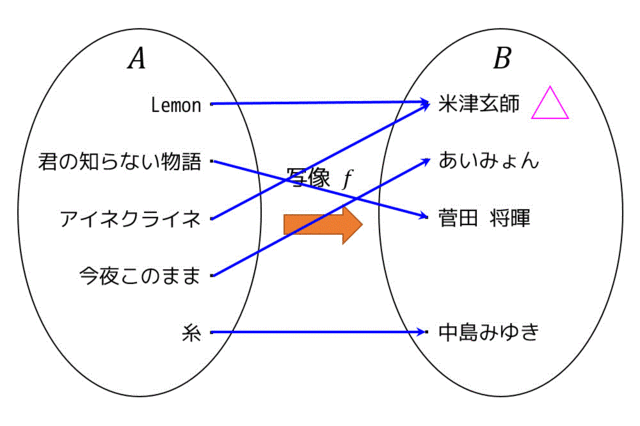
ちなみに(1),(2)の図が全単射でない理由は、
(1) △の部分に要素が2つ集まっているので単射ではない。
(2) △の地点に1つも矢印が刺されていないので全射ではない。
だからです。
さらに「2.写像」の図の写像 \( f \) はすべて全射でも単射でもありません。米津玄師に矢印が2つ集まっているから単射ではなく、supercellに矢印が刺されていないため全射でもないからです。
ではここで例題を2つ解いてみましょう。
例題1
集合 \( A \) を \( A = \{1,2,3,4\} \) とし、集合 \( B \) を \( B = \{a,b,c,d\} \) とする。このとき、次の(1)~(4)の関係は写像であるかないかを答えなさい。さらに写像の場合、全射、単射であるかどうかも答えなさい。
(1) \( R_1: A \to B, \ \ R_1 = \{(1,a),(2,c),(3,b)\} \)
(2) \( R_2: A \to B, \ \ R_2 = \{(1,b),(2,c),(3,d),(4,a)\} \)
(3) \( R_3: A \to B, \ \ R_3 = \{(1,c),(4,a),(3,b),(2,b)\} \)
(4) \( R_4: B \to A, \ \ R_4 = \{(a,4),(b,3),(a,1),(c,2)\} \)
解答1
(1) 要素4から集合 \( B \) の要素への関係ないので写像とは言えない。
(2) 要素 1,2,3,4 からそれぞれ集合 \( B \) の要素への関係があるので写像である。また、集合 \( B \) の各要素に集合 \( A \) から1つずつ関係(矢印)があるので全射でも単射でもある。
(3) 要素 1,2,3,4 からそれぞれ集合 \( B \) の要素への関係があるので写像である。しかし、要素 \( d \) への関係がないため全射とは言えず、要素 \( b \) への関係が2つあるため単射とも言えない。
(4) 要素 \( a \) から2つの関係があるため写像と言えない。
例題2
\( x,y \in \mathbb{R} \) (\( x,y \) を実数)とする。このとき、つぎの \( x \) から \( y \) への関数は全射、単射であるかどうか答えなさい。
(1) \( y = 2x - 3 \)
(2) \( y = 2^{x} \)
(3) \( y = \frac{1}{2} x^{2} \)
(4) \( y = \cos x \)
(5) \( y = x^{3} - 3 x + 4 \)
解答2
実際にグラフを書いてみるのをおすすめします。今回はこちらのDesmosというサイトで図示したものを埋め込みました。
(1) \( y = 2x - 3 \)
グラフを見ればわかるのですが、\( x \) の値と \( y \) の値が1対1で対応していますよね。なので全射、単射のどちらとも満たします。
(2) \( y = 2^{x} \)
\( x \) の値と \( y \) の値が1対1で対応するので単射ではあるのですが、\( y \leqq 0 \) になることはありませんよね。なので全射とは言えません。
(3) \( y = \frac{1}{2} x^{2} \)
例えば \( y = 2 \) のときの \( x \) の取りうる値は \( x = 2,-2 \) の2つ存在しますよね。なので1対1対応してるとは言えませんよね。さらに \( y \lt 0 \) になることもないので全射とも言えません。
(4) \( y = \cos x \)
例えば \( y = 1 \) のとき、\( x \) の取りうる値としては \( x = 0 \) 以外にもたくさんありますよね。なので1対1対応とは言えません。\( -1 \leqq y \leqq 1 \) が値域なので全射でもありません。
(5) \( y = x^{3} - 3 x + 4 \)
このグラフを図示するためには、極値を調べて増減表を書く必要があります。
\( y' = 3 x^{2} - 3 = 3 (x + 1)( x - 1) \)
\( x = -1 \) のとき極大値 \( 6 \) 、\( x = 1 \) のとき極小値 \( 2 \)
あとは増減表(省略します)を書けば、
のようなグラフになります。
グラフより、全射であるのはわかるだろう。しかし、例えば \( y = 6 \) のとき \( x = -1,2 \) となり、1対1対応ではないので単射ではない。
ここら編から少し発展的な内容なので話がかなりややこしくなってきます。おまけ程度に見てください。うさぎでも多分わかりません…(;_:)
4.合成関数・合成写像
2つの関数 \( y = f(x) \) 、\( z = g(y) \) がある。\( f(x) \) の値域が\( g(y) \) の定義域に含まれているとき、\( z = g(y) = g(f(x)) \) を \( f(x),g(y) \) の合成関数という。\( z = g \circ f (x) \) とも書けます。
例えば、\( \sin(3x + 5) \) というのは、\( f(x) = 3x + 5 \) と \( g(x) = \sin x \) の合成である。
合成する順番を逆にする場合は注意してください。\( f \) と\( g \) の合成 \( g \circ f \) が定義できても、 \( g \) と \( f \) の合成 \( f \circ g \) が定義されないこともある。また、両方とも定義できた場合でも計算結果は異なることが多い。[交換則は成り立たない]
例としては、
\( f(x) = x + 1 \) , \( g(x) = 2x^{2} \) とする。
\( g \circ f (x) = g(f(x)) = g(x+1) = 2(x+1)^{2} = 2x^{2} + 4x + 2 \)
\( f \circ g (x) = f(g(x)) = f(2x^{2}) = 2x^{2} + 1 \)
なので計算結果が変わりますよね。
ただし、\( h \circ g \circ f \) のように3つ以上の合成を行うときは、\( (h \circ g) \circ f \)、\( h \circ (g \circ f) \) のどちらから計算を行っても計算結果は同じになります。カッコを省略することもあります。[結合則は成り立つ]
\( (h \circ g) \circ f(x) = (h \circ g)(f(x) ) = h(g(f(x))) \)
\( h \circ (g \circ f)(x) = h[1]g \circ f)(x) ) = h(g(f(x) \)
ご覧のようにどちらから計算しても結果は変わりませんよね。
写像の場合でも、関数と同じように合成写像があります。
写像 \( f : A \to B \)、\( g : B \to C \) があるとします。この時、2つの写像を使って、\( A \to B \to C \) とできますよね。これを合成写像と言い、合成関数のように \( g \circ f: A \to C \) とすることができます。合成写像を図でわかりやすく書くと下のようになります。
※集合 \( A \) を曲名の集合、集合 \( B \) をアーティスト名の集合、集合 \( C \) を性別の集合としています。
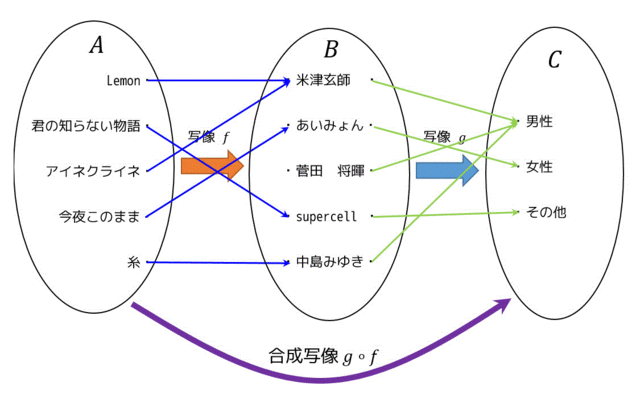
5.逆写像
写像 \( f : A \to B \) が全射でも単射でもある場合、逆写像 \( f^{-1} : B \to A \) が存在します。図で例を出してみます。
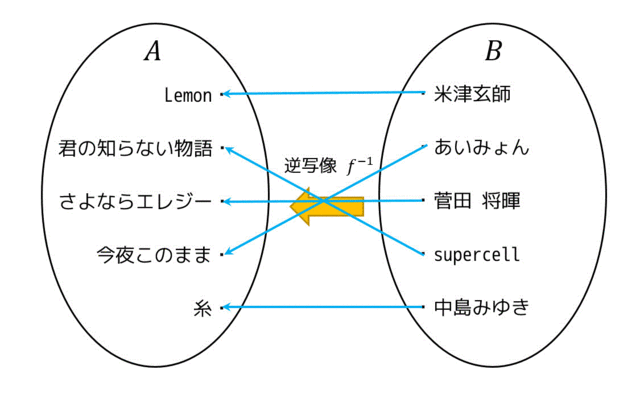
矢印の向きがすべて逆になっているのがわかりますね。
写像 \( f \) が全射・単射のどちらかでも満たしていない場合、逆写像 \( f^{-1} \) が存在しない理由を簡単に説明したいと思います。
(1) 全射でない場合は、\( B \) 側に矢印が向けられていない要素がある。逆写像の場合、矢印の向きが逆になるのでスタート地点に矢印がない要素が存在することになるので逆写像は存在しなくなる。
(2) 単射ではない場合、\( B \) 側の要素に \( A \) からの矢印が2箇所以上指されている要素がある。しかし逆写像の場合、矢印の向きは逆になるので2箇所以上の要素から矢印が出ることになり、これもおかしい。
この2つの理由から、写像 \( f \) は全単射の場合のみ逆写像 \( f^{-1} \) は存在するといえます。
ちなみに合成写像 \( g \circ f \) の逆写像は \( f^{-1} \circ g^{-1} \) となります。順番も変わるので要注意です。
6.全域関数(全域写像)・部分関数(部分写像)
写像の話から少し離れて、最後に全域関数と部分関数について説明しましょう。
全域写像、部分写像と言うことがあまりないみたいなのでこの部分だけ全域関数、部分関数と表記します。
(1) 全域関数(全域写像)
これは今まで言ってきた関数と全く同じです。あえて説明すると、定義域のすべての要素に対して、対応する値が1つに定まる関数のことです。特に説明なしに「関数」と言われた場合は、全域関数だと思って大丈夫です。
(2) 部分関数(部分写像)
全域関数の条件を少し緩めて、定義域の部分集合の要素(一部の要素)に対して、対応する値が定まる関数のことです。少しわかりにくいので例を示してみましょう。
\( f(x) = 1 \div x \) 定義域: \( x \in \mathbb{R} \) (実数範囲)
この関数の場合、\( x = 0 \) のときは \( f(x) \) は定義されませんよね。このように1つでも対応する値がない関数は全域関数と言うことができません。
ちなみに全域関数である場合、その関数は必ず部分関数です。逆に部分関数である関数が全域関数とは限りません。
ではさらに練習問題を2つ解いてみましょう。
例題3(証明)
集合 \( X,Y,Z \) に対して、写像 \( f : X \to Y \) 、\( g: Y \to Z \) と合成写像 \( g \circ f \) とする。このとき、つぎの(1)~(4)を証明しなさい。
(1) 写像 \( f,g \) がともに全射ならば合成写像 \( g \circ f \) も全射である
(2) 写像 \( f,g \) がともに単射ならば合成写像 \( g \circ f \) も単射である
(3) 合成写像 \( g \circ f \) が全射ならば写像 \( g \) も全射である
(4) 合成写像 \( g \circ f \) が単射ならば写像 \( f \) も単射である
ヒント:定義を使いましょう。
全射の定義
\( \forall b\in B,\,\exists a\in A \;\text{ s.t. }f(a)=b \)
単射の定義
\( (\forall a_1, a_2 \in A)\; a_1 \neq a_2 \ \Longrightarrow \ f(a_1) \neq f(a_2) \)
\( (\forall a_1, a_2 \in A)\; f(a_1)=f(a_2) \ \Longrightarrow \ a_1=a_2 \)
解説3
(1)
すべての \( z \) に対して、\( z = g(f(x) ) \) を満たすような \( x \) が存在することを示せばよい。
\( g \) が全射であるので、すべての \( z \in Z \) に対して、\( z = g(y) \) となるような \( y \) が存在する。
また、\( y \) が全射であるので、すべての \( y \in Z \) に対して、\( y = f(x) \) となるような \( x \) が存在する。
よって、\( z = g(y) = g(f(x) ) \) を満たせるので合成写像 \( g \circ f \) も全射であることが示された。
(2)
\( x_1,x_2 \in X \) とする。
\( x_1 \not= x_2 \) ならば \( g(f(x_1) ) \not= g(f(x_2) ) \) となることを示せばよい。
\( f \) は単射かつ \( x_1 \not= x_2 \) なので \( f(x_1) \not= f(x_2) \) となる。
\( g \) も同様に、単射かつ \( f(x_1) \not= f(x_2) \) なので \( g(f(x_1) ) \not= g(f(x_2) ) \) となる。
よって、合成写像 \( g \circ f \) も単射であることが示された。
(3)
合成写像 \( g \circ f \) が全射なので、すべての \( z \) に対して、 \( z = g \circ f(x) \) を満たすような \( x \in X \) が存在する。\( y in Y \) となるように \( y = f(x) \) とおくと、\( z = g \circ f(x) = g(f(x) ) = g(y) \) と変形できる。
よって任意の \( z \) に対して \( g \) の像(終域)となるので題意が満たされた。
(4)
(2) と違って対偶を使うパターン。
\( x_1,x_2 \in X \) とする。
\( f(x_1) = f(x_2) \) ならば \( x_1 = x_2 \) となることを示せばよい。
\( f(x_1) = f(x_2) \) なので、\( g \circ f(x_1) = g( f(x_1) ) = g( f(x_2) ) = g \circ f(x_2) \) と変形できる。ここで合成写像 \( g \circ f \) は単射なので \( x_1 = x_2 \) となり、題意は示された。
解答には東北大学のこちらのPDFを参考にさせていただきました。
参考文献:「解析学入門」東北大学大学院情報科学研究科 尾畑研究室
例題4
集合 \( A \) を、\( A = \{1,2,3, \cdots, n\} \) 、集合 \( B \) を \( B = \{1,2,3, \cdots, m\} \) とする。(ただし \( n,m \) は4以上の自然数)
(1) \( A \) から \( B \) への全域関数(全域写像)で相異なるものは全部で何個ありますか。
(2) \( B \) から \( A \) への全域関数で相異なるものは全部で何個ありますか。
(3) \( A \) から \( A \) への部分関数(部分写像)で相異なるものは全部で何個ありますか。
(4) \( A \) から 集合 \( \{a,b\} \) への全域関数で全射であるものは全部で何個ありますか。
(5) \( A \) から \( A \) への全域関数で1対1対応(全単射)であるものは全部で何個ありますか。
解答4
(1) 集合 \( B \) の要素は \( m \) 個ある。つまり、1つの要素ごとに \( m \) 通りの関係がある。集合 \( A \) の要素が \( n \) 個あるので、\( m \) 通りの関係が \( n \) 個あることとなる。つまり、\( m \) を \( n \) 回かけた分だけ存在する。よって答えは \( m^{n} \) 個となる。
(2) (1)のパターンの逆である。集合 \( A \) の要素は \( n \) 個ある。つまり、1つの要素ごとに \( n \) 通りの関係がある。集合 \( B \) の要素が \( m \) 個あるので、\( n \) 通りの関係が \( m \) 個あることとなる。つまり、\( n \) を \( m \) 回かけた分だけ存在する。よって答えは \( n^{m} \) 個となる。
(3) 全域関数ではなく部分関数のパターンである。部分関数の場合、対応先の集合 \( A \) は要素ではなく、未定義 \( K \)(空集合)でもOKになるので、\( \{1,2,3, \cdots, n,K\} \) の中から1つを選べるので、1つの要素ごとに \( n + 1 \) 通りの関係が生まれる。\( n+1 \) 通りの関係が \( n \) 個あることとなるので答えは \( (n+1)^{n} \) 通りとなります。
(4) まず、\( A \) から 集合 \( \{a,b\} \) への全域関数の個数を求めます。
各要素2パターンあり、それが \( n \) 個あるので全部で \( 2^n \) 個あります。
全射であるということは、「対応先の要素に矢印が向けられていない状態」にならないようにしないといけません。そのような場合は、
(i) すべての要素が \( a \) に対応付けられている
(ii) すべての要素が \( b \) に対応付けられている
この2パターン以外です。よって答えは \( 2^n - 2 \) 個です。
(5) 1対1対応ということは、1つめの要素だと \( n \) 通りの決め方、2つ目だと1つ目に決めた要素を除いた \( n-1 \) 通り、3つ目は2つ目までに決めた要素を除いた \( n-2 \) 通りと続いていくので、
\( n \times (n-1) \times \cdots \times 2 \times 1 = n! \)
となり、答えは \( n! \) 個です。(1から \( n \) の並び替えの数だけあるのとおなじ)
7.さいごに
今回は、写像(関数)についてかなり長い文章でしたがまとめてみました。
途中どうしても簡単な用語でまとめられなかったところは難しい表現になってしまっています。ご了承ください。
この記事で写像というのがどんなものなのか、そして全射、単射の意味、全射、単射かどうかの判別がわかるようになれば非常にうれしいです。
お知らせなのですが、今回でうさぎでもわかる離散数学は一旦更新を止めようとおもいます…
番外編として差分方程式はやるのですがあれは離散数学というより数2Bの漸化式に似てるので…
ということで全6回+おまけとなりましたが今まで読んでいただきありがとうございました!
では、さようなら。
*1:ただし、先生によっては写像と関数は名前だけが違ってて名前以外は全く同じという先生がいるので要注意。
注釈
| ↑1 | g \circ f)(x) ) = h(g(f(x |
|---|
関連広告・スポンサードリンク