スポンサードリンク
※ 動的システムではなく、ディジタルシステムの周波数特性(振幅特性、位相特性)について知りたい人は、この記事ではなく、下のリンク先の記事をご覧ください。
こんにちは、ももやまです。
前回は、伝達関数 \( G(s) \) の分子(ゼロ点)と分母(極)に着目することで、ラプラス変換をすることなくシステムがどんな振る舞いをするのかを把握する安定性の判定について説明しました。
今回は、伝達関数自体に値を代入することで、逆ラプラス変換なしにシステムがどんな振る舞いをするかを見ていきましょう。
目次
スポンサードリンク
0. 対数関数と複素数の復習
周波数応答について説明する前に、今回使う高校数学・大学の解析学の知識の確認をしておきましょう。
(1) 対数関数の計算法則
対数関数では、底が同じ対数どうしの足し算は掛け算になります。\[\begin{align*}
\textcolor{blue}{\log_2 8} + \textcolor{red}{\log_2 4} & = \log_2 (8\times4) = \textcolor{green}{\log_2 32} \\
\textcolor{blue}{3} + \textcolor{red}{2} & = \textcolor{green}{5}
\end{align*}\]
また、底が同じ対数同士の引き算は割り算になります。 \[\begin{align*}
\textcolor{blue}{\log_2 64} - \textcolor{red}{\log_2 16} & = \log_2 (64 \div 16) = \textcolor{green}{\log_2 4} \\
\textcolor{blue}{6} - \textcolor{red}{4} & = \textcolor{green}{2}
\end{align*}\]
(2) 複素数と偏角
(i) 複素数の大きさと偏角
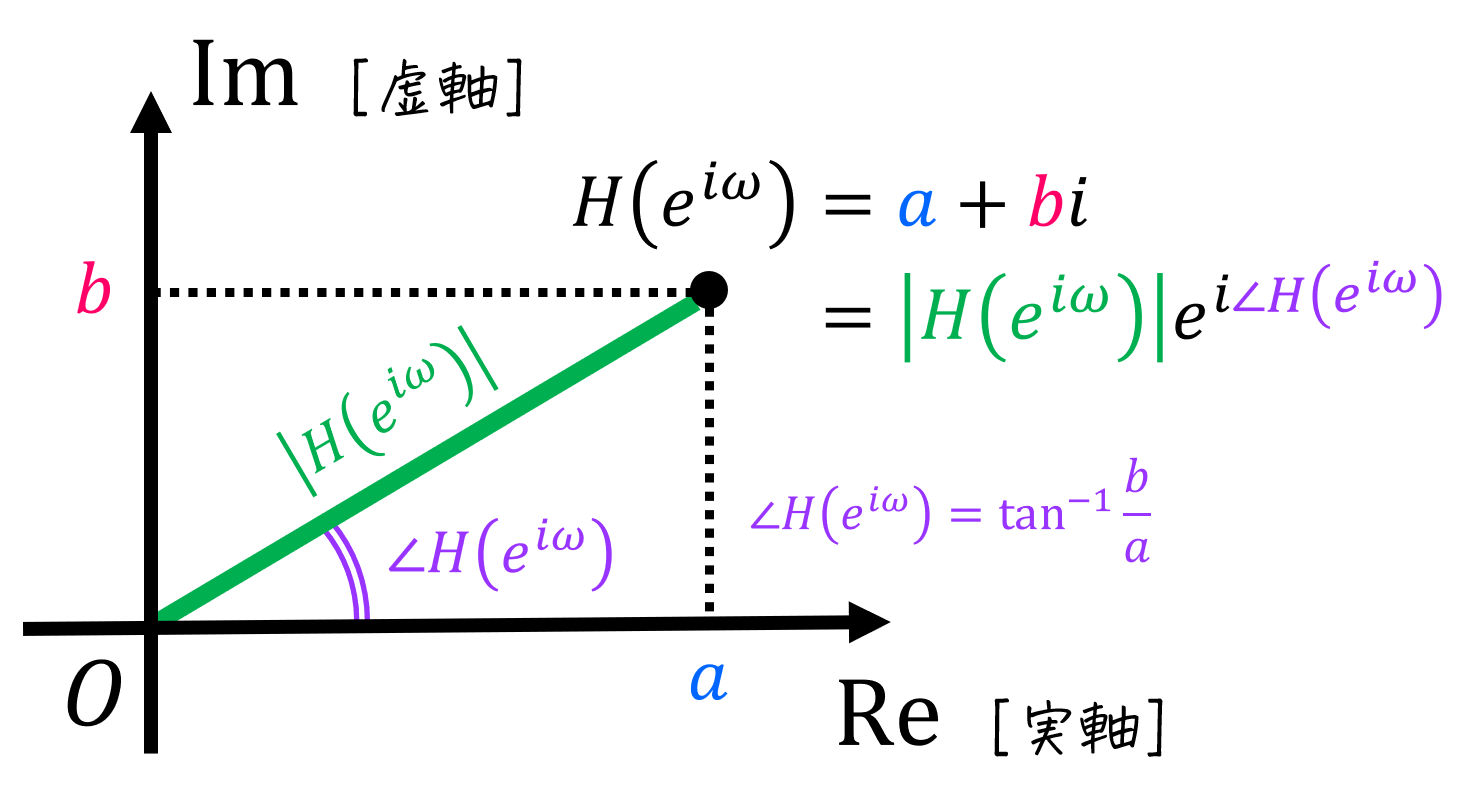
ある複素数 \( z = a + bi \) は、大きさ \( r = |z| \) と偏角 \( \theta \) を用いて\[
z = r ( \cos \theta + i \sin \theta )
\]\[
r = \sqrt{a^2 + b^2} \]\[ \tan \theta = \frac{b}{a} \ \ \left( \theta = \tan^{-1} \frac{b}{a} \right)
\]と分解することができます[1]逆三角関数 \( \tan^{-1} \theta \) … Continue reading。
さらに、大学数学で習ったオイラーの法則を使うことで、複素数を \( z = r e^{i \theta} \) の形に置き換えることも可能です。
(ii) 偏角の計算法則
ある複素数 \( z_1 \), \( z_2 \) の偏角が \( \arg z_1 = \theta_1 \), \( \arg z_2 = \theta_2 \) だとします。
このとき、2つの複素数 \( z_1 \), \( z_2\) の積で表された複素数の偏角 \( \arg (z_1 z_2) \) は、2つの複素数の偏角の和となります。\[
\arg (z_1 z_2) = \arg z_1 + \arg z_2
\]
また、複素数の割り算を行う場合、偏角は引き算となります。\[
\arg \frac{z_1}{z_2} = \arg z_1 - \arg z_2
\]
2つの複素数\[
z_1 = 1 + i , \ \ \ z_2 = \frac{1}{2} + \frac{ \sqrt{3} }{2} i
\]がある。
(1) \( z_1 \), \( z_2 \) の偏角 \( \arg z_1 \), \( \arg z_2 \) を求めなさい。
(2) \( z_1 z_2 \) の偏角 \( \arg z_1 z_2 \) を求めなさい。
(3) \( \frac{z_1}{z_2} \) の偏角 \( \arg \frac{z_1}{z_2} \) を求めなさい。
(1)
\( z_1 = \textcolor{blue}{1} + \textcolor{red}{1}i \) より、\[
\tan \theta = \frac{\textcolor{red}{1}}{\textcolor{blue}{1}} = 1
\]を満たす \( \theta \) が偏角 \( \arg z_1 \) となる。よって、\( \arg z_1 = 45^{\circ} \)
また、\( z_2 = \textcolor{blue}{ \frac{1}{2} } + \textcolor{red}{ \frac{ \sqrt{3} }{2} } i \) より、\[
\tan \theta = \frac{\textcolor{red}{ \frac{\sqrt{3} }{2} }}{\textcolor{blue}{ \frac{1}{2} }} = \sqrt{3}
\]を満たす \( \theta \) が偏角 \( \arg z_2 \) となる。よって、\( \arg z_2 = 60^{\circ} \)
(2) \[\begin{align*}
\arg (z_1 z_2) & = \arg z_1 + \arg z_2
\\ & = 45^{\circ} + 60^{\circ}
\\ & = 105^{\circ}
\end{align*}\]
(3) \[\begin{align*}
\arg \frac{z_1}{z_2} & = \arg z_1 - \arg z_2
\\ & = 45^{\circ} - 60^{\circ}
\\ & = - 15^{\circ}
\end{align*}\]
これで今回使う高校数学の知識が復習できたので、本題に入っていきましょう!
スポンサードリンク
1. 周波数特性(周波数応答)
(1) 周波数特性(周波数応答)とは
例えばある未知の関数 \( f(x) \) という関数があるとします。
この関数がどんな振る舞いをするかは、\( x \) の値を適当に代入することである程度予測することができます。例えば、\( x = 0 \) を代入すると1、\( x = 1 \) を代入すると3、\( x = 2 \) を代入すると5、…、という結果が得られたとします。すると、この関数 \( f(x) \) は、「\( x \) の値を1増やすと \( y \) の値が2増える関数」であることがわかりますね。
同じように信号処理の世界でも、ある値を代入したときの結果からシステムの振る舞いを予測するということを行います。
具体的には、伝達関数[2]システムの振る舞いをラプラス変換上で表した関数で \( G(s) \) で表されます。 に大きさが1の正弦波 \( s = i \omega \) が入力されたときにどれくらいの強さの波がどれくらいの周期で出てくるかを調べます[3]※ なぜ \( s = i \omega \) … Continue reading。
この \( s = i \omega \) を代入したときの値のことを周波数特性(周波数応答)と呼び、\( G(i \omega) \) で表します。
※ \( i \) は虚数、\( \omega \) は位相を表します。
(2) 振幅(ゲイン)特性・位相特性
周波数特性は \( G(i \omega) \) は複素数を代入することにより出てきた関数なので、\( G(i \omega) \) は複素数 \( z = a + bi \) の形で表すことができますね。
なので、大きさ \( r = |z| \) と位相 \( \theta \) に分解することができますね!
この周波数特性 \( G(i \omega) \) の大きさ(複素数でいう \( r \) に相当)のことを振幅特性(ゲイン特性)と呼び、\( | G (i \omega)| \) と書きます。
また、位相(複素数でいう \( \theta \) に相当)のことを位相特性と呼び、\( \angle G(i \omega) \) と書きます。
伝達関数 \( G(s) \) に対し、\( s = i \omega \) と代入したものを周波数特性と呼び、\( G(i \omega) \) と呼ぶ。
また、周波数特性 \( G(i \omega) = a + bi \) の大きさ \( | G(i \omega) | \) を振幅特性、もしくはゲイン特性と呼び、位相 \( \angle G( i \omega ) \) のことを位相特性と呼ぶ。
なお、周波数特性から振幅特性、位相特性は以下のように計算できる。\[
| G(i \omega) | = \sqrt{a^2 + b^2}
\]\[
\angle G(i \omega) = \tan^{-1} \frac{b}{a} \ \ \ \left( \tan \angle G(i \omega) = \frac{b}{a} \right)
\]
(3) 例題で確認
それでは、実際に例題で周波数特性、振幅特性、位相特性を求めてみましょう!
次の伝達関数 \( G(s) \) で表されるシステムがある。\[
G(s) = \frac{1}{2s-1}
\]
(1) 周波数特性 \( G(i \omega ) \) を求め、\( a + bi \) の形で表しなさい。
(2) 振幅特性 \( | G(i \omega ) | \)、位相特性 \( \angle G ( i \omega ) \) を求めなさい。
[解答]
(1)
\( s = i \omega \) を代入するだけでOK。\[\begin{align*}
G( i \omega ) & = \frac{1}{2 (i \omega) - 1}
\\ & = \frac{1}{(2 i \omega - 1)(2 i \omega + 1)}
\\ & = \frac{1 (2 i \omega + 1) }{4i^2 \omega^2 -1}
\\ & = \frac{2i \omega + 1}{-4 \omega^2 - 1}
\\ & = - \frac{1}{4 \omega^2 + 1} ( 1 + 2 i \omega )
\\ & = \textcolor{blue}{- \frac{1}{4 \omega^2 + 1}} \textcolor{red}{ - \frac{2 \omega}{ 4 \omega^2 + 1 } } i
\end{align*}\]
(2)
(i) 振幅特性
\( G( i \omega ) = a + bi \) から \( | G( i \omega ) | = \sqrt{ \textcolor{blue}{a}^2 + \textcolor{red}{b}^2 } \) を下のように計算するのもありだが、少し時間がもったいない。
\[\begin{align*}
| G ( i \omega ) | & = \sqrt{ \left( \textcolor{blue}{ - \frac{1}{4 \omega^2 + 1} } \right)^2 + \left( \textcolor{red}{ - \frac{2 \omega}{ 4 \omega^2 + 1 } } \right)^2 }
\\ & = \sqrt{ \frac{1}{( 4 \omega^2 + 1 )^2} + \frac{4 \omega^2 }{( 4 \omega^2 + 1 )^2} }
\\ & = \sqrt{ \frac{ 4 \omega^2 + 1}{(4 \omega^2 + 1)^2} }
\\ & = \sqrt{ \frac{1}{4 \omega^2 + 1} }
\\ & = \frac{1}{ \sqrt{ 4 \omega^2 + 1 } }
\end{align*}\]
おすすめはこの計算。\[\begin{align*}
| G( i \omega ) | & = \left| \frac{1}{2 (i \omega) - 1} \right|
\\ & = \frac{1}{ \left| 2i \omega - 1 \right| }
\\ & = \frac{1}{ \sqrt{ (-1)^2 + (2 \omega )^2 } }
\\ & = \frac{1}{ \sqrt{ 4 \omega^2 + 1 } }
\end{align*}\]
(ii) 位相特性
\[\begin{align*}
\angle G ( i \omega ) & = \tan^{-1} \frac{\textcolor{red}{ b } }{\textcolor{blue}{a} }
\\ & = \tan^{-1} \frac{ \textcolor{red}{- \frac{2 \omega}{4 \omega^2 + 1} } }{ \textcolor{blue}{ - \frac{1}{ 4 \omega^2 + 1 } } }
\\ & = \tan^{-1} 2 \omega
\end{align*}\]
スポンサードリンク
2. ボード線図
第1章では、ある角周波数 \( \omega \) に対しての振幅 \( | G(i \omega )| \)、および位相 \( \angle G ( i \omega ) \) を求める計算をしていきました。
ここからは、角周波数 \( \omega \) を変えたときの振幅と位相の対応関係を表すグラフ、ボード線図を「伝達関数からで自力で書く方法」について説明していきます!
(1) 大きさのレベルを表す単位:デシベル
信号処理の世界では、振幅の大きさ \( | G( i \omega ) | \) を表すのに「デシベル」という単位が使われます。音とかのうるささを表す単位として聞いた事がある人も多いと思います。
具体的には、常用対数(底が10のlog)をとってから20倍した値をとり、単位はデシベル [dB]となります。\[
\mathrm{ [ dB] }
\]
ボード線図でゲインに関するグラフを書く際には \( | G( i \omega )| \) の値そのままではなく、\( 20 \log_{10} | G ( i \omega ) | \) にしたを使います。
なぜこの式を使うかは、実際にグラフの例を見てみるとわかります!
(2) 目盛りが対数…?
今回は、角周波数 \( \omega \) を0.01 ~ 100 のかなり広い範囲で振幅と位相をグラフに書いていきます。
その際、普通の目盛りを使ってしまうと、\( \omega \) が小さいときの変化がほとんど見れなくなってしまいます。
そのため、ボード線図では値が小さいときでも変化を見やすくするために片方の軸が対数の目盛りが使用されます。
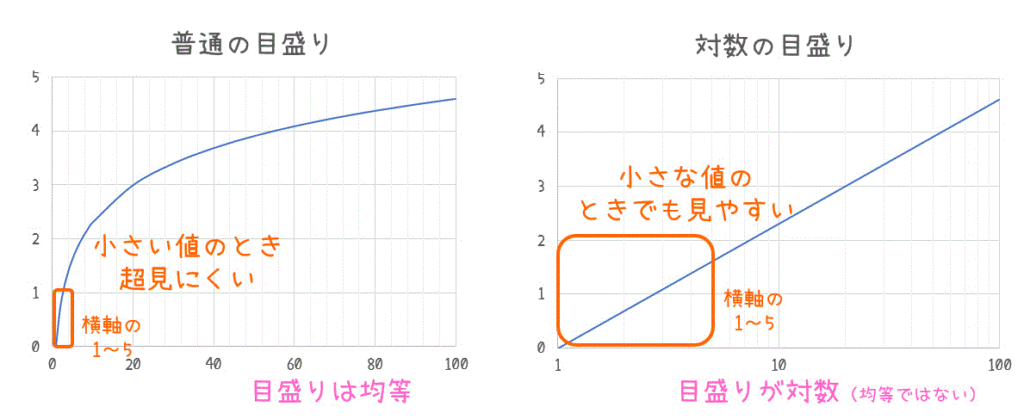
なお、対数グラフ(片対数・両対数)の書き方や仕組みが気になる人は、こちらの記事に詳しく書いているので、ぜひご覧ください!
(3) ボード線図の書き方
それでは、ボード線図の書き方について見ていきましょう。
とは言っても、覚えることはたった4つです。
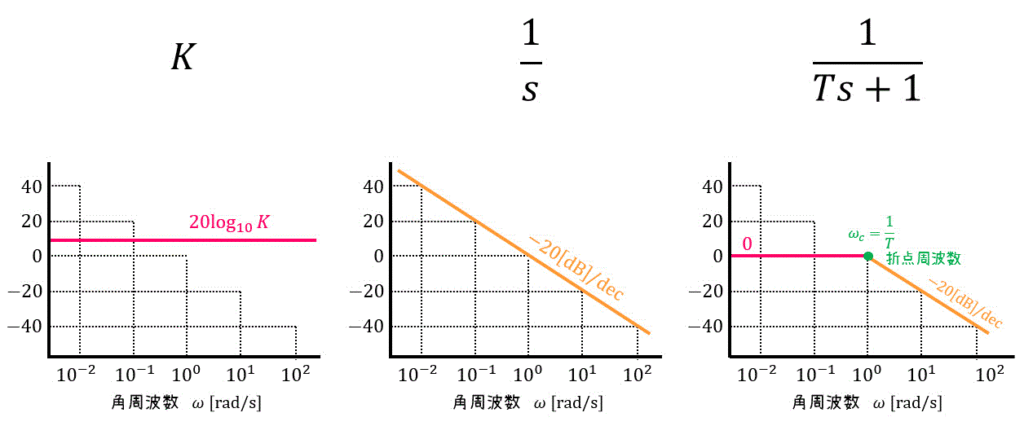
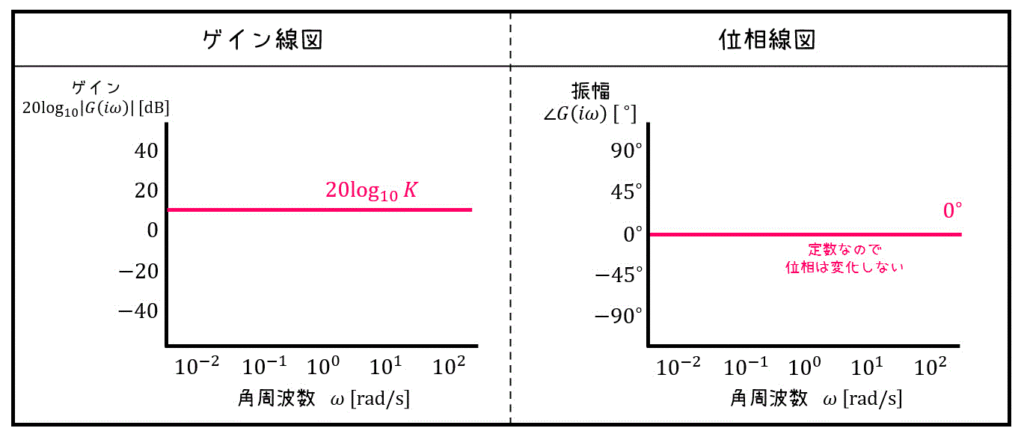
その1 定数
定数 \( K \) の場合は簡単です。
ゲイン:角周波数に関係なく \( 20 \log_{10} K \) となります。
位相:角周波数に関係なく位相は変化しません(0°です)。定数なので。
その2 1/s系
伝達関数、および周波数応答が\[
G(s) = \frac{1}{s} , \ \ \ G( i \omega ) = \frac{1}{i \omega}
\]のときも見ていきましょう。
まず、ゲインは\[\begin{align*}
20 \log_{10} | G( i \omega ) | & = 20 \log_{10} \left| \frac{1}{i \omega } \right|
\\ & = 20 \log_{10} \frac{1}{ | i \omega | }
\\ & = 20 \log_{10} \frac{1}{ \omega }
\\ & = - 20 \log_{10} \omega
\end{align*}\]となりますね。
ここで、\( \omega \) は対数目盛りなので、ゲインのグラフは傾き-20の直線となります。
つぎに角周波数は\[\begin{align*}
\angle G( i \omega ) & = \arg \frac{1}{i \omega}
\\ & = \arg 1 - \arg i \omega
\\ & = 0^{\circ} - 90^{\circ}
\\ & = - 90^{\circ}
\end{align*}\]となり、定数となります。
よって、グラフは下のように書くことができます。
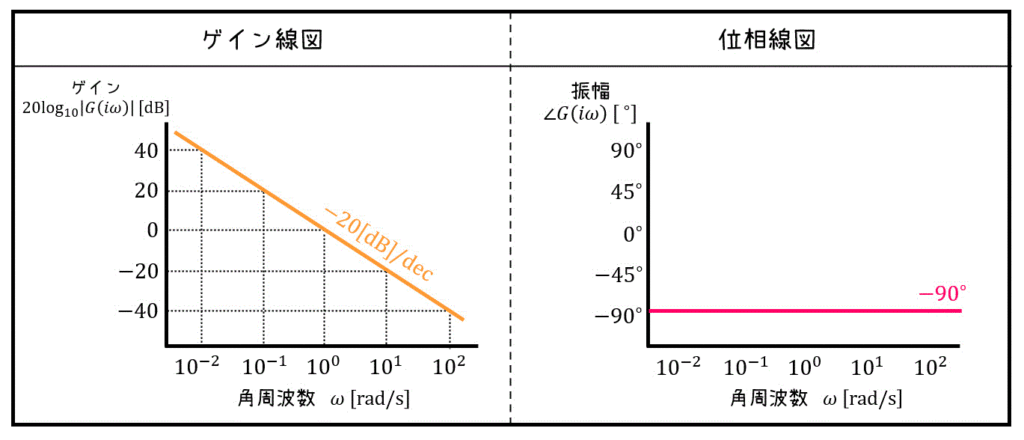
\( \omega \) の目盛りを対数+ゲインをデシベル値にしたことで、グラフの形が傾き-20[dB]の直線になっているのがポイントです。
これが「\( \omega \) の目盛りを対数」、および「ゲインをデシベル値を表現」する理由です。
なお、対数世界でのグラフの傾きを表す際には値を10倍にしたときの変化量 "/dec" が用いられます。
例えば、-20[dB]/dec であれば、対数世界での傾きが-20[dB]であることを表します[4]decは、decade(10)を略したもの。10倍にしたときに値がどれくらい増えるかを示している。。
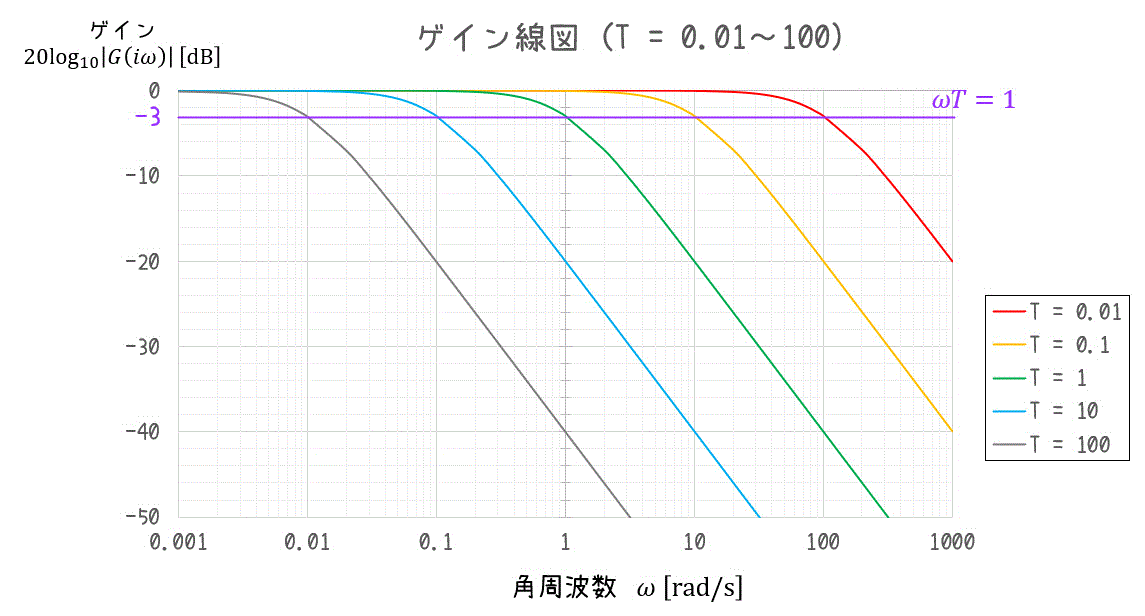
その3 1/(Ts+1)系
伝達関数、および周波数応答が\[
G(s) = \frac{1}{Ts+1} , \ \ \ G( i \omega ) = \frac{1}{i \omega T + 1}
\]のときも見ていきましょう。 (ただし \( T \) は0より大きい定数))
(a) ゲイン
まず、ゲインは\[\begin{align*}
20 \log_{10} | G( i \omega ) | & = 20 \log_{10} \left| \frac{1}{i \omega T + 1} \right|
\\ & = 20 \log_{10} \frac{1}{ | i \omega T + 1 | }
\\ & = 20 \log_{10} \frac{1}{\sqrt{1 + (\omega T)^2} }
\end{align*}\]となりますね。
ここで、この形だと少しグラフを書くのが難しいので近似をします。
(i) \( \omega T \) が1より十分に小さいとき
最初に、\( \omega T \) が1より十分小さい場合 \( \omega T \ll 1 \) を仮定します。
このとき、\( \omega T \) が1よりも十分小さいため、分母の \( \omega T \) を無視することができます。\[\begin{align*}
20 \log_{10} | G( i \omega ) | & = 20 \log_{10} \frac{1}{\sqrt{1 + (\textcolor{red}{\omega T})^2} }
\\ & \fallingdotseq 20 \log_{10} \frac{1}{\sqrt{1} } \ \ \ ( \omega T \ll 1 \ \mathrm{より})
\\ & = 20 \log_{10} 1
\\ & = 0
\end{align*}\]となります。
(ii) \( \omega T \) が1より十分に大きいとき
次に、\( \omega T \) が1より十分大きい場合 \( \omega T \gg 1 \) を仮定します。
このとき、\( \omega T \) が1よりも十分大きいため、分母の1を無視することができます。\( \omega T \to \infty \) に、\[\begin{align*}
20 \log_{10} | G( i \omega ) | & = 20 \log_{10} \frac{1}{\sqrt{\textcolor{red}{1} + (\omega T)^2} }
\\ & \fallingdotseq 20 \log_{10} \frac{1}{\sqrt{ (\omega T)^2 } } \ \ \ ( \omega T \gg 1 \ \mathrm{より})
\\ & = 20 \log_{10} \frac{1}{ \omega T }
\\ & = - 20 \log_{10} \omega T
\end{align*}\] となります。
(iii) \( \omega T \) が1のとき
最後に \( \omega T = 1 \) のときも考えましょう。このときは、\[\begin{align*}
20 \log_{10} | G( i \omega ) | & = 20 \log_{10} \frac{1}{ \sqrt{ 1 + ( \omega T)^2 } }
\\ & = 20 \log_{10} \frac{1}{ \sqrt{ 1 + (1)^2 } }
\\ & = 20 \log_{10} \frac{1}{ \sqrt{2} }
\\ & = -10 \log_{10} 2 \ \ \ ( \log_{10} 2 \fallingdotseq 0.3010 )
\\ & \fallingdotseq -3
\end{align*}\]となります。
よって、\[ 20 \log_{10} | G( i \omega ) | \fallingdotseq \left\{ \begin{array}{l} 0 & ( \omega t \ll 1 ) \\ -3 & ( \omega T = 1) \\ - 20 \log_{10} \omega T & ( \omega T \gg 1 ) \end{array} \right. \]となります。
これを踏まえて、\( T = 0.01 , 0.1 , 1, 10 ,100 \) のゲイン線図を見てみましょう。
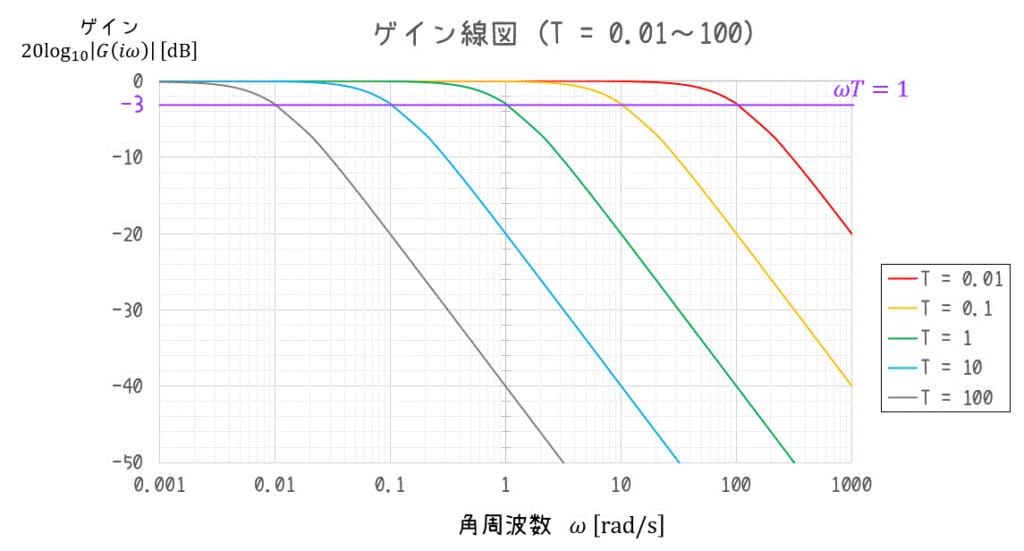
(b) 位相
つぎに角周波数は\[\begin{align*}
\angle G( i \omega ) & = \arg \frac{1}{i \omega T + 1}
\\ & = \arg 1 - \arg ( i \omega T + 1 )
\\ & = 0^{\circ} - \tan^{-1} \frac{\omega T}{1}
\\ & = - \tan^{-1} \omega T
\end{align*}\]となります。
\( \tan^{-1} \) のグラフさえわかれば簡単にグラフがかけそうですが、ゲインのときと同じように場合分けしてみましょう。
(i) \( \omega T \) が1より十分に小さいとき
最初に、\( \omega T \) が1より十分小さい場合 \( \omega T \ll 1 \) を仮定します。このときは、\( \omega T \to 0 \) として、\[\begin{align*}
\lim_{ \omega T \to 0 } \angle G( i \omega ) & = \lim_{ \omega T \to 0 } - \tan^{-1} \omega T
\\ & = - \tan^{-1} 0
\\ & = 0 ( = 0^{\circ} )
\end{align*}\]となります[5] \( \omega T \) を1つの変数として極限をとっています。。
(ii) \( \omega T \) が1より十分に大きいとき
同じように \( \omega T \) が1より十分大きい場合 \( \omega T \gg 1 \) も見ていきましょう。
このときは、\( \omega T \to \infty \) として、\[\begin{align*}
\lim_{ \omega T \to \infty } \angle G( i \omega ) & = \lim_{ \omega T \to \infty } - \tan^{-1} \omega T
\\ & = \frac{\pi}{2} ( = 90^{\circ} )
\end{align*}\]となります。
(iii) \( \omega T \) が1のとき
最後に \( \omega T = 1 \) も見ていきましょう。
このときは、、\[\begin{align*}
\angle G( i \omega ) & = - \tan^{-1} \omega T
\\ & = - \tan^{-1} 1
\\ & = \frac{\pi}{4} ( = 45^{\circ} )
\end{align*}\]となります。
よって、\[ \angle G( i \omega ) \fallingdotseq \left\{ \begin{array}{l} 0^{\circ} & ( \omega t \ll 1 ) \\ -45^{\circ} & ( \omega T = 1) \\ -90^{\circ} & ( \omega T \gg 1 ) \end{array} \right. \]となります。
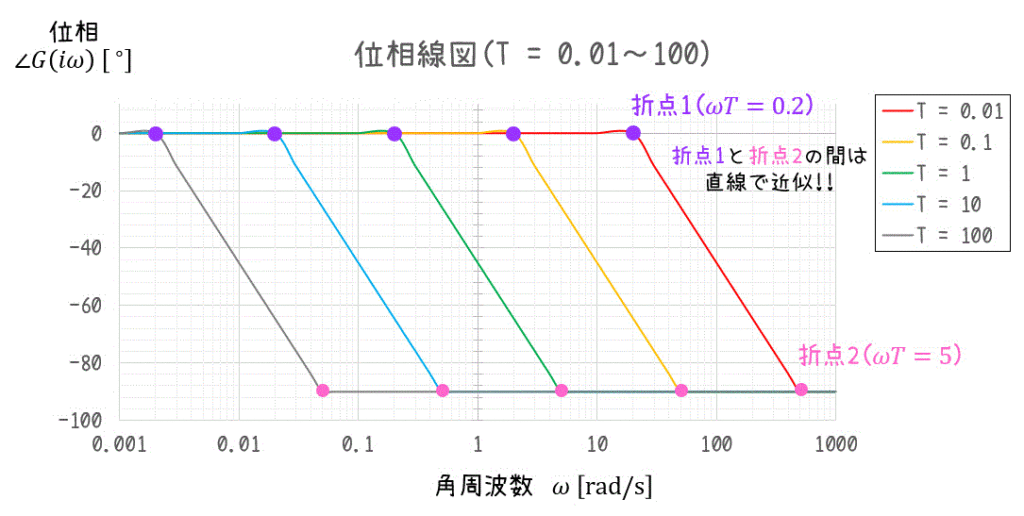
これを踏まえて、\( T = 0.01 , 0.1 , 1, 10 ,100 \) の位相線図を見てみましょう。
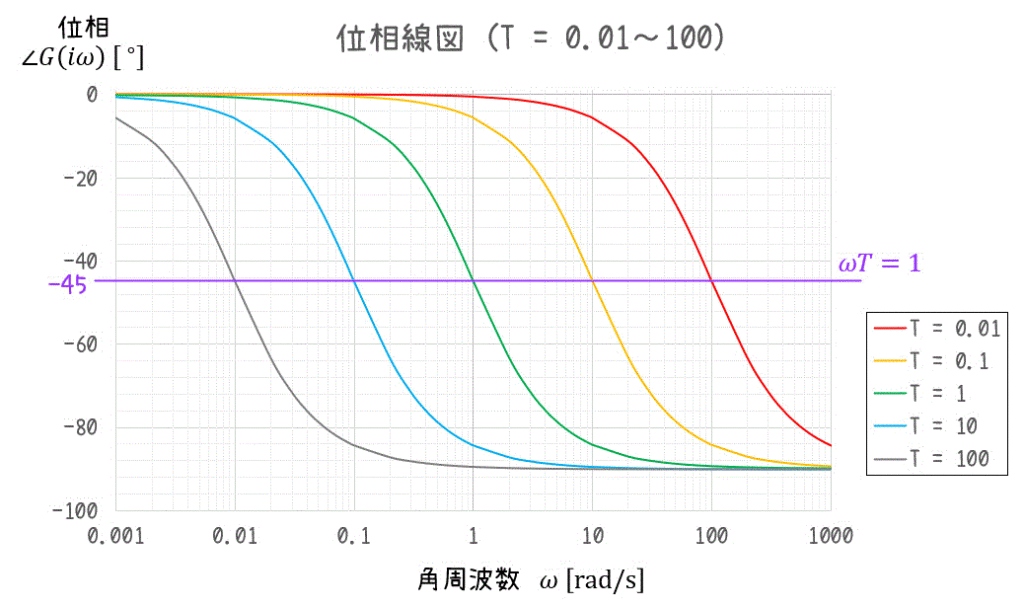
(c) グラフを近似して書いてみよう
グラフを書くときにいちいち \( \omega T \) の値で場合分けするのは少しめんどくさいですね。
なので、グラフを直線と近似しちゃいましょう。(この近似方法を折線近似と呼びます。)
ゲイン線図は、\( \omega T = 1 \) となる点 \( \omega \) までは0[dB]、それ以降は -20[dB]/dec の傾きの直線で近似を行います。数式で書くと近似式はこんな感じ。\[
20 \log_{10} | G ( i \omega ) | \fallingdotseq \left\{ \begin{array}{l} 0 & ( \omega t \leqq 1 ) \\ - 20 ( \log_{10} \omega T ) & ( \omega T > 1) \end{array} \right.
\]
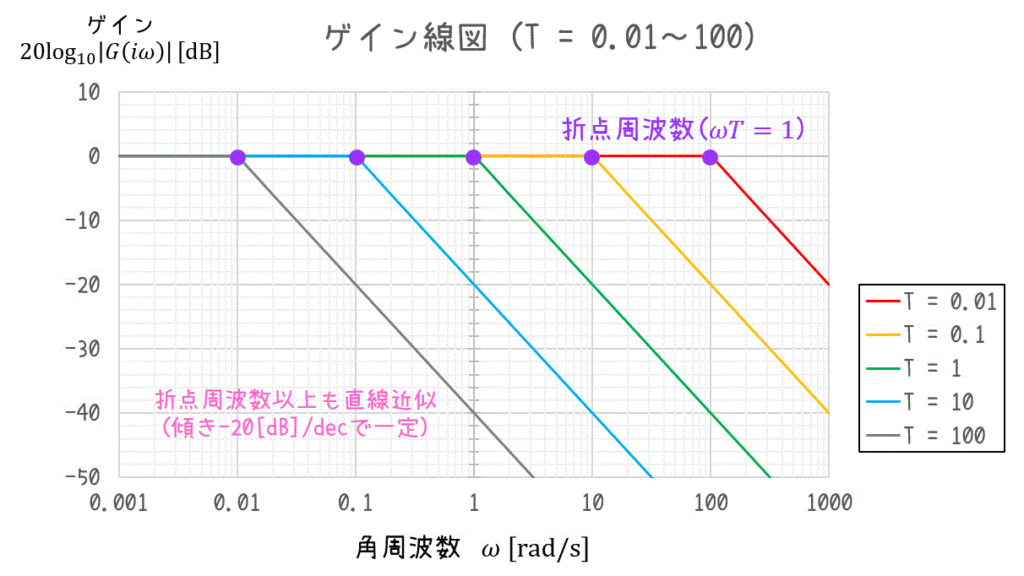
また、位相線図では \( \omega T = 0.2 \) 以下となる \( \omega \) 0°、\( \omega T = 5 \) 以上となる \( \omega \) では90°とし、その間を直線で結ぶことで近似を行います。
(\( \omega T = 0.2 \) となる点を折点1、\( \omega T = 5 \) となる点を折点2と勝手に名付けましょう。)
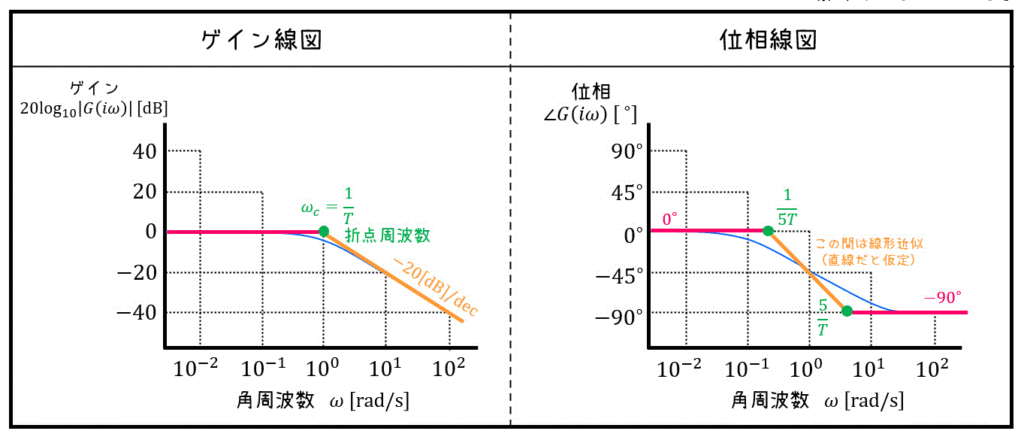
最後に、\( T = 1 \) においてゲイン線図と位相線図の書き方の確認をしましょう。
余談ですが、\( \omega T = 1 \) となる \( \omega \) は折点周波数と呼ばれ、\( \omega_c \) などの記号で表されます。
その1~3のグラフまとめ
★ゲイン線図★
★位相線図★
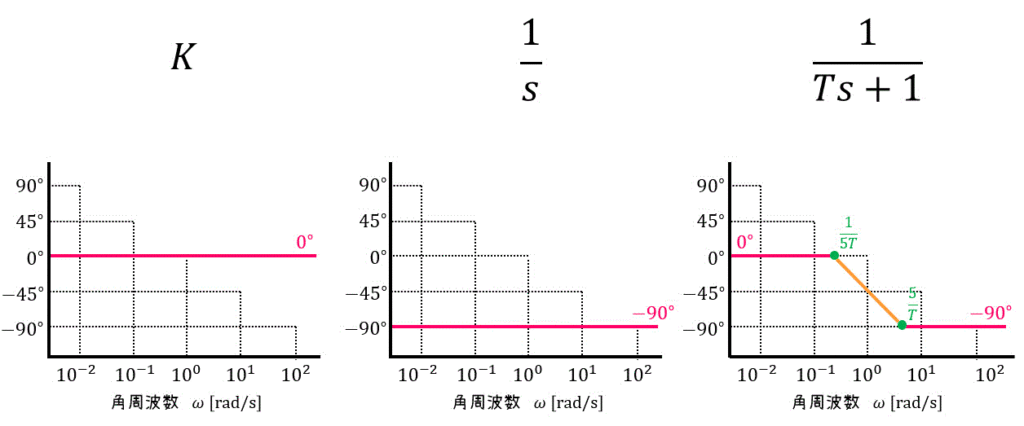
※ \( T = 1 \) のときのグラフを示しています。
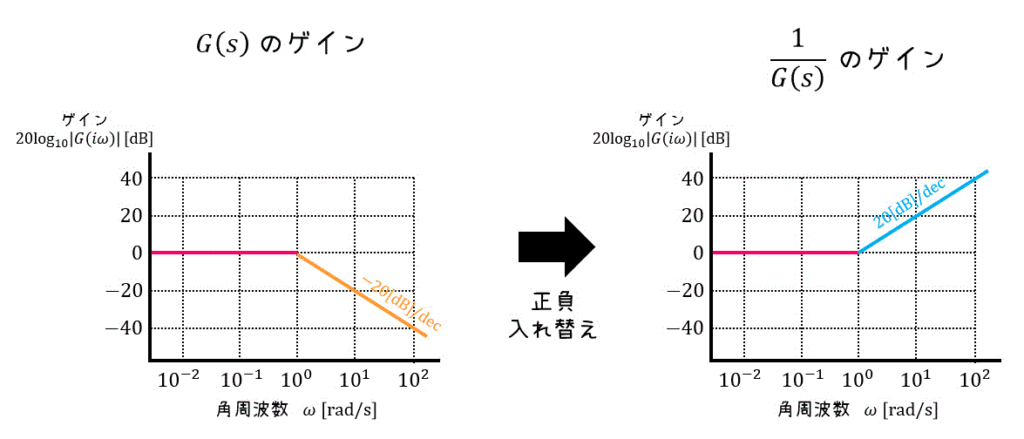
その4 1/G(s)のグラフ
その1~その3の分子分母が入れ替わったパターン\[
\frac{1}{G(s)}
\]のボード線図が、\( G(s) \) と比べてどう変化するかを見ていきましょう。
20 \log_{10} \left| \frac{1}{G(i \omega)} \right| & = 20 \log_{10} \frac{1}{| G( i \omega )|}
\\ & = - 20 \log_{10} G( i \omega )
\end{align*}\]
\angle \frac{1}{G(i \omega)} & = \angle 1 - \angle G(i \omega)
\\ & = 0 - \angle G(i \omega)
\\ & = - \angle G(i \omega)
\end{align*}\]
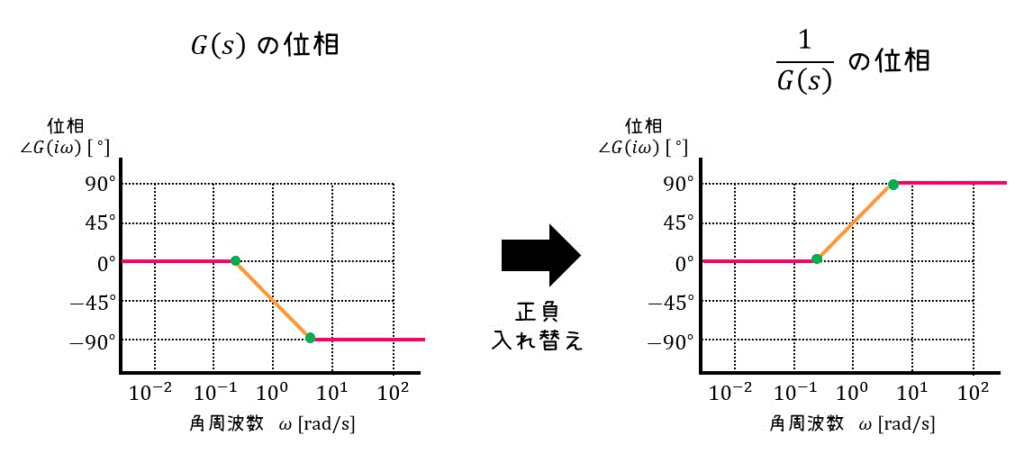
このように、伝達関数が \( 1/G(s) \) で表されるシステムのボード線図は、もとの \( G(s) \) の正負を入れ替えることで簡単にグラフを書くことができます!
その5 複数の組み合わせは足し算!
実際に試験で出てくる伝達関数 \( G(s) \) は複雑ですが、\( \log \) の計算法や位相の分解などを使うことで、掛け算を足し算に分解することができます。
早速例題を見ていきましょう!
次の伝達関数\[
G(s) = \frac{10s}{s+1}
\]で表されるシステムがある。
このシステムのボード線図(ゲイン線図・位相線図)を折れ線近似で記しなさい。ただし、\( 0.01 \leqq \omega \leqq 100 \) の範囲で図示すること。
[解説]
周波数特性は\[
G(i \omega) = \frac{10 i \omega}{i \omega + 1}
\]となる。
この周波数特性を\[\begin{align*}
G( i \omega ) & = \textcolor{blue}{10} \cdot \textcolor{red}{i \omega} \cdot \textcolor{green}{\frac{1}{i \omega + 1}}
\\ & = \textcolor{blue}{10} \cdot \textcolor{red}{ \frac{1}{ \frac{1}{i \omega} }} \cdot \textcolor{green}{\frac{1}{i \omega + 1}}
\\ & = \textcolor{blue}{G_1 ( i \omega )} \cdot \textcolor{red}{G_2 ( i \omega )} \cdot \textcolor{green}{ G_3 ( i \omega ) }
\end{align*}\]と3つに分解する[6]分解方法としては\[ \textcolor{blue}{G_1 ( i \omega )} \cdot \frac{1}{\textcolor{red}{G_2 ( i \omega )}} \cdot \textcolor{green}{ G_3 ( i \omega ) } \]とするのもあり。 … Continue reading。
※ \( G_2 \) はその4で紹介した逆数の形に持ち込みます
すると、\[\begin{align*}
20 \log_{10} | G( i \omega ) | & = 20 \log_{10} \left| \textcolor{blue}{G_1 ( i \omega )} \cdot \textcolor{red}{G_2 ( i \omega )} \cdot \textcolor{green}{ G_3 ( i \omega ) } \right|
\\ & = 20 \log_{10} \left( \left| \textcolor{blue}{G_1 ( i \omega )} \right| \cdot \left| \textcolor{red}{G_2 ( i \omega )} \right| \cdot \left| \textcolor{green}{G_3 ( i \omega )} \right| \right)
\\ & = 20 \log_{10} | \textcolor{blue}{G_1 ( i \omega )} | + 20 \log_{10} | \textcolor{red}{G_2 ( i \omega )} | + 20 \log_{10} | \textcolor{green}{G_3 ( i \omega )} |
\end{align*}\]となるため、\( G_1 \) ~ \( G_3 \) それぞれのゲインを求め、最後に足すことでゲイン線図を書くことができます。
あとは、\( \omega = 0.01, 0.1, 1, 10, 100 \) それぞれにおいて \( G_1 \) ~ \( G_3 \) のゲインを求め、\( \omega \) ごとに\[
20 \log_{10} | \textcolor{blue}{G_1 ( i \omega )} | + 20 \log_{10} | \textcolor{red}{G_2 ( i \omega )} | + 20 \log_{10} | \textcolor{green}{G_3 ( i \omega )} |
\]を計算し、直線で結んでしまえばOKです!
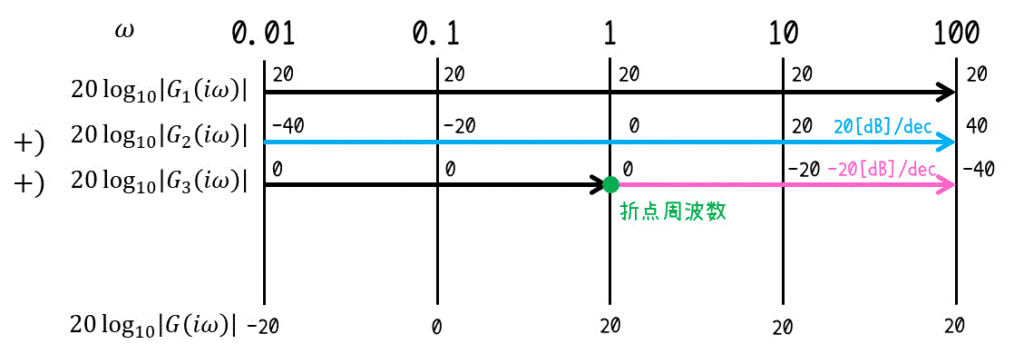
※1 計算のときは上のような数直線を書くと、グラフをいちいち書かなくても足し合わせることができます。
※2 折点周波数が \( \omega = 0.01, 0.1, 1, 10, 100 \) 以外にある場合は、折点周波数の値も求める必要があります。
また、位相は\[\begin{align*}
\angle G( i \omega ) & = \angle \left( \textcolor{blue}{G_1 ( i \omega )} \cdot \textcolor{red}{G_2 ( i \omega )} \cdot \textcolor{green}{ G_3 ( i \omega ) } \right)
\\ & = \angle \textcolor{blue}{G_1 ( i \omega )} + \angle \textcolor{red}{G_2 ( i \omega )} + \angle \textcolor{green}{ G_3 ( i \omega ) }
\end{align*}\]となるため、\( G_1 \) ~ \( G_3 \) それぞれの位相を求め、最後に足し合わせることで位相線図を書くことができます。
ゲインのときと同じように \( \omega = 0.01, 0.1, 1, 10, 100 \)、および折点それぞれにおいて \( \angle G_1 ( i \omega ) \), \( \angle G_2 ( i \omega ) \), \( \angle G_3 ( i \omega ) \) の値を求め、\( \omega \) ごとに\[
\angle \textcolor{blue}{G_1 ( i \omega )} + \angle \textcolor{red}{G_2 ( i \omega )} + \angle \textcolor{green}{ G_3 ( i \omega ) }
\]を求めて、直線で結んでしまえばOKです!
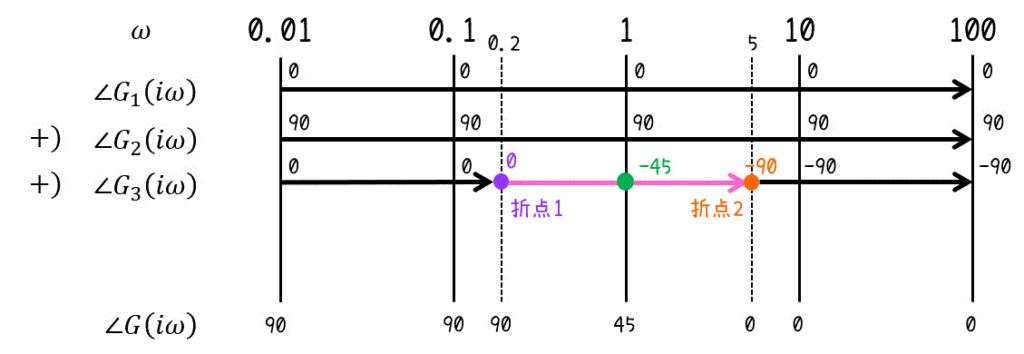
よって、ボード線図(ゲイン線図・位相線図)は下のようになります。
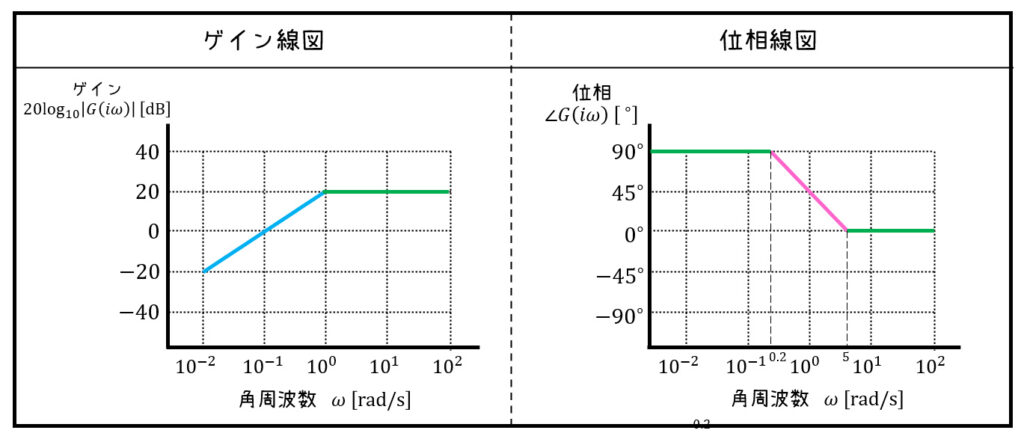
3. 練習問題
最後にボード線図について1問練習してみましょう。
つぎの伝達関数 \[
G(s) = \frac{(0.1s+1)(10s+1)}{(2s+1)(0.5s+1)}
\]で表されるシステムがある。
このシステムのボード線図(ゲイン線図のみ)を折れ線近似を用いて書きなさい。位相線図は書かなくてよい。
必要があれば \( \log_{10} 2 = 0.3 \) を用いてもよい。
★解説★
\( G(i \omega ) \) を\[\begin{align*}
G(i \omega) & = \frac{(0.1 i \omega +1)(10 i \omega +1)}{(2 i \omega +1)(0.5 i \omega +1)}
\\ & = \textcolor{blue}{ 0.1 i \omega +1 } \cdot \textcolor{red}{ 10 i \omega +1 } \cdot \textcolor{green}{ \frac{1}{2 i \omega + 1} } \cdot \textcolor{orange}{ \frac{1}{0.5 i \omega + 1} }
\ & = \textcolor{blue}{ \frac{1}{ \frac{1}{0.1 i \omega +1} } } \cdot \textcolor{red}{ \frac{1}{ \frac{1}{ 10 i \omega +1 } } } \cdot \textcolor{green}{ \frac{1}{2 i \omega + 1} } \cdot \textcolor{orange}{ \frac{1}{0.5 i \omega + 1} }
\\ & = \textcolor{blue}{ G_1 ( i \omega ) } \cdot \textcolor{red}{ G_2 ( i \omega ) } \cdot \textcolor{green}{ G_3( i \omega ) } \cdot \textcolor{orange}{ G_4( i \omega ) }
\end{align*}\]としてから、下のような数直線や表などを書きながら \( \omega = 0.01, 0.1, 1, 10, 100 \) と各折点周波数の値を求めていきましょう。
※ 慣れた人は、\( \omega = 0.01 \) の値のみを求めてから傾きに着目したほうが早くグラフが書けるかもしれません。
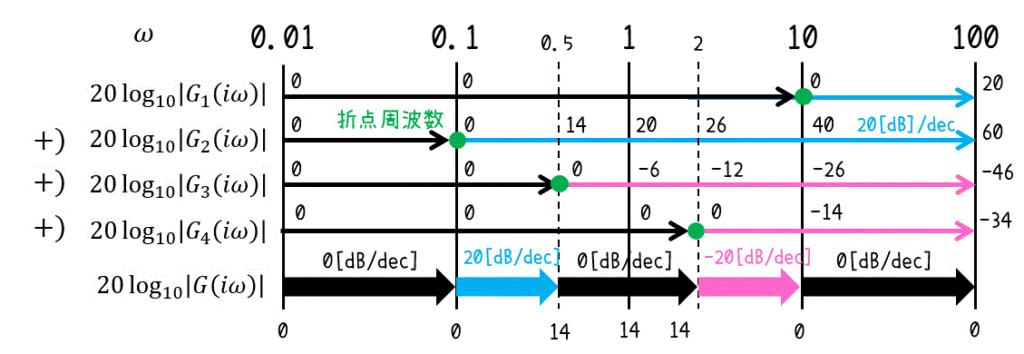
少し「傾きに着目した解き方」も説明しましょう。
傾きに着目する場合、まずは初期値(どこでもいい)としてある \( \omega \) におけるゲインを1つ求めます。今回は \( \omega = 0.01 \) のときで考えましょう(ゲインは0)。
つぎに、\( \omega = \textcolor{blue}{ 0.1 } \) から \( \omega = \textcolor{red}{ 0.5 } \) では、傾きが20[dB/dec] なため、\( \omega = 0.5 \) のときのゲインは\[\begin{align*}
20 \times ( \log_{10} \textcolor{red}{0.5} - \log_{10} \textcolor{blue}{0.1} ) & = 20 \log_{10} \frac{0.5}{0.1}
\\ & = 20 \log_{10} 5
\\ & = 20 ( \log_{10} 10 - \log_{10} 2 )
\\ & = 20 ( 1 - 0.3)
\\ & = 14
\end{align*}\]と計算することができます。
ここで \( \omega = 0.5 \) から \( \omega = 2 \) の値は傾きが変化しないため、\( \omega = 1 \), \( \omega = 2 \) の値を追加で求める必要はありません。
\( \omega = \textcolor{blue}{ 2 } \) から \( \omega = \textcolor{red}{ 10 } \) では、傾きが-20[dB/dec] なため、\( \omega = 10 \) のときのゲインは\[\begin{align*}
14 - 20 \times ( \log_{10} \textcolor{red}{10} - \log_{10} \textcolor{blue}{2} ) & = 20 \log_{10} \frac{10}{2}
\\ & = 14 - 20 \log_{10} 5
\\ & = 14 - 20 ( \log_{10} 10 - \log_{10} 2 )
\\ & = 0
\end{align*}\]と計算することができます。
\( \omega = 10 \) 以降は傾きが変化しないため、ずっとゲインは0です。
これらを踏まえると、下のようなグラフが書けます。
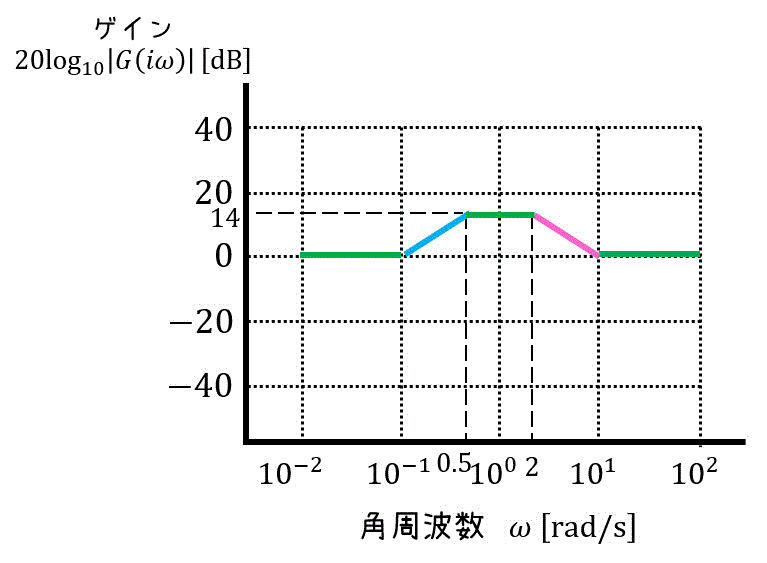
4. さいごに
今回は、伝達関数 \( G(s) \) から逆ラプラス変換を行わずにシステムの振る舞いを調べる方法の1つであるボード線図をメインに説明していきました!
次回からは、フーリエ関連の説明に入っていきたいと思います!
注釈
| ↑1 | 逆三角関数 \( \tan^{-1} \theta \) は大学数学範囲ですが、偏角を表す際に必要なことがあるので、もし慣れていない人はこちらで復習することをおすすめします。 |
|---|---|
| ↑2 | システムの振る舞いをラプラス変換上で表した関数で \( G(s) \) で表されます。 |
| ↑3 | ※ なぜ \( s = i \omega \) を代入するかについては、ここでは省略します。大きさが1の波を入力したときの出力の度合いでシステムの振る舞いを調べる方法があると思っていただけたらOKです。 |
| ↑4 | decは、decade(10)を略したもの。10倍にしたときに値がどれくらい増えるかを示している。 |
| ↑5 | \( \omega T \) を1つの変数として極限をとっています。 |
| ↑6 | 分解方法としては\[ \textcolor{blue}{G_1 ( i \omega )} \cdot \frac{1}{\textcolor{red}{G_2 ( i \omega )}} \cdot \textcolor{green}{ G_3 ( i \omega ) } \]とするのもあり。 ただしこの場合、\( G_2 \) が逆数になっているため、ゲインの式が\[ 20 \log_{10} | \textcolor{blue}{G_1 ( i \omega )} | - 20 \log_{10} | \textcolor{red}{G_2 ( i \omega )} | + 20 \log_{10} | \textcolor{green}{G_3 ( i \omega )} | \]となる点に注意。 |
関連広告・スポンサードリンク