スポンサードリンク
こんにちは、ももやまです。
今回は2重積分における広義積分、および解析学を習った理系学生なら必ず知っておきたいガウス積分についてまとめました。
前回の記事(Part25)はこちら!
(上の記事の内容が前提となっていますので、もし極座標変換を用いた2重積分がわからない人は復習しましょう。)
目次
スポンサードリンク
1.2重積分における広義積分
1変数の広義積分で、例えば\[
\int^1_0 \frac{1}{\sqrt{x}} \ dx , \ \ \ \int^{\infty}_0 \frac{1}{(1+x)^4}
\]のような積分区間に定義されない値が含まれていたり、積分範囲が無限大であるような積分は、いったん極限をとってから計算していましたね。
1変数関数の広義積分があれぇってなった人はこちらに復習記事を用意したのでご覧ください↓
2重積分の場合でも、積分領域内に定義されない点や領域が無限に広がっている(有界ではない)場合は今までの2重積分の方法では計算ができません。そのため、1変数の場合と同様にいったん極限をとってから計算をします。
しかし、無限の領域がどの方向に続くのか*1によって極限の取り方も様々なので、1変数関数に比べて2重積分の広義積分は少しめんどくさいのです。
(1変数関数はプラスとマイナスの2方向を考えるだけでOKだが、2変数になると平面全体あらゆる方向を考える必要があるため。)
大雑把にですが2変数広義積分の定義を書きました。
領域 \( D \) で表される2重積分\[
\iint_D f(x,y) \ dxdy
\]の積分領域が有界ではない(無限に広がる)or ある点において定義されていないために2重積分が計算できない場合でも、
パターン1:有界ではない場合
→\( n \to \infty \) に飛ばした際に \( D \) に近づく有限な領域 \( D_n \) を考える。
パターン2:ある点において定義されていない場合
→定義されない点の周辺を除いた領域 \( D_n \) が \( n \to \infty \) に飛ばした際に \( D \) に近づくように考える。
(1), (2)の場合でも極限\[
\lim_{n \to \infty} \iint_{D_n} f(x,y) \ dxdy
\]がどのような \( D_n \) の取り方をしても同じ値(かつ存在する)場合、広義積分可能といい、広義積分が存在し、そのときの値は\[
\lim_{n \to \infty} \iint_{D_n} f(x,y) \ dxdy
\]の計算結果となる。
実際に例題などでみていったほうがわかりやすいのでそれぞれのパターンについて1つずつ例題で説明していきましょう。
パターン1 積分領域が無限に広がっている場合
まずは、積分領域が無限に広がっている場合について説明していきましょう。
例題1
つぎの広義2重積分\[
\iint_D \frac{1}{(1+x+y)^{\alpha}} \ dxdy \]\[ D = \{ (x,y) \mid x \geqq 0, \ y \geqq 0 \ \}
\]について、つぎの問いに答えなさい。
(1) \( \alpha = 3 \) のときの広義2重積分の値を求めなさい。
(2) 広義積分が収束するための \( \alpha \) の条件を求め、その条件のもとでの広義積分の値を求めなさい。
解説1
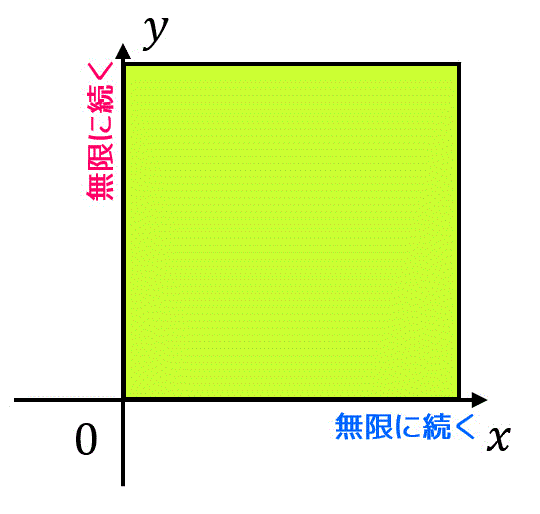
積分範囲を見ると \( x \), \( y \) の正の方向に無限に広がっていますね。
図示すると、
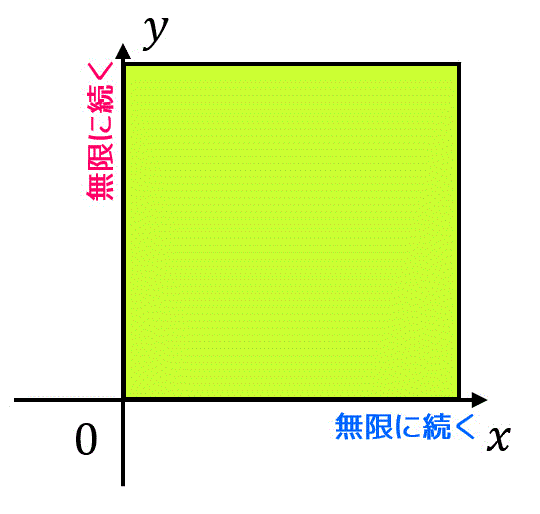
となります。
なので、いったん\[
D_n = \{ (x,y) \mid 0 \leqq x \leqq n , \ 0 \leqq y \leqq n \ \}
\]としてあげます。
すると、\[
\iint_{D_n} \frac{1}{(1+x+y)^{\alpha}} \ dxdy = \int^n_0 \left( \int^n_0 \frac{1}{(1+x+y)^{\alpha}} \ dx \right) \ dy
\]と変形できる。
(1)
\( \alpha = 3 \) なので、\[
\int^n_0 \left( \int^n_0 \frac{1}{(1+x+y)^{3}} \ dx \right) \ dy
\]を計算すればよい。
\[\begin{align*} &
\int^n_0 \frac{1}{(1+x+y)^{3}} \ dx
\\ = & \int^n_0 (1+x+y)^{-3} \ dx
\\ = & - \left[ \frac{1}{2} \cdot (1+x+y)^{-2} \right]^n_0
\\ = & - \frac{1}{2} (1+n+y)^{-2} + \frac{1}{2} (1+y)^{-2}
\end{align*} \]より、\[\begin{align*} &
\int^n_0 \left( \int^n_0 \frac{1}{(1+x+y)^{3}} \ dx \right) \ dy
\\ = & \int^n_0 - \frac{1}{2} (1+n+y)^{-2} + \frac{1}{2} (1+y)^{-2} \ dy
\\ = & \left[ \frac{1}{2} (1+n+y)^{-1} - \frac{1}{2} (1+y)^{-1} \right]^n_0
\\ = & \frac{1}{2} (1+2n)^{-1} - \frac{1}{2} (1+n)^{-1} - \left( \frac{1}{2} (1+n)^{-1} - \frac{1}{2} \cdot 1 \right)
\\ = & \ \frac{1}{2} \cdot \frac{1}{1+2n} - \frac{1}{1+n} + \frac{1}{2}
\end{align*} \]となる。
ここで、\[\begin{align*} &
\lim_{n \to \infty} \left( \frac{1}{2} \cdot \frac{1}{1+2n} - \frac{1}{1+n} + \frac{1}{2} \right)
\\ = & \ 0 - 0 + \frac{1}{2}
\\ = & \ \frac{1}{2}
\end{align*} \]なので、\[\begin{align*}
\iint_D \frac{1}{(1+x+y)^{3}} \ dxdy & = \lim_{n \to \infty} \iint_{D_n} \frac{1}{(1+x+y)^{3}} \ dxdy \\ & = \ \frac{1}{2}
\end{align*} \]となる。
(2)
(1)と同じように計算するだけ。 \[\begin{align*} &
\int^n_0 \frac{1}{(1+x+y)^{\alpha}} \ dx
\\ = & \int^n_0 (1+x+y)^{-\alpha} \ dx
\\ = & - \left[ \frac{1}{1-\alpha} \cdot (1+x+y)^{1-\alpha} \right]^n_0
\\ = & - \frac{1}{1-\alpha} (1+n+y)^{1-\alpha} + \frac{1}{1-\alpha} (1+y)^{1-\alpha}
\end{align*} \]より、\[\begin{align*} &
\int^n_0 \left( \int^n_0 \frac{1}{(1+x+y)^{\alpha}} \ dx \right) \ dy
\\ = & \int^n_0 - \frac{1}{1-\alpha} (1+n+y)^{1-\alpha} + \frac{1}{1-\alpha} (1+y)^{1-\alpha} \ dy
\\ = & \left[ \frac{1}{(1-\alpha)(2-\alpha)} (1+n+y)^{2-\alpha} - \frac{1}{(1-\alpha)(2-\alpha)} (1+y)^{2-\alpha} \right]^n_0
\\ = & \left[ \frac{1}{(1-\alpha)(2-\alpha)} \left( \frac{1}{(1+n+y)^{\alpha - 2}} - \frac{1}{(1+y)^{\alpha - 2}} \right) \right]^n_0
\\ = & \ \frac{1}{(1-\alpha)(2-\alpha)} \left\{ \left( \frac{1}{(1+2n)^{\alpha - 2}} - \frac{1}{(1+n)^{\alpha - 2}} \right) - \left( \frac{1}{(1+n)^{\alpha - 2}} - 1 \right) \right\}
\\ = & \ \frac{1}{(1-\alpha)(2-\alpha)} \left( \frac{1}{(1+2n)^{\alpha - 2}} -2 \cdot \frac{1}{(1+n)^{\alpha - 2}} + 1 \right)
\end{align*} \]となる。
また、\( \alpha \gt 2 \) のときに限り \[\begin{align*} &
\lim_{n \to \infty} \frac{1}{(1+2n)^{2-\alpha}} -2 \cdot \frac{1}{(1+n)^{2-\alpha}} + 1
\\ = & \ 0 - 0 + 1
\\ = & \ 1
\end{align*} \]と収束する*2。
よって、\( \alpha \gt 2 \) のとき、広義2重積分は収束し、\[\begin{align*}
\iint_D \frac{1}{(1+x+y)^{\alpha}} \ dxdy & = \lim_{n \to \infty} \iint_{D_n} \frac{1}{(1+x+y)^{\alpha}} \ dxdy \\ & = \ \frac{1}{(1-\alpha)(2-\alpha)}
\end{align*} \]となる。
パターン2 積分領域内のある点が定義されていない場合
つぎに積分領域内のどこかしらの点において定義されていない点があるパターンについて説明していきましょう。
例題2
つぎの広義2重積分\[
\iint_D \frac{1}{(x^2+y^2)^{\alpha}} \ dxdy \]\[ D = \{ (x,y) \mid \ x^2 + y^2 \leqq 1 \}
\]について、つぎの問いに答えなさい。
(1) \( \alpha = 1/2 \) のときの広義2重積分の値を求めなさい。
(2) 広義積分が収束するための \( \alpha \) の条件を求め、その条件のもとでの広義積分の値を求めなさい。
解説2
積分範囲を見ると原点 \( (x,y) = (0,0) \) のときは積分したい関数が定義されていませんね。図示すると、
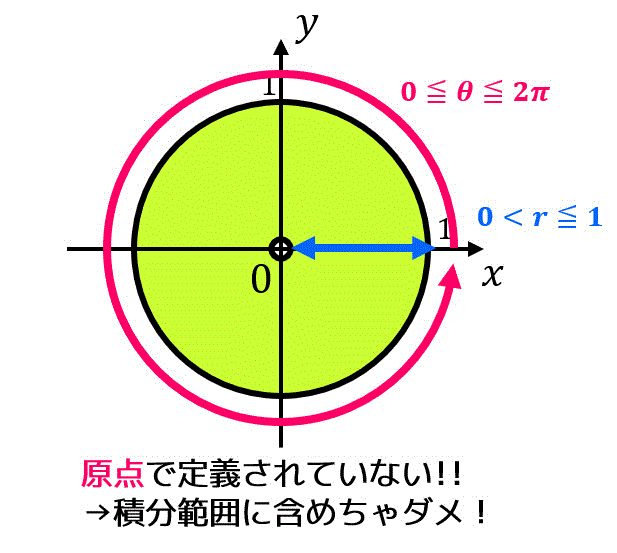
となります。なので原点を避けて積分を行います。そのため、\[
D_n = \left\{ (x,y) \middle| \frac{1}{n^2} \leqq x^2 + y^2 \leqq 1 \ \right\}
\]としてあげます。
すると、\[
\iint_{D_n} \frac{1}{(x^2+y^2)^{\alpha}} \ dxdy = \int^{1}_{\frac{1}{n^2}} \left( \int^{1}_{\frac{1}{n^2}} \frac{1}{(x^2+y^2)^{\alpha}} \ dx \right) \ dy
\]と変形できますね。
ここで積分範囲が円の形になっていますね。なので極座標変換\[
x = r \cos \theta , \ \ \ y = r \sin \theta \\ \left( r \geqq 0, \ \ 0 \leqq \theta \leqq 2 \pi \right)
\]を行いましょう。
また、このときのヤコビアン \( J \) は \( r \) となるので、\[
dxdy = r \ dr d \theta
\]となる(ヤコビアンが \( r \) になる過程を知りたい方はこちらの記事をご覧ください)。
また、積分範囲は\[
\frac{1}{n^2} \leqq r^2 \leqq 1, \ \ \ r \sin \theta \geqq 0
\]となるので変換後の積分範囲 \( D_{n}' \) は\[
D_{n}' = \left\{ (r,\theta) \middle| \ \frac{1}{n} \leqq r \leqq 1, \ 0 \leqq \theta \leqq 2 \pi \ \right\}
\]となる。
(1)
\( \alpha = 1/2 \) なので、\[\begin{align*} &
\iint_{D_n} \frac{1}{\sqrt{x^2+y^2}} \ dxdy
\\ = & \iint_{D_{n}'} \frac{r}{r} \ dr d \theta
\\ = & \int^1_{ \frac{1}{n} } 1 \ dr \cdot \int^{ 2 \pi }_0 1 \ d \theta
\end{align*} \]を計算すればよい。
それぞれの積分の値は\[\begin{align*}
\int^1_{ \frac{1}{n} } 1 \ dr = & \left[ r \right]^1_{ \frac{1}{n} }
\\ = & \ 1 - \frac{1}{n}
\end{align*} \]\[\begin{align*}
\int^{ 2 \pi }_0 1 \ d \theta = & \left[ \theta \right]^{ 2 \pi }_0
\\ = & 2 \pi
\end{align*} \]となるので、\[\begin{align*}
\iint_{D_n} \frac{1}{ \sqrt{x^2+y^2} } \ dxdy
= & \ 2 \pi \left( 1 - \frac{1}{n} \right)
\end{align*} \]となる。
ここで、\[
\lim_{n \to \infty} \ 2 \pi \left( 1 - \frac{1}{n} \right) = \ 2 \pi
\]なので、\[\begin{align*}
\iint_D \frac{1}{ \sqrt{x^2+y^2} } \ dxdy = 2 \pi
\end{align*} \]となる。
(2)
\[\begin{align*} &
\iint_{D_n} \frac{1}{(x^2+y^2)^{\alpha}} \ dxdy
\\ = & \iint_{D_{n}'} \frac{r}{r^{2 \alpha}} \ dr d \theta
\\ = & \int^1_{ \frac{1}{n} } r^{1 - 2 \alpha} \ dr \cdot \int^{ 2 \pi }_0 1 \ d \theta
\end{align*} \]を計算すればよい。
それぞれの積分の値は\[\begin{align*}
\int^1_{ \frac{1}{n} } r^{1 - 2 \alpha} \ dr = & \left[ \frac{1}{2- 2 \alpha} r^{2 - 2 \alpha} \right]^1_{ \frac{1}{n} }
\\ = & \ \frac{1}{2(1- \alpha)} \left( 1 - \left( \frac{1}{n} \right)^{2 - 2 \alpha} \right)
\end{align*} \]\[\begin{align*}
\int^{ 2 \pi }_0 1 \ d \theta = & \left[ \theta \right]^{ 2 \pi }_0
\\ = & 2 \pi
\end{align*} \]となるので、\[\begin{align*}
\iint_D \frac{1}{(x^2+y^2)^{\alpha}} \ dxdy
= & \ \frac{\pi}{1- \alpha} \left( 1 - \left( \frac{1}{n} \right)^{2 - 2 \alpha} \right)
\end{align*} \]となる。
また、\( \alpha \lt 1 \) のときに限り \[ \begin{align*} &
\lim_{n \to \infty} 1 - \left( \frac{1}{n} \right)^{2 - 2 \alpha}
\\ = & \ 1 - 0
\\ = & \ 1
\end{align*} \]と収束する。
よって、\( \alpha \lt 1 \) のとき、広義2重積分は収束し、\[\begin{align*}
\iint_D \frac{1}{(x^2+y^2)^{\alpha}} \ dxdy & = \lim_{n \to \infty} \iint_{D_n} \frac{1}{(x^2+y^2)^{\alpha}} \ dxdy \\ & = \ \frac{\pi}{1- \alpha}
\end{align*} \]となる。
スポンサードリンク
2.ガウス積分
ではいよいよガウス積分について説明しましょう。
ガウス積分とは、ガウス関数 \( e^{-x^2} \) を\[
\int^{\infty}_{- \infty} e^{-x^2} \ dx
\]のように積分する広義積分を表します。
ガウス関数 \( e^{-x^2} \) をグラフに図示すると、下のようになります。
ガウス関数のグラフ、正規分布にそっくりですよね。
このグラフの \( x \) 軸と赤色の \( e^{-x^2} \) で囲まれた面積を求めるのがガウス積分となります。
この広義積分の結果は、統計学(正規分布など)や物理学などの様々な部分で使われています。
では、実際にこの値を今まで習った解析学の力を駆使して計算してみましょう。
Step1: 2変数関数の形に変形
まず、被積分関数は偶関数なので\[
2 \int^{\infty}_{0} e^{-x^2} \ dx
\]ですね。また、広義積分になっているので、\[
2 \lim_{R \to \infty} \int^{R}_{0} e^{-x^2} \ dx
\]としましょう。ここで \( I \) を\[
I = \int^{\infty}_{0} e^{-x^2} \ dx
\]とします。
皆さんは1変数関数の定積分を求める際には1変数関数をいったん不定積分しますね。しかし、 \( e^{-x^2} \) はどう頑張っても不定積分を行うことができません。
しかし、\( x e^{-x^2} \) ならどうでしょうか。この形なら数3レベルの不定積分に変化しますよね。なので、なんとか \( e^{-x^2} \) を \( x e^{-x^2} \) の形に持ち込めないかな、と考えます。
ここで、\[
\int^{R}_{0} e^{-x^2} \ dx = \int^{R}_{0} e^{-y^2} \ dy
\]なのは当たり前ですよね。
なので、2つの積、つまり\[\begin{align*}
I^2 = & \int^{R}_{0} e^{-x^2} \ dx \cdot \int^{R}_{0} e^{-y^2} \ dy
\\ = & \int^{R}_{0} \int^{R}_{0} e^{-x^2-y^2} \ dy
\\ = & \iint_{E_R} e^{-x^2-y^2} \ dx dy
\end{align*} \]の計算を考えます。積分領域は、\[
E_R = \{ (x,y) \mid \ 0 \leqq x \leqq R , \ 0 \leqq y \leqq R \ \}
\]となります。
Step2: 2つの別の領域を用意
\( x^2 + y^2 \) が含まれた積分は、極座標変換をすればうまく \( r^2 \) が出てきてくれて簡単に積分できますね。さらにヤコビアンにより \( r \) 倍されるので、\( r e^{r^2} \) の形にできて簡単に積分ができます。
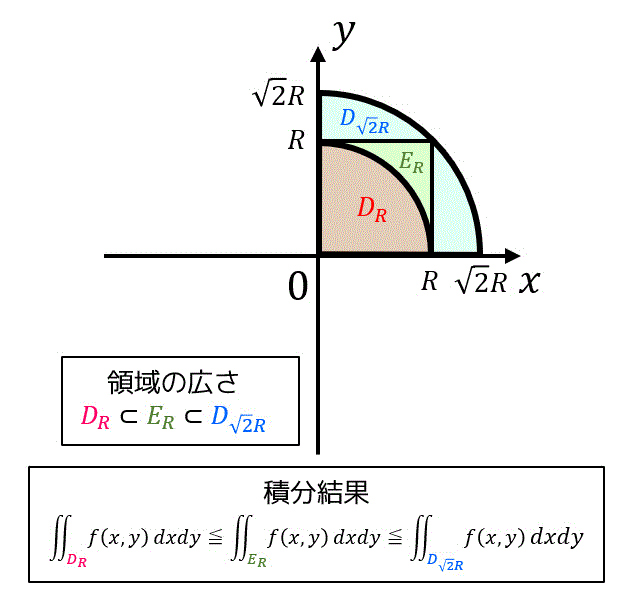
しかし、このままだと領域が円上になっていないので極座標変換ができませんね。なので、実際に計算に使う積分領域よりも少し小さい円上の領域 \( D_1 \) と少し大きい円上の領域 \( D_2 \) を用意します。
\( D_1 \), \( D_2 \) どちらの領域で計算しても同じ答えになることが示せれば、実際に計算したい2重積分の積分領域における計算結果と領域 \( D_1 \), \( D_2 \) で計算したときの計算結果が等しくなることが示せますね!
(はさみうちの定理の2変数バージョンだと思っていただければOKです!)
今回の場合、実際に求めたい2重積分の積分領域\[
E_R = \{ (x,y) \mid \ 0 \leqq x \leqq R , \ 0 \leqq y \leqq R \ \}
\]に対し、少し小さい領域\[
D_R = \{ (x,y) \mid x^2 + y^2 \leqq R^2 , \ x \geqq 0, \ y \geqq 0 \}
\]と少し大きい領域\[
D_{\sqrt{2} R} = \{ (x,y) \mid x^2 + y^2 \leqq 2R^2 , \ x \geqq 0, \ y \geqq 0 \}
\]を考え、\[
\int_{D_R} e^{-x^2-y^2} \ dx dy \leqq \int_{E_R} e^{-x^2-y^2} \ dx dy \leqq \int_{D_{\sqrt{2} R}} e^{-x^2-y^2} \ dx dy
\]を用いて2重積分を計算していこうと思います。
↓領域を図示してみると大小関係がわかりやすいので図示するのがおすすめです!
Step3: 2つの別の領域を計算
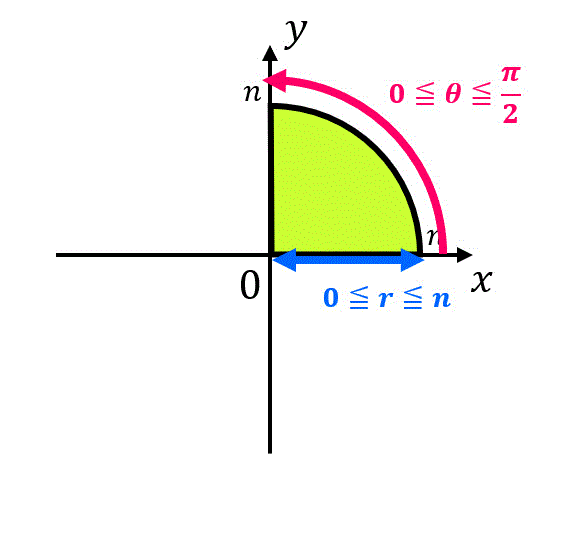
上の2重積分を求めるために、まず2重積分\[
\int_{D_n} e^{-x^2-y^2} \ dx dy \\
D_n = \left\{ (r,\theta) \middle| \ x^2 + y^2 \leqq n^2 , \ x \geqq 0, \ y \geqq 0, \right\}
\]を求めます。\[
x = r \cos \theta , \ \ \ y = r \sin \theta \\ \left( r \geqq 0, \ \ 0 \leqq \theta \leqq 2 \pi \right)
\]を行い、積分領域 \( D_n ' \) を\[
D_n ' = \left\{ (r,\theta) \middle| \ 0 \leqq r \leqq n, \ 0 \leqq \theta \leqq \frac{\pi}{2} \ \right\}
\]となります。
↓図示すると下のようになります
また、このときのヤコビアン \( J \) は \( r \) となるので、\[
dxdy = r \ dr d \theta
\]となる。
よって、[\begin{align*} &
\iint_{D_n} e^{-x^2-y^2} \ dx dy
\\ = & \int^{n}_{0} r e^{-r^2} \ dr \cdot \int^{ \frac{\pi}{2} }_0 1 \ d \theta
\end{align*} \]を計算すればよい。
(ヤコビアン \( r \) が掛けられることで \( r e^{-r^2} \) という不定積分ができる形に持ち込めましたね!)
それぞれの積分の値は\[\begin{align*}
\int^{n}_{ 0 } r e^{-r^2} \ dr = & - \frac{1}{2} \int^{R}_{ 0 } -2r e^{-r^2} \ dr
\\ = & - \frac{1}{2} \left[ e^{-r^2} \right]^{R}_{ 0 }
\\ = & - \frac{1}{2} \left(e^{-n^2} - 1 \right)
\\ = & \ \frac{1}{2} \left( 1 - e^{-n^2} \right)
\end{align*} \]\[\begin{align*}
\int^{ \frac{\pi}{2} }_0 1 \ d \theta = & \left[ \theta \right]^{ \frac{\pi}{2} }_0
\\ = & \frac{\pi}{2}
\end{align*} \]となる。よって、\[\begin{align*} &
\iint_{D_n} e^{-x^2-y^2} \ dx dy
\\ = & \int^{n}_{0} r e^{-r^2} \ dr \cdot \int^{ \frac{\pi}{2} }_0 1 \ d \theta
\\ = & \ \frac{1}{2} \left( 1 - e^{-n^2} \right) \cdot \frac{\pi}{2}
\\ = & \ \frac{\pi}{4} \left( 1 - e^{-n^2} \right)
\end{align*} \]と計算できます。\( n = R \), \( n = \sqrt{2} R \) を代入すると、\[ \begin{align*}
\int_{D_R} e^{-x^2-y^2} \ dx dy = \frac{\pi}{4} \left( 1 - e^{-R^2} \right) \\
\int_{D_{ \sqrt{2} R}} e^{-x^2-y^2} \ dx dy = \frac{\pi}{4} \left( 1 - e^{-2R^2} \right)
\end{align*} \]となります。
Step4: それぞれの計算結果に極限を取り、はさみうち
よって、\[
\frac{\pi}{4} \left( 1 - e^{-R^2} \right) \leqq \int_{E_R} e^{-x^2-y^2} \ dx dy \leqq \frac{\pi}{4} \left( 1 - e^{-2R^2} \right)
\]が成り立ちます。さきほど求めた積分結果を \( R \to \infty \) に飛ばします。\[
\lim_{R \to \infty} e^{-R^2} = 0 \ \ \ \lim_{R \to \infty} e^{- 2 R^2} = 0
\]なので、\[
\lim_{R \to \infty} \frac{\pi}{4} \left( 1 - e^{-R^2} \right) = \frac{\pi}{4} \\
\lim_{R \to \infty} \frac{\pi}{4} \left( 1 - e^{-2R^2} \right) = \frac{\pi}{4}
\]となります。よって、\[
\frac{\pi}{4} \leqq I^2 \leqq \frac{\pi}{4}
\]となり、\[
I^2 = \frac{\pi}{4}
\]となることがわかります。よって、\( I \gt 0 \) より\[
I = \int^{\infty}_{0} e^{-x^2} \ dx = \frac{ \sqrt{ \pi }}{2}
\]と求められます。よって、\[
\int^{\infty}_{- \infty} e^{-x^2} \ dx = \sqrt{ \pi }
\]となります!
期末試験とか院試とかではガウス積分の導出過程を聞かれることが多いので過程は頭にいれておきましょう。
スポンサードリンク
3.練習
では、3問ほど練習してみましょう。
練習1
つぎの広義2重積分\[
\iint_D e^{ax+by} \ dxdy \]\[ D = \{ (x,y) \mid x \geqq 0, \ y \geqq 0 \ \}
\]を求めなさい。ただし \( a \lt 0 \), \( b \lt 0 \) とする。
練習2
つぎの広義2重積分\[
\iint_D \frac{1}{ \sqrt{1-x^2-y^2} } \ dxdy \]\[ D = \{ (x,y) \mid x^2 + y^2 < 1, \ 0 \leqq y \ \}
\]を求めなさい。
練習3 ガウス積分と正規分布(応用)
つぎの積分\[
\int^{\infty}_{- \infty} e^{-ax^2} \ dx
\]を計算しなさい。さらに\[
\int^{\infty}_{- \infty} \frac{1}{ \sqrt{2 \pi} \sigma } e^{ - \frac{(x- \mu)^2}{2 \sigma^2} } \ dx = 1
\]を示しなさい。
4.練習問題の解答
解答1
積分範囲が \( x \), \( y \) の正の方向に無限に広がっているので、\[
D_n = \{ (x,y) \mid 0 \leqq x \leqq n , \ 0 \leqq y \leqq n \ \}
\]とする。
すると、\[
\iint_{D_n} e^{ax+by} \ dxdy = \int^n_0 \left( \int^n_0 e^{ax+by} \ dx \right) \ dy
\]と変形できる。
\[\begin{align*} &
\int^n_0 e^{ax+by} \ dx
\\ = & \left[ \frac{1}{a} e^{ax+by} \right]^n_0
\\ = & \frac{1}{a} \left( e^{an + by} - e^{by} \right)
\\ = & \frac{1}{a} e^{by} \left( e^{an} - 1 \right)
\end{align*} \]より、\[\begin{align*} &
\int^n_0 \left( \int^n_0 e^{ax+by} \ dx \right) \ dy
\\ = & \frac{1}{a} \left( e^{an} - 1 \right) \int^n_0 e^{by} \ dy
\\ = & \frac{1}{a} \left( e^{an} - 1 \right) \left[ \frac{1}{b} e^{by} \right]^n_0
\\ = & \frac{1}{ab} \left( e^{an} - 1 \right) \left( e^{bn} - 1 \right)
\end{align*} \]となる。
ここで、\( a \lt 0 \), \( b \lt 0 \) なので、\[
\lim_{n \to \infty} e^{an} = 0 ,\ \ \ \lim_{n \to \infty} e^{bn} = 0
\]となる。よって、\[\begin{align*}
\lim_{n \to \infty} \left( e^{an} - 1 \right) \left( e^{bn} - 1 \right) = 1
\end{align*} \]なので、\[\begin{align*}
\iint_D e^{ax+by} \ dxdy & = \lim_{n \to \infty} \iint_{D_n} e^{ax+by} \ dxdy \\ & = \ \frac{1}{ab}
\end{align*} \]となる。
解答2
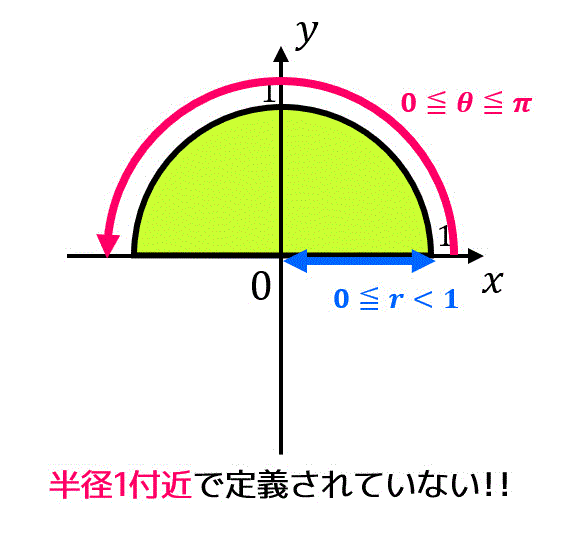
\( x^2 + y^2 = 1 \) を満たすときは積分したい関数が定義されていませんね。なので定義されていない部分を避けて積分を行います。そのため、\[
D_n = \{ (x,y) \mid 0 \leqq x^2 + y^2 \leqq 1 - \frac{1}{n} \ \}
\]としてあげます。さらに\[
R^2 = 1 - \frac{1}{n}
\]とすると*3、\[
D_n = \{ (x,y) \mid 0 \leqq x^2 + y^2 \leqq R^2 \ \}
\]となります。
ここで積分範囲が円の形になっていますね。なので極座標変換\[
x = r \cos \theta , \ \ \ y = r \sin \theta \]\[ \left( r \geqq 0, \ \ 0 \leqq \theta \leqq 2 \pi \right)
\]を行いましょう。ヤコビアン \( J \) は \( r \) となるので、\[
dxdy = r \ dr d \theta
\]ですね。
また、積分範囲は\[
0 \leqq r^2 \leqq R^2, \ \ \ r \sin \theta \geqq 0
\]となるので変換後の積分範囲 \( D_{n}' \) は\[
D_{n}' = \left\{ (r,\theta) \middle| \ 0 \leqq r \leqq R, \ 0 \leqq \theta \leqq \pi \ \right\}
\]となる。
↓図示して確認すると
よって、\[\begin{align*} &
\iint_D \frac{1}{ \sqrt{1-x^2-y^2} } \ dx dy
\\ = & \left( \lim_{n \to \infty} \int^{R}_{0} \frac{r}{1-r^2} dr \right) \cdot \int^{ \pi }_0 1 \ d \theta
\end{align*} \]を計算すればよい。
それぞれの積分の値は\[\begin{align*}
\int^{R}_{0} \frac{r}{1-r^2} dr = & - \frac{1}{2} \int^{R}_{0} \frac{-2r}{1-r^2} dr
\\ = & - \frac{1}{2} \left[ 2 \sqrt{1-r^2} \right]^{R}_{ 0 }
\\ = & - \frac{1}{2} \left( 2 \sqrt{1-R^2} - 2 \right)
\\ = & \ 1 - \sqrt{1-R^2}
\end{align*} \]\[\begin{align*}
\int^{ \pi }_0 1 \ d \theta = & \left[ \theta \right]^{ \pi }_0
\\ = & \pi
\end{align*} \]となる。
ここで、\[\begin{align*} &
\lim_{n \to \infty} \left( 1 - \sqrt{1-R^2} \right)
\\ = & \lim_{n \to \infty} \left( 1 - \sqrt{1- \left( 1- \frac{1}{n} \right)} \right)
\\ = & \lim_{n \to \infty} \left( 1 - \sqrt{ \frac{1}{n} } \right)
\\ = & 1
\end{align*} \]なので、\[\begin{align*} &
\iint_D \frac{1}{ \sqrt{1-x^2-y^2} } \ dx dy
\\ = & \left( \lim_{n \to \infty} \int^{R}_{0} \frac{r}{1-r^2} dr \right) \cdot \int^{ \pi }_0 1 \ d \theta
\\ = & \ \pi
\end{align*} \]と計算できます。
解答3
Step1: 2変数関数の形に変形
まず、被積分関数は偶関数なので\[
2 \int^{\infty}_{0} e^{-ax^2} \ dx
\]となる。また範囲が無限大になっているため、\[
2 \lim_{R \to \infty} \int^{R}_{0} e^{-ax^2} \ dx
\]とし、 \( I \) を\[
I = \int^{\infty}_{0} e^{-ax^2} \ dx
\]とします。
ここで、\[
\int^{R}_{0} e^{-x^2} \ dx = \int^{R}_{0} e^{-y^2} \ dy
\]なので、\[\begin{align*}
I^2 = & \int^{R}_{0} e^{-ax^2} \ dx \cdot \int^{R}_{0} e^{-ay^2} \ dy
\\ = & \int^{R}_{0} \int^{R}_{0} e^{-ax^2-ay^2} \ dy
\\ = & \iint_{E_R} e^{-a(x^2+y^2)} \ dx dy
\end{align*} \]の計算を考えます。積分領域は、\[
E_R = \{ (x,y) \mid \ 0 \leqq x \leqq R , \ 0 \leqq y \leqq R \ \}
\]となります。
Step2: 2つの別の領域を用意
実際に求めたい2重積分の積分領域\[
E_R = \{ (x,y) \mid \ 0 \leqq x \leqq R , \ 0 \leqq y \leqq R \ \}
\]に対し、少し小さい領域\[
D_R = \{ (x,y) \mid x^2 + y^2 \leqq R^2 , \ x \geqq 0, \ y \geqq 0 \}
\]と少し大きい領域\[
D_{\sqrt{2} R} = \{ (x,y) \mid x^2 + y^2 \leqq 2R^2 , \ x \geqq 0, \ y \geqq 0 \}
\]を考え、\[
\int_{D_R} e^{-x^2-y^2} \ dx dy \leqq \int_{E_R} e^{-x^2-y^2} \ dx dy \leqq \int_{D_{\sqrt{2} R}} e^{-x^2-y^2} \ dx dy
\]を用いて2重積分を計算する。すると、\[
D_R \subset E_R \subset D_{\sqrt{2} R}
\]の関係が成り立つ。
(ここは例題と全く同じです)
Step3: 2つの別の領域を計算
上の2重積分を求めるために、まず2重積分\[
\int_{D_n} e^{-a(x^2-y^2)} \ dx dy \\
D_n = \left\{ (r,\theta) \middle| \ x^2 + y^2 \leqq n^2 , \ x \geqq 0, \ y \geqq 0, \right\}
\]を求めます。\[
x = r \cos \theta , \ \ \ y = r \sin \theta \\ \left( r \geqq 0, \ \ 0 \leqq \theta \leqq 2 \pi \right)
\]を行い、積分領域 \( D_n ' \) を\[
D_n ' = \left\{ (r,\theta) \middle| \ 0 \leqq r \leqq n, \ 0 \leqq \theta \leqq \frac{\pi}{2} \ \right\}
\]となります。
また、このときのヤコビアン \( J \) は \( r \) となるので、\[
dxdy = r \ dr d \theta
\]となる。
よって、[\begin{align*} &
\iint_{D_n} e^{-a(x^2-y^2)} \ dx dy
\\ = & \int^{n}_{0} r e^{-ar^2} \ dr \cdot \int^{ \frac{\pi}{2} }_0 1 \ d \theta
\end{align*} \]を計算すればよい。
それぞれの積分の値は\[\begin{align*}
\int^{n}_{ 0 } r e^{-ar^2} \ dr = & - \frac{1}{2a} \int^{R}_{ 0 } -2ar e^{-ar^2} \ dr
\\ = & - \frac{1}{2a} \left[ e^{-ar^2} \right]^{R}_{ 0 }
\\ = & - \frac{1}{2a} \left(e^{-an^2} - 1 \right)
\\ = & \ \frac{1}{2a} \left( 1 - e^{-an^2} \right)
\end{align*} \]\[\begin{align*}
\int^{ \frac{\pi}{2} }_0 1 \ d \theta = & \left[ \theta \right]^{ \frac{\pi}{2} }_0
\\ = & \frac{\pi}{2}
\end{align*} \]となる。よって、\[\begin{align*} &
\iint_{D_n} e^{-ax^2-ay^2} \ dx dy
\\ = & \int^{n}_{0} r e^{-ar^2} \ dr \cdot \int^{ \frac{\pi}{2} }_0 1 \ d \theta
\\ = & \ \frac{1}{2a} \left( 1 - e^{-an^2} \right) \cdot \frac{\pi}{2}
\\ = & \ \frac{\pi}{4a} \left( 1 - e^{-an^2} \right)
\end{align*} \]と計算できます。\( n = R \), \( n = \sqrt{2} R \) を代入すると、\[ \begin{align*}
\int_{D_R} e^{-ax^2-ay^2} \ dx dy = \frac{\pi}{4a} \left( 1 - e^{-aR^2} \right) \\
\int_{D_{ \sqrt{2} R}} e^{-ax^2-ay^2} \ dx dy = \frac{\pi}{4a} \left( 1 - e^{-2aR^2} \right)
\end{align*} \]となります。
Step4: それぞれの計算結果に極限を取り、はさみうち
よって、\[
\frac{\pi}{4} \left( 1 - e^{-aR^2} \right) \leqq \int_{E_R} e^{-ax^2-ay^2} \ dx dy \leqq \frac{\pi}{4} \left( 1 - e^{-2aR^2} \right)
\]が成り立ちます。さきほど求めた積分結果を \( R \to \infty \) に飛ばします。\[
\lim_{R \to \infty} e^{-aR^2} = 0 \ \ \ \lim_{R \to \infty} e^{- 2 aR^2} = 0
\]なので、\[
\lim_{R \to \infty} \frac{\pi}{4a} \left( 1 - e^{-aR^2} \right) = \frac{\pi}{4a} \\
\lim_{R \to \infty} \frac{\pi}{4a} \left( 1 - e^{-2aR^2} \right) = \frac{\pi}{4a}
\]となります。よって、\[
\frac{\pi}{4a} \leqq I^2 \leqq \frac{\pi}{4a}
\]となり、\[
I^2 = \frac{\pi}{4a}
\]となることがわかります。よって、\( I \gt 0 \) より\[
I = \int^{\infty}_{0} e^{-ax^2} \ dx = \frac{1}{2} \sqrt{ \frac{\pi}{a} }
\]と求められます。よって、\[
\int^{\infty}_{- \infty} e^{-ax^2} \ dx = \sqrt{ \frac{\pi}{a} }
\]と求められる。
つぎに、\[
\int^{\infty}_{- \infty} \frac{1}{ \sqrt{2 \pi} \sigma } e^{ - \frac{(x- \mu)^2}{2 \sigma^2} } \ dx = 1\]を示す。\( \frac{x- \mu}{\sigma} = t \) とすると、\( dx = \sigma dt \) となる。
よって、\[ \begin{align*} &
\int^{\infty}_{- \infty} \frac{1}{ \sqrt{2 \pi} \sigma } e^{ - \frac{(x- \mu)^2}{2 \sigma^2} } \ dx
\\ = & \int^{\infty}_{- \infty} \frac{1}{ \sqrt{2 \pi} \sigma } e^{\frac{ - t^2 }{2 } } \cdot \sigma dt
\\ = & \int^{\infty}_{- \infty} \frac{1}{ \sqrt{2 \pi} } e^{\frac{ - t^2 }{2 } } dt
\end{align*} \]となる。
ここで、\[
\int^{\infty}_{- \infty} e^{-ax^2} \ dx = \sqrt{ \frac{\pi}{a} }
\]なので、\( a = 1/2 \) を代入すると、\[
\int^{\infty}_{- \infty} e^{- \frac{x^2}{2} } \ dx = \sqrt{ 2 \pi }
\]となる。よって、\[ \begin{align*} &
\int^{\infty}_{- \infty} \frac{1}{ \sqrt{2 \pi} } e^{\frac{ - t^2 }{2 } } dt
\\ = & \frac{1}{ \sqrt{2 \pi} } \int^{\infty}_{- \infty} e^{\frac{ - t^2 }{2 } } dt
\\ = & \frac{1}{ \sqrt{2 \pi} } \cdot \sqrt{ 2 \pi }
\\ = & \ 1
\end{align*} \]となるので、\[
\int^{\infty}_{- \infty} \frac{1}{ \sqrt{2 \pi} \sigma } e^{ - \frac{(x- \mu)^2}{2 \sigma^2} } \ dx = 1
\]となることが示された。
5.さいごに
今回は2重積分の広義積分、およびガウス積分の導出方法とその応用についてまとめました。
1変数の広義積分に比べ、定義などが若干めんどくさいので
ガウス積分は理系で解析学を習った人の総復習としてふさわしい積分だと思います。この積分が理解できた人は解析学がある程度理解できている、といっていいと思います!
6.引用
(2019年9月25日アクセス)
関連広告・スポンサードリンク