うさぎでもわかる画像処理Part05　画像の幾何学的変換（後編）　同次座標・アフィン変換

こんにちは、ももうさです。

今回は、前回に引き続き画像の幾何学的変換について、同次座標を用いた方法を中心に説明していきます。

※ 前編（Part04）を見ていない方は、前編を見てからこちらの記事をご覧になることをおすすめします。前編では、幾何学的変換の中でも同次座標を使わない基本的な変換を紹介しています。

うさぎでもわかる画像処理　Part04　画像の幾何学的変換（前編）　線形変換

2021.12.5

大学の線形代数で習った線形変換（線形写像）の力を借りて、画像に対して、拡大縮小、回転、スキューなどの幾何学的変換をする方法について、数学的にも画像処理的にもわかりやすくまとめていま...

スポンサードリンク

1. 画像の平行移動

まずはじめに、下のようなある画像を \( x \) 軸方向に \( t_x \)、\( y \) 軸方向に \( t_y \) 移動した場合の変換を考えてみましょう。

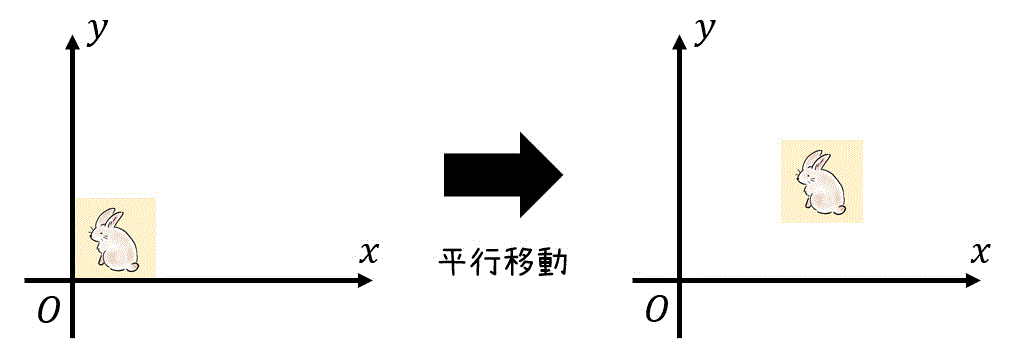
この変換式は、下のように行列とベクトルを使って表すことができます。

しかし、こんなに単純な変換であるにも関わらず、前回のように変換行列 \( A \) を用いた \( \vec{x}' = A \vec{x} \) の形では表すことができません。

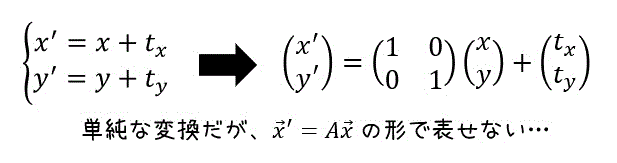
そこで、\( \vec{x}' = A \vec{x} \) で表せるように変換式に一工夫することを考えましょう。

スポンサードリンク

2. 座標を1つ付け足してみよう

ここで、平行移動に \( 1 = 1 \) という余分な式を付け加えてあげます。すると、式は\[
\left\{ \begin{array}{l} x' & = x + t_x \\ y' & = y + t_y \\ 1 & = 1 \end{array} \right.
\]の3つとなりましたね。

この3つの式を行列を使って表すと、下のように \( \vec{x}' = A \vec{x} \) の形で変換を表現することができましたね！

ここで、変換式のベクトルに注目すると、\( x \), \( y \) の他に1がありますね。このように、実際の座標に加えて、仮想的な座標を1個付け加えた座標のことを同次座標と呼びます。

この同次座標については、次の章にて少し詳しく説明していきます。

さらに、Part04で説明してきた下の4つの変換も同次座標ありVerの式を見ていきましょう。

• 画像の拡大・縮小変換
• 鏡映変換
• 回転変換
• スキュー変換

これらの式を同次変換ありVerで表現することで、「画像の平行移動」との合成変換を計算できるようになります。

(1) 画像の拡大・縮小 (同次座標ありVer）

(2) 鏡映変換 (同次座標ありVer）

(3) 回転変換 (同次座標ありVer）

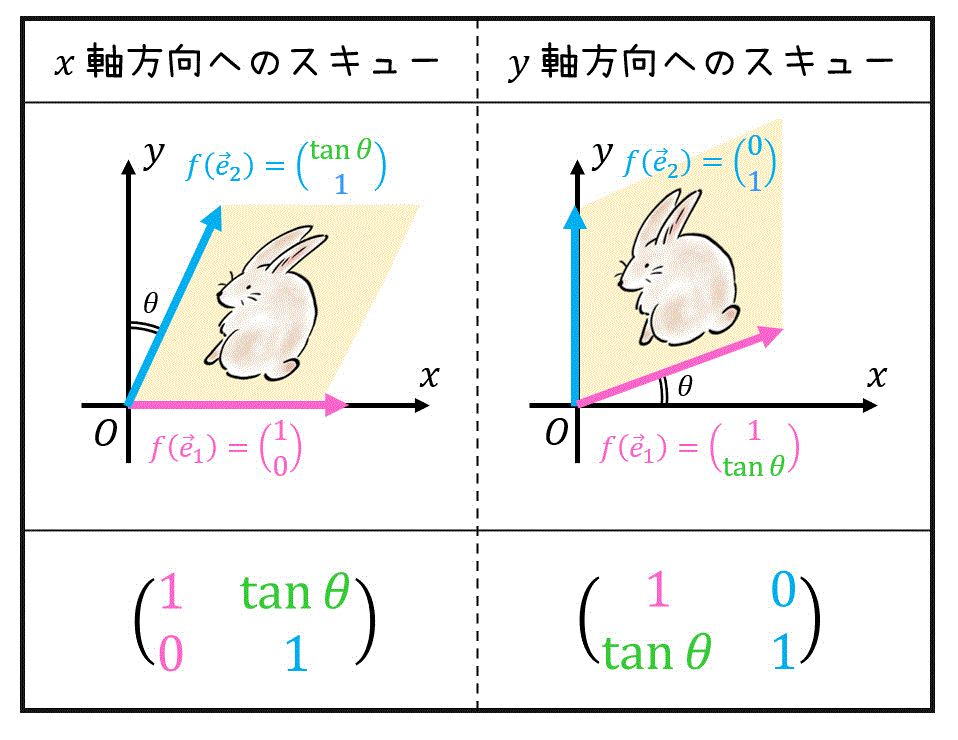
(4) スキュー変換 (同次座標ありVer）

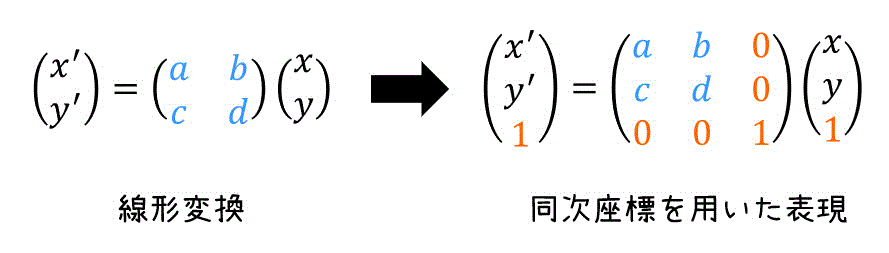
式が複雑そうになっているように見えますが、実際はPart04で出てきた線形変換な式を、下のように変換しているだけです。

スポンサードリンク

3. 同次座標（発展）

※ 少し難しめな内容のため、スキップしてもOKです。

(1) 同次座標の付け方

本来の座標 \( (x,y) \) に加えて、1つ仮想的な座標を付け加えた座標 \( (x,y, \textcolor{red}{1}) \) のことを同次座標系と呼ぶのでしたね。

先ほどの章では、適当に1を付け加えていましたが、実際にはとあるルールに従って同次座標が定義されます。

2次元の場合、ある座標 \( (x,y) \) の同次座標 \( (w_1, w_2, w_3) \) は、\( w_3 \not = 0 \) かつ\[
x = \frac{w_1}{w_3}, \ \ \ y = \frac{w_2}{w_3}
\]の条件を満たすように定義されます。

ただし、\( w_3 = 1 \) 以外の場合、拡大縮小変換、回転変換などの線形変換の式が少し複雑になるため、ほとんどの場合 \( w_3 = 1 \) とし、同次座標を \( (w_1,w_2,w_3) = (x,y,1) \) とします。

(2) 見た目は違うのに同じ座標？

同次座標 \( (w_1, w_2, w_3) \) は、\( w_3 \not = 0 \) かつ\[
x = \frac{w_1}{w_3}, \ \ \ y = \frac{w_2}{w_3}
\]で定義されるのでしたね。

そのため、例えば \[ (w_1,w_2,w_3) = (2,1,1), (4,2,2), \cdots ,(2k,k,k) \] は共に同じ座標 \( (x,y) = (2,1) \) を指しています。同次座標系は定数倍してもすべて同じ座標ということですね。

参考書によっては、ある同次座標系とその定数倍が同値であることを明記するために、下のように同値記号 \( \sim \) を使っている本もあります。\[
\left( \begin{array}{ccc} w_1 \\ w_2 \\ w_3 \end{array} \right) \sim k \left( \begin{array}{ccc} w_1 \\ w_2 \\ w_3 \end{array} \right)
\]

(3) 線形変換式の厳密な表し方

先ほど、2章で、Part04で説明した\[
\left( \begin{array}{ccc} x' \\ y' \end{array} \right) = \left( \begin{array}{ccc} \textcolor{deepskyblue}{a} & \textcolor{deepskyblue}{b} \\ \textcolor{deepskyblue}{c} & \textcolor{deepskyblue}{d} \end{array} \right) \left( \begin{array}{ccc} x \\ y \end{array} \right)
\]の数式を同次座標系で\[
\left( \begin{array}{ccc} x' \\ y' \end{array} \right) \textcolor{red}{=} \left( \begin{array}{ccc} \textcolor{deepskyblue}{a} & \textcolor{deepskyblue}{b} & 0 \\ \textcolor{deepskyblue}{c} & \textcolor{deepskyblue}{d} & 0 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} x \\ y \end{array} \right)
\]と表現しました。

実は、この式の等号＝は同次座標の \( (x,y,\textcolor{red}{1}) \) の赤色要素が1のみで成立する式でした。

この式を、赤色座標部分が1以外で使えるようにするためには、下のように定数倍（\( k \) 倍（の自由度）を考慮する必要があります。 \[
\left( \begin{array}{ccc} x' \\ y' \\ 1 \end{array} \right) = \textcolor{red}{k} \left( \begin{array}{ccc} \textcolor{deepskyblue}{a} & \textcolor{deepskyblue}{b} & 0 \\ \textcolor{deepskyblue}{c} & \textcolor{deepskyblue}{d} & 0 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} x \\ y \\ 1 \end{array} \right)
\]

また、参考書によっては定数倍の考慮を先ほど説明した同値記号 \( \textcolor{red}{\sim} \) を用いて表現しているものもあります。\[
\left( \begin{array}{ccc} x' \\ y' \\ 1 \end{array} \right) \textcolor{red}{\sim} \left( \begin{array}{ccc} \textcolor{deepskyblue}{a} & \textcolor{deepskyblue}{b} & 0 \\ \textcolor{deepskyblue}{c} & \textcolor{deepskyblue}{d} & 0 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} x \\ y \\ 1 \end{array} \right)
\]

4. よく使うアフィン変換

任意の線形変換 → 平行移動の順に行う変換をアフィン変換と呼び、その変換式は以下のように表せます。\[
\left( \begin{array}{ccc} x' \\ y' \\ \textcolor{red}{1} \end{array} \right) = \left( \begin{array}{ccc} a & b & 0 \\ c & d & 0 \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} x \\ y \\ \textcolor{red}{1} \end{array} \right)
\]※赤色の要素が1以外の場合、定数倍を考慮する必要があり。（詳しくは本記事の3-(3)章にて）

そのアフィン変換の中でもよく使うアフィン変換を紹介しましょう。

(1) ユークリッド変換（回転 → 平行移動）

画像を原点中心に反時計回りに \( \theta \) 回転させる変換の後に、\( x \) 軸方向に \( t_x \)、\( y \) 軸方向に \( t_y \) 移動する変換です。

ここで、回転変換の変換行列を \( A \)、平行移動の変換行列を \( B \) とすると、ユークリッド変換を表す変換行列 \( X \) は、\[\begin{align*}
X & = BA
\\ & = \left( \begin{array}{ccc} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} \cos \theta & - \sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} \cos \theta & - \sin \theta & t_x \\ \sin \theta & \cos \theta & t_y \\ 0 & 0 & 1 \end{array} \right)
\end{align*}\]と導出することができます。

(2) 相似変換（拡大 → ユークリッド変換）

ユークリッド変換の前に、画像の縦横の大きさを \( s \) 倍に拡大する変換です。

ここで、 拡大変換の変換行列を \( C \)、ユークリッド変換の変換行列を \( X \) とすると、相似変換の変換行列 \( Y \) は下のように計算できます。\[\begin{align*}
Y & = XC
\\ & = \left( \begin{array}{ccc} \cos \theta & - \sin \theta & t_x \\ \sin \theta & \cos \theta & t_y \\ 0 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} s & 0 & 0 \\ 0 & s & 0 \\ 0 & 0 & 1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} s \cos \theta & - s \sin \theta & t_x \\ s \sin \theta & s \cos \theta & t_y \\ 0 & 0 & 1 \end{array} \right)
\end{align*}\]

5. 練習問題を解いてみよう！

では、実際に2問ほど練習問題で練習をしてみましょう！

☆解答☆

(1) 平行移動させる変換行列に \( t_x = 3 \), \( t_y = 2 \) を代入すればOK。\[
\textcolor{magenta}{ \left( \begin{array}{ccc} 1 & 0 & 3 \\ 0 & 1 & -2 \\ 0 & 0 & 1 \end{array} \right) }
\]

(2) 回転変換の行列に対して、\( \theta = 60^{\circ} \) を代入すればOK。\[\begin{align*}
\left( \begin{array}{ccc} \cos 60^{\circ} & - \sin 60^{\circ} & 0 \\ \sin 60^{\circ} & \cos 60^{\circ} & 0 \\ 0 & 0 & 1 \end{array} \right) & = \left( \begin{array}{ccc} \frac{1}{2} & - \frac{ \sqrt{3} }{2} & 0 \\ \frac{ \sqrt{3} }{2} & \frac{1}{2} & 0 \\ 0 & 0 & 1 \end{array} \right)
\\ & = \textcolor{deepskyblue}{ \frac{1}{2} \left( \begin{array}{ccc} 1 & - \sqrt{3} & 0 \\ \sqrt{3} & 1 & 0 \\ 0 & 0 & 2 \end{array} \right) }
\end{align*}\]

(3) 拡大・縮小変換を行う行列に対して、\( s_x = 2 \), \( s_y = 0.5 \) を代入すればOK。 \[
\textcolor{purple}{ \left( \begin{array}{ccc} 2 & 0 & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & 0 & 1 \end{array} \right) }
\]

☆解答☆

(1)→(2)\[\begin{align*}
X & = \textcolor{deepskyblue}{ \frac{1}{2} \left( \begin{array}{ccc} 1 & - \sqrt{3} & 0 \\ \sqrt{3} & 1 & 0 \\ 0 & 0 & 1 \end{array} \right) } \textcolor{magenta}{ \left( \begin{array}{ccc} 1 & 0 & 3 \\ 0 & 1 & -2 \\ 0 & 0 & 1 \end{array} \right) }
\\ & = \frac{1}{2} \left( \begin{array}{ccc} 1 & - \sqrt{3} & 3 + 2 \sqrt{3} \\ \sqrt{3} & 1 & 3 \sqrt{3} - 2 \\ 0 & 0 & 2 \end{array} \right)
\end{align*}\]

(2)→(3)\[\begin{align*}
Y & = \textcolor{purple}{ \left( \begin{array}{ccc} 2 & 0 & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & 0 & 1 \end{array} \right) } \cdot \textcolor{deepskyblue}{ \frac{1}{2} \left( \begin{array}{ccc} 1 & - \sqrt{3} & 0 \\ \sqrt{3} & 1 & 0 \\ 0 & 0 & 1 \end{array} \right) }
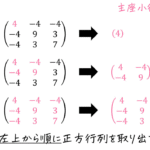
\\ & = \frac{1}{4} \left( \begin{array}{ccc} 4 & -4 \sqrt{3} & 0 \\ \sqrt{3} & 1 & 0 \\ 0 & 0 & 4 \end{array} \right)
\end{align*}\]

(3)→(1)\[\begin{align*}
Z & = \textcolor{magenta}{ \left( \begin{array}{ccc} 1 & 0 & 3 \\ 0 & 1 & -2 \\ 0 & 0 & 1 \end{array} \right) } \textcolor{purple}{ \left( \begin{array}{ccc} 2 & 0 & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & 0 & 1 \end{array} \right) }
\\ & = \left( \begin{array}{ccc} 2 & 0 & 3 \\ 0 & \frac{1}{2} & -2 \\ 0 & 0 & 1 \end{array} \right)
\end{align*}\]

6. さいごに

今回は、同次座標を用いた画像の幾何学的変換を説明していきました。

2回にわたって、様々な変換行列 \( A \) や変換規則が出てきましたが、この行列や規則を丸覚えするのではなく、仕組みを理解しながら導出できるようにすると、試験でど忘れすることが減ると思います。