スポンサードリンク
こんにちは、ももやまです。
今回は2重積分を使って立体の体積や曲面積(表面積)を求める方法についてまとめています。
前回の記事(Part26)はこちら!
広義積分・ガウス積分についてまとめています。こちらも期末試験、院試に頻出項目です。
スポンサードリンク
1.体積
2重積分のイメージは立体を \( x \) 軸方向、\( y \) 軸方向の両方で細かく刻んだ立方体の体積を足したものと以前こちらの記事で説明しましたね。
今回は実際に2変数関数で与えられた立体の体積を求めてみましょう。
2変数関数 \( z = f(x,y) \geqq 0 \) で与えられる立体の体積は\[
\iint_D f(x,y) \ dxdy
\]で求めることができる。ただし、領域 \( D \) は立体の底面である。
例題1
半径 \( a \) の球の体積は\[
\frac{4}{3} \pi a^3
\]である。これを二重積分を用いて示しなさい。
ヒント:原点を中心とした半径 \( a \) の球の方程式は\[
x^2 + y^2 + z^2 = a^2
\]で表される。
解説1
まずは球の式 \( x^2 + y^2 + z^2 = a^2 \) を \( z = f(x,y) \geqq 0 \) の形にしましょう。すると、\[
z = f(x,y) = \sqrt{ a^2 - x^2 - y^2}
\]となりますね。
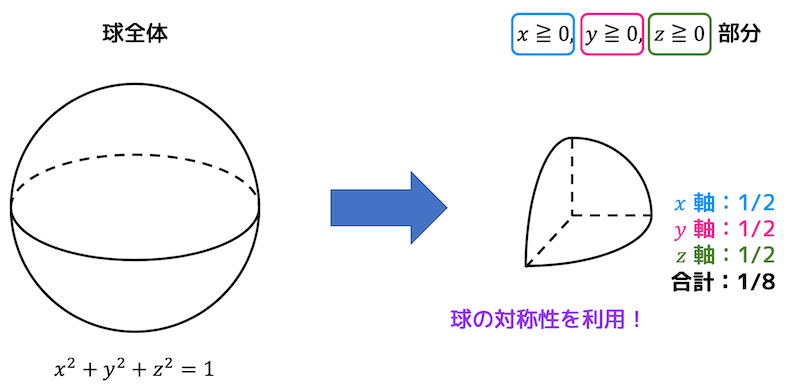
つまり、下の図のような\( x \) 軸, \( y \) 軸, \( z \) 軸の正の部分からなる図形の体積を求めます。
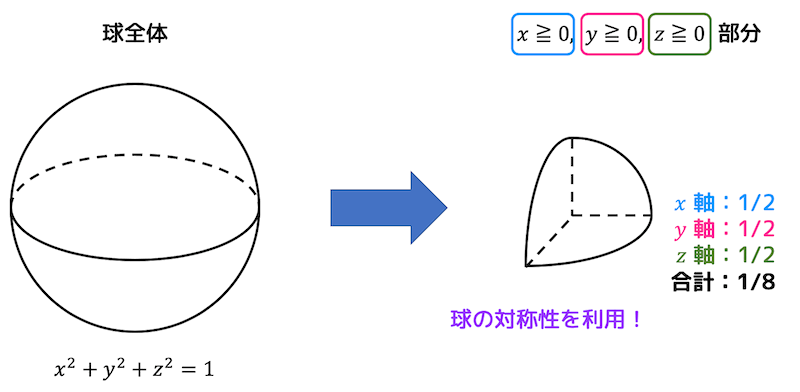
ただし、3つの軸で2等分した図形の体積を求めているので、二重積分で求められる体積の結果は求めたい立体の体積の1/8となります。
なので、球の体積 \( V \) は\[
V = 8 \iint_D \sqrt{ a^2 - x^2 - y^2} \ dxdy
\]で求めることができます。
また、積分領域 \( D \) は下のようになります。
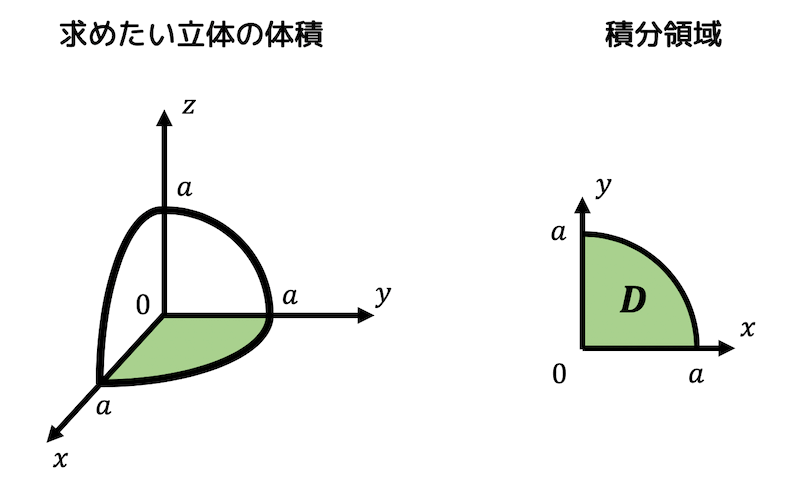
数式で表すと、\[
D = \{ (x,y) \mid x^2 + y^2 \leqq a^2 , x \geqq 0 , y \geqq 0 \ \}
\]となります。
では2重積分\[
\iint_D \sqrt{ a^2 - x^2 - y^2} \ dxdy
\]を計算していきましょう。
積分範囲が円なので、極座標変換\[
x = r \cos \theta , \ \ \ y = r \sin \theta \]\[ \left( r \geqq 0, \ \ 0 \leqq \theta \leqq 2 \pi \right)
\]を行いましょう。
もし極座標変換があやふやな人がいればこちらの記事で復習しましょう。
体積・曲面積を求める問題では極座標変換を使うことが多いので極座標変換は必須項目です。
極座標変換のヤコビアン \( J \) は \( r \) となるので、\[
dxdy = r \ dr d \theta
\]でしたね。
また、積分範囲は\[
r^2 \leqq a^2, \ \ \ r \sin \theta \geqq 0 , \ r \cos \theta \geqq 0
\]となり、\( r \geqq 0 \) のため、\[
0 \leqq r \leqq a, \ \ \ \sin \theta \geqq 0, \ \cos \theta \geqq 0
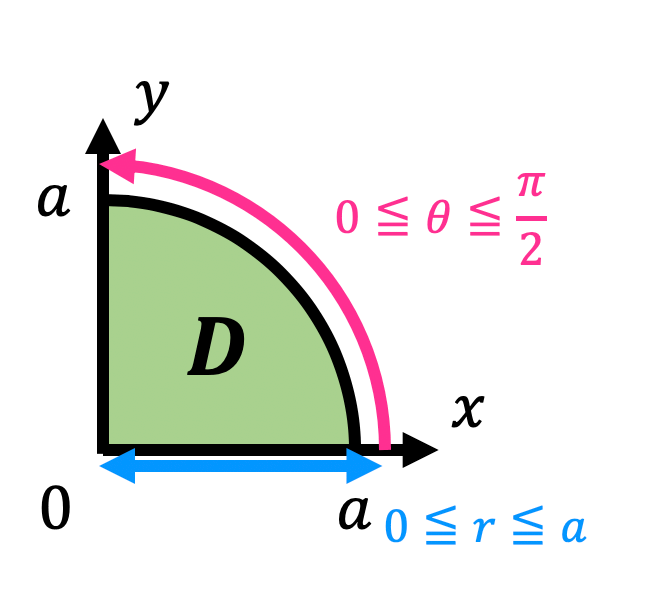
\]となり、変換後の積分範囲 \( D' \) は\[
D' = \left\{ (r,\theta) \ \middle| \ 0 \leqq r \leqq a, \ 0 \leqq \theta \leqq \frac{\pi}{2} \ \right\}
\]となりますね。
自信がない人は図示した領域から積分範囲が正しくなるかを確認しておきましょう。
よって、\[\begin{align*} &
\iint_D \sqrt{ a^2 - x^2 - y^2} \ dxdy
\\ = & \iint_{D'} r \sqrt{ a^2 - r^2 } \ drd \theta
\\ = & \int^a_0 r \sqrt{ a^2 - r^2 } \ dr \cdot \int^{ \frac{\pi}{2} }_{0} 1 \ d \theta
\end{align*} \]を計算すればよい。
それぞれの積分の値は\[\begin{align*}
\int^a_0 r \sqrt{ a^2 - r^2 } \ dr & = - \frac{1}{2} \int^a_0 -2r \sqrt{ a^2 - r^2 } \ dr
\\ & = - \frac{1}{2} \left[ - \frac{2}{3} (a^2 - r^2)^{ \frac{3}{2} } \right]^a_0
\\ & = - \frac{1}{3} ( - a^2 )^{ \frac{3}{2} }
\\ & = \frac{1}{3} a^3
\end{align*} \]\[\begin{align*}
\int^{ \frac{\pi}{2} }_{0} 1 \ d \theta = \frac{\pi}{2}
\end{align*} \]となるので、\[\begin{align*}
\iint_D \sqrt{ a^2 - x^2 - y^2} \ dxdy
= & \frac{1}{3} a^3 \cdot \frac{\pi}{2}
\\ = & \frac{1}{6} \pi a^3
\end{align*} \]となる。
よって、球の体積 \( V \) は\[\begin{align*}
V & = 8 \iint_D \sqrt{ a^2 - x^2 - y^2} \ dxdy
\\ & = 8 \cdot \frac{1}{6} \pi a^3
\\ & = \frac{4}{3} \pi a^3
\end{align*} \]となり、題意は満たされた。
余談ですが、\[
\int^a_0 r \sqrt{ a^2 - r^2 } \ dr = - \frac{1}{2} \left[ - \frac{2}{3} (a^2 - r^2)^{ \frac{3}{2} } \right]^a_0
\]のように途中で置換積分の省略公式を適用させています。
省略公式について詳しく知りたい人はこちらの記事をご覧ください。
置換積分の省略公式は覚えておくと計算速度をかなり早めることができるのでぜひ習得しておきましょう!
スポンサードリンク
2.曲面積(表面積)
2重積分を使うことで立体の曲面の面積を求めることができます。
ある立体の曲面の面積のことを曲面積、もしくは表面積と呼びます。
まずは曲面積の公式をみてみましょう。
2変数関数 \( z = f(x,y) \geqq 0 \) で与えられる立体の曲面の面積 \( S \) は\[
S = \iint_D \sqrt{ 1 + \left( \frac{\partial f}{\partial x} \right)^2 + \left( \frac{\partial f}{\partial y} \right)^2 } \ dxdy
\]で求めることができる。ただし、領域 \( D \) は立体の底面である。
曲面積の公式の仕組みを少しだけですが解説します。
曲面積を求めるにあたって、\( x \), \( y \) をそれぞれ \( \Delta x \), \( \Delta y \) だけ微小変化させることで作った微小な面積の平行四辺形を考えます。
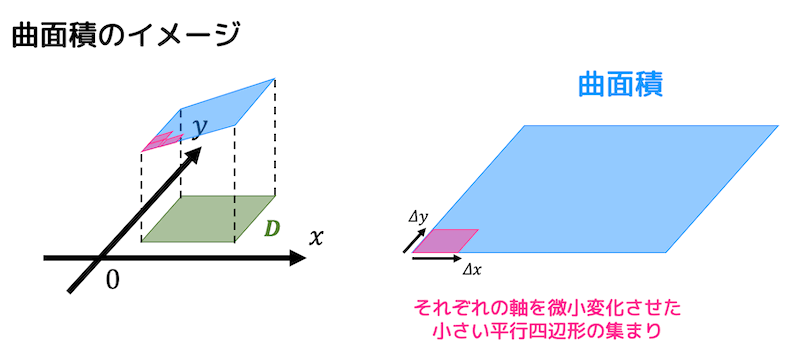
曲面 \( z = f(x,y) \) で与えられた面を微小な平行四辺形に分割し、分割した平行四辺形の面積の総和をとり、極限を取ったものが曲面積となります。
実際に曲面積の公式を導出してみましょう。
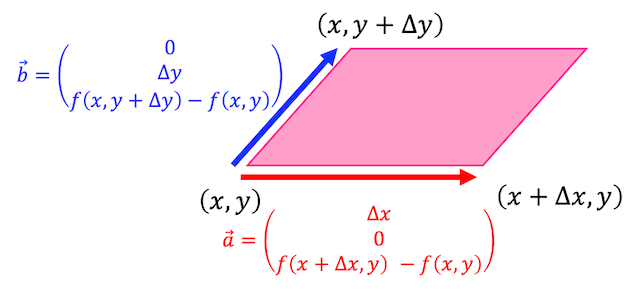
上の図のような平行四辺形を考えるためにベクトル \( \vec{a} \), \( \vec{b} \) を考えます。
すると、平行四辺形の面積は \( \vec{a} \) と \( \vec{b} \) の外積の長さで求めることができますね。
ベクトル \( \vec{a} \), \( \vec{b} \) の外積を求めると*1、\[\begin{align*}
\vec{a} \times \vec{b} & = \left( \begin{array}{ccc} \Delta x \\ 0 \\ F( \Delta x) \end{array} \right) \times \left( \begin{array}{ccc} 0 \\ \Delta y \\ F( \Delta y) \end{array} \right)
\\ & = \left| \begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ \Delta x & 0 & F( \Delta x) \\ 0 & \Delta y & F(\Delta y) \end{array} \right|
\\ & = - \Delta y \cdot F(\Delta x) \vec{i} - \Delta x \cdot F( \Delta y) \vec{j} + \Delta x \cdot \Delta y \vec{k}
\\ & = \left( \begin{array}{ccc} - \Delta y \cdot F(\Delta x) \\ - \Delta x \cdot F( \Delta y) \\ \Delta x \cdot \Delta y \end{array} \right)
\\ & = \left( \begin{array}{ccc} - \Delta y \cdot ( f(x + \Delta x, y) - f(x,y) ) \\ - \Delta x \cdot ( f(x, y +\Delta y) - f(x,y) ) \\ \Delta x \cdot \Delta y \end{array} \right)
\end{align*}\]となるので面積 \( S_i \) は\[\begin{align*}
S_i & = | \vec{a} \times \vec{b} |
\\ & = \sqrt{ 1 + \left( \frac{ f(x + \Delta x, y) - f(x,y) }{\Delta x} \right)^2 + \left( \frac{ f(x,y + \Delta y) - f(x,y) }{\Delta y} \right)^2 } \Delta x \Delta y
\\ & \fallingdotseq \sqrt{ 1 + \left( \frac{\partial f}{\partial x} \right)^2 + \left( \frac{\partial f}{\partial y} \right)^2 } \Delta x \Delta y
\end{align*}\]
と求めることができます。この分割した平行四辺形の面積 \( S_i \) の総和をとり、極限を取ったものが曲面積となります。なので、曲面積 \( S \) は\[\begin{align*}
S & =
\sum^{\infty}_{i = 1} S_i
\\ & = \sum^{\infty}_{i = 1} \sqrt{ 1 + \left( \frac{\partial f}{\partial x_i} \right)^2 + \left( \frac{\partial f}{\partial y_i} \right)^2 } \Delta x_i \Delta y_i
\\ & = \iint_D \sqrt{ 1 + \left( \frac{\partial f}{\partial x} \right)^2 + \left( \frac{\partial f}{\partial y} \right)^2 } \ dxdy
\end{align*}\]となります。
(\( i \) 番目の \( x \), \( y \), \( \Delta x \), \( \Delta y \) をそれぞれ \( x_i \), \( y_i \), \( \Delta x_i \), \( \Delta y_i \) とし、\( x_i \), \( y_i \), \( \Delta x_i \), \( \Delta y_i \) からできる微小な平行四辺形の面積を \( S_i \) としています。)
例題2
半径 \( a \) の球の表面積は\[
4 \pi a^2
\]である。これを二重積分を用いて示しなさい。
ヒント:例題1と同じように球の対称性を利用できる。
解説2
まずは球の式 \( x^2 + y^2 + z^2 = a^2 \) を \( z = f(x,y) \geqq 0 \) の形にしましょう。すると、\[
z = f(x,y) = \sqrt{ a^2 - x^2 - y^2}
\]となりますね。
つぎに例題1とおなじように球の対称性を利用します。つまり、\( x \) 軸, \( y \) 軸, \( z \) 軸の正の部分からなる図形の表面積を求め、最後に8倍します。
(3つの軸で2等分した図形の曲面積を計算すると計算結果は求めたい立体の表面積(曲面積)の1/8となるため)
なので、球の表面積 \( S \) は\[
S = 8 \iint_D \sqrt{ 1 + \left( \frac{\partial f}{\partial x} \right)^2 + \left( \frac{\partial f}{\partial y} \right)^2 } \ dxdy \\
f(x,y) = \sqrt{ a^2 - x^2 - y^2} \\
D = \{ (x,y) \mid x^2 + y^2 \leqq a^2 , x \geqq 0 , y \geqq 0 \ \}
\]で求めることができます。
ここで、\[\begin{align*}
\frac{\partial f}{\partial x} & = -2x \cdot \frac{1}{2 \sqrt{ a^2 - x^2 - y^2} }
\\ & = - \frac{x}{ \sqrt{ a^2 - x^2 - y^2} }
\end{align*} \]\[\begin{align*}
\frac{\partial f}{\partial y} & = -2y \cdot \frac{1}{2 \sqrt{ a^2 - x^2 - y^2} }
\\ & = - \frac{y}{ \sqrt{ a^2 - x^2 - y^2} }
\end{align*} \]と計算できるので、\[\begin{align*} &
\sqrt{ 1 + \left( \frac{\partial f}{\partial x} \right)^2 + \left( \frac{\partial f}{\partial y} \right)^2 }
\\ = & \ \sqrt{ 1 + \left( - \frac{x}{ \sqrt{ a^2 - x^2 - y^2} } \right)^2 + \left( - \frac{y}{ \sqrt{ a^2 - x^2 - y^2} } \right)^2 }
\\ = & \ \sqrt{ 1 + \frac{x^2}{a^2 - x^2 - y^2} + \frac{y^2}{a^2 - x^2 - y^2} }
\\ = & \ \sqrt{ \frac{ a^2 - x^2 - y^2 + x^2 + y^2}{a^2 - x^2 - y^2} }
\\ = & \ \sqrt{ \frac{ a^2 }{a^2 - x^2 - y^2} }
\\ = & \ \frac{a}{ \sqrt{ a^2 - x^2 - y^2} }
\end{align*} \]となります。
つぎに\[
\iint_D \sqrt{ 1 + \left( \frac{\partial f}{\partial x} \right)^2 + \left( \frac{\partial f}{\partial y} \right)^2 } \ dxdy = \iint_D \frac{a}{ \sqrt{ a^2 - x^2 - y^2} }
\]を計算します。
積分範囲が円なので、極座標変換\[
x = r \cos \theta , \ \ \ y = r \sin \theta \]\[ \left( r \geqq 0, \ \ 0 \leqq \theta \leqq 2 \pi \right)
\]を行いましょう。
極座標変換のヤコビアン \( J \) は \( r \) となるので、\[
dxdy = r \ dr d \theta
\]でしたね。
また、積分範囲は\[
r^2 \leqq a^2, \ \ \ r \sin \theta \geqq 0 , \ r \cos \theta \geqq 0
\]となり、\( r \geqq 0 \) のため、\[
0 \leqq r \leqq a, \ \ \ \sin \theta \geqq 0, \ \cos \theta \geqq 0
\]となり、変換後の積分範囲 \( D' \) は\[
D' = \left\{ (r,\theta) \ \middle| \ 0 \leqq r \leqq a, \ 0 \leqq \theta \leqq \frac{\pi}{2} \ \right\}
\]となりますね。
(体積のときと同じ積分範囲になります)
よって、\[\begin{align*} &
\iint_D \frac{a}{ \sqrt{ a^2 - x^2 - y^2} } \ dxdy
\\ = & \iint_{D'} \iint_D \frac{ar}{ \sqrt{ a^2 - r^2} } \ drd \theta
\\ = & \int^a_0 \frac{ar}{ \sqrt{ a^2 - r^2} } \ dr \cdot \int^{ \frac{\pi}{2} }_{0} 1 \ d \theta
\end{align*} \]を計算すればよい。
それぞれの積分の値は\[\begin{align*}
\int^a_0 \frac{ar}{ \sqrt{ a^2 - r^2} } \ dr = & -\frac{1}{2} a \int^a_0 \frac{-2r}{ \sqrt{ a^2 - r^2} } \ dr
\\ = & - \frac{1}{2} a \left[ 2 \sqrt{a^2 - r^2} \right]^a_0
\\ = & - \frac{1}{2} a \cdot (- 2 \sqrt{a^2})
\\ = & a^2
\end{align*} \]\[\begin{align*}
\int^{ \frac{\pi}{2} }_{0} 1 \ d \theta = \frac{\pi}{2}
\end{align*} \]となるので、\[\begin{align*}
\iint_D \sqrt{ a^2 - x^2 - y^2} \ dxdy
& = a^2 \cdot \frac{\pi}{2}
\\ & = \frac{1}{2} \pi a^2
\end{align*} \]となる。
よって、球の表面積 \( S \) は\[\begin{align*}
S & = 8 \sqrt{ 1 + \left( \frac{\partial f}{\partial x} \right)^2 + \left( \frac{\partial f}{\partial y} \right)^2 } \ dxdy
\\ & = 8 \cdot \frac{1}{2} \pi a^2
\\ & = 4 \pi a^2
\end{align*} \]となり、題意は満たされた。
スポンサードリンク
3.練習問題
では実際に体積と表面積(曲面積)を求める問題を1問ずつ練習してみましょう。
練習1
円柱 \( x^2 + z^2 = a^2 \) の \( x^2 + y^2 \leqq a^2 \) にある部分の体積 \( V \) と表面積 \( S \) を求めなさい。
練習2
球 \( x^2 + y^2 + z^2 = 1 \) の \( x^2 + y^2 \leqq x \) にある部分の体積 \( V \) と表面積 \( S \) を求めなさい。
4.練習問題の答え
解答1
概形と底面は下の図のようになる。
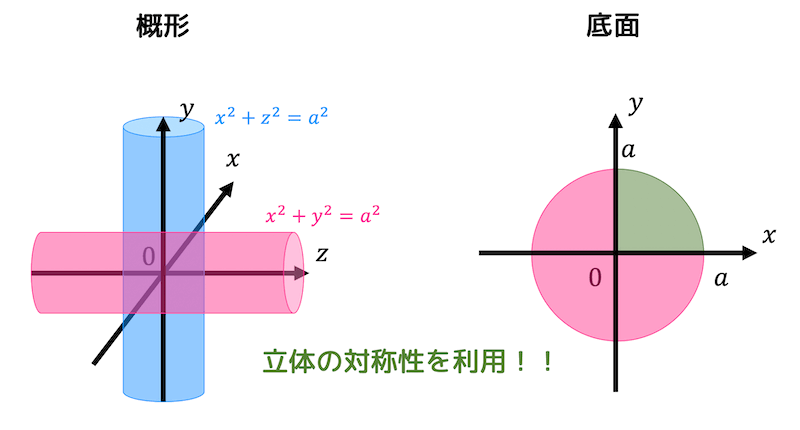
円柱の式 \( x^2 + z^2 = a^2 \) を \( z = f(x,y) \geqq 0 \) の形にすると、\[
z = f(x,y) = \sqrt{a^2 - x^2}
\]となる。
また、\( x \) 軸, \( y \) 軸, \( z \) 軸それぞれに対して図形の対称性があるので、体積、表面積ともに \( x \geqq 0 \), \( y \geqq 0 \), \( z \geqq 0 \) の部分を求めてから答えを8倍にすればよい。
体積の導出
円柱の体積 \( V \) は\[
V = 8 \iint_D \sqrt{a^2 - x^2} \]\[
D = \{ (x,y) \mid x^2 + y^2 \leqq a^2 , x \geqq 0 , y \geqq 0 \ \}
\]で求めることができる。
ここで積分領域 \( D \) が円なので極座標に置きたくなるが、極座標にしてしまうと \( f(x,y) \) の部分が計算しにくくなるので今回は極座標には変換しない。
[2重積分ができる形に積分範囲を置き換え]ここで、\[
y^2 \leqq a^2 - x^2
\]である。さらに \( y \geqq 0 \) より、\[
0 \leqq y \leqq \sqrt{a^2 - x^2}
\]となる。さらに \( x \geqq 0 \) かつ \( a^2 - x^2 \geqq 0 \) (ルートの中身は0以上)なので、\[
0 \leqq x \leqq a
\]となる。よって、積分範囲は\[
D = \{ (x,y) \ \mid \ 0 \leqq x \leqq a , \ 0 \leqq y \leqq \sqrt{a^2 - x^2} \}
\]と書き換えることができる。
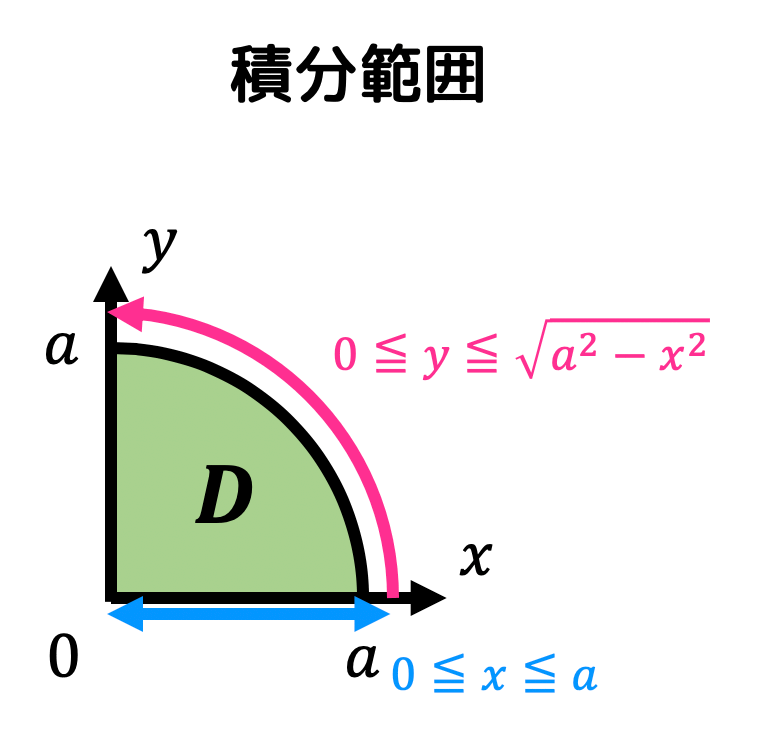
よって、\[\begin{align*} &
\iint_D \sqrt{a^2 - x^2} \ dxdy
\\ = & \ \int^{a}_0 \left( \int^{ \sqrt{a^2-x^2} }_{0} \sqrt{a^2 - x^2} \ dy \right) \ dx
\end{align*} \]を計算すればよい。
ここで、\[\begin{align*}
\int^{ \sqrt{a^2-x^2} }_{0} \sqrt{a^2 - x^2} \ dy & = \sqrt{a^2 - x^2} \int^{ \sqrt{a^2-x^2} }_{0} 1 \ dy
\\ & = a^2 - x^2
\end{align*} \]となるので、\[\begin{align*} &
\iint_D \sqrt{a^2 - x^2} \ dxdy
\\ = & \ \int^{a}_0 \left( \int^{ \sqrt{a^2-x^2} }_{0} \sqrt{a^2 - x^2} \ dy \right) \ dx
\\ = & \ \int^{a}_0 a^2 - x^2 \ dx
\\ = & \left[ a^2 x - \frac{1}{3} x^3 \right]^{a}_0
\\ = & a^3 - \frac{1}{3} a^3
\\ = & \frac{2}{3} a^3
\end{align*} \]となる。
よって体積 \( V \) は\[\begin{align*}
V & = 8 \iint_D \sqrt{a^2 - x^2}
\\ & = 8 \cdot \frac{2}{3} a^3
\\ & = \frac{16}{3} a^3
\end{align*}\]となる。
表面積の導出
円柱の表面積 \( S \) は\[
S = 8 \iint_D \sqrt{ 1 + \left( \frac{\partial f}{\partial x} \right)^2 + \left( \frac{\partial f}{\partial y} \right)^2 } \ dxdy \]\[
f(x,y) = \sqrt{a^2 - x^2} \]\[
D = \{ (x,y) \mid x^2 + y^2 \leqq a^2 , x \geqq 0 , y \geqq 0 \ \}
\]で求めることができる。
ここで、\[\begin{align*}
\frac{\partial f}{\partial x} & = -2x \cdot \frac{1}{2 \sqrt{ a^2 - x^2 } }
\\ & = - \frac{x}{ \sqrt{ a^2 - x^2} }
\end{align*} \]\[\begin{align*}
\frac{\partial f}{\partial y} & = 0
\end{align*} \]と計算できるので、\[\begin{align*} &
\sqrt{ 1 + \left( \frac{\partial f}{\partial x} \right)^2 + \left( \frac{\partial f}{\partial y} \right)^2 }
\\ = & \ \sqrt{ 1 + \left(- \frac{x}{ \sqrt{ a^2 - x^2} } \right)^2 }
\\ = & \ \sqrt{ 1 + \frac{x^2}{a^2 - x^2} }
\\ = & \ \sqrt{ \frac{ a^2 - x^2 + x^2}{a^2 - x^2} }
\\ = & \ \sqrt{ \frac{ a^2 }{a^2 - x^2 } }
\\ = & \ \frac{a}{ \sqrt{ a^2 - x^2 } }
\end{align*} \]となる。
よって\[
\iint_D \sqrt{ 1 + \left( \frac{\partial f}{\partial x} \right)^2 + \left( \frac{\partial f}{\partial y} \right)^2 } \ dxdy = \iint_D \frac{a}{ \sqrt{ a^2 - x^2 } }
\]を計算して最後に答えを8倍すればよい。
体積を求めたときと全く同じように積分範囲を\[
D = \{ (x,y) \ \mid \ 0 \leqq x \leqq a , \ 0 \leqq y \leqq \sqrt{a^2 - x^2} \}
\]と書き換える。
つまり、\[\begin{align*} &
\iint_D \sqrt{a^2 - x^2} \ dxdy
\\ = & \ \int^{a}_0 \left( \int^{ \sqrt{a^2-x^2} }_{0} \frac{a}{ \sqrt{ a^2 - x^2 } } \ dy \right) \ dx
\end{align*} \]を計算すればよい。
ここで、\[\begin{align*}
\int^{ \sqrt{a^2-x^2} }_{0} \frac{a}{ \sqrt{ a^2 - x^2 } } \ dy & = \frac{a}{ \sqrt{ a^2 - x^2 } } \int^{ \sqrt{a^2-x^2} }_{0} 1 \ dy
\\ & = a
\end{align*} \]となるので、\[\begin{align*} &
\iint_D \sqrt{a^2 - x^2} \ dxdy
\\ = & \ \int^{a}_0 \left( \int^{ \sqrt{a^2-x^2} }_{0} \frac{a}{ \sqrt{ a^2 - x^2 } } \ dy \right) \ dx
\\ = & \ a \int^{a}_0 1 \ dx
\\ = & \ a^2
\end{align*} \]となる。
よって、表面積 \( S \) は\[\begin{align*}
S & = 8 \sqrt{ 1 + \left( \frac{\partial f}{\partial x} \right)^2 + \left( \frac{\partial f}{\partial y} \right)^2 } \ dxdy
\\ & = 8 \cdot a^2
\\ & = 8 a^2
\end{align*} \]となる。
解答2
概形と底面は下の図のようになる。
(概形が球っぽく見えないのは仕様です……。)
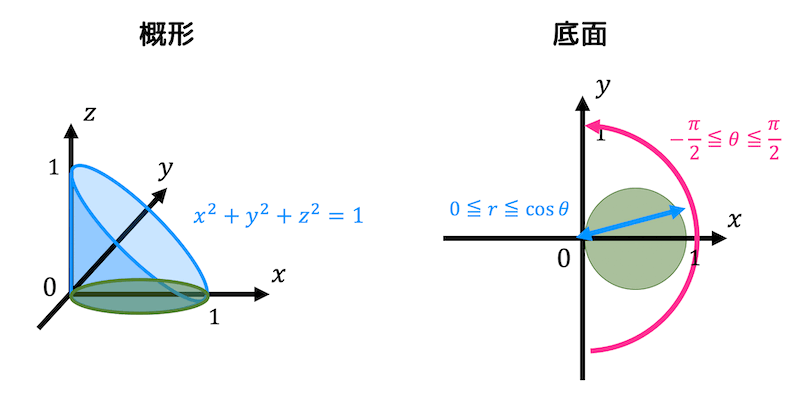
球の式 \( x^2 + y^2 + z^2 = 1 \) を \( z = f(x,y) \geqq 0 \) の形にすると、\[
z = f(x,y) = \sqrt{1 - x^2 - y^2}
\]となる。
また、体積に関しては \( z \) 軸に対して図形の対称性があるので、\( z \geqq 0 \) の部分を求めてから答えを2倍にすればよい。
( \( x \) 軸に対しては図形の対称性がないので間違えて答えを8倍にしないこと。なお、\( y \) 軸に対しても対称性を適用させてもOK。)
また、表面積に関しては \( z \) 軸に加え、\( y \) 軸に対して図形の対称性があるので、\( z \geqq 0 \), \( y \geqq 0 \) の部分を求めてから答えを4倍にすればよい。
表面積の場合、体積の場合と異なり \( y \geqq 0 \) を無視すると正しい答えが出ないので注意してください。
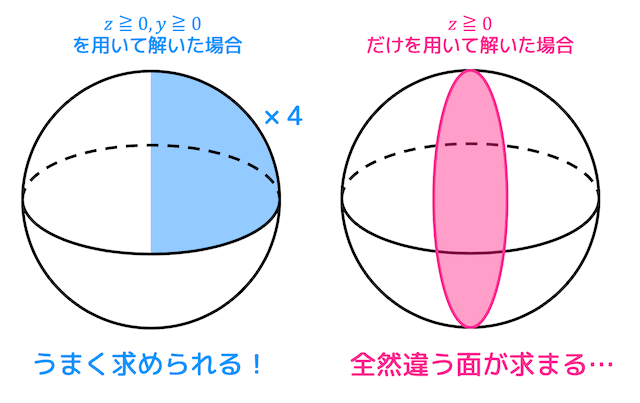
対称性をうまく使わないと違う面の面積が求まることもあります……。
体積の導出
円柱の体積 \( V \) は\[
V = 2 \iint_D \sqrt{1 - x^2 - y^2} \]\[
D = \{ (x,y) \mid x^2 + y^2 \leqq x \}
\]で求めることができる。
積分範囲を変換するため、極座標変換\[
x = r \cos \theta , \ \ \ y = r \sin \theta \]\[ \left( r \geqq 0, \ \ - \pi \leqq \theta \leqq \pi \right)
\]を行う。
極座標変換のヤコビアン \( J \) は \( r \) となるので、\[
dxdy = r \ dr d \theta
\]が成立する。
また、積分範囲は\[
r^2 \leqq r \cos \theta
\]となり、\( r \geqq 0 \) のため、\[
r \leqq a \cos \theta , \cos \theta \geqq 0
\]となります( \( \cos \theta \geqq 0 \) に要注意。)
変換後の積分範囲 \( D' \) は\[
D' = \left\{ (r,\theta) \ \middle| \ 0 \leqq r \leqq \cos \theta, \ - \frac{\pi}{2} \leqq \theta \leqq \frac{\pi}{2} \ \right\}
\]となる。
よって、\[\begin{align*} &
\iint_D \sqrt{ 1 - x^2 - y^2} \ dxdy
\\ = & \iint_{D'} r \sqrt{ 1 - r^2 } \ drd \theta
\\ = & \int^{ \frac{\pi}{2} }_{ - \frac{\pi}{2} } \left( \int^{\cos \theta}_{0} r \sqrt{ 1 - r^2 } \ dr \right) \ d \theta
\end{align*} \]を計算すればよい。
ここで、\[\begin{align*}
\int^{\cos \theta}_{0} r \sqrt{ 1 - r^2 } \ dr & = -\frac{1}{2} \int^{\cos \theta}_{0} -2r \sqrt{ 1 - r^2 } \ dr
\\ & = - \frac{1}{2} \left[ - \frac{2}{3} (1 - r^2)^{ \frac{3}{2} } \right]^{\cos \theta}_{0}
\\ & = - \frac{1}{3} ( 1 - \cos^2 \theta )^{ \frac{3}{2} } + \frac{1}{3}
\\ & = \frac{1}{3} - \frac{1}{3} ( \sin^2 \theta )^{ \frac{3}{2} }
\\ & = \frac{1}{3} - \frac{1}{3} \left| \sin \theta \right|^3
\end{align*} \]と計算できるので、\[\begin{align*} &
\iint_D \sqrt{ 1 - x^2 - y^2} \ dxdy
\\ = & \ \int^{ \frac{\pi}{2} }_{ - \frac{\pi}{2} } \left( \int^{\cos \theta}_{0} r \sqrt{ 1 - r^2 } \ dr \right) \ d \theta
\\ = & \ \int^{ \frac{\pi}{2} }_{ - \frac{\pi}{2} } \frac{1}{3} - \frac{1}{3} \left| \sin \theta \right|^3 \ d \theta
\\ = & \ 2 \int^{ \frac{\pi}{2} }_{ 0 } \frac{1}{3} - \frac{1}{3} \left| \sin \theta \right|^3 \ d \theta
\\ = & \ 2 \int^{ \frac{\pi}{2} }_{ 0 } \frac{1}{3} - \frac{1}{3} \sin^3 \theta \ d \theta
\\ = & \ \frac{2}{3} \int^{ \frac{\pi}{2} }_{ 0 } 1 \ d \theta - \frac{2}{3} \int^{ \frac{\pi}{2} }_{ 0 } \sin^3 \theta \ d \theta
\\ = & \ \frac{\pi}{3} - \frac{4}{9}
\end{align*} \]となる*2。
よって、体積 \( V \) は\[\begin{align*}
V & = 2 \iint_D \iint_D \sqrt{ 1 - x^2 - y^2} \ dxdy
\\ & = 2 \left( \frac{\pi}{3} - \frac{4}{9} \right)
\\ & = \frac{2}{3} \pi - \frac{8}{9}
\end{align*} \]となる。
表面積の導出
対称性に注意しましょう。\( y \geqq 0 \), \( z \geqq 0 \) の両方の対称性を用いないと正しい答えが出せません。
表面積 \( S \) は\[
S = 2 \iint_D \sqrt{ 1 + \left( \frac{\partial f}{\partial x} \right)^2 + \left( \frac{\partial f}{\partial y} \right)^2 } \ dxdy \]\[
f(x,y) = \sqrt{ 1 - x^2 - y^2} \]\[
D = \{ (x,y) \mid x^2 + y^2 \leqq x \}
\]で求めることができます。
ここで、\[\begin{align*}
\frac{\partial f}{\partial x} & = -2x \cdot \frac{1}{2 \sqrt{ 1 - x^2 - y^2} }
\\ & = - \frac{x}{ \sqrt{ 1 - x^2 - y^2} }
\end{align*} \]\[\begin{align*}
\frac{\partial f}{\partial y} & = -2y \cdot \frac{1}{2 \sqrt{ 1 - x^2 - y^2} }
\\ & = - \frac{y}{ \sqrt{ 1 - x^2 - y^2} }
\end{align*} \]と計算できるので、\[\begin{align*} &
\sqrt{ 1 + \left( \frac{\partial f}{\partial x} \right)^2 + \left( \frac{\partial f}{\partial y} \right)^2 }
\\ = & \ \sqrt{ 1 + \left( - \frac{x}{ \sqrt{ 1 - x^2 - y^2} } \right)^2 + \left( - \frac{y}{ \sqrt{ 1 - x^2 - y^2} } \right)^2 }
\\ = & \ \sqrt{ 1 + \frac{x^2}{1 - x^2 - y^2} + \frac{y^2}{1 - x^2 - y^2} }
\\ = & \ \sqrt{ \frac{ 1 - x^2 - y^2 + x^2 + y^2}{1 - x^2 - y^2} }
\\ = & \ \sqrt{ \frac{ 1 }{1 - x^2 - y^2} }
\\ = & \ \frac{1}{ \sqrt{ 1 - x^2 - y^2} }
\end{align*} \]となる。
よって、\[
\iint_D \sqrt{ 1 + \left( \frac{\partial f}{\partial x} \right)^2 + \left( \frac{\partial f}{\partial y} \right)^2 } \ dxdy = \iint_D \frac{1}{ \sqrt{ 1 - x^2 - y^2} }
\]を計算して最後に答えを4倍すればよい。
\( y \geqq 0 \) ( \( r \sin \theta \geqq 0 \) )の条件が加わるため積分範囲は、\[
D' = \left\{ (r,\theta) \ \middle| \ 0 \leqq r \leqq \cos \theta, \ 0 \leqq \theta \leqq \frac{\pi}{2} \ \right\}
\]と変わるので注意してください。
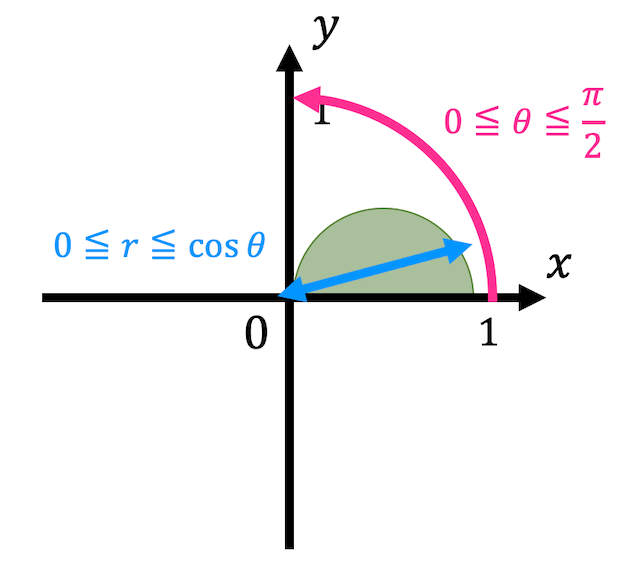
よって、\[\begin{align*} &
\iint_D \frac{1}{ \sqrt{ 1 - x^2 - y^2} } \ dxdy
\\ = & \iint_{D'} \frac{r}{ \sqrt{ 1 - r^2} } \ dr d \theta
\\ = & \int^{ \frac{\pi}{2} }_{ 0 } \left( \int^{\cos \theta}_{0} \frac{r}{ \sqrt{ 1 - r^2} } \ dr \right) \ d \theta
\end{align*} \]を計算すればよい。
ここで、\[\begin{align*}
\int^{\cos \theta}_{0} \frac{r}{ \sqrt{ 1 - r^2} } \ dr = & -\frac{1}{2} \int^{\cos \theta}_{0} \frac{-2r}{ \sqrt{ 1 - r^2} } \ dr
\\ = & - \frac{1}{2} \left[ 2 \sqrt{1 - r^2} \right]^{\cos \theta}_{0}
\\ = & - \sqrt{1 - \cos^2 \theta} + 1
\\ = & 1 - \sqrt{\sin^2 \theta}
\\ = & 1 - \sin \theta
\end{align*} \]と計算できるので、\[\begin{align*} &
\iint_D \frac{1}{ \sqrt{ 1 - x^2 - y^2} } \ dxdy
\\ = & \int^{ \frac{\pi}{2} }_{ 0 } \left( \int^{\cos \theta}_{0} \frac{r}{ \sqrt{ 1 - r^2} } \ dr \right) \ d \theta
\\ = & \int^{ \frac{\pi}{2} }_{ 0 } 1 - \sin \theta \ d \theta
\\ = & \left[ \theta + \cos \theta \right]^{ \frac{\pi}{2} }_{ 0 }
\\ = & \frac{\pi}{2} - 1
\end{align*} \]となる。
よって、表面積 \( S \) は\[\begin{align*}
S & = 4 \sqrt{ 1 + \left( \frac{\partial f}{\partial x} \right)^2 + \left( \frac{\partial f}{\partial y} \right)^2 } \ dxdy
\\ & = 4 \cdot \left( \frac{\pi}{2} - 1 \right)
\\ & = 2 \pi - 4
\end{align*} \]となる。
5.さいごに
今回は2重積分を用いて立体の体積・表面積を求める方法についてまとめました。
2重積分の応用問題として期末試験、院試などに出題されやすいのでぜひ対策をしましょう。
うさぎでもわかる解析は今回が「一応」最終回となります。
Part27までお付き合いいただき、ありがとうございました!
p.s. Part28「3重積分」ができました。
興味があればご覧ください!
*1:省略のため\[
F(\Delta x) = f(x + \Delta x, y) - f(x,y) \\
F(\Delta y) = f(x, y +\Delta y) - f(x,y)
\]としています。
*2:
\( | \sin \theta |^3 \) は偶関数なのを積分計算の途中で利用している。
また、ウォリスの公式から、\[
\int^{ \frac{\pi}{2} }_{ 0 } \sin^3 \theta \ d \theta = \frac{2}{3}
\]を導き出している。わからなければ3倍角の公式から\[ \begin{align*} &
\int^{ \frac{\pi}{2} }_{ 0 } \sin^3 \theta \ d \theta
\\ = & \ \frac{1}{4} \int^{ \frac{\pi}{2} }_{ 0 } 3 \sin \theta - \sin 3 \theta \ d \theta
\\ = & \ \frac{1}{4} \left[ - 3 \cos \theta + \frac{1}{3} \cos \theta \right]^{ \frac{\pi}{2} }_{ 0 }
\\ = & \ \frac{1}{4} \left( 3 - \frac{1}{3} \right)
\\ = & \ \frac{1}{4} \cdot \frac{8}{3}
\\ = & \ \frac{2}{3}
\end{align*} \]と導いてもOK。
関連広告・スポンサードリンク