【誤差伝播の法則】うさぎでもわかる実験の基礎　第1羽　誤差の取り扱い（誤差論）と有効数字

こんにちは、ももやまです！

みなさんは実験で測定をしたことはありますか？

実験に出てくる理論ってかなり難しく書いてありますよね。難しすぎて嫌になって（うさぎのように）逃げだしたくなります。

今回はそんな難しい理論をなるべく（うさぎでもわかるように）簡単に書いてみようということでこのページを作りました。

特に実験でよく使う誤差処理（誤差論）と有効数字についてまとめています。

※注意

厳密な定義とかは省いています。あくまでもわかりやすさ重視です。

また、もしかしたら間違えてまとめてしまっている部分があるかもしれません。そのような部分を見つけた方は私のTwitter、もしくはメールなどでお知らせいただけたらありがたいです。

また、数1の「データの分析」が怪しい人は、必ず復習しておきましょう。

下に1時間で復習できる記事を用意しているので、もしよかったらご覧ください。

www.momoyama-usagi.com

スポンサードリンク

１．有効数字のいろは

では、まずは有効数字について説明していきます。

高校のときに化学や物理で有効数字について習った人がおおいかと思いますが、習っていない（or忘れた）人用にうさぎでもわかるように記述しております。

(1) 有効数字とは

機械なのでデータを測定する際、測定できる値には限りがありますよね。例えば（人用の）体重計であれば小数第1位（0.1の位）までしか測れませんね。

実験の際には正しく測定できた値を明記する必要があります。これを有効数字と呼びます。

たとえば体重の測定結果が50kgであった場合、（小数第1位を四捨五入し、）1の位まで正しく測定できたことを示しています。そのため、体重の測定結果が49.5kg以上50.5kg未満であることがわかります。

一方測定結果が50.0kgであった場合、（小数第2位を四捨五入し、）小数第1位まで正しく測定できたことを示しています。そのため、体重の測定結果が49.95kg以上50.05kg未満であることがわかります。

このように測定結果の50kgと50.0kgは同じ値に見えても意味がかなり異なるものになってくるのです。

(2) 有効数字の桁数

有効数字の桁数は測定できた値の範囲を表します。有効数字の桁数が増えれば増えるほどより多くの桁数が測定できたことを表しています。

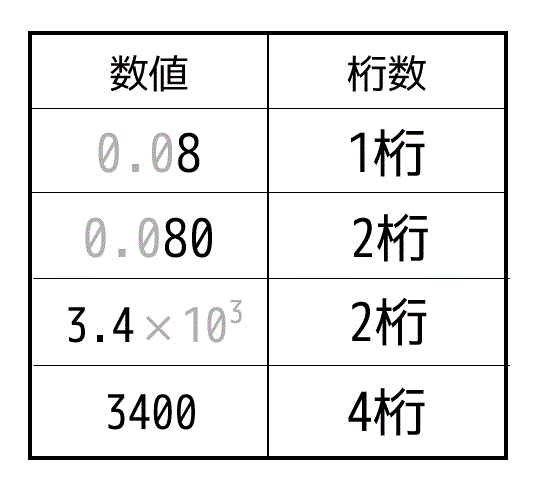
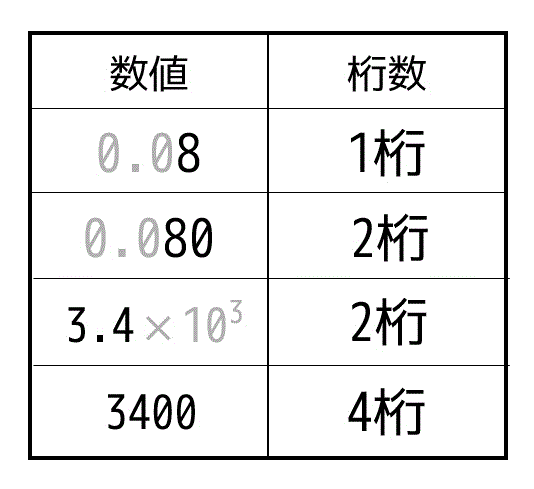
例えば50kgであれば有効数字2桁であり、50.0kgであれば有効数字が3桁となります。数学の場合と異なり、.0 には意味があるものというところに注意してください。

また、小数の場合は左側の0は有効数字としてはカウントしません。例えば、0.08であれば有効数字は1桁、0.080であれば有効数字は2桁となります。

しかし、数がすごく大きいor小さい場合は\[
a \times 10^n \ \ \  \ \ \left( \ 1 \leqq a \lt 10 \ \right)
\]のように表現を行います。このように表現することで有効数字の桁数がわかりやすくなります。例えば、\( 3.34 \times 10^5 \) であれば有効数字は3桁、\( - 6.0 \times 10^{-23} \) であれば有効数字は2桁となります。

（決して \( 3.34 \times 10^5 \) を334000と書いてはいけません。有効数字が3桁と6桁で全然違う結果となります。ただし、\( 2.0 \times 10^{-3} \) を 0.0020 と書くように有効数字が変化しない書き方の場合は書き換えてもOKです。）

↓何個か例をまとめてみました。

(3) 測定値を読む場合の有効数字

実際に測定した値を読む際、どこまでを有効数字にしたらいいか迷いますよね。

デジタル値で測定結果が表示されている場合、デジタル値の値をそのまま有効数字としてOKです。（事前に測定器具の目盛りの単位を取扱説明書などで確認しましょう。）

一方アナログ表示の場合、最小目盛りの1/10の値までを読み取り、有効数字としましょう。たとえば皆さんがよく使う1[mm]刻みの定規の場合、0.1mm単位までを有効数字としてください。

(4) 各種演算における有効数字の桁数

つぎは、各種演算を行った際に有効数字の桁数がどのように変わるのかについてみていきたいと思います。

(1) 足し算・引き算の場合

まず、足し算・引き算の場合について説明していきます。

たとえば19.19 + 33.4 の計算を普通にすると 52.59 になります。しかし、33.4は33.40とは限りませんよね*1。（イメージとしては33.4の後には未知の数字?が続いてる（33.4????…）と考えてください。

足し算や引き算の場合、値の一番小さい位が大きいほうに桁を合わせます。

19.19と33.4の場合は19.19が小数第2位に対し、33.4が小数第1位なのでより位が大きい小数第1位に合わせましょう。

わかりやすく筆算で書いてみます。

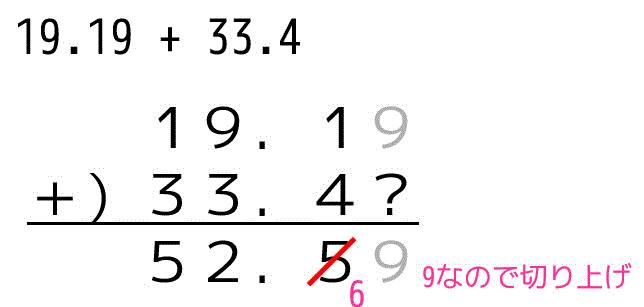
すると、52.6 となることがわかります。

有効数字の範囲外の数字には？をつけて計算するとわかりやすくなると思います。

引き算の場合も足し算と同じように計算を行います。

8.93 - 5.2 の計算の場合、値の一番小さい位がより大きい5.2（小数第1位まで）に合わせます。筆算で書くと、

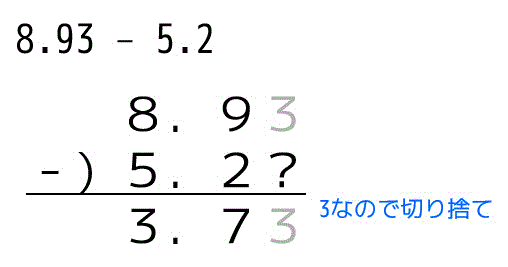
となり、3.7となることがわかります。

(2) 掛け算・割り算・べき乗の場合

つぎに掛け算、割り算の場合について説明します。

掛け算や割り算の場合は、2つの数のうち有効数字が小さい方に合わせます。例えば、3.53×5.6の場合、3桁×2桁なので有効数字は2桁とします。

有効数字を考慮すると、\[
3.53 \times 5.6 = 20
\]となります。同様に3.53÷5.6を計算すると、\[
3.53 \div 5.6 = 0.63
\]となります。（同じく有効数字は2桁）

値のべき乗や平方根を求める際は、有効数字の桁数を元の値と同じにします。例えば、\[
4.1^3 = 69 , \ \ \ \ \sqrt{57} = 7.5
\]となります（計算元も計算先も有効数字は2桁ですね。）。

(3) 定数や無理数などを計算に使う場合

公式などに代入する場合、\( 4 \pi r^2 \) の4や \( \frac{1}{2} mv^2 \) の1/2のような定数がよく出てきます。

定数に誤差は絶対にないので*2、定数は有効数字が無限大と考えてください。

（同じく \( \sin 30^{\circ} = 1/2 \) なども定数となります。）

また、無理数の \( \pi \) や \( e \) は丸める箇所までが有効数字となります。例えば \( \pi \) を3.14とした場合は有効数字が3桁に、3.14159とした場合は有効数字が6桁となります。

どこまで有効数字を取るかについてですが、他の実験データの桁数よりも1桁多くとれば他の有効数字などに影響を与えないので、1桁多く取ることを習慣にしましょう。

（逆に無意味な桁まで有効数字を取ることはしないようにしましょう。誤差の原因となります。Excelなどで処理する人は、出た値をむやみやたらに使用することは避け、Round関数などで有効数字+1桁までの桁で四捨五入させてから計算させましょう。）

(4) 計算過程と有効数字

結果を計算する際に、1つの式だけで計算結果が求められることは多くはありません。2段階以上にわけて計算をする必要も出てきます。

2段階以上にわけて計算をする場合、本来取るべき有効数字より1桁多く取るようにしましょう。

（後ほど紹介する例題などで実際に2段階に分けて計算する場面があるのでそこで確認してください。）

例題1　有効数字の計算

つぎの(1)～(4)の計算を有効数字を考えながら計算しなさい。

(1) \( 11.4 + 5.14 \)
(2) \( 10.0 - 4.55 \)
(3) \( 1.5 \times 2.53 \)
(4) \( \sqrt{33.4} \)

解説1

(1)

11.4は小数第1位、5.14は小数第2位なので小数第1位に合わせる。よって\[
11.4 + 5.14 = 16.5
\]となる。（筆算は下に示しています。）

(2)

10.0は小数第1位、4.55は小数第2位なので小数第1位に合わせる。よって\[
10.0 - 4.55 = 5.5
\]となる。（筆算は下に示しています。）

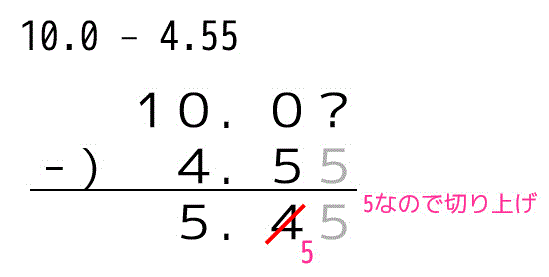
(3)

1.5は有効数字2桁、2.53は有効数字3桁なので有効数字2桁に合わせる。よって\[
1.5 \times 2.53 = 3.8
\]となる。（筆算は下に示しています。）

(4)

33.4は有効数字が3桁なので計算結果も有効数字3桁。よって\[
\sqrt{33.4} = 5.78
\]となる。

スポンサードリンク

２．誤差のいろは

(1) 誤差とは

まず、誤差とはどのようなものかについて説明していきましょう。

皆さんは何かしらのものを測ったことはありますよね。例えば長さを測ったり重さを測ったり時間を測ったり…。

しかし、全く狂いのない正確な値（真値）を我々人間が計測することは不可能です。必ずどこかで誤差が発生してしまいます。

誤差論において誤差 \( \Delta x \) とは、測定した値 \( x \) と真値 \( X \) との差を表します。数式で表すと、\[
\Delta x = x - X
\]となります。

（1回1回測定した結果に対する誤差は正負を考える必要があります。）

(2) 絶対誤差と相対誤差

つぎに絶対誤差と相対誤差の2つの違いについて説明していきたいと思います。この2つでは、誤差の表記の仕方が異なります。

絶対誤差

絶対誤差とは、真値 \( X \) と測定値 \( x \) の差を直接表す方法です。絶対誤差のことを単に誤差と表すこともよくあります。絶対誤差を数式で表すと、\[
(絶対誤差) = x - X
\]となります。（上の誤差は絶対誤差を表しています。）

たとえば、真値160.0[cm]の人を158.4[cm]と測定してしまった場合、絶対誤差は\[
158.4 - 160.0 = -1.6
\]となり、絶対誤差は -1.6[cm] となります。

（絶対）誤差には単位が必要なので単位を忘れていないか確認しましょう！

相対誤差

相対誤差とは、真値 \( x \) と測定値との誤差を割合で表す方法です。

同じ「10cm」の誤差でも、

• 身長160cmの人を170cmと測定し、10cmの誤差が発生
• スカイツリーの高さを63400cmと63410cmと測定し、10cmの誤差が発生

この2つの誤差は規模が全然違いますよね。身長の10cm誤差に比べたらスカイツリーの10cm誤差なんて微々たるものですね。

このように誤差の規模を比べたいときは相対誤差を使い、測定値と真値との誤差を割合で表します。相対誤差を数式で表すと、\[
(相対誤差) = \frac{ x - X}{ X } =\frac{ \Delta x}{ X }
\]となります。

たとえば、真値160.0[cm]の人を158.4[cm]と測定してしまった場合、相対誤差は\[
\frac{158.4 - 160.0}{160.0} = \frac{-1.6}{160.0} = -0.01
\]となり、相対誤差は -0.01（つまり-1%）となります。

相対誤差には割合なので単位を付けないようにしましょう！（パーセントはつけてもOK！）

(3) 誤差の種類

測定において、誤差の原因は主に2つに分かれます。

系統誤差

系統誤差とは主に

• 理論とか原理を誤って解釈したことによっておこる誤差（理論的誤差）
• 測定装置のバグなどによって発生する誤差（機械的誤差）
• 測定者の癖による誤差（個人的誤差）

の3つを表します。系統誤差は誤差の原因さえ取り除くことで完全に誤差をなくすことができます。

偶然誤差

偶然誤差は、測定者がどんなプロでも、測定機械がどんなに高性能なものでも発生してしまう誤差を表します。偶然誤差は、確率的に発生する誤差（誤差ガチャみたいなもん）なので、誤差の原因として取り除くことはできません。

しかし確率的に発生するので、あとで紹介する統計的処理によって、偶然誤差を減らすことができます。

(4) 正規分布

偶然誤差は確率的に発生すると説明しましたね。十分な回数（とにかくたくさん）測定したときの誤差の分布は下のようなグラフで近似することができます。

このグラフを正規分布と呼びます*3。

正規分布については、こちらのサイトで詳しく説明しているのでもしよかったらご覧ください！

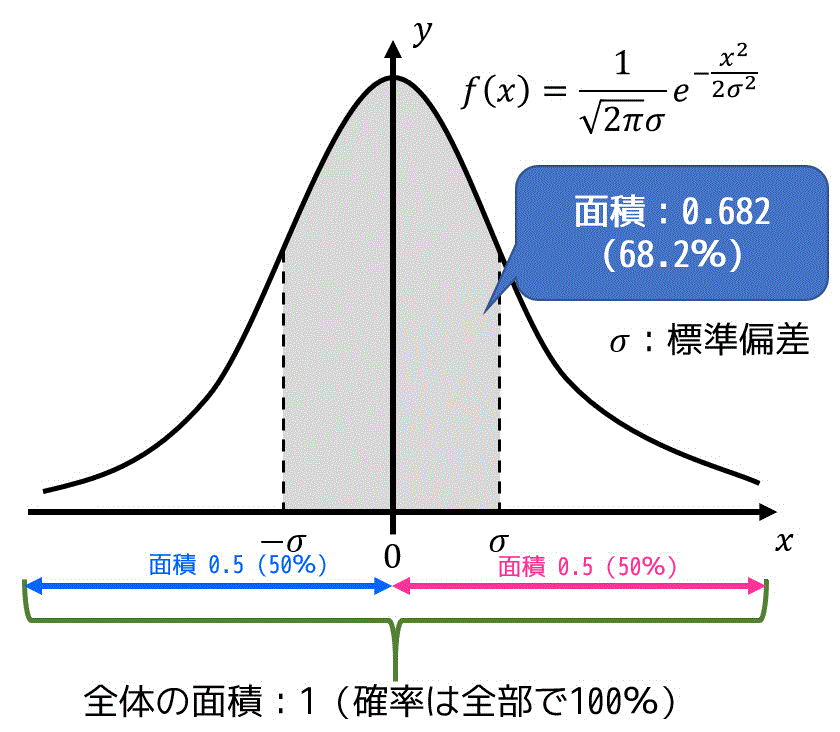
ここで \( \sigma \) は標準偏差*4を表します。

例えば、誤差が \( \pm \sigma \) 以下となる確率は、上の図の灰色部分の面積で表され、0.682（68.2%）となります。標準偏差誤差の基準としてよく使われます。

このグラフの特徴としては、

• \( x \) 軸と \( f(x) \) の面積が1（全体の確率は100%なので当たり前）
• 絶対値の小さい誤差は絶対値の大きい誤差よりも起こりやすい*5
• 絶対値が等しい誤差は（正負に関係なく）等しく発生する*6

ことを示しています。

[おまけ]

誤差の基準として、標準偏差のかわりに確率誤差 \( r \) を使うことがあります。この \( r \) は、誤差が \( r \) 以下となる確率が50％になるようにとった値を指します。

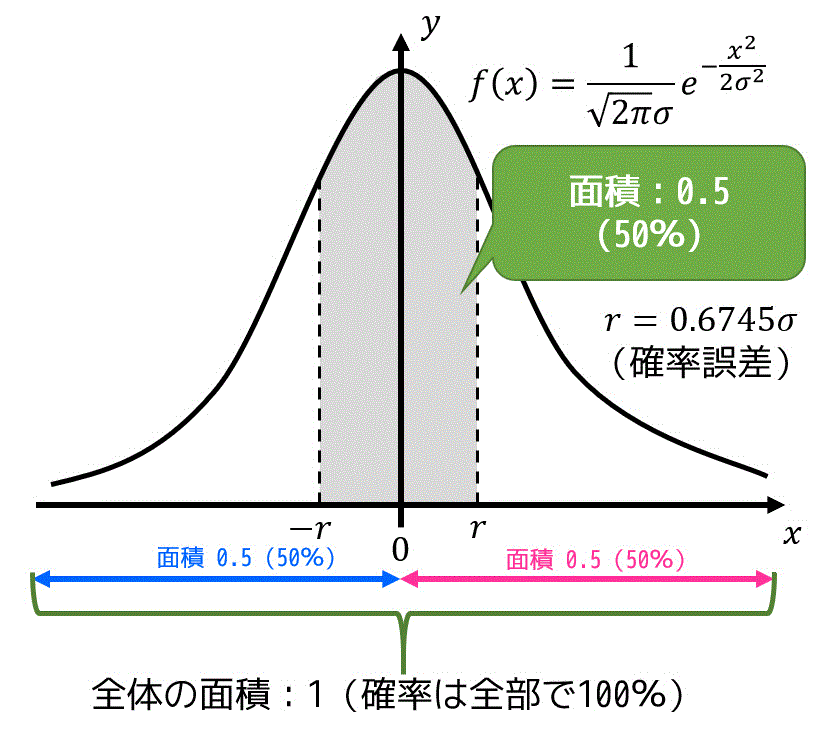
この \( r \) を \( \sigma \) を用いて表すと\[
r = 0.6745 \sigma
\]となります。

(5) 最確値と誤差

第２章の最初の方で説明しましたが、正確な値（真値）を我々人間が計測することは不可能です。

なので、真値の代わりに最確値を使います。

最確値や、最確値に対する誤差を求める際には複数回測定を行い、複数回測定を行った結果から最確値や誤差を求めていきます。

最確値

\( n \) 個の測定値 \( x_1 \), \( x_2 \), …, \( x_n \) の最確値 \( \bar{X} \) は下のような式で求めることができます。\[ \begin{align*}
\bar{X} & = \frac{1}{n} \left( x_1 + x_2 + \cdots + x_n \right)
\\ & = \frac{1}{n} \sum_{i=1}^{n} x_i
\end{align*} \]（測定値の平均が最確値と頭に入れておけばOK！）

最確値は、ある標本における平均から出せるので標本平均と呼ばれることもあります。

（なぜ最確値が平均になるのかの証明は今回はおいておきます……）

最確値に対する誤差（標準誤差）

最確値に対する誤差には、標準偏差を使うのですが、そのまま標準偏差を誤差として使うのには問題があります。

上に書かれている標準偏差 \( \sigma \) は無限回測定した場合の標準偏差 \( \sigma \) に適応されますが、無限回測定することなんてできないので、測定の誤差に標準偏差をそのまま適応することはできません。

（今まで説明してきた標準偏差 \( \sigma \) は全体のデータの標準偏差を求めるものだったが、今回は全体のデータの中から一部のデータを抜き取って計算するので今までの標準偏差の公式が適用できないってことです！*7）

今回の場合、最確値に対する誤差は、標準誤差 \( s_m \) を使用します。では、標準誤差を求める方法について説明していきましょう。

まず、普通の分散（母分散） \( \sigma^2 \) を求める公式は、\[\begin{align*}
\sigma^2  = \frac{1}{n} \sum^n_{ i = 1} \left( x_i - \bar{X} \right)^2
\end{align*} \]でしたね。

（それぞれのデータと平均との差（残差）を2乗した平均）

しかし、\( n \) 個のデータの平均が分かっている場合、\( n-1 \) 個のデータが分かっていれば残りのデータ1つの値は平均と \( n - 1 \) 個のデータから求めることができますね*8。\( n - 1 \) 個のデータからわかるのに \( n \) で割るのは少しおかしいですよね。なので分散 \( s^2 \) は \( n \) ではなく、\( n - 1 \) で割ったもの、つまり\[
s^2 = \frac{1}{n-1} \sum^n_{ i = 1} \left( x_i - \bar{X} \right)^2
\]と求められます。この分散 \( s^2 \) のことを不偏分散と呼びます。

不変分散は、全体のデータ*9からいくつか抜き出して、抜き出したデータの中から全体のデータの分散を推定した値を表しています。

（全体のデータに対する分散が母分散、一部のデータを抜き出して母分散を予測したものが不偏分散です。）

さらに \( n \) 回の測定から得られた最確値（標本平均）\( \bar{X} \) に対する不偏分散 \( s_m^2 \) は、\[
s_m^2 = \frac{s^2}{n} = \frac{1}{n(n-1)} \sum^n_{ i = 1} \left( x_i - \bar{X} \right)^2
\]と求めることができます。あとは不偏分散の平方根を取ることで標準誤差 \( s_m \) を\[
s_m = \sqrt{s_m^2}
\]と求めることができます。

（標準偏差 \( \sigma \) を使うと、\[
s_m = \frac{1}{\sqrt{n-1}} \sigma
\]と表現することもできます。）

※注意

誤差を標準誤差（や標準偏差）で表す場合、各データと最確値の差の2乗を誤差計算に利用していますね。2乗をすることで誤差の正負がなくなるので、標準誤差（や標準偏差）を誤差とする場合、誤差は絶対値となる点に注意してください。

（例：標準誤差が3[cm]だった場合、-3[cm]〜3[cm]の誤差が生まれていることを表す。）

実験結果の表し方

実験結果を示す際には、最確値 \( \bar{X} \) と標準誤差 \( s_m \) を用いて\[
\bar{X} \pm s_m
\]の形にします（単位忘れないように！）。標準誤差の方は原則有効数字1桁にするようにしましょう。例えば、最確値が 3.6 [kg]、誤差が 0.13 [kg] であれば、\[
3.6 \pm 0.1 \ \mathrm{[kg]}
\]と表します。（誤差は絶対値なので ± となることに注意。）

では、1つ例題で試してみましょう！

例題2

筆者が食べた「たけのこの里」のうち、ランダムに10個抽出し、測定したところ、それぞれの重さは下のようになった。

このときの最確値と標準誤差を計算し、たけのこの里の重さを（3.34±0.03 [g]）のような）誤差を含めて表しなさい。

解説2

まずはたけのこの里の最確値 \( \bar{X} \) を出していきます。\[\begin{align*}
\bar{X} & = \frac{1}{10} (2.4 + 2.6 + 2.3 + 2.5 + 2.3 + 2.8 + 2.5 + 2.3 + 2.9 + 2.4)
\\ & = \frac{1}{10} \cdot 25.0
\\ & = 2.50
\end{align*} \]となり、最確値は2.50 [g] となります。（10個すべて足すと有効数字が3桁になる点に注意）

つぎに標準誤差を計算します。

標準誤差を求める際には、

1. 残差（測定値 - 最確値）の2乗の和を計算
2. 1で求めた値を \( \frac{1}{n(n-1)} \) 倍
3. 最後にルートを取る

の流れで計算をしましょう。

今回の場合、残差と残差の2乗は下のようになります。

残差の2乗をすべて足すと0.040となる（有効数字2桁）。

よって、標準誤差 \( s_m \) は、\[\begin{align*}
s_m & = \sqrt{ \frac{1}{10 \cdot 9} } \cdot 0.040
\\ & = \sqrt{4.44 \times 10^{-3} }
\\ & = 0.067
\end{align*} \]となる。

よって、たけのこの里の重さは、2.50 ± 0.07 [g] となる。

※誤差部分の有効数字は原則1桁！

スポンサードリンク

３．偏微分・全微分

次の4章で偏微分と全微分について使うので、ここで簡単に偏微分と全微分についてさらっと説明しておきましょう。

(1) 偏微分

偏微分とは、微分したい変数を1つ決め、残りの変数をすべて定数とみなして微分するだけです。

高校までで習った微分（常微分では）と記号が若干異なるので少し気を付けてください。例えば、\[
f(x,y) = 3x^2 + 5xy + 9y^2
\]を \( x \) で偏微分すると、\[
\frac{\partial f}{\partial x} = 6x + 5y
\]となり、\( y \) で偏微分すると、\[
\frac{\partial f}{\partial y} = 5x + 18y
\]となります。

（3変数以上の場合も同様に計算ができます。）

より詳しい偏微分の説明はこちらの記事をご覧ください。

www.momoyama-usagi.com

(2) 全微分

全微分とは、関数 \( w = f(x_1, x_2, \cdots, x_n) \) の変化量に対しての、\( w \) の変化量 \( dw \) を表します。

たとえば、3変数関数 \( w = f(x,y,z) \) の増加量が \( dx \), \( dy \), \( dz \) のときの増加量 \( dw \) は、\[
dw = \frac{\partial f}{\partial x} dx + \frac{\partial f}{\partial y} dy + \frac{\partial f}{\partial z} dz
\]と表すことができます。

（4変数以上の場合も同様に計算ができます。）

より詳しい全微分の説明はこちらの記事をご覧ください。

www.momoyama-usagi.com

４．間接測定における誤差

(1) 直接測定・間接測定

たとえば体重、身長などは測定器などで直接得ることができましたね。このように測定器具から数値を直接測定することを直接測定と言います。

一方測定器では直接得ることができず、計算をしなければ得ることができない値のことを間接測定と言います。

関数測定の結果は直接測定で得ることができた値（例：\( x \), \( y \), \( z \) の3つ）の関数（例： \( f(x,y,z) \) ）として表すことができます。

(2) 間接測定と相対誤差

間接測定で結果を求める場合、間接測定で使うそれぞれの直接測定の相対誤差の影響が同程度になるようにすることで無駄なく測定することができます。

無駄なく測定するために、間接測定でつかうそれぞれの直接測定の結果の相対誤差の影響がどうなるのかを計算によって求めてみましょう。

測定結果 \( w \) が\[
w = f(x,y,z) = C x^a y^b z^c
\]で得ることができる関数があるとします。（\( C \) は定数）

この関数の対数をとると\[
\log w = a \log x + b \log y + c \log z
\]と変形することができますね。

さらに両辺を微分すると、\[
\frac{dw}{w} = a \cdot \frac{dx}{x} + b \cdot \frac{dy}{y} + c \cdot \frac{dz}{z}
\]と表すことができます。

誤差は絶対値なので正と負と両方が考えられる。間接誤差は\[
\left| \frac{dw}{w} \right| \leqq \left| a \cdot \frac{dx}{x} \right| + \left| b \cdot \frac{dy}{y} \right| + \left| c \cdot \frac{dz}{z} \right|
\]と表すことができます。

（\( x^n \) は \( x \) にくらべて相対誤差の影響が \( n \) 倍となる。）

この式から、測定結果 \( w \) がそれぞれの直接測定から得られた値のべき乗の積 \( C x^a y^b z^c \) で表せる場合、絶対値の大きい指数がかかっているものほど誤差の影響が大きい*10ことがわかりますね。（言い換えると、絶対値の大きい指数であればあるほどより正確に測定する必要がある。）

もちろんもっと多変数の場合であっても同じ手順で計算ができます。例えば、金属の直径 \( D \)、長さ \( L \)、電圧 \( V \)、電流 \( I \) の4つから金属の電気抵抗を計算できる公式\[
w = \frac{\pi D^2 V}{4 L I}
\]について考えてみましょう。このように多くの変数があった場合でも、直接測定から得られた値のべき乗の積\[
w = \frac{\pi}{4} D^2 V L^{-1} I^{-1}
\]で表せるので、\[
\log w = \log \frac{\pi}{4} + 2 \log D + \log V - \log L - \log I
\]とし、両辺を微分すると、\[
\frac{dw}{w} = 2 \frac{dD}{D} + \frac{dV}{V} - \frac{dL}{L} - \frac{dI}{I}
\]とし、絶対値を付けて\[
\left| \frac{dw}{w} \right| = 2 \left| \frac{dD}{D} \right| + \left| \frac{dV}{V} \right| + \left| \frac{dL}{L} \right| + \left| \frac{dI}{I} \right|
\]とすることで金属の直径 \( D \) は他の測定値より2倍正確*11に測定する必要があることがわかります。

例題3

身長 \( h \) [m] と体重 \( m \) [kg] からBMI \( b \) を誤差0.1以下で求めたい。ただし、BMIは、\[
b = \frac{m}{h^2} = mh^{-2}
\]で求めることができる。

このとき、

(1) より正確に測定する必要があるのは身長、体重のどちらですか？
(2) 身長、体重をどれくらいの精度で測ればBMIの誤差を0.1にできるでしょうか？　ただし平均BMIは20前後である。

解説3

(1)

BMI \( b = f(m,h) \) は、\[
b = f(m,h) = mh^{-2}
\]と求めることができる。対数をとると\[
\log b = \log m - 2 \log h
\]となる。両辺を微分し、\[
\frac{db}{b} = \frac{dm}{m} - 2 \frac{dh}{h}
\]となる。

誤差には絶対値なので正と負と両方が考えられる。よって間接誤差は\[
\left| \frac{db}{b} \right| \leqq \left| \frac{dm}{m} \right| + 2 \left| \frac{dh}{h} \right|
\]となり、身長は体重に比べて相対誤差の影響が2倍となる。

よって身長をより正確に測定する必要がある。

(2)

BMIの誤差が0.1以下を相対誤差で表すと、\[
\frac{0.1}{20} = \frac{1}{200}
\]となる。

身長、体重それぞれの項が同程度の影響を持つようにしたいので身長の相対後誤差が1/400、体重の相対誤差が1/400となるようにする。

平均身長を1.6 [m]、平均体重を 60 [kg]と仮定すると、身長、体重の絶対誤差は\[
1.6 \cdot \frac{1}{800} = 0.0020 \mathrm{[m]} \]\[
60 \cdot \frac{1}{400} = 0.15 \mathrm{[kg}] \]となるので、身長は誤差 2[mm] 以下、体重は誤差 0.15[kg] 以下で測定すればよい。

（つまり保健室とかにある身長系や体重計で余裕ってことですね！）

(3) 誤差の四則演算は単純じゃない！

1つ目の測定結果 \( x \) から2つ目の測定結果 \( y \) を引くことで求められる値 \( x - y \) があるとします。

たとえば1つ目の測定結果の誤差が0.3で2つ目の測定結果の誤差も0.3だとします。

このとき、測定結果の誤差も1つ目の結果から2つ目の測定結果を引くと 0.3 - 0.3 だから誤差は0.0である、とするのはさすがにおかしいな、と思いますよね。

（こんな理論がもし成り立ったら全く誤差がないデータを1つでも掛けるだけで誤差が0になってしまいますし。）

今回の例でいくと、誤差を計算する際には絶対値で考える必要があります。誤差には正と負の2つのパターンが考えられるます。なので、今回の場合は最悪の場合、\( x \) が +0.3の誤差、\( y \) が -0.3の誤差で合計0.6の誤差が生まれます。

このように誤差の計算はたとえ四則演算であっても複雑なのです。

ではどうやって計算するのかを下のほうで説明していこうと思います。

(4) 誤差の伝播（誤差伝播の法則）

間接測定の誤差を求める際には、誤差の伝播法則を使います。

ここでは、誤差は偶然誤差のみ起こると仮定します。

例えば、間接測定 \( w \) が2つの独立した測定結果 \( x \), \( y \) （誤差はそれぞれ \( \delta_x \), \( \delta_y \) ）の関数、つまり \( w = f(x,y) \) で求められるときの誤差 \( \delta_w \) を求めるとしましょう。

まず、\( w = f(x,y) \) を全微分すると、\[
| \delta_w | = \frac{\partial f}{\partial x} \delta_x + \frac{\partial f}{\partial y} \delta_y
\]となりますね。絶対値があると邪魔なので両辺を2乗します。

ここで、\( x \), \( y \) は独立してるので互いの相関係数は0となります。よって、\[
\delta_w^2 = \left( \frac{\partial f}{\partial x} \right)^2 \delta_x^2 + \left( \frac{\partial f}{\partial y} \right)^2 \delta_y^2
\]と変形ができます*12。

さらに測定結果 \( w \) がそれぞれの直接測定から得られた値のべき乗 \( w = x^a y^b \) の積で表せる場合、両辺を \( w^2 \) で割ることで\[
\frac{\delta_w^2}{w^2} = a^2 \left(  \frac{\delta_x}{x} \right)^2   + b^2  \left( \frac{\delta_y}{y} \right)^2
\]と変形ができます*13。

この法則を使って直接測定で得られた値 \( x,y \) の積 \( xy \) の誤差と商 \( x \div y \) の誤差を求めてみましょう。

2つの積ということは、関数を用いて\[
f(x,y) = xy
\]と表すことができますね。よって誤差は\[\begin{align*}
\delta_w^2 & = \left( \frac{\partial f}{\partial x} \right)^2 \delta_x^2 + \left( \frac{\partial f}{\partial y} \right)^2 \delta_y^2
\\ & = \left( y \right)^2 \delta_x^2 + \left( x \right)^2 \delta_y^2
\\
\delta_w &  = \sqrt{ (y \ \delta_x)^2 + (x \ \delta_y)^2 }
\end{align*} \]と計算できます。

また、商 \( x \div y \) は関数を用いて\[
f(x,y) = \frac{x}{y}
\]と表すことができますね。よって誤差は\[\begin{align*}
\delta_w^2 & = \left( \frac{\partial f}{\partial x} \right)^2 \delta_x^2 + \left( \frac{\partial f}{\partial y} \right)^2 \delta_y^2
\\ & = \left( \frac{1}{y} \right)^2 \delta_x^2 + \left( - \frac{x}{y^2} \right)^2 \delta_y^2
\\
\delta_w  & = \sqrt{ \left( \frac{1}{y} \delta_x \right)^2 + \left( \frac{x}{y^2} \delta_y \right)^2 }
\end{align*} \]と計算できます。

下に誤差の伝播法則について3変数の場合でまとめています。

主な計算の間接測定のおける誤差の計算法を下にまとめたので参考にしてください。

では、また練習をしてみましょう。

例題4

身長 \( h \)、体重 \( m \) がそれぞれ 1.640 ± 0.004 [m]、51.0 ± 0.3 [kg] で与えられる際のBMI \( b \)を誤差を含めて計算しなさい。

（ただし身長と体重の相関関係が0と仮定して計算してよい。）

解答4

まずは最確値を求める。最確値の計算は普通に計算すればよい。\[
b = \frac{m}{h^2} = \frac{51.0}{1.640^2} = 18.96
\]となる。（計算のため有効数字を1桁余計にとった）

よって最確値は19.0となる。

次に誤差を求める。身長の誤差 \( \delta_h = 0.004 \)、体重の誤差 \( \delta_m = 0.3 \) を誤差伝播の式に代入すると、\[\begin{align*}
\frac{\delta_b^2}{b^2} & = \left( 4 \cdot \frac{\delta_h}{h} \right)^2  +  \left( \frac{\delta_m}{m} \right)^2
\\ & = \left( 4 \cdot \frac{0.004}{1.640} \right)^2  +  \left( \frac{0.3}{51.0} \right)^2
\\ & = \left( 4 \cdot 5.9 \times 10^{-6} + 3.5 \times 10^{-5} \right)
\\ & = 5.9 \times 10^{-5}
\end{align*}\]となる[有効数字1桁]。（1桁多く計算ではとっています）

よって、誤差 \( \delta b \) は、\[\begin{align*}
\delta b & = \sqrt{ \frac{\delta_b^2}{b^2} } \cdot b
\\ & = \sqrt{ 5.9 \times 10^{-5} } \cdot 18.96
\\ & = 0.146
\end{align*} \]となる[有効数字1桁]ので、誤差は0.1となることがわかる*14。

よって、\[
b = 19.0 \pm 0.1
\]となる。

５．さいごに

今回は実験でならう誤差の取り扱いについてメインにまとめていきました。

私も昔この実験をした際に誤差論を習ったのですが当時は全然わからなくてすごい大変だった思い出があります。

この記事で1人でも多くの人に誤差論の基礎部分だけでも理解していただけたら幸いです。

需要があれば最小2乗法についても書いてきたいとおもいます。

６．参考文献

今回はこちらの記事を作成するにあたり、以下のPDFを参考にさせていただきました。

富山大学理学部 光田暁弘「誤差の取り扱い」
（2019年9月28日アクセス）

東京学芸大学「理科生の理科生による理科生のための誤差論基礎 」
（2019年9月28日アクセス）