スポンサードリンク
2020年09月01日 諸事情により内容修正
2022年05月25日 改行バグを修正・行列を用いた計算方法のリンクを追加
こんにちは、ももやまです!
実験で出てくる「最小二乗法」ってとっても難しいですよね!
そこで、今回は実験やデータの分析でよく使う「最小二乗法」についてうさぎでもわかるように説明します!
目次
スポンサードリンク
1.最小2乗法を使う理由
大学になると「基礎物理実験」で、物理実験をすることがありますね。
私も大学1年生のときに、未知の抵抗を渡され、抵抗を求めなさいと言われました。
ということで、今回は抵抗を例に説明して
中学生のときに抵抗を求める関係式\[
I = \frac{V}{R}
\]を習いましたね。
( \( I \) は電流[A]、\( V \) は電圧[V]、\( R \) は抵抗[Ω]です。)
もしかしたら\[
V = IR
\]と(Vには愛があーる)とおぼえてる人もいるかもしれません。
では、この関係式\[
V = IR
\]を \( I \) の関数 \( V = f(I) \) として考えてみましょう。
ちなみに \( I \) の関数というのは、\( I \) に何かしらの値を代入すると、それに対応した値が帰ってくる箱みたいなものです。
今回は抵抗 \( R \) を 2[Ω]としてみましょうか。すると、\[
V = 2I
\]という式が成り立ちますね。
例えば、\( I = 0.5 \) とすると、\( V = 1.0 \) となり、\( I = 3.0 \) とすると \( V = 6.0 \) となりますね*1。
ただし、こんなに都合よくオームの法則は成り立ちません。
成り立つのはセンター試験、二次試験などのテストくらいです。
ということで、オームの法則(理論値)と実世界の値はどれくらい異なるのかをここからとある方法を使ってみていきましょう。
ここで、1年生のときに実験で得た値を過去のレポートから引っ張り出してきました。
随分前のレポートなのですが、未だにパソコンに残っているとは思いませんでしたよほんとに。
| 電圧V [V] | 電流I [A] |
| 0.000 | -0.001 |
| 1.000 | 0.502 |
| 2.000 | 1.005 |
| 3.000 | 1.508 |
| 4.001 | 2.012 |
| 5.001 | 2.516 |
| 6.001 | 3.019 |
当然理論値ではありません。小数第2位やら3位やらに余計な値が残ってます。
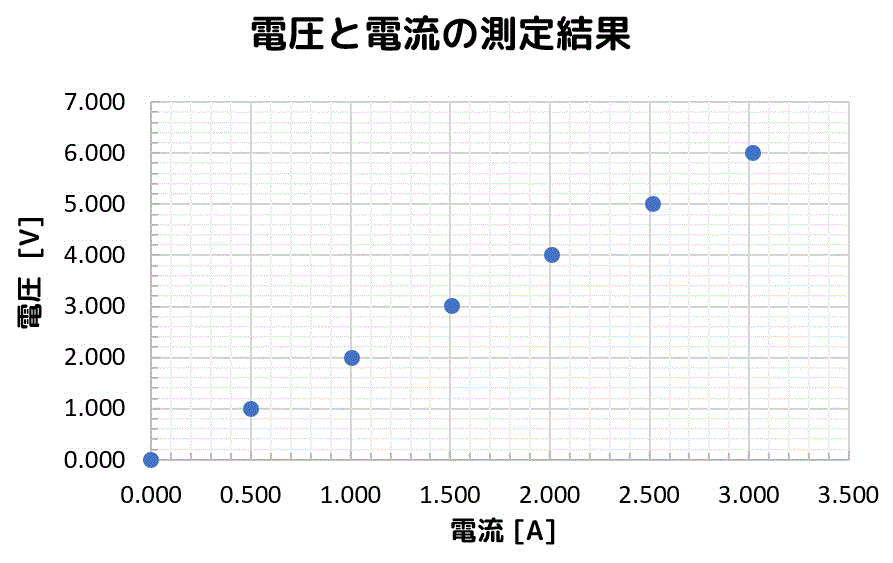
つぎに、グラフ用紙の測定した箇所(対応する電圧と電流)に点を打ってみましょう。
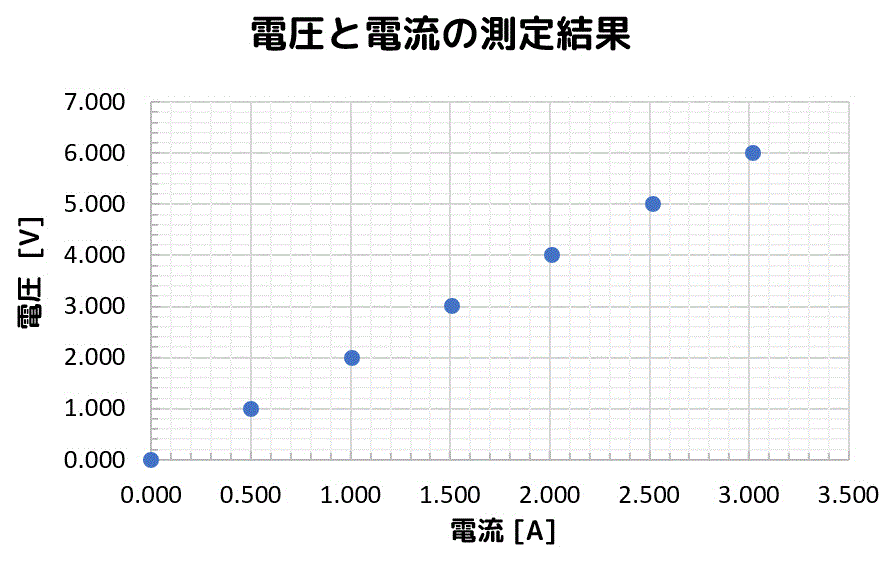
ここで、心を小中学生に戻してみましょう。
いくつか点があると…、
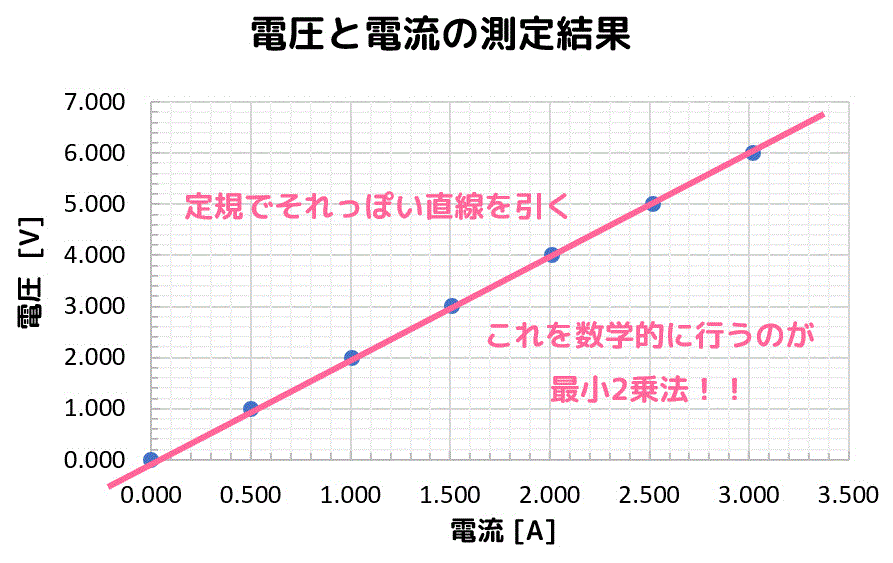
こんな感じに定規でだいたいの点を通るような線を引きたくなりますよね。
線を引けば、だいたいの傾きがわかりますね。この傾きが \( R \) に相当します。
この「だいたいの点を通るけど、どうやって線を引けばどの点にも近くなるんだろう…」というのを数学的に求めるのが最小2乗法の仕組みです。
スポンサードリンク
2.最小2乗法の仕組み
ここから少し理論的なお話に入っていきます。眠くなりますね。
ある実験により得られたデータが \( x \) を独立変数、\( y \) を従属変数として \( x \) の関数 \( y(x) \) として関係式\[
y = ax + b
\]を満たしていると予想できているとします*2。
このとき、\( x \), \( y \) の \( n \) 個の測定値の組をそれぞれ \( (x_i, y_i) \) \( (i = 1, 2, 3, \cdots, n) \) とし、これらの方程式からつぎの方程式\[
y_i = a x_i + b
\]における係数 \( a \), \( nb \) の最確値を求めることを考えてみましょう。
この係数 \( a \), \( b \) の最確値を複数の測定値から求めようとするのが最小二乗法です。
次の章では、さらに詳しく最小2乗法を導出する計算法を見ていきましょう。
スポンサードリンク
3.最小2乗法を用いた計算法
測定の組 \( (x_i, y_i) \) で生じた誤差(測定の不確かさ)を \( r_i \) とすると、つぎの式(誤差方程式といいます)\[
r_i = y_i - a x_i - b
\]が成立します。
(ここでの \( y \) は実際に得た値、\( ax + b \) は計算によって得た値なので測定値と理論値の差が誤差 \( r \) となります。)
この誤差ができるだけ小さくなる(誤差が0に近づく) \( a \) と \( b \) の値を求めればOKと言い換えられます。
実際は \( n\) 個すべてのデータに対して適用するので、\[
\sum^n_{i = 1} r_i
\]が0に近づくときの \( a \) と \( b \) の値を求めればいいことになります。
しかし、上の式の場合、誤差 \( r_i \) が負になることがありますね。
そのため、正の誤差と負の誤差が打ち消しあって、誤差がありまくりなのに0になる、というわけが分からないことがおこります。
そこで、誤差 \( r_i \) を2乗したものを全部足していくことにしましょう。
(実は、分散を求めるときも偏差を2乗するのですが、まったく同じ理由で2乗を行っています。)
すると、式は\[
\sum^n_{i = 1} r_i^2
\]となりますね。この式が0に最も近くなる \( a \), \( b \) を求めるのが最小2乗法です。
(2乗したものが最も小さくなるものを求めるため、最小2乗法と呼ばれます。)
ここで直線を、\( a \), \( b \) の2変数関数 \( S(a,b) \) と考えてみましょう。
(2変数関数というのは、2つの変数 \( a \), \( b \) を入れると値が1つ決まる魔法の箱です。)
2変数関数 \( S(a, b) \) が最小値となる点は当然極小値になります。
極小値ということは、極値となりうる点(停留点)の中のどれかですね。
(停留点は解析学で習うと思います。「停留点ってなんだ?」と思った人のようなまだ習っていない人はこちらの記事で復習お願いします。)
さて、では停留点を求めていきましょう。\( S \) は \( a \) と \( b \) の関数ですので \( S \) を \( a , b \)それぞれについて「偏微分」しましょう。
実際に計算すると、\[\begin{align*}
S(a,b) = & \sum^n_{i = 1} r_i^2
\\ = & \sum^n_{i = 1} \left( y_i - a x_i - b \right)^2
\\ = &\sum^n_{i = 1} \left( y_i^2 + a^2 x_i^2 +b^2 - 2a x_i y_i - 2b y_i + 2ab x_i \right)
\end{align*}\]ですので、\[\begin{align*}
\frac{\partial S}{\partial a} = &
\sum^n_{i = 1} \frac{\partial}{\partial a} \left( y_i^2 + a^2 x_i^2 +b^2 - 2a x_i y_i - 2b y_i + 2ab x_i \right)
\\ = & \sum^n_{i = 1} \left( 2ax_i^2 - 2x_i y_i + 2 b x_i \right)
\end{align*}\]\[\begin{align*}
\frac{\partial S}{\partial b} = &
\sum^n_{i = 1} \frac{\partial}{\partial b} \left( y_i^2 + a^2 x_i^2 +b^2 - 2a x_i y_i - 2b y_i + 2ab x_i \right)
\\ = & \sum^n_{i = 1} \left( 2b - 2 y_i + 2a x_i \right)
\end{align*}\]となっていますから、このとき\[
\frac{\partial S}{\partial a} = 0, \ \ \ \frac{\partial S}{\partial b} = 0
\]ですので、\[\begin{align*} &
\sum^n_{i = 1} \left( 2ax_i^2 - 2x_i y_i + 2 b x_i \right)
\\ = & \ 2 \sum^n_{i = 1} \left( ax_i^2 - x_i y_i + b x_i \right)
\\ = & \ 2 \left( a \sum^n_{i = 1} x_i^2 - \sum^n_{i = 1} x_i y_i + b \sum^n_{i = 1} x_i \right) = 0
\end{align*} \]\[\begin{align*} &
\sum^n_{i = 1} \left( 2b - 2 y_i + 2a x_i \right)
\\ = & \ 2 \sum^n_{i = 1} \left( b - y_i + a x_i \right)
\\ = & \ 2 \left( b \sum^n_{i = 1} 1 - \sum^n_{i = 1} y_i + a \sum^n_{i = 1} x_i \right) = 0
\end{align*} \]となり、\[
a \sum^n_{i = 1} x_i^2 - \sum^n_{i = 1} x_i y_i + b \sum^n_{i = 1} x_i = 0 \]\[
bn - \sum^n_{i = 1} y_i + a \sum^n_{i = 1} x_i = 0
\]という2つの関係式が出てきました。*3
シグマが多くてごちゃごちゃするので、シグマを別の記号 [ ] をつかって\[
\sum^n_{i = 1} x_i y_i = [xy]
\]のように書いて式を整理しましょう。
先ほどの2つの関係式は\[
a [ x^2] - [xy] + b [x] = 0 , \ \ \ \ a[x] - [y] + nb = 0
\]という見た目だけは簡単な式になりますね。
この2式はただの連立1次方程式なので、これを解くことで \( a \), \( b \) の値を求めることができます!
実際に解いてみると、\[
a = \frac{n [xy] - [x][y]}{n [x^2] - [x]^2} , \ \ \ \ b = \frac{[x^2][y] - [x][xy]}{n [x^2] - [x]^2}
\]と求めることができます。
これが、実験の教科書によく出てくる最小2乗法の計算式です。
r_i = y_i - a x_i - b
\]の \( r \) の2乗の総和\[
\sum^{n}_{i = 1} r^2
\]が最小になるような \( a \), \( b \) を、\[
a = \frac{n [xy] - [x][y]}{n [x^2] - [x]^2} = \frac{ n \sum^n_{i = 1} x_i y_i - \sum^n_{i = 1} x_i \sum^n_{i = 1} y_i }{ n \sum^n_{i = 1} x_i^2 - \left( \sum^n_{i = 1} x_i \right)^2 }
\]\[ b = \frac{[x^2][y] - [x][xy]}{n [x^2] - [x]^2} = \frac{ \sum^n_{i = 1} x_i^2 \sum^n_{i = 1} y_i - \sum^n_{i = 1} (x_i y_i) \sum^n_{i = 1} x_i }{ n \sum^n_{i = 1} x_i^2 - \left( \sum^n_{i = 1} x_i \right)^2 }
\]と取ることで回帰直線 \( y = ax + b \) を求めることができる。
4.具体例(電流と電圧)
電流と電圧の話に戻りましょう。
オームの法則の式は\[
V = IR
\]でしたね。
しかし、実世界では「初期の起電力」というものが出てきます。
この起電力を \( V_0 \) とでもすると、\[
V = IR + V_0
\]と書けます。
すると、この式は最小2乗法の式 \( y = ax+b \) と似ていますね。
この式の \( a \) の部分を \( R \)、\( b \) の部分を \( V_0 \) にすると、最小2乗法が適用できますね。
( \( y\) の部分は \( V \)、\( x \) の部分は \( R \) となります。)
実際に、最初に出した実験データから最小2乗法を使って抵抗 \( R \) と起電力 \( V_0 \) を求めましょう。
| 電流 I [A] | 電圧 V [V] |
| -0.001 | 0.000 |
| 0.502 | 1.000 |
| 1.005 | 2.000 |
| 1.508 | 3.000 |
| 2.012 | 4.001 |
| 2.516 | 5.001 |
| 3.019 | 6.001 |
ここで、最小2乗法の式の \( x \) が電流 \( I \)、\( y \) が電圧 \( V \) に対応付けができるので、具体的に\[
R = \frac{n [IV] - [I][V]}{n [I^2] - [I]^2} , \ \ \ \ V_0 = \frac{[I^2][V] - [I][IV]}{n [I^2] - [I]^2}
\]となりますね。
計算の注意点としては、
- \( [I]^2 \) は \( [I] \) を2乗したもの、\( [ I^2 ] \) は各電流の値を2乗したものの総和と、互いに異なっているものを求めていること
- \( [IV] \) は、\( [I] \times [V] \) ではなく、各データの電流値と電圧値をかけたものの総和であること
の2点に注意が必要です。
計算はめんどくさいと思うので手でせず、Excelやら電卓でやることをおすすめします。
ただし、Excelで行う場合は有効数字の処理に気を付けましょう。(round関数などできちんと有効数字の処理しましょう。)
有効数字がいまいちよくわかってない人はこちらの記事で確認しましょう!
実際に求めると、\[\begin{align*}
[I] & = \sum^{n}_{i = 1} x_i
\\ & = 10.562
\end{align*}\]\[\begin{align*}
[V] & = \sum^{n}_{i = 1} y_i
\\ & = 21.003
\end{align*}\]\[\begin{align*}
[IV] & = \sum^{n}_{i = 1} x_i y_i
\\ & = 45.786
\end{align*}\]\[\begin{align*}
[I^2] & = \sum^{n}_{i = 1} x_i^2
\\ & = 23.029
\end{align*}\]\[\begin{align*}
[I]^2 & = (10.562)^2
\\ & = 111.556
\end{align*}\]
あとは、実際に求めた値を代入し、 \( R \) と \( V_0 \) を求めると、
\[
R = 1.987, \ \ \ V_0 = 0.001774
\]と求まり、直線の傾き \( R \) および切片 \( V_0 \) を求めることができます。
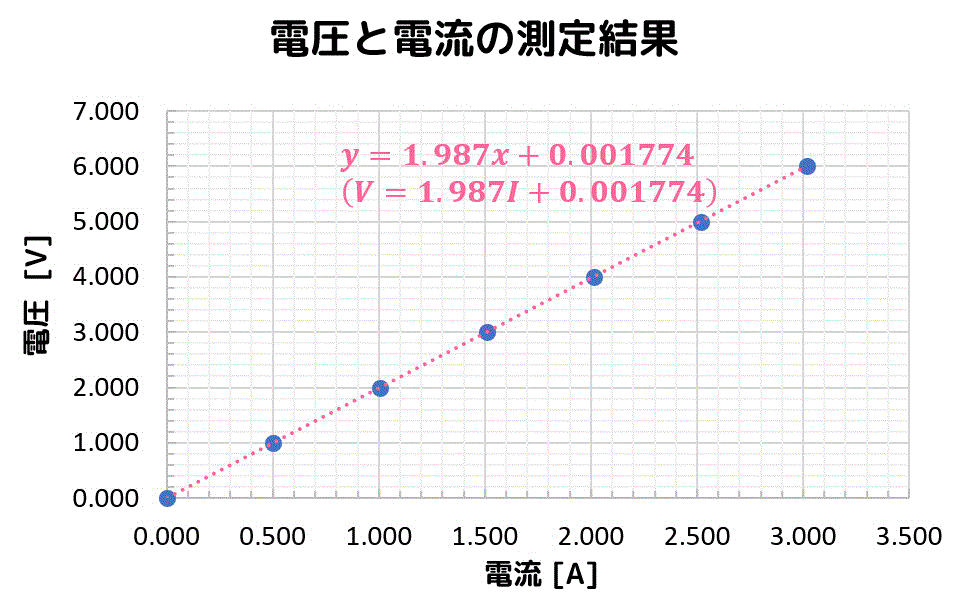
これが、最小2乗法の使い方の例です。
実は実験の後、教授から「この抵抗、本当は2[Ω]なんだよ~」と教えてくれました。
このように、実際の値かどうかはわからないが、表向きに言われている値のことを公称値とよびます*4。
2[Ω]だといわれている抵抗に対して、1.987[Ω] (相対誤差約1%) の結果が出せたのはなかなかな精度だと思います。
当時1年生だった私すごい!(すいませんでした。)
5.最小2乗法の応用
少し応用例も紹介してみましょう。
最小2乗法は、線形なもの(直線なもの)適用できないと思われがちですが、実は何個か式を挟むことで、線形以外なものにも適用することができます。
例えば、\[
y = \frac{a}{x} + b
\]というような反比例の式があるとします。
この式を、\[
X = \frac{1}{x} , \ \ \ \ Y = y
\]とおくことで、\[
Y = aX + b
\]という1次式に変形できますね。この形は、まさに最小2乗法ですね。
もう1つ比熱の式で例を出しましょう。比熱の式は、\[
C = \gamma T + A T^3
\]なのですが、この式の両辺を \( T \) で割ると、\[
\frac{C}{T} = \gamma + AT^2
\]となりますね(ただし \( T \not = 0 \) を仮定することに注意)。
さらに、\[
X = T^2 , \ \ \ \ Y = \frac{C}{T}
\]とおくことで\[
Y = AX + \gamma
\]という最小2乗法の形になりますね。
そのため、 \( A \), \( \gamma \) の値を求める際にも最小2乗法を使うことができます。
6.最小2乗法の式の簡単化
先ほど紹介した最小2乗法の式\[
a = \frac{n [xy] - [x][y]}{n [x^2] - [x]^2} = \frac{ n \sum^n_{i = 1} x_i y_i - \sum^n_{i = 1} x_i \sum^n_{i = 1} y_i }{ n \sum^n_{i = 1} x_i^2 - \left( \sum^n_{i = 1} x_i \right)^2 }
\]\[ b = \frac{[x^2][y] - [x][xy]}{n [x^2] - [x]^2} = \frac{ \sum^n_{i = 1} x_i^2 \sum^n_{i = 1} y_i - \sum^n_{i = 1} (x_i y_i) \sum^n_{i = 1} x_i }{ n \sum^n_{i = 1} x_i^2 - \left( \sum^n_{i = 1} x_i \right)^2 }
\]の形はかなり複雑ですよね。
手計算をするのは言うまでもなく嫌だし、Excelなどで計算させるのもかなり式入力がめんどくさいですよね。
なので、この式を簡単化しましょう。
(1) 共分散
式を簡単化する前に、簡単化に使う共分散について説明しましょう。
共分散 \( s_{xy} \) は、ある \( i \) 番目(\( i = 1,2,3, \cdots, n \))データ \( x_i \) における平均 \( \overline{x} \) のずれ(\( x \) の残差)と別のデータ \( y_i \) における平均 \( \overline{y} \) からのずれ(\( y \) の残差)の積の平均を表します。式で書くと、\[
\frac{1}{n} \sum^n_{i = 1} (x_i - \overline{x})(y_i - \overline{y})
\]と表せます。
この式を変形すると、\[\begin{align*} &
\frac{1}{n} \sum^n_{i = 1} \left( x_i y_i - x_i \overline{y} - y_i \overline{x} + \overline{x} \cdot \overline{y} \right)
\\ = & \overline{x_i y_i} - \overline{y} \cdot \frac{1}{n} \sum^n_{i = 1} x_i - \overline{x} \cdot\frac{1}{n} \sum^n_{i = 1} y_i + \frac{1}{n} \cdot n \overline{x} \cdot \overline{y}
\\ = & \overline{x_i y_i} - \overline{y} \cdot \overline{x} - \overline{x} \cdot \overline{y} + \overline{x} \cdot \overline{y}
\\ = & \overline{x_i y_i} - \overline{x} \cdot \overline{y}
\end{align*} \]となり、2つの積の平均 - それぞれの平均の積からも共分散を出せることがわかりましたね。
(2) 式の変形
では、実際に共分散を使って式を変形してみましょう。式変形がめんどくさいので基本的には結果だけわかればOKです。
\( \overline{x} \), \( \overline{y} \) はそれぞれ \( x \) の平均、\( y \) の平均、\( \sigma_x^2 \) は \( x \) の分散\[
\sigma_x^2 = \frac{1}{n} \sum^n_{i = 1} x_i^2 - \left( \frac{1}{n} \sum^n_{i = 1} x_i \right)^2
\]を表しています。
\[ \begin{align*}
a & = \frac{ n \sum^n_{i = 1} (x_i y_i) - \sum^n_{i = 1} x_i \sum^n_{i = 1} y_i }{ n \sum^n_{i = 1} x_i^2 - \left( \sum^n_{i = 1} x_i \right)^2 }
\\ & = \frac{ \frac{1}{n^2} \left( n \sum^n_{i = 1} x_i y_i - \sum^n_{i = 1} x_i \sum^n_{i = 1} y_i \right) }{ \frac{1}{n^2} \left( n \sum^n_{i = 1} x_i^2 - \left( \sum^n_{i = 1} x_i \right)^2 \right) }
\\ & = \frac{ \frac{1}{n} \sum^n_{i = 1} (x_i y_i) - \frac{1}{n} \sum^n_{i = 1} x_i \cdot\frac{1}{n} \sum^n_{i = 1} y_i }{ \frac{1}{n} \sum^n_{i = 1} x_i^2 - \left( \frac{1}{n} \sum^n_{i = 1} x_i \right)^2 }
\\ & = \frac{ \overline{x y} - \overline{x} \cdot \overline{y} }{ \sigma_x^2 }
\\ & = \frac{ s_{xy} }{ \sigma_x^2 }
\end{align*} \]となり、\( a \) は \( x \), \( y \) の共分散 \( s_{xy} \) および \( x \) の分散 \( \sigma_x^2 \) を用いて\[
a =\frac{ s_{xy} }{ \sigma_x^2 }
\]で求めることができますね!
(\( a \) は「 \( x \), \( y \) の共分散 ÷ \( x \) の分散 」で計算できる!)
同様に \( b \) も\[\begin{align*}
b & = \frac{ \sum^n_{i = 1} x_i^2 \sum^n_{i = 1} y_i - \sum^n_{i = 1} (x_i y_i) \sum^n_{i = 1} x_i }{ n \sum^n_{i = 1} x_i^2 - \left( \sum^n_{i = 1} x_i \right)^2 }
\\ & = \frac{ \frac{1}{n^2} \left( \sum^n_{i = 1} x_i^2 \sum^n_{i = 1} y_i - \sum^n_{i = 1} (x_i y_i) \sum^n_{i = 1} x_i \right) }{ \frac{1}{n^2} \left( n \sum^n_{i = 1} x_i^2 - \left( \sum^n_{i = 1} x_i \right)^2 \right) }
\\ & = \frac{ \frac{1}{n^2} \sum^n_{i = 1} x_i^2 \sum^n_{i = 1} y_i - \frac{1}{n^2} \sum^n_{i = 1} (x_i y_i) \sum^n_{i = 1} x_i }{ \frac{1}{n} \sum^n_{i = 1} x_i^2 - \left( \frac{1}{n} \sum^n_{i = 1} x_i \right)^2 }
\\ & = \frac{ \frac{1}{n^2} \sum^n_{i = 1} x_i^2 \sum^n_{i = 1} y_i - \frac{1}{n^2} \sum^n_{i = 1} (x_i y_i) \sum^n_{i = 1} x_i }{ \sigma_x^2 }
\end{align*} \]となる。
ここから先は分子のみの変形を考える。\[\begin{align*} &
\frac{1}{n^2} \sum^n_{i = 1} x_i^2 \sum^n_{i = 1} y_i - \frac{1}{n^2} \sum^n_{i = 1} (x_i y_i) \sum^n_{i = 1} x_i
\\ = & \frac{1}{n^2} \sum^n_{i = 1} x_i^2 \sum^n_{i = 1} y_i - \frac{1}{n^2} \sum^n_{i = 1} (x_i y_i) \sum^n_{i = 1} x_i + ( \overline{x} )^2 \overline{y} - ( \overline{x} )^2 \overline{y}
\\ = & \frac{1}{n^2} \sum^n_{i = 1} x_i^2 \sum^n_{i = 1} y_i - \frac{1}{n} \sum^n_{i = 1} (x_i y_i) \cdot \sum^n_{i = 1} x_i + \frac{1}{n} \sum^n_{i = 1} x_i \cdot \overline{x} \cdot \overline{y} - \frac{1}{n^3} \sum^n_{i = 1} x_i \sum^n_{i = 1} x_i \sum^n_{i = 1} y_i
\\ = & \frac{1}{n^2} \sum^n_{i = 1} x_i^2 \sum^n_{i = 1} y_i - \frac{1}{n^3} \sum^n_{i = 1} x_i \sum^n_{i = 1} x_i \sum^n_{i = 1} y_i - \frac{1}{n} \sum^n_{i = 1} (x_i y_i) \cdot \frac{1}{n} \sum^n_{i = 1} x_i + \frac{1}{n} \sum^n_{i = 1} x_i \cdot \overline{x} \cdot \overline{y}
\\ = & \frac{1}{n} \sum^n_{i = 1} y_i \left( \sum^n_{i = 1} x_i^2 - \left( \sum^n_{i = 1} x_i \right)^2 \right) - \frac{1}{n} \sum^n_{i = 1} x_i \left( \frac{1}{n}\sum^n_{i = 1} (x_i y_i) -\overline{x} \cdot \overline{y} \right)
\\ = & \overline{y} \sigma_x^2 - \overline{x} \left( \overline{xy} - \overline{x} \cdot \overline{y} \right)
\\ = & \overline{y} \sigma_x^2 - \overline{x} s_{xy}
\end{align*} \]となる。
よって、\[\begin{align*} &
\frac{ \frac{1}{n^2} \sum^n_{i = 1} x_i^2 \sum^n_{i = 1} y_i - \frac{1}{n^2} \sum^n_{i = 1} (x_i y_i) \sum^n_{i = 1} x_i }{ \sigma_x^2 }
\\ = & \frac{ \overline{y} \sigma_x^2 - \overline{x} s_{xy} }{ \sigma_{x}^2 }
\\ = & \overline{y} -\overline{x} \cdot \frac{s_{xy}}{\sigma_x^2}
\\ = & \overline{y} - a \overline{x} \ \left( \because a = \frac{ s_{xy} }{ \sigma_x^2 } \right)
\end{align*} \]となる。
※変形はこちらのページを参考にさせていただきました!
参考文献:「Black学科へようこそ! 自然科学のための数学 最小2乗法」
(2019年9月29日アクセス)
よって、下のような結果が得られます。(結果が理解できれていれば十分です)
2つの測定の組 \( (x_i, y_i) \) で生じた誤差(測定の不確かさ)を \( r_i \) とし、誤差方程式\[
r_i = y_i - a x_i - b
\]の \( r \) の2乗の総和\[
\sum^{n}_{i = 1} r^2
\]が最小になるような \( a \), \( b \) を、\[
a = \frac{ s_{xy} }{ \sigma_x^2 }
\]\[ b = \overline{y} - a \overline{x}
\]と取ることで回帰直線 \( y = ax + b \) を求めることができる。
※ \( \overline{x} \), \( \overline{y} \) はそれぞれ \( x \), \( y \) の平均、\( \sigma_x^2 \) は \( x \) の分散、\( s_{xy} \) は \( x \), \( y \) の共分散を表します。
(こちらの方が簡単に求められますね!)
最小2乗法における回帰直線 y = ax + b の簡単な求め方
実際に第3章で計算したデータと同じ電圧と電流で正しい値がでるかを調べてみましょう。
(電流 \( I \) が \( x \)、電圧 \( V \) が \( y \)、抵抗 \( R \) が \( a \)、起電力 \( V_0 \) が \( b \) に相当)
| 電流 I [mA] | 電圧 V [V] |
| 0.000 | 0.000 |
| 0.502 | 1.000 |
| 1.005 | 2.000 |
| 1.508 | 3.000 |
| 2.012 | 4.001 |
| 2.516 | 5.001 |
| 3.019 | 6.001 |
すると、\[
s_{xy} = 2.013 , \ \ \
\sigma_{x}^2 = 1.013
\]なので、\[
a = R = \frac{s_{xy}}{\sigma_{x}^2} = 1.987
\]となります[有効数字4桁]。
同様に \( b \) も求めます。\( x \) の平均 \( \overline{x} \) と \( y \) の平均 \( \overline{y} \) はそれぞれ、\[
\overline{x} = 1.509 , \ \ \
\overline{y} = 3.000
\]なので、\[\begin{align*}
b & = V_0
\\ & = \overline{y} - a \overline{x}
\\ & = 3.000 - 1.509 \times 1.987
\\ & = 0.001774
\end{align*} \]となります。
先ほどの計算式より比較的ラクに計算できましたね!
(ちなみにExcelでは共分散は covar 関数、分散は var.p 関数を使ってラクラク計算することができます!)
おまけ
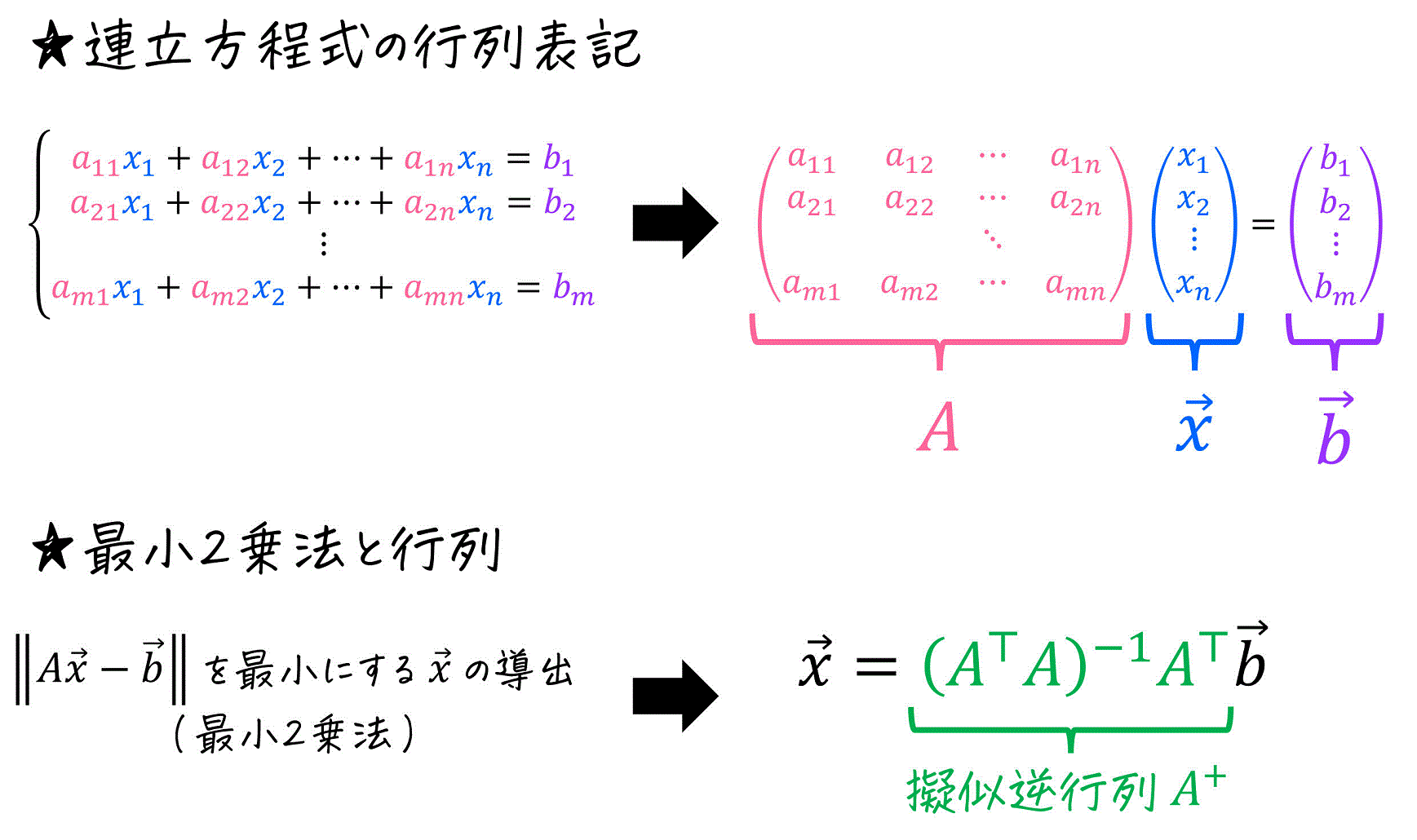
最小2乗法は、線形代数(行列やベクトル)の力を使うことで、行列を使って計算することもできます。
もし行列を使った最小2乗法の計算に興味がある方は、こちらの記事をご覧ください。
7.Excelで最小2乗法を自動計算させる方法
実は、回帰直線 \( y = ax + b \) はExcel上で簡単に計算をさせることができます。
今回はExcelで回帰直線の値を求める方法についてわかりやすくまとめました!
皆さん、Excelの準備はいいですか!?
Step1:データを入力
まずは、データを入力してください。今回は上の例で挙げた電流と電圧から抵抗 \( R \) と起電力 \( V_0 \) を求めます。
なお、電流の値は [mA] など単位がずれていた場合 \( A \) に直してから入力してください。
データの入力が終わったら挿入ボタンをクリックしてください。
Step2:散布図を表示させる
つぎに入力したデータをすべて選択し、上側にある「おすすめグラフ」をクリックします。
すると、グラフの種類が出てきます。
その中から「散布図」を選び、OKをクリックします!
(おそらく一番上に「散布図」が出てきます)
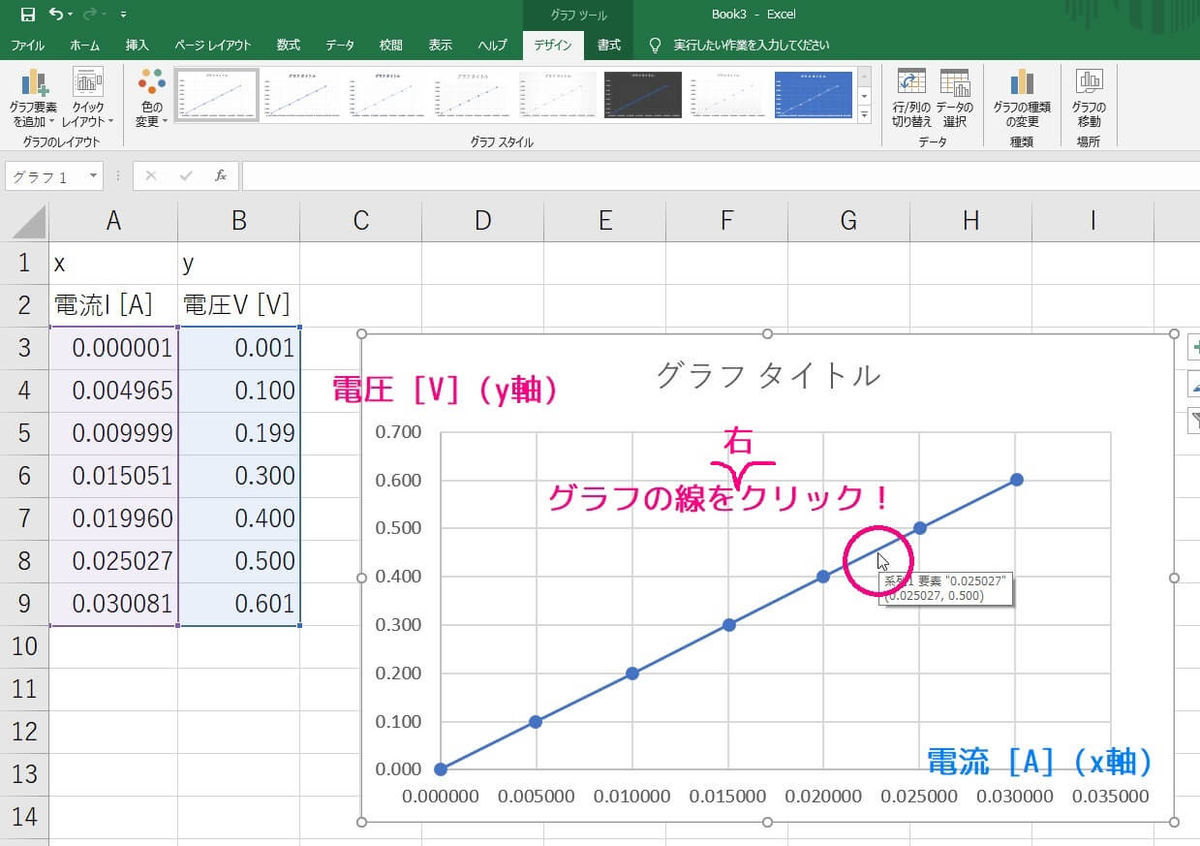
すると、グラフが出てきます。
Step3:y = ax + b の a,b の値を表示させる
つぎに、出てきたグラフの線を右クリックしてください。
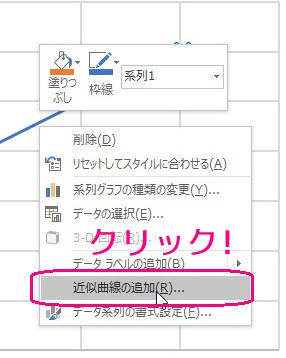
すると、色々出てくるので「近似直線の追加」を選んでください。
すると、右側に「近似直線の書式設定」ウィンドウが出てくるので、線形近似であることを確認してから「グラフに数式を表示する」をクリックしてください。
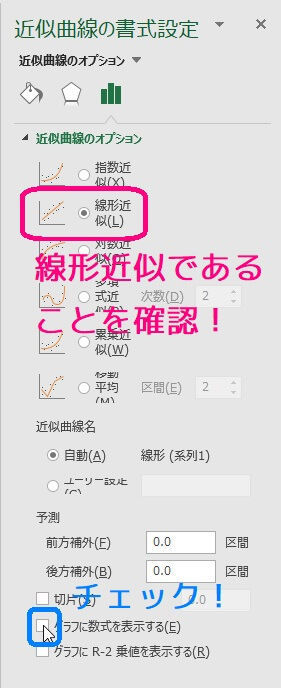
すると、下のように \( y = ax + b \) の \( a,b \) の値が表示されます。
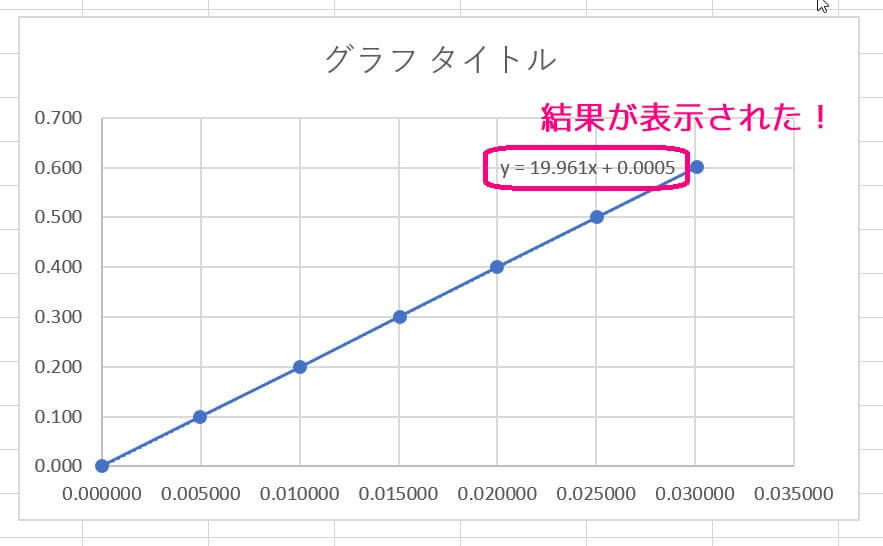
今回の場合は \[ y = 19.961x + 0.0005\] なので \( a = R = 19.961 \), \( b = V_0 = 0.0005 \) となることがわかります。
しかし、\( b \) の部分の有効数字が1桁しか表示されていませんね。
なので \( a \), \( b \) の桁数をもっと多く表示させる設定をしてみましょう。
(表示させる必要がないときはここで終了です。)
Step4:表示桁数を変える
\( y = ax + b \) の値(今回は \( y = 19.961x + 0.0005 \))が表示されている部分をクリックしてください。
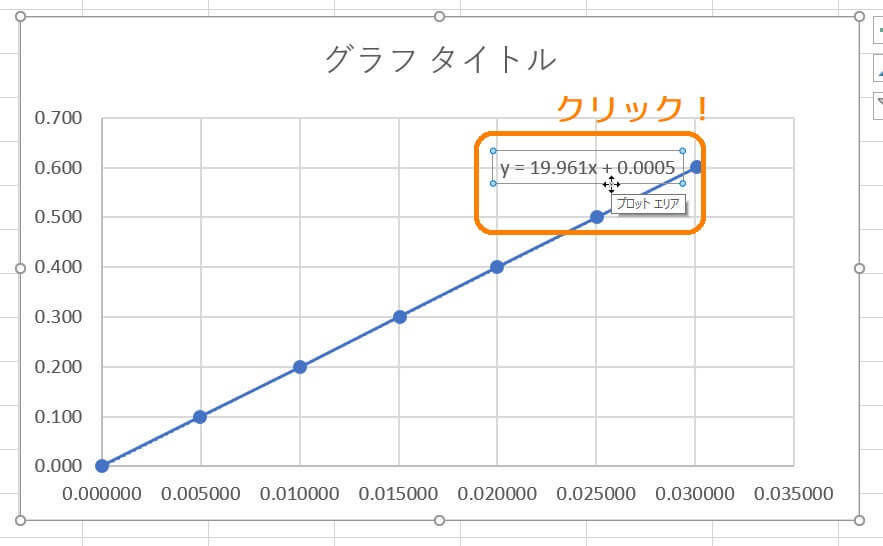
すると、このようなウィンドウが右側に表示されています。
そこからカテゴリを「数値」もしくは「指数」を選んでください。
(指数を選ぶと \( a \times 10^n \) の形で表示されます。)
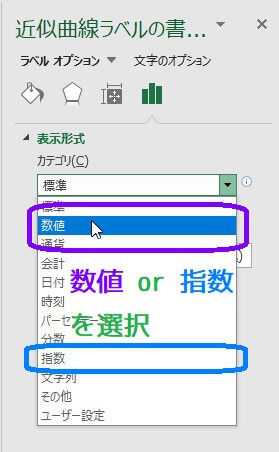
※万が一この表示になっていない場合、この画像にある棒グラフのアイコンをクリックすると出てくるはずです。
(1) 数字を選んだ場合
表示させる小数点以下の桁数を入力してください。
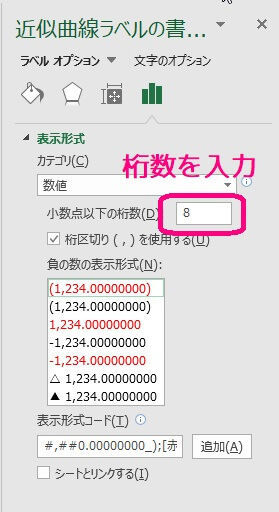
桁数を入力してから、適当な箇所をクリックすると自動的に設定が反映されます。
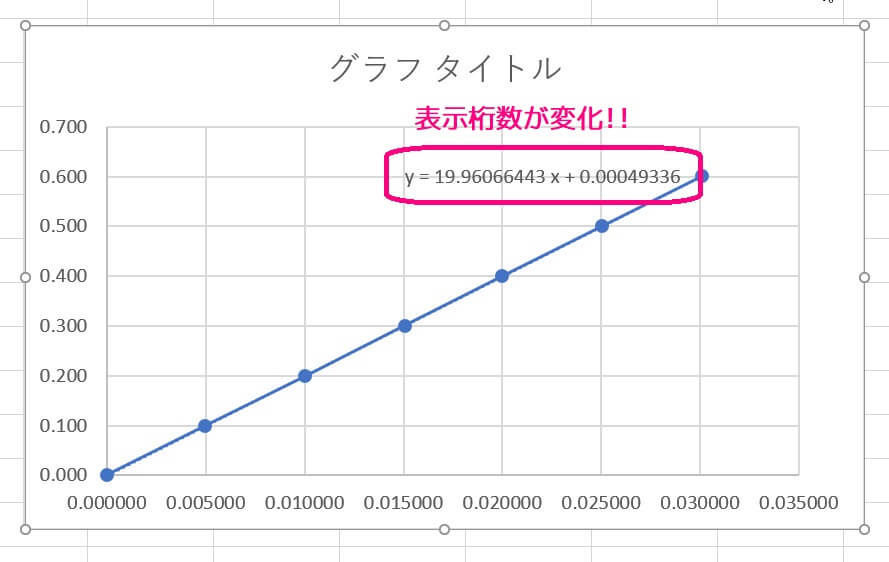
ちゃんと小数第8位まで表示されましたね。
(2) 指数を選んだ場合
指数を選んだ場合、\( a \times 10^n \) の形で表示されます。
\( a \) の部分に表示させたい桁数を入力してください。
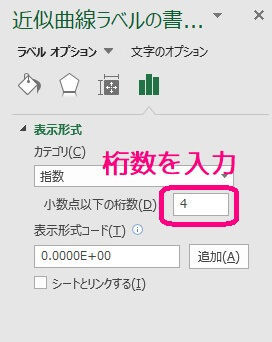
桁数を入力してから、適当な箇所をクリックすると自動的に設定が反映されます。
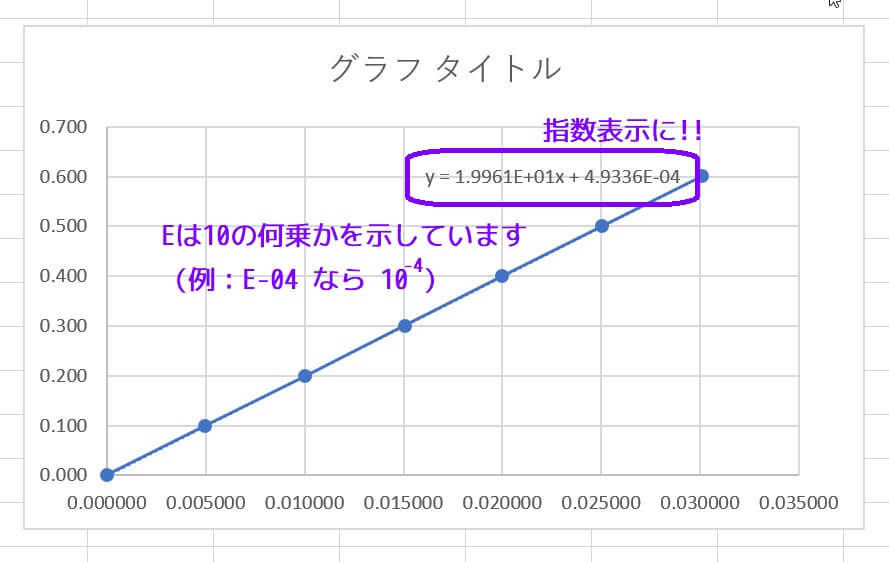
ちゃんと \( a \times 10^n \) の形(\( a \) は小数第4位まで)で表示されましたね。
※ Eは10の何乗かを表しています。例えば E-04 であれば \( 10^{-4} \)、E+01であれば \( 10^{1} \) を表しています。
8.さいごに
今回は最小2乗法についてうさぎでもわかるように、仕組みをわかりやすく説明しました。
次回の第3章では、普通のグラフではなく、
- 片対数、両対数グラフによるプロット
- 片対数、両対数グラフを用いた最小2乗法
について説明しています。
*1:有効数字2桁を意識するため、わざと \( V = 1.0 \) と .0 を残しています。
*2:\( y(x) \) の \( x \) のように、自身の値が変化する以外に値の変わりようがない変数を独立変数、 \( y \) のように、独立変数である \( x \) の値が変化することで自身の値が変化するような変数を従属変数といいます。
*3:シグマと微分演算子は有限の和であればいつでも順番を変えることができます。つまり、 \( n \)が有限の値であれば\[
\frac{d}{dx} \sum^n_{i = 1} S(x) = \sum^n_{i = 1} \frac{d}{dx} S(x)
\]は常に成立します。
*4:例えばですが、ジュースとかで「内容量 500mL」とか書かれていますね。この 500mLというのは、表向きに(パッケージなどで)言われている値で、実際に 500mL入っているかはわかりませんね。測ったら499mLかもしれませんし501mLくらいあるかもしれません。
関連広告・スポンサードリンク