うさぎでもわかる線形代数　第01羽　行基本変形で行列の階数を求めよう

こんにちは、ももやまです。

今回は、行基本変形についてまとめてみました。

行基本変形計算のコツ、行基本変形を使って階段行列を作ったり階数を求める方法などをわかりやすくまとめてみました。

前回の行列の四則演算編はこちら！

www.momoyama-usagi.com

\( a \) 

スポンサードリンク

１．行基本変形における３つのルール

行基本変形では次の3つのルールがあります。

その3つのルールについて紹介したいと思います。

階段行列を作るときはこの3つのルールに基づいて行います。

(1) 1つの行を何倍（何分の1倍）する

例：2行目を2倍にする

\[\left( \begin{array}{ccc} 1 & 2 & 2  \\ 0 & 1_{\times 2} & 1_{\times 2}  \end{array} \right) \to\left( \begin{array}{ccc} 1 & 2 & 2  \\ 0 & 2 & 2  \end{array} \right) \]

文字式が入っている式の文字をまとめて消すときによく使います

(2) 2つの行を入れ替える

例：1行目と2行目を入れ替える

\[\left( \begin{array}{ccc} 1 & 1 & 1  \\ 2 & 3 & 4  \end{array} \right) \to\left( \begin{array}{ccc} 2 & 3 & 4  \\ 1 & 1 & 1  \end{array} \right) \]

(3) 1つの行から他の行を何倍かしたものを加えるor引く

例：1行目に2行目を2倍したものを引く

\[\left( \begin{array}{ccc} 1 & 2_{-2} & 2_{-2}  \\ 0 & 1 & 1  \end{array} \right) \to\left( \begin{array}{ccc} 1 & 0 & 0  \\ 0 & 1 & 1  \end{array} \right) \]

この3つの行列を使って、行の下のほうにいけばいくほど左側に並ぶ0の数が増えるように階段行列を作っていくのが目標です！

スポンサードリンク

２．計算のコツ

行基本変形のコツを書いていきます

(1) 極力分数は出さない

計算の途中で分数を出すと、計算がややこしくなります。
さらにただでさえ小さいスペースに分数を入れるとすごく見にくくなります。
なので極力分数を出さないように計算しましょう！
やむを得ずに分数を出す場合は変形の最後の最後に分数にするようにしましょう！

(2) 0が多く、1か-1が含まれている行で他の列に0を作る

基本的に0が多く含まれていて、かつなるべく1か-1が含まれている行を使って他の列を0にしていきましょう。
行にある0の数が同じで、かつ1か-1が複数ある行列の場合はどっちから計算してもいいです。この場合私は左側の列に1や-1ある方を優先して使います。
1つ変形例を書いてみます。

\[
\left( \begin{array}{ccc} 2_{-4} & 1_{-4} & -3_{+4} & 2_{-2} \\ -2 & -2 & 2 & -1 \\ 2 & 3 & -1 & 0   \end{array} \right) \ \to \
\left( \begin{array}{ccc} -2 & -3 & 1 & 0 \\ -2 & -2 & 2 & -1 \\  2 & 3 & -1 & 0   \end{array} \right)
\]

1回他の列を0にしたら、0が多く含まれている行（最初とは違う行）でまた行基本変形を行います。
\[
\left( \begin{array}{ccc} -2 & -3 & 1 & 0 \\ -2_{+2} & -2_{+3} & 2_{-1} & -1 \\ 2_{-2} & 3_{-3} & -1_{+1} & 0   \end{array} \right) \ \to \
\left( \begin{array}{ccc} -2 & -3 & 1 & 0 \\ 0 & 1 & -1 & -1 \\ 0 & 0 & 0 & 0  \end{array} \right)
\]

今回の場合、2ステップで階段行列ができましたね。この場合、3行に対して、全部0の行が1つあるので、この行列の階数は2となります。

階段行列を求める際に、一番左の要素を1にしろ、っていう先生もいるのでその場合は一番左の要素が1になるように割り算をします。（この手段は行列の階数を求めるためには不要の操作）
\[
\left( \begin{array}{ccc} -2_{\div (-2)} & -3_{\div (-2)} & 1_{\div (-2)} & 0 \\ 0 & 1 & -1 & -1 \\ 0 & 0 & 0 & 0  \end{array} \right) \ \to \
\left( \begin{array}{ccc} 1 & \frac{3}{2} & -\frac{1}{2} & 0 \\ 0 & 1 & -1 & -1 \\ 0 & 0 & 0 & 0  \end{array} \right)
\]

しかし、全然0どころか1や-1ですら行列内に含まれていない場合がありますよね。

そのときは下のように変形して1や-1を作り出しましょう。

\[
\left( \begin{array}{ccc} 2 & 3 & 4 & 5 \\ 3_{-2} & 4_{-3} & 5_{-4} &  6_{-5} \\ 4 & 5 & 6 & 7   \end{array} \right) \ \to \
\left( \begin{array}{ccc} 2 & 3 & 4 & 5 \\ 1 & 1 & 1 &  1 \\ 4 & 5 & 6 & 7   \end{array} \right)
\]

ただし、下の例のように全然1や-1がなくても分数計算なしで計算できる場合はそのまま計算することをおすすめします。

\[
\left( \begin{array}{ccc} 2 & 5 & -3 & -2 \\ -2_{+2} & -7_{+5} & 3_{-3} &  4_{-2} \\ 4_{-4} & 14_{-10} & -6_{+6} & -8_{+4}   \end{array} \right) \ \to \
\left( \begin{array}{ccc}2 & 5 & -3 & -2 \\ 0 & -2 & 0 &  2 \\ 0 & 4 & 0 & -4   \end{array} \right)
\]

(4) 計算課程を下にメモ

1の(3)の「1つの行から他の行を何倍かしたものを足したり引いたりする」ときに、「他の行を何倍かする」動作と「1つの行から他の行の値を加減する」動作を同時に頭で計算すると計算ミスが多発します（暗算できる人はいいですが…）。

私は計算するときに、他の行を何倍か足したり引いたりした結果を下にメモするようにしています。例えば、

\[
\left( \begin{array}{ccc} 2_{+6} & 1 & -3_{+8} & 2_{-2} \\ 3 & 0 & 4 & -1 \\ -2 & 3 & 2 & 0   \end{array} \right) \ \to \
\left( \begin{array}{ccc} 8 & 1 & 5 & 0 \\ 3 & 0 & 4 & -1 \\ -2 & 3 & 2 & 0   \end{array} \right)
\]

のように、いくら足す（もしくは引く）かを下にメモして置くことで2つの操作を脳内で同時でする必要がなくなり、それぞれを別々に処理できるので計算ミスの確率が低下します。

今回の記事では計算過程を示すためにもこのメモをあえて表記しています。

スポンサードリンク

３．行列の階数

階数の説明をする前に、まずは階段行列について説明したいと思います。

階段行列とは、下に行けばいくほど左側の0の数が増えていき、左側の0の隣が0以外の数字になっているような行列のことを階段行列といいます。*1

下に階段行列の例を載せました。

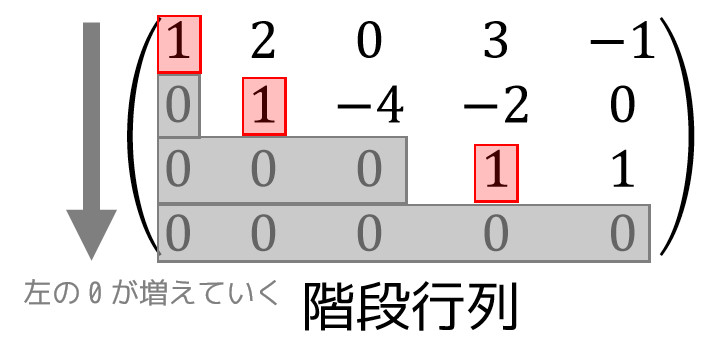
階数の求め方は、まず行列を行基本変形して階段行列にしてください。

階段行列にしたときに、それぞれの行の中に0ではない成分が1つでも残っている行の数の総数が行列の階数となり、Rankで表されます。

階段行列への変形例を1つ示しましょう。

\[ \begin{align*}  &
\left( \begin{array}{ccc} 3 & -1 & 9 & -5  \\ 2 & 1 & 1 & 0 \\ -3 & -2 & 0 & -1  \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 3_{+2} & -1_{+1} & 9_{+1} & -5  \\ 2 & 1 & 1 & 0 \\ -3_{+4} & -2_{+2} & 0_{+2} & -1  \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 5_{-5} & 0 & 10_{-10} & -5_{+5}  \\ 2_{-2} & 1 & 1_{-4} & 0_{+2} \\ 1 & 0 & 2 & -1  \end{array} \right)  \\ \to \ &
\left( \begin{array}{ccc} 0 & 0 & 0 & 0  \\ 0 & 1 & -3 & 2 \\ 1 & 0 & 2 & -1  \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 0 & 2 & -1  \\ 0 & 1 & -3 & 2 \\ 0 & 0 & 0 & 0  \end{array} \right)
\end{align*}
\]

この場合は、1行目と2行目には0でない成分が残っていますね。しかし、3行目はすべての行列の成分が0となっています。なので階数は2となります。

このように全部0の行があって階数が「行数」ではなくなるとき、私は階数（ランク）が減ると勝手に呼んでます。（例：4行の行列でランクが2→ランクが2減った）

なお、多くの試験、例えば大学の定期試験、数検1級、大学院入試問題などでは、階数に関する問題が出た場合はほぼ確実に行基本変形をすると全部0の行が現れ、ランクが減る問題がほとんどです。

４．練習してみよう！

次の行列 \( A, B \) を階段行列に直し、階数を求めなさい。

\[A = \left( \begin{array}{ccc} 2 & -1 & -2 & 9  \\ 4 & 5 & 0 & -3 \\ -2 & -6 & -2 & 12 \\ 3 & 2 & -1 & 4  \end{array} \right) \]

\[B = \left( \begin{array}{ccc} 1 & 1 & a \\ 1 & a & 1 \\ a & 1 & 1  \end{array} \right) \]

解答

\[ \begin{align*} A = &
\left( \begin{array}{ccc} 2 & -1 & -2 & 9  \\ 4_{+10} & 5_{-5} & 0_{-10} & -3_{+45} \\ -2_{-12} & -6_{+6} & -2_{+12} & 12_{-54} \\ 3_{+4} & 2_{-2} & -1_{-4} & 4_{+18}  \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 2 & -1 & -2 & 9  \\ 14 & 0 & -10 & 42 \\ -14_{+14}& 0 & 10_{-10} & -42_{+42} \\ 7 & 0 & -5 & 22 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 2 & -1 & -2 & 9  \\ 14 & 0 & -10 & 42 \\ 0 & 0 & 0 & 0 \\ 7 & 0 & -5 & 22 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 2 & -1 & -2 & 9  \\ 7 & 0 & -5 & 21 \\ 0 & 0 & 0 & 0 \\ 7_{-7} & 0 & -5_{+5} & 22_{-21} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 2 & -1 & -2 & 9_{-9}  \\ 7 & 0 & -5 & 21_{-21} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 14_{-14} & -7 & -14_{+10} & 0  \\ 7 & 0 & -5 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 0 & -7 & -4 & 0  \\ 7 & 0 & -5 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 7 & 0 & -5 & 0  \\ 0 & -7 & -4 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 0 & -\frac{5}{7} & 0  \\ 0 & 1 & \frac{4}{7} & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{array} \right)
\end{align*}
\]

と階段行列に変形でき、階数は3となる。

行列 \( B \) に関しては、途中 \( a + 2 \) で割るところがあるので、0除算しないように \( a = 2 \) かそれ以外で場合分けが必要である。

\[ \begin{align*} B = &
\left( \begin{array}{ccc} 1 & 1 & a \\ 1 & a & 1 \\ a_{+1} & 1_{+1} & 1_{+a}  \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 1 & a \\ 1 & a & 1 \\ a+1_{+1} & 2_{+a} & 1+a_{+1}\end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 1 & a \\ 1 & a & 1 \\ a+2_{\div (a+2)} & a+2_{\div (a+2)} & a+2_{\div (a+2)} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1_{-1} & 1_{-1} & a_{-1} \\ 1_{-1} & a_{-1} & 1_{-1} \\ 1 & 1 & 1  \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 0 & 0 & a-1 \\ 0 & a-1 & 0 \\ 1 & 1 & 1  \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 1 & 1 \\ 0 & a-1 & 0 \\ 0 & 0 & a-1  \end{array} \right)
\end{align*}
\]

となる。また、\( a = -2 \) のときは、

\[ \begin{align*} C = &
\left( \begin{array}{ccc} 1 & 1 & -2 \\ 1 & -2 & 1 \\ -2_{+1} & 1_{+1} & 1_{-2}  \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 1 & -2 \\ 1 & -2 & 1 \\ -1_{+1} & 2_{-2} & -1_{+1} \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 1 & -2 \\ 1_{-1} & -2_{-1} & 1_{+2} \\ 0 & 0 & 0 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 1 & -2 \\ 0 & -3_{\div (-3)} & 3_{\div (-3)} \\ 0 & 0 & 0 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 1_{-1} & -2_{+1} \\ 0 & 1 & -1 \\ 0 & 0 & 0 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 0 & -1 \\ 0 & 1 & -1 \\ 0 & 0 & 0 \end{array} \right)
\end{align*}
\]

となり、

• \( a = 1 \) のとき、階数は1
• \( a = -2 \) のとき、階数は2
• 上記以外、つまり \( a \not=1,-2 \) のとき、階数は3

となる。

５．さいごに

今回は行基本変形を用いた階段行列の作り方、作り方のコツ、行列の階数についてまとめてみました。

行基本変形は階段行列以外にも様々な分野で必要になってくるのでぜひ得意になってください。次回は、行基本変形を使った連立方程式の解き方が説明できたらいいなと思ってます。

ではまた次回。

Next：行基本変形を用いた連立方程式の算出法

www.momoyama-usagi.com