うさぎでもわかる線形代数　第22羽　ジョルダン標準形

こんにちは、ももやまです。

今回は、線形代数の中でもかなりの難易度を誇り、期末試験や院試などで出題されるジョルダン標準形がどんなものなのかを簡単に説明し、3次ジョルダン標準形までの求め方を例題や練習問題を用意し、（たぶん）わかりやすくまとめています。

※注意

ジョルダン標準形の求め方が知りたい方は、項目3以降をご覧ください。

前回の記事「うさぎでもわかる線形代数　第21羽」はこちら↓

www.momoyama-usagi.com

スポンサードリンク

１．ジョルダン標準形とは

行列の中には対角化ができないものもありました。例えば、\[
\left( \begin{array}{ccc} 2 & 1 \\ -1 & 4 \end{array} \right)
\]は、2次正方行列なのに固有ベクトルが1つしか求められないため、対角化ができませんね*1。

しかし、対角化できない行列でもできる限り対角行列に近い形にすることはできます。この形のことをジョルダン標準形と呼ばれます。

ジョルダン標準形は、ジョルダンブロック（下で説明します）を対角線上に並べた行列を表します。

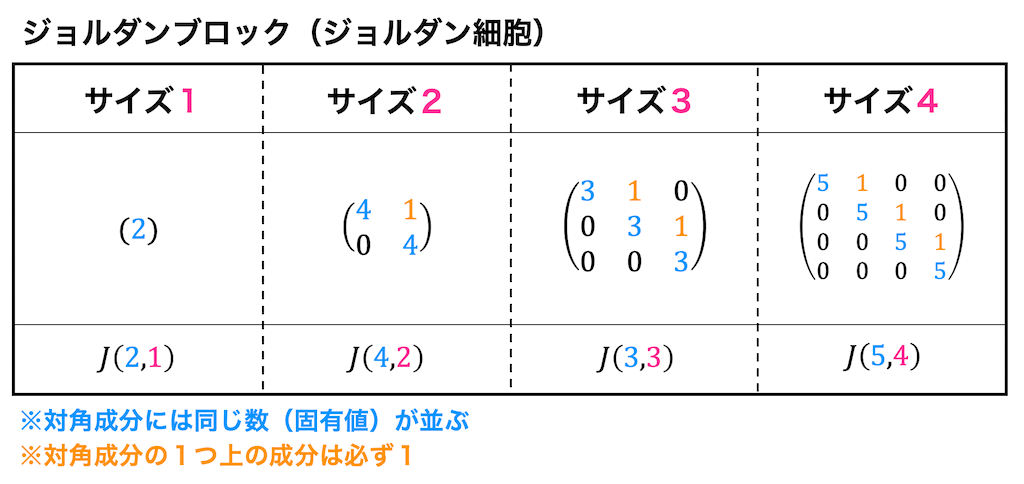
ジョルダンブロック（ジョルダン細胞）

ジョルダンブロックは下のように対角成分に同じ数（固有値）を並べ、対角成分の1つ上が1となる行列のことを表し、

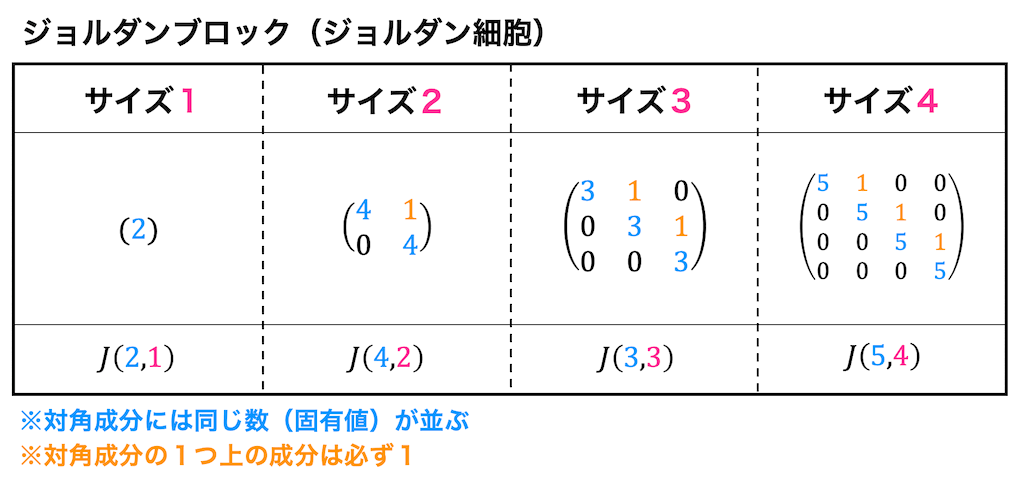
ジョルダンブロックは、対角成分に並んでいる数（固有値）を \( \alpha \)、ジョルダンブロックのサイズ（行列の大きさ）を \( n \) とし、 \( J(\alpha,n) \) と表すことができます。

ジョルダン標準形とジョルダンブロック

ジョルダン標準形は下のようにジョルダンブロックを対角線上に並べ、残りの成分が0であるような行列を表します。

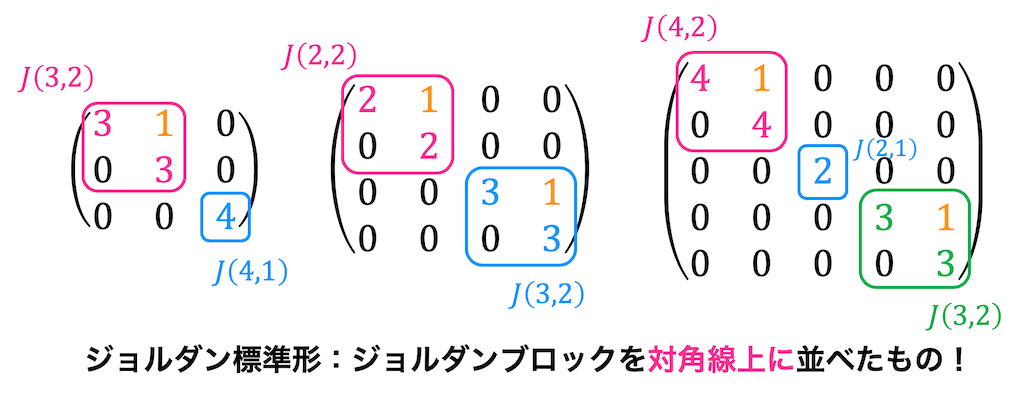
ジョルダン標準形を記号で表現する際には、どんな

例えば、図の一番左の行列は、\( J(3,2) \) と \( J(4,1) \) のジョルダンブロックで構成されていますね。なので、\[
J(3,2) \oplus J(4,1)
\]と表現します。

行列が対角化できる場合、ジョルダン標準形はすべてサイズ1のジョルダンブロック \( J(x,1) \) で構成されます。

対角化はジョルダン標準形の特殊なパターンなのです。

（もし対角化がまだわからない人は早急にこちらの記事で復習しましょう！）

スポンサードリンク

２．2次・3次のジョルダン標準形とジョルダンブロック

2次平方行列、3次平方行列の場合のジョルダン標準形とジョルダンブロックの組み合わせを下に記しておきます。

2次正方行列の場合

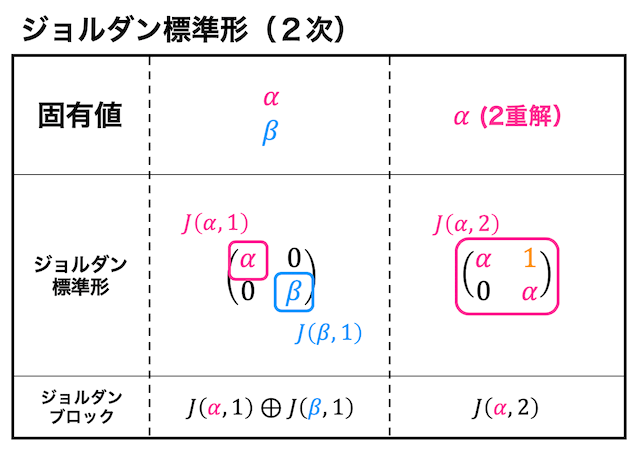
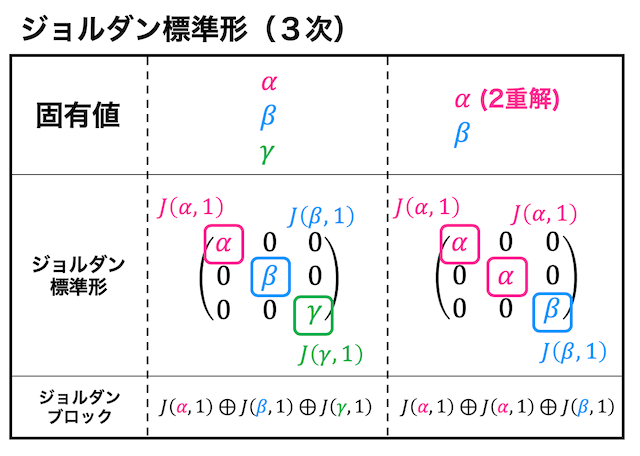
3次正方行列の場合

ジョルダン標準形が対角行列

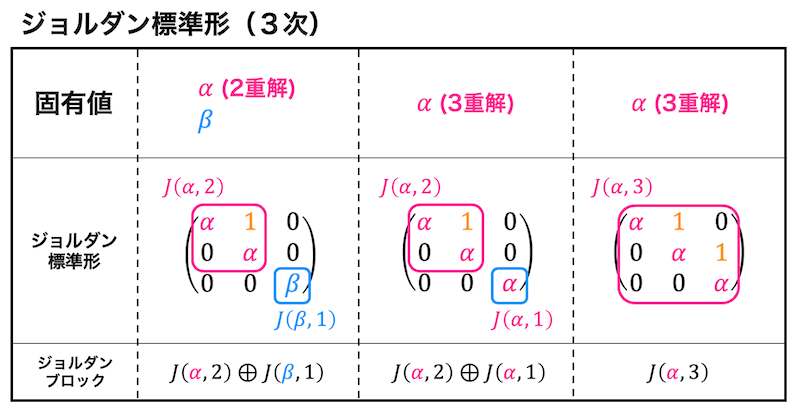
対角化できない場合

スポンサードリンク

３．ジョルダン標準形の求め方（2次）

ではまずは2次正方行列のジョルダン標準形を求める方法を例題を使って説明していきましょう。

例題1

行列\[ \left( \begin{array}{ccc} 2 & 1 \\ -1 & 4 \end{array} \right)  \]を正則行列 \( P \) を用いて \( P^{-1} AP \) をジョルダン標準形にしなさい。

解説1

(1)

Step1：固有値を求める

固有値を \( t \) とすると、固有方程式は、\[\begin{align*}
|A-tE| = & \left| \begin{array}{ccc} 2-t & 1 \\ -1 & 4-t \end{array} \right|
\\ = & (t-4)(t-2) + 1 \\ = & t^2 - 6t + 9 \\ = & (t-3)^2 = 0
\end{align*} \]より固有値は3（2重解）

Step2：固有ベクトルを求める

固有値が3のときの固有ベクトルは、\[ \begin{align*}
(A-3E) = &
\left( \begin{array}{ccc} -1 & 1 \\ -1 & 1  \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & -1 \\ 0 & 0  \end{array} \right)
\end{align*} \]となる。\[
x - y = 0
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y  \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)
\]と表せるので、固有ベクトルは1本あり、固有ベクトル \( \vec{p_1} \) は、\[
\vec{p_1} = \left( \begin{array}{ccc} 1 \\ 1   \end{array} \right)
\]となる。

ここまでは通常の対角化と全く同じ流れです。

Step3：広義固有ベクトルを求める

このままでは固有ベクトルが1本足りないため、ジョルダン標準形がつくれませんね。

そこで、\[
(A - 3E) \vec{p_2} = \vec{p_1}
\]を満たすような \( \vec{p_2} \) を探します。1つ前に求めた固有ベクトルを借りてくるのです。これを広義固有ベクトルと呼びます。

※通常の固有ベクトルも広義固有ベクトルの中に含まれるので「広義固有ベクトルを求めなさい」という問題が出た際には通常の固有ベクトルを答えに入れ忘れないように注意しましょう。

固有値3に対する広義固有ベクトル \( \vec{p_2} \) は、\[ \begin{align*} &
\left( \begin{array}{cc|c} -1 & 1 & 1 \\ -1 & 1 & 1  \end{array} \right)  \\ \to \ &
\left( \begin{array}{cc|c} 1 & -1 & -1  \\ 0 & 0 & 0  \end{array} \right)
\end{align*} \]となる。\[
x - y = -1
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y  \end{array} \right) =\left( \begin{array}{ccc} 0 \\ 1 \end{array} \right) + k \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)
\]と表せますね。
（実はここは任意定数とおかなくても \( x - y = -1 \) を満たすような解を1つ見つければOK、例題2からは任意定数とおかずに解を1つ見つける書き方に変えます。）

よって広義固有ベクトル \( \vec{p_2} \) は \( k = 0 \) として\[
\vec{p_2} = \left( \begin{array}{ccc} 0 \\ 1   \end{array} \right)
\]となります。

Step4：ジョルダン標準形を求める

よって、\[
\left\{ \begin{array}{l} (A - 3E) \vec{p_1} = \vec{0} \\ A \vec{p_1} = 3 \vec{p_1} \end{array}\right.  \ \ \
\left\{ \begin{array}{l} (A - 3E) \vec{p_2} = \vec{p_1} \\ A \vec{p_2} = \vec{p_1} +  3 \vec{p_2} \end{array}\right.
\]が成立するので、\[ P = \left( \vec{p_1}, \vec{p_2} \right) = \left( \begin{array}{ccc} 1 & 0 \\ 1 & 1 \end{array} \right)\]とすると、\[ \begin{align*}
AP & = A \left( \vec{p_1}, \vec{p_2} \right) \\ & = \left( 3 \vec{p_1}, \vec{p_1} + 3 \vec{p_2} \right)  \\ & =   \left( \vec{p_1}, \vec{p_2} \right) \left( \begin{array}{ccc} 3 & 1 \\ 0 & 3 \end{array} \right) \\ & = P \left( \begin{array}{ccc} 3 & 1 \\ 0 & 3 \end{array} \right)
\end{align*} \]となります。

ここで、\[
J = \left( \begin{array}{ccc} 3 & 1 \\ 0 & 3 \end{array} \right)
\]とすると、\[
AP = PJ \\
P^{-1} AP = J = \left( \begin{array}{ccc} 3 & 1 \\ 0 & 3 \end{array} \right)
\]となり、うまくジョルダン標準形が求められますできますね。
（ジョルダン標準形の検算も対角化と同じように \( AP = PJ \) で検算ができます。）

ジョルダンブロック：\( J(3,2) \)

広義固有ベクトルと広義固有空間

広義固有ベクトルも固有ベクトルと同じようにベクトル空間を用いて表すことができます。

例題1の広義固有空間は、\[
\tilde{V}(3) = \left\{ \left( \begin{array}{ccc} 1 \\ 1   \end{array} \right) , \left( \begin{array}{ccc} 0 \\ 1   \end{array} \right)  \right\}
\]となります。

下のほうに一応定義は示しておきますが、参考程度にどうぞ。
固有値ごとに広義固有ベクトルをまとめたものが広義固有空間だと思ってもらってOKです。

さきほどの例題で広義固有ベクトルを求めるときに\[
(A - 3E) \vec{p_2} = \vec{p_1}
\]を解きましたね。実は、\[
(A - 3E) \vec{p_1} = (A - 3E)^2 \vec{p_2} = \vec{0}
\]と変形できるので、\( k = 2 \) のときの広義固有ベクトル（広義固有空間）を求めていることと同じなのです！

４．ジョルダン標準形の求め方（3次）

3次のジョルダン標準形も2次と同じように計算をすることができます。

ただし、重解のパターンによって解き方が3パターンにわかれるので注意してください。

パターン1　2重解の固有値があり、固有ベクトルが1本足りない場合

例題2

行列\[ \left( \begin{array}{ccc} 1 & 0 & -1 \\ 0 & 2 & 0 \\ 0 & 1 & 1 \end{array} \right)  \]を正則行列 \( P \) を用いて \( P^{-1} AP \) をジョルダン標準形にしなさい。

解説2

固有方程式は、\[\begin{align*}
|A-tE| = & \left| \begin{array}{ccc} 1-t & 0 & -1 \\ 0 & 2-t & 0 \\ 0 & 1 & 1-t \end{array} \right|
\\ = & (1-t) \left| \begin{array}{ccc} 2-t & 0 \\ 1 & 1-t  \end{array} \right|
\\ = & (1-t)^2 (2-t) = 0
\end{align*} \]より固有値は1（2重解）、2となる。

つぎに、広義固有ベクトル（および固有ベクトル）を求めていく。

(1) 固有値が1のとき

固有値1に属する固有ベクトルは、\[ \begin{align*}
(A-E) = &
\left( \begin{array}{ccc} 0 & 0 & -1 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc}  0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0  \end{array} \right)
\end{align*} \]となる。\[
\left\{ \begin{array}{l} y = 0 \\ z = 0 \end{array}\right.
\]を解くと（要注意）、\[
\left( \begin{array}{ccc} x \\ y \\ z  \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right)
\]となるので、固有ベクトルは1本あり、固有ベクトル \( \vec{p_1} \) は、\[
\vec{p_1} = \left( \begin{array}{ccc} 1 \\ 0 \\ 0    \end{array} \right)
\]となる。

2重解に対し、固有ベクトルが1本しかないので、\[
(A - E) \vec{p_2} = \vec{p_1}
\]を満たすような \( \vec{p_2} \) を求める。\[ \begin{align*} &
\left( \begin{array}{ccc|c} 0 & 0 & -1 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0  \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc|c} 0 & 0 & 1 & -1 \\ 0 & 1 & 0 & 0 \end{array} \right)
\end{align*} \]となる。\[
y = 0, z = -1
\]の解の1つに\[ \left( \begin{array}{ccc} x \\ y \\ z  \end{array} \right) =  \left( \begin{array}{ccc} 0 \\ 0 \\ -1 \end{array} \right) \]があるので*2、広義固有ベクトル \( \vec{p_2} \) は\[
\vec{p_2} = \left( \begin{array}{ccc} 0 \\ 0 \\ -1   \end{array} \right)
\]となります。

(ii)

固有値が2のときの固有ベクトル

固有値2に属する固有ベクトルは、\[ \begin{align*}
(A-2E) = &
\left( \begin{array}{ccc} -1 & 0 & -1 \\ 0 & 0 & 0 \\ 0 & 1 & -1 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc}  1 & 0 & 1 \\ 0 & 1 & -1 \\ 0 & 0 & 0  \end{array} \right)
\end{align*} \]となる。\[
\left\{ \begin{array}{l} x + z \\ y - z = 0 \end{array}\right.
\]を解くと（要注意）、\[
\left( \begin{array}{ccc} x \\ y \\ z  \end{array} \right) = k \left( \begin{array}{ccc} -1 \\ 1 \\ 1 \end{array} \right)
\]となるので、固有ベクトルは1本あり、固有ベクトル \( \vec{p_3} \) は、\[
\vec{p_3} = \left( \begin{array}{ccc} -1 \\ 1 \\ 1    \end{array} \right)
\]となる。

よって、\[
\left\{ \begin{array}{l} (A - E) \vec{p_1} = \vec{0} \\ A \vec{p_1} = \vec{p_1} \end{array}\right.  \ \ \
\left\{ \begin{array}{l} (A - E) \vec{p_2} = \vec{p_1} \\ A \vec{p_2} = \vec{p_1} +  \vec{p_2} \end{array}\right.   \ \ \
\left\{ \begin{array}{l} (A - 2E) \vec{p_3} = \vec{0} \\ A \vec{p_3} = 2 \vec{p_3} \end{array}\right. \]が成り立つ。ここで\[ P = \left( \vec{p_1}, \vec{p_2}, \vec{p_3} \right) = \left( \begin{array}{ccc} 1 & 0 & -1 \\ 0 & 0 & 1 \\ 0 & -1 & 1 \end{array} \right)\]とすると、\[ \begin{align*}
AP & = A \left( \vec{p_1}, \vec{p_2}, \vec{p_3} \right) \\ & = \left( \vec{p_1}, \vec{p_1} +  \vec{p_2}, \vec{p_3} \right)  \\ & =   \left( \vec{p_1}, \vec{p_2}, \vec{p_3} \right) \left( \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{array} \right) \\ & = P \left( \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{array} \right)
\end{align*} \]となります。

よって、\[
P = \left( \begin{array}{ccc} 1 & 0 & -1 \\ 0 & 0 & 1 \\ 0 & -1 & 1 \end{array} \right) \ \ \
J = P^{-1} AP =  \left( \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{array} \right)
\]とジョルダン標準形にできます。

ジョルダンブロックの構成：\( J(1,2) \oplus J(2,1) \)

[検算] \[
AP = PJ = \left( \begin{array}{ccc} 1 & 1 & -2 \\ 0 & 0 & 2 \\ 0 & -1 & 2 \end{array} \right)
\]

※広義固有空間は\[
\tilde{V}(1) = \left\{\left( \begin{array}{ccc} 1 \\ 0 \\ 0   \end{array} \right) , \left( \begin{array}{ccc} 0 \\ 0 \\ -1   \end{array} \right) , \left( \begin{array}{ccc} -1 \\ 1 \\ 1    \end{array} \right)  \right\} \\
\]となる。

パターン2　3重解の固有値があり、固有ベクトルが2本足りない場合

つぎに固有値が3重解となり、固有ベクトルが1本しか出てこないパターンをみていきましょう。

例題3

行列\[ \left( \begin{array}{ccc} 7 & -1 & 1 \\ 8 & 1 & 2 \\ -6 & 1 & 1 \end{array} \right)  \]を正則行列 \( P \) を用いて \( P^{-1} AP \) をジョルダン標準形にしなさい。

解説3

変形がめんどくさいの

固有多項式は、\[ \begin{align*}
|A - tE| & = \left| \begin{array}{ccc} 7-t & -1 & 1 \\ 8 & 1-t & 2 \\ -6 & 1 & 1-t \end{array} \right|
\\ & = \left| \begin{array}{ccc} 1-t & 0 & 2-t \\ 8 & 1-t & 2 \\ -6 & 1 & 1-t \end{array} \right|
\\ & = (1-t) \left| \begin{array}{ccc} 1-t & 2 \\ 1 & 1-t  \end{array} \right| + (2-t) \left| \begin{array}{ccc}  8 & 1-t \\ -6 & 1 \end{array} \right|
\\ & = (1-t) \left( t^2-2t-1 \right) + (2-t) \left( 8 + (6-6t)  \right)
\\ & = -(t^3-9t^2+27t-27)
\\ & = - (t-3)(t^2-6t+9)
\\ & = -(t-3)^3
\end{align*}\]と変形できる。

よって固有値は3（3重解）となる。

(1) 固有値が3のとき

固有値3に属する固有ベクトルは、\[ \begin{align*}
(A-3E) = \ &
\left( \begin{array}{ccc} 4 & -1 & 1 \\ 8 & -2 & 2 \\ -6 & 1 & -2 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} -2 & 0 & -1 \\ -4 & 0 & -2 \\ -6 & 1 & -2  \end{array} \right)  \\ \to \ &
\left( \begin{array}{ccc} 2 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 0  \end{array} \right)  \\ \to \ &
\end{align*} \]となる。\[
\left\{ \begin{array}{l} 2x+z = 0 \\ y+z = 0 \end{array}\right.
\]を解くと（要注意）、\[
\left( \begin{array}{ccc} x \\ y \\ z  \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 2 \\ -2 \end{array} \right)
\]となるので、固有ベクトルは1本あり、固有ベクトル \( \vec{p_1} \) は、\[
\vec{p_1} = \left( \begin{array}{ccc} 1 \\ 2 \\ -2    \end{array} \right)
\]となる。

広義固有ベクトルが2本足りないので、まずは\[
(A - 3E) \vec{p_2} = \vec{p_1}
\]を満たすようなベクトルを求める。

\[ \begin{align*} &
\left( \begin{array}{ccc|c} 4 & -1 & 1 & 1 \\ 8 & -2 & 2 & 2 \\ -6 & 1 & -2 & -2  \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc|c} -2 & 0 & -1 & -1 \\ -4 & 0 & -2 & -2 \\ -6 & 1 & -2 & -2  \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc|c} 2 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1  \end{array} \right)
\end{align*} \]となる。

\[
\left\{ \begin{array}{l} 2x + z = 1 \\ y + z = 1 \end{array}\right.
\]の解の1つに\[ \left( \begin{array}{ccc} x \\ y \\ z  \end{array} \right) =  \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \end{array} \right) \]があるので、広義固有ベクトル \( \vec{p_2} \) は\[
\vec{p_2} = \left( \begin{array}{ccc} 0 \\ 0 \\ 1   \end{array} \right)
\]となります。

しかし、まだ1つ広義固有ベクトルが足りませんね。

なので、今度は、\[
(A - 3E) \vec{p_3} = \vec{p_2}
\]を満たすベクトルを求めます*3。

\[ \begin{align*} &
\left( \begin{array}{ccc|c} 4 & -1 & 1 & 0 \\ 8 & -2 & 2 & 0 \\ -6 & 1 & -2 & 1  \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc|c} -2 & 0 & -1 & 1 \\ -4 & 0 & -2 & 2 \\ -6 & 1 & -2 & 1  \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc|c} 2 & 0 & 1 & -1 \\ 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & -2  \end{array} \right)
\end{align*} \]となる。

\[
2x + z = -1, y + z = -2
\]の解の1つに\[ \left( \begin{array}{ccc} x \\ y \\ z  \end{array} \right) =  \left( \begin{array}{ccc} 0 \\ -1 \\ -1 \end{array} \right) \]があるので、広義固有ベクトル \( \vec{p_3} \) は\[
\vec{p_3} = \left( \begin{array}{ccc} 0 \\ 0 \\ 1   \end{array} \right)
\]となります。

※解の1つを選ぶ際に \( \vec{p_1} \), \( \vec{p_2} \), \( \vec{p_3} \) が1次独立かを確認すること！

よって、\[
\left\{ \begin{array}{l} (A - 3E) \vec{p_1} = \vec{0} \\ A \vec{p_1} = 3 \vec{p_1} \end{array}\right.  \ \ \
\left\{ \begin{array}{l} (A - 3E) \vec{p_2} = \vec{p_1} \\ A \vec{p_2} = \vec{p_1} +  3 \vec{p_2} \end{array}\right.   \ \ \
\left\{ \begin{array}{l} (A - 3E) \vec{p_3} = \vec{p_2} \\ A \vec{p_3} = \vec{p_2} + 3 \vec{p_3} \end{array}\right. \]が成り立つ。ここで\[ P = \left( \vec{p_1}, \vec{p_2}, \vec{p_3} \right) = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 2 & 0 & -1 \\ -2 & 1 & -1 \end{array} \right)\]とすると、\[ \begin{align*}
AP & = A \left( \vec{p_1}, \vec{p_2}, \vec{p_3} \right) \\ & = \left( \vec{p_1}, \vec{p_1} +  \vec{p_2},\vec{p_2} +  \vec{p_3} \right)  \\ & =  \left( \vec{p_1}, \vec{p_2}, \vec{p_3} \right) \left( \begin{array}{ccc} 3 & 1 & 0 \\ 0 & 3 & 1 \\ 0 & 0 & 3 \end{array} \right) \\ & = P \left( \begin{array}{ccc} 3 & 1 & 0 \\ 0 & 3 & 1 \\ 0 & 0 & 3 \end{array} \right)
\end{align*} \]となります。

よって、\[
P = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 2 & 0 & -1 \\ -2 & 1 & -1 \end{array} \right) \ \ \
J = P^{-1} AP =  \left( \begin{array}{ccc} 3 & 1 & 0 \\ 0 & 3 & 1 \\ 0 & 0 & 3 \end{array} \right)
\]とジョルダン標準形にできます。

ジョルダンブロックの構成：\( J(3,3) \)

[検算] \[
AP = PJ = \left( \begin{array}{ccc} 3 & 1 & 0 \\ 6 & 2 & -3 \\ -6 & 1 & -2 \end{array} \right)
\]

※広義固有空間は\[
\tilde{V}(3) = \left\{ \left( \begin{array}{ccc} 1 \\ 2 \\ -2    \end{array} \right), \left( \begin{array}{ccc} 0 \\ 0 \\ 1   \end{array} \right)  \right\} \\
\]となる。

パターン3　3重解の固有値があり、固有ベクトルが1本足りない場合

例題4

行列\[ \left( \begin{array}{ccc} 3 & 1 & 1 \\ 1 & 3 & -1 \\ -2 & 2 & 6 \end{array} \right)  \]を正則行列 \( P \) を用いて \( P^{-1} AP \) をジョルダン標準形にしなさい。

解説4

Step1：固有値を求める

固有値を \( t \) とする。

固有多項式は、\[ \begin{align*}
|A - tE| & = \left| \begin{array}{ccc} 3-t & 1 & 1 \\ 1 & 3-t & -1 \\ -2 & 2 & 6-t \end{array} \right|
\\ & =\left| \begin{array}{ccc} 4-t & 4-t & 0 \\ 1 & 3-t & -1 \\ -2 & 2 & 6-t \end{array} \right|
\\ & = (4-t) \left| \begin{array}{ccc} 1 & 1 & 0 \\ 1 & 3-t & -1 \\ -2 & 2 & 6-t \end{array} \right|
\\ & = (4-t) \left| \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 2-t & -1 \\ 0 & 4 & 6-t \end{array} \right|
\\ & = (4-t) \left| \begin{array}{ccc} 2-t & -1 \\ 4 & 6-t \end{array} \right|
\end{align*}\]と変形できる。

ここで、\[\begin{align*} &
\left| \begin{array}{ccc} 2-t & -1 \\ 4 & 6-t \end{array} \right|
\\ = & (t-2)(t-6) + 4 \\ = & t^2 - 8t + 16 \\ = & (t-4)^2
\end{align*} \]となるので、固有方程式は\[
|A - tE| = (4-t)(t-4)^2 = -(t-4)^3
\]を満たす \( t \) が固有値となり、固有値は4（3重解）となる。

Step2：広義固有ベクトル（広義固有空間）を求める

固有値4に属する固有ベクトルは、\[ \begin{align*}
(A-4E) = \ &
\left( \begin{array}{ccc} -1 & 1 & 1 \\ 1 & -1 & -1 \\ -2 & 2 & 2 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & -1 & -1 \\ 0 & 0 & 0 \\ 0 & 0 & 0  \end{array} \right)
\end{align*} \]となる。\[
x-y-z=0
\]を解くと（要注意）、任意定数 \( s,t \) を用いて\[
\left( \begin{array}{ccc} x \\ y \\ z  \end{array} \right) = s \left( \begin{array}{ccc} 1 \\ 1 \\ 0 \end{array} \right) + t \left( \begin{array}{ccc} 1 \\ 0 \\ 1 \end{array} \right)
\]となります。なので、固有ベクトルを2本求めることができます。
（ただしこの時点では解が出せないので注意）

広義固有ベクトルが1本足りないので先ほどの例題のように固有ベクトルを持ってくるのですが、\( \vec{p_1} \), \( \vec{p_2} \) と候補の固有ベクトルが2つあるため、どのように固有

なので、定義にしたがって、\[
(A - 4E)^2 \vec{p_3} = \vec{0}
\]を満たすベクトルを探します。\[
(A - 4E)^2 = \left( \begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0  \end{array} \right)  = O
\]となるので、どのような広義固有ベクトル \( \vec{p_3} \) を持ってきてもOKなことがわかりますね。

例えば、\[
\vec{p_3} =  \left( \begin{array}{ccc} 1 \\ 0 \\ 0  \end{array} \right)
\]とします。つぎに、\[
(A - 4E) \vec{p_3} = \vec{p_2}
\]を満たすような固有ベクトル \( \vec{p_2} \) を求めます。

すると、\[
(A-4E) \vec{p_3} = \left( \begin{array}{ccc}  2 & 1 & 1 \\ 1 & -1 & -1 \\ -2 & 2 & 2 \end{array} \right) \left( \begin{array}{ccc} 1 \\ 0 \\ 0  \end{array} \right) = \left( \begin{array}{ccc} -1 \\ 1 \\ -2  \end{array} \right) = \vec{p_2}
\]となります。これは、\[
s \left( \begin{array}{ccc} 1 \\ 1 \\ 0 \end{array} \right) + t \left( \begin{array}{ccc} 1 \\ 0 \\ 1 \end{array} \right)
\]の \( s = 1 \), \( t = -2 \) に相当します。

よって、\[
(A - 4E) \vec{p_3} = \vec{p_2}
\]を成立させるためには広義固有ベクトル \( \vec{p_2} \), \( \vec{p_3} \) を\[
\vec{p_2} = \left( \begin{array}{ccc} -1 \\ 1 \\ -2  \end{array} \right) , \ \ \
\vec{p_3} = \left( \begin{array}{ccc} 1 \\ 0 \\ 0  \end{array} \right)
\]とする必要があります。

残りの固有ベクトル \( \vec{p_1} \) は先ほどの解の \( (s,t) = (1,0) \) もしくは \( (s,t) = (0,1) \) どちらを選んでもOKです*4。

なので、\[
\vec{p_1} = \left( \begin{array}{ccc} 1 \\ 1 \\ 0 \end{array} \right)
\]とします。

よって、\[
\left\{ \begin{array}{l} (A - 4E) \vec{p_1} = \vec{0} \\ A \vec{p_1} = 4\vec{p_1} \end{array}\right.  \ \ \
\left\{ \begin{array}{l} (A - 4E) \vec{p_2} = \vec{0} \\ A \vec{p_2} = 4 \vec{p_2} \end{array}\right.   \ \ \
\left\{ \begin{array}{l} (A - 4E) \vec{p_3} = \vec{p_2} \\ A \vec{p_3} = \vec{p_2} + 4 \vec{p_3} \end{array}\right.
\]が成り立つ。ここで\[ P = \left( \vec{p_1}, \vec{p_2}, \vec{p_3} \right) = \left( \begin{array}{ccc} 1 & -1 & 1 \\ 1 & 1 & 0 \\ 0 & -2  & 0 \end{array} \right)\]とすると、\[ \begin{align*}
AP & = A \left( \vec{p_1}, \vec{p_2}, \vec{p_3} \right) \\ & = \left( 4 \vec{p_1}, 4 \vec{p_2} , \vec{p_2} + 4\vec{p_3} \right)  \\ & =   \left( \vec{p_1}, \vec{p_2}, \vec{p_3} \right) \left( \begin{array}{ccc} 4 & 0 & 0 \\ 0 & 4 & 1 \\ 0 & 0 & 4 \end{array} \right) \\ & = P \left( \begin{array}{ccc} 4 & 0 & 0 \\ 0 & 4 & 1 \\ 0 & 0 & 4 \end{array} \right)
\end{align*} \]となります。

よって、\[
P = \left( \begin{array}{ccc} 1 & -1 & 1 \\ 1 & 1 & 0 \\ 0 & -2  & 0 \end{array} \right) \ \ \
J = P^{-1} AP =  \left( \begin{array}{ccc} 4 & 0 & 0 \\ 0 & 4 & 1 \\ 0 & 0 & 4 \end{array} \right)
\]とジョルダン標準形にできます。

ジョルダンブロックの構成：\( J(4,2) \oplus J(4,1) \)

※広義固有空間は\[
\tilde{V}(4) =
\left\{
\left( \begin{array}{ccc} 1 \\ 1 \\ 0 \end{array} \right),
\left( \begin{array}{ccc} -1 \\ 1 \\ -2  \end{array} \right)  ,
\left( \begin{array}{ccc} 1 \\ 0 \\ 0  \end{array} \right)
\right\}
\]となる。

このように同じ固有値から複数の固有値を求められ、かつ固有ベクトルが重解の数存在しない場合の広義固有ベクトルの求め方は少しめんどくさいです。

５．ジョルダン標準形の求め方のまとめ

ジョルダン標準形がどんなものなのか、そしてどうやって求めるかについてを簡単にですがまとめました。

確認用にご覧ください。

3次までのジョルダン標準形を求めるためのステップを簡単にまとめたいと思います。

1. 行列の固有値を求める
2. 行列の固有ベクトルを求め、重解分だけ固有ベクトルが出るかを確認
3. 重解分だけ固有ベクトルが求められなかった固有値に対し、\[
   (A- tE) \vec{p_i} = \vec{p_{i-1}}
   \]のように1つ前の固有ベクトル（or 広義固有ベクトル）を用いて広義固有ベクトルを出す
4. 求めた広義固有ベクトルを並べて正則行列 \( P \) を作成し、ジョルダン標準形 \( J = P^{-1}AP \) を作成する。

注意点としては、固有ベクトルが複数本求められたにも関わらず、広義固有ベクトルを用いないとジョルダン標準形が求められない場合は、\[
(A- tE) \vec{p_i} = \vec{p_{i-1}}
\]がうまく成立するように \( \vec{p_{i-1}} \) を決める必要があるため、\[
(A - tE)^2 \vec{p_i} = \vec{0}
\]を解き、\( \vec{p_i} \) を決めてから \( \vec{p_{i-1}} \) を決める必要があります。

６．練習問題

では、ジョルダン標準形を求める練習をしましょう。

練習1→練習2→練習3の順に難易度があがります。

練習1

行列\[ \left( \begin{array}{ccc} 3 & -4 \\ 1 & -1 \end{array} \right)  \]についてつぎの問いに答えなさい。

(1) 行列の固有値を求めなさい。
(2) 固有ベクトル（もしくは固有空間）を求めなさい。
(3) 広義固有ベクトル（もしくは広義固有空間）を求めなさい。
(4) 正則行列 \( P \) を用いて \( P^{-1} AP \) をジョルダン標準形にしなさい。

練習2

行列\[ A = \left( \begin{array}{ccc} -1 & 5 & -8 \\ 3 & 1 & 4 \\ 6 & -6 & 13 \end{array} \right)  \]についてつぎの問いに答えなさい。

(1) 行列 \( A \) のの固有値を求めなさい。
(2) 固有ベクトル（もしくは固有空間）を求めなさい。
(3) 広義固有ベクトル（もしくは広義固有空間）を求めなさい。
(4) 正則行列 \( P \) を用いて \( P^{-1} AP = J \) をジョルダン標準形にしなさい。

練習3

行列\[ A = \left( \begin{array}{ccc} 3 & 3 & 1 \\ -1 & -1 & -1 \\ 2 & 6 & 4 \end{array} \right)  \]についてつぎの問いに答えなさい。

(1) 行列 \( A \) のの固有値を求めなさい。
(2) 固有ベクトル（もしくは固有空間）を求めなさい。
(3) 広義固有ベクトル（もしくは広義固有空間）を求めなさい。
(4) 正則行列 \( P \) を用いて \( P^{-1} AP \) をジョルダン標準形にしなさい。

７．練習問題の答え

解答1

(1) 固有値を求める

固有値を \( t \) とすると、固有方程式は、\[\begin{align*}
|A-tE| = & \left| \begin{array}{ccc} 3-t & -4 \\ 1 & -1-t \end{array} \right|
\\ = & (t-3)(t+1) + 4
\\ = & t^2 - 2t + 1
\\ = & (t-1)^2 = 0
\end{align*} \]より固有値は1（2重解）となる。

(2) 固有ベクトルを求める

固有値が1のときの固有ベクトルは、\[ \begin{align*}
(A-E) = &
\left( \begin{array}{ccc} 2 & -4 \\ 1 & -2  \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & -2 \\ 0 & 0  \end{array} \right)
\end{align*} \]となる。\[
x - 2y = 0
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y  \end{array} \right) = k \left( \begin{array}{ccc} 2 \\ 1 \end{array} \right)
\]と表せるので、固有ベクトルは1本あり、固有ベクトル \( \vec{p_1} \) は、\[
\vec{p_1} = \left( \begin{array}{ccc} 2 \\ 1   \end{array} \right)
\]となる。

固有空間は\[
V(1) = \left\{\left( \begin{array}{ccc} 2 \\ 1  \end{array} \right) \right\}
\]となる。

(3) 広義固有ベクトルを求める

固有ベクトル \( \vec{p_1} \) はもちろん広義固有ベクトルである。\[
(A - E) \vec{p_2} = \vec{p_1}
\]を満たすような \( \vec{p_2} \) を求める。

\[ \begin{align*} &
\left( \begin{array}{cc|c} 2 & -4 & 2  \\ 1 & -2 & 1  \end{array} \right) \\ \to \ &
\left( \begin{array}{cc|c} 1 & -2 & 1  \\ 0 & 0 & 0  \end{array} \right)
\end{align*} \]となる。\[
x - 2y = 1
\]の解の1つに\[ \left( \begin{array}{ccc} x \\ y   \end{array} \right) =  \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right) \]があるので、広義固有ベクトル \( \vec{p_2} \) は\[
\vec{p_2} = \left( \begin{array}{ccc} 1 \\ 0  \end{array} \right)
\]となります。
（広義固有ベクトルは \( \vec{p_1} \), \( \vec{p_2} \) の2つ存在）

広義固有空間は\[
\tilde{V}(1) = \left\{\left( \begin{array}{ccc} 2 \\ 1   \end{array} \right) , \left( \begin{array}{ccc} 1 \\ 0  \end{array} \right)   \right\}
\]となる。

(4) ジョルダン標準形を求める

よって、\[
\left\{ \begin{array}{l} (A - E) \vec{p_1} = \vec{0} \\ A \vec{p_1} = 3 \vec{p_1} \end{array} \right.  \ \ \
\left\{ \begin{array}{l} (A - E) \vec{p_2} = \vec{p_1} \\ A \vec{p_2} = \vec{p_1} +   \vec{p_2} \end{array} \right.
\]が成立するので、\[ P = \left( \vec{p_1}, \vec{p_2} \right) = \left( \begin{array}{ccc} 2 & 1 \\ 1 & 0 \end{array} \right)\]とすると、\[ \begin{align*}
AP & = A \left( \vec{p_1}, \vec{p_2} \right) \\ & = \left(  \vec{p_1}, \vec{p_1} + \vec{p_2} \right)  \\ & =   \left( \vec{p_1}, \vec{p_2} \right) \left( \begin{array}{ccc} 1 & 1 \\ 0 & 1 \end{array} \right) \\ & = P \left( \begin{array}{ccc} 1 & 1 \\ 0 & 1 \end{array} \right)
\end{align*} \]となります。

よって、\[
P = \left( \begin{array}{ccc} 2 & 1 \\ 1 & 0 \end{array} \right) , \ \ \
J = P^{-1} AP =  \left( \begin{array}{ccc} 1 & 1 \\ 0 & 1 \end{array} \right)
\]とジョルダン標準形にできる。

[検算] \[
AP = PJ = \left( \begin{array}{ccc} 2 & 3 \\  1 & 1  \end{array} \right)
\]

解答2

(1) 固有値を求める

行列式では列基本変形も行えるというのを忘れないようにしましょう。

固有値を \( t \) とする。固有多項式は、\[ \begin{align*}
|A - tE| & = \left| \begin{array}{ccc} -1-t & 5 & -8 \\ 3 & 1-t & 4 \\ 6 & -6 & 13-t \end{array} \right|
\\ & = \left| \begin{array}{ccc} -1-t & 4-t & -8 \\ 3 & 4-t & 4 \\ 6 & 0 & 13-t \end{array} \right|
\\ & = (4-t) \left| \begin{array}{ccc} -1-t & 1 & -8 \\ 3 & 1 & 4 \\ 6 & 0 & 13-t \end{array} \right|
\\ & = (4-t) \left| \begin{array}{ccc} -4-t & 0 & -12 \\ 3 & 1 & 4 \\ 6 & 0 & 13-t \end{array} \right|
\\ & = (4-t) \left| \begin{array}{ccc} -4-t & -12 \\  6 & 13-t \end{array} \right|
\end{align*}\]と変形できる。

ここで、\[\begin{align*} &
\left| \begin{array}{ccc} -4-t & -12 \\ 6 & 13-t \end{array} \right|
\\ = & (t-13)(t+4) + 72
\\ = & t^2 - 9t + 20
\\ = & (t-4)(t-5) = 0
\end{align*} \]となるので、固有方程式は\[
|A - tE| = (4-t)(t-4)(t-5) = -(t-4)^2 (t-5)
\]を満たす \( t \) が固有値となり、固有値は4（2重解）、5となる。

(2) 固有ベクトルを求める

固有値が4のときの固有ベクトルは、\[ \begin{align*}
(A-4E) = &
\left( \begin{array}{ccc} -5 & 5 & -8 \\ 3 & -3 & 4 \\ 6 & -6 & 9  \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} -5 & 5 & -8 \\ 3 & -3 & 4 \\ 0 & 0 & 1  \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} -5 & 5 & 0 \\ 3 & -3 & 0 \\ 0 & 0 & 1  \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & -1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0  \end{array} \right) \\ \to \ &
\end{align*} \]となる。\[
\left\{ \begin{array}{l} x - y = 0 \\  z = 0 \end{array}\right.
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \\ z  \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 1 \\ 0 \end{array} \right)
\]と表せるので、固有ベクトルは1本あり、固有ベクトル \( \vec{p_1} \) は、\[
\vec{p_1} = \left( \begin{array}{ccc} 1 \\ 1 \\ 0   \end{array} \right)
\]となる。

（2重解なのに固有ベクトルが1本なので、残り1本は広義固有ベクトル \( \vec{p_2} \) は(3)で求める）

固有値が5のときの固有ベクトルは、\[ \begin{align*}
(A-5E) = &
\left( \begin{array}{ccc} -6 & 5 & -8 \\ 3 & -4 & 4 \\ 6 & -6 & 8  \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 0 & -3 & 0 \\ 3 & -4 & 4 \\ 0 & 2 & 0  \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 3 & -4 & 4 \\ 0 & 2 & 0 \\ 0 & 0 & 0  \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 3 & 0 & 4 \\ 0 & 1 & 0 \\ 0 & 0 & 0  \end{array} \right)
\end{align*} \]となる。\[
\left\{ \begin{array}{l} 3x + 4z = 0 \\  y = 0 \end{array}\right.
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \\ z  \end{array} \right) = k \left( \begin{array}{ccc} 4 \\ 0 \\ -3 \end{array} \right)
\]と表せるので、固有ベクトルは1本あり、固有ベクトル \( \vec{p_3} \) は、\[
\vec{p_3} = \left( \begin{array}{ccc} 4 \\ 0 \\ -3   \end{array} \right)
\]となる。

よって固有空間は\[
V(4) = \left\{ \left( \begin{array}{ccc} 1 \\ 1 \\ 0   \end{array} \right) \right\} \ \ \
V(5) = \left\{ \left( \begin{array}{ccc} 4 \\ 0 \\ -3   \end{array} \right) \right\}
\]となる。

(3) 広義固有ベクトルを求める

固有値4に対する広義固有ベクトルが1本不足しているので、\[
(A - 4E) \vec{p_2} = \vec{p_1}
\]を満たすようなベクトルを求める。

固有値が4のときの固有ベクトルは、\[ \begin{align*}
(A-4E) = &
\left( \begin{array}{ccc|c} -5 & 5 & -8 & 1 \\ 3 & -3 & 4 & 1 \\ 6 & -6 & 9 & 0  \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc|c} -5 & 5 & -8 & 1  \\ 3 & -3 & 4 & 1 \\ 0 & 0 & 1 & -2  \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc|c} -5 & 5 & -0 & -15  \\ 3 & -3 & 0 & 9 \\ 0 & 0 & 1 & -2  \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc|c} 1 & -1 & 0 & 3  \\ 0 & 0 & 1 & -2 \\ 0 & 0 & 0 & 0  \end{array} \right) \\ \to \ &
\end{align*} \]となる。\[
\left\{ \begin{array}{l} x - y = 3 \\  z = -2 \end{array}\right.
\]の解の1つに\[ \left( \begin{array}{ccc} x \\ y \\ z   \end{array} \right) =  \left( \begin{array}{ccc} 3 \\ 0 \\ -2 \end{array} \right) \]があるので、広義固有ベクトル \( \vec{p_2} \) は\[
\vec{p_2} = \left( \begin{array}{ccc} 3 \\ 0 \\ -2  \end{array} \right)
\]となります。
（広義固有ベクトルは \( \vec{p_1} \), \( \vec{p_2} \), \( \vec{p_3} \) の3つ）

また、広義固有空間は\[
\tilde{V}(4) = \left\{ \left( \begin{array}{ccc} 1 \\ 1 \\ 0   \end{array} \right), \left( \begin{array}{ccc} 3 \\ 0 \\ -2   \end{array} \right)  \right\}
\tilde{V}(5) = \left\{ \left( \begin{array}{ccc} 4 \\ 0 \\ -3   \end{array} \right) \right\}
\]となる。

(4) ジョルダン標準形を求める

よって、\[
\left\{ \begin{array}{l} (A - 4E) \vec{p_1} = \vec{0} \\ A \vec{p_1} = 4 \vec{p_1} \end{array} \right.  \ \ \
\left\{ \begin{array}{l} (A - 4E) \vec{p_2} = \vec{p_1} \\ A \vec{p_2} = \vec{p_1} +  4  \vec{p_2} \end{array} \right.  \ \ \
\left\{ \begin{array}{l} (A - 5E) \vec{p_3} = \vec{0} \\ A \vec{p_3} = 5 \vec{p_3} \end{array} \right.
\]が成立する。

ここで\[ P = \left( \vec{p_1}, \vec{p_2}, \vec{p_3} \right) = \left( \begin{array}{ccc} 1 & 3 & 4 \\ 1 & 0 & 0 \\ 0 & -2 & -3 \end{array} \right)\]とすると、\[ \begin{align*}
AP & = A \left( \vec{p_1}, \vec{p_2}, \vec{p_3} \right) \\ & = \left( 4\vec{p_1}, \vec{p_1} +  4\vec{p_2},5 \vec{p_3} \right)  \\ & =  \left( \vec{p_1}, \vec{p_2}, \vec{p_3} \right) \left( \begin{array}{ccc} 4 & 1 & 0 \\ 0 & 4 & 0 \\ 0 & 0 & 5 \end{array} \right) \\ & = P \left( \begin{array}{ccc} 4 & 1 & 0 \\ 0 & 4 & 0 \\ 0 & 0 & 5 \end{array} \right)
\end{align*} \]となります。

よって、\[
P = \left( \begin{array}{ccc} 1 & 3 & 4 \\ 1 & 0 & 0 \\ 0 & -2 & -3 \end{array} \right) \ \ \
J = P^{-1} AP =  \left( \begin{array}{ccc} 4 & 1 & 0 \\ 0 & 4 & 0 \\ 0 & 0 & 5 \end{array} \right)
\]とジョルダン標準形にできる。

[検算] \[
AP = PJ = \left( \begin{array}{ccc} 4 & 13 & 20 \\ 4 & 1 & 0 \\ 0 & -8 & -15 \end{array} \right)
\]

解答3

(1) 固有値を求める

行列式では列基本変形も行えるというのを忘れないようにしましょう。

固有値を \( t \) とする。固有多項式は、\[ \begin{align*}
|A - tE| & = \left| \begin{array}{ccc} 3-t & 3 & 1 \\ -1 & -1-t & -1 \\ 2 & 6 & 4-t \end{array} \right|
\\ & = \left| \begin{array}{ccc} 2-t & 2-t & 0 \\ -1 & -1-t & -1 \\ 2 & 6 & 4-t \end{array} \right|
\\ & = (2-t) \left| \begin{array}{ccc} 1 & 1 & 0 \\ -1 & -1-t & -1 \\ 2 & 6 & 4-t \end{array} \right|
\\ & = (2-t) \left| \begin{array}{ccc} 1 & 1 & 0 \\ 0 & -t & -1 \\ 0 & 4 & 4-t \end{array} \right|
\\ & = (2-t) \left| \begin{array}{ccc} -t & -1 \\  4 & 4-t \end{array} \right|
\end{align*}\]と変形できる。

ここで、\[\begin{align*} &
\left| \begin{array}{ccc} -t & -1 \\  4 & 4-t \end{array} \right|
\\ = & t(t-4) + 4
\\ = & t^2 - 4t + 4
\\ = & (t-2)^2 = 0
\end{align*} \]となるので、固有方程式は\[
|A - tE| = (2-t)(t-2)^2 = -(t-2)^2 = 0
\]を満たす \( t \) が固有値となり、固有値は2（3重解）となる。

(2), (3) 固有ベクトル・広義固有ベクトルを求める

固有値2に属する固有ベクトルは、\[ \begin{align*}
(A-2E) = \ &
\left( \begin{array}{ccc} 1 & 3 & 1 \\ -1 & -3 & -1 \\ 2 & 6 & 2 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 3 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0  \end{array} \right)
\end{align*} \]となる。\[
x+3y+z=0
\]を解くと（要注意）、任意定数 \( s,t \) を用いて\[
\left( \begin{array}{ccc} x \\ y \\ z  \end{array} \right) = s \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \end{array} \right) + t \left( \begin{array}{ccc} 3 \\ -1 \\ 0 \end{array} \right)
\]となります。なので、固有ベクトルを2本求めることができます。
（ただしこの時点では解が出せないので注意）

なので、定義にしたがって、\[
(A - 2E)^2 \vec{p_3} = \vec{0}
\]を満たすベクトルを探します。\[
(A - 4E)^2 = \left( \begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0  \end{array} \right)  = O
\]となるので、どのような広義固有ベクトル \( \vec{p_3} \) を持ってきてもOKなことがわかりますね。

ここで、\[
\vec{p_3} = \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right)
\]とする*5。\[
(A - 2E) \vec{p_3} = \vec{p_2}
\]を満たすような固有ベクトル \( \vec{p_2} \) を探す。

すると、\[
(A-4E) \vec{p_3} = \left( \begin{array}{ccc}  1 & 3 & 1 \\ -1 & -3 & -1 \\ 2 & 6 & 2 \end{array} \right) \left( \begin{array}{ccc} 1 \\ 0 \\ 0  \end{array} \right) = \left( \begin{array}{ccc} 1 \\ -1 \\ 2  \end{array} \right) = \vec{p_2}
\]となります。これは、\[
s \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \end{array} \right) + t \left( \begin{array}{ccc} 3 \\ -1 \\ 0 \end{array} \right)
\]の \( s = -2 \), \( t = 1 \) に相当します。

よって、\[
(A - 4E) \vec{p_3} = \vec{p_2}
\]を成立させるためには広義固有ベクトル \( \vec{p_2} \), \( \vec{p_3} \) を\[
\vec{p_2} = \left( \begin{array}{ccc} 1 \\ -1 \\ 2  \end{array} \right) , \ \ \
\vec{p_3} = \left( \begin{array}{ccc} 1 \\ 0 \\ 0  \end{array} \right)
\]とする必要があります。

残りの固有ベクトル \( \vec{p_1} \) は先ほどの解の \( (s,t) = (1,0) \) もしくは \( (s,t) = (0,1) \) どちらを選んでもOK。

なので、\[
\vec{p_1} = \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \end{array} \right)
\]とします。

よって固有ベクトルは \( \vec{p_1} \), \( \vec{p_2} \) となり、固有空間は\[
V(2) = \left\{ \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \end{array} \right), \left( \begin{array}{ccc} 1 \\ -1 \\ 2  \end{array} \right)   \right\}
\]となる。

また、広義固有ベクトルは \( \vec{p_1} \), \( \vec{p_2} \), \( \vec{p_3} \) となり、広義固有空間は\[
V(2) = \left\{ \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \end{array} \right), \left( \begin{array}{ccc} 1 \\ -1 \\ 2  \end{array} \right), \left( \begin{array}{ccc} 1 \\ 0 \\ 0  \end{array} \right)   \right\}
\]となる。

(4) ジョルダン標準形を求める

よって、\[
\left\{ \begin{array}{l} (A - 2E) \vec{p_1} = \vec{0} \\ A \vec{p_1} = 2 \vec{p_1} \end{array} \right.  \ \ \
\left\{ \begin{array}{l} (A - 2E) \vec{p_2} = \vec{0} \\ A \vec{p_2} =  2 \vec{p_2} \end{array} \right.  \ \ \
\left\{ \begin{array}{l} (A - 2E) \vec{p_3} = \vec{p_2} \\ A \vec{p_3} = \vec{p_2} + 2 \vec{p_3} \end{array} \right.
\]が成立する。

ここで\[ P = \left( \vec{p_1}, \vec{p_2}, \vec{p_3} \right) = \left( \begin{array}{ccc} 1 & 1 & 1 \\ 0 & -1 & 0 \\ -1 & 2 & 0 \end{array} \right)\]とすると、\[ \begin{align*}
AP & = A \left( \vec{p_1}, \vec{p_2}, \vec{p_3} \right) \\ & = \left( 2 \vec{p_1},  2 \vec{p_2}, \vec{p_2} + 2 \vec{p_3} \right)  \\ & =  \left( \vec{p_1}, \vec{p_2}, \vec{p_3} \right) \left( \begin{array}{ccc} 2 & 0 & 0 \\ 0 & 2 & 1 \\ 0 & 0 & 2 \end{array} \right) \\ & = P \left( \begin{array}{ccc} 2 & 0 & 0 \\ 0 & 2 & 1 \\ 0 & 0 & 2 \end{array} \right)
\end{align*} \]となります。

よって、\[
P = \left( \begin{array}{ccc} 1 & 1 & 1 \\ 0 & -1 & 0 \\ -1 & 2 & 0 \end{array} \right) \ \ \
J = P^{-1} AP =  \left( \begin{array}{ccc} 2 & 0 & 0 \\ 0 & 2 & 1 \\ 0 & 0 & 2 \end{array} \right)
\]とジョルダン標準形にできる。

[検算] \[
AP = PJ = \left( \begin{array}{ccc} 2 & 2 & 3 \\ 0 & -2 & -1 \\ -2 & 4 & 2 \end{array} \right)
\]

８．さいごに

今回は、ジョルダン標準形についての簡単な説明と、3次までのジョルダン標準形の求め方を例題などを用いてまとめました。

ジョルダン標準形を求める際には、固有ベクトルを求めていき、足りなくなったら1つ前の固有ベクトル（もしくは広義固有ベクトル）を借りて\[
(A - tE) \vec{p_i} = \vec{p_{i-1}}
\]のようにドミノ倒しのように求めていくものだというのを覚えておきましょう。

また、ドミノ倒し的にもとめていくため、1つ前の固有ベクトル（もしくは広義固有ベクトル）が間違っていくと連鎖的に間違ってしまうため、慎重に計算していきましょう。

次回はジョルダン標準形の応用として行列の \( n \) 乗の求め方について簡単にですがまとめていきたいと思います。