スポンサードリンク
※修正(2020/01/12)
\( v_6 \) の距離が10ではなく13になっていたのを修正しています。
こんにちは、ももやまです。
乗り換え案内アプリやカーナビってすぐに最短経路を計算してくれてすごい便利ですよね。路線が複雑な東京都内であってもあっという間に最短経路を計算してくれますよね。
↓こんな感じに一瞬で経路を計算してくれます!
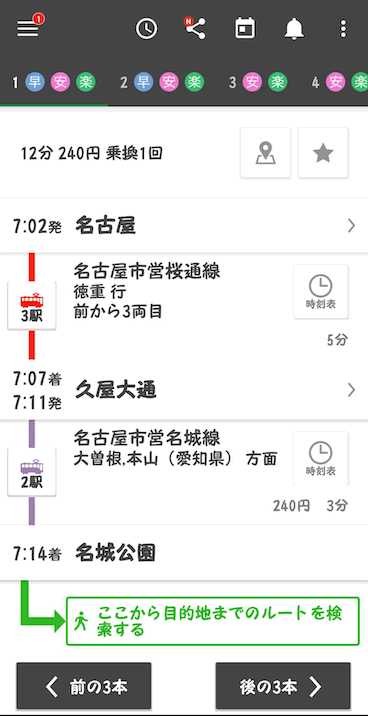
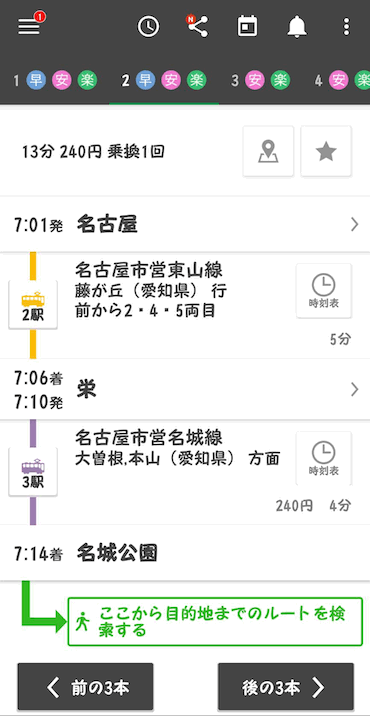
「この最短経路っていったいどうやって求まっているんだろう??」と気になった人はいませんか? 気になりますよね。
今回はある地点からある地点までの最短ルート(時間・距離など)を求める方法の1つとしてダイクストラ法を説明していきたいと思います。
(ダイクストラ法以外に有名な最短経路を求めるアルゴリズムとしてはA*アルゴリズムもありますがこちらはまた別の機会に紹介したいと思います。)
前回の記事(第13羽・最小全域木の求め方)はこちら!
目次
スポンサードリンク
1.経路とは
グラフに重み(コスト)という概念を追加した重み付きグラフを考えます。
今回は辺の重みを距離や時間と考えます。
ある点からある点までにたどった辺の重み(距離)の合計が合計距離(合計時間)となります。
例えば、赤色のルートの場合、\[
3 + 7 + 4 + 5 + 4 = 23
\]となるので合計の距離は23となり、青色のルートの場合、\[
5 + 4 + 6 + 3 = 18
\]となり、合計の距離は18となります。
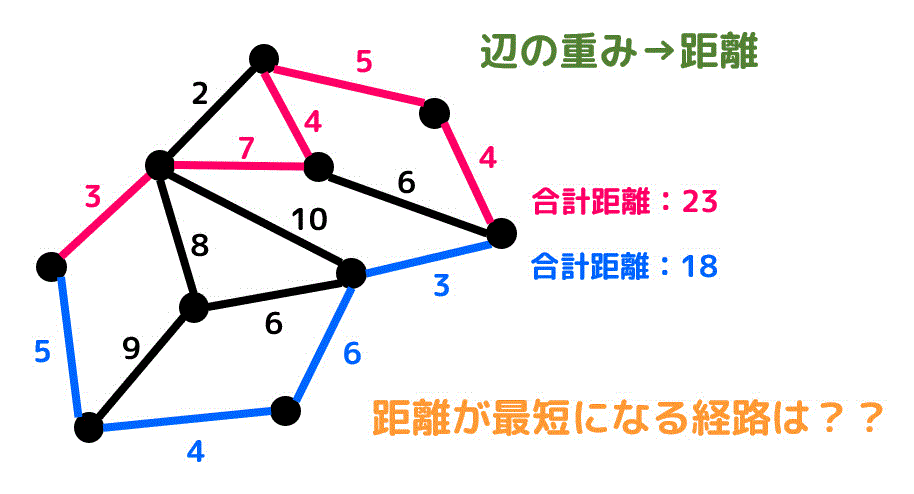
このようにある点からある点までの辺のたどり方が変わると当然合計距離も変化しますよね。
しかし、すべてのパターンの合計距離を求め、最短距離を求めていくゴリ押し戦法だと計算に時間がかかってしまいます。たった点が10個であったとしても \( 10! \) 通り(約300万通り)もあります。点が20, 30と増えたらコンピュータ上でも何年も計算がかかってしまいます*1。
そこで使われる方法がダイクストラ法です。ダイクストラ法を使うことで 100, 200 と点が増えたとしてもあっという間に最短経路を求めることができるのです。
スポンサードリンク
2.ダイクストラ法
(1) ダイクストラ法の仕組み・アルゴリズム
例えば、「東京から名古屋経由で大阪に行く」最短ルートがあるとします。
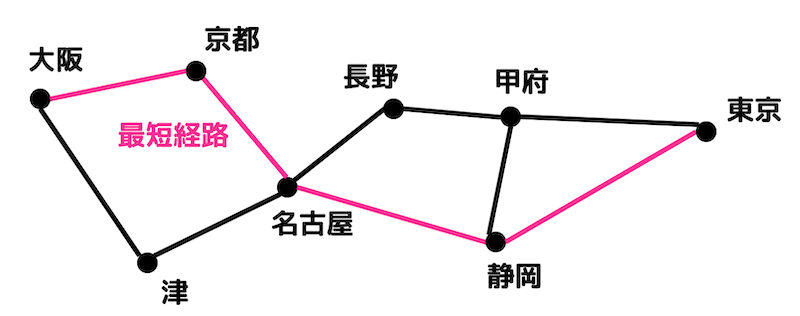
このとき、「東京から名古屋」のように最短ルートの一部分を切り取ったルートも最短ルートになりますよね。
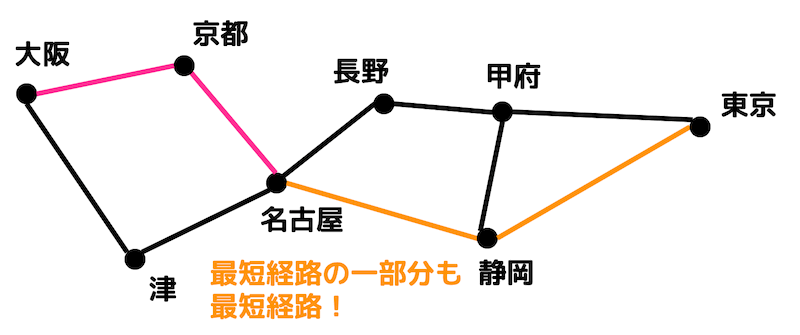
(もし「東京→名古屋→大阪」が最短ルートなのに「東京→名古屋」が最短ルートでなかったら、「東京→名古屋→大阪」の「東京→名古屋」の部分を「東京→甲府→静岡→名古屋」のような別の最短ルートに付け替えて「東京→甲府→静岡→名古屋→大阪」とすることでさらに短いルートが出来てしまうのでおかしくなりますね。)
ダイクストラ法の大まかな方針としては、「まずスタートに近い点から最短経路を決定し、徐々にゴールに近い点の最短経路を求めていく」アルゴリズムです。
(このようにそのまま解くと難しい問題*2を手短に解ける簡単な問題に分割し、分割した簡単な問題の答えを使うことで徐々に複雑な問題を解いていく方法のことを動的計画法(Dynamic Programming・DP)と呼びます。)
ダイクストラ法のアルゴリズムは、下のようになっています。
文章だけでは理解するのが少し大変だと思うので、実際に下のほうにある例を見ることをおすすめします。
それぞれの点から点までの距離が確定したものを確定距離、確定はしてないものの距離を計算している点を暫定距離とする。
- スタート点からスタート点までの確定距離を0とする。
- 距離が確定した点と隣り合っている点までの暫定距離とたどる元の点を求める。
(暫定距離 = 確定距離 + 隣り合っている点までの移動距離)
ただし、隣り合っている点の暫定距離がすでに求まっている場合、より短い暫定距離が出た場合のみ上書きする。また、隣り合っている点の確定距離がすでに求まっている場合は無視する(すでに確定してるので更新されない)。 - 暫定距離が出ている点の中で、一番暫定距離が小さいものを確定距離とする。
- すべての距離が確定するまで2, 3を繰り返す。距離が確定した際の経路は、ゴールから元の点をたどっていることで求めることができる。
ダイクストラ法のアルゴリズム
「確定距離が出た点と隣接している点の暫定距離を出す → 暫定距離が最小のものを確定させる」をゴール点の距離が確定するまで繰り返すと頭に入れておけばOKです。
ここで、3の「暫定距離が出ている点の中で、一番暫定距離が小さいものを確定距離とできる」理屈を簡単にですが説明したいと思います。
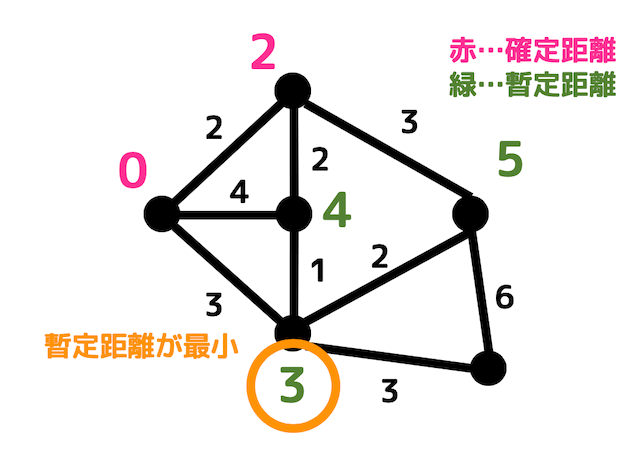
例えば、上のようなグラフの場合、暫定距離が3, 4, 5の3つの点がありますね。ここで一番暫定距離が短いノードは距離が3のノードですね。
このとき、距離(重み)が負の辺が存在しなければ距離3未満の経路は絶対に見つかりませんよね*3。
(ある点 \( x \) からどこか \( y \) へたどる場合、必ず行き先の点 \( y \) は元の点 \( x \) 以上の距離になりますよね。)
なので暫定距離が一番小さいノードを確定ノードにすることができるのです!
計算時間も \( n \) 個の点それぞれに対し、最大 \( n-1 \) 個暫定経路を出していくだけなのでオーダーでいうと \( O(n^2) \) 以下に抑えることができます!
( \( n! \) と \( n^2 \) は大きな違いですよね。)
(2) ダイクストラ法の実例
では、実際に下のグラフの \( s \) から \( t \) までの最短経路を求めてみましょう。
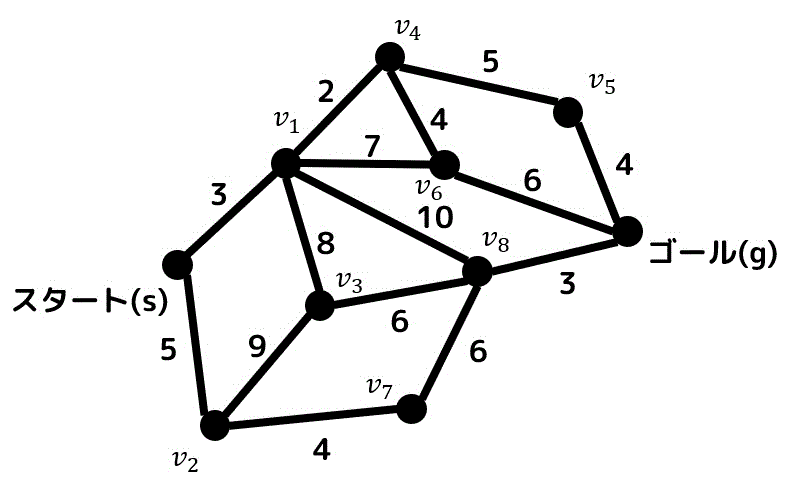
まず、スタートからスタートまでの距離は、移動しなくてもいいのでなにがあっても0ですよね。なので距離0で確定ですね。
さらにスタート点から隣り合っている点までの暫定の距離を出していきます。
(距離を出す際にたどる元の点もメモしておきましょう。最後に経路を求めるときに使います。)
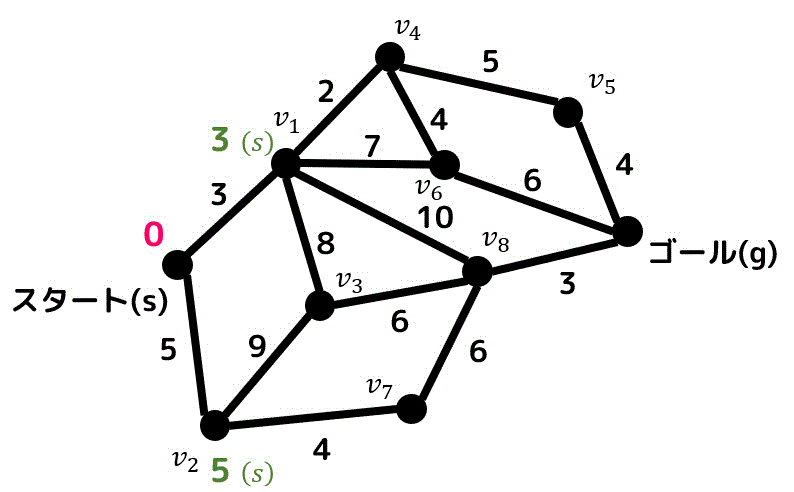
これでスタートから \( v_1 \) までの暫定距離が3、\( v_2 \) までの暫定距離が5であることがわかりましたね。
暫定距離が出ている2つの点のうち、より近いのは \( v_1 \) の3ですよね。なのでどう頑張っても距離が3未満の経路はもうみつかりません。よって \( v_1 \) までの距離が3であることが確定します。
つぎに距離が確定した \( v_1 \) からたどれる点の暫定距離を求めていきます。
暫定距離は、「(たどる元の距離)+(辺に示された距離)」で求めることができます。
暫定距離を更新したので再び暫定距離が一番短い点を探しましょう。
(修正:\( v_6 \) の距離が10ではなくなぜか13と間違えていたので修正しています。)
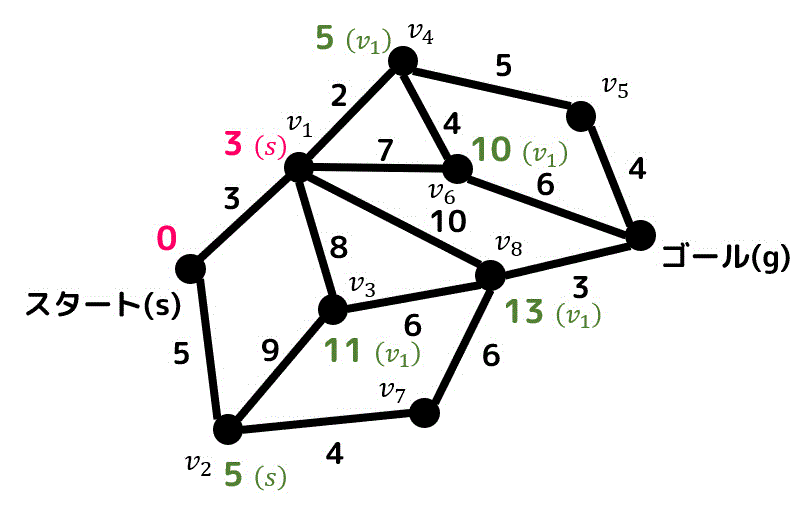
今回の場合、暫定距離が短い点が2点ありますね。このように同じ距離の点が2つ以上ある場合、どちらを先に確定距離にしてもOKです。
今回は番号が若い \( v_2 \) を先に確定させましょう。
さらに \( v_2 \) と隣り合っている点の暫定距離を更新していきましょう。
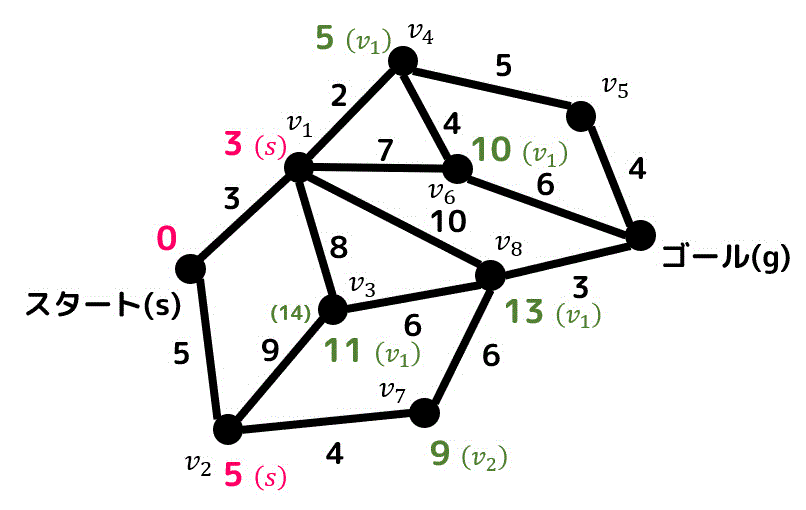
暫定距離を更新したのでまた暫定距離が最小の点を探します。
すると \( v_4 \) の距離が一番短いため、距離が確定します。
さらに \( v_4 \) と隣り合っている点を探索すると、\( v_6 \) の距離が9に更新されます。(更新された距離は水色で示しています)
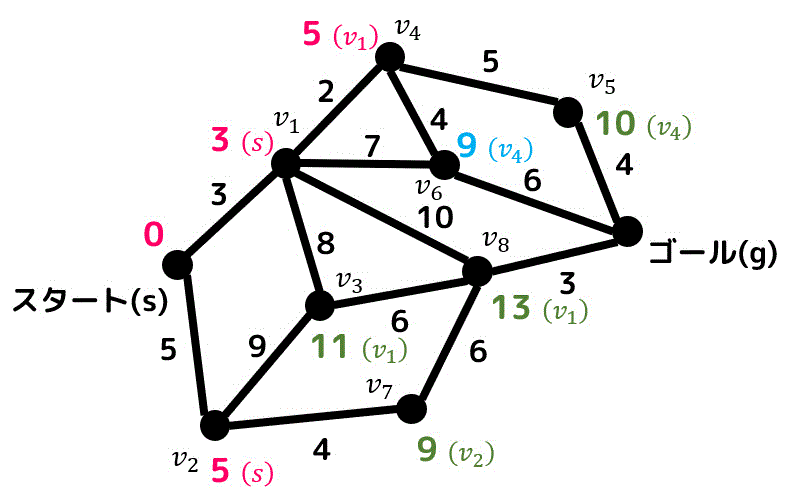
暫定距離が一番小さいのは9の点ですが、9の点が2つあります。
なので番号が若い \( v_6 \) から先に確定させましょう。
いつものように \( v_6 \) と隣り合っている点の距離を更新します。
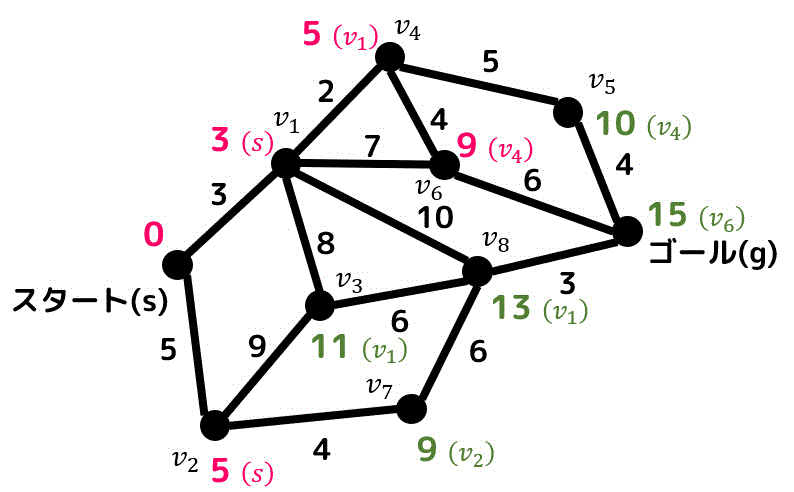
もう1つの暫定距離9の点 \( v_7 \) も確定させ、隣り合っている点の距離を求めていきましょう。
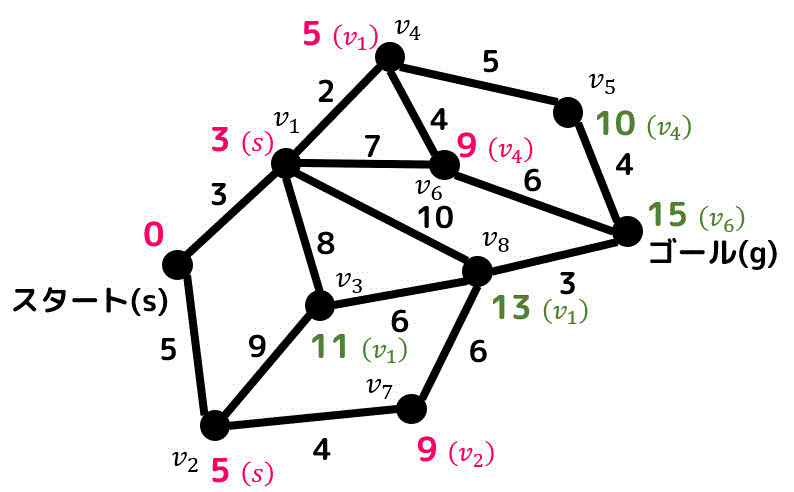
暫定距離が出ている4つの点の中で一番距離が短い点は距離10の点 \( v_5 \) ですね。
なので \( v_5 \) が確定し、\( v_5 \) と隣り合っている点の距離を更新します。
すると、点 \( g \) の距離が14に更新されます。
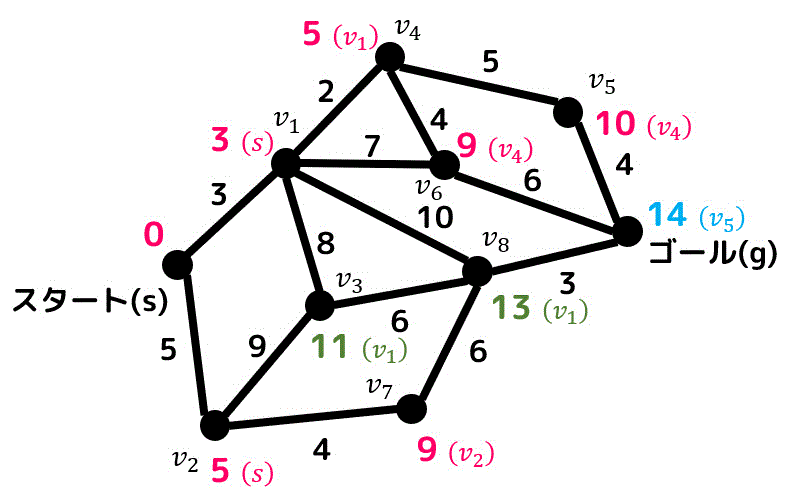
まだ確定していない点は3つですね。3点の中で一番距離が短い距離11の点 \( v_3 \) を確定させます。
\( v_3 \) の隣り合っている点の距離を更新させるのですが、\( v_8 \) の距離が17と最短距離以上となってしまうので更新しません。
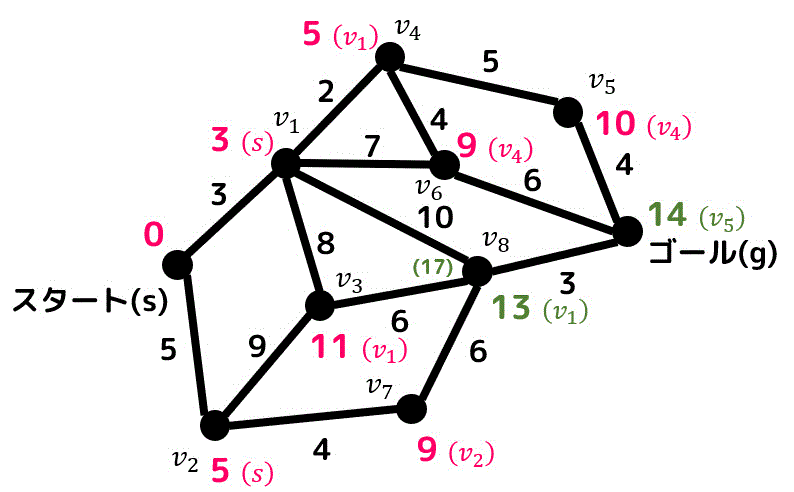
つぎに \( v_1 \) を確定させます。(2点のうちより暫定距離が短いので)
隣り合ってる点 \( g \) の距離が16と求まりますが、最小距離以上なので無視します。
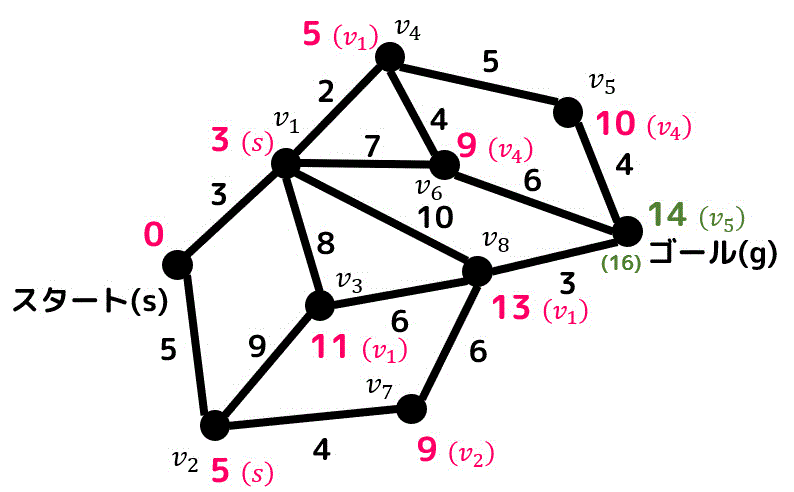
最後にゴール点の距離を更新すれば最短距離が導出完了です。
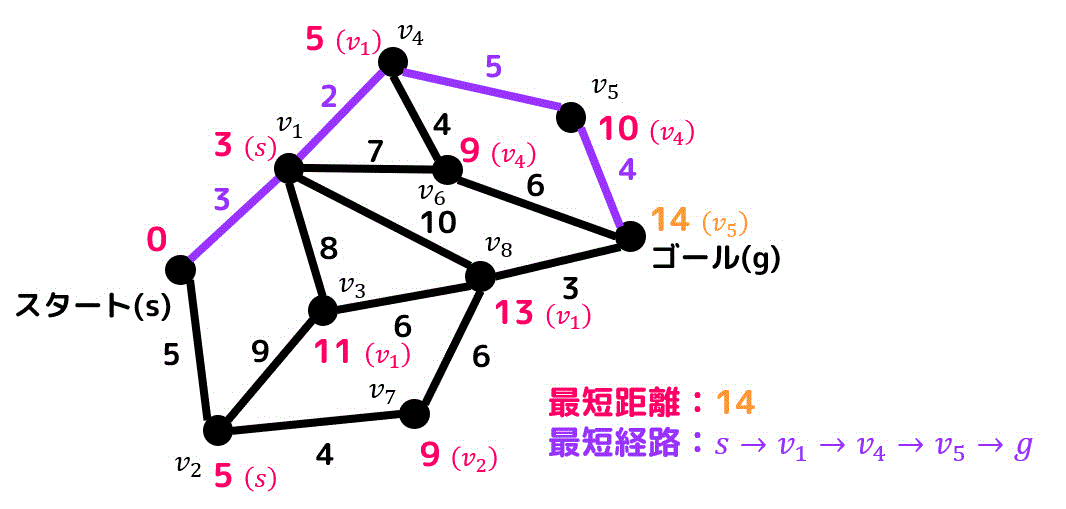
最短経路は、ゴールからたどったもとの点を確認していくと求めることができます。ゴールからたどっていくと、\[
g \to v_5 \to v_4 \to v_1 \to s
\]と求められるので、スタートからゴールまでの経路は\[
s \to v_1 \to v_4 \to v_5 \to g
\]と求めることができます。
スポンサードリンク
3.動画でわかるダイクストラ法
ダイクストラ法を求める方法を動画でわかりやすく説明したものがYouTubeにあったのでこちらも紹介しておきたいと思います。
4.練習問題
では2問ほど練習しましょう。
練習1
つぎのグラフの \( s \) から \( g \) の最短距離、およびそのときの経路を求めなさい。
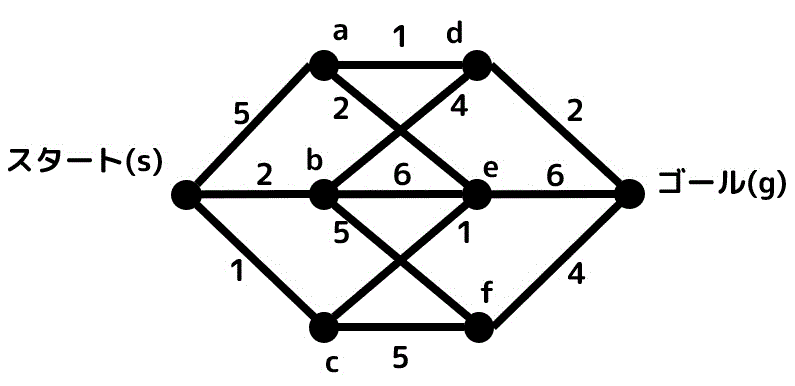
練習2
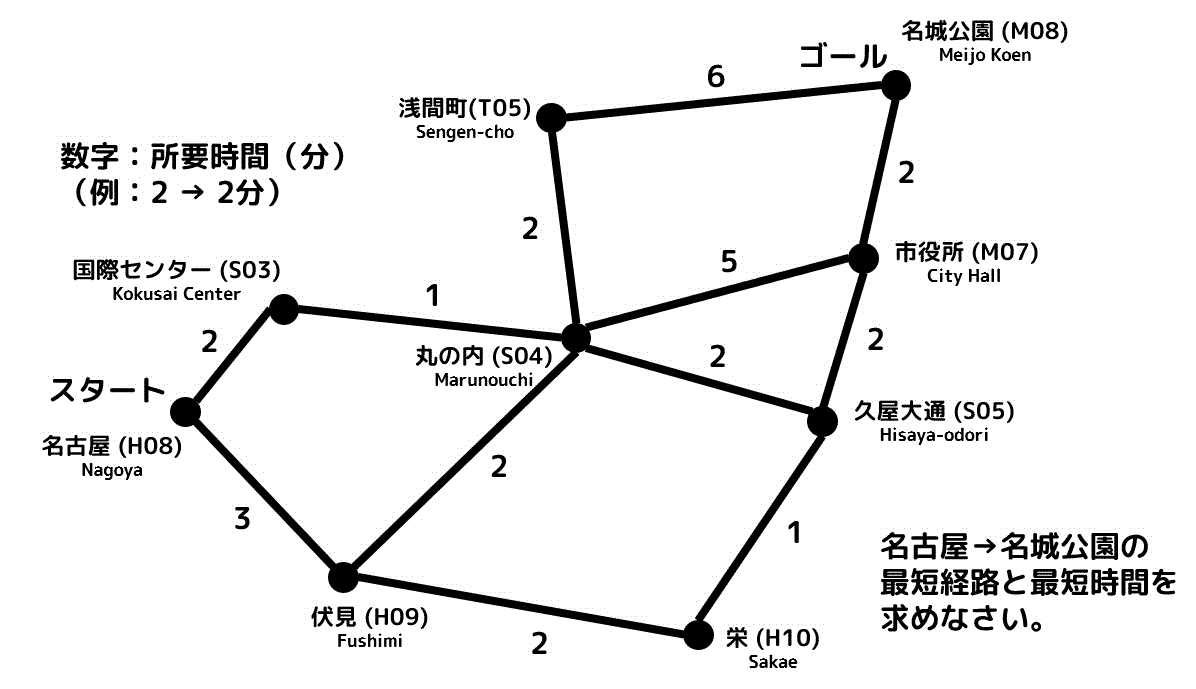
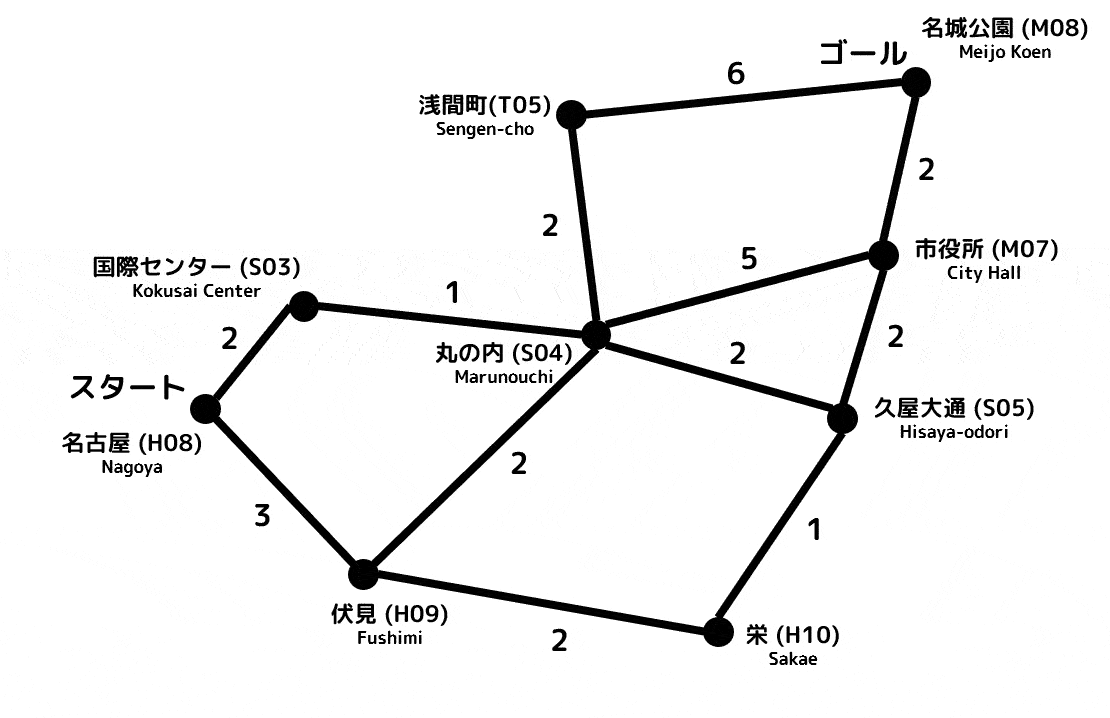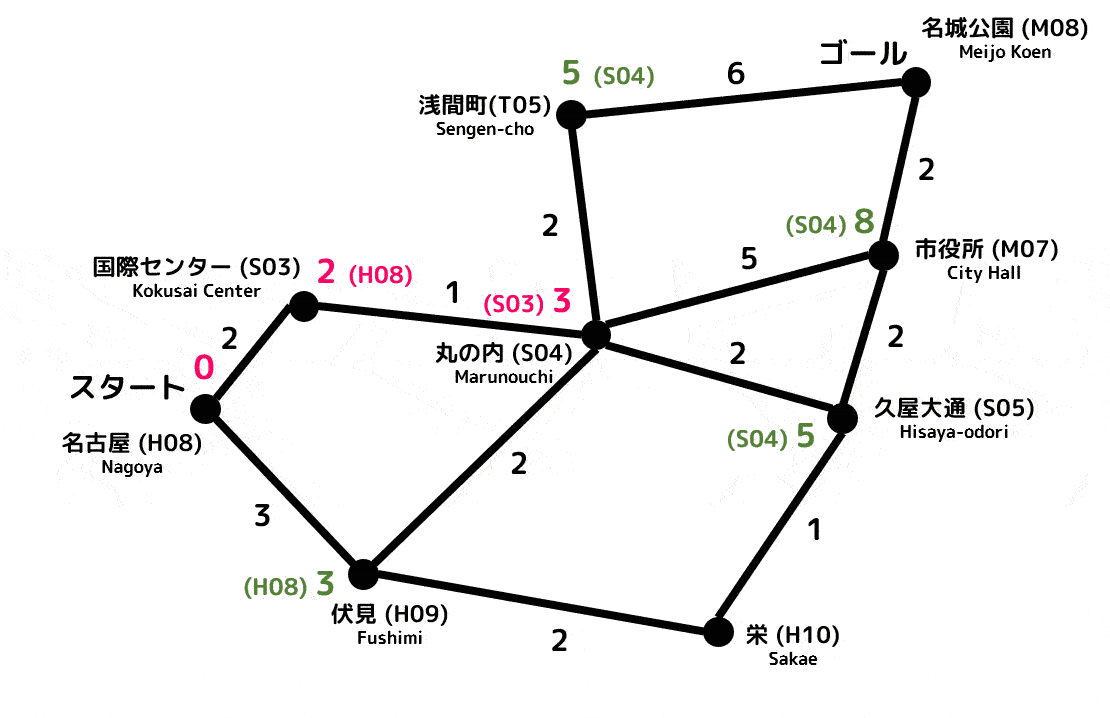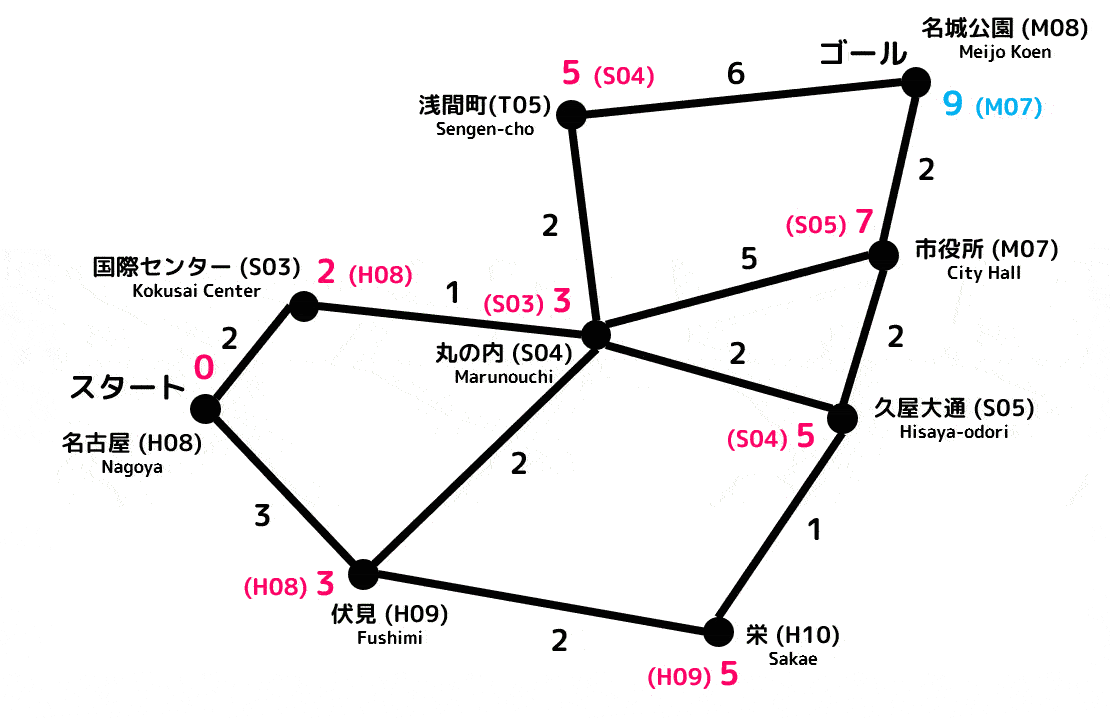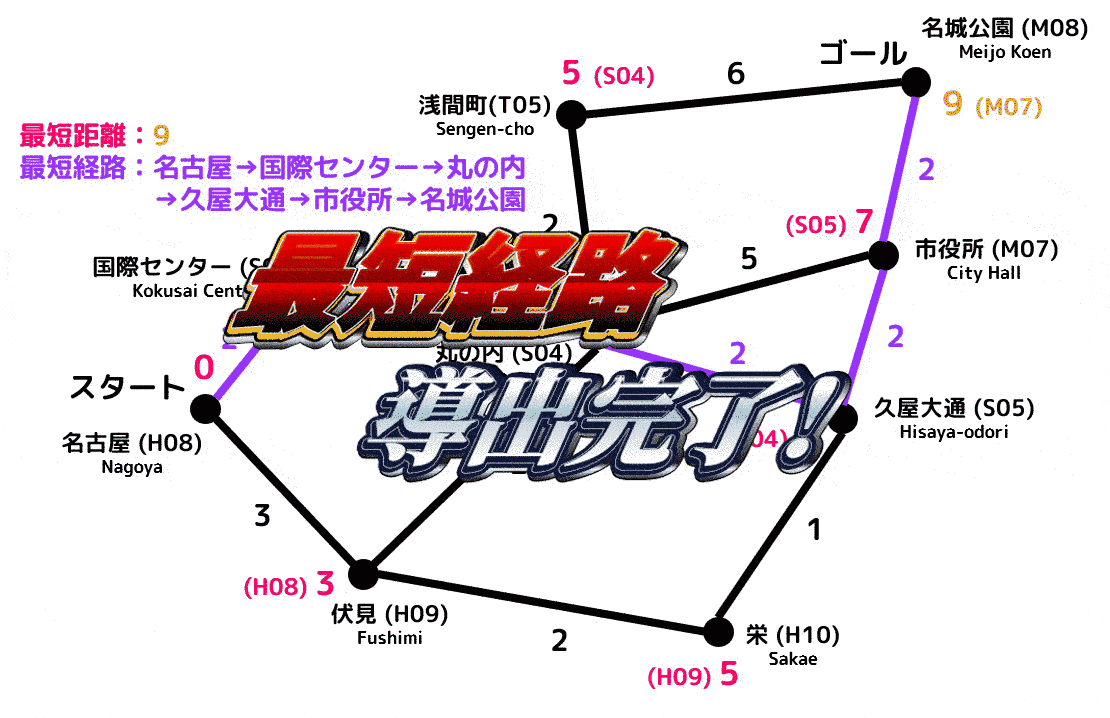
つぎの路線図は、駅間を移動するためにかかる時間を表している。例えば、名古屋と伏見の間の辺には3と表記されているため、3分かかることをしめしている。
このとき、名古屋(H08)から名城公園(M08)までは最短何分で移動することができますか。また、最短時間で移動できる経路を答えなさい。
(移動以外の時間(例:乗り換え)は考慮しないものとする。)
5.練習問題の答え
解答1
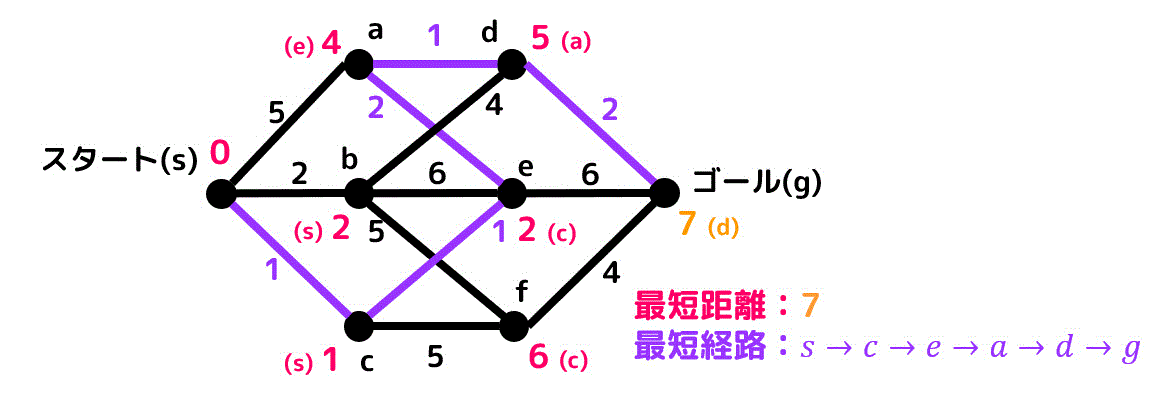
最短距離:7
最短経路:s → c → e → a → d → g
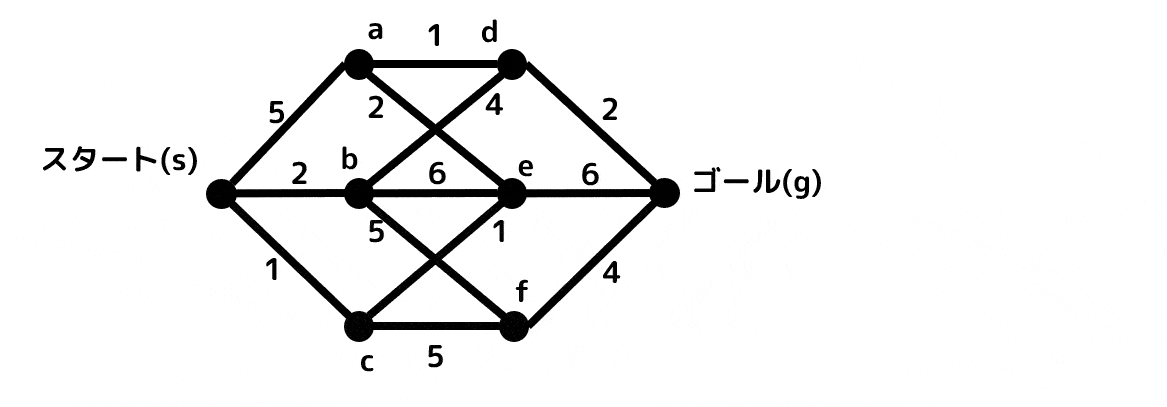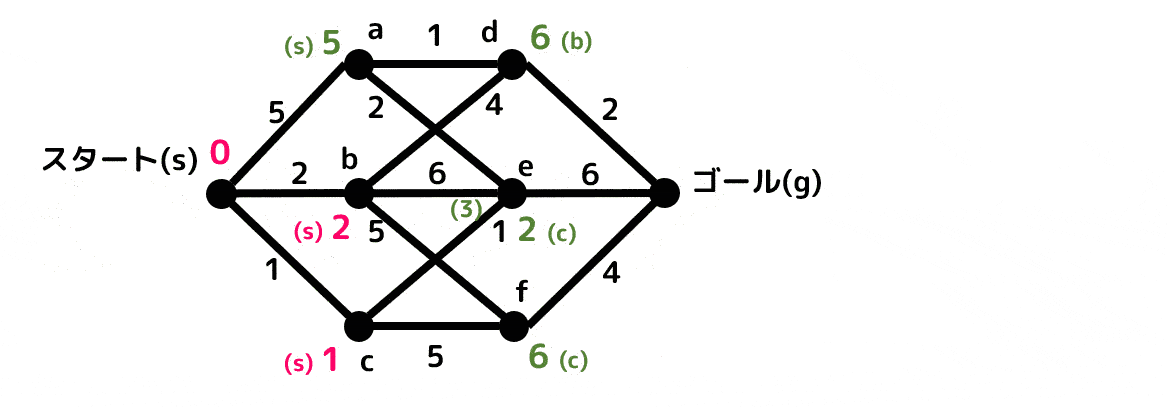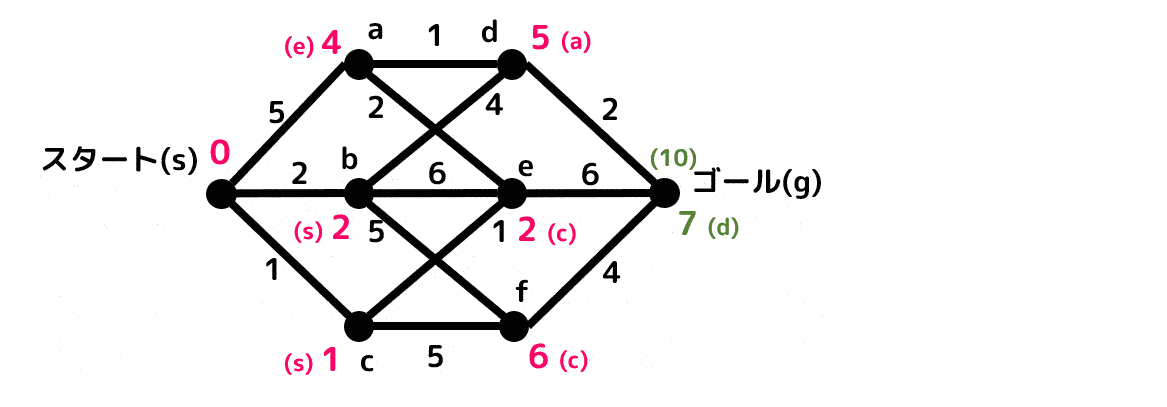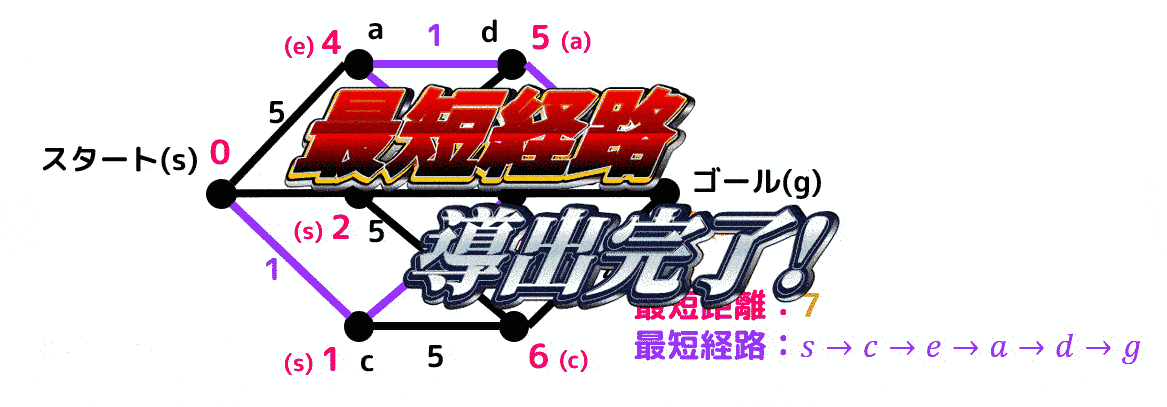
ダイクストラ法を適用していく過程(アニメーション)
(赤色が確定距離、緑色が暫定距離、水色が更新された暫定距離を表します)
解答2
最短距離:9
最短経路:名古屋(H08)→国際センター(S03)→丸の内(S04)→久屋大通(S05)→市役所(M07)→名城公園(M08)
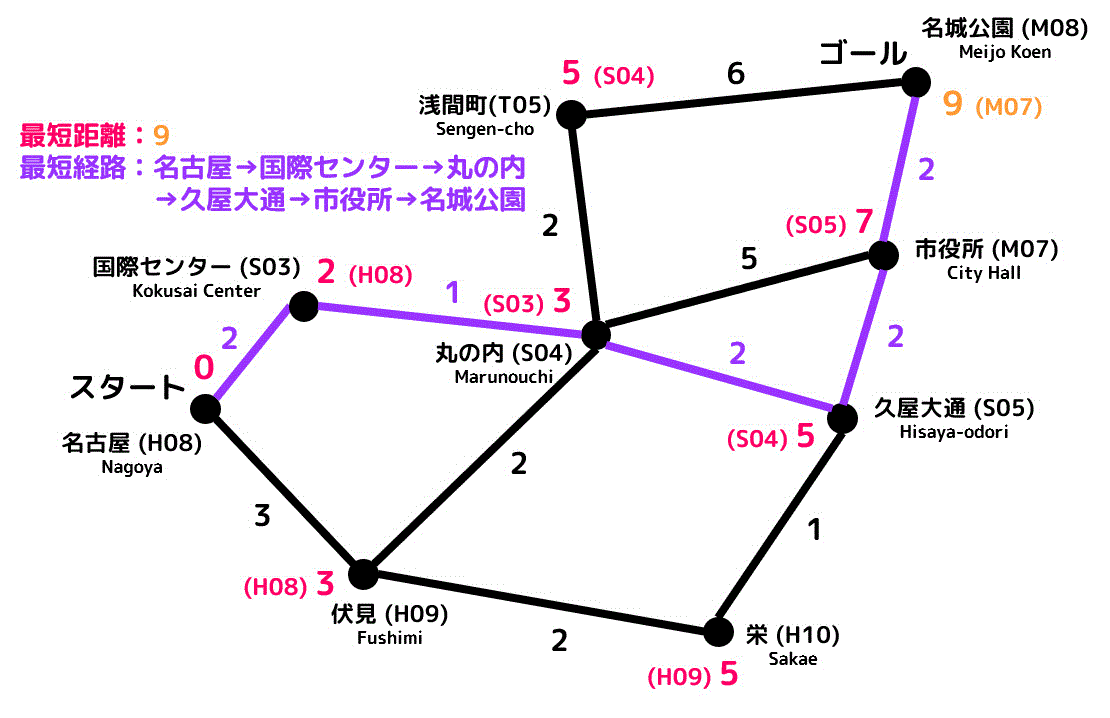
ダイクストラ法を適用していく過程(アニメーション)
(赤色が確定距離、緑色が暫定距離、水色が更新された暫定距離を表します)
6.さいごに
今回は最短経路を求める方法の1つであるダイクストラ法についてまとめました。
そのまま解くと膨大な計算時間がかかるような問題でも、ダイクストラ法のように分割して求めるとかなり簡単に求めることができることがわかりましたね。
次回は「ある地点からある地点に一度に送ることのできる量の上限が決まっているとき、全体で一度に送れる量の最大値を求めるような問題」(最小フロー)についてまとめていきたいと思います。
関連広告・スポンサードリンク