【CG・CV入門】拡散反射と鏡面反射の特徴

こんにちは。ももやまです。

今回は、コンピュータビジョン(CG)、コンピュータビジョン(CV)の基礎の1つである反射についてお勉強しましょう。

さらに、反射の知識と、PythonとMATLABを使ってCG上で球を作成する手順についても紹介します。

１．反射とは

皆さんの周りにはたくさんの物体がありますね。身の回りにあるものだけでも、財布・椅子・机… と色々なものがありますね。

しかし、多くの身の回りのものは自分から光を発していません。それなのに、なぜ我々は自分自身の目で見ることができるのでしょうか。

それは、明かり（専門用語で光源*1といいます）が反射しているからなのです！

ということで、CG上の球に光を当ててみる前に2つの反射についてお勉強しましょう！

２．拡散反射（反射その1）

(1) 拡散反射とは

拡散反射とは、光源から発せられた光が物体の表面で散乱をくりかえすことにより発生する反射です。鈍い反射、乱反射とも呼ばれます。

拡散反射が起こりやすい物体としては、物体の表面に光沢がほとんどない石膏などがあげられます。

CG（コンピュータグラフィックス）やCV（コンピュータビジョン）の世界では、拡散反射の理想的なモデルの1つで、最も単純なランバートモデルを取り扱うことが多いです*2。

(2) 拡散反射と輝度

拡散反射における明るさ（専門用語で輝度）の特徴には、以下の2つがあげられます。

• 法線*3と光源方向のなす角が小さいほど明るい
• どの方向から見ても同じ明るさに見える
  (視点方向に依存しない)

(3) 拡散反射での輝度

拡散反射における輝度は、先ほど説明した理想的なモデルの1つであるランバートモデルで考えられることが多いです。

ランバートモデル（理想的な拡散反射を行う物体）の場合の輝度値（明るさの度合い）\( L_{d} \) は、光源の明るさ \( I \), 拡散反射率*4 \( K_{d} \), 物体表面の法線と光源方向のなす角度 \( \theta \) を用いて、以下の式(1)で表されます。\[ L_{d} = I \ K_{d} \cos \theta \tag{1} \]

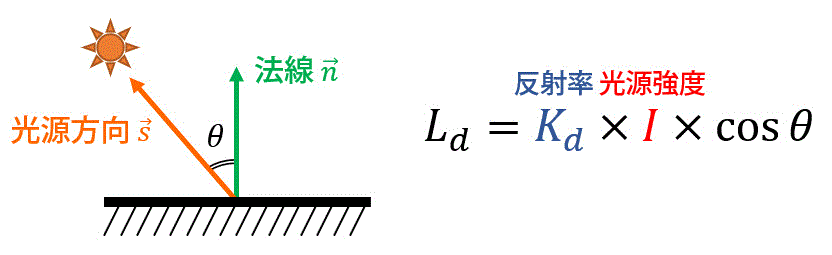
（※ ただし、角度 \( \theta \) は \( 0^{\circ} \leqq \theta \leqq 90^{\circ} \) です。\( \theta \geqq 90^{\circ} \) のとき、つまり \( \cos \theta \leqq 0 \) になるときは、下の図のように光が全く当たらないので輝度値 \( L_{d} \) は0となります。）

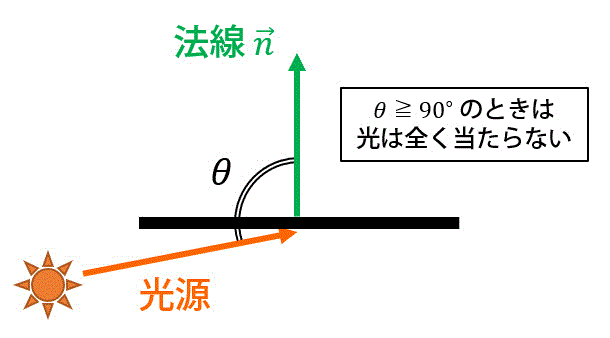
さらに物体表面の法線を \( \vec{n} \), 光源方向を \( \vec{s} \) とし、どちらのベクトルの大きさも1とすると、式(2)の変形が成立します。\[\begin{align} \vec{s} \cdot \vec{n} & = | \vec{s} | | \vec{n} | \cos \theta
\\ & = 1 \cdot 1 \cos \theta
\\ & = \cos \theta \tag{2} \end{align}\]

そのため、式(1)を以下の式(3)に書き換えることができます。

\[\begin{align} L_{d} & = I \ K_{d} \cos \theta \\ & = I \ K_{d} ( \vec{s} \cdot \vec{n} ) \tag{3} \end{align}\]

３．鏡面反射（反射その2）

(1) 鏡面反射とは

スマホのライトを鏡に当ててみてください。すごい反射して眩しいですよね。このように、鏡のように境界面における反射のことを鏡面反射と呼びます。鋭い反射、正反射とも呼ばれます。

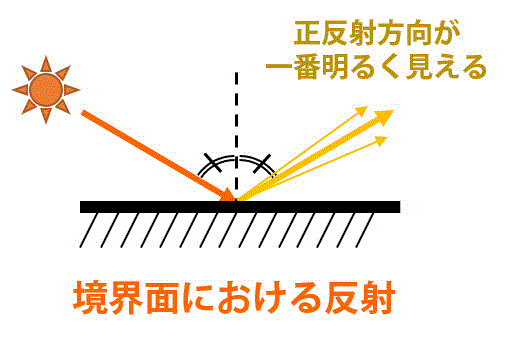
鏡面反射が起こりやすい物体としては、鏡のほかに光沢のある物体（例：陶磁器）などがあげられます。

CG（コンピュータグラフィックス）やCV（コンピュータビジョン）の世界では、拡散反射の理想的なモデルの1つで、最も単純なランバートモデルを取り扱うことが多いです*5。

(2) 鏡面反射と輝度

鏡面反射における明るさ（専門用語で輝度）の特徴には、以下の2つがあげられます。

• 視点によって明るさが変わる
• 光が正反射する方向から見たときが一番明るい

(3) 鏡面反射における輝度

鏡面反射における輝度は、先ほど説明した理想的なモデルの1つであるフォンモデルで考えられることが多いです。

フォンモデル（理想的な鏡面反射を行う物体）の場合の輝度値（明るさの度合い）\( L_{s} \) は、光源の明るさ \( I \), 鏡面反射率*6 \( K_{s} \), 視線方向と光源方向のなす角度 \( \alpha \)、表面のあらさを表す係数 \( n \) を用いて、以下の式(1)で表されます。\[ L_{s} = I \ K_{s} ( \cos \alpha )^{n} \tag{4} \]

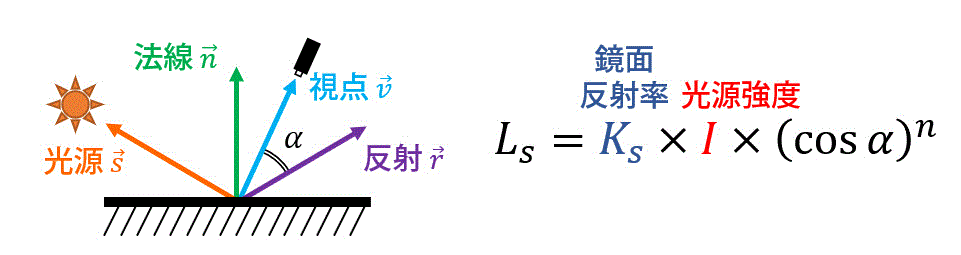
（※ ただし、角度 \( \alpha \) は \( 0^{\circ} \leqq \alpha \leqq 90^{\circ} \) です。\( \alpha \geqq 90^{\circ} \) のとき、つまり \( \cos \alpha \leqq 0 \) になるときは輝度値 \( L_{s} \) は0となります。意外とプログラミングするときの落とし穴になるので気をつけましょう*7。）

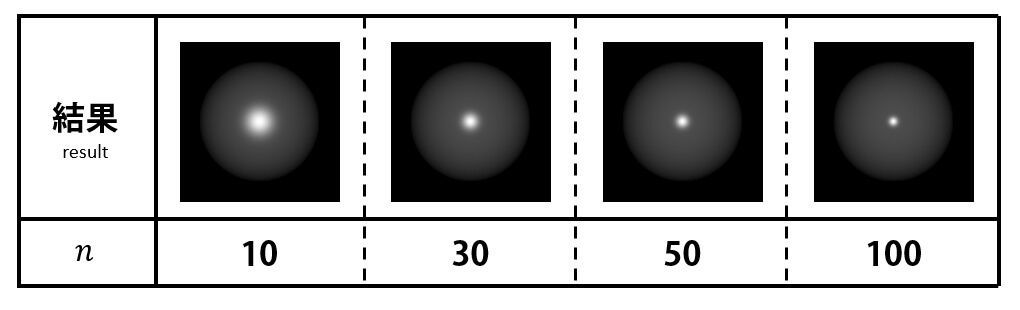
表面のあらさを表す係数 ( n ) には、以下の関係があります。

• 大きい → 鏡に近い鋭い反射（理想的な鏡面反射）
• 小さい → 鈍い反射（拡散反射に近い）

フォンモデルの場合の輝度値 \( L_{s} \) は、拡散反射と同じく物体表面の法線を \( \vec{n} \), 光源方向を \( \vec{s} \) から求めることができますが、一工夫必要です。

正反射ベクトルの求め方

まずは正反射方向を表すベクトル \( \vec{r} \) を求めてみましょう。

ベクトル \( \vec{a} \) を\[ \vec{a} = \frac{1}{2} ( \vec{s} + \vec{r} ) \tag{5} \]とします。すると、ベクトル \( \vec{a} \) は \( \vec{s} \cos \theta \) と等しくなりますね。

さらに、式(2)より \( \theta = \vec{s} \cdot \vec{n} \) となるので、\[\begin{align} \vec{a} & = \vec{s} \cos \theta \\ & = \vec{s} ( \vec{s} \cdot \vec{n} ) \tag{6} \end{align} \]の関係式が成り立ちます。

あとは、式(5)を使うことで、\[\begin{align} \frac{1}{2} ( \vec{s} + \vec{r} ) &= \vec{s} ( \vec{s} \cdot \vec{n} ) \\ \vec{s} + \vec{r} & = 2 ( \vec{s} \cdot \vec{n} ) \vec{s} \\ \vec{r} & = 2 ( \vec{s} \cdot \vec{n} ) \vec{s} - \vec{s} \tag{7} \end{align} \]と反射ベクトルを求めることができます。

最後に、式(7)で計算される反射ベクトル \( \vec{r} \) を使うことで、フォンモデルの輝度値 \( L_{s} \) を\[\begin{align} L_{s} & = I \ K_{s} ( \cos \alpha )^{n} \\ & = I \ K_{s} ( \vec{v} \cdot \vec{r} )^{n} \tag{8} \end{align}\]と求めることができます。

４．球の作成プログラム紹介

拡散反射、鏡面反射の説明が終わったので、実際に球を作るプログラムを見てみましょう。

ある画素の画素値は、拡散反射と鏡面反射の和、つまり式(9)のように考えることができます*8。

\[ L = L_{d} + L_{s} \tag{9} \]

そのため、

• ランバートモデルと仮定したときの輝度値（拡散反射）
• フォンモデルと仮定したときの輝度値（鏡面反射）

の2つを足し合わせることでCG上で球を作成することができます。

下にPythonとMATLAB上でのプログラムをおくので、設定部分を色々変えて遊んでみてはいかがでしょうか。

Python

import math
import numpy as np
import cv2

# 設定ここから

## 画像設定
N_ROW = 128 # 画像の行 (縦方向) の数
N_COL = 128 # 画像の列 (横方向) の数
view  = [0.1,0.3,0.4] # 視点方向

## 球の設定
radius = 48  # 球の半径
kyu_x  = 64  # 中心のx座標
kyu_y  = 64  # 中心のy座標
K_d    = 0.5 # 球の拡散反射率
K_s    = 0.5 # 球の鏡面反射率 (0→ランバート拡散反射を仮定)
n      = 30  # 鏡面反射パラメタ

## 光源の情報
light = [0,0,1] # 光源方向 (自動的に1に正規化)
I     = 1;       # 光源強度

## 出力先
OUTPUT_DIR = "img_output.png"; # 球を出力する場所

# 設定ここまで


## 各種初期化
light = light / np.linalg.norm(light)
view  = view / np.linalg.norm(view)
sn = np.zeros([N_ROW, N_COL, 3])


## 球の作成
for i in range(0,N_ROW):
    for j in range(0,N_COL):
        if (i - kyu_x) ** 2 + (j - kyu_y) ** 2 <= radius ** 2:
            k = math.sqrt(radius ** 2 - (i - kyu_x) ** 2 - (j - kyu_y) ** 2)
            sn_tmp =  [i - kyu_x, j - kyu_y , k]
            sn_tmp = sn_tmp / np.linalg.norm(sn_tmp)
            sn[i,j,:] = sn_tmp


## 正しく法線が求まっているかの確認用 (普段はコメントアウト)
# check_sn = (sn + 1) * 255 / 2
# check_sn_bgr = check_sn[:, :, [2, 1, 0]] # CV2はBGRの順に認識されるため  


## 拡散反射の考慮
img_diffuse = np.zeros([N_ROW, N_COL])

for i in range(0,N_ROW):
    for j in range(0,N_COL):
        sn_tmp =  sn[i,j,:]
        if np.linalg.norm(sn_tmp) > 0:
            cos_theta = np.dot(light,sn_tmp)
            if cos_theta > 0:
                img_diffuse[i,j] = K_d * I * cos_theta * 255


## 鏡面反射の考慮
img_specular = np.zeros([N_ROW, N_COL])

for i in range(0,N_ROW):
    for j in range(0,N_COL):
        sn_tmp =  sn[i,j,:]
        if np.linalg.norm(sn_tmp) > 0:
            r = 2 * np.dot(sn_tmp,light) * sn_tmp - light
            cos_alpha = np.dot(view,r)
            if cos_alpha > 0:
                img_specular[i,j] = K_s * I * (cos_alpha ** n) * 255


## 出力
img_output = img_diffuse + img_specular
cv2.imwrite(OUTPUT_DIR, img_output)

MATLAB

% 設定ここから

%% 画像の設定
N_ROW = 128; % 画像の行（縦方向）の数
N_COL = 128; % 画像の列（横方向）の数 
view = [0.1 0.3 0.4]'; % 視点 (鏡面反射に影響)

%% 球の設定
radius = 48;   % 球の半径
kyu_x  = 64;   % 中心のx座標
kyu_y  = 64;   % 中心のy座標
K_d    = 0.5;  % 球の拡散反射率
K_s    = 0.5;  % 球の鏡面反射率 (0→ランバート拡散反射を仮定)
n      = 30;   % 鏡面反射パラメタ

%% 光源の情報
light = [0 0 1]'; % 光源方向 (自動的に1に正規化)
I     = 1;        % 光源強度

%% 出力情報
OUTPUT_DIR = "img_output.png"; % 球を出力する場所

% 設定ここまで

%% 各種初期化
light = light / norm(light); % 光源ベクトル正規化
view  = view / norm(view); % 視点ベクトル正規化
sn = zeros(N_ROW,N_COL,3); 

%% 球の作成
for i = 1:N_ROW
   for j = 1:N_COL
       if (i - kyu_x) ^ 2 + (j - kyu_y) ^ 2 <= radius ^ 2
            k = sqrt(radius ^ 2 - (i - kyu_x) ^ 2 - (j - kyu_y) ^ 2);
            sn_tmp =  [i - kyu_x, j - kyu_y , k]';
            sn_tmp = sn_tmp / norm(sn_tmp);
            sn(i,j,:) = sn_tmp;
       end
   end
end

%% 法線デバッグ用 普段はコメントアウト
% check_sn = uint8((sn + 1) * 255 / 2);
% imwrite(check_sn,"true_hosen.ppm");

%% 拡散反射の考慮
img_diffuse = zeros(N_ROW,N_COL);

for i = 1:N_ROW
   for j = 1:N_COL
       sn_tmp = [sn(i,j,1) sn(i,j,2) sn(i,j,3)]';
       if norm(sn_tmp) > 0
           cos_theta = dot(light,sn_tmp);
           if cos_theta > 0
               img_diffuse(i,j) = K_d * I * cos_theta;
           end
       end
   end
end

%% 鏡面反射の考慮
img_specular = zeros(N_ROW,N_COL);

for i = 1:N_ROW
   for j = 1:N_COL
       sn_tmp = [sn(i,j,1) sn(i,j,2) sn(i,j,3)]';
       if norm(sn_tmp) > 0
           r = 2 * dot(sn_tmp,light) * sn_tmp - light; % 正規化の必要なし
           cos_alpha = dot(view,r);
           if cos_alpha > 0
               img_specular(i,j) = K_s * I * (cos_alpha ^ n);
               % img_specular(i,j) = K_s * I * specular(sn(i,j,1),sn(i,j,2),sn(i,j,3),light,view,n);
               % ライブラリ関数 specular を使ってもOK
           end
       end
   end
end

%% 出力
img_output = img_diffuse + img_specular; 
img_output(img_output > 1) = 1; % 輝度値の上限を考慮

imwrite(img_output,OUTPUT_DIR);

５．さいごに

今回は、

• 拡散反射と鏡面反射の紹介
• PythonとMATLABを用いてCG上で球を作るプログラムの紹介

の2つについて説明しました。

次回はどんなCG, CVの分野について語ろうかしら。

余談：\( K_{d} \) とかの小さい \( d \) は拡散 (diffuse) の頭文字を、\( K_{s} \) とかの小さい \( s \) は鏡面 (specular) の頭文字をとったものです。

*1:屋外だと明かりは「太陽」や「街灯」、屋内だと明かりは「蛍光灯」や「LED」が光源の例となります。

*2:より厳密な拡散反射の理想的なモデルに、オーレン・ネイヤーモデルなどがあります。

*3:物体表面が向いている方向のことです。

*4:どれくらい拡散反射をするかを数値で表したもの

*5:より厳密な拡散反射の理想的なモデルに、オーレン・ネイヤーモデルなどがあります。

*6:どれくらい拡散反射をするかを数値で表したもの

*7:\( \cos \alpha \leqq 0 \) のときに \( L_{s} = 0 \) としない場合、\( n \) を偶数にしたときに \( \cos \alpha \) が正になってしまうので、思いもよらない方向に鏡面反射があることになってしまいます。例えば \( \alpha = 150^{\circ} \), \( n = 30 \) くらいで考えるとわかりやすいと思います。

*8:CGの世界では環境光（間接光などによって全体的にちょっと明るくなるため、全体的に与える明るさのこと。）も考える必要があるのですが、今回は省略します。