スポンサードリンク
こんにちは、ももやまです。
前回(応用編第3羽)では、ベクトルの大小を比べるための道具であるpノルム(\( L^p \) ノルム)について説明しました。
今回は、行列の大小を比べるための道具、行列ノルムを説明しましょう。
目次
スポンサードリンク
復習(ベクトルのpノルム)
行列のノルムを学習する前に、前回説明したベクトルの \( p \) ノルム(\(L^p \) ノルム)の復習をしましょう。
なお、説明の際にはベクトル \( \vec{a} \) の成分は、\[
\vec{a} = \left( \begin{array}{ccc} a_1 \\ a_2 \\ \vdots \\ a_n \end{array} \right)
\]とします。
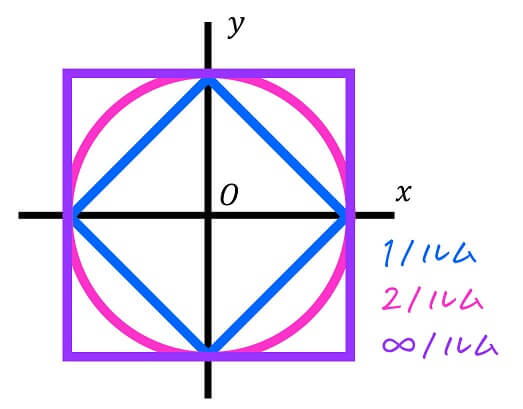
(1) 1ノルム(絶対値ノルム)
各成分の絶対値をすべて足したものが1ノルムとなります。
\[\begin{align*}
\| \vec{a} \|_1 & = |a_1| + |a_2| + \cdots + |a_n|
\\ & = \sum^{n}_{k = 1} | a_k |
\end{align*}\]
(2) 2ノルム(ユークリッドノルム)
皆さんお馴染み、ユークリッドノルムです。
高校数学で出てくるベクトルの長さ(大きさ)と全く同じです。
\[\begin{align*}
\| \vec{a} \|_2 & = \sqrt{ a_1^2 + a_2^2 + \cdots + a_n^2 }
\\ & = \sqrt{ \sum^{n}_{k = 1} a_k^2 }
\end{align*}\]
(3) ∞ノルム(最大値ノルム)
ベクトルの成分の絶対値の中で、最も大きい値が∞ノルムとなります。
\[\begin{align*}
\| \vec{a} \|_\infty & = \max \left( |a_1|, |a_2|, \cdots , | a_n | \right)
\\ & = \max_{1 \leqq k \leqq n} | a_k |
\end{align*}\]
スポンサードリンク
1. 行列の誘導ノルムpの定義
行列のノルムには様々な定義方法があります。
まずは、その中の1つである誘導pノルム(作用素ノルム)の定義式を紹介しましょう。
\( m \) 行 \( n \) 列の行列 \( A \) の誘導 \( p \) ノルムは、\( n \) 次元ベクトル \( \vec{x} \) を用いて次のように定義される。\[\begin{align*}
\| A \|_p = \max_{\vec{x} \not = \vec{0}} \frac{ \| A \vec{x} \|_p }{ \| \vec{x} \|_p }
= \max_{ \| \vec{x} \|_p = 1} \| A \vec{x} \|_p
\end{align*}\]
式の意味としては、ベクトル \( \vec{x} \) に行列 \( A \) を掛けると、ノルムが何倍になるかを表しています[1]\( \vec{x} = \vec{0} \) の場合、\( \| \vec{0} \|_p= 0 \) となり、\( \frac{ \| A \vec{x} \|_p }{ \| \vec{x} \|_p } \) の分母が0になってしまうため、\( \vec{x} \not = \vec{0} \) … Continue reading。\[
\| A \|_p = \max_{\vec{x} \not = \vec{0}} \frac{ \| A \vec{x} \|_p }{ \| \vec{x} \|_p }
\]
さらに、元のベクトル \( \vec{x} \) のノルムを1に固定してしまえば、\( \| \vec{x} \|_p \) から \( \| A \vec{x} \|_p \) に変化させたときの倍率がそのまま \( \| A \vec{x} \| \) の値となりますね。そのため、\[
\max_{\vec{x} \not = \vec{0}} \frac{ \| A \vec{x} \|_p }{ \| \vec{x} \|_p } = \max_{ \textcolor{magenta}{ \| \vec{x} \|_p = 1} } \| A \vec{x} \|_p
\]と変形ができます。
スポンサードリンク
2. 行列の誘導pノルムの計算公式 (p = 1, 2, ∞)
1章の定義に従って行列の誘導pノルムを計算することはできますが、少し時間がかかってしまいます。
そこで、\( p = 1 , 2, \infty \) のとき(誘導1ノルム、誘導2ノルム、誘導∞ノルム)の誘導 \( p \) ノルムの計算公式とその導出を見てみましょう。
(1) 誘導1ノルム (p = 1)
(i) 計算公式
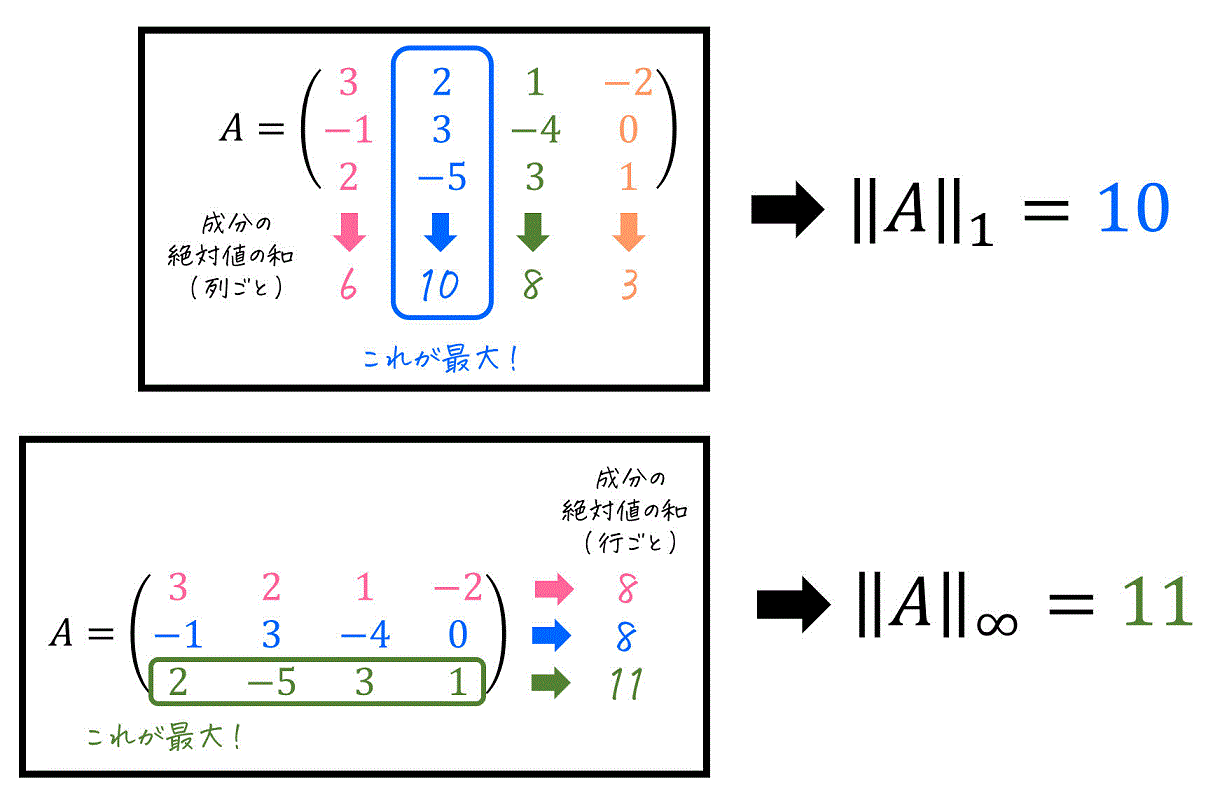
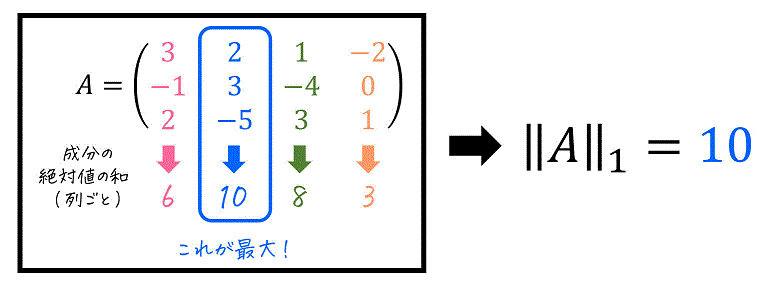
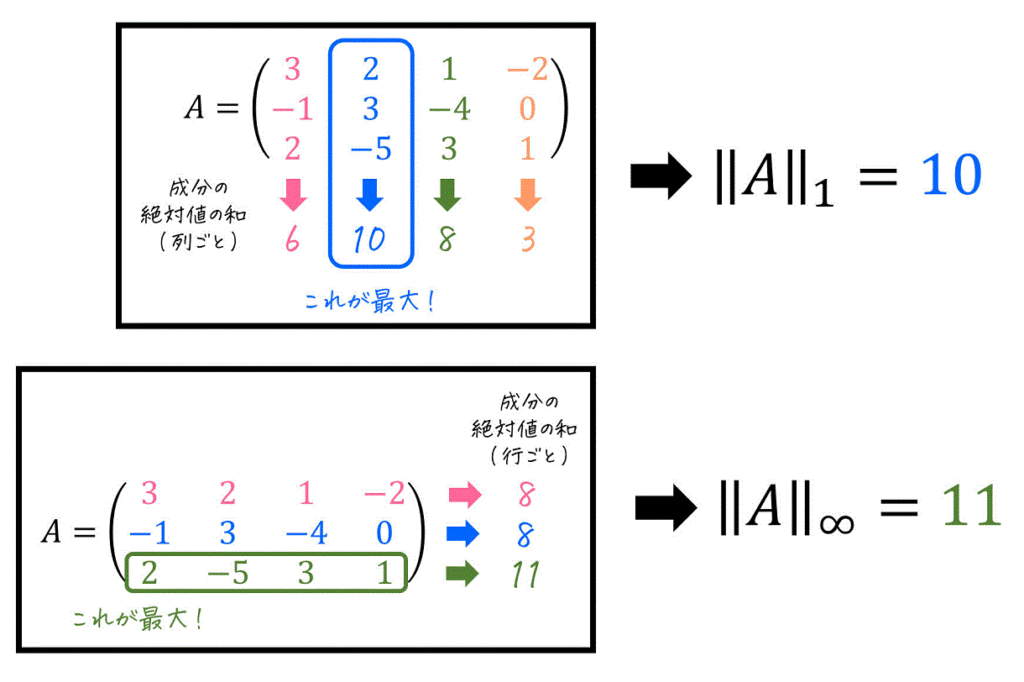
行列 \( A \) の誘導1ノルム \( \| A \|_1 \) は、行列の各列ごとに「成分の絶対値の合計」を計算したときの、和が最も大きい列の「成分の絶対値の合計」が誘導1ノルムとなります。
例えばつぎの行列\[
A = \left( \begin{array}{ccc} 3 & 2 & 1 & -2 \\ -1 & 3 & -4 & 0 \\ 2 & -5 & 3 & 1 \end{array} \right)
\]の場合、各列ごとの成分の絶対値の和は下のように計算ができますね。
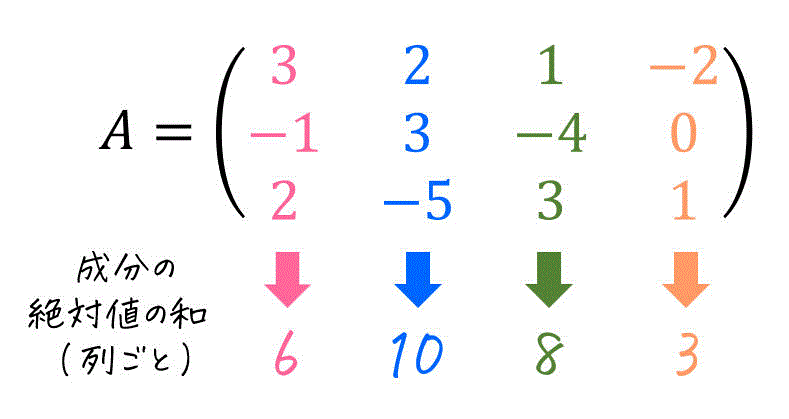
計算をすると、2列目(青部分)が「成分の絶対値の和が最も大きい列」であることがわかりますね。そのため、この列(成分の和が最も大きい2列目)の「成分の絶対値の和」である 10 が誘導1ノルム \( \| A \|_1 \) となります。
次のような \( m \) 行 \( n \) 列の行列 \( A \) がある。\[
A = \left( \begin{array}{ccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array} \right)
\]この行列 \( A \) の誘導1ノルム \( \| A \|_1 \) は、行列の各列ごとに「成分の絶対値の合計」を計算したときの、和が最も大きい列の「成分の絶対値の合計」となる。\[\begin{align*}
\| A \|_1 & = \textcolor{blue}{\max_{1 \leqq j \leqq n}} \textcolor{red}{\sum^{m}_{i = 1} | a_{ij} | }
\end{align*}\]
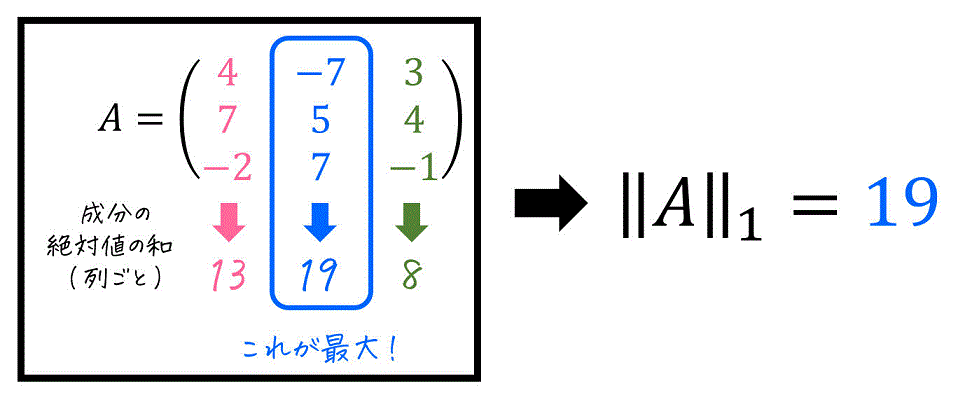
(ii) 例題
次の行列 \( A \) に対し、誘導1ノルム \( \| A \|_{1} \) を計算しなさい。\[
A = \left( \begin{array}{ccc} 4 & -7 & 3 \\ 7 & 5 & 4 \\ -2 & 7 & -1 \end{array} \right)
\]
[解説1]
(iii) 公式の仕組み
行列 \( A \) の誘導1ノルム \( \| A \|_1 \) は次のような式で計算できますね。\[
\| A \|_1 = \max_{\vec{x} \not = \vec{0}} \frac{ \| A \vec{x} \|_1 }{ \| \vec{x} \|_1 }
= \max_{ \| \vec{x} \|_1 = 1} \| A \vec{x} \|_1
\]
つまり、\( \| \vec{x} \|_1 = 1 \) の条件の下で\[\begin{align*}
\| A \vec{x} \|_1 & = \left\| \left( \begin{array}{ccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array} \right) \left( \begin{array}{ccc} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right) \right\|_1
\\ &= \left\| \left( \begin{array}{ccc} a_{11} x_1 +a_{12} x_2 + \cdots + a_{1n} x_n \\ a_{21} x_1 +a_{22} x_2 + \cdots + a_{2n} x_n \\ \vdots \\ a_{m1} x_1 +a_{m2} x_2 + \cdots + a_{1n} x_n \end{array} \right) \right\|_1
\\ &= \left\| \left( \begin{array}{ccc} a_{11} x_1 \\ a_{21} x_1 \\ \vdots \\ a_{m1} x_1 \end{array} \right) + \left( \begin{array}{ccc} a_{12} x_2 \\ a_{22} x_2 \\ \vdots \\ a_{m2} x_2 \end{array} \right) + \cdots + \left( \begin{array}{ccc} a_{1n} x_n \\ a_{2n} x_n \\ \vdots \\ a_{mn} x_n \end{array} \right) \right\|_1
\\ &= \left\| x_1 \underbrace{ \left( \begin{array}{ccc} a_{11} \\ a_{21} \\ \vdots \\ a_{m1} \end{array} \right) }_{\vec{a}_1} + x_2 \underbrace{ \left( \begin{array}{ccc} a_{12} \\ a_{22} \\ \vdots \\ a_{m2} \end{array} \right) }_{\vec{a}_2} + \cdots + x_n \underbrace{ \left( \begin{array}{ccc} a_{1n} \\ a_{2n} \\ \vdots \\ a_{mn} \end{array} \right)}_{\vec{a}_n} \right\|_1
\end{align*}\]が最も大きくなるときのノルム \( \| A \vec{x} \|_1 \) が \( \| A \|_1 \) の値ですね。( \( A = (\vec{a}_1, \vec{a}_2, \cdots, \vec{a}_n ) \) です。)
ここで、条件 \( \| \vec{x} \|_1 = 1 \) を言い換えると、ベクトル \( \vec{x} \) の各成分の絶対値 \( |x_1| \), \( |x_2| \), …, \( |x_n| \) の和が1、つまり\[
|x_1| + |x_2| + \cdots + |x_n| = 1
\] となりますね。
そのため、行列 \( A \) の各列ベクトル \( \vec{a}_1 \), \( \vec{a}_2 \), … \( \vec{a}_n \) ごとに「ベクトルの各成分を絶対値したものの和」を計算し、一番大きくなった列ベクトルに対応するベクトル \( \vec{x} \) の成分を1もしくは-1、それ以外の成分を0とすることで \( \| A \vec{x} \|_1 \) の最大値、つまり \( \| A \|_1 \) を求めることができます。
具体例で確認しましょう。例えば行列 \( A \) が下のような値だったとします。\[\begin{align*}
A & = \left( \begin{array}{ccc} \textcolor{red}{2} & \textcolor{blue}{-1} & \textcolor{green}{3} & \textcolor{orange}{4} \\ \textcolor{red}{-1} & \textcolor{blue}{0} & \textcolor{green}{-5} & \textcolor{orange}{-1} \\ \textcolor{red}{0} & \textcolor{blue}{1} & \textcolor{green}{3} & \textcolor{orange}{2} \end{array} \right)
\\ & = ( \textcolor{red}{\vec{a}_1}, \textcolor{blue}{\vec{a}_2} , \textcolor{green}{\vec{a}_3} , \textcolor{orange}{\vec{a}_4} )
\end{align*}\]
このとき、各列ベクトルごとの「各成分を絶対値したものの和」は、次のように計算できます。
- \( \textcolor{red}{ \vec{a}_1 \to |2| +|-1|+|0| = 3 } \)
- \( \textcolor{blue}{ \vec{a}_2 \to |-1| +|0|+|1| = 2 } \)
- \( \textcolor{green}{ \vec{a}_3 \to |3| +|-5|+|3| = 11 } \)
- \( \textcolor{orange}{ \vec{a}_4 \to |4| +|-1|+|2| = 7 } \)
よって、ベクトル \( \vec{a}_3 \) に対応する \( \vec{x} \) の成分 \( x_3 \) を1(もしくは-1)、それ以外の \( \vec{x} \) の成分が0のときに \( \| A \vec{x} \|_1 \) の最大値、つまり \( \| A \|_1 \) が求まります。\[\begin{align*}
\| A \|_1 & = \max_{\| \vec{x} \|_ 1 } \| A \vec{x} \|_1
\\ & = \left( \begin{array}{ccc} \textcolor{red}{2} & \textcolor{blue}{-1} & \textcolor{green}{3} & \textcolor{orange}{4} \\ \textcolor{red}{-1} & \textcolor{blue}{0} & \textcolor{green}{-5} & \textcolor{orange}{-1} \\ \textcolor{red}{0} & \textcolor{blue}{1} & \textcolor{green}{3} & \textcolor{orange}{2} \end{array} \right) \left( \begin{array}{ccc} \textcolor{red}{0} \\ \textcolor{blue}{0} \\ \textcolor{green}{1} \\ \textcolor{orange}{0} \end{array} \right)
\\ & = |3| + |-5| + |3|
\\ & = 11
\end{align*}\]
つまり、誘導1ノルム \( \| A \|_1 \) は各列ごとに「成分の絶対値の合計」を計算したときの最大値で求めることができます!\[
\| A \|_1 = \max ( \| \vec{a}_1 \|_1, \| \vec{a}_2 \|_1, \cdots , \| \vec{a}_n \|_1 )
\]※ \( A = ( \vec{a}_1, \vec{a}_2 , \cdots, \vec{a}_n ) \)
(2) 誘導2ノルム (p = 2)
誘導2ノルムは、誘導1ノルム・誘導∞ノルムに比べて公式が少し複雑です。
(i) 計算公式
行列 \( A \) の誘導2ノルム \( \| A \|_{2} \) は、行列 \( A \) の最大特異値(もしくは行列 \( A A^{\top} \) もしくは \( A^{\top} A \) の最大固有値)を計算することにより求めることができます。
↓↓特異値についての詳しい解説はこちらをご覧ください!↓↓
\( m \) 行 \( n \) 列の行列 \( A \) の誘導ノルム \( \| A \|_2 \) は、下の1, 2のどちらかを計算することで求められる。
- 行列 \( A \) の最大特異値 \( \sigma_1 \)
- 行列 \( A A^{\top} \) もしくは \( A^{\top} A \) の最大固有値 \( t_1 \) の平方根 \( \sqrt{t_1} \)
(ii) 例題
まずは例題で行列 \( A \) の誘導ノルム \( \| A \|_p \) を計算してみましょう。
※ 公式の威力を確認してもらうため、定義からもノルムを計算してみましょう。
次の行列 \( A \) に対して、(1), (2)の方法で誘導ノルム \( \| A \|_2 \) を求めなさい。\[
A = \left( \begin{array}{ccc} -8 & 1 \\ -4 & -7 \end{array} \right)
\]
(1) 行列 \( A \) の特異値から求める方法
(2) ベクトル \( \vec{x} \) を\[
\vec{x} = \left( \begin{array}{ccc} \cos \theta \\ \sin \theta \end{array} \right)
\]とおき、定義\[
\| A \|_2 = \max_{\vec{x} \not = \vec{0}} \frac{ \| A \vec{x} \|_2 }{ \| \vec{x} \|_2 }
= \max_{ \| \vec{x} \|_2 = 1} \| A \vec{x} \|_2
\]から求める方法
[解説2]
(1)
行列 \( A A^{\top} \) の固有値を求めて[2]もちろん \( A^{\top} A \) の固有値を求めてもOKから平方根を取ればOK。。
まずは、\( A A^{\top} \) を計算する。\[
A^{\top} = \left( \begin{array}{ccc} -8 & -4 \\ 1 & -7 \end{array} \right)
\]より、\[\begin{align*}
A A^{\top} & = \left( \begin{array}{ccc} -8 & 1 \\ -4 & -7 \end{array} \right) \left( \begin{array}{ccc} -8 & -4 \\ 1 & -7 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 65 & 25 \\ 25 & 65 \end{array} \right)
\end{align*}\]
ここで、\( A A^{\top} \) の固有値を \( t \) とすると、\[\begin{align*}
| A A^{\top} - tE | & = \left| \begin{array}{ccc} 65-t & 25 \\ 25 & 65-t \end{array} \right|
\\ & = (65-t)^2 - 25 \cdot 25
\\ & = t^2 - 130t + 4225 - 625
\\ & = t^2 - 130t + 3600
\\ & = (t-40)(t-90) = 0
\end{align*}\]が成立する。
よって、\( A A^{\top} \) の固有値は40, 90となるため、行列 \( A \) の特異値は \( 2 \sqrt{10} \), \( 3 \sqrt{10} \) となる。
ここで誘導ノルム \( \| A \|_2 \) は行列 \( A \) の最大特異値となるので、\( \| A \|_2 = 3 \sqrt{10} \) が答え。
(2)
\[\begin{align*}
A \vec{x} & = \left( \begin{array}{ccc} -8 & 1 \\ -4 & -7 \end{array} \right) \left( \begin{array}{ccc} \cos \theta \\ \sin \theta \end{array} \right)
\\ & = \left( \begin{array}{ccc} -8 \cos \theta + \sin \theta \\ -4 \cos \theta - 7 \sin \theta \end{array} \right)
\end{align*}\]となるので、あとは \( \| A \vec{x} \|_2 \) の最大値を求めるだけ。\[\begin{align*}
\| A \vec{x} \|_2
& = \left\| \left( \begin{array}{ccc} -8 \cos \theta + \sin \theta \\ -4 \cos \theta - 7 \sin \theta \end{array} \right) \right\|_2
\\ & = \sqrt{ (-8 \cos \theta + \sin \theta)^2 + (-4 \cos \theta - 7 \sin \theta)^2 }
\\ & = \sqrt{ (64 \cos^2 \theta - 16 \sin \theta \cos \theta + \sin^2 \theta) + (16 \cos^2 \theta + 56 \sin \theta \cos \theta + 49 \sin^2 \theta) }
\\ & = \sqrt{ 80 \cos^2 \theta + 50 \sin^2 \theta + 40 \sin \theta \cos \theta }
\\ & = \sqrt{ (65 \cos^2 \theta + 65 \sin^2 \theta)+ (15 \cos^2 \theta - 15 \sin^2 \theta) + 20 \sin 2 \theta}
\\ & = \sqrt{ 65 + (15 \cos^2 \theta - 15 \sin^2 \theta) + 20 \sin 2 \theta}
\\ & = \sqrt{ 65 + 15 \cos 2 \theta + 20 \sin 2 \theta}
\\ & = \sqrt{ 65 + \sqrt{15^2+20^2} \cos (2 \theta + \alpha) }
\\ & = \sqrt{ 65 + 25 \cos (2 \theta + \alpha) }
\end{align*}\]となるため、\( \cos (2 \theta + \alpha) = 1 \) のとき、\[\begin{align*}
\| A \|_2 & = \max_{ \| \vec{x} \|_2 = 1} \| A \vec{x} \|_2
\\ & = \sqrt{90}
\\ & = 3 \sqrt{10}
\end{align*}\]となることがわかる。
(2)のように定義に沿って計算すると、膨大な計算量が必要なことがわかりましたね。
(iii) 公式の仕組みと特異値分解・特異値
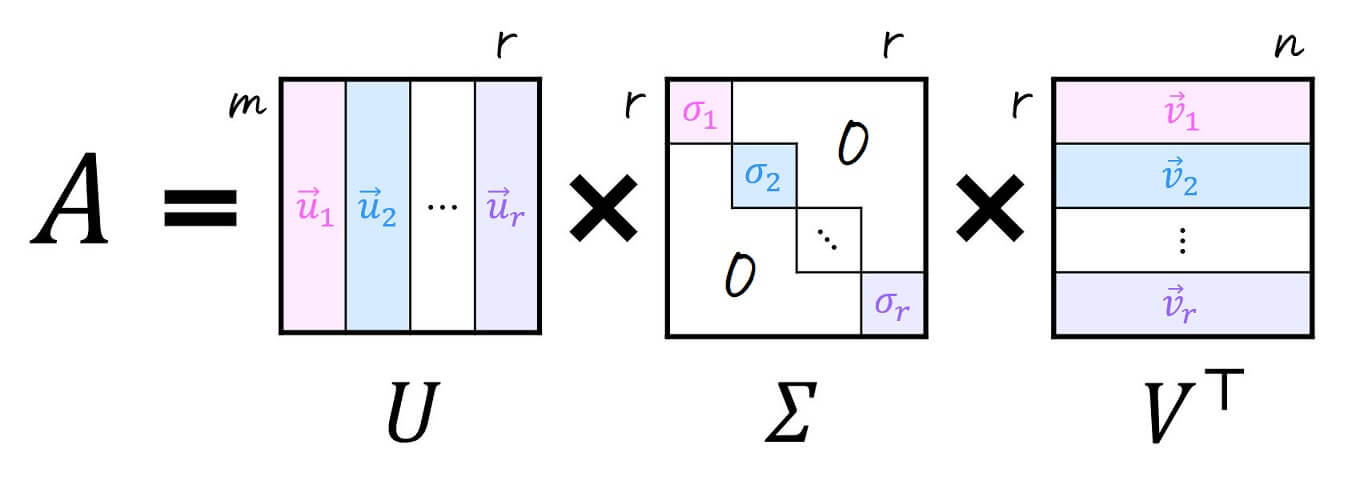
まず、行列 \( A \) を直交行列 \( U \), \( V \) および対角成分以外が0の行列 \( \Sigma \) を用いて、\(
A = U \Sigma V^{\top}
\) と分解することにしましょう。この分解のことを(フルサイズの)特異値分解と呼びます[3]フルサイズではない特異値分解としては、\( m \times r \) の行列 \( U \)、\( r \times r \) の対角行列 \( \Sigma \)、\( r \times n \) の行列 \( V \) を用いて \( U … Continue reading。
(特異値分解について詳しく知りたい人は、こちらの記事をご覧ください。)

また、特異値分解をした際に出てくる行列 \( \Sigma \) の対角成分 \( \sigma_1 \), \( \sigma_2 \), …, \( \sigma_n \) を特異値と呼び、\( AA^{\top} \) または \( A^{\top} A \) の固有値の平方根に等しくなります。
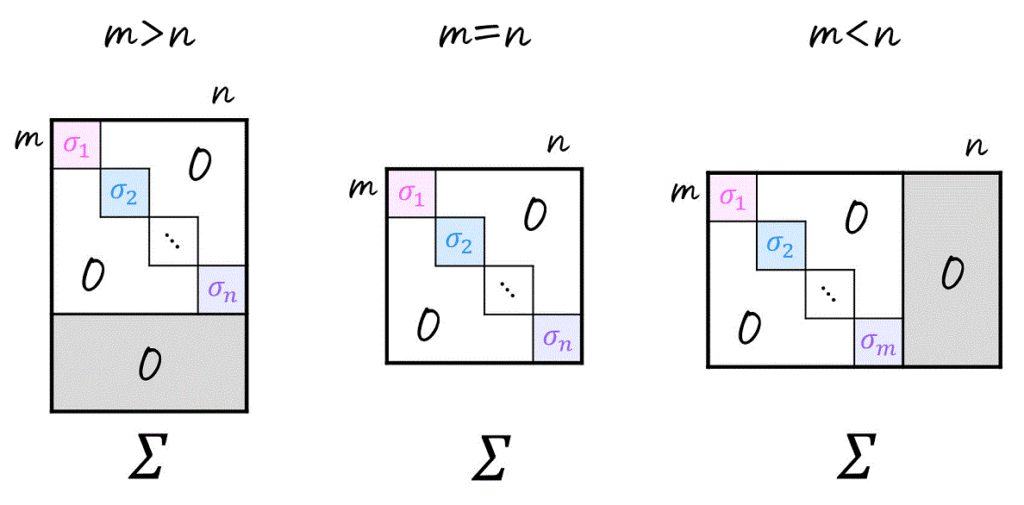
対角行列 \( \Sigma \) の成分は、直交行列 \( U \), \( V \) の値の決め方によって変わりますが、今回は行列の上の方ほど特異値が大きくなるように並べましょう。つまり、\( \sigma_1 \geqq \sigma_2 \geqq \cdots \geqq \sigma_r \) となるように並べます。
ここで、ベクトル \( \vec{x} \) に直交行列 \( U \) を掛けても、2ノルムは変わりません。つまり、\[
\| U \vec{x} \|_2 = \| \vec{x} \|_2
\]が成り立ちます。(直交変換と呼びます。)
この変換を利用することで、\[\begin{align*}
\| A \|_p & = \max_{ \| \vec{x} \|_2 = 1} \| A \vec{x} \|_2
\\ & = \max_{ \| \vec{x} \|_2 = 1} \| U \Sigma V^{\top} \vec{x} \|_2
\\ & = \max_{ \| \vec{x}' \|_2 = 1} \| U ( \Sigma \vec{y} ) \|_2 \ \ \ ( \vec{y} = V^{\top} \vec{x} )
\\ & = \max_{ \| \vec{y} \|_2 = 1} \| \Sigma \vec{y} \|_2
\end{align*}\]と変形できます。
ここで、\( \| \vec{y} \|_2 = 1 \) の条件下で \( \| \Sigma \vec{y} \|_2 \) を最大化するような \( \vec{y} \) について考えましょう。
まずは、\( \Sigma \vec{y} \) を計算してみましょう。
(見やすさ重視のために「\( m \geqq n \) のとき」と「\( m < n \) のとき」で場合分けして計算しています。)
\[\begin{align*}
\Sigma \vec{y} & = \left( \begin{array}{ccc} \textcolor{red}{\sigma_1} & 0 & \cdots & 0 \\ 0 & \sigma_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \sigma_n \\ \vdots & \vdots & & \vdots \\ 0 & 0 & 0 & 0 \end{array} \right) \left( \begin{array}{ccc} \textcolor{red}{y_1} \\ y_2 \\ \vdots \\ y_n \end{array} \right)
\\ & = \left( \begin{array}{ccc} \textcolor{red}{\sigma_1 y_1} \\ \sigma_2 y_2 \\ \vdots \\ \sigma_r y_n \end{array} \right)
\end{align*}\]
[\( m < n \) のとき]
\[\begin{align*}
\Sigma \vec{y} & = \left( \begin{array}{ccc} \textcolor{red}{\sigma_1} & 0 & \cdots & 0 & \cdots & 0 \\ 0 & \sigma_2 & \cdots & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & 0 & & 0 \\ 0 & 0 & \cdots & \sigma_m & \cdots & 0\end{array} \right) \left( \begin{array}{ccc} \textcolor{red}{y_1} \\ y_2 \\ \vdots \\ y_n \end{array} \right)
\\ & = \left( \begin{array}{ccc} \textcolor{red}{\sigma_1 y_1} \\ \sigma_2 y_2 \\ \vdots \\ \sigma_r y_n \end{array} \right)
\end{align*}\]
上の式のように変形[4]\( r < n \) のとき、\( r+1\) 番目以降の \( \Sigma \vec{y} \) の成分はすべて0。すると、行列 \( A \) の最大特異値 \( \textcolor{red}{\sigma_1} \) に対応するベクトル \( \vec{y} \) の第1成分 \( y_1 \)を1、それ以外を0とすれば \( \| \vec{y} \|_2 = 1 \) の条件下で \( \| \Sigma \vec{y} \|_2 \) が最大化しますね。
よって、誘導2ノルム \( \| A \|_2 \) の計算公式を下のように導出することができます。\[\begin{align*}
\| A \|_2 & = \max_{ \| \vec{x} \|_2 = 1} \| A \vec{x} \|_2
\\ & = \max_{ \| \vec{y} \|_2 = 1} \| \Sigma \vec{y} \|_2
\\ & = \left\| \left( \begin{array}{ccc} \textcolor{red}{\sigma_1} & 0 & \cdots & 0 \\ 0 & \sigma_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \sigma_r \end{array} \right) \left( \begin{array}{ccc} \textcolor{red}{1} \\ 0 \\ \vdots \\ 0 \end{array} \right) \right\|_2
\\ & = \left\| \left( \begin{array}{ccc} \sigma_1 \\ 0 \\ \vdots \\ 0 \end{array} \right) \right\|_2
\\ & = \sigma_1
\end{align*}\]
(3) 誘導∞ノルム (p = ∞)
(i) 計算公式
行列 \( A \) の誘導∞ノルム \( \| A \|_{\infty} \) は、行列の各行ごとに「成分の絶対値の合計」を計算したときの、和が最も大きい行の「成分の絶対値の合計」が誘導∞ノルムとなります。
例えば、つぎの行列\[
A = \left( \begin{array}{ccc} 3 & 2 & 1 & -2 \\ -1 & 3 & -4 & 0 \\ 2 & -5 & 3 & 1 \end{array} \right)
\]の場合、各行ごとの成分の絶対値の和は下のように計算ができますね。
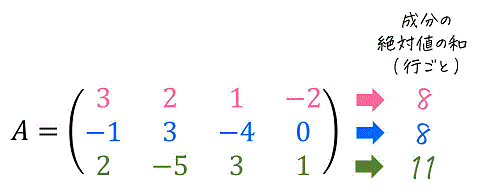
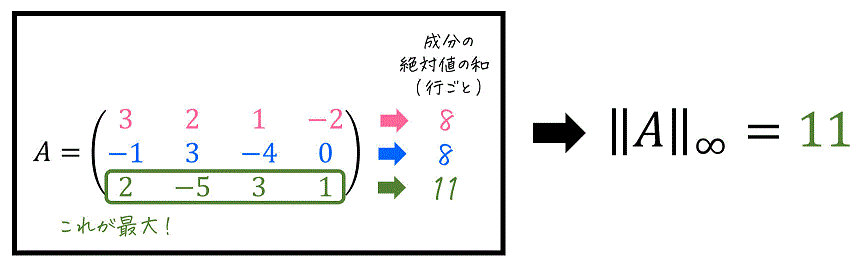
計算をすると、3行目(緑部分)が「成分の絶対値の和が最も大きい行」であることがわかりますね。そのため、この行(成分の和が最も大きい3行目)の「成分の絶対値の和」である 11 が誘導∞ノルム \( \| A \|_{\infty} \) となります。
次のような \( m \) 行 \( n \) 列の行列 \( A \) がある。\[
A = \left( \begin{array}{ccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array} \right)
\]この行列 \( A \) の誘導∞ノルム \( \| A \|_{\infty} \) は、行列の各行ごとに「成分の絶対値の合計」を計算したときの、和が最も大きい行の「成分の絶対値の合計」となる。\[\begin{align*}
\| A \|_{\infty} & = \textcolor{blue}{\max_{1 \leqq i \leqq n}} \textcolor{red}{\sum^{m}_{j = 1} | a_{ij} | }
\end{align*}\]
(ii) 例題
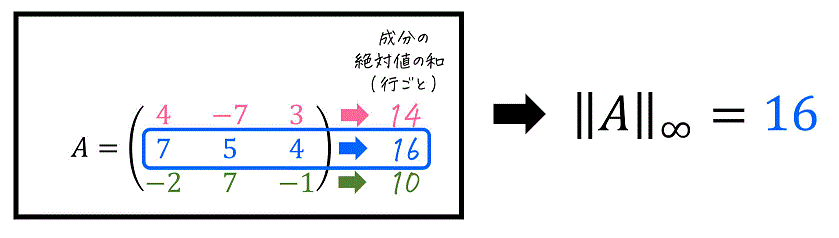
次の行列 \( A \) に対し、誘導∞ノルム \( \| A \|_{\infty} \) を計算しなさい。\[
A = \left( \begin{array}{ccc} 4 & -7 & 3 \\ 7 & 5 & 4 \\ -2 & 7 & -1 \end{array} \right)
\]
[解説3]
(iii) 公式の仕組み
行列 \( A \) の誘導∞ノルム \( \| A \|_{\infty} \) の定義は次のような式でしたね。\[
\| A \|_{\infty} = \max_{\vec{x} \not = \vec{0}} \frac{ \| A \vec{x} \|_{\infty} }{ \| \vec{x} \|_{\infty} }
= \max_{ \| \vec{x} \|_{\infty} = 1} \| A \vec{x} \|_{\infty}
\]
つまり、\( \| \vec{x} \|_{\infty} = 1 \) の条件の下で\[\begin{align*}
\| A \vec{x} \|_{\infty} & = \left\| \left( \begin{array}{ccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array} \right) \left( \begin{array}{ccc} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right) \right\|_{\infty}
\\ &= \left\| \left( \begin{array}{ccc} a_{11} x_1 +a_{12} x_2 + \cdots + a_{1n} x_n \\ a_{21} x_1 +a_{22} x_2 + \cdots + a_{2n} x_n \\ \vdots \\ a_{m1} x_1 +a_{m2} x_2 + \cdots + a_{1n} x_n \end{array} \right) \right\|_{\infty}
\\ & = \max_{1 \leqq i \leqq m} \textcolor{red}{ | a_{i1} x_1 + a_{i2} x_2 + \cdots + a_{in} x_n | }
\end{align*}\]が最も大きくなるときが \( \| A \|_{\infty} \) の値ですね。
なので、\( \| A \|_{\infty} \) を計算するために、各行ごとに計算される上の式の赤色部分をなるべく大きくすることを考えましょう。
ここで、条件 \( \| \vec{x} \|_{\infty} = 1 \) を満たすためには、ベクトル \( \vec{x} \) のうち、1つは 1 もしくは -1で、残りの各成分の絶対値が1以下になっていればOKですね。
そのため、各行ごとの赤色部分を大きくするためには、要素 \( a_{ij} \) が正であれば対応するベクトル の成分は1、要素 \( a_{ij} \) が負であれば対応するベクトルの成分 \( x_{j} \) を-1とすればOKですね。
例えば、次の行列の1行目を大きくすることを考えましょう。\[
\left( \begin{array}{ccc} \textcolor{red}{2} & \textcolor{blue}{-1} & \textcolor{red}{3} & \textcolor{red}{4} \\ -1 & 0 & -5 & -1 \\ 0 & 1 & 3 & 2 \end{array} \right)
\]この場合、\( \vec{x} \) を次のようにすることで、1行目に対応する \( A \vec{x} \) の成分を最大化できますね。\[\begin{align*}
A \vec{x} & = \left( \begin{array}{ccc} \textcolor{red}{2} & \textcolor{blue}{-1} & \textcolor{red}{3} & \textcolor{red}{4} \\ -1 & 0 & -5 & -1 \\ 0 & 1 & 3 & 2 \end{array} \right) \left( \begin{array}{ccc} \textcolor{red}{1} \\ \textcolor{blue}{-1} \\ \textcolor{red}{1} \\ \textcolor{red}{1} \end{array} \right)
\\ & = \left( \begin{array}{ccc} 10 \\ * \\ * \end{array} \right)
\end{align*}\]
また、「1行目における各成分の絶対値の和」が(1行目に)対応する \( A \vec{x} \) の成分となっていますね。
同じように、2行目・3行目に対応する \( A \vec{x} \) の成分は下のように最大化できます。
[2行目]\[\begin{align*}A \vec{x} & = \left( \begin{array}{ccc} 2 & -1 & 3 & 4 \\ \textcolor{blue}{-1} & 0 & \textcolor{blue}{-5} & \textcolor{blue}{-1} \\ 0 & 1 & 3 & 2 \end{array} \right) \left( \begin{array}{ccc} \textcolor{blue}{-1} \\ 0 \\ \textcolor{blue}{-1} \\ \textcolor{blue}{-1} \end{array} \right)
\\ & = \left( \begin{array}{ccc} * \\ 7 \\ * \end{array} \right)
\end{align*}\]※0に対応するベクトル \( \vec{x} \) の成分は「絶対値が1以下」であればなんでもOK。 [3行目]\[\begin{align*}
A \vec{x} & = \left( \begin{array}{ccc} 2 & -1 & 3 & 4 \\ -1 & 0 & -5 & -1 \\ 0 & \textcolor{red}{1} & \textcolor{red}{3} & \textcolor{red}{2} \end{array} \right) \left( \begin{array}{ccc} 0 \\ \textcolor{red}{1} \\ \textcolor{red}{1} \\ \textcolor{red}{1} \end{array} \right)
\\ & = \left( \begin{array}{ccc} * \\ * \\ 6 \end{array} \right)
\end{align*}\]
※2行目、3行目ともに「各行における各成分の絶対値の和」が(2行目、3行目に)対応する \( A \vec{x} \) の成分となっていますね。
ここで、\( \| A \vec{x} \|_{\infty} \) は、「\( A \vec{x} \) の各成分中で最も大きい値」をとるのでしたね。
例えば上の例の場合、各行ごとの赤色部分を最大化したベクトル \( A \vec{x} \) は\[
\vec{x} = \left( \begin{array}{ccc} 10 \\ 7 \\ 6 \end{array} \right)
\]となるため、\( \| A \vec{x} \|_{\infty} = 10 \) ですね。
この一連の動作から、「行列の各行(1行目、2行目、…)ごとに成分の絶対値の和を計算」し、成分の絶対値の和が最も大きくなる行の計算結果(成分の絶対値の和)が \( \| A \|_{\infty} \) となることが確認できますね。
3. 行列のフロベニウスノルム
ここからは誘導ノルム以外のノルムも紹介していきましょう。
先ほど紹介した「誘導2ノルム」は行列の固有値を計算するため、計算処理が少し複雑です。
なので、もう少し簡単に2ノルムを計算できるようなノルムが作られました。それがフロベニウスノルム \( \| A \|_F \) です。
(1) 計算公式
フロベニウスノルムは、\( m \) 行 \( n \) 列 の行列を1列に並べ、ベクトルにした後、2ノルムの計算をすることで求められます[5]\( m \) 行 \( n \) 列の行列を1列に並べることで作ったベクトルのpノルムのことを成分ノルムと呼びます。なお、フロベニウスノルムは \( p = 2 \) … Continue reading。
例えば、下の行列\[
A = \left( \begin{array}{ccc} \textcolor{red}{2} & \textcolor{blue}{1} & \textcolor{green}{-3} \\ \textcolor{red}{3} & \textcolor{blue}{0} & \textcolor{green}{1} \end{array} \right)
\]の場合、1行に並べたベクトル \( \vec{a}' = \mathrm{vec} (A) \) は下のようになります。\[ \vec{a}' = \left( \begin{array}{ccc} \textcolor{red}{2} \\ \textcolor{red}{3} \\ \textcolor{blue}{1} \\ \textcolor{blue}{0} \\ \textcolor{green}{-3} \\ \textcolor{green}{1} \end{array} \right) = \mathrm{vec} (A)
\]※ 行列 \( A \) を1行に並べる処理を \( \mathrm{vec} (A) \) と書きます。
あとはこのベクトル \( \vec{a}' \) の2ノルム \( \| \vec{a}' \|_2 \) を求めるだけでOKです。\[\begin{align*}
\| A \|_F & = \sqrt{ 2^2 + 3^2 + 1^2 + 0^2 + (-3)^2 + 1^2 }
\\ & = \sqrt{24}
\\ & = 2 \sqrt{6}
\end{align*}\]
なお、行列をベクトルにする前後で各成分の値自体は変化しないため、フロベニウスノルムを計算する際には行列の各成分を2乗した値の和に平方根を取ることで計算ができます。
次のような \( m \) 行 \( n \) 列の行列 \( A \) がある。\[
A = \left( \begin{array}{ccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array} \right)
\]この行列 \( A \) のフロベニウスノルム \( \| A \|_F \) は、行列の各成分を2乗した値の和の平方根で計算できる。\[
\| A \|_F = \sqrt{ \textcolor{red}{\sum^{m}_{i = 1}\left( \sum^{n}_{j = 1} a_{ij}^2 \right)}}
\]
(2) フロベニウスノルムと行列の対角成分の和(トレース)
フロベニウスノルムの2乗 \( \| A \|_F^2 \) は、行列 \( A A^{\top} \) もしくは \( A^{\top} A \) の対角成分の和 \( \mathrm{trace} \left[ A A^{\top} \right] \), \( \mathrm{trace} \left[ A^{\top} A \right] \) に等しくなります。
言い換えると、行列 \( A A^{\top} \) もしくは \( A^{\top} A \) の対角成分の和の平方根がフロベニウスノルム \( \| A \|_F \) となります。
実際に計算して確かめてみましょう。
まず、行列 \( A A^{\top} \)、\( A^{\top} A \) は下のように計算できますね。\[\begin{align*}
A A^{\top} & = \left( \begin{array}{ccc} 2 & 1 & -3 \\ 3 & 0 & 1 \end{array} \right) \left( \begin{array}{ccc} 2 & 3 \\ 1 & 0 \\ -3 & 1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} \textcolor{red}{14} & 3 \\ 3 & \textcolor{red}{10} \end{array} \right)
\end{align*}\]
\[\begin{align*}
A^{\top} A & = \left( \begin{array}{ccc} 2 & 3 \\ 1 & 0 \\ -3 & 1 \end{array} \right) \left( \begin{array}{ccc} 2 & 1 & -3 \\ 3 & 0 & 1 \end{array} \right)
\\ & = \left( \begin{array}{ccc} \textcolor{red}{13} & 2 & -3 \\ 2 & \textcolor{red}{1} & -3 \\ -3 & -3 & \textcolor{red}{10} \end{array} \right)
\end{align*}\]
そのため、\[\begin{align*}
\mathrm{trace} \left[ A A^{\top} \right] & = 14 + 10 = 24 \\
\mathrm{trace} \left[ A^{\top} A \right] & = 13 + 1 + 10 = 24
\end{align*}\]となり、確かに \( \| A \|_F^2 = 24 \)、\( \| A \|_F = \sqrt{24} = 2 \sqrt{6} \) となっていますね。
この行列 \( A \) のフロベニウスノルムの2乗は \( \| A \|_F^2 \) は、\( A A^{\top} \) もしくは \( A^{\top} A \) の対角成分の和に一致する。\[
\| A \|_F^2 = \mathrm{trace} \left[ A A^{\top} \right] = \mathrm{trace} \left[ A^{\top} A \right]
\]
(3) 例題
次の行列 \( A \) に対し、フロベニウスノルム \( \| A \|_{F} \) を計算しなさい。\[
A = \left( \begin{array}{ccc} 1 & -2 \\ 4 & -3 \end{array} \right)
\]
また、計算したフロベニウスノルム \( \| A \|_F \) に対し、\[
\| A \|_F^2 = \mathrm{trace} \left[ A A^{\top} \right] = \mathrm{trace} \left[ A^{\top} A \right]
\]が成立することを確認しなさい。
\| A \|_F & = \sqrt{ 1^2 + (-2)^2 + 4^2 + (-3)^2 }
\\ & = \sqrt{1 + 4 + 16 + 9}
\\ & = \sqrt{30}
\end{align*}\]と計算できる。
また、行列 \( A A^{\top} \)、\( A^{\top} A \) は下のように計算できる。\[\begin{align*}
A A^{\top} & = \left( \begin{array}{ccc} 1 & -2 \\ 4 & -3 \end{array} \right) \left( \begin{array}{ccc} 1 & 4 \\ -2 & -3 \end{array} \right)
\\ & = \left( \begin{array}{ccc} \textcolor{red}{5} & 10 \\ 10 & \textcolor{red}{25} \end{array} \right)
\end{align*}\]
\[\begin{align*}
A^{\top} A & = \left( \begin{array}{ccc} 1 & 4 \\ -2 & -3 \end{array} \right) \left( \begin{array}{ccc} 1 & -2 \\ 4 & -3 \end{array} \right)
\\ & = \left( \begin{array}{ccc} \textcolor{red}{17} & -14 \\ -14 & \textcolor{red}{13} \end{array} \right)
\end{align*}\]
そのため、\[\begin{align*}
\mathrm{trace} \left[ A A^{\top} \right] & = 5 + 25 = 30 \\
\mathrm{trace} \left[ A^{\top} A \right] & = 17 + 13 = 30
\end{align*}\]となり、確かに \( \| A \|_F^2 = 30 \) と一致することが確認できた。
(4) なぜ行列のトレースからフロベニウスノルムが出せるのか
(2)が成立することを確かめるためには、\( m \) 行 \( n \) 列の行列\[
A = \left( \begin{array}{ccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array} \right)
\]に対して、\( A A^{\top} \) および \( A^{\top} A \) を計算し、その対角成分の和を計算することで求めることができます。
ここでは、計算を省略しますが実際に計算することで、下の式が導出されます。\[\begin{align*}
\mathrm{trace} \left[ A A^{\top} \right] & = \sum^{m}_{i = 1} \left( \sum^{n}_{j = 1} a_{ij}^2 \right)
\\ & = \mathrm{trace} \left[ A^{\top} A \right]
\end{align*}\]
4. 行列の最大値ノルム
(1) 計算公式
行列の最大値ノルム \( \| A \|_{\mathrm{max}} \) は、フロベニウスノルムのときと同じように \( m \) 行 \( n \) 列 の行列 \( A \) を1列に並べ、ベクトルにした後、∞ノルムの計算をすることで求められます。
例えば、下の行列\[
A = \left( \begin{array}{ccc} \textcolor{red}{-4} & \textcolor{blue}{2} & \textcolor{green}{3} \\ \textcolor{red}{1} & \textcolor{blue}{0} & \textcolor{green}{-2} \end{array} \right)
\]の場合、1行に並べたベクトル \( \vec{a}' = \mathrm{vec} (A) \) は下のようになります。\[ \vec{a}' = \left( \begin{array}{ccc} \textcolor{red}{-4} \\ \textcolor{red}{1} \\ \textcolor{blue}{2} \\ \textcolor{blue}{0} \\ \textcolor{green}{3} \\ \textcolor{green}{-2} \end{array} \right) = \mathrm{vec} (A)
\]
あとはこのベクトル \( \vec{a}' \) の∞ノルム \( \| \vec{a}' \|_{\infty} \) を求めるだけでOKです。\[\begin{align*}
\| A \|_{\mathrm{max}} & = \max (|-4|,|1|,|2|,|0|,|3|,|-2|)
\\ & = 4
\end{align*}\]
なお、行列をベクトルにする前後で各成分の値自体は変化しませんね。
そのため、最大値ノルムは「行列内の各成分の絶対値」の中で最も大きい値となります。
次のような \( m \) 行 \( n \) 列の行列 \( A \) がある。\[
A = \left( \begin{array}{ccc} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{array} \right)
\]この行列 \( A \) の最大値ノルム \( \| A \|_{\mathrm{max}} \) は、「行列の各成分の絶対値」の中で、最も大きな値となる。\[
\| A \|_{\mathrm{max}} = \textcolor{red}{ \max_{i, j} | a_{ij} | }
\]
[2022/08/26 修正] 公式の数式部分が誤っていたため、正しい数式に修正いたしました。申し訳ございません。
(2) 例題
次の行列 \( A \) に対し、最大値ノルム \( \| A \|_{ \mathrm{max} } \) を計算しなさい。\[
A = \left( \begin{array}{ccc} -1 & 2 \\ -4 & 3 \end{array} \right)
\]
[解説5]
\[\begin{align*}
\| A \|_{ \mathrm{max} } & = \max (|-1|,|2|,|-4|,|3| )
\\ & = 4
\end{align*}\]
5. 練習問題
それでは、今回出てきた様々なノルムを計算する練習をしてみましょう。
次の行列\[
A = \left( \begin{array}{ccc} 10 & 5 & 5 \\ 2 & -5 & 1 \\ -2 & 2 & 2 \end{array} \right)
\]に対して、(1)~(5)を計算しなさい。
(1) 誘導1ノルム \( \| A \|_1 \)
(2) 誘導2ノルム \( \| A \|_2 \)
(3) 誘導∞ノルム \( \| A \|_{\infty} \)
(4) フロベニウスノルム \( \| A \|_F \)
(5) 最大値ノルム \( \| A \|_{\mathrm{max}} \)
6. 練習問題の答え
(1) 誘導1ノルム

(2) 誘導2ノルム
行列 \( A A^{\top} \) は次のように求められる。\[\begin{align*}
A A^{\top} & = \left( \begin{array}{ccc} 10 & 5 & 5 \\ 2 & -5 & 1 \\ -2 & 2 & 2 \end{array} \right) \left( \begin{array}{ccc} 10 & 5 & 5 \\ 2 & -5 & 1 \\ -2 & 2 & 2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 150 & 0 & 0 \\ 0 & 30 & -12 \\ 0 & -12 & 12 \end{array} \right)
\end{align*}\]
ここで、\( A A^{\top} \) の固有値を \( t \) とする。すると、\[\begin{align*}
| A A^{\top} - tE | & = \left| \begin{array}{ccc} 150-t & 0 & 0 \\ 0 & 30-t & -12 \\ 0 & -12 & 12-t \end{array} \right|
\\ & = (150-t) \left| \begin{array}{ccc} 30-t & -12 \\ -12 & 12-t \end{array} \right|
\\ & = (150-t) \left\{ (30-t)(12-t) - 144 \right\}
\\ & = (150-t) ( t^2 - 42t + 360 - 144 )
\\ & = (150-t) ( t^2 - 42t + 216)
\\ & = (150-t)( t-6)(t-36)
\\ & = 0
\end{align*}\]の関係式が成立する。
よって、\( A A^{\top} \) の固有値 \( t \) は6, 36, 150となる。
よって最大固有値150の平方根 \( \sqrt{150} = 5 \sqrt{6} \) が誘導2ノルムとなり、\( \| A \|_2 = 5 \sqrt{6} \) と求められる。
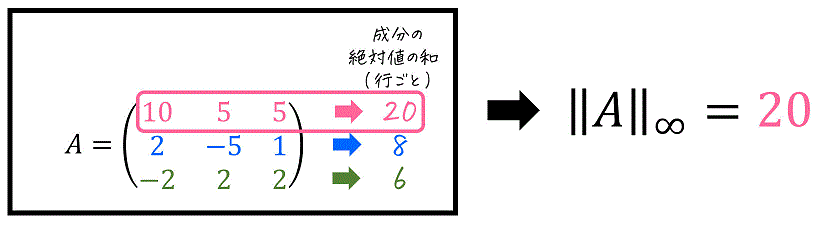
(3) 誘導∞ノルム
(4) フロベニウスノルム
[素直に各成分を2乗したものの和を平方根で求める]\[\begin{align*}
\| A \|_F & = \sqrt{10^2 + 5^2 + 5^2 + 2^2 + (-5)^2 + 1^2 + (-2)^2 + 2^2 + 2^2}
\\ & = \sqrt{100 + 25 + 25 + 4 + 25 + 1 + 4 + 4 + 4}
\\ & = \sqrt{192}
\\ & = 8 \sqrt{3}
\end{align*}\]
[(2)で求めた \( A A^{\top} \) の対角成分の和から求める]
\[\begin{align*}
\mathrm {trace} \left[ A A^{\top} \right] & = 150 + 30 + 12
\\ & = 192
\end{align*}\]より、\[\begin{align*}
\| A \|_F & = \sqrt{192}
\\ & = 8 \sqrt{3}
\end{align*}\]
(5) 最大値ノルム
\[\begin{align*}
\| A \|_{ \mathrm{max} } & = \max ( |10|,|5|,|5|,|2|,|-5|,|1|,|-2|,|2|,|2|)
\\ & = 10
\end{align*}\]
※ 絶対値を取り忘れても正解できてしまいますが、必ず絶対値を取るようにしましょう。
7. さいごに
今回は、行列のノルムとして、「誘導pノルム」、「フロベニウスノルム」、「最大値ノルム」の3種類を紹介しました。
行列のノルムは様々な種類があり、計算方法も似たような手順(誘導1ノルムと誘導∞ノルム)なものが多いので、ほかの行列のノルムとごちゃごちゃにならないようにきちんと復習しましょう。
次回は、関数のノルム・ベクトルの成分が関数となっているノルム(連続信号のノルム)についてみていきましょう。
注釈
| ↑1 | \( \vec{x} = \vec{0} \) の場合、\( \| \vec{0} \|_p= 0 \) となり、\( \frac{ \| A \vec{x} \|_p }{ \| \vec{x} \|_p } \) の分母が0になってしまうため、\( \vec{x} \not = \vec{0} \) と定義し、分母が0にならないようにしている。 |
|---|---|
| ↑2 | もちろん \( A^{\top} A \) の固有値を求めてもOK |
| ↑3 | フルサイズではない特異値分解としては、\( m \times r \) の行列 \( U \)、\( r \times r \) の対角行列 \( \Sigma \)、\( r \times n \) の行列 \( V \) を用いて \( U \Sigma V^{\top} \) と分解する手法もあります(ただし \( r = \min (m,n) \) とします)。この手法のことをエコノミーサイズの特異値分解と呼びます。 |
| ↑4 | \( r < n \) のとき、\( r+1\) 番目以降の \( \Sigma \vec{y} \) の成分はすべて0。 |
| ↑5 | \( m \) 行 \( n \) 列の行列を1列に並べることで作ったベクトルのpノルムのことを成分ノルムと呼びます。なお、フロベニウスノルムは \( p = 2 \) のときの成分ノルム(つまり特殊例)です。 |
関連広告・スポンサードリンク