スポンサードリンク
こんにちは、ももやまです!
この記事は、試験前日寝る前や、当日起きてから試験前までにサクッと1年後期の線形代数の範囲を復習できる記事となっております。
試験直前に是非読んでみてください!
スポンサードリンク
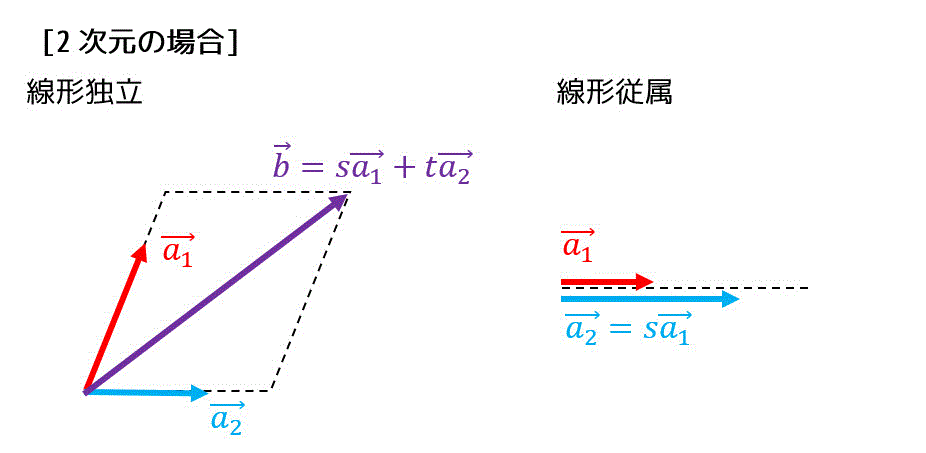
1. 線形独立・線形従属(1次独立・1次従属)
※ 線形独立のことを1次独立、線形従属のことを1次従属とも呼ぶ。
(1) 定義の確認
該当するうさぎ塾の記事↓↓
\( n \) 本のベクトルの組 \( \vec{a}_1 \), \( \vec{a}_2 \), …, \( \vec{a}_n \) に対して、\[
c_1 \vec{a}_1 + c_2 \vec{a}_2 + \cdots + c_n \vec{a}_n
\]を満たす実数 \( c_1 \), \( c_2 \), …, \( c_n \) が\[
c_1 = c_2 = \cdots = c_n = 0
\]しか存在しないとき、線形独立(1次独立)と呼ぶ。
逆に1つでも\[
c_1 \vec{a}_1 + c_2 \vec{a}_2 + \cdots + c_n \vec{a}_n = 0
\]を満たすような実数 \( c_1 \), \( c_2 \), …, \( c_n \) が \( c_1 = c_2 = \cdots = c_n = 0 \) 以外に存在すれば、線形従属(1次従属)となる。
また、線形従属のときは、 ベクトルの組 \( \vec{a}_1 \), \( \vec{a}_2 \), …, \( \vec{a}_n \) の中の1つのベクトルを、他のベクトルのペア(線形結合)で表すことができる。例えば、\( \vec{a}_1 \) であれば下のような関係式となる。\[
\vec{a}_1 = t_1 \vec{a}_2 + t_2 \vec{a}_3 + \cdots + t_{n-1} \vec{n}
\]※
(2) 線形独立の判定法
\( n \) 本の \( m \) 次元ベクトル \( \vec{a}_1 \), \( \vec{a}_2 \), …, \( \vec{a}_n \) を並べた行列\[
A = ( \vec{a}_1 , \vec{a}_2 , \cdots , \vec{a}_n )
\]を考える。
このとき、線形独立かどうかを判定するには行列の階数を調べればOK。
- \( \mathrm{Rank} \ A = n \) → 線形独立
- \( \mathrm{Rank} \ A < n \) → 線形従属
また、\( m = n \) となり、行列 \( A \) が正方行列であれば、行列式 \( |A| \) を計算することで線形独立性を判定することもできる。
- \( |A| \not = 0 \) → 線形独立
- \( |A| = 0 \) → 線形従属
ベクトル\[
\vec{a}_1 = \left( \begin{array}{ccc} 1 \\ 3 \end{array} \right) , \ \ \ \vec{a}_2 = \left( \begin{array}{ccc} 2 \\ -1 \end{array} \right)
\]は線形独立? 線形従属?
行列 \( A \) を\[\begin{align*}
A & = ( \vec{a}_1 , \vec{a}_2 )
\\ & = \left( \begin{array}{ccc} 1 & 2 \\ 3 & -1 \end{array} \right)
\end{align*}\]とする。
(i) 行列の階数による判定
\[\begin{align*}
A & = \left( \begin{array}{ccc} 1 & 2 \\ 3 & -1 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 2 \\ 0 & -7 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 2 \\ 0 & 1 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 0 \\ 0 & 1 \end{array} \right)
\end{align*}\]より、\( A \) の階数は2。
2本のベクトル(\( n = 2 \))に対し、階数は2。
よって、線形独立である。
(ii) 行列式による判定
\[\begin{align*}
A & = \left| \begin{array}{ccc} 1 & 2 \\ 3 & -1 \end{array} \right|
\\ & = -1 - 6
\\ & = -7 \not = 0
\end{align*}\]より、線形独立である。
行基本変形・列基本変形するときの注意点
(1) 行列の階数 \( \mathrm{Rank} \ A \) など、行列式 \( |A| \) 以外を求めるときの基本変形
- 行基本変形と列基本変形を混合して行うのは×
- 基本的に行基本変形のみを使うこと
- 変形次には → を使うこと(=を使ってはいけない)
(2) 行列式 \( |A| \) を求めるときの基本変形
- 行基本変形と列基本変形は混合して行ってもOK
- 変形時には = を使うこと
(3) 線形結合
あるベクトル \( \vec{b} \) を、線形独立なベクトルの組 \( \vec{a}_1 \), \( \vec{a}_2 \), …, \( \vec{a}_n \) を使って\[
\vec{b} = c_1 \vec{a}_1 + c_2 \vec{a}_2 + \cdots + c_n \vec{a}_n
\]と表すことを \( \vec{b} \) を \( \vec{a}_1 \), \( \vec{a}_2 \), …, \( \vec{a}_n \) の線形結合(1次結合)で表すと呼ぶ。
また、行基本変形の前後で1次結合の関係式(ベクトル間の関係式)は変化しない。
(4) 線形独立(1次独立)の最大数と最大組
線形独立なベクトルの組から、なるべく多くのベクトルを取り出して、線形独立な組を作り出すことを考えます。
\( n \) 本の \( m \) 次元ベクトル \( \vec{a}_1 \), \( \vec{a}_2 \), …, \( \vec{a}_n \) からなるべく多くのベクトルを取り出し、取り出したベクトルが線形独立にすることを考える。
ここで、\[
A = ( \vec{a}_1 , \vec{a}_2 , \cdots , \vec{a}_n )
\]を考える。
すると、線形独立な組の最大数は \( \mathrm{Rank} \ A \) となる。
また、行基本変形の前後で線形結合の関係式は変化しないため、線形独立な組の最大組も変化しない。
(5) 基底
\[
\left( \begin{array}{ccc} x \\ y \end{array} \right) = s \left( \begin{array}{ccc} 1 \\ 2 \end{array} \right) + t \left( \begin{array}{ccc} -3 \\ 1 \end{array} \right)
\]
のように、線形独立なベクトルの線形結合で表されているベクトルを下のように組で表したものを基底と呼ぶ。\[
\left\{ \left( \begin{array}{ccc} 1 \\ 2 \end{array} \right), \left( \begin{array}{ccc} -3 \\ 1 \end{array} \right) \right\}
\]
ベクトル\[
\vec{a}_1 = \left( \begin{array}{ccc} 5 \\ 5 \end{array} \right) , \ \ \ \vec{a}_2 = \left( \begin{array}{ccc} 1 \\ -2 \end{array} \right) , \ \ \ \vec{a}_3 = \left( \begin{array}{ccc} -3 \\ 1 \end{array} \right)
\]がある。このベクトルの中から、線形独立な組の最大組を基底とする。
(1) \( \vec{a}_1 \), \( \vec{a}_2 \), \( \vec{a}_3 \) の中から線形独立な組の最大組を求め、基底を作りなさい。
(2) (1)で答えた基底以外のベクトルを、基底のベクトルを用いて表しなさい。
[解説]
(1) 行列 \( A \) を\[\begin{align*}
A &= ( \vec{a}_1, \vec{a}_2, \vec{a}_3 )
\\ & = \left( \begin{array}{ccc} 5 & 1 & -3 \\ 5 & -2 & 1 \end{array} \right)
\end{align*}\]とする。行基本変形を行うと\[\begin{align*}
A & = \left( \begin{array}{ccc} 5 & 1 & -3 \\ 5 & -2 & 1 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 5 & 1 & -3 \\ 15 & 0 & -5 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 5 & 1 & -3 \\ 3 & 0 & -1 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} -4 & 1 & 0 \\ 3 & 0 & -1 \end{array} \right)
\end{align*}\]となる。
ここで、行基本変形の行列を\[\begin{align*}
B & = (\vec{b}_1, \textcolor{red}{\vec{b}_2}, \textcolor{blue}{\vec{b}_3})
\\ & = \left( \begin{array}{ccc} -4 & \textcolor{red}{1} & \textcolor{blue}{0} \\ 3 & \textcolor{red}{0} & \textcolor{blue}{-1} \end{array} \right)
\end{align*}\]とおく。
すると、\( \vec{b}_2 \), \( \vec{b}_3 \) は明らかに線形独立[1]もし明らかじゃないだろっていう人がいたら素直に行列式 \( |(\vec{b}_2, \vec{b}_3)| \) を計算してください。。
ここで行基本変形の前後で線形独立性は変化しないので、\( \vec{a}_2 \), \( \vec{a}_3 \) は線形独立な組の最大組となる。(最大数は \( \mathrm{Rank} \ A = 2 \))
(2) まず、\( \vec{b}_1 \) を \( \vec{b}_2 \)、\( \vec{b}_3 \) を用いて表すと、\[
\vec{b}_1 = -4 \vec{b}_2 - 3 \vec{b}_3\]となる。
ここで、行基本変形の前後でベクトルの関係式(線形結合の係数)は変化しないため、\[
\vec{a}_1 = -4 \vec{a}_2 - 3 \vec{a}_3
\]も成立。
スポンサードリンク
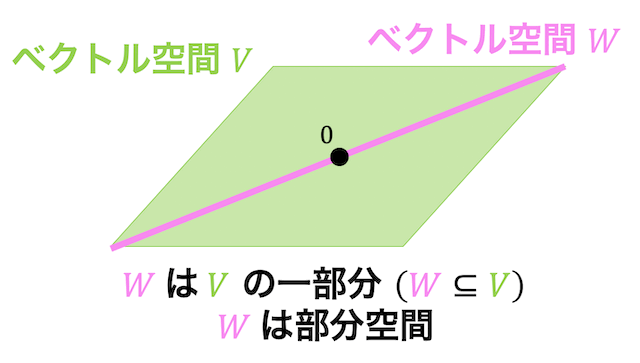
2. 部分空間
該当するうさぎ塾の記事↓↓
(1) 定義の確認
次の(1), (2)をともに満たすとき、集合 \( W \) が部分空間であるといえる。
(1) 部分空間に属するベクトル \( \vec{x} \), \( \vec{y} \) を足しても必ず部分空間となる。\[
\vec{x} \in W \ \mathrm{かつ} \ \vec{y} \in W \to \vec{x}+\vec{y} \in W
\]
(2) 部分空間に属するベクトル \( \vec{x} \) を定数倍しても必ず部分空間になる。\[
\vec{x} \in W \to k \vec{x} \in W
\]※ \( k \) は実数
なお、部分空間を証明する際には、練習3のように行列を使って証明すると手っ取り早い。
次の2次元ベクトル空間 \( \mathbb{R}^2 \) 上の空間 \( W_1 \), \( W_2 \) が部分空間であるかを判定しなさい。
(時間がある人は、部分空間であれば証明を、部分空間でなければ反例を1つ挙げなさい。)
(1)\[
W_1 = \left\{ \left( \begin{array}{ccc} x \\ y \end{array} \right) \middle| \ 2x-3y=0 \right\}
\]
(2)\[
W_1 = \left\{ \left( \begin{array}{ccc} x \\ y \end{array} \right) \middle| \ 2x-3y \geqq 0 \right\}
\]
[解説]
(1) 部分空間である
行列 \( A \)、およびベクトル \( \vec{x} \) を\[
A = \left( \begin{array}{ccc} 2 & 0 \\ 0 & 3 \end{array} \right) , \ \ \
\vec{x} = \left( \begin{array}{ccc} x \\ y \end{array} \right)
\]とする。
すると、\[
W_1 = \left\{ \vec{x} \middle| \ A \vec{x} = \vec{0} \right\}
\]と書き換えることができる。
ここで、部分空間であることを示すためには、\( \vec{x} \), \( \vec{y} \) が部分空間であるときに、
(a) \( \vec{x} + \vec{y} \in W_1 \)
(b) \( k \vec{x} \in W_1 \)
を示せばOK。
(a) \( \vec{x} + \vec{y} \in W_1 \)
\( \vec{x} \), \( \vec{y} \) は部分空間なので \( A \vec{x}=0 \), \( A \vec{y}=0 \) が成立。
ここで、\( \vec{x} + \vec{y} \in W_1 \) を示すためには \( A( \vec{x} + \vec{y}) = 0 \) を示せばOK。
\[\begin{align*}
A ( \vec{x} + \vec{y} ) & = A \vec{x} + A \vec{y}
\\ & = 0 + 0 = 0
\end{align*}\]より、(a)成立。
(b) \( k \vec{x} \in W_1 \)
\( \vec{x} \) は部分空間なので \( A \vec{x}=0 \) が成立。
ここで、\(k \vec{x} \in W_1 \) を示すためには \( k \vec{x} = 0 \) を示せばOK。
\[\begin{align*}
A ( k \vec{x} ) & = Ak \vec{x}
\\ & = k (A \vec{x})
\\ & = k \cdot 0 = 0
\end{align*}\]より、(b)成立。
(a), (b)より \( W_1 \) が部分空間であることが示された。
(2) 部分空間ではない。
\( W_2 \) が部分空間であると仮定する。例えば、\[
\vec{x} = \left( \begin{array}{ccc} 2 \\ 1 \end{array} \right)
\]を考える。これは、\( 2 \cdot 2 - 3 \cdot 1 = 1 \geqq 0 \) となり、部分空間となる。
ここで、\( W_2 \) は部分空間なので、-1倍した\[
- \vec{x} = \left( \begin{array}{ccc} -2 \\ -1 \end{array} \right)
\]も部分空間となる。
しかし、実際は \( 2 \cdot (-2) - 3 \cdot (-1) = -1 < 0 \) となり、部分空間とはならない。
よって仮定は矛盾。よって部分空間ではない。
(2) 部分空間が解空間のときの次元と基底
未知数が \( n \) 個の連立方程式 \( A \vec{x} = \vec{0} \) を解を要素とする集合\[
V = \left\{ \vec{x} \in \mathbb{R}^n \middle| \ A \vec{x} = \vec{0} \right\}
\]を考える。
このとき、部分空間 \( \vec{V} \) の次元と基底は以下のようになる。
- 次元: \( \dim V = n - \mathrm{Rank} \ A \)
- 基底: \( A \vec{x} = \vec{0} \) の解を基底で表したもの
以下の行列 \( A \) で与えられる部分空間 \( V \) の次元と基底を求めなさい。\[
A = \left( \begin{array}{ccc} 1 & 1 & -3 \\ -2 & 1 & 0 \\ 1 & -1 & 1 \end{array} \right)
\]\[
V = \left\{ \vec{x} \in \mathbb{R}^3 \middle| \ A \vec{x} = \vec{0} \right\}
\]
[解答]
連立方程式を解くための行基本変形を行う。\[\begin{align*}
A & = \left( \begin{array}{ccc} 1 & 1 & -3 \\ -2 & 1 & 0 \\ 1 & -1 & 1 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 1 & -3 \\ 0 & 3 & -6 \\ 0 & -2 & 4 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 1 & -3 \\ 0 & 1 & -2 \\ 0 & 0 & 0 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 0 & -1 \\ 0 & 1 & -2 \\ 0 & 0 & 0 \end{array} \right)
\end{align*}\]
となるので、\[
\left\{ \begin{array}{l} x - z = 0 \\ y - 2z = 0 \end{array} \right.
\]と同じ連立方程式となる。
ここで、\( \mathrm{Rank} \ A = 2 \) より、解空間の次元は 3 - 2 = 1。つまり、連立方程式の解を表すためには任意定数が1つ必要。その任意定数を \( k \) とする。
すると、解は\[
\vec{x} = k \left( \begin{array}{ccc} 1 \\ 2 \\ 1 \end{array} \right)
\]となるため、解空間の基底 \( V \) は\[
V = \left\{ \left( \begin{array}{ccc} 1 \\ 2 \\ 1 \end{array} \right) \right\}
\]となる。
検算にかかる時間: 30秒~1分
検算する価値: ★★☆
基底となるすべてのベクトル \( \vec{x} \) に対し、\( A \vec{x} = \vec{0} \) となることを確認すればOK。
(2) 部分空間が生成系のときの次元と基底
ベクトル \( \vec{a}_1 \), \( \vec{a}_2 \), …, \( \vec{a}_n \) が生成する部分空間\[
V = \left< \vec{a}_1 , \vec{a}_2, \cdots, \vec{a}_n \right>
\]の次元と基底は以下のように求められる。
- 次元: \( \dim V = \mathrm{Rank} \ A \)
- 基底: \( V \) 内のベクトルから選べる1次独立な最大組
次の \( \mathbb{R}^3 \) のベクトル\[
\vec{a}_1 = \left( \begin{array}{ccc} 0 \\ -1 \\ 3 \end{array} \right) , \ \ \
\vec{a}_2 = \left( \begin{array}{ccc} 1 \\ 1 \\ 0 \end{array} \right) , \ \ \
\vec{a}_3 = \left( \begin{array}{ccc} 2 \\ 1 \\ 3 \end{array} \right)
\]が生成する部分空間 \( V \) の次元とその基底を求めなさい。
[解説]
行列 \( A \) を\[\begin{align*}
A & = ( \vec{a}_1, \vec{a}_2, \vec{a}_3 )
\\ & = \left( \begin{array}{ccc} 0 & 1 & 2 \\ -1 & 1 & 1 \\ 3 & 0 & 3 \end{array} \right)
\end{align*}\]とし、行基本変形を行う。\[\begin{align*}
A & = \left( \begin{array}{ccc} 0 & 1 & 2 \\ -1 & 1 & 1 \\ 3 & 0 & 3 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 0 & 1 & 2 \\ -1 & 1 & 1 \\ 0 & 3 & 6 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 0 & 1 & 2 \\ -1 & 0 & -1 \\ 0 & 0 & 0 \end{array} \right)
\\ & \to \left( \begin{array}{ccc} 1 & 0 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & 0 \end{array} \right)
\end{align*}\]
ここで、行列 \( A \) の階数は2なので、部分空間 \( V \) の次元は2となる。
さらに、行基本変形後の行列に対し、ベクトル \( \vec{b}_1 \), \( \vec{b}_2 \), \( \vec{b}_3 \) を次のように定義する。\[
\left( \begin{array}{ccc} \textcolor{red}{1} & \textcolor{blue}{0} & 1 \\ \textcolor{red}{0} & \textcolor{blue}{1} & 2 \\ \textcolor{red}{0} & \textcolor{blue}{0} & 0 \end{array} \right) = ( \textcolor{red}{ \vec{b}_1}, \textcolor{blue}{ \vec{b}_2 }, \vec{b}_3)
\]ここで、\( \vec{b}_1 \), \( \vec{b}_2 \) は明らかに線形独立である。
行基本変形を加えても線形独立性は変わらないため、\( \vec{a}_1 \), \( \vec{a}_2 \) も線形独立となり、この2本が部分空間の基底となる。\[\begin{align*}
V & = \left\{ \vec{a}_1, \vec{a}_2 \right\}
\\ & = \left\{ \left( \begin{array}{ccc} 0 \\ -1 \\ 3 \end{array} \right) , \left( \begin{array}{ccc} 1 \\ 1 \\ 0 \end{array} \right) \right\}
\end{align*}\]
※ 2本の線形独立なベクトルが選べていれば \( \vec{a}_1 \), \( \vec{a}_2 \) を基底としなくてもOK
検算にかかる時間: 1分程度
検算する価値: ★☆☆
線形独立なベクトルを並べた行列 \( A' \) を作り、実際に行列 \( A' \) の階数が次元に一致することを確かめればOK。
今回の場合は、\[\begin{align*}
A' & = (\vec{a}_1, \vec{a}_2)
\\ & = \left( \begin{array}{ccc} 0 & 1 \\ -1 & 1 \\ 3 & 0 \end{array} \right)
\end{align*}\]の階数が2になることを確かめればOK。
スポンサードリンク
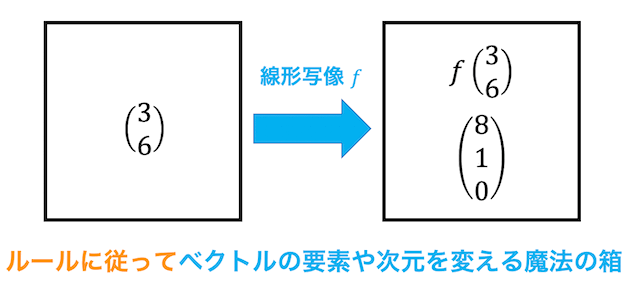
3. 線形写像
(1) 定義の確認
(1), (2)の該当するうさぎ塾の記事↓↓
まずは定義を確認しましょう。
- ある写像 \( f \) が次の1, 2を満たすとき、線形写像となる。
(1) 足し算の分離が可能\[
f( \vec{x} + \vec{y} ) = f( \vec{x} ) + f ( \vec{y} )
\]
(2) 定数倍の分離が可能\[
f( k \vec{x}) = k f ( \vec{x} )
\]
※1 \( \vec{x} \), \( \vec{y} \) はn次元ベクトル、\( k \) は実数
※2 証明の際は、部分空間のときのように行列 \( A \) をおき、行列の計算法則を使うと簡単に証明できます。
次の(1), (2)の写像 \( f \) は線形写像か。
(時間がある人は、線形写像であれば証明を、線形写像でなければ反例を書いてみましょう)
(1)\[
f: \ \mathbb{R}^2 \to \mathbb{R}^2 , \ \ \ f \left( \begin{array}{ccc} x_1 \\ x_2 \end{array} \right) = \left( \begin{array}{ccc} x_1 + x_2 \\ x_1 x_2 \end{array} \right)
\]
\]
(2)\[
f : \ \mathbb{R}^2 \to \mathbb{R}^2 , \ \ \ f \left( \begin{array}{ccc} x_1 \\ x_2 \end{array} \right) = \left( \begin{array}{ccc} x_1 \\ 2 x_1 - 3x_2 \end{array} \right)
\]
[解答]
(1) 線形写像ではない。
例えば、\[\begin{align*}
f \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right) & = \left( \begin{array}{ccc} 1+1 \\ 1 \cdot 1 \end{array} \right) \\ & = \left( \begin{array}{ccc} 2 \\ 1 \end{array} \right)
\end{align*}\] \[\begin{align*}
f \left( \begin{array}{ccc} 2 \\ 2 \end{array} \right) & = \left( \begin{array}{ccc} 2+2 \\ 2 \cdot 2 \end{array} \right) \\ & = \left( \begin{array}{ccc} 4 \\ 4 \end{array} \right)
\end{align*}\] が成立する。
ここで、\( f \) が線形写像と仮定すると、\[\begin{align*}
f \left( \begin{array}{ccc} 3 \\ 3 \end{array} \right) & =
f \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right) + f \left( \begin{array}{ccc} 2 \\ 2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 2 \\ 1 \end{array} \right) + \left( \begin{array}{ccc} 4 \\ 4 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 6 \\ 5 \end{array} \right)
\end{align*}\]と計算できる。
しかし、実際は\[\begin{align*}
f \left( \begin{array}{ccc} 3 \\ 3 \end{array} \right) & = \left( \begin{array}{ccc} 3+3 \\ 3 \cdot 3 \end{array} \right) \\ & = \left( \begin{array}{ccc} 6 \\ 9 \end{array} \right)
\end{align*}\]となり、仮定に矛盾する。
よって、線形写像ではない。
(2) 線形写像である。
線形写像であることは、任意のベクトル \( \vec{x}, \vec{y} \)、および任意の実数 \( k \) において、\[
\begin{array}{l} f ( \vec{x} + \vec{y} ) & = f ( \vec{x} ) + f ( \vec{y} ) \\
f (k \vec{x} ) & = k f ( \vec{x} ) \end{array}
\]が成立することを確かめればよい。
ここで、行列 \( A \)、ベクトル \( \vec{x} \) を\[
A = \left( \begin{array}{ccc} 1 & 0 \\ 2 & -3 \end{array} \right) , \ \ \
\vec{x} = \left( \begin{array}{ccc} x \\ y \end{array} \right)
\]とおく。すると、\[\begin{align*}
f \left( \begin{array}{ccc} x_1 \\ x_2 \end{array} \right) & = \left( \begin{array}{ccc} x_1 \\ 2 x_1 - 3x_2 \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 & 0 \\ 2 & -3 \end{array} \right) \left( \begin{array}{ccc} x_1 \\ x_2 \end{array} \right)
\\ & = A \vec{x}
\end{align*}\]となり、\( f ( \vec{x} ) = A \vec{x} \) と表せる。
(a) \( f ( \vec{x} + \vec{y} ) = f ( \vec{x} ) + f ( \vec{y} ) \) の証明
\[\begin{align*}
f ( \vec{x} + \vec{y} ) & = A ( \vec{x} + \vec{y} )
\\ & = A \vec{x} + A \vec{y}
\\ & = f( \vec{x} ) + f ( \vec{y} )
\end{align*}\]
より、(a)成立。
(b) \( f (k \vec{x} ) = k f ( \vec{x} ) \) の証明
\[\begin{align*}
f ( k \vec{x} ) & = A ( k \vec{x} )
\\ & = k A \vec{x}
\\ & =k f( \vec{x} )
\end{align*}\]
より、(b)成立。
(a), (b) より、\( f \) が線形写像であることが示された。
(2) 線形写像の表現行列
\( \mathbb{R}^n \to \mathbb{R}^m \) の線形写像 \( f \) の表現行列 \( A \) を考える。
(1) 表現行列 \( A \) は \( m \) 行 \( n \) 列となる。
(2) \( m = n \) の線形写像(表現行列が正方行列)、つまり線形写像の前後でベクトルの次元が変化しないとき、\( f \) は線形変換と呼ばれる。
(3) 表現行列 \( A \) は各基本ベクトルに対して線形写像を適用したものを並べたものである。\[
A = \left( \begin{array}{ccc} f \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right) & f \left( \begin{array}{ccc} 0 \\ 1 \\ 0 \end{array} \right) & f \left( \begin{array}{ccc} 0 \\ 0 \\ 1 \end{array} \right) \end{array} \right)
\]
(4) \( f \left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right) \) などを求める際には、加減算 \( f( \vec{x} + \vec{y} ) = f( \vec{x} ) + f( \vec{y} ) \) や定数倍 \( f( k \vec{x} ) = k f ( \vec{x} ) \)を駆使して基本ベクトルを作り出せばよい。
※1 \( \mathbb{R}^3 \) で例をしめしていますが、次元に関係なく同じ方法で求めることができます。
※2 逆行列を使って求める方法もありますが、個人的にはあまりおすすめではありません。
検算にかかる時間: 30秒程度
検算する価値: ★★☆
表現行列 \( A \) を求めたあとは、与えられた変換法則に対して、実際に \( f( \vec{x} ) = A \vec{x} \) が成り立つかを確認することで検算をすることができる。
※ 時間がもったいないので、与えられた変換法則のうちの1つを試せばOK。
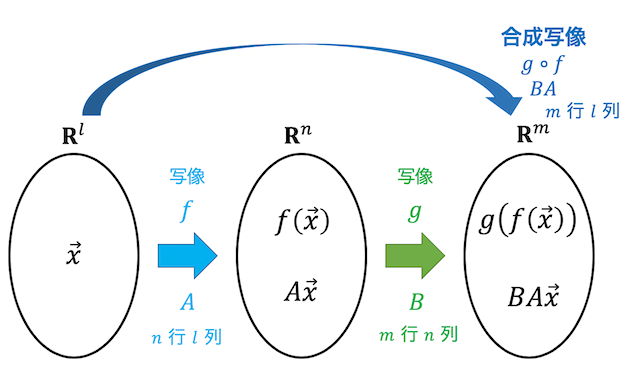
(3) 合成写像の表現行列
(3), (4)の該当するうさぎ塾の記事↓↓
ある線形写像 \( f \) の表現行列を \( A \)、線形写像 \( g \) の表現行列を \( B \) とする。
このとき、写像 \( f \) → 写像 \( g \) の順に適用する合成写像を \( g \circ f \) と書き、その表現行列は \( BA \) となる。
また、写像 \( g \) → 写像 \( f \) の順に適用する合成写像を \( f \circ g \) と書き、その表現行列は \( AB \) となる。
- 行列の積は交換不可(\( AB \not = BA \) )なので注意! 写像の適用順序を変えると、表現行列は変わります。
- 行列の積が計算できないときは、その合成写像は適用できない。
検算にかかる時間: 1分
検算する価値: ★☆☆(それなりにあり)
例えば、表現行列 \( A \) の写像 \( f \) → 表現行列 \( B \) の写像 \( g \) の順に適用する合成写像 \( g \circ f \) は \( C = BA \) となる。
これを検算するためには、\[\begin{align*}
\vec{x}'' & = g(f(\vec{x}) )
\\ & = g(A \vec{x} )
\\ & = g( \vec{x}' )
\\ & = B \vec{x}'
\end{align*}\]のように地道に求めた \( \vec{x}'' \) と、\( \vec{x}'' = C \vec{x} \) が一致するかを確かめればOK。
(4) 逆変換の表現行列
表現行列 \( A \) の線形変換 \( f \) の逆変換 \( f^{-1} \) を考える。このとき、逆変換が計算できる条件は以下の2つである。
- 表現行列 \( A \) が正方行列である。(変換の前後でベクトルの次元が変わらない)
- 表現行列 \( A \) が逆行列を持つ。(\( |A| \not = 0 \) である
また、逆変換が存在するとき、逆変換 \( f^{-1} \) の表現行列は \( A^{-1} \) で計算できる。
検算にかかる時間: 2次正方行列 30秒、3次正方行列 1分
検算する価値: ★★☆
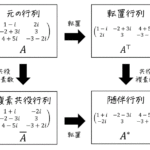
(1) 元の行列 \( A \) とその逆行列 \( A^{-1} \) の積は必ず単位行列となる。つまり、\[
A A^{-1} = E
\]が成立するかどうかを確かめれば検算が可能。
(5) 核と像
該当するうさぎ塾の記事↓↓
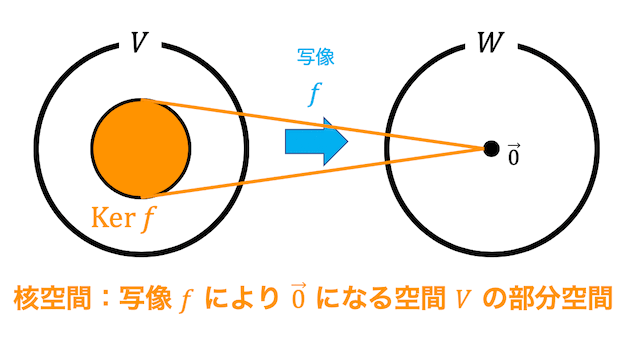
\( \mathbb{R}^n \to \mathbb{R}^m \) への線形写像 \( f \) の表現行列を \( A \) とする。このとき、核空間 \( \mathrm{Ker} \ f \)、像空間 \( \mathrm{Im} \ f \) の次元と基底は以下のように求められる。
(1) 核空間 \( \mathrm{Ker} \ f \)
次元: \( n - \mathrm{Rank} \ A \)
基底: 連立方程式 \( A \vec{x} = \vec{0} \) の解空間
(2) 像空間 \( \mathrm{Im} \ f \)
次元: \( \mathrm{Rank} \ A \)
基底: \( A = ( \vec{a}_1, \vec{a}_2, \cdots, \vec{a}_n ) \) としたときの、ベクトルが生成する部分空間[2]\( \vec{a}_1, \vec{a}_2, \cdots, \vec{a}_n \) から選べる線形独立(1次独立)なベクトルの最大組。
検算にかかる時間: 核 30秒~1分 像 1分程度
検算する価値: 核 ★★☆ 像 ★☆☆
※ 線形写像 \( f \) の表現行列 \( A \) とする。
核空間:基底となるすべてのベクトル \( \vec{x} \) に対し、\( A \vec{x} = \vec{0} \) となることを確認すればOK。
像空間:基底となるすべてのベクトルを並べて \( A' = ( \vec{a}_1, \vec{a}_2, \cdots ) \) と行列を作り、\( A' \) の階数が核空間の次元と等しくなることを確認すればOK。
4. 正規直交基底の作成
該当するうさぎ塾の記事↓↓
(1) 正規直交基底の重要な性質
ある基底 \( \left\{ \vec{u}_1 , \vec{u}_2, \cdots, \vec{u}_n \right\} \) が正規直交基底であるとする。このとき、
(1) どのベクトルの大きさも1である。\[
| \vec{u}_1 | = | \vec{u}_2 | = \cdots = | \vec{u}_n | = 1
\]
(2) 正規直交基底内のどの2つのベクトルを取ってきても内積が0である(直交する)。\[
\vec{u}_1 \cdot \vec{u}_2 = \vec{u}_1 \cdot \vec{u}_3 = \vec{u}_2 \cdot \vec{u}_3 = \cdots
\]
(3) 正規直交基底を並べて作った行列 \( U \) は直交行列となる。\[
U = ( \vec{u}_1, \vec{u}_2, \cdots, \vec{u}_n )
\]
(2) 直交行列の重要な性質
ある行列 \( U \) が直交行列のとき、以下の性質が成立する。
(1) 直交行列とその転値の積(順不同)は必ず単位行列となる\[
{}^t U U = U \ {}^t U = E
\]
(2) 直交行列を転置させたものは逆行列となる\[
{}^t U = U^{-1}
\]
(3) 直交行列の行列式は1か-1のいずれかである\[
|U| = \pm 1
\]
(4) ある直交行列 \( U \) を下のような縦ベクトルで分解する。\[
U = ( \vec{u}_1, \vec{u}_2, \cdots, \vec{u}_n )
\]このとき、これらのベクトルを基底 \( \{ \vec{u}_1, \vec{u}_2, \cdots, \vec{u}_n \} \)としたものは、正規直交基底となる。
(3) グラム・シュミットの直交化法
ベクトル \( \vec{a}_1 \), \( \vec{a}_2 \), \( \vec{a}_3 \) に対して、以下の演算を行うことで正規直交基底 \( { \vec{u}_1, \vec{u}_2, \vec{u}_3 } \) を得ることができる。
\[
\vec{u}_1 = \frac{ \vec{a}_1 }{ | \vec{a}_1 | }
\]\[
\vec{b}_2 = \vec{a}_2 - ( \vec{a}_2 \cdot \vec{u}_1 ) \vec{u}_1 , \ \ \ \vec{u}_2 = \frac{ \vec{b}_2 }{ | \vec{b}_2 | }
\]\[
\vec{b}_3 = \vec{a}_3 - ( \vec{a}_3 \cdot \vec{u}_1 ) \vec{u}_1 - ( \vec{a}_3 \cdot \vec{u}_2 ) \vec{u}_2 , \ \ \ \vec{u}_3 = \frac{ \vec{b}_3 }{ | \vec{b}_3 | }
\]
また、この公式を一般化したものを示す。
\[\begin{align*}
\vec{b}_n & = \vec {a}_n - ( \vec {a}_n \cdot \vec{u}_1 ) \vec{u}_1 - ( \vec{a}_n \cdot \vec{u}_2 ) - \cdots
\\ & = \vec{a}_n - \sum^{n-1}_{k = 1} ( \vec{a}_n \cdot \vec{u}_k ) \vec{u}_k
\end{align*}\]\[
\vec{u}_n = \frac{ \vec{b}_n }{ | \vec{b}_n | }
\]
検算にかかる時間: 10秒
検算する価値: ★★★(非常にあり!)
\( \vec{b}_2 \) を出した段階で、\( \vec{u}_1 \cdot \vec{b}_2 = 0 \) を、 \( \vec{b}_3 \) を出した段階で、\( \vec{u}_1 \cdot \vec{b}_3 = \vec{u}_2 \cdot \vec{b}_3 = 0 \) を確かめればOK。
5. 対角化・2次形式
(1) 固有値・固有ベクトル・固有空間の定義
該当するうさぎ塾の記事↓↓
ある正方行列 \( A \) の固有値を \( t \)、固有ベクトルを \( \vec{x} \) とする。
このとき、以下の関係式が成立する。\[
A \vec{x} = t \vec{x}
\]
また、固有空間 \( V( t ) \) は、ある固有値 \( t \) に対する固有ベクトルの基底となる。
ある \( n \) 次正方行列 \( A \) の固有値 \( t\)、固有ベクトル \( \vec{x} \) の計算方法は以下の通り。
(1) 固有値は \( |A - t E | = 0 \) となるような \( t \) を求める。
※ \( |tE - A| = 0 \) でもいいですが、\( A \) を-1倍するときにミスが発生する可能性があるのでおすすめしません。
(2) 固有ベクトルは連立方程式 \( (A - t E) \vec{x} = \vec{0} \) を解くことによって求められる。
ある \( n \) 次正方行列 \( A \) の固有値を \( t \)、固有ベクトルを \( \vec{x} \) とする。
(1) 固有ベクトルは、\( \vec{0} \) にはならない。
(2) ある固有値に対する固有ベクトルの数は、\( n - \mathrm{Rank} \ (A - tE) \) 本存在する。
(3) それぞれの固有値に対する固有ベクトルの数は最小で1本、最大で重解の数存在する。
(4) ある固有値に対して固有ベクトルが複数ある場合、それらのベクトルは必ず線形独立になるように取る必要がある。(異なる固有値に対する固有ベクトルとは勝手に線形独立になってくれます)
(5) ある固有値に対する固有ベクトルが存在しないなんてことはない。そんな状態になったら100%計算ミスをしている。
検算にかかる時間: 10秒
検算する価値: ★★★(非常にあり!)
例えば\[
A = \left( \begin{array}{ccc} \textcolor{red}{6} & 0 & -2 \\ 3 & \textcolor{red}{3} & -3 \\ 4 & 0 & \textcolor{red}{0} \end{array} \right)
\]であれば、対角成分の和は 6+3+0=9 なので、固有値の総和が9になることを確かめればOK。
※ 実際に固有値の総和を計算すると、2 + 3 + 4 = 9 になります。
※ 固有値に重解が含まれる場合は、重解の数だけカウントする。例えば固有値が4の3重解であれば、4×3=12となる。
検算にかかる時間: 20秒
検算する価値: ★☆☆(それなり)
固有値と固有ベクトルの定義 \( A \vec{x} = t \vec{x} \) が成立するかを実際に確認する。
次に紹介する \( AP = PD \) もしくはジョルダン標準形の検算で使われる \( AP = PJ \) で一致しなかったときに、どこで間違えているのかを把握するために使うのはあり。
(2) 行列の対角化
該当するうさぎ塾の記事 ↓↓
(2-i) 対角化できる条件
ある \( n \) 正方行列 \( A \) から、合計 \( n \) 本の固有ベクトルを計算することができるとき、行列 \( A \) を対角化することができる。
また、行列 \( A \) の固有値を \( t_1 \), \( t_2 \), …, とするとき、対角化ができる条件は、固有空間の次元を用いて以下のようにあらわせる\[
\dim V(t_1) + \dim V(t_2) + \cdots = n
\]
(2-ii) 対角化の計算
3次正方行列 ( A ) の対角化の流れは以下の通り。
※ 3次以外でも基本的な流れは同じです。
Step1. \( |A-tE|=0 \) と解いて固有値 \( t_1 \), \( t_2 \), \( t_3 \) を求める
※ 重解が含まれることもある
※ 計算後に \( t_1 + t_2 + t_3 = \) [行列の対角成分の和] を確認!
Step2. 各固有値ごとに固有ベクトル \( \vec{p}_1 \), \( \vec{p}_2 \), \( \vec{p}_3 \) を求める
※ 固有ベクトルが3本なければ対角化できない[3]固有空間でいうと、\[ \dim V(t_1) + \dim V(t_2) + \dim V(t_3) = 3 \]を満たしていれば対角化OK
Step3. 正則行列 \( P \) を用いて、以下のように \( P^{-1} AP = D \) を対角化する。\[
P = ( \textcolor{red}{\vec{p}_1}, \textcolor{blue}{\vec{p}_2}, \textcolor{green}{\vec{p}_3} ) , \ \ \ D = \left( \begin{array}{ccc} \textcolor{red}{t_1} & \textcolor{blue}{0} & \textcolor{green}{0} \\ \textcolor{red}{0} & \textcolor{blue}{t_2} & \textcolor{green}{0} \\ \textcolor{red}{0} & \textcolor{blue}{0} & \textcolor{green}{t_3} \end{array} \right)
\]※ 各列に対して、固有値と固有ベクトルが組になっているのがポイント
検算にかかる時間: 1分~2分
検算する価値: ★★☆(結構あり)
\( AP = PD \) を計算してみる。時間は少しかかるが、対角化の問題は配点が高いことが多いため、検算してあっていることが確認できればかなりメンタルが安定する。
※ 直交行列の対角化でも使えます。
(3) 直交行列による対角化
該当するうさぎ塾の記事↓↓
ある行列 \( A \) の行と列を転置させても変わらない行列、つまり \( {}^t \! A = A \) が成立する行列に対しては、直交行列を用いて対角化をすることができる。
また、 \( {}^t \! A = A \) を満たす行列のことを実対称行列(対称行列)と呼ぶ。
3次実正方行列 \( A \) を直交行列 \( P \) により対角化する流れは下の通り
※ 3次以外でも基本的な流れは同じ
Step1. \( |A-tE|=0 \) と解いて固有値 \( \alpha \), \( \beta \), \( \gamma \) を求める
※ ここまでは通常の対角化と同じ
※ 重解が含まれることもある
※ 計算後に \( \alpha + \beta + \gamma = \) [行列の対角成分の和] を確認!
Step2. 各固有値ごとに大きさが1の固有ベクトル \( \vec{p}_1 \), \( \vec{p}_2 \), \( \vec{p}_3 \) を求める。
ただし、重解となる固有値に対する固有ベクトルの組は、そのままでは正規直交基底にはならないので、グラム・シュミットの直交化法により正規直交基底になるようにする。
※ 異なる固有値に対する固有ベクトルは、正規化さえしていれば勝手に正規直交基底になるので、固有値が重解でなければ正規化だけをすればOK。
Step3. 直交行列 \( P \) を用いて、以下のように \( P^{-1} AP \) を対角化する。\[
P = ( \textcolor{red}{\vec{p}_1}, \textcolor{blue}{\vec{p}_2}, \textcolor{green}{\vec{p}_3} ) , \ \ \ D = \left( \begin{array}{ccc} \textcolor{red}{\alpha} & \textcolor{blue}{0} & \textcolor{green}{0} \\ \textcolor{red}{0} & \textcolor{blue}{\beta} & \textcolor{green}{0} \\ \textcolor{red}{0} & \textcolor{blue}{0} & \textcolor{green}{\gamma} \end{array} \right)
\]※ 各列に対して、固有値と固有ベクトルが組になっているのがポイント
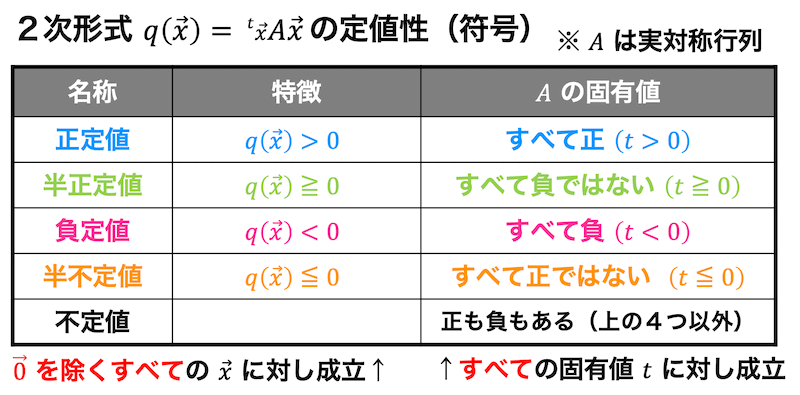
(4) 2次形式
該当するうさぎ塾の記事↓↓
2次形式\[
q(x_1, x_2, x_3) a x_1^2 + b x_2^2 + c x_3^2 + 2p x_1 x_2 + 2q x_1 x_3 + 2r x_2 x_3
\]の標準形を求める方法は以下の通り。
Step1. 2次形式行列 \( A \)、ベクトル \( \vec{x} \) を\[
A = \left( \begin{array}{ccc} a & p & q \\ p & b & r \\ q & r & c \end{array} \right), \ \ \ \vec{x} = \left( \begin{array}{ccc} x_1 \\ x_2 \\ x_3 \end{array} \right)
\]とおき、\( q(x_1,x_2,x_3) = {}^t \! \vec{x} A \vec{x} \) とする。
Step2・Step3は直交行列の対角化の方法と同じです!
Step2. \( |A-tE|=0 \) と解いて固有値 \( \alpha \), \( \beta \), \( \gamma \) を求める
※ 計算後に \( \alpha + \beta + \gamma = \) [行列の対角成分の和] を確認!
Step3. 各固有値ごとに大きさが1の固有ベクトル \( \vec{p}_1 \), \( \vec{p}_2 \), \( \vec{p}_3 \) を求める。
ただし、重解となる固有値に対する固有ベクトルの組は、そのままでは正規直交基底にはならないので、グラム・シュミットの直交化法により正規直交基底になるようにする。
※ 異なる固有値に対する固有ベクトルは、正規化さえしていれば勝手に正規直交基底になるので、固有値が重解でなければ正規化だけをすればOK。
Step3. 直交行列 \( P \) を用いて、以下のように \( P^{-1} AP \) を対角化する。\[
P = ( \textcolor{red}{\vec{p}_1}, \textcolor{blue}{\vec{p}_2}, \textcolor{green}{\vec{p}_3} ) , \ \ \ D = \left( \begin{array}{ccc} \textcolor{red}{\alpha} & \textcolor{blue}{0} & \textcolor{green}{0} \\ \textcolor{red}{0} & \textcolor{blue}{\beta} & \textcolor{green}{0} \\ \textcolor{red}{0} & \textcolor{blue}{0} & \textcolor{green}{\gamma} \end{array} \right)
\]※ 各列に対して、固有値と固有ベクトルが組になっているのがポイント
Step4. \[
\vec{y} = \left( \begin{array}{ccc} y_1 \\ y_2 \\ y_3 \end{array} \right)
\]とし、変換法則 \( \vec{y} = {}^t \! P \vec{x} \) もしくは \( \vec{x} = P \vec{y} \) を用いることで\[
a x_1^2 + b x_2^2 + c x_3^2 + 2p x_1 x_2 + 2q x_1 x_3 + 2r x_2 x_3 = \textcolor{red}{\alpha} y_1^2 + \textcolor{blue}{\beta} y_2^2 + \textcolor{green}{\gamma} y_3^2
\]と標準形にする。
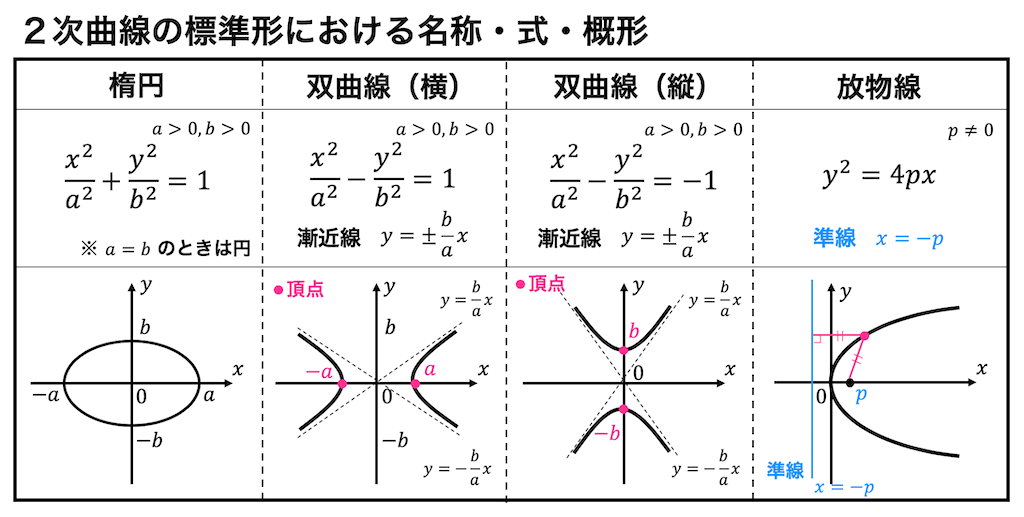
(5) 2次曲線
該当するうさぎ塾の記事↓↓
2次曲線\[
a x^2 + 2p xy + b y^2 + 2qx + 2ry + c = 0
\]のグラフを書く手順は以下の通り。
※ 3次以外でも基本的な流れは同じ
※ 主要部分 \( a x^2 + 2p xy + b y^2 = 0 \) のグラフであればStep3までの段階でグラフを書ける。
Step1. 主要部分 \( ax^2 + 2p xy + b^2 \) を行列 \( A \)、ベクトル \( \vec{x} \) で表す。\[
A = \left( \begin{array}{ccc} a & p \\ p & b \end{array} \right) , \ \ \
\vec{x} = \left( \begin{array}{ccc} x \\ y \end{array} \right)
\]で
Step2. 行列 \( A \) を直交行列 \( P \) になるように \( P^{-1} AP \) を対角化する。\[
P^{-1} AP = \left( \begin{array}{ccc} \alpha & 0 \\ 0 & \beta \end{array} \right)
\]その際に \( P \) が回転行列\[
P = \left( \begin{array}{ccc} \textcolor{magenta}{\cos \theta} & - \textcolor{deepskyblue}{\sin \theta} \\ \textcolor{deepskyblue}{\sin \theta} & \textcolor{magenta}{\cos \theta} \end{array} \right)
\]になるようにする。
※ 2×2の行列の場合、固有値に重解は発生しないため、グラム・シュミットの直交化を使うことは基本ない[4]異なる固有値に対する固有ベクトルは、正規化さえしていれば勝手に正規直交基底になるので、固有値が重解でなければ正規化だけをすればOK。。
Step3. \( P \vec{y} = \vec{x} \) を用いて、以下のように主要部分を標準形にする。\[
ax^2 + 2p xy + b^2 = \alpha X^2 + \beta Y^2
\]
Step4. \( \vec{x} = P \vec{y} \) の関係式から、主要部分以外も \( X \), \( Y \) を用いて表す。
さらに、\[
\textcolor{red}{\frac{(X-a')^2}{p^2} + \frac{(Y-a')^2}{q^2} = 1} \ \ \
\textcolor{blue}{\frac{(X-a')^2}{p^2} - \frac{(Y-a')^2}{q^2} = 1}
\]の形にする。(前者は楕円、後者は双曲線となる。)
Step5. 標準形から、図形の意味を考える。
Step6. 回転行列 \( P \) はどのように回転しているのかを調べ、さらに中心点を回転させる。
Step7. グラフを書く
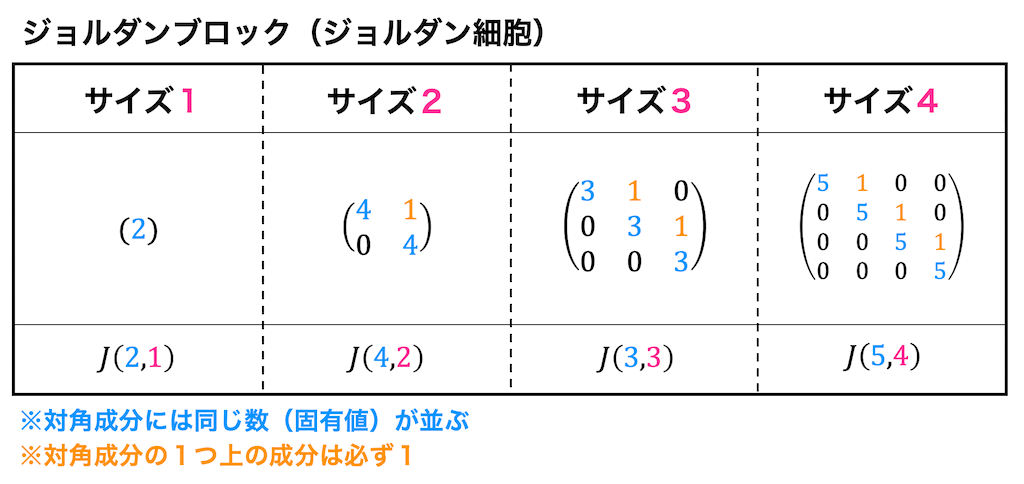
6. ジョルダン標準形
該当するうさぎ塾の記事↓↓
3次正方行列 ( A ) のジョルダン標準形の流れは以下の通り。
※ 3次以外でも基本的な流れは同じです。
Step1. \( |A-tE|=0 \) と解いて固有値 \( t_1 \), \( t_2 \), \( t_3 \) を求める
※ ジョルダン標準形を求める問題の場合、必ず固有値に重解が現れる
※ 計算後に \( t_1 + t_2 + t_3 = \) [行列の対角成分の和] を確認!
Step2. 各固有値ごとに広義固有ベクトル \( \vec{p}_1 \), \( \vec{p}_2 \), \( \vec{p}_3 \) を求める。
ここで、広義固有ベクトルの求め方は下の通り
- 固有ベクトルが固有値の重解の数だけ出てきたとき
→ 普通の固有ベクトルの求め方と同じ - ある固有値 \( t \) が2重解で、固有ベクトルが1本しかないとき
→ まず普通に固有ベクトル \( \vec{p}_1 \) を求め、\( A \vec{p}_2 = \vec{p}_1 \) となるような \( \vec{p}_2 \) を固有ベクトルの代わりにする - る固有値 \( t \) が3重解で、固有ベクトルが1本しかないとき
→ まず普通に固有ベクトル \( \vec{p}_1 \) を求め、\( A \vec{p}_2 = \vec{p}_1 \) となるような \( \vec{p}_2 \) を固有ベクトルの代わりにし、さらに \( A \vec{p}_3 = \vec{p}_2 \) となるような \( \vec{p}_3 \) を固有ベクトルの代わりにする。 - ある固有値 \( t \) が2重解で、固有ベクトルが1本しかないとき
→ 定義 \( (A-tE)^2 \vec{p} = \vec{0} \) を満たすような固有ベクトルを探す
Step3. 正則行列 \( P \) を用いて、以下のように \( P^{-1} AP = J \) を対角化する。\[
P = ( \textcolor{red}{\vec{p}_1}, \textcolor{blue}{\vec{p}_2}, \textcolor{green}{\vec{p}_3} ) , \ \ \ J = \left( \begin{array}{ccc} \textcolor{red}{t_1} & \textcolor{blue}{*} & \textcolor{green}{0} \\ \textcolor{red}{0} & \textcolor{blue}{t_2} & \textcolor{green}{*} \\ \textcolor{red}{0} & \textcolor{blue}{0} & \textcolor{green}{t_3} \end{array} \right)
\]※ ここで、対角成分の上の \( * \) は、以下の法則によって決まる。
- \( (A - tE) \vec{p} = \vec{0} \) で求めた \( \vec{p} \) の列 → 0
- それ以外の列 → 1
関連広告・スポンサードリンク