z変換で差分方程式（漸化式）を解いてみよう！

2021年6月19日 2021年6月21日 69分49秒

ももうさ

スポンサードリンク

こんにちは、ももやまです。

高校生の頃、漸化式ですごく苦労した思い出はありませんか？　公式ごとに計算方法が色々あって頭に入れるのが大変でしたよね。

今回は、制御数学や信号処理で習うz変換を使って、差分方程式（漸化式）を機械的に解く方法を紹介したいと思います…！

（練習問題の後半では、国公立大学の2次試験問題で出題された漸化式をz変換を用いて解いていただきます！）

1. 差分方程式を解く前に
2. z変換を用いた差分方程式の解き方
3. z変換で連立差分方程式を解いてみよう！
4. 練習問題
5. 練習問題の答え
6. さいごに
7. 参考文献

スポンサードリンク

1. 差分方程式を解く前に

まず、差分方程式をz変換で解く際に、必要になってくる公式を簡単に説明していきます。

(1) 差分方程式で使う基本z変換法則

z変換の公式には、様々なものがあります。

しかし、差分方程式を解くだけであれば下の2つの法則さえ覚えておけばOKです。

(2) 差分方程式で使うz変換公式

差分方程式を解く際に、z変換 \( X(z) \) をいちいち定義\[
X(z) = \sum^{\infty}_{n = 0} x_n z^{-n}
\]から計算してたら時間がかかってしまいます。

そこで、差分方程式でよく出てくる z 変換は覚えてしまいましょう！

差分方程式で必ず使うz変換

変換後 \( X(z) \)	変換前 \( x_n \)
\[ \frac{z}{(z-\textcolor{red}{a})^{\textcolor{blue}{0}+1}} \]	\( {}_n \mathrm{C}_\textcolor{blue}{0} \cdot \textcolor{red}{a}^{n-\textcolor{blue}{0}} \)
\[ \frac{z}{(z-\textcolor{red}{a})^{\textcolor{blue}{1}+1}} \]	\( {}_n \mathrm{C}_\textcolor{blue}{1} \cdot \textcolor{red}{a}^{n-\textcolor{blue}{1}} \)
\[ \frac{z}{(z-\textcolor{red}{a})^{\textcolor{blue}{2}+1}} \]	\( {}_n \mathrm{C}_\textcolor{blue}{2} \cdot \textcolor{red}{a}^{n-\textcolor{blue}{2}} \)
\[ \frac{z}{(z-\textcolor{red}{a})^{ \textcolor{blue}{3}+1} } \]	\( {}_n \mathrm{C}_\textcolor{blue}{3} \cdot \textcolor{red}{a}^{n-\textcolor{blue}{3}} \)
\[ \frac{z}{(z - \textcolor{red}{a})^{\textcolor{blue}{k}+1}} \]	\( {}_n \mathrm{C}_\textcolor{blue}{k} \cdot \textcolor{red}{a}^{n-k} \)

上の式の赤色の文字と青色の文字は対応していると思っていただけたらOKです！

(3) 逆z変換特有の部分分数分解

上の表の変換後 \( X(z) \) に注目していただくと、分子がすべて \( z \) になっていることがわかりますね。

そこで、逆z変換する際には、分子が \( a \cdot z \) のような定数 \( a \) × \( z \) の形にするために部分分数分解を行います。

(i) 普通の部分分数分解の場合

通常の部分分数分解の場合、\[
\frac{x + 3}{(x-1)(x-2)} = \frac{a}{x-1} + \frac{b}{x-2}
\]分子に \( x \) の項は来ません。

しかし、差分方程式を解く際には、計算効率を上げるため、下の式のようにわざと分子に \( z \) をおきます。\[
\frac{z+3}{(z-1)(z-2)} = \frac{az}{z-1} + \frac{bz}{z-2}
\]

ただし、わざと \( z \) をおく以外は普通の部分分数分解と変わりません。例えば、\[
\frac{z^2+6z}{(z-1)(z-2)^2}
\]であれば、\[
\frac{z^2+6z}{(z-1)(z-2)^2} = \frac{az}{z-1} + \frac{bz}{z-2} + \frac{cz}{(z-2)^2}
\]おき、\( a \), \( b \), \( c \) を解いていきます。

（解く際には左辺の分母（今回であれば \( (z-1)(z-2)^2 \) ）を両辺に掛けて、部分分数分解先の分子に相当する変数 \( a \), \( b \), … のうち、1つしか残らないような値を代入する方法がおすすめです。解説もこの方法で書いております。）

(4) z変換表

実際にz変換を求めて差分方程式を求める際には、下のようなz変換表からある数列 \( x_n \) と、z変換後の関数 \( X(z) \) の対応が読み解ければOKです。

数列 \( x_n \)	z変換 \( X(z) \)
\( 1 \)	\[ \frac{1}{z-1} \]
\( a^n \)	\[ \frac{1}{z-a} \]
\( n \)	\[ \frac{1}{(z-1)^2} \]
\( n a^{n-1} \)	\[ \frac{1}{(z-a)^2} \]
⋮	⋮

(i) z変換をする場合

z変換は、表の左側 \( x_n \) から右側 \( X(z) \) への変換に相当します。

例えば、\( f(t) = 2^n \) をz変換すると考えましょう。まず、左側に \( 2^n \) に該当する項目がないかを探します。

すると、\( f(t) = a^n \) の \( a = 2 \) のときが該当しますね。該当する項目( \( a^n \) の右側を見ると、\[
\frac{1}{z-a}
\]と書かれていますね。ここに \( a = 2 \) を入れた\[
\frac{1}{z-2}
\]が \( 2^n \) のz変換の結果に相当します。

(ii) 逆z変換をする場合

逆z変換は、表の右側 \( X(z) \) から左側 \( x_n \) への変換に相当します。

例えば、\[ \frac{1}{(z-4)^2} \] を変換すると考えましょう。まず、右側に \( \frac{1}{(z-4)^2} \) に該当する項目がないかを探します。

すると、\[ X(z) = \frac{1}{(z-a)^2} \] の \( a = 4 \) のときが該当しますね。該当する項目 \( \frac{1}{(z-a)^2} \) の左側を見ると、\( n a^{n-1} \) と書かれていますね。ここに \( a = 4 \) を入れた\[
n 4^{n-1}
\]が \( \frac{1}{(z-4)^2} \) の逆z変換の結果に相当します。

(iii) PDF版z変換表

z変換表がPDFでほしい方は、下のボタンからダウンロードを行うことができます！

z変換表のダウンロードはこちら！

スポンサードリンク

2. z変換を用いた差分方程式の解き方

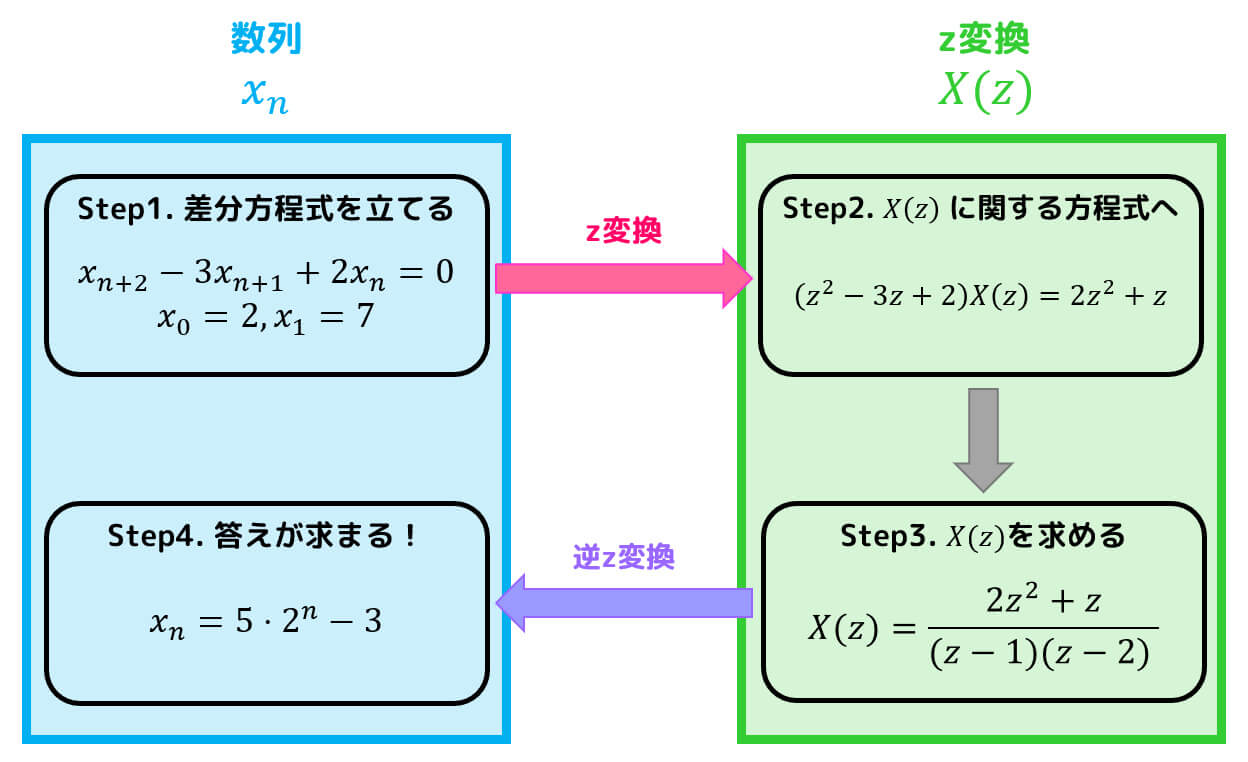
では、早速z変換を使った差分方程式の解き方を例題を用いて説明しましょう。

例題1

次の差分方程式\[
x_{n+2} - 3 x_{n+1} + 2 x_{n} = 0 , \ \ \ x_{0} = 2 , \ \ \ x_{1} = 7
\]を解きなさい。

Step1. 差分方程式を立てる

文章問題などで、差分方程式を立式する必要があれば最初に立式します。

今回は、問題文で式が与えられているため、立式は不要です。

ただし、以下の場合は式が与えられている場合であっても、変形が必要です。

(例外1) 式に \( x_{n-1} \), \( x_{n-2} \) のような \( x_{n-k} \) の形がある場合

この場合は、\( n \to n+k \) に変換することで、\( x_{n-a} \) の形が出ないようにしましょう。例えば、\[
x_{n} - 2 x_{n-1} = n^2
\]であれば、\( n \to n+1 \) とし、\[
x_{n+1} - 2 x_n = (n+1)^2
\]とすればOKです。

(例外2) 初項が \( x_0 \) ではない場合

特に高校数学の場合でよく見られるパターンです。（高校数学は初項が \( x_1 \) として与えられる場合がほとんど）

この場合は漸化式を逆算することで \( x_0 \) を出しましょう。例えば、\[
x_{n+1} - x_{n} = 2n + 1 , \ \ \ x_1 = 2
\]と与えられている場合、\( n = 0 \) を代入し、\( x_1 - x_0 = 1 \) から \( x_0 = 1 \) を計算します。

Step2. 両辺をz変換する

次に差分方程式の両辺をz変換しましょう。

ここで、\( \textcolor{orange}{x_{0} = 2} \), \( \ \textcolor{magenta}{x_{1} = 7} \) なので、\( x_{n+2} \), \( x_{n+1} \), \( x_{n} \) をz変換すると、\[\begin{align*}
\mathcal{Z} [ x_{n+2} ] & = z^2 X(z) - \textcolor{orange}{x_0} z^2 - \textcolor{magenta}{x_1} z
\\ & = z^2 X(z) - \textcolor{orange}{2} z^2 - \textcolor{magenta}{7} z
\end{align*}\]\[\begin{align*}
\mathcal{Z} [ x_{n+1} ] & = z X(z) - \textcolor{orange}{x_0} z
\\ & = z X(z) - \textcolor{orange}{2} z
\end{align*}\]\[\begin{align*}
\mathcal{Z} [ x_{n} ] = X(z)
\end{align*}\]となりますね。

なので、両辺をz変換すると、\[\begin{align*}
\mathcal{Z} \left[ x_{n+2} - 3 x_{n+1} + 2 x_{n}\right] & = \mathcal{Z} \left[ 0 \right] \\
\mathcal{Z} [ x_{n+2} ] - 3 \ \mathcal{Z} [ x_{n+1} ] + 2 \ \mathcal{Z} [ x_{n} ] & = \mathcal{Z} [ 0 ] \\
z^2 X(z) - 2 z^2 - 7z - 3 (z X(z) - 2z) + 2 X(z) &= 0
\end{align*}\]となり、さらに整理することで、\[
(z^2 - 3z + 2) X(z) = 2z^2 + z
\]と \( X(z) \) の1次方程式の形にすることができます。

Step3. X(z)をzの形で求める

Step2で求めた1次方程式の形を変形し、\( X(z) \) を \( z \) の形で求めます。

先程の1次方程式の両辺を \( z^2 - 3z + 2 \) で割ると、\[\begin{align*}
X(z) & = \frac{2z^2+z}{z^2-3z+2}
\\ & = \frac{2z^2+z}{(z-1)(z-2)}
\end{align*} \]と求めることができます。

（※ Step4で \( x_n \) を求める際に逆z変換がしやすいよう、分母を因数分解しておきましょう）

Step4. X(z)を逆z変換し、\( x_n \) を求める

(i) まずは部分分数分解し、公式の形に変形

あとは、\( X(z) \) を逆z変換することで差分方程式を満たす数列 \( x_n \) を求めることができます。

ここで、\( X(z) \) を\[
\frac{2z^2 + z}{(z-1)(z-2)} = \frac{az}{z-1} + \frac{bz}{z-2}
\]の形（部分分数分解）にするために \( a \), \( b \) の値を求めます。両辺を \( (z-1)(z-2) \) 倍すると、\[\begin{align*}
2z^2 + z & = az(z-2) + bz(z-1)
\end{align*}\]となります。

あとは、括弧内が0となるような \( z \) の値を代入し、\( a \), \( b \) を求めればOK。

\( z = 2 \) とする → \( 10 = 2b \) より \( b = 5 \)
\( z = 1 \) とする → \( 3 = -a \) より \( a = -3 \)

よって、\[
X(z) = - \frac{3z}{z-1} + \frac{5z}{z-2}
\]と変形ができます。

(ii) あとは公式を適用するのみ

最後に、公式を適用できる形になった \( X(z) \) を逆z変換し、元の数列 \( x_n \) を求めましょう。\[\begin{align*}
x_n & = \mathcal{Z}^{-1} \left[ x_n \right]
\\ & = \mathcal{Z}^{-1} \left[ - \frac{3z}{z-1} + \frac{5z}{z-2} \right]
\\ & = -3 \cdot \mathcal{Z}^{-1} \left[ \frac{z}{z-\textcolor{red}{1}} \right] + 5 \cdot \mathcal{Z}^{-1} \left[ \frac{z}{z-\textcolor{red}{2}} \right]
\\ & = -3 \cdot \textcolor{red}{1}^n + 5 \cdot \textcolor{red}{2}^n
\\ & = 5 \cdot 2^n - 3
\end{align*} \]

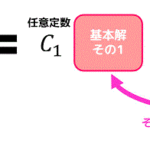
解き方の確認をしよう！

z変換を用いて、差分方程式を解く場合の流れを図で確認しましょう！

スポンサードリンク

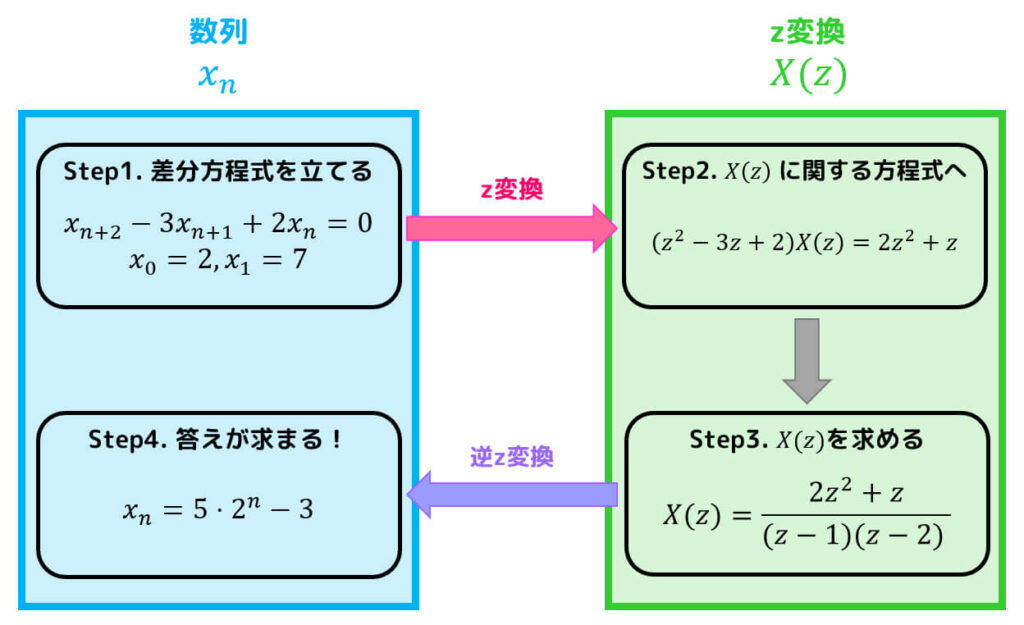
3. z変換で連立差分方程式を解いてみよう！

z変換を用いることで、連立差分方程式（連立漸化式）も解くことができます。

例題2

次の連立差分方程式\[
\left\{ \begin{array}{l}
x_{n+1} = 2 x_{n} + \ \ y_{n} \\
y_{n+1} = 2 x_{n} + 3 y_{n}
\end{array}\right.
\]を解きなさい。ただし、\( x_0 = 7 \), \( y_0 = -4 \) とする。

Step1. 差分方程式を立てる

すでに問題文で与えられているため、連立差分方程式を立てる必要はありません。

ただし、普通の差分方程式と同じように、以下の例外の場合は式が与えられている場合であっても、変形が必要です。

差分方程式に \( x_{n-a} \ )のようなマイナス方向へのシフトが入っている場合
初項が \( x_0 \) 始まりではない場合

Step2. 両辺をz変換する

次に、与えられた2つの式を両方ともz変換しましょう。
\( x_n \) のz変換を \( X(z) \)、\( y_n \) のz変換を \( Y(z) \) とおきましょうか。

ここで、\( \textcolor{orange}{x_0 = 7} \), \( \textcolor{magenta}{y_0 = -4} \) なので、\( x_{n+1} \), \( y_{n+1} \), \( x_{n} \), \( y_n \) をz変換すると、\[\begin{align*}
\mathcal{Z} [ x_{n+1} ] & = z X(z) - \textcolor{orange}{x_0} z
\\ & = z X(z) - \textcolor{orange}{7} z
\end{align*}\]\[\begin{align*}
\mathcal{Z} [ y_{n+1} ] & = z Y(z) - \textcolor{magenta}{y_0} z
\\ & = z Y(z) - \textcolor{magenta}{(-4)} z
\end{align*}\]\[\begin{align*}
\mathcal{Z} [ x_{n} ] = X(z) \\
\mathcal{Z} [ y_{n} ] = Y(z)
\end{align*}\]となりますね。

よって、\( x_{n+1} = 2 x_{n} + y_{n} \) は\[
z X(z) - 7 z = 2 X(z) + Y(z)
\]とz変換ができる。

同様に \( y_{n+1} = 2 x_{n} + 3 y_{n} \) をz変換すると、\[
z Y(z) + 4z = 2 X(z) + 3 Y(z)
\]となる。

z変換した結果をともに変形することで、\[
\left\{ \begin{array}{l}
(z-2) X(z) - Y(z) = 7z \\
-2 X(z) + (z-3) Y(z) = -4z
\end{array}\right.
\]となり、\( X(z) \), \( Y(z) \) の2元連立方程式の形に書き換えることができます。

連立漸化式は解くのが面倒くさいですが、ただの連立方程式に変形することができちゃえばもうこちらのものですね！

Step3. 連立方程式を解く

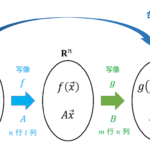
連立方程式は線形代数の力を使って解くことができます。

先程の連立方程式を行列を用いて表すと、\[
\left( \begin{array}{ccc} z-2 & -1 \\ -2 & z-3 \end{array} \right) \left( \begin{array}{ccc} X(z) \\ Y(z) \end{array} \right) = \left( \begin{array}{ccc} 7z \\ -4z \end{array} \right)
\]となり、\( A \vec{x} = \vec{b} \) の形に変形することができますね。

ここで、\( |A| \not = 0 \)（行列 \(A \) が正則）であれば、解を \( \vec{x} = A^{-1} \vec{b} \) と求めることができます。

\[\begin{align*}
|A| & = \left| \begin{array}{ccc} z-2 & -1 \\ -2 & z-3 \end{array} \right|
\\ & = (z-2)(z-3) - 2
\\ & = z^2 - 5z + 4
\\ & = (z-1)(z-4) \not = 0
\end{align*}\]となるため、行列 \( A \) は正則ですね。

ここで、逆行列 \( A^{-1} \) は、\[\begin{align*}
A^{-1} & = \frac{1}{|A|} \left( \begin{array}{ccc} z-3 & 1 \\ 2 & z-2 \end{array} \right)
\\ &= \frac{1}{(z-1)(z-4)} \left( \begin{array}{ccc} z-3 & 1 \\ 2 & z-2 \end{array} \right)
\end{align*}\]

となるため、\( X(z) \), \( Y(z) \) は\[\begin{align*}
\left( \begin{array}{ccc} X(z) \\ Y(z) \end{array} \right) & = \left( \begin{array}{ccc} z-2 & -1 \\ -2 & z-3 \end{array} \right)^{-1} \left( \begin{array}{ccc} 7z \\ -4z \end{array} \right)
\\ & = \frac{1}{(z-1)(z-4)} \left( \begin{array}{ccc} z-3 & 1 \\ 2 & z-2 \end{array} \right) \left( \begin{array}{ccc} 7z \\ -4z \end{array} \right)
\\ & = \frac{1}{(z-1)(z-4)} \left( \begin{array}{ccc} 7z(z-3) - 4z \\ 14z - 4z(z-2) \end{array} \right)
\\ & = \frac{1}{(z-1)(z-4)} \left( \begin{array}{ccc} 7z^2 - 25z \\ -4z^2 + 22z \end{array} \right)
\end{align*}\]となるため、\[
X(z) = \frac{7z^2 - 25z}{(z-1)(z-4)}
\]\[
Y(z) = \frac{-4z^2 + 22z}{(z-1)(z-4)}
\]と求めることができる。

Step4. あとは逆z変換するのみ！

Step3で求めた \( X(z) \), \( Y(z) \) を逆z変換しましょう。

まず、逆z変換公式に適用させるための部分分数分解を \( X(z) \), \( Y(z) \) それぞれに行います。

(1) X(z)に対する計算

(i) 部分分数分解

\[\begin{align*}
X(z) & = \frac{7z^2 - 25z}{(z-1)(z-4)}
\\ & = \frac{az}{z-1} + \frac{bz}{z-4}
\end{align*}\]の \( a \), \( b \) を求める。

両辺を \( (z-1)(z-4) \) 倍すると、\[
X(z) = 7z^2 - 25z = az(z-4) + bz(z-1)
\]となる。

\( z = 4 \) を代入 → \( 12 = 12b \) より \( b = 1 \)
\( z = 1 \) を代入 → \( -18 = -3a \) より \( a = 6 \)

よって、\[\begin{align*}
X(z) & = \frac{7z^2 - 25z}{(z-1)(z-4)}
\\ & = \frac{6z}{z-1} + \frac{z}{z-4}
\end{align*}\]と部分分数分解できる。

(ii) 逆z変換

部分分数分解後の \( X(z) \) を逆z変換し、元の数列 \( x_n \) を求めましょう。\[\begin{align*}
x_n & = \mathcal{Z}^{-1} \left[ x_n \right]
\\ & = \mathcal{Z}^{-1} \left[ \frac{6z}{z-1} + \frac{z}{z-4} \right]
\\ & = 6 \ \mathcal{Z}^{-1} \left[ \frac{z}{z-\textcolor{red}{1}} \right] + \mathcal{Z}^{-1} \left[ \frac{z}{z-\textcolor{red}{4}} \right]
\\ & = 6 \cdot \textcolor{red}{1}^n + \textcolor{red}{4}^n
\\ & = 4^n + 6
\end{align*} \]

(2) Y(z)に対する計算

(i) 部分分数分解

\[\begin{align*}
Y(z) & = \frac{-4z^2 + 22z}{(z-1)(z-4)}
\\ & = \frac{az}{z-1} + \frac{bz}{z-4}
\end{align*}\]の \( a \), \( b \) を求める。

両辺を \( (z-1)(z-4) \) 倍すると、\[
X(z) = -4z^2 + 22z = az(z-4) + bz(z-1)
\]となる。

\( z = 4 \) を代入 → \( 24 = 12b \) より \( b = 2 \)
\( z = 1 \) を代入 → \( 18 = -3a \) より \( a = -6 \)

よって、\[\begin{align*}
Y(z) & = \frac{-4z^2 + 22z}{(z-1)(z-4)}
\\ & = - \frac{6z}{z-1} + \frac{2z}{z-4}
\end{align*}\]と部分分数分解できる。

(ii) 逆z変換

\( X(z) \) と同じように \( Y(z) \) を逆z変換し、元の数列 \( y_n \) を求めましょう。\[\begin{align*}
y_n & = \mathcal{Z}^{-1} \left[ y_n \right]
\\ & = \mathcal{Z}^{-1} \left[ - \frac{6z}{z-1} + \frac{2z}{z-4} \right]
\\ & = -6 \ \mathcal{Z}^{-1} \left[ \frac{z}{z-\textcolor{red}{1}} \right] + 2 \ \mathcal{Z}^{-1} \left[ \frac{z}{z-\textcolor{red}{4}} \right]
\\ & = -6 \cdot \textcolor{red}{1}^n + 2 \ \textcolor{red}{4}^n
\\ & = 2 \cdot 4^n - 6
\end{align*} \]

よって、\( x_n \), \( y_n \) は\[
\left\{ \begin{array}{l}
x_{n} = 4^n + 6 \\
y_{n} = 2 \cdot 4^n - 6
\end{array}\right.
\]と求められる。

解き方の確認をしよう！

z変換を用いて、連立差分方程式を解く場合の流れを図で確認しましょう！

4. 練習問題

練習問題を4問用意しました。後半の2問は、国公立の入試問題となっております。ぜひ、国公立の入試問題をz変換で解いてみてください。

練習1

次の差分方程式\[
x_{n} - 4 x_{n-1} + 4 x_{n-2} = 3^n , \ \ \ x_{0} = 0 , \ \ \ x_{1} = 1
\]を解きなさい。

練習2

次の差分方程式\[
x_{n} - 4 x_{n-1} + 3 x_{n-2} = 4n , \ \ \ x_{0} = 1 , \ \ \ x_{1} = 2
\]を解きなさい。

※ 計算量がかなり多いので、覚悟して計算に挑んでください

練習3

次の漸化式（差分方程式）\[
a_{n+3} = 10 a_{n+2} - 31 a_{n+1} + 30 a_{n}
\]が存在する。\( a_0 = 1 \), \( a_1 = 2 \), \( a_2 = 5 \) のとき、\( a_n \) を \( n \) の式で表わせ。

[横浜国立大学　入試問題より(途中の誘導を飛ばしました)]

練習4

次の条件によって定められる数列 \( a_n \), \( b_n \) がある。

\[ a_1 = 3 , \ \ \ b_1 = 1 \]\[\begin{align*}
2 a_{n+1} & = 5 a_n + b_n + 2^{n+1} + 4 \ \ \ ( n = 1, \ 2 , \ 3, \cdots ) \\
2 b_{n+1} & = a_n + 5b_n - 2^{n+1} + 4 \ \ \ ( n = 1, \ 2 , \ 3, \cdots )
\end{align*} \]が存在する。

このとき、数列 \( a_n \) の一般項 \( a_n \) を \( n \) の式で表しなさい。

※ ヒント \( a_0 = 0 \), \( b_0 = 0 \) となる

[大分大学　入試問題より(途中の誘導を飛ばしました)]

5. 練習問題の答え

解答1

Step1. 方程式の書き換え

両辺をz変換しましょう。しかし、\( x_{n-1} \), \( x_{n-2} \) をz変換してしまうと、\( x_{-1} \), \( x_{-2} \) を求める必要があり、少し面倒くさいです。

そこで \( n \to n+2 \) と置き換えてあげましょう。すると、\[
x_{n+2} - 4 x_{n+1} + 4 x_{n} = 3^{n+2}
\]と書き換えることができます。

Step2. 両辺をz変換

ここで、\( \textcolor{orange}{x_{0} = 0} \), \( \ \textcolor{magenta}{x_{1} = 1} \) なので、\( x_{n+2} \), \( x_{n+1} \), \( x_{n} \) をz変換すると、\[\begin{align*}
\mathcal{Z} [ x_{n+2} ] & = z^2 X(z) - \textcolor{orange}{x_0} z^2 - \textcolor{magenta}{x_1} z
\\ & = z^2 X(z) - \textcolor{orange}{0} z^2 - \textcolor{magenta}{1} z
\\ & = z^2 X(z) - z
\end{align*}\]\[\begin{align*}
\mathcal{Z} [ x_{n+1} ] & = z X(z) - \textcolor{orange}{x_0} z
\\ & = z X(z) - \textcolor{orange}{0} z
\\ & = z X(z)
\end{align*}\]\[\begin{align*}
\mathcal{Z} [ x_{n} ] = X(z)
\end{align*}\]となりますね。

よって、両辺をz変換すると、\[\begin{align*}
\mathcal{Z} \left[ x_{n+2} - 4 x_{n+1} + 4 x_{n}\right] & = \mathcal{Z} \left[ 3^{n+2} \right] \\
\mathcal{Z} [ x_{n+2} ] - 4 \ \mathcal{Z} [ x_{n+1} ] + 4 \ \mathcal{Z} [ x_{n} ] & = 9 \mathcal{Z} [ \textcolor{red}{3}^n ] \\
z^2 X(z) - z - 4 \cdot z X(z) + 4 X(z) &= \frac{9z}{ z - \textcolor{red}{3} }
\end{align*}\]となり、さらに整理することで、\[\begin{align*}
(z^2-4z+4)X(z) & = \frac{9z}{z-3} + z
\\ & = \frac{9z + z(z-3)}{z-3}
\\ & = \frac{z^2 + 6z}{z-3}
\end{align*}\]と \( X(z) \) の1次方程式の形にすることができます。

Step3. X(z)を求める

ここで、両辺を \( z^2 - 4z + 4 \) で割ることで、\[\begin{align*}
X(z) & = \frac{z^2+6z}{(z^2-4z+4)(z-3)}
\\ & = \frac{z^2+6z}{(z-2)^2(z-3)}
\end{align*}\]と \( X(z) \) を求めることができます。

Step4. あとは逆z変換するのみ！

(i) 部分分数分解

ここで、\( X(z) \) を\[
\frac{z^2+6z}{(z-2)^2(z-3)} = \frac{az}{z-2} + \frac{bz}{(z-2)^2} + \frac{cz}{z-3}
\]の形（部分分数分解）にするために \( a \), \( b \), \( c \) の値を求めます。両辺を \( (z-2)^2(z-3)\) 倍すると、\[\begin{align*}
z^2+6z = az(z-2)(z-3) + bz(z-3) + cz(z-2)^2
\end{align*}\]となります。

あとは、括弧内が0となるような \( z \) の値を代入し、\( a \), \( b \) を求めればOK。

\( z = 2 \) とする → \( 16 = -2b \) より \( b = -8 \)
\( z = 3 \) とする → \( 27 = 3c \) より \( c = 9 \)
\( z = 1 \) とする → \( 7 = 2a - 2b + c = -34 + c \) より、\( a = -9 \)
※ \( z \) の値を何にしてもうまく \( b \), \( c \) が消えないため、適当な値を1つ代入した

よって、\[
X(z) = - \frac{9z}{z-2} - \frac{8z}{(z-2)^2} + \frac{9z}{z-3}
\]と変形ができます。

(ii) 逆z変換

最後に、公式を適用できる形になった \( X(z) \) を逆z変換し、元の数列 \( x_n \) を求めましょう。\[\begin{align*}
x_n & = \mathcal{Z}^{-1} \left[ x_n \right]
\\ & = \mathcal{Z}^{-1} \left[ - \frac{9z}{z-2} - \frac{8z}{(z-2)^2} + \frac{9z}{z-3} \right]
\\ & = -9 \mathcal{Z}^{-1} \left[ \frac{z}{z-\textcolor{red}{2}} \right] - 8 \mathcal{Z}^{-1} \left[ \frac{z}{(z-\textcolor{red}{2})}^{2} \right] + 9 \mathcal{Z}^{-1} \left[ \frac{z}{z-\textcolor{red}{3}} \right]
\\ & = -9 \cdot \textcolor{red}{2}^n - 8 \cdot n \cdot \textcolor{red}{2}^{n-1} + 9 \cdot \textcolor{red}{3}^n
\\ & = - 9 \cdot 2^n - 4n \cdot 2^{n} + 3^{n+2}
\\ & = 3^{n+2} - (4n+9) 2^n
\end{align*} \]となる。

解答2

Step1. 方程式の書き換え

練習1と同じく、\( x_{n-1} \), \( x_{n-2} \) をz変換してしまうと、\( x_{-1} \), \( x_{-2} \) を求める必要があり、少し面倒くさいです。

同じように \( n \to n+2 \) と置き換えてあげましょう。すると、\[\begin{align*}
x_{n+2} - 4 x_{n+1} + 3 x_{n} & = 4(n+2) = 4
\\ & = 4n + 8
\end{align*}\]と書き換えることができます。

Step2. 両辺をz変換

ここで、\( \textcolor{orange}{x_{0} = 1} \), \( \ \textcolor{magenta}{x_{1} = 2} \) なので、\( x_{n+2} \), \( x_{n+1} \), \( x_{n} \) をz変換すると、\[\begin{align*}
\mathcal{Z} [ x_{n+2} ] & = z^2 X(z) - \textcolor{orange}{x_0} z^2 - \textcolor{magenta}{x_1} z
\\ & = z^2 X(z) - \textcolor{orange}{1} z^2 - \textcolor{magenta}{2} z
\\ & = z^2 X(z) - z^2 - 2z
\end{align*}\]\[\begin{align*}
\mathcal{Z} [ x_{n+1} ] & = z X(z) - \textcolor{orange}{x_0} z
\\ & = z X(z) - \textcolor{orange}{1} z
\\ & = z X(z) - z
\end{align*}\]\[\begin{align*}
\mathcal{Z} [ x_{n} ] = X(z)
\end{align*}\]となりますね。

よって、両辺をz変換すると、\[\begin{align*}
\mathcal{Z} \left[ x_{n+2} - 4 x_{n+1} + 3 x_{n}\right] & = \mathcal{Z} \left[ 4n+8 \right] \\
\mathcal{Z} [ x_{n+2} ] - 4 \ \mathcal{Z} [ x_{n+1} ] + 3 \ \mathcal{Z} [ x_{n} ] & = 4 \mathcal{Z} [ n ] + 8 \mathcal{Z} [ 1 ] \\
z^2 X(z) - z^2 - 2z - 4 (z X(z) - z) + 3 X(z) &= \frac{4z}{(z-1)^2} + \frac{8z}{(z-1)}
\end{align*}\]となり、さらに整理することで、\[\begin{align*}
(z^2-4z+3)X(z) & = \frac{4z}{(z-1)^2} + \frac{8z}{(z-1)} + z^2 - 2z
\\ & = \frac{(z^2-2z)(z-1)^2 + 4z + 8z(z-1)}{(z-1)^2}
\\ & = \frac{z^4 - 4z^3 + 13z^2 - 6z}{(z-1)^2}
\end{align*}\]と \( X(z) \) の1次方程式の形にすることができます。

Step3. X(z)を求める

ここで、両辺を \( z^2-4z+3 \) で割ることで、\[\begin{align*}
X(z) & = \frac{z^4 - 4z^3 + 13z^2 - 6z}{(z^2-4z+3)(z-1)^2}
\\ & = \frac{z^4 - 4z^3 + 13z^2 - 6z}{(z-1)^3(z-3)}
\end{align*}\]と \( X(z) \) を求めることができます。

Step4. あとは逆z変換するのみ！

(i) 部分分数分解

ここで、\( X(z) \) を\[
\frac{z^4 - 4z^3 + 13z^2 - 6z}{(z-1)^3 (z-3)} = \frac{az}{z-1} + \frac{bz}{(z-1)^2} + \frac{cz}{(z-1)^3} + \frac{dz}{z-3}
\]の形（部分分数分解）にするために \( a \), \( b \), \( c \), \( d \) の値を求めます。両辺を \( (z-1)^3(z-3)\) 倍すると、\[\small \begin{align*}
z^4 - 4z^3 + 13z^2 - 6z & = az (z-1)^2 (z-3) + bz (z-1) (z-3) + cz (z-3) + d z (z-1)^3
\end{align*}\]となります。

あとは、括弧内が0となるような \( z \) の値を代入し、\( a \), \( b \) を求めればOK。

\( z = 1 \) とする → \( 4 = -2c \) より \( c = -2 \)
\( z = 3 \) とする → \( 72 = 24d \) より \( d = 3 \)
\( z = -1 \) とする → \( 24 = 16a-8b+4c+8d = 16a - 8b -8 + 24 \) より、\( 16a - 8b = 8 \)
\( z = 2 \) とする → \( 24 = -2a-2b-2c+2d = -2a-2b+4+6 \) より、\( -2a - 2b = 2 \)
- ※ \( z \) の値を何にしてもうまく \( a \), \( b \) が消えないため、適当な値を2つ代入した
- \( 16a - 8b = 8 \), \( -2a-2b = 2 \) を連立すると \( a = -2 \), \( b = -5 \) が求まる

よって、\[
X(z) = - \frac{2z}{z-1} - \frac{5z}{(z-1)^2} - \frac{2z}{(z-1)^3} + \frac{3z}{z-3}
\]と変形ができます。

(ii) 逆z変換

最後に、公式を適用できる形になった \( X(z) \) を逆z変換し、元の数列 \( x_n \) を求めましょう。\[\small \begin{align*}
x_n & = \mathcal{Z}^{-1} \left[ x_n \right]
\\ & = \mathcal{Z}^{-1} \left[ - \frac{2z}{z-1} - \frac{5z}{(z-1)^2} - \frac{2z}{(z-1)^3} + \frac{3z}{z-3} \right]
\\ & = -2 \mathcal{Z}^{-1} \left[ \frac{z}{z-\textcolor{red}{1}} \right] - 5 \mathcal{Z}^{-1} \left[ \frac{z}{(z-\textcolor{red}{1})^{2}} \right] - 2 \mathcal{Z}^{-1} \left[ \frac{z}{(z-\textcolor{red}{1})^{3}} \right] + 3 \mathcal{Z}^{-1} \left[ \frac{z}{z-\textcolor{red}{3}} \right]
\\ & = -2 - 5n - 2 {}_n \mathrm{C}_2 + 3\cdot \textcolor{red}{3}^n
\\ & = 3^{n+1} - n(n-1) - 5n - 2
\\ & = 3^{n+1} - n^2 - 4n - 2
\end{align*} \]となる。

※ 計算量えげつなかったですね……。

解答3

Step1. 方程式の書き換え

\( a_{n+3} \), \( a_{n+2} \), \( a_{n+1} \), \( a_{n} \) をすべて左辺に移行しましょう。すると、\[
a_{n+3} - 10 a_{n+2} + 31 a_{n+1} - 30 a_{n} = 0
\]となります。ついでに、\[
x_{n+3} - 10 x_{n+2} + 31 x_{n+1} - 30 x_{n} = 0
\]としましょうか。（\( x_n = a_n \) とした）

Step2. 両辺をz変換

ここで、\( \textcolor{orange}{x_{0} = 1} \), \( \ \textcolor{magenta}{x_{1} = 2} \), \( \ \textcolor{deepskyblue}{x_{2} = 5} \) なので、\( x_{n+3} \), \( x_{n+2} \), \( x_{n+1} \), \( x_{n} \) をz変換すると、\[\begin{align*}
\mathcal{Z} [ x_{n+3} ] & = z^2 X(z) - \textcolor{orange}{x_0} z^3 - \textcolor{magenta}{x_1} z^2 - \textcolor{deepskyblue}{x_2} z
\\ & = z^2 X(z) - \textcolor{orange}{1} z^3 - \textcolor{magenta}{2} z^2 - \textcolor{deepskyblue}{5} z
\\ & = z^3 X(z) - z^3 - 2z^2 - 5z
\end{align*}\]\[\begin{align*}
\mathcal{Z} [ x_{n+2} ] & = z^2 X(z) - \textcolor{orange}{x_0} z^2 - \textcolor{magenta}{x_1} z
\\ & = z^2 X(z) - \textcolor{orange}{1} z^2 - \textcolor{magenta}{2} z
\\ & = z^2 X(z) - z^2 - 2z
\end{align*}\]\[\begin{align*}
\mathcal{Z} [ x_{n+1} ] & = z X(z) - \textcolor{orange}{x_0} z
\\ & = z X(z) - \textcolor{orange}{1} z
\\ & = z X(z) - z
\end{align*}\]\[\begin{align*}
\mathcal{Z} [ x_{n} ] = X(z)
\end{align*}\]となりますね。

よって、両辺をz変換すると、\[\small \begin{align*}
\mathcal{Z} \left[ x_{n+3} - 10 x_{n+2} + 31 x_{n+1} - 30 x_{n} \right] & = \mathcal{Z} \left[ 0 \right] \\
\mathcal{Z} [ x_{n+3} ] - 10 \mathcal{Z} [ x_{n+2} ] + 31 \mathcal{Z} [ x_{n+1} ] - 30 \mathcal{Z} [ x_{n} ] & = \mathcal{Z} [ 0 ] \\
z^3 X(z) - z^3 - 2z^2 - 5z - 10(z^2 X(z) - z^2 - 2z) + 31(z X(z) - z) - 30 X(z) &= 0
\end{align*}\]となり、さらに整理することで、\[\begin{align*}
(z^3 -10z^2 + 31z - 30)X(z) & = z^3 - 8z^2 + 16z
\end{align*}\]と \( X(z) \) の1次方程式の形にすることができます。

Step3. X(z)を求める

ここで、両辺を \( z^3 -10z^2 + 31z - 30 \) で割ることで、\[\begin{align*}
X(z) & = \frac{z^3 - 8z^2 + 16z}{z^3 -10z^2 + 31z - 30}
\\ & = \frac{z^3 - 8z^2 + 16z}{(z-2)(z^2-8z+15)}
\\ & = \frac{z^3 - 8z^2 + 16z}{(z-2)(z-3)(z-5)}
\end{align*}\]と \( X(z) \) を求めることができます。

Step4. あとは逆z変換するのみ！

(i) 部分分数分解

ここで、\( X(z) \) を\[
\frac{z^3 - 8z^2 + 16z}{(z-2)(z-3)(z-5)} = \frac{az}{z-2} + \frac{bz}{z-3} + \frac{cz}{z-5}
\]の形（部分分数分解）にするために \( a \), \( b \), \( c \) の値を求めます。両辺を \( (z-2)(z-3)(z-5)\) 倍すると、\[\small \begin{align*}
z^3 - 8z^2 + 16z = az(z-3)(z-5) + bz(z-2)(z-5) + cz(z-2)(z-3)
\end{align*}\]となります。

あとは、括弧内が0となるような \( z \) の値を代入し、\( a \), \( b \) を求めればOK。

\( z = 2 \) とする → \( 8 = 6a \) より \( a = 4/3 \)
\( z = 3 \) とする → \( 3 = -6b \) より \( b = -1/2 \)
\( z = 5 \) とする → \( 5 = 30 \) より、\( c = 1/6 \)

よって、\[
X(z) = \frac{4}{3} \cdot \frac{z}{z-2} - \frac{1}{2} \cdot \frac{z}{z-3} + \frac{1}{6} \cdot \frac{z}{z-5}
\]と変形ができます。

(ii) 逆z変換

最後に、公式を適用できる形になった \( X(z) \) を逆z変換し、元の数列 \( x_n \) を求めましょう。\[\begin{align*}
x_n & = \mathcal{Z}^{-1} \left[ x_n \right]
\\ & = \mathcal{Z}^{-1} \left[ \frac{4}{3} \cdot \frac{z}{z-2} - \frac{1}{2} \cdot \frac{z}{z-3} + \frac{1}{6} \cdot \frac{z}{z-5} \right]
\\ & = \frac{4}{3} \mathcal{Z}^{-1} \left[ \frac{z}{z-\textcolor{red}{2}} \right] - \frac{1}{2} \mathcal{Z}^{-1} \left[ \frac{z}{z-\textcolor{red}{3}} \right] + \frac{1}{6} \mathcal{Z}^{-1} \left[ \frac{z}{z-\textcolor{red}{5}} \right]
\\ & = \frac{4}{3} \cdot \textcolor{red}{2}^n - \frac{1}{2} \cdot \textcolor{red}{3}^{n} + \frac{1}{6} \cdot \textcolor{red}{5}^n
\\ & = \frac{1}{6} ( 8 \cdot 2^n - 3 \cdot 3^n + 5^n )
\\ & = \frac{1}{6} ( 2^{n+3} - 3^{n+1} + 5^n )
\end{align*} \]となる。

よって、\( a_n \) は\[
a_n = \frac{1}{6} ( 2^{n+3} - 3^{n+1} + 5^n )
\]と表すことができます。

解答4

Step1. 方程式の書き換え

特に書き換える必要はありませんが、\( x_n = a_n \), \( y_n = b_n \) にしましょうか。

つまり、\[
\left\{ \begin{array}{l}
2 x_{n+1} = 5 x_{n} + \ \ y_{n} + 2^{n+1} + 4 \\
2 y_{n+1} = \ \ x_{n} + 5 y_{n} - 2^{n+1} + 4
\end{array}\right.
\]の \( x_n \) を求めればOKです。

Step2. 両辺をz変換する

次に、与えられた2つの式を両方ともz変換しましょう。
\( x_n \) のz変換を \( X(z) \)、\( y_n \) のz変換を \( Y(z) \) とおきましょうか。

ここで、\( \textcolor{orange}{x_0 = 0} \), \( \textcolor{magenta}{y_0 = 0} \) なので、\( x_{n+1} \), \( y_{n+1} \), \( x_{n} \), \( y_n \) をz変換すると、\[\begin{align*}
\mathcal{Z} [ x_{n+1} ] & = z X(z) - \textcolor{orange}{x_0} z
\\ & = z X(z) - \textcolor{orange}{0} z
\\ & = z X(z)
\end{align*}\]\[\begin{align*}
\mathcal{Z} [ y_{n+1} ] & = z Y(z) - \textcolor{magenta}{y_0} z
\\ & = z Y(z) - \textcolor{magenta}{0} z
\\ & = z Y(z)
\end{align*}\]\[\begin{align*}
\mathcal{Z} [ x_{n} ] = X(z) \\
\mathcal{Z} [ y_{n} ] = Y(z)
\end{align*}\]となりますね。

よって、\( 2x_{n+1} = 5 x_{n} + y_{n} + 2^{n+1} + 4 \) は\[\begin{align*}
2 z X(z) & = 5 X(z) + Y(z) + \frac{2z}{z-2} + \frac{4z}{z-1}
\\ & = 5 X(z) + Y(z) + \frac{2z(z-1)+4z(z-2)}{(z-1)(z-2)}
\\ & = 5 X(z) + Y(z) + \frac{6z^2-10z}{(z-1)(z-2)}
\end{align*}\]とz変換ができる。

同様に \( 2y_{n+1} = x_{n} + 5 y_{n} - 2^{n+1} + 4 \) をz変換すると、\[\begin{align*}
2 z Y(z) & = X(z) + 5 Y(z) - \frac{2z}{z-2} + \frac{4z}{z-1}
\\ & = X(z) + 5 Y(z) + \frac{-2z(z-1)+4z(z-2)}{(z-1)(z-2)}
\\ & = X(z) + 5 Y(z) + \frac{2z^2-6z}{(z-1)(z-2)}
\end{align*} \]となる。

z変換した結果をともに変形することで、\[
\left\{ \begin{array}{l}
(2z-5) X(z) - Y(z) = \frac{2}{z-2} + \frac{4z}{z-1} \\
- X(z) + (2z-5) Y(z) = - \frac{2}{z-2} + \frac{4z}{z-1}
\end{array}\right.
\]となり、\( X(z) \), \( Y(z) \) の2元連立方程式の形に書き換えることができます。

Step3. X(z)の導出

先程の連立方程式を行列を用いて表すと、\[
\left( \begin{array}{ccc} 2z-5 & -1 \\ -1 & 2z-5 \end{array} \right) \left( \begin{array}{ccc} X(z) \\ Y(z) \end{array} \right) = \left( \begin{array}{ccc} 7z \\ -4z \end{array} \right)
\]となり、\( A \vec{x} = \vec{b} \) の形に変形することができますね。

ここで、\( |A| \not = 0 \)（行列 \(A \) が正則）であれば、解を \( \vec{x} = A^{-1} \vec{b} \) と求めることができます。

\[\begin{align*}
|A| & = \left| \begin{array}{ccc} 2z-5 & -1 \\ -1 & 2z-5 \end{array} \right|
\\ & = (2z-5)(2z-5) - 1
\\ & = 4^2 -20z + 24
\\ & = 4(z^2-5z+6)
\\ & = 4(z-2)(z-3) \not = 0
\end{align*}\]となるため、行列 \( A \) は正則ですね。

ここで、逆行列 \( A^{-1} \) は、\[\begin{align*}
A^{-1} & = \frac{1}{|A|} \left( \begin{array}{ccc} 2z-5 & -1 \\ -1 & 2z-5 \end{array} \right)
\\ &= \frac{1}{4(z-2)(z-3)} \left( \begin{array}{ccc} 2z-5 & 1 \\ 1 & 2z-5 \end{array} \right)
\end{align*}\]となるため、\( X(z) \), \( Y(z) \) は\[\begin{align*}
\left( \begin{array}{ccc} X(z) \\ Y(z) \end{array} \right) & = \left( \begin{array}{ccc} 2z-5 & -1 \\ -1 & 2z-5 \end{array} \right)^{-1} \left( \begin{array}{ccc} \frac{4z^2-6z-2}{(z-1)(z-2)} \\ \frac{4z^2-10z+2}{(z-1)(z-2)} \end{array} \right)
\\ & = \frac{1}{4(z-1)(z-2)^2 (z-3)} \left( \begin{array}{ccc} 2z-5 & 1 \\ 1 & 2z-5 \end{array} \right) \left( \begin{array}{ccc} 4z^2-6z-2 \\ 4z^2-10z+2 \end{array} \right)
\\ & = \frac{1}{4(z-1)(z-2)^2 (z-3)} \left( \begin{array}{ccc} (2z-5)(6z^2-10z) + 2z^2-6z \\ 6z^2-10z + (2z-5)(2z^2-6z) \end{array} \right)
\\ & = \frac{1}{4(z-1)(z-2)^2 (z-3)} \left( \begin{array}{ccc} 12z^3 - 48z^2 + 44z \\ 4z^3 - 16z^2 + 20 \end{array} \right)
\\ & = \frac{1}{(z-1)(z-2)^2 (z-3)} \left( \begin{array}{ccc} 3z^3 - 12z^2 + 11z \\ z^3 - 4z^2 + 5z \end{array} \right)
\end{align*}\]となるため、\[
X(z) = \frac{3z^3 - 12z^2 + 11z}{(z-1)(z-2)^2 (z-3)}
\]\[
Y(z) = \frac{z^3 - 4z^2 + 5z}{(z-1)(z-2)^2 (z-3)}
\]と求めることができる。

（ \( Y(z) \) は今回の問題では不要ですが、一応出してみました）

Step4. あとはX(z)を逆z変換するのみ！

(i) 部分分数分解

ここで、\( X(z) \) を\[\small
\frac{3z^3 - 12z^2 + 11z}{(z-1)(z-2)^2 (z-3)} = \frac{az}{z-1} + \frac{bz}{z-2} + \frac{cz}{(z-2)^2} + \frac{dz}{z-3}
\]の形（部分分数分解）にするために \( a \), \( b \), \( c \), \( d \) の値を求めます。両辺を \( (z-1)(z-2)^2 (z-3) \) 倍すると、\[\small \begin{align*}
3z^3 - 12z^2 + 11z & = az (z-2)^2 (z-3) + bz (z-1)(z-2)(z-3) + cz (z-1)(z-3) + dz (z-1)(z-2)^2
\end{align*}\]となります。

あとは、括弧内が0となるような \( z \) の値を代入し、\( a \), \( b \) を求めればOK。

\( z = 1 \) とする → \( 2 = -2a \) より \( a = -1 \)
\( z = 2 \) とする → \( -2 = -2c \) より \( c = 1 \)
\( z = 3 \) とする → \( 6 = 6d \) より、\( d = 1 \)
\( z = 4 \) とする → \( 44 = 16a + 24b + 12c + 48d = 44+12b \) より、\( b = 0 \)

となるため、\[
X(z) = - \frac{z}{z-1} + \frac{z}{(z-2)^2} + \frac{z}{z-3}
\]と部分分数分解できる。

(ii) 逆z変換

最後に、\( X(z) \) を逆z変換し、元の数列 \( x_n \) を求めましょう。\[\begin{align*}
x_n & = \mathcal{Z}^{-1} \left[ x_n \right]
\\ & = \mathcal{Z}^{-1} \left[ - \frac{z}{z-1} + \frac{z}{(z-2)^2} + \frac{z}{z-3} \right]
\\ & = - \mathcal{Z}^{-1} \left[ \frac{z}{z-\textcolor{red}{1}} \right] + \mathcal{Z}^{-1} \left[ \frac{z}{(z-\textcolor{red}{2})^2} \right] + \mathcal{Z}^{-1} \left[ \frac{z}{z-\textcolor{red}{3}} \right]
\\ & = - \textcolor{red}{1}^n + n \textcolor{red}{2}^{n-1} + \textcolor{red}{3}^n
\\ & = 3^n + n \cdot 2^{n-1} + 1
\end{align*} \]となる。

よって、\( a_n \) は\[
a_n = 3^n + n \cdot 2^{n-1} + 1
\]と表せる。

※ ちなみに \( b_n \) は\[
b_n = 3^n - n \cdot 2^{n-1} + 1
\]となります。