スポンサードリンク
こんにちは、ももやまです。
前編の「うさぎ模試 1年後期解析学 フォーム編」にて、解析学で使う知識の確認はできましたでしょうか。
後編ではより実践的な解析学の力をつけるために、記述型の問題を5問用意しました!
※ まだ前編(フォーム式)にチャレンジしていない方は、前編からすることをおすすめします!
- 50分間で問題を解く。
- 記事内の解説を見て、間違った箇所を確認し、どこ間違えたのか(理解ができていないのか)を確認する。
- 間違えた箇所を参考書や記事などで練習する。
- 寝る。
時間がある人はじっくり、時間がない人は素早くこの記事にて1年後期で習う解析学の復習をしましょう!
本記事では、前編と同じく練習問題の解説を載せております。さらに、要点を
- 試験で必要な知識:青色の枠
- 試験で必要な解き方:赤色の枠
などでまとめております。
※ 採点は各自でお願いします。
スポンサードリンク
問題1. 2変数関数の極値
2変数関数\[
f(x,y) = x^4 + 2y^2 + 6x^2 - 8xy
\]の極値を求めたい。(1), (2)の問いに答えなさい。(配点 10)
(1) 点 (1,2) 以外の極値をとるすべての候補点(停留点)を答えなさい。
(2) 点 (1,2) が極値を持つかどうか調べなさい。
(1) (0,0), (-1,-2) [2点+3点=5点]
(2) 極小値をもつ(極小値:-1)[5点]
[解説]
(1) 2変数関数 \( f(x,y) \) が点 \( (a,b) \) において、\[
f_{x} (a,b) =f_{y} (a,b) = 0
\]を満たす点が停留点となる。
まず、2変数関数 \( f(x,y) \) を \( x \), \( y \) それぞれで偏微分する。\[
f_{x} = 4x^3 + 12x - 8y \]\[
f_{y} = 4y - 8x
\]ここで、停留点であれば、\[
f_{y} = 4y - 8x = 0
\]が成り立つので、\( 4y = 8x \)、つまり \( y = 2x \) が成立する。
また、停留点であれば\[\begin{align*}
f_{x} & = 4x^3 + 12x - 8y
\\ & = 4x^3 + 12x - 16x
\\ & = 4x^3 - 4x
\\ & = 4x (x^2 - 1)
\\ & = 4x (x + 1)(x - 1) = 0
\end{align*}\]も成立する。
よって停留点の \( x \) 座標は \( x = -1, 0, 1 \) の3つにしぼられる。
また、\( y = 2x \) より、それぞれの停留点は \( (0,0) \), \( (1,2) \), \( (-1,-2) \) となる。
よって \( (1,2) \) 以外の停留点は \( (-1,-2) \), \( (0,0) \) となる。
(2) \( f(x,y) \) の2次導関数を求めると、\[
f_{xx} = 12x^2 + 12 \]\[
f_{xy} = -8 \]\[
f_{yy} = 4
\]となる。\( (x,y) = (1,2) \) のとき、ヘッセ行列 \( H \) は\[\begin{align*}
H & = \left| \begin{array}{ccc} f_{xx} & f_{xy} \\ f_{yx} & f_{yy} \end{array} \right|
\\ & = \left| \begin{array}{ccc} 24 & -8 \\ -8 & 4 \end{array} \right|
\\ & = 8 \cdot 4 \left| \begin{array}{ccc} 3 & -1 \\ -2 & 1 \end{array} \right|
\\ & = 32 \cdot (3-2)
\\ & = 32 > 0
\end{align*} \]なので、\( (1,2) \) は極値となることがわかる。さらに \( (1,2) \) のとき、\[
f_{xx} = 24 > 0
\]なので、点 \( (1,2) \) は極小値を持つ。
前編でも公式を紹介しましたが、念のためもう1度確認しておきましょう。
Step1. 極値を持つ候補点(停留点)を以下の式で確認。\[
f_x (a,b) = f_y (a,b) = 0
\]
Step2. 停留点 \( (a,b) \) ごとに極値を持つかどうかを下の行列式\[H = \left| \begin{array}{ccc} f_{xx} (a,b) & f_{xy}(a,b) \\ f_{yx}(a,b) & f_{yy}(a,b) \end{array} \right|
\]の値で確認。(\( H \) はヘッシアン・ヘッセ行列と呼ばれる)
- \( H > 0 \) … 点 \( (a,b) \) は極値
- \( H < 0 \) … 点 \( (a,b) \) は極値ではない
- \( H = 0 \) … 点 \( (a,b) \) は極値かどうかわからない(試験に出ない)
Step3. 極値となる点 \( (a,b) \) ごとに、その極値が極大値・極小値のどちらになるかは、\( f_{xx} \) の値を計算することで確認。
- \( f_{xx} (a,b) > 0 \) … 点 \( (a,b) \) は極小値
- \( f_{xx} (a,b) < 0 \) … 点 \( (a,b) \) は極大値
2変数関数の極値を求める方法についての更なる復習はこちらをご覧ください。
スポンサードリンク
問題2. 条件付き2変数関数の極値
ラグランジュの未定乗数法を用いてつぎの条件付き極値を求めたい。
\( x^2 + y^2 = 1 \) の条件下において、\( f(x,y) = xy \) の極値
このとき、極値があればそれぞれ答えなさい。(配点 10)
極値:1/2, -1/2
[解説]\( g(x,y) = x^2 + y^2 - 1 = 0 \) とする。すると、\[
f_{x} = y , \ \ \ f_{y} = x \]\[
g_{x} = 2x, \ \ \ g_{y} = 2y
\]となるのでラグランジュの未定乗数法により\[\begin{align*}
H & = \left| \begin{array}{ccc} f_{x} & g_{x} \\ f_{y} & g_{y} \end{array} \right|
\\ & = \left| \begin{array}{ccc} y & 2x \\ x & 2y \end{array} \right|
\\ & = 2y^2 - 2x^2
\\ & = 2(y^2 - x^2)
\\ & = 2(y-x)(y+x)
\\ & = 0
\end{align*} \]つまり \( y - x = 0 \) or \( y + x = 0 \) が成立する。
よって、\( y = \pm x \) も成立するので、\( g(x,y) = 0 \) に代入して候補点を求める。\[\begin{align*}
g(x) & =
x^2 + (\pm x)^2 - 1
\\ & = x^2 + x^2 - 1
\\ & = 2x^2 - 1
\\ & = 0
\end{align*} \]となるので、\( x = \pm \frac{\sqrt{2}}{2} \) が候補点の \( x \) 座標。
ここで \( y = \pm x \) より、\[
(x,y) = \left( \pm \frac{ \sqrt{2} }{2}, \pm \frac{ \sqrt{2} }{2} \right)
\]が極値の候補点(全部で4点)となる。ただし符号は複号任意。
あとは4点を \( f(x,y) \) に代入することで極値を求める。
(i) \( (x,y) = \left( \pm \frac{ \sqrt{2} }{2} ,\pm \frac{ \sqrt{2} }{2} \right) \) のとき(複号同順)
\[\begin{align*}
f(x,y) & = xy \\ & = \left( \pm \frac{ \sqrt{2} }{2} \right) \cdot \left( \pm \frac{ \sqrt{2} }{2} \right) \\ & = \frac{1}{2}
\end{align*}\]
(ii) \( (x,y) = \left( \pm \frac{ \sqrt{2} }{2} ,\mp \frac{ \sqrt{2} }{2} \right) \) のとき(複号同順)
\[\begin{align*}
f(x,y) & = xy \\ & = \left( \pm \frac{ \sqrt{2} }{2} \right) \cdot \left( \mp \frac{ \sqrt{2} }{2} \right) \\ & = - \frac{1}{2}
\end{align*}\] となるので、
極値は、1/2, -1/2 となる。(極大値は1/2、極小値は-1/2)
条件 \( g(x,y) = 0 \) のもとで関数 \( f(x,y) \) の極値、および最大値・最小値は以下のように求める。
Step1. 極値を持つ候補点を以下の式で確認。\[
g(x,y) = 0
\]\[
\left| \begin{array}{ccc} f_{x} & g_{x} \\ f_{y} & g_{y} \end{array} \right| = 0
\]
Step2. Step1で出てきた候補点を実際に \( f(x,y) \) を代入し、出てきた値が極値である。
Step3. 極値が最大値・最小値になるかを確認する。
(有界閉集合であれば一番大きい極値が最大値、一番小さい極値が最小値という確認でOK)
条件付きの2変数関数の極値(ラグランジュの未定乗数法)についてさらなる復習をしたい人はこちら!
スポンサードリンク
問題3. 2重積分の基礎
2重積分\[
\iint_{D} \frac{ \sin y }{ y} \ dxdy
\]\[ D = \{ (x,y) \mid 0 \leqq x \leqq \pi, \ x \leqq y \leqq \pi \ \}
\]を求めたい。つぎの(1), (2)の問いに答えなさい。(配点 10)
(1) 積分領域 \( D \) を図示しなさい。
(2) この2重積分の値を求めなさい。
(1) 下の解説を参照
(2) 2
(1) 下の図のようになる。
ついでに積分範囲も交換する。
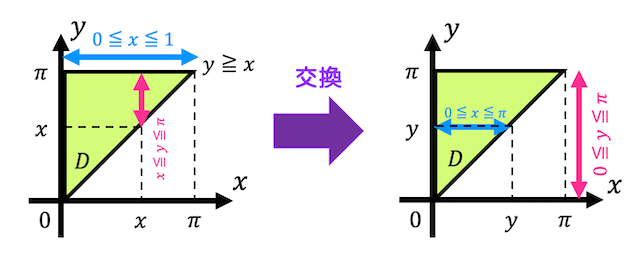
(2) \( y \) 側の積分領域に文字が含まれているため、\( y \) から先に積分しなければならない。
しかし、積分 \[ \int \frac{ \sin y }{ y } \ dy \] の不定積分は求められない。
そこで、積分順序を入れ替えることで、\( x \) から積分できるようにする。積分範囲を入れ替えると、\[
D = \{ (x,y) \mid 0 \leqq x \leqq y, \ 0 \leqq y \leqq \pi \ \}
\]となる。よって、\[
\iint_{D} \frac{ \sin y }{ y} \ dxdy = \int^{\pi}_0 \left( \int^{y}_0 \frac{ \sin y }{ y } \ dx \right) \ dy
\]の計算をすればよい。
ここで、\[\begin{align*}
\int^{y}_0 \frac{ \sin y }{ y } \ dx & =
\frac{ \sin y }{ y } \int^{y}_0 1 \ dx \\ & =
\frac{ \sin y }{ y } \left[ x \right]^{y}_0 \\ & =
\frac{ \sin y }{ y } \cdot y \\ & =
\sin y
\end{align*}\]となるので、\[\begin{align*}
\iint_{D} \frac{ \sin y }{ y} \ dxdy & = \int^{\pi}_0 \left( \int^{y}_0 \frac{ \sin y }{ y } \ dx \right) \ dy
\\ & = \int^{\pi}_0 \sin y \ dy
\\ & = \left[ - \cos y \right]^{\pi}_0
\\ & = 1 + 1
\\ & = 2
\end{align*}\]と計算できる。
積分範囲の交換、および2重積分の基本的な問題を解く練習をさらにしたい方はこちら!
問題4. 2重積分と変数変換
2重積分\[
\iint_{D} (x^2 - y^2) e^{ (x-y)^2 } \ dxdy \]\[
D = \{ (x,y) \mid 0 \leqq x+y \leqq 6, \ 0 \leqq x-y \leqq 2 \ \}
\]を求めたい。つぎの(1), (2)の問いに答えなさい。(配点 10)
(1) どのように変数変換したのか、変数変換によるヤコビアンを求めなさい。
(2) この2重積分の値を求めなさい。
(1) 変数変換:\( x + y = 2p \), \( x - y = 2q \)、ヤコビアン:2 [5点]
(2) \( \frac{9}{2} (e^4 - 1) \) [5点]
[解説]
(1) \( x + y = 2p \), \( x - y = 2q \) とする。すると、\[
2x = 2p + 2q, \ \ \ 2y = 2p - 2q
\]より、\[
\left\{ \begin{array}{l} x = p + q \\ y = p - q \end{array}\right.
\]となる。よってヤコビアン \( J \) は\[\begin{align*}
J = & \left| \begin{array}{ccc} \frac{\partial x}{\partial p} & \frac{\partial x}{\partial q} \\ \frac{\partial y}{\partial p} & \frac{\partial y}{\partial q} \end{array} \right|
\\ = & \left| \begin{array}{ccc} 1 & 1 \\ 1 & -1 \end{array} \right|
\\ = & -2
\end{align*}\]の絶対値となるので、\[
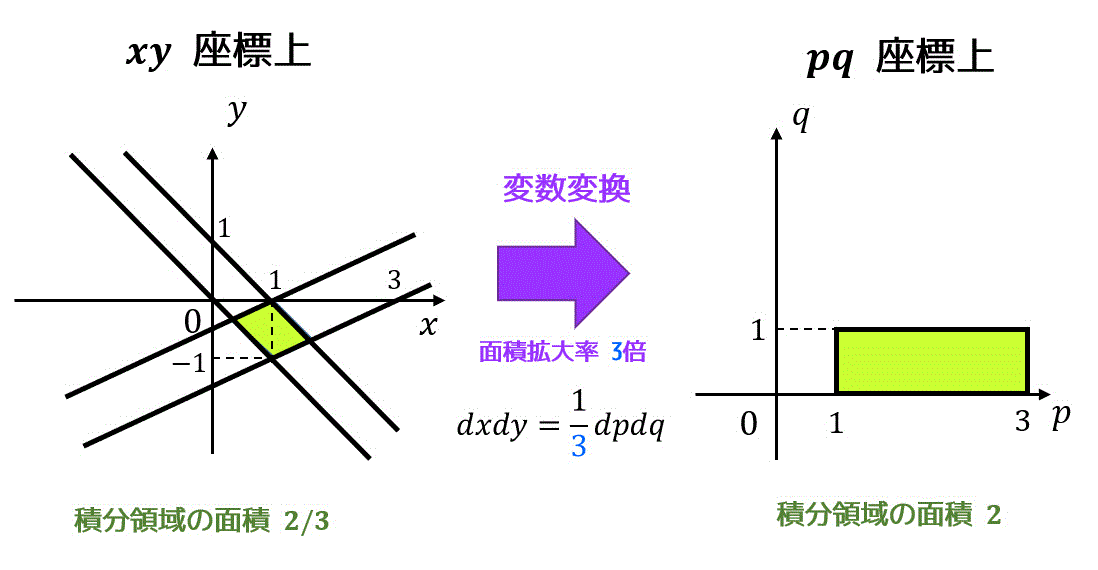
dxdy = 2 \ dpdq \]\[
D'= \{ (p,q) \mid 0 \leqq p \leqq 3, \ 0 \leqq q \leqq 1 \ \}
\]となる。
(2) (1)より、\[\begin{align*}
\iint_{D} (x^2 - y^2) e^{ (x-y)^2 } \ dxdy & =
\iint_{D'} 2 \cdot 4pq e^{ 4q^2 } \ dpdq \\ & =
\int^{3}_{0} p \ dp \cdot \int^{1}_{0} 8 qe^{ 4q^{2} } \ dq
\end{align*}\]を計算すればよい。
それぞれの積分を求めると、\[\begin{align*}
\int^{3}_{0} p \ dp & = \left[ \frac{1}{2} p^2 \right]^{3}_{0}
\\ & = \frac{1}{2} \cdot 3^2
\\ & = \frac{9}{2}
\end{align*} \]、\[\begin{align*}
\int^{1}_{0} 8 qe^{ 4q^{2} } \ dq & = \left[ e^{ 4q^{2} } \right]^{1}_{0}
\\ & = e^4 - 1
\end{align*} \]となるので、\[\begin{align*}
\iint_{D} (x^2 - y^2) e^{ (x-y)^2 } \ dxdy & =
\iint_{D'} 2 \cdot 4pq e^{ 4q^2 } \ dpdq \\ & =
\int^{3}_{0} p \ dp \cdot \int^{1}_{0} 8 qe^{ 4q^{2} } \ dq \\ & =
\frac{9}{2}(e^4 - 1)
\end{align*}\]となる。
被積分関数が \( x \), \( y \) の2重積分の変数を \( x = x(p,q) \), \( y = y(p,q) \) でおく。
このときのヤコビアン \( J \) を下のように計算できる。\[\begin{align*}
J = \left| \begin{array}{ccc} \frac{\partial x}{\partial p} & \frac{\partial x}{\partial q} \\ \frac{\partial y}{\partial p} & \frac{\partial y}{\partial q} \end{array} \right|
\end{align*}\]
また、ヤコビアン \( J \) を用いて、変数変換の前後の関係は下のように書き表せる。\[
dxdy = |J| \ dpdq
\]
※ 絶対値が付くところに要注意!
※ 計算時にヤコビアンを考慮し忘れないように!!
変数変換(ヤコビアン)を用いた2重積分の練習をさらにしたい方はこちら!
問題5. 2重積分と変数変換
つぎの広義積分\[
\iint_{D} \frac{1}{ (x^2 + y^2 + 1)^a } \ dxdy
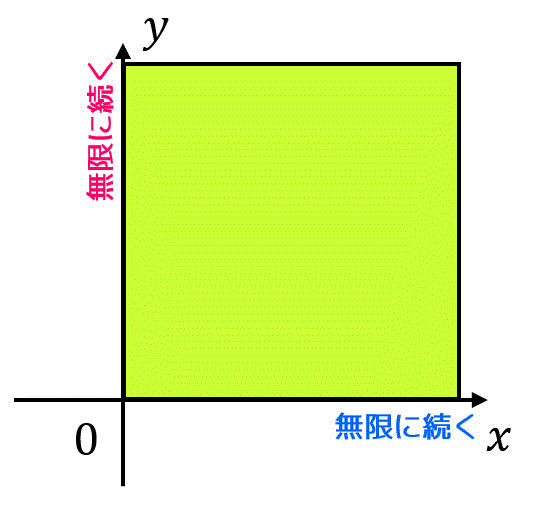
\]\( D \) は \( xy \) 平面全体
について(1), (2)の問いに答えなさい。(配点 10)
(1) 広義積分が存在するための \( a \) の条件を求めなさい。
(2) (1)の条件のもとで広義積分を計算しなさい。
(1) \( a \gt 1 \) [5点]
(2) \( \frac{\pi}{a-1} \) [5点]
[解説]
(1) \( x = r \cos \theta \), \( y = r \sin \theta \) とすると、ヤコビアンは \( r \) となるので、\[
dxdy = r \ dr d \theta
\]となる。また、積分領域 \( D' \) は、\[\begin{align*}
D' = \{ (r, \theta ) \mid 0 \leqq r , \ 0 \leqq \theta \leqq 2 \pi \ \}
\end{align*}\]となる。よって、\[\begin{align*}
\iint_{D} \frac{1}{ (x^2 + y^2 + 1)^a } \ dxdy & = \iint_{D'} \frac{r}{ (r^2 + 1)^a } \ dr d \theta
\\ & = \int^{2 \pi}_{0} 1 \ d \theta \cdot \lim_{R \to \infty} \int^{R}_{0} \frac{r}{ (r^2 + 1)^a } \ dr
\end{align*}\]を求めればよい(広義積分に注意)。
ここで広義積分となっている \( r \) の積分について考える。\[\begin{align*}
\int^{R}_{0} \frac{r}{ (r^2 + 1)^a } \ dr & = \frac{1}{2} \int^{R}_{0} 2r (r^2+1)^{-a} \ dr
\\ & = \frac{1}{2} \left[ \frac{1}{1-a} \cdot (r^2+1)^{-a+1} \right]^{R}_{0}
\\ & = \frac{1}{2(1-a)} \cdot \left( (R^2+1)^{1-a} - 1 \right)
\\ & = \frac{1}{2(1-a)} \cdot \left( (R^2+1)^{1-a} - 1 \right)
\end{align*} \]となる。
よって\( R \to \infty \) のときに \( (R^2+1)^{1-a} \) を収束させるためには、\( 1 - a \lt 0 \) であればよい。
つまり、\( a \gt 1 \) のときに広義積分が存在(収束)する。
(2) \( a \gt 1 \) とすると、\[\begin{align*} &
\lim_{R \to \infty} \int^{R}_{0} \frac{r}{ (r^2 + 1)^a } \ dr \\ = \ &
\lim_{R \to \infty} \left (\frac{1}{2(1-a)} \cdot \left( (R^2+1)^{1-a} - 1 \right) \right)\\ = \ &
\left (\frac{1}{2(1-a)} \cdot \left( 0 - 1 \right) \right)\\ = \ &
\frac{1}{2(a-1)}
\end{align*} \]となる。
さらに、\[ \begin{align*}
\int^{2 \pi}_{0} 1 \ d \theta = 2 \pi
\end{align*} \]なので、\[\begin{align*}
\iint_{D} \frac{1}{ (x^2 + y^2 + 1)^a } \ dxdy & = \iint_{D'} \frac{r}{ (r^2 + 1)^a } \ dr d \theta
\\ & = \int^{2 \pi}_{0} 1 \ d \theta \cdot \lim_{R \to \infty} \int^{R}_{0} \frac{r}{ (r^2 + 1)^a } \ dr
\\ & = 2 \pi \cdot \frac{1}{2(a-1)}
\\ & = \frac{\pi}{a-1}
\end{align*}\]となる。
2変数の広義積分を解く練習をさらにしたい人はこちら!
関連広告・スポンサードリンク