うさぎでもわかる線形代数　第19羽　行列を用いた差分方程式（漸化式）の解き方

こんにちは、ももやまです。
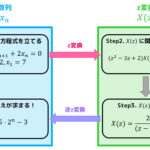
今回は差分方程式（漸化式）を行列の \( n \) 乗を使って解くテクニックを紹介します！

 

 

前回の記事（行列の \( n \) 乗の求め方）はこちらから↓

www.momoyama-usagi.com

 

普通に差分方程式（漸化式）を解く方法はこちら！

www.momoyama-usagi.com

 

 

★注意★

この記事では、初項を \( a_1 \) ではなく \( a_0 \) としてるので気をつけてください。初項が \( a_1 \) だと特殊解は \( a^{n-1} \) のような形で出ますが、\( a_0 \) の場合は \( a^n \) の形で出てきます。

また、人によっては \( a_n \) という形ではなく、\( f(n) \) を使って表す人もいるので気をつけてください。

例：\( a_{n} = 2 a_{n-1} + 1 \) は \( f(n) = 2f(n-1) + 1 \) と同じ

スポンサードリンク

１．行列を用いた連立漸化式

まずは、2次連立漸化式を行列で解く流れを誘導付きの例題で見ていきましょう。

例題1

初項 \( a_0 = 7 \), \( b_0 = -4 \) で表される漸化式、

 \[\left\{ \begin{array}{l} a_n = 2a_{n-1} + \ \ b_{n-1}\\ b_n = 2a_{n-1} + 3b_{n-1}  \end{array}\right.\]

の \( a_n \), \( b_n \) を求めたい。つぎの問いに答えなさい。

(1) \[ \vec{x}_n = \left( \begin{array}{ccc} a_n \\ b_n \end{array} \right) \]とおく。このとき、\[ \vec{x}_{n} = A \vec{x}_{n-1} \]を満たす行列 \( A \) を求めなさい。

(2) \( \vec{x}_0 \), \( \vec{x}_1 \) の値を求めなさい。

(3) 行列 \( A \) の固有値 \( t_1 \), \( t_2 \) とそれぞれの固有値に属する固有ベクトル \( \vec{p_1} \), \( \vec{p_2} \) を求めなさい。

(4) \( \vec{x}_0 \) を固有ベクトル \( \vec{p_1} \), \( \vec{p_2} \) の1次結合で表しなさい。

(5) \( \vec{x}_n \) を求めることで、\( a_n \), \( b_n \) の特殊解を求めなさい。

 

解説1

(1)

与えられた漸化式（差分方程式）を行列で表すだけ。\[
 \left( \begin{array}{ccc} a_n \\ b_n \end{array} \right) =  \left( \begin{array}{ccc} 2 & 1 \\ 2 & 3 \end{array} \right) \left( \begin{array}{ccc} a_{n-1} \\ b_{n-1} \end{array} \right)
\]と表せるので、\[
A = \left( \begin{array}{ccc} 2 & 1 \\ 2 & 3 \end{array} \right)
\]となる。

 

(2) \[
\vec{x}_0 = \left( \begin{array}{ccc} a_0 \\ b_0 \end{array} \right) = \left( \begin{array}{ccc} 7 \\ -4 \end{array} \right) \\ 
\vec{x}_1 = \left( \begin{array}{ccc} 2 & 1 \\ 2 & 3 \end{array} \right) \left( \begin{array}{ccc} 7 \\ -4 \end{array} \right) = \left( \begin{array}{ccc} 10 \\ 2 \end{array} \right)
\]

 

(3)

固有値を \( t \) とすると、固有方程式は、\[\begin{align*}
|A-tE| = & \left| \begin{array}{ccc} 2-t & 1 \\ 2 & 3-t \end{array} \right|
\\ = & (t-3)(t-2) - 2
\\ = & t^2 - 5t + 4
\\ = & (t-1)(t-4) = 0
\end{align*} \]より固有値は1, 4となる。

よって、\( t_1 = 1 \), \( t_2 = 4 \) となる。

[検算ポイント：固有値の和は対角成分の和になっていることを確認（5になればOK）]

 

(i) 固有値が1のときの固有ベクトル \( \vec{p_1} \)\[ \begin{align*}
(A-E) = &
\left( \begin{array}{ccc} 1 & 1 \\ 2 & 2  \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 1 & 1 \\ 0 & 0  \end{array} \right)
\end{align*} \]となる。\[
x + y = 0
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y  \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ -1 \end{array} \right)
\]と表せるので、固有ベクトル \( \vec{p_1} \) は、\[
\vec{p_1} = \left( \begin{array}{ccc} 1 \\ -1   \end{array} \right)
\]となる。

 

(ii) 固有値が4のときの固有ベクトル \( \vec{p_1} \)\[ \begin{align*}
(A-4E) = &
\left( \begin{array}{ccc} -2 & 1 \\ 2 & -1  \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 2 & -1 \\ 0 & 0  \end{array} \right)
\end{align*} \]となる。\[
2x - y = 0
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y  \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 2 \end{array} \right)
\]と表せるので、固有ベクトル \( \vec{p_2} \) は、\[
\vec{p_2} = \left( \begin{array}{ccc} 1 \\ 2   \end{array} \right)
\]となる。

 

(4)\[
\vec{x}_0 = c_1 \vec{p_1} + c_2 \vec{p_2} \\
\left( \begin{array}{ccc} 7 \\ -4 \end{array} \right) = c_1 \left( \begin{array}{ccc} 1 \\ -1   \end{array} \right) + c_2 \left( \begin{array}{ccc} 1 \\ 2   \end{array} \right) \\
\left( \begin{array}{ccc} 1 & 1 \\ -1 & 2   \end{array} \right) \left( \begin{array}{ccc} c_1 \\ c_2   \end{array} \right) = \left( \begin{array}{ccc} 7 \\ -4   \end{array} \right)
\]となるような \( c_1 \), \( c_2 \) の値をもとめればよい。

求め方は2パターン

[パターン1：行基本変形で求める] \[
 \begin{align*}
C = \ & \left( \begin{array}{cc|c} 1 & 1 & 7 \\ -1 & 2 & -4 \end{array} \right)
 \\ \to \ & \left( \begin{array}{cc|c} 1 & 1 & 7 \\ 0 & 3 & 3 \end{array} \right)
 \\ \to \ & \left( \begin{array}{cc|c} 1 & 1 & 7 \\ 0 & 1 & 1 \end{array} \right)
 \\ \to \ & \left( \begin{array}{cc|c} 1 & 0 & 6 \\ 0 & 1 & 1 \end{array} \right)
\end{align*} \]\]となるので、\( c_1 = 6 \), \( c_2 = 1 \) となる。よって、\[
\vec{x}_0 = 6 \vec{p_1} + \vec{p_2}
\]となる。

 

[パターン2：逆行列を用いる]　\[
\left( \begin{array}{ccc} 1 & 1 \\ -1 & 2   \end{array} \right)^{-1} = \frac{1}{3} \left( \begin{array}{ccc} 2 & -1 \\ 1 & 1   \end{array} \right)
\]となるので、\[\begin{align*}
\left( \begin{array}{ccc} c_1 \\ c_2   \end{array} \right) & = \left( \begin{array}{ccc} 1 & 1 \\ -1 & 2   \end{array} \right)^{-1} \left( \begin{array}{ccc} 7 \\ -4   \end{array} \right)
\\ & = \frac{1}{3} \left( \begin{array}{ccc} 2 & -1 \\ 1 & 1   \end{array} \right)\left( \begin{array}{ccc} 7 \\ -4   \end{array} \right)
\\ & = \frac{1}{3} \left( \begin{array}{ccc} 18 \\ 3   \end{array} \right)
\\ & = \left( \begin{array}{ccc} 6 \\ 1   \end{array} \right)
\end{align*} \]

より、\[
\vec{x}_0 = 6 \vec{p_1} + \vec{p_2}
\]となる。

※1次結合は2次の場合は逆行列（パターン2）を、3次以上の場合は行基本変形で求めること（パターン1）をおすすめします。

 

(5)

行列のべき乗 \( A^n \) を使って求めてもよいのですが、せっかく \( \vec{x}_0 \) を \( \vec{p_1} \), \( \vec{p_2} \) で表したので利用してしまいましょう。

 

固有値 \( t \) と \( t \) に属する固有ベクトル \( \vec{p} \) には、\[
A \vec{p} = t \vec{p}
\]の関係がありますね。（忘れていたら早急に復習しましょう。）

 

ここで、\[ \begin{align*}
A^n \vec{p} & = A^{n-1} \left( A \vec{p} \right)
\\ & = A^{n-1} \left( t \vec{p} \right)
\\ & = t A^{n-1} \vec{p}
\\ & = t A^{n-2} \left( A \vec{p} \right)
\\ & = t A^{n-2} \left( t \vec{p} \right)
\\ & = t^2 A^{n-2}
\\ & = \cdots
\\ & = t^n \vec{p}
\end{align*} \]となるので、\[
A^n \vec{p} = t^n \vec{p}
\]の関係も成立しますよね。

 

ここで、\[ \begin{align*}
 \left( \begin{array}{ccc} a_n \\ b_n   \end{array} \right)
\vec{x}_n & = A^n \vec{x}_0
\\ & = A^n \left( 6\vec{p_1} + \vec{p_2} \right)
\\ & = 6 A^n \vec{p_1} + A^n \vec{p_2}
\\ & = 6 \cdot 1 \vec{p_1} + 4^n \vec{p_2}
\\ & = 6 \cdot \left( \begin{array}{ccc} 1 \\ -1   \end{array} \right) + 4^n \left( \begin{array}{ccc} 1 \\ 2   \end{array} \right)
\\ & = \left( \begin{array}{ccc} 4^n + 6 \\ 2 \cdot 4^n - 6   \end{array} \right)
\end{align*} \]と求められますね。

よって、一般項は\[
a_n = 4^n + 6 \\ b_n = 4^n - 6
\]と求められます。

 

ポイントは、\[
A^n \vec{p} = t^n \vec{p}
\]を使うことです。

 

今回は \( \vec{x} \) が \( a_n \), \( b_n \) の2次でしたが、\( a_n \), \( b_n \), \( c_n \) と3次（もしくは4次以上）になった場合でも同じ方法で求めることができます。

 

一般項を求めるまでの流れは、

1. 漸化式を行列やベクトルを用いて表す
2. 行列の固有値、（固有値に属する）固有ベクトルを求める
3. 初項ベクトルを2で求めた固有ベクトルの1次結合で求める
4. \( \vec{x}_n = A^n \vec{x}_0 \) を用いて一般項を求める

となります。

 

スポンサードリンク

２．隣接3項間漸化式（差分方程式）

行列の置き方を工夫することで、隣接3項間漸化式を解くこともできます。\[
a_n = p a_{n-1} + q a_{n-2}
\]で表される漸化式を、\[
\left\{ \begin{array}{l} a_n = p a_{n-1} + q a_{n-2} \\ a_{n-1} = 1 a_{n-1}
\end{array}\right.\]と式を2つおくことにより、\[
\left( \begin{array}{ccc} a_n \\ a_{n-1}   \end{array} \right) = \left( \begin{array}{ccc} p & q \\ 1 & 0   \end{array} \right) \left( \begin{array}{ccc} a_{n-1} \\ a_{n-2}   \end{array} \right)
\]とおくことができます。

 

 

例題2

\[ a_0 = 2, \  a_1 = 7, \  a_{n} - 3a_{n-1} + 2 a_{n-2} = 0 \]

の初期値による特殊解を求めたい。

(1) \[
\left( \begin{array}{ccc} a_n \\ a_{n-1}   \end{array} \right) = \left( \begin{array}{ccc} a & b \\ c & d   \end{array} \right) \left( \begin{array}{ccc} a_{n-1} \\ a_{n-2}   \end{array} \right) \ \ \ 
\]を満たすような \( a \), \( b \), \( c \), \( d \) を求めなさい。

以降、\[
A = \left( \begin{array}{ccc} a & b \\ c & d   \end{array} \right)
\]とする。

(2) 行列 \( A \) の固有値 \( t_1 \), \( t_2 \) とそれぞれの固有値に属する固有ベクトル \( \vec{p_1} \), \( \vec{p_2} \) を求めなさい。

(3) 初項を表すベクトル \( \vec{x}_0 \) を、\[
\left( \begin{array}{ccc} a_1 \\ a_0   \end{array} \right) = \left( \begin{array}{ccc} 7 \\ 2   \end{array} \right)
\]とする。\( \vec{x}_0 \) を \( \vec{p_1} \), \( \vec{p_2} \) の1次結合で表しなさい。

(4) \[
\vec{x}_n =  \left( \begin{array}{ccc} a_{n+1} \\ a_{n}   \end{array} \right)
\]とし、\( a_n \) の特殊解を求めなさい。

解説2

(1)

差分方程式の形を変え、\[
\left\{ \begin{array}{l} a_n = 3 a_{n-1} - 2 a_{n-2} \\ a_{n-1} = 1 a_{n-1} \end{array}\right.
\]とします。すると、行列 \( A \) は、\[
\left( \begin{array}{ccc} 3 & -2 \\ 1 & 0   \end{array} \right)
\]となります。よって、\[
a = 3, \ \ b = -2, \ \ c = 1, \ \ d = 0
\]となる。

 

(2)

固有値を \( t \) とすると、固有方程式は、\[\begin{align*}
|A-tE| = & \left| \begin{array}{ccc} 3-t & -2 \\ 1 & -t \end{array} \right|
\\ = & t(t-3) + 2
\\ = & t^2 - 3t + 2
\\ = & (t-1)(t-2) = 0
\end{align*} \]より固有値は1, 2となる。

よって、\( t_1 = 1 \), \( t_2 = 2 \) となる。

[検算ポイント：固有値の和は対角成分の和になっていることを確認（3になればOK）]

 

(3)

固有値を \( t \) とすると、固有方程式は、\[\begin{align*}
|A-tE| = & \left| \begin{array}{ccc} 3-t & -2 \\ 1 & -t \end{array} \right|
\\ = & t(t-3) + 2
\\ = & t^2 - 3t + 2
\\ = & (t-1)(t-2) = 0
\end{align*} \]より固有値は1, 2となる。

よって、\( t_1 = 1 \), \( t_2 = 2 \) となる。

[検算ポイント：固有値の和は対角成分の和になっていることを確認（3になればOK）]

 

固有値が1のときの固有ベクトル \( \vec{p_1} \) \[ \begin{align*}
(A-1E) = &
\left( \begin{array}{ccc} 2 & -2 \\ 1 & -1  \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 1 & -1 \\ 0 & 0  \end{array} \right)
\end{align*} \]となる。\[
x + y = 0
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y  \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)
\]と表せるので、固有ベクトル \( \vec{p_1} \) は、\[
\vec{p_1} = \left( \begin{array}{ccc} 1 \\ 1   \end{array} \right)
\]となる。

 

 固有値が2のときの固有ベクトル \( \vec{p_2} \)\[ \begin{align*}
(A-3E) = &
\left( \begin{array}{ccc} 1 & -2 \\ 1 & -2  \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 1 & -2 \\ 0 & 0  \end{array} \right)
\end{align*} \]となる。\[
x - 2y = 0
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y  \end{array} \right) = k \left( \begin{array}{ccc} 2 \\ 1 \end{array} \right)
\]と表せるので、固有ベクトル \( \vec{p_2} \) は、\[
\vec{p_2} = \left( \begin{array}{ccc} 2 \\ 1   \end{array} \right)
\]となる。

 

(4)

\[
\vec{x}_0 = c_1 \vec{p_1} + c_2 \vec{p_2} \\
\left( \begin{array}{ccc} 7 \\ 2 \end{array} \right) = c_1 \left( \begin{array}{ccc} 1 \\ 1   \end{array} \right) + c_2 \left( \begin{array}{ccc} 2 \\ 1   \end{array} \right) \\
\left( \begin{array}{ccc} 1 & 2 \\ 1 & 1   \end{array} \right) \left( \begin{array}{ccc} c_1 \\ c_2   \end{array} \right) = \left( \begin{array}{ccc} 7 \\ 2   \end{array} \right)
\]となるような \( c_1 \), \( c_2 \) の値をもとめればよい。

求め方は2パターン

[パターン1：行基本変形で求める] \[
 \begin{align*}
C = \ & \left( \begin{array}{cc|c} 1 & 2 & 7 \\ 1 & 1 & 2 \end{array} \right)
 \\ \to \ & \left( \begin{array}{cc|c} 1 & 2 & 7 \\ 0 & -1 & -5 \end{array} \right)
 \\ \to \ & \left( \begin{array}{cc|c} 1 & 0 & -3 \\ 0 & 1 & 5 \end{array} \right)
\end{align*} \]\]となるので、\( c_1 = -3 \), \( c_2 = 5 \) となる。よって、\[
\vec{x}_0 = -3 \vec{p_1} + 5 \vec{p_2}
\]となる。

 

[パターン2：逆行列を用いる]　\[
\left( \begin{array}{ccc} 1 & 2 \\ 1 & 1 \end{array} \right)^{-1} =  \left( \begin{array}{ccc} -1 & 2 \\ 1 & -1   \end{array} \right)
\]となるので、\[\begin{align*}
\left( \begin{array}{ccc} c_1 \\ c_2   \end{array} \right) & = \left( \begin{array}{ccc} 1 & 2 \\ 1 & 1   \end{array} \right)^{-1} \left( \begin{array}{ccc} 7 \\ 2   \end{array} \right)
\\ & = \left( \begin{array}{ccc} -1 & 2 \\ 1 & -1   \end{array} \right)\left( \begin{array}{ccc} 7 \\ 2   \end{array} \right)
\\ & = \frac{1}{3} \left( \begin{array}{ccc} -3 \\ 5   \end{array} \right)
\end{align*} \]

となり、\[
\vec{x}_0 = -3 \vec{p_1} + 5 \vec{p_2}
\]と表せる。

 

(5)

ここで、\[ \begin{align*}
 \left( \begin{array}{ccc} a_{n+1} \\ a_{n}   \end{array} \right) & = 
\vec{x}_n  \\ & = A^n \vec{x}_0
\\ & = A^n \left( -3 \vec{p_1} + 5 \vec{p_2} \right)
\\ & = -3 A^n \vec{p_1} + 5 A^n \vec{p_2}
\\ & = -3 \cdot 1 \vec{p_1} + 5 \cdot 2^n \vec{p_2}
\\ & = -3 \cdot \left( \begin{array}{ccc} 1 \\ 1   \end{array} \right) + 5 \cdot 2^n \left( \begin{array}{ccc} 2 \\ 1   \end{array} \right)
\\ & = \left( \begin{array}{ccc} -3 + 10 \cdot 2^n \\ -3 + 5 \cdot 2^n    \end{array} \right)
\end{align*} \]と求められますね。

よって、一般項は\[
a_n = 5 \cdot 2^n - 3
\]と求められます。

 

\[ a_{n+1} = 5 \cdot 2^{n+1} -3 = 10 \cdot 2^n - 3\] とすることで検算することができますね。）

 

参考までに隣接4項間の差分方程式を行列に変換する方法も下に記しておきます。

 

 隣接4項間漸化式は練習問題のほうに1問用意したのでチャレンジしたい方はぜひチャレンジしてみてください！

 

スポンサードリンク

３．練習問題

では、3問ほど練習してみましょう。

練習1

とある大学の休憩コーナー（通称：LA）では、毎日12時になるとご飯を食べるための座席（陣地）を占領するために大量の人が訪れる。

しかし、LAの陣地はあまり広くないため、陣地を占領するためのナワバリバトルが生徒組と教授組の間で毎日繰り広げられ戦争となる。

ナワバリバトルの結果は不思議なことにつぎのような一定確率で決まる。

\( n \) 日目（ただし \( n \) は0以上の整数）のナワバリバトルで生徒組が勝利する確率を \( a_n \)、教授組が敗北する確率を \( b_n \) とする。

戦争開始日を0日目とし、0日目の争いでは生徒組が勝利したとき、つまり \( a_0 = 1 \), \( b_0 = 0 \) のとき、つぎの問いに答えなさい。

(1) \[
\vec{x}_n =   \left( \begin{array}{ccc} a_n \\ b_n  \end{array} \right) 
\]としたとき、\[ \vec{x}_n = A \vec{x}_{n-1} \]を満たすような行列 \( A \) を求めなさい。

(2) \( \vec{x}_0 \), \( \vec{x}_1 \) を求めなさい。
（ヒント \( a_n + b_n = 1 \) は必ず成立する）

(3) 行列 \( A \) の固有値 \( t_1 \), \( t_2 \) およびそれぞれの固有値に対応する固有ベクトル \( \vec{p_1} \), \( \vec{p_2} \) を求めなさい。

(4) ベクトル \( \vec{x}_0 \) を \( \vec{p_1} \), \( \vec{p_2} \) の1次結合で表しなさい。

(5) \( \vec{x}_n \) を求めなさい。

(6) 十分長い間ナワバリバトルが行われたときの生徒お組の勝利確率を\[
\lim_{x \to \infty} \vec{x}_n 
\]を求めて答えなさい。

練習2 [名古屋大学（理系）前期日程　問題3]

大学入試の問題を行列を使って解いてみましょう！
もとの問題はこちらから！

はじめにAくんが赤玉を1個、Bくんが白玉を1個、Cくんが青玉を1個もっている。表裏の出る確率がそれぞれ1/2の硬貨を投げ、表が出ればAとBの玉を交換し、裏が出ればBとCを玉が交換する。という操作を考える。この操作を \( n \) 回繰り返したあとにAくん、Bくん、Cくんが赤玉を持っている確率を \( a_n \), \( b_n \), \( c_n \) とおく。

このとき、 
\[\left\{ \begin{array}{l}
a_{n+1} =  \frac{1}{2} a_n   +   \frac{1}{2} b_n  \\
b_{n+1} =  \frac{1}{2} a_n +  \frac{1}{2} c_n  \\
c_{n+1} =  \frac{1}{2} b_n  +  \frac{1}{2} c_n 
\end{array}\right.\]の差分方程式（漸化式）が成り立つ。

このとき、つぎの問いに答えなさい。

(1) \[
\vec{x}_n = \left( \begin{array}{ccc} a_n \\ b_n \\ c_n   \end{array} \right) 
\]とおく。このとき、\[ \vec{x}_{n+1} = A \vec{x}_{n} \]を満たす行列 \( A \) を求めなさい。

(2) \( \vec{x}_1 \), \( \vec{x}_2 \) の値を答えなさい。

(3) 行列 \( A \) の固有値 \( t_1 \), \( t_2 \), \( t_3 \) と固有値に対応する固有ベクトル \( \vec{p_1} \), \( \vec{p_2} \), \( \vec{p_3} \) を求めなさい。

(4) \( \vec{x}_0 \) を \( \vec{p_1} \), \( \vec{p_2} \), \( \vec{p_3} \) の1次結合で表しなさい。

(5) \( \vec{x}_n \) を求め、\( a_n \), \( b_n \), \( c_n \) の一般項を求めなさい。

(6) \[
\lim_{x \to \infty} \vec{x}_n 
\]を求め、十分な回数硬貨を投げたとき（\( n \) が大きくなったとき）、\( a_n \), \( b_n \), \( c_n \) にはどのような関係が生まれるかを答えなさい。

 

練習3

差分方程式\[ a_{n+3} = 10 a_{n+2} - 31 a_{n+1} + 30 a_n \\ a_0 = 1, \  a_1 = 2, a_2 = 5 \]

の初期値による特殊解を求めたい。差分方程式を変形し、\[
\left\{ \begin{array}{l} a_n = 3 a_{n-1} - 2 a_{n-2} \\ a_{n-1} = 1 a_{n-1} \\ a_{n-2} = 1 a_{n-2} \end{array}\right.
\]としてみることにより、\[
\vec{x}_n = \left( \begin{array}{ccc} a_{n+2} \\ b_{n+1} \\ c_n   \end{array} \right)  \ \ \ A = \left( \begin{array}{ccc} 10 & -31 & 30 \\ 1 & 0 & 0 \\ 0 & 1 & 0   \end{array} \right) \\ \vec{x}_n = A \vec{x}_{n-1}
\]と表すことができる。

(1) \( \vec{x}_0 \), \( \vec{x}_1 \) の値を求めなさい。

(2) 行列 \( A \) の固有値、固有ベクトルを求めなさい

(3) 行列 \( A \) の固有値 \( t_1 \), \( t_2 \), \( t_3 \) と固有値に対応する固有ベクトル \( \vec{p_1} \), \( \vec{p_2} \), \( \vec{p_3} \) を求めなさい。

(4) \( \vec{x}_0 \) を \( \vec{p_1} \), \( \vec{p_2} \), \( \vec{p_3} \) の1次結合で表しなさい。

(5) \( \vec{x}_n \) を求め、\( a_n \) の一般項を求めなさい。

 

解答1

(1) 

\( n \) 日目のナワバリバトルの勝利確率 \( a_{n} \), \( b_{n} \) は前日の勝利確率 \( a_{n-1} \)、敗北確率 \( b_{n-1} \) を用いて
\[\left\{ \begin{array}{l}
a_{n} =  \frac{6}{7} a_{n-1}   +   \frac{3}{7} b_{n-1}  \\
b_{n} =  \frac{1}{7} a_{n-1} +  \frac{4}{7} b_{n-1}  \\
\end{array}\right.\]となる。これを行列を用いて表すと、\[
 \left( \begin{array}{ccc} a_{n} \\ b_{n} \end{array} \right) =  \left( \begin{array}{ccc} \frac{6}{7} & \frac{3}{7} \\ \frac{1}{7} & \frac{4}{7} \end{array} \right) \left( \begin{array}{ccc} a_{n-1} \\ b_{n-1} \end{array} \right)
\]とかけるため、行列 \( A \) は、\[
A = \left( \begin{array}{ccc} \frac{6}{7} & \frac{3}{7} \\ \frac{1}{7} & \frac{4}{7} \end{array} \right) = \frac{1}{7} \left( \begin{array}{ccc} 6 & 3 \\ 1 & 4 \end{array} \right)
\]となる。

 

(2) \[
\vec{x}_0 =  \left( \begin{array}{ccc} a_{0} \\ b_{0}  \end{array} \right) =   \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right)
\\
\vec{x}_1 = A \vec{x}_0 = \frac{1}{7} \left( \begin{array}{ccc} 6 & 3 \\ 1 & 4 \end{array} \right)  \left( \begin{array}{ccc} 1 \\ 0 \end{array} \right)
=  \frac{1}{7} \left( \begin{array}{ccc} 6 \\ 1 \end{array} \right)
\]

 

(3)

固有値を \( t \) とすると、固有方程式は、\[\begin{align*}
|A-tE| = &  \left| \begin{array}{ccc} \frac{6}{7} - t & \frac{3}{7} \\ \frac{1}{7} & \frac{4}{7} - t \end{array} \right|
\\ = & \frac{1}{7} \left| \begin{array}{ccc} 6 - 7t & 3 \\ 1 & 4  - 7t \end{array} \right|
\\ = & (7t-6)(7t-4) - 3
\\ = & 49t^2 - 70t + 21
\\ = & (7t-3)(7t-7) = 0
\end{align*} \]より固有値は \( 3/7, 1 \) となる。

 

(i) 固有値が1のときの固有ベクトル \( \vec{p_1} \)\[ \begin{align*}
\frac{1}{7} (A-7E) = &
\frac{1}{7} \left( \begin{array}{ccc} -1 & 3 \\ 1 & -3  \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 1 & -3 \\ 0 & 0  \end{array} \right)
\end{align*} \]となる。\[
x - 3y = 0
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y  \end{array} \right) = k \left( \begin{array}{ccc} 3 \\ 1 \end{array} \right)
\]と表せるので、固有ベクトル \( \vec{p_1} \) は、\[
\vec{p_1} = \left( \begin{array}{ccc} 3 \\ 1   \end{array} \right)
\]となる。

 

(ii) 固有値が3/7のときの固有ベクトル \( \vec{p_1} \)\[ \begin{align*}
\frac{1}{7} (A-3E) = &
\frac{1}{7} \left( \begin{array}{ccc} 3 & 3 \\ 1 & 1  \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 1 & 1 \\ 0 & 0  \end{array} \right)
\end{align*} \]となる。\[
x + y = 0
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y  \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ -1 \end{array} \right)
\]と表せるので、固有ベクトル \( \vec{p_2} \) は、\[
\vec{p_2} = \left( \begin{array}{ccc} 1 \\ -1   \end{array} \right)
\]となる。

 

(4)\[
\vec{x}_0 = c_1 \vec{p_1} + c_2 \vec{p_2} \\
\left( \begin{array}{ccc} 1 \\ 0 \end{array} \right) = c_1 \left( \begin{array}{ccc} 3 \\ 1   \end{array} \right) + c_2 \left( \begin{array}{ccc} 1 \\ -1   \end{array} \right) \\
\left( \begin{array}{ccc} 3 & 1 \\ 1 & -1   \end{array} \right) \left( \begin{array}{ccc} c_1 \\ c_2   \end{array} \right) = \left( \begin{array}{ccc} 1 \\ 0   \end{array} \right)
\]となるような \( c_1 \), \( c_2 \) の値をもとめればよい。

求め方は2パターン

[パターン1：行基本変形で求める] \[
 \begin{align*}
& \left( \begin{array}{cc|c} 3 & 1 & 1 \\ 1 & -1 & 0 \end{array} \right)
 \\ \to \ & \left( \begin{array}{cc|c} 4 & 0 & 1 \\ -4 & 4 & 0 \end{array} \right)
 \\ \to \ & \left( \begin{array}{cc|c} 4 & 0 & 0 \\ 0 & 4 & 1 \end{array} \right)
 \\ \to \ & \left( \begin{array}{cc|c} 1 & 0 & \frac{1}{4} \\ 0 & 1 & \frac{1}{4} \end{array} \right)
\end{align*} \]\]となるので、\( c_1 = 1/4 \), \( c_2 = 1/4 \) となる。よって、\[
\vec{x}_0 = \frac{1}{4} \vec{p_1} + \frac{1}{4} \vec{p_2}
\]となる。

 

[パターン2：逆行列を用いる]　\[
\left( \begin{array}{ccc} 3 & 1 \\ 1 & -1   \end{array} \right)^{-1} = \frac{1}{4} \left( \begin{array}{ccc} 1 & 1 \\ 1 & -3   \end{array} \right)
\]となるので、\[\begin{align*}
\left( \begin{array}{ccc} c_1 \\ c_2   \end{array} \right) & = \left( \begin{array}{ccc} 3 & 1 \\ 1 & -1   \end{array} \right)^{-1} \left( \begin{array}{ccc} 1 \\ 0   \end{array} \right)
\\ & = \frac{1}{4} \left( \begin{array}{ccc} 1 & 1 \\ 1 & -3   \end{array} \right)\left( \begin{array}{ccc} 1 \\ 0   \end{array} \right)
\\ & = \frac{1}{4} \left( \begin{array}{ccc} 1 \\ 1   \end{array} \right)
\end{align*} \]

となる。よって、\[
\vec{x}_0 = \frac{1}{4} \vec{p_1} + \frac{1}{4} \vec{p_2}
\]が求められる。

 

(5)

ここで、\[ \begin{align*}
 \left( \begin{array}{ccc} a_n \\ b_n   \end{array} \right) & = 
\vec{x}_n \\ & = A^n \vec{x}_0
\\ & = A^n \left( \frac{1}{4} \vec{p_1} + \frac{1}{4} \vec{p_2} \right)
\\ & = \frac{1}{4} A^n \vec{p_1} + \frac{1}{4} A^n \vec{p_2}
\\ & = \frac{1}{4} \cdot 1 \vec{p_1} + \frac{1}{4} \left( \frac{3}{7} \right)^n \vec{p_2}
\\ & = \frac{1}{4} \cdot \left( \begin{array}{ccc} 3 \\ 1   \end{array} \right) + \frac{1}{4} \left( \frac{3}{7} \right)^n \left( \begin{array}{ccc} 1 \\ -1   \end{array} \right)
\\ & = \frac{1}{4} \left( \begin{array}{ccc} 3 + \left( \frac{3}{7} \right)^n  \\ 1 - \left( \frac{3}{7} \right)^n   \end{array} \right)
\end{align*} \]と求められますね。

よって、一般項は\[
a_n = \frac{1}{4} \left\{ 3 +  \left( \frac{3}{7} \right)^n \right\} 
\\ b_n = \frac{1}{4}  \left\{ 1 - \left( \frac{3}{7} \right)^n   \right\}
\]と求められます。

 

(6)

（(5)の計算よりもこちらのほうが簡単かも）

\[
\vec{x}_n = \frac{1}{4} \cdot \left( \begin{array}{ccc} 3 \\ 1   \end{array} \right) + \frac{1}{4} \left( \frac{3}{7} \right)^n \left( \begin{array}{ccc} 1 \\ -1   \end{array} \right)
\]の \( n \) を十分大きくすると、\[
\lim_{x \to \infty} \vec{x}_n = \frac{1}{4} \cdot \left( \begin{array}{ccc} 3 \\ 1   \end{array} \right)
\]となる*1。

よって、十分な回数硬貨を投げると\[
a_n = \frac{3}{4} \ \ \ b_n = \frac{1}{4}
\]に収束する。

 

解答2

(1) 

与えられた漸化式（差分方程式）を行列で表すだけ。\[
 \left( \begin{array}{ccc} a_{n+1} \\ b_{n+1} \\ c_{n+1} \end{array} \right) =  \left( \begin{array}{ccc} \frac{1}{2} & \frac{1}{2} & 0 \\ \frac{1}{2} & 0 & \frac{1}{2} \\ 0 & \frac{1}{2} & \frac{1}{2}  \end{array} \right) \left( \begin{array}{ccc} a_{n} \\ b_{n} \\ c_{n} \end{array} \right)
\]と表せるので、\[
A = \frac{1}{2} \left( \begin{array}{ccc} \frac{1}{2} & \frac{1}{2} & 0 \\ \frac{1}{2} & 0 &\frac{1}{2} \\ 0 & \frac{1}{2} & \frac{1}{2} \end{array} \right) = \frac{1}{2} \left( \begin{array}{ccc} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1   \end{array} \right)
\]となる。

 

(2)

行列の積を計算するだけ。

\[
\vec{x}_1 = A \vec{x}_0 \frac{1}{2} \left( \begin{array}{ccc} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1   \end{array} \right) \left( \begin{array}{ccc} 1 \\ 0 \\ 0   \end{array} \right) = \frac{1}{2} \left( \begin{array}{ccc} 1 \\ 1 \\ 0   \end{array} \right) \\
\vec{x}_2 = A^2 \vec{x}_0 = A \vec{x}_1 = \frac{1}{4} \left( \begin{array}{ccc} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1   \end{array} \right) \left( \begin{array}{ccc} 1 \\ 1 \\ 0   \end{array} \right) = \frac{1}{4} \left( \begin{array}{ccc} 2 \\ 1 \\ 1   \end{array} \right)
\]ちなみに名古屋大の入試でも \( a_1 \), \( b_1 \), \( c_1 \), \( a_2 \), \( b_2 \), \( c_2 \) の値を答えさせる問題は出題されている。

 

(3)

ここからがオリジナル問題。

固有値を \( t \) とすると、固有方程式は、\[\begin{align*}
|A-tE| = &  \left| \begin{array}{ccc} \frac{1}{2} - t & \frac{1}{2} & 0 \\ \frac{1}{2} & -t & \frac{1}{2} \\ 0 & \frac{1}{2} & \frac{1}{2} -t \end{array} \right|
\\ = & \frac{1}{2} \left| \begin{array}{ccc} 1-2t & 1 & 0 \\ 1 & -2t & 1 \\ 0 & 1 & 1-2t \end{array} \right|
\\ = & \frac{1}{2} \left| \begin{array}{ccc} 2-2t & 2-2t & 2-2t \\ 1 & -2t & 1 \\ 0 & 1 & 1-2t \end{array} \right|
\\ = & (1-t) \left| \begin{array}{ccc} 1 & 1 & 1 \\ 1 & -2t & 1 \\ 0 & 1 & 1-2t \end{array} \right|
\\ = & (1-t) \left| \begin{array}{ccc} 1 & 1 & 1 \\ 0 & -2t-1 & 0 \\ 0 & 1 & 1-2t \end{array} \right|
\\ = & (1-t) \left| \begin{array}{ccc} -2t-1 & 0 \\ 1 & 1-2t \end{array} \right|
\end{align*} \]となる。

となる。

ここで、\[\begin{align*} 
\left| \begin{array}{ccc} -2t-1 & 0 \\ 1 & 1-2t \end{array} \right| = -(1-2t)(1+2t)
\end{align*} \]となるので、\[
|A - tE| = -(1-t)(1-2t)(1+2t)
\]を満たす \( t \) が固有値となり、固有値は1, 1/2, -1/2となる。

 

(i) 固有値が1のときの固有ベクトル \( \vec{p_1} \) \[ \begin{align*}
\frac{1}{2} (A-2E) = &
\frac{1}{2} \left( \begin{array}{ccc} -1 & 1 & 0 \\ 1 & -2 & 1 \\ 0 & 1 & -1  \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 0 & 1 & -1  \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 1 & -1 & 0 \\ 0 & 1 & -1 \\ 0 & 0 & 0  \end{array} \right)
\end{align*} \]となる。\[
\left\{ \begin{array}{l} x - y = 0 \\ y - z = 0 \end{array}\right. 
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \\ z  \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 1 \\ 1 \end{array} \right)
\]と表せるので、固有ベクトル \( \vec{p_1} \) は、\[
\vec{p_1} = \left( \begin{array}{ccc} 1 \\ 1 \\ 1 \end{array} \right)
\]となる。

 

(ii) 固有値が1/2のときの固有ベクトル \( \vec{p_2} \) \[ \begin{align*}
\frac{1}{2} (A-1E) = &
\frac{1}{2} \left( \begin{array}{ccc} 0 & 1 & 0 \\ 1 & -1 & 1 \\ 0 & 1 & 0  \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 0  \end{array} \right) 
\end{align*} \]となる。\[
\left\{ \begin{array}{l} x + z = 0 \\ y  = 0 \end{array}\right. 
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \\ z  \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \end{array} \right)
\]と表せるので、固有ベクトル \( \vec{p_2} \) は、\[
\vec{p_2} = \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \end{array} \right)
\]となる。

 

(iii) 固有値が-1/2のときの固有ベクトル \( \vec{p_3} \) \[ \begin{align*}
\frac{1}{2} (A+1E) = &
\frac{1}{2} \left( \begin{array}{ccc} 2 & 1 & 0 \\ 1 & 1 & 1 \\ 0 & 1 & 2  \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 0 & -1 & -2 \\ 1 & 1 & 1 \\ 0 & 1 & 2  \end{array} \right)  \\ \to \ & 
\left( \begin{array}{ccc} 1 & 0 & -1 \\ 0 & 1 & 2 \\ 0 & 0 & 0  \end{array} \right) 
\end{align*} \]となる。\[
\left\{ \begin{array}{l} x + z = 0 \\ y  = 0 \end{array}\right. 
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \\ z  \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ -2 \\ 1 \end{array} \right)
\]と表せるので、固有ベクトル \( \vec{p_3} \) は、\[
\vec{p_3} = \left( \begin{array}{ccc} 1 \\ -2 \\ 1 \end{array} \right)
\]となる。

 

(4)

\[
\vec{x}_0 = c_1 \vec{p_1} + c_2 \vec{p_2} + c_3 \vec{p_3} \\
\left( \begin{array}{ccc} 1 \\ 0 \\ 0 \end{array} \right) = c_1 \left( \begin{array}{ccc} 1 \\ 1 \\ 1  \end{array} \right) + c_2 \left( \begin{array}{ccc} 1 \\ 0 \\ -1   \end{array} \right) + c_3 \left( \begin{array}{ccc} 1 \\ -2 \\ 1  \end{array} \right) \\
\left( \begin{array}{ccc} 1 & 1 & 1\\ 1 & 0 & -2 \\ 1 & -1 & 1   \end{array} \right) \left( \begin{array}{ccc} c_1 \\ c_2 \\ c_3  \end{array} \right) = \left( \begin{array}{ccc} 1 \\ 0 \\ 0   \end{array} \right)
\]となるような \( c_1 \), \( c_2 \), \( c_3 \) の値をもとめればよい。

 

3次正方行列の逆行列はあまりおすすめしないので素直に行基本変形で求める。

[パターン1：行基本変形で求める] \[
 \begin{align*} &
 \left( \begin{array}{ccc|c} 1 & 1 & 1 & 1 \\ 1 & 0 & -2 & 0 \\ 1 & -1 & 1 & 0 \end{array} \right) \\ \to \ & 
 \left( \begin{array}{ccc|c} 1 & 1 & 1 & 1 \\ 0 & -1 & -3 & -1 \\ 0 & -2 & 0 & -1 \end{array} \right) \\ \to \ & 
 \left( \begin{array}{ccc|c} 6 & 6 & 6 & 6 \\ 0 & -2 & -6 & -2 \\ 0 & -2 & 0 & -1 \end{array} \right) \\ \to \ & 
 \left( \begin{array}{ccc|c} 6 & 0 & 6 & 3 \\ 0 & 0 & -6 & -1 \\ 0 & -2 & 0 & -1 \end{array} \right) \\ \to \ & 
 \left( \begin{array}{ccc|c} 6 & 0 & 0 & 2 \\ 0 & 0 & -6 & -1 \\ 0 & -2 & 0 & -1 \end{array} \right) \\ \to \ & 
 \left( \begin{array}{ccc|c} 1 & 0 & 0 & \frac{1}{3} \\ 0 & 1 & 0 & \frac{1}{2} \\ 0 & 0 & 1 & \frac{1}{6} \end{array} \right) 
\end{align*} \]\]となるので、\( c_1 = 1/3 \), \( c_2 = 1/2 \), \( c_3 = 1/6 \) となる。よって、\[
\vec{x}_0 = \frac{1}{3} \vec{p_1} + \frac{1}{2} \vec{p_2} + \frac{1}{6} \vec{p_3}
\]となる。

 

(5)

ここで、\[ \begin{align*}
 \left( \begin{array}{ccc} a_n \\ b_n \\ c_n   \end{array} \right) & =
\vec{x}_n \\ & = A^n \vec{x}_0
\\ & = A^n \left( \frac{1}{3} \vec{p_1} + \frac{1}{2} \vec{p_2} + \frac{1}{6} \vec{p_3} \right)
\\ & = \frac{1}{3} A^n \vec{p_1} + A^n \frac{1}{2} \vec{p_2} + A^n \frac{1}{6} \vec{p_3}
\\ & = \frac{1}{3} \cdot 1 \vec{p_1} + \frac{1}{2} \cdot \left( \frac{1}{2} \right )^n \vec{p_2} +  \frac{1}{6} \left( - \frac{1}{2} \right )^n \vec{p_3}
\\ & = \frac{1}{3} \cdot \left( \begin{array}{ccc} 1 \\ 1 \\ 1   \end{array} \right) +  \left( \frac{1}{2} \right )^{n+1} \left( \begin{array}{ccc} 1 \\ 0 \\ -1   \end{array} \right) + \frac{1}{6} \cdot \left( - \frac{1}{2} \right )^{n} \left( \begin{array}{ccc} 1 \\ -2 \\ 1   \end{array} \right)
\\ & =
\left( \begin{array}{ccc} \frac{1}{3} + \left( \frac{1}{2} \right )^{n+1} + \frac{1}{6} \left( - \frac{1}{2} \right )^{n+1} \\ \frac{1}{3} - \frac{1}{3} \left( - \frac{1}{2} \right )^{n+1} \\ \frac{1}{3} - \left( \frac{1}{2} \right )^{n+1} + \frac{1}{6} \left( - \frac{1}{2} \right)^{n+1} \end{array} \right)
\end{align*} \]と求められますね。

よって、一般項は\[
a_n = \frac{1}{3} + \left( \frac{1}{2} \right )^{n+1} + \frac{1}{6} \left( - \frac{1}{2} \right )^{n+1} \\
b_n = \frac{1}{3} - \frac{1}{3} \left( - \frac{1}{2} \right)^{n+1}
\\ c_n = \frac{1}{6} \left( - \frac{1}{2} \right)^{n+1} 
\]と求められます。

 

(6)

（(5)の計算よりもこちらのほうが簡単かも）

\[
\vec{x}_n =  \frac{1}{3} \cdot \left( \begin{array}{ccc} 1 \\ 1 \\ 1   \end{array} \right) +  \left( \frac{1}{2} \right )^{n+1} \left( \begin{array}{ccc} 1 \\ 0 \\ -1   \end{array} \right) + \frac{1}{6} \cdot \left( - \frac{1}{2} \right )^{n} \left( \begin{array}{ccc} 1 \\ -2 \\ 1   \end{array} \right)
\]の \( n \) を十分大きくすると、\[
\lim_{x \to \infty} \vec{x}_n = \frac{1}{3} \cdot \left( \begin{array}{ccc} 1 \\ 1 \\ 1   \end{array} \right)
\]となる*2。

よって、十分な回数硬貨を投げると\[
a_n = b_n = c_n
\]となるので、Aくん、Bくん、Cくんがそれぞれ均等な確率で赤玉をもつ。

 

解答3

(1) 

\[
\vec{x}_0 = \left( \begin{array}{ccc} a_2 \\ a_1 \\ a_0   \end{array} \right) = \left( \begin{array}{ccc} 5 \\ 2 \\ 1   \end{array} \right)
\begin{align*}
\vec{x}_1 & = A \vec{x}_0 \\ & =  \left( \begin{array}{ccc} 10 & -31 & 30 \\ 1 & 0 & 0 \\ 0 & 1 & 0   \end{array} \right) \left( \begin{array}{ccc} 5 \\ 2 \\ 1   \end{array} \right) \\ & =  \left( \begin{array}{ccc} 18 \\ 5 \\ 2   \end{array} \right) 
\end{align*}
\]

 

(2) 

実はこの固有値問題は行基本変形で簡単な形にするのが難しい、行列の0の成分が2つあることなどからサラスの公式でゴリ押しで求めたほうが早く固有値を出せる。

固有値を \( t \) とすると、固有方程式は、\[\begin{align*}
|A-tE| = &  \left| \begin{array}{ccc} 10-t & -31 & 30 \\ 1 & -t & 0 \\ 0 & 1 & -t \end{array} \right|
\\ = & t^2 (10-t) + 30 - 31t
\\ = & -t^3 + 10t^2 -31t + 30
\\ = & -(t^3 - 10t^2 +31t - 30)
\\ = & -2(t-2)(t^2 - 8t +15)
\\ = & -2(t-2)(t-3)(t-5)
\end{align*} \]より固有値は 2,3,5 となる。

 

(i) 固有値が2のときの固有ベクトル \( \vec{p_1} \) \[ \begin{align*}
(A-2E) = &
\left( \begin{array}{ccc} 8 & -31 & 30 \\ 1 & -2 & 0 \\ 0 & 1 & -2  \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 0 & -15 & 30 \\ 1 & -2 & 0 \\ 0 & 1 & -2  \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 1 & -2 & 0 \\ 0 & 1 & -2 \\ 0 & 1 & -2  \end{array} \right)  
\end{align*} \]となる。\[
\left\{ \begin{array}{l} x - 2y = 0 \\ y - 2z = 0 \end{array}\right. 
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \\ z  \end{array} \right) = k \left( \begin{array}{ccc} 4 \\ 2 \\ 1 \end{array} \right)
\]と表せるので、固有ベクトル \( \vec{p_1} \) は、\[
\vec{p_1} = \left( \begin{array}{ccc} 4 \\ 2 \\ 1 \end{array} \right)
\]となる。

 

(ii) 固有値が3のときの固有ベクトル \( \vec{p_2} \) \[ \begin{align*}
(A-2E) = &
\left( \begin{array}{ccc} 7 & -31 & 30 \\ 1 & -3 & 0 \\ 0 & 1 & -3  \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 0 & -10 & 30 \\ 1 & -3 & 0 \\ 0 & 1 & -3  \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 1 & -3 & 0 \\ 0 & 1 & -3 \\ 0 & 0 & 0  \end{array} \right)  
\end{align*} \]となる。\[
\left\{ \begin{array}{l} x - 3y = 0 \\ y - 3z = 0 \end{array}\right. 
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \\ z  \end{array} \right) = k \left( \begin{array}{ccc} 9 \\ 4 \\ 1 \end{array} \right)
\]と表せるので、固有ベクトル \( \vec{p_2} \) は、\[
\vec{p_2} = \left( \begin{array}{ccc} 9 \\ 4 \\ 1 \end{array} \right)
\]となる。

 

(iii) 固有値が5のときの固有ベクトル \( \vec{p_3} \) \[ \begin{align*}
(A-5E) = &
\left( \begin{array}{ccc} 5 & -31 & 30 \\ 1 & -5 & 0 \\ 0 & 1 & -5  \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 0 & -6 & 30 \\ 1 & -5 & 0 \\ 0 & 1 & -5  \end{array} \right) \\ \to \ & 
\left( \begin{array}{ccc} 1 & -5 & 0 \\ 0 & 1 & -5 \\ 0 & 0 & 0  \end{array} \right) 
\end{align*} \]となる。\[
\left\{ \begin{array}{l} x - 5y = 0 \\ y - 5z = 0 \end{array}\right. 
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \\ z  \end{array} \right) = k \left( \begin{array}{ccc} 25 \\ 5 \\ 1 \end{array} \right)
\]と表せるので、固有ベクトル \( \vec{p_3} \) は、\[
\vec{p_3} = \left( \begin{array}{ccc} 25 \\ 5 \\ 1 \end{array} \right)
\]となる。

 

(4) \[
\vec{x}_0 = c_1 \vec{p_1} + c_2 \vec{p_2} + c_3 \vec{p_3} \\
\left( \begin{array}{ccc} 5 \\ 2 \\ 1 \end{array} \right) = c_1 \left( \begin{array}{ccc} 4 \\ 2 \\ 1  \end{array} \right) + c_2 \left( \begin{array}{ccc} 9 \\ 4 \\ 1   \end{array} \right) + c_3 \left( \begin{array}{ccc} 25 \\ 5 \\ 1  \end{array} \right) \\
\left( \begin{array}{ccc} 4 & 9 & 25 \\ 2 & 4 & 5 \\ 1 & 1 & 1   \end{array} \right) \left( \begin{array}{ccc} c_1 \\ c_2 \\ c_3   \end{array} \right) = \left( \begin{array}{ccc} 5 \\ 2 \\ 1   \end{array} \right)
\]となるような \( c_1 \), \( c_2 \), \( c_3 \) の値をもとめればよい。

 

3次正方行列の逆行列はあまりおすすめしないので素直に行基本変形で求める。

 \[
 \begin{align*} &
 \left( \begin{array}{ccc|c} 4 & 9 & 25 & 5 \\ 2 & 3 & 5 & 2 \\ 1 & 1 & 1 & 1 \end{array} \right) \\ \to \ & 
 \left( \begin{array}{ccc|c} 0 & 5 & 21 & 1 \\ 0 & 1 & 3 & 0 \\ 1 & 1 & 1 & 1 \end{array} \right) \\ \to \ & 
 \left( \begin{array}{ccc|c} 0 & 0 & 6 & 1 \\ 0 & 2 & 6 & 0 \\ 6 & 6 & 6 & 6 \end{array} \right) \\ \to \ & 
 \left( \begin{array}{ccc|c} 0 & 0 & 6 & 1 \\ 0 & 2 & 0 & -1 \\ 6 & 6 & 0 & 5 \end{array} \right) \\ \to \ & 
 \left( \begin{array}{ccc|c} 0 & 0 & 6 & 1 \\ 0 & 2 & 0 & -1 \\ 6 & 0 & 0 & 8 \end{array} \right) \\ \to \ & 
 \left( \begin{array}{ccc|c} 6 & 0 & 0 & 8 \\ 0 & 2 & 0 & -1 \\ 0 & 0 & 6 & 1 \end{array} \right) \\ \to \ & 
 \left( \begin{array}{ccc|c} 1 & 0 & 0 & \frac{4}{3} \\ 0 & 1 & 0 & - \frac{1}{2} \\ 0 & 0 & 1 & \frac{1}{6} \end{array} \right) 
\end{align*} \]\]となるので、\( c_1 = 4/3 \), \( c_2 = - 1/2 \), \( c_3 = 1/6 \) となる。よって、\[
\vec{x}_0 = \frac{4}{3} \vec{p_1} - \frac{1}{2} \vec{p_2} + \frac{1}{6} \vec{p_3}
\]となる。

 

(5)

ここで、\[ \begin{align*}
 \left( \begin{array}{ccc} a_{n+2} \\ a_{n+1} \\ a_n   \end{array} \right) & =
\vec{x}_n \\ & = A^n \vec{x}_0
\\ & = A^n \left( \frac{4}{3} \vec{p_1} - \frac{1}{2} \vec{p_2} + \frac{1}{6} \vec{p_3} \right)
\\ & = \frac{4}{3} A^n \vec{p_1} - A^n \frac{1}{2} \vec{p_2} + A^n \frac{1}{6} \vec{p_3}
\\ & = \frac{4}{3} \cdot 2^n \vec{p_1} - \frac{1}{2} \cdot 3^n \left( \frac{1}{2} \right )^n \vec{p_2} +  \frac{1}{6} \cdot 5^n \vec{p_3}
\\ & =  \frac{4}{3} \cdot 2^n \left( \begin{array}{ccc} 4 \\ 2 \\ 1 \end{array} \right) - \frac{1}{2} \cdot 3^n \left( \begin{array}{ccc} 9 \\ 3 \\ 1 \end{array} \right) + \frac{1}{6} \cdot 5^n \left( \begin{array}{ccc} 25 \\ 5 \\ 1 \end{array} \right)  \\ & = 
\left( \begin{array}{ccc}
\frac{4}{3} \cdot 2^{n+2} - \frac{1}{2}  \cdot 3^{n+2} + \frac{1}{6} \cdot 5^{n+2} \\
\frac{4}{3} \cdot 2^{n+1} - \frac{1}{2}  \cdot 3^{n+1} + \frac{1}{6} \cdot 5^{n+1} \\
\frac{4}{3} \cdot 2^{n} - \frac{1}{2}  \cdot 3^{n} + \frac{1}{6} \cdot 5^{n} 
\end{array} \right)
\end{align*} \]と求められますね。

よって、一般項は\[
a_n =  2^{n} - \frac{1}{2}  \cdot 3^{n} + \frac{1}{6} \cdot 5^{n} 
\]と求められます。

 

４．さいごに

今回は差分方程式（漸化式）を行列を用いて解く流れを例題などで説明しました。

 

実際に差分方程式を解く際にはおそらく行列を使わないこちらの解き方のほうがかなり早く出せるので、線形代数の練習をしたいときや問題文で指示されたとき以外は行列で解かないほうがいいかもしれません。

 

また、万が一漸化式を直した行列 \( A \) が対角化できない場合は、ジョルダン標準形を求めたり、\( A^n \vec{p} = t^n \vec{p} \) が使えなくなるので計算過程がさらに複雑になります。