スポンサードリンク
こんにちは、ももやまです。
今回は、2次形式についてのまとめました。
2次形式を標準形にする方法、2次形式の正定値、負定値などの符号についてまとめています。
前回の記事はこちら!(行列の \( n \) 乗を用いた差分方程式の解き方!)
目次
スポンサードリンク
1.2次形式とは
2次形式とは、\[
4 x_1^2 + 2 x_1 x_2 + 4 x_2^2
\]のように、2次の項だけで構成される多項式のことを表します。
2次の項だけで構成されるので、1次以下の項も存在しないことにも注意が必要です。
スポンサードリンク
2.実対象行列を用いた2次形式の表現
変数が \( x_1 \), \( x_2 \) の2つの場合の2次形式を行列に表すことを考えましょう。
変数ベクトル \( \vec{x} \) 、行列 \( A \) をそれぞれ\[
\vec{x} = \left( \begin{array}{ccc} x_1 \\ x_2 \end{array} \right) \ \ \ A = \left( \begin{array}{ccc} a & p \\ p & b \end{array} \right)
\]とします。
すると、\[ \begin{align*}
{}^t\! \vec{x} A \vec{x} & = \left( x_1 , x_2 \right) \left( \begin{array}{ccc} a & p \\ p & b \end{array} \right) \left( \begin{array}{ccc} x_1 \\ x_2 \end{array} \right)
\\ & = \left( a x_1 + p x_2 , p x_1 + b x_2 \right) \left( \begin{array}{ccc} x_1 \\ x_2 \end{array} \right)
\\ & = a x_1^2 + p x_1 x_2 + p x_1 x_2 + b x_2^2
\\ & = a x_1^2 + 2p x_1 x_2 + b x_2^2
\end{align*} \]と変形できます。
変数が \( x_1 \), \( x_2 \), \( x_3 \) の3つになった場合も同じように 変数ベクトル \( \vec{x} \) 、行列 \( A \) をそれぞれ\[
\vec{x} = \left( \begin{array}{ccc} x_1 \\ x_2 \\ x_3 \end{array} \right) \ \ \ A = \left( \begin{array}{ccc} a & p & q \\ p & b & r \\ q & r & c \end{array} \right)
\]とします。
すると、\[ \begin{align*}
{}^t\! \vec{x} A \vec{x} & = \left( x_1, x_2, x_3 \right) \left( \begin{array}{ccc} a & p & q \\ p & b & r \\ q & r & c \end{array} \right) \left( \begin{array}{ccc} x_1 \\ x_2 \\ x_3 \end{array} \right)
\\ & = \left( a x_1 + p x_2 + q x_3, p x_1 + b x_2 + r x_3 + q x_1 + r x_2 + c x_3 \right) \left( \begin{array}{ccc} x_1 \\ x_2 \\ x_3 \end{array} \right)
\\ & = a x_1^2 + p x_1 x_2 + q x_1 x_3 + p x_1 x_2 + b x_2^2 + r x_1 x_3 + q x_1 x_3 + r x_2 x_3 + c x_3^2
\\ & = a x_1^2 + b x_2^2 + c x_2^2 + 2p x_1 x_2 + 2q x_1 x_3 + 2r x_2 x_3
\end{align*} \]と変形できます。
2変数 \( x_1 \), \( x_2 \) の2次形式 \[
a x_1^2 + 2p x_1 x_2 + b x_2^2
\]は実対称行列 \( A \)、ベクトル \( \vec{x} \) を用いて\[\begin{align*}
a x_1^2 + 2p x_1 x_2 + b x_2^2 & = \left( x_1 , x_2 \right) \left( \begin{array}{ccc} a & p \\ p & b \end{array} \right) \left( \begin{array}{ccc} x_1 \\ x_2 \end{array} \right) \\ & = {}^t\! \vec{x} A \vec{x}
\end{align*} \]と変形できる。
また、3変数 \( x_1 \), \( x_2 \), \( x_3 \) の2次形式 \[
a x_1^2 + b x_2^2 + c x_2^2 + 2p x_1 x_2 + 2q x_1 x_3 + 2r x_2 x_3
\]も同様に\[\begin{align*} &
a x_1^2 + b x_2^2 + c x_2^2 + 2p x_1 x_2 + 2q x_1 x_3 + 2r x_2 x_3 \\ = & \left( x_1 , x_2 , x_3 \right) \left( \begin{array}{ccc} a & p & q \\ p & b & r \\ q & r & c \end{array} \right) \left( \begin{array}{ccc} x_1 \\ x_2 \\ x_3 \end{array} \right) \\ = & {}^t\! \vec{x} A \vec{x}
\end{align*} \]と変形できる。
(4変数以上についても同様に変形できる。)
スポンサードリンク
3.2次形式の標準形
2次形式の標準形とは、\[
3 x_1^2 + 3 x_2^2 + 4 x_3^2 \cdots
\]のように、すべての項が1変数の2次式となっているもの*1(つまり \( x_1 x_2 \) や \( x_2 x_3 \) のように2変数の2次式がないもの)を2次形式の標準形と呼びます。
もともと標準形ではない2次形式も、変換することで標準形にすることができます。
ということで、標準形に変換する過程を例題を1問解きながら説明していきましょう。
例題1
2次形式\[
4 x_1^2 + 2 x_1 x_2 + 4 x_2^2
\]を標準形にしなさい。
解説1
\( A \) 、ベクトル \( \vec{x} \) をそれぞれ\[
A = \left( \begin{array}{ccc} 4 & 1 \\ 1 & 4 \end{array} \right) \ \ \ \vec{x} = \left( \begin{array}{ccc} x_1 \\ x_2 \end{array} \right)
\]とすると、\[
4 x_1^2 + 2 x_1 x_2 + 4 x_2^2 = {}^t\! \vec{x} A \vec{x}
\]と変形できる。
直交行列を用いた対角化を行うため、行列 \( A \) の固有値、固有ベクトルを求める。
直交行列を用いた対角化について忘れてしまった人やまだわからない〜って人はこちらで復習しましょう↓
固有値を \( t \) とすると、固有方程式は、\[\begin{align*}
|A-tE| = & \left| \begin{array}{ccc} 4-t & 1 \\ 1 & 4-t \end{array} \right|
\\ = & (t-4)^2 - 1
\\ = & t^2 - 8t + 15
\\ = & (t-3)(t-5) = 0
\end{align*} \]より固有値は3, 5となる。
(1) 固有値が3のとき\[ \begin{align*}
(A-3E) = &
\left( \begin{array}{ccc} 1 & 1 \\ 1 & 1 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 1 \\ 0 & 0 \end{array} \right)
\end{align*} \]となる。\[
x + y = 0
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ -1 \end{array} \right)
\]と表せる。
固有ベクトル \( \vec{p_1} \) は大きさを1に正規化したベクトル、\[
\vec{p_1} = \frac{1}{\sqrt{2}}\left( \begin{array}{ccc} 1 \\ -1 \end{array} \right)
\]となる。
(2) 固有値が5のとき\[ \begin{align*}
(A-5E) = &
\left( \begin{array}{ccc} -1 & 1 \\ 1 & -1 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & -1 \\ 0 & 0 \end{array} \right)
\end{align*} \]となる。\[
x - y = 0
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)
\]と表せる。
固有ベクトル \( \vec{p_1} \) は大きさを1に正規化したベクトルなので、\[
\vec{p_1} = \frac{1}{\sqrt{2}}\left( \begin{array}{ccc} 1 \\ 1 \end{array} \right)
\]となる。
\( \vec{p_1} \), \( \vec{p_2} \) は正規直交基底となるので、直交行列\[
P = \left( \vec{p_1}, \vec{p_2} \right) = \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 & 1 \\ -1 & 1 \end{array} \right)
\]を用いて、\[
P^{-1} AP = \left( \begin{array}{ccc} 3 & 0 \\ 0 & 5 \end{array} \right) = D
\]と対角化できますね。
よって、\[
P P^{-1} A P P^{-1} = A = P D P^{-1}
\]と変形でき、行列 \( A \) は、\[
A = P D P^{-1} = P D {}^t\! P
\]と変形できます*2。
ここで、変数 \( y_1 \), \( y_2 \)、ベクトル \( \vec{y} \) を\[
\vec{y} = \left( \begin{array}{ccc} y_1 \\ y_2 \end{array} \right) = {}^t\! P \left( \begin{array}{ccc} x_1 \\ x_2 \end{array} \right) = {}^t\! P \vec{x}
\]となるようにおきます。
すると、\[\begin{align*}
\left( \begin{array}{ccc} y_1 \\ y_2 \end{array} \right) & = \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 & -1 \\ 1 & 1 \end{array} \right) \left( \begin{array}{ccc} x_1 \\ x_2 \end{array} \right)
\\ & = \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} x_1 - x_2 \\ x_1 + x_2 \end{array} \right)
\end{align*} \]、つまり\[
y_1 = \frac{1}{\sqrt{2}} \left( x_1 - x_2 \right) \\
y_2 = \frac{1}{\sqrt{2}} \left( x_1 + x_2 \right)
\]と変数変換となりますね。
また、\( \vec{y} = {}^t\! P \vec{x} \) なので、\( P \vec{y} = \vec{x} \) となりますね*3。
よって、\[\begin{align*}
{}^t\! \vec{x} A \vec{x} & = {}^t\! \left( P \vec{y} \right) A \left( P \vec{y} \right)
\\ & = {}^t\! \vec{y} {}^t\! P A P \vec{y}
\\ & = {}^t\! \vec{y} P^{-1} A P \vec{y}
\\ & = {}^t\! \vec{y} D \vec{y}
\end{align*} \]と変形できます。
よって、\[\begin{align*}
4 x_1^2 + 2 x_1 x_2 + 4 x_2^2 & = {}^t\! \vec{x} A \vec{x}
\\ & = {}^t\! \vec{y} D \vec{y}
\\ & = 3 y_1^2 + 5y_2^2
\end{align*} \]となり、標準形に変形できました!
2変数の2次形式の標準形の変換法をまとめると、下のようになります。
2変数 \( x_1 \), \( x_2 \) の2次形式 \[
a x_1^2 + 2p x_1 x_2 + b x_2^2
\]は実対称行列 \( A \)、ベクトル \( \vec{x} \)\[\begin{align*}
A = \left( \begin{array}{ccc} a & p \\ p & b \end{array} \right) \ \ \
\vec{x} = \left( \begin{array}{ccc} x_1 \\ x_2 \end{array} \right) = {}^t\! \vec{x} A \vec{x}
\end{align*} \]を用いて\[
a x_1^2 + 2p x_1 x_2 + b x_2^2 = {}^t\! \vec{x} A \vec{x}
\]と変形できる。
行列 \( A \) を直交行列 \( P \) により\[
P^{-1} AP = \left( \begin{array}{ccc} \alpha & 0 \\ 0 & \beta \end{array} \right)
\]と対角化し、\( y_1 \), \( y_2 \) を\[
\left( \begin{array}{ccc} y_1 \\ y_2 \end{array} \right) ={}^t\! P \left( \begin{array}{ccc} x_1 \\ x_2 \end{array} \right)
\]とおくと、2次形式を\[
a x_1^2 + 2p x_1 x_2 + b x_2^2 = \alpha y_1^2 + \beta y_2^2
\]と標準形に変換できる。
2次形式の標準形のそれぞれの係数は2次形式を表す実対称行列のそれぞれの固有値となっていることがわかりますね。
3変数の場合も載せておきます。2変数の場合と同様の手順で2次形式に変換できます。
3変数 \( x_1 \), \( x_2 \), \( x_3 \) の2次形式 \[
a x_1^2 + b x_2^2 + c x_2^2 + 2p x_1 x_2 + 2q x_1 x_3 + 2r x_2 x_3
\]は実対称行列 \( A \)、ベクトル \( \vec{x} \)\[\begin{align*}
A = \left( \begin{array}{ccc} a & p & q \\ p & b & r \\ q & r & c \end{array} \right) \ \ \
\vec{x} = \left( \begin{array}{ccc} x_1 \\ x_2 \\ x_3 \end{array} \right)= {}^t\! \vec{x} A \vec{x}
\end{align*} \]を用いて\[
a x_1^2 + b x_2^2 + c x_2^2 + 2p x_1 x_2 + 2q x_1 x_3 + 2r x_2 x_3 = {}^t\! \vec{x} A \vec{x}
\]と変形できる。
行列 \( A \) を直交行列 \( P \) により\[
P^{-1} AP = \left( \begin{array}{ccc} \alpha & 0 & 0 \\ 0 & \beta & 0 \\ 0 & 0 & \gamma \end{array} \right)
\]と対角化し、\( y_1 \), \( y_2 \), \( y_3 \) を\[
\left( \begin{array}{ccc} y_1 \\ y_2 \\ y_3 \end{array} \right) ={}^t\! P \left( \begin{array}{ccc} x_1 \\ x_2 \\ y_3 \end{array} \right)
\]とおくと、2次形式を\[
a x_1^2 + b x_2^2 + c x_3^2 + 2p x_1 x_2 + 2q x_1 x_3 + 2r x_2 x_3 = \alpha y_1^2 + \beta y_2^2 + \gamma y_3^2
\]と標準形に変換できる。
練習問題では3変数の2次形式の標準形変換問題を用意しましたのでチャレンジしてみましょう。
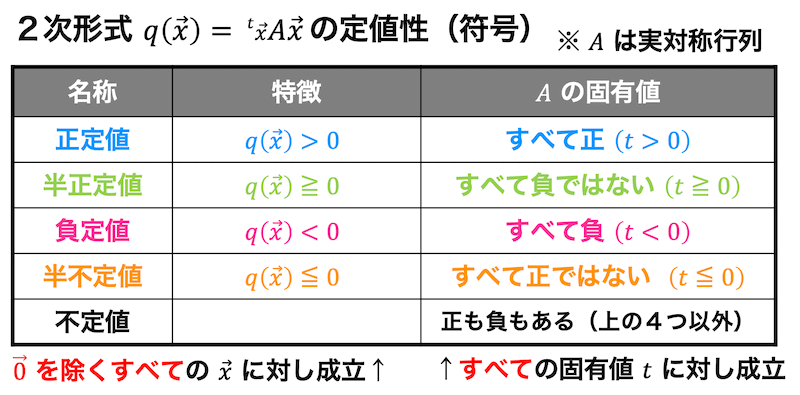
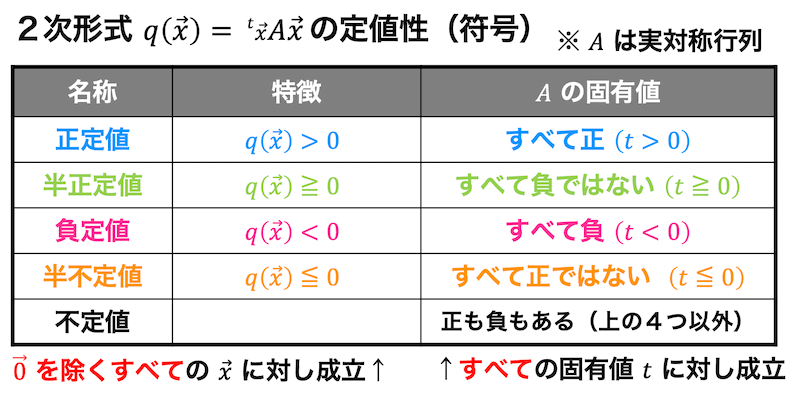
4.2次形式の定値性・符号(正定値・負定値など)
2次形式 \( q(\vec{x}) \) を標準形に変換することで、2次形式が取りうる値の範囲が正だけなのか、負だけなのか、あるいはその両方なのかを係数を見るだけでパッと見て確認することができますね。
2次形式の標準形の係数を見るだけで取りうる値の範囲がわかるということは、2次形式を表す実対象行列の固有値を見るだけで取りうる値の範囲がわかりますね。
2次形式の取りうる値の範囲ごとにそれぞれ名前がつけられています。
値の範囲と名前について下のほうにまとめていこうと思います。
(1) 2次形式が常に正となる場合 \( q(\vec{x}) \gt 0 \)
例題1の2次形式を標準形にすると\[
3 y_1^2 + 5y_2^2
\]となりましたね。
この標準形の \( y_1^2 \), \( y_2^2 \) の係数は3, 5とともに正ですね。このように、標準形の係数がすべて正のときは、\( y_1 \), \( y_2 \) にどのような値を(ただし \( y_1 \), \( y_2 \) がともに0のとき以外)入れても正になりますね*4。
\( y_1 \), \( y_2 \) がどんな値でも正なら当然 \( x_1 \), \( x_2 \) がどんな値でも正ですよね。
このように、\[
\vec{x} \not = \vec{0}
\]のとき、常に正となる2次形式を正定値といいます。
標準形の係数がすべて正というのは、2次形式を表現する実対称行列の固有値がすべて正と言い換えることができますね。
つまり、2次形式が正定値かどうかを判定するためには、正定値かどうかを判定したい2次形式の実対称行列の固有値が正になることを確認すればOKです。
(2) 2次形式が常に負とならない場合 \( q(\vec{x}) \geqq 0 \)
例えば、\[
3 y_1^2 + 0 y_2^2
\]のような2次形式を考えましょう。
この標準形に負の係数は含まれていませんが、\( y_2^2 \) の係数が0ですね。
このとき、\( y_1 \) のとき、\( y_2 \) の値に関わらず例の2次形式は0になってしまいます。しかし、それ以外のときは2次形式は正となりますね(つまり、2次形式が負になることはない)。
このように、\[
\vec{x} \not = \vec{0}
\]のとき、常に負にならない(0か正になる)2次形式を半正定値といいます。
半正定値も正定値のときと同じように2次形式を表現する実対称行列の固有値をすべて確認することで確認ができます。
半正定値の場合2次形式に負の係数が含まれないことが条件なので、実対称行列の固有値が0以上(負とならない)ことが条件となります。
(3) 2次形式が常に負となる場合 \( q(\vec{x}) \lt 0 \)
例えば、\[
- 3 y_1^2 - 5 y_2^2
\]のような2次形式の場合、\( y_1 \), \( y_2 \) の値に関わらず2次形式が負となりますね(両方0のときを除く)。
このように、\[
\vec{x} \not = \vec{0}
\]のとき、常に負となる2次形式を負定値といいます。
正定値のときのときと同様に実対称行列の固有値で判定が可能です。負定値の場合、2次の形式がすべて負となるので、実対称行列の固有値がすべて負となるときに負定値となります。
(4) 2次形式が常に正とならない場合 \( q(\vec{x}) \leqq 0 \)
例えば、\[
- 3 y_1^2 - 0 y_2^2
\]のような2次形式の場合、係数が0の項があるため、2次形式が0となることがありますが、\( y_1 \), \( y_2 \) の値に関わらず2次形式が正となることはありませんね。
このように、\[
\vec{x} \not = \vec{0}
\]のとき、常に正とならない(0か負となる)2次形式を半負定値といいます。
実対称行列の固有値で判定する場合、固有値が0以下(負とならないこと)が条件となります。
(5) それ以外(2次形式が正にも負にもなる場合)
次の(1)〜(4)に当てはまらなかった2次形式は正、負ともにとる可能性がある2次形式ですね。例えば、\[
1 y_1^2 + 1 y_2^2 - 4 y_3^2
\]の係数は正、負ともにありますね。
このような2次形式のことを不定値と呼びます。
2次形式が不定値の場合、実対称行列の固有値は正、負のものがそれぞれ少なくとも1つ存在します。
(1)〜(5)をまとめると、下のような表で表せます。
5.練習問題
では2問ほど練習してみましょう。
例題では2変数の2次形式でしたが、練習では3変数の2次形式にチャレンジしてみましょう!
練習1
2次形式\[
3 x_1^2 + 4 x_2^2 + 3x_3^2 + 2 x_1 x_2 + 4 x_1 x_3 + 2 x_2 x_3
\]の標準形を求めなさい。また、この2次形式の符号を調べ、正定値、負定値となるかを調べなさい。
練習2
2次形式\[
3 x_1^2 + 3 x_2^2 - x_3^2 + 4 x_1 x_2 + 4 x_1 x_3 - 4 x_2 x_3
\]の標準形を求めなさい。また、この2次形式の符号を調べ、正定値、負定値となるかを調べなさい。
解答1
Step1:2次形式を表す実対称行列を作成
\( A \) 、ベクトル \( \vec{x} \) をそれぞれ\[
A = \left( \begin{array}{ccc} 3 & 1 & 2 \\ 1 & 4 & 1 \\ 2 & 1 & 3 \end{array} \right) \ \ \ \vec{x} = \left( \begin{array}{ccc} x_1 \\ x_2 \\ x_3 \end{array} \right)
\]とすると、\[
3 x_1^2 + 4 x_2^2 + 3 x_3^2 + 2 x_1 x_2 + 4 x_1 x_3 + 2 x_2 x_3 = {}^t\! \vec{x} A \vec{x}
\]と変形できる。
Step2:行列の固有値を求める
固有値を \( t \) とすると、固有方程式は、\[\begin{align*}
|A-tE| = & \left| \begin{array}{ccc} 3-t_{-2} & 1_{-1} & 2_{-3+t} \\ 1 & 4-t & 1 \\ 2 & 1 & 3-t \end{array} \right|
\\ = & \left| \begin{array}{ccc} 1-t & 0 & -1+t \\ 1 & 4-t & 1 \\ 2 & 1 & 3-t \end{array} \right|
\\ = & (1-t) \left| \begin{array}{ccc} 1 & 0 & -1 \\ 1 & 4-t & 1 \\ 2 & 1 & 3-t \end{array} \right|
\\ = & (1-t) \left| \begin{array}{ccc} 1 & 0 & -1 \\ 0 & 4-t & 2 \\ 0 & 1 & 5-t \end{array} \right|
\\ = & (1-t) \left| \begin{array}{ccc} 4-t & 2 \\ 1 & 5-t \end{array} \right|
\end{align*} \]となる。
ここで、\[\begin{align*} &
\left| \begin{array}{ccc} 4-t & 2 \\ 1 & 5-t \end{array} \right|
\\ = & (t-4)(t-5) - 2
\\ = & t^2 - 9t + 18
\\ = & (t-3)(t-6)
\end{align*} \]となるので、\[
|A - tE| = (1-t)(t-3)(t-6)= 0
\]を満たす \( t \) が固有値となり、固有値は1, 3, 6となる。
Step3:大きさ1の直交する固有ベクトルを求め、対角化
(1) 固有値が1のとき\[ \begin{align*}
(A-1E) = &
\left( \begin{array}{ccc} 2 & 1 & 2 \\ 1 & 3 & 1 \\ 2 & 1 & 2 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 0 & -5 & 0 \\ 1 & 3 & 1 \\ 0 & 0 & 0 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array} \right)
\end{align*} \]となる。\[
\left\{ \begin{array}{l} x + z = 0 \\ y = 0 \end{array}\right.
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \end{array} \right)
\]と表せる。
固有ベクトル \( \vec{p_1} \) は大きさを1に正規化したベクトル、\[
\vec{p_1} = \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 \\ 0 \\ -1 \end{array} \right)
\]となる。
(2) 固有値が3のとき\[ \begin{align*}
(A-3E) = &
\left( \begin{array}{ccc} 0 & 1 & 2 \\ 1 & 1 & 1 \\ 2 & 1 & 0 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 0 & 1 & 2 \\ 1 & 1 & 1 \\ 0 & -1 & -2 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 0 & 1 & 2 \\ 1 & 0 & -1 \\ 0 & 0 & 0 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 0 & -1 \\ 0 & 1 & 2 \\ 0 & 0 & 0 \end{array} \right)
\end{align*} \]となる。\[
\left\{ \begin{array}{l} x - z = 0 \\ y + 2z = 0 \end{array}\right.
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ -2 \\ 1 \end{array} \right)
\]と表せる。
固有ベクトル \( \vec{p_2} \) は大きさを1に正規化したベクトル、\[
\vec{p_2} = \frac{1}{\sqrt{6}} \left( \begin{array}{ccc} 1 \\ -2 \\ 1 \end{array} \right)
\]となる。
(3) 固有値が6のとき\[ \begin{align*}
(A-6E) = &
\left( \begin{array}{ccc} -3 & 1 & 2 \\ 1 & -2 & 1 \\ 2 & 1 & -3 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 0 & -5 & 5 \\ 1 & -2 & 1 \\ 0 & 5 & -5 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 0 & 1 & -1 \\ 1 & 0 & -1 \\ 2 & 0 & 1 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 0 & -1 \\ 0 & 1 & -1 \\ 0 & 0 & 0 \end{array} \right)
\end{align*} \]となる。\[
\left\{ \begin{array}{l} x - z = 0 \\ y - z = 0 \end{array}\right.
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 1 \\ 1 \end{array} \right)
\]と表せる。
固有ベクトル \( \vec{p_3} \) は大きさを1に正規化したベクトル、\[
\vec{p_3} = \frac{1}{\sqrt{3}} \left( \begin{array}{ccc} 1 \\ 1 \\ 1 \end{array} \right)
\]となる。
よって、\( \vec{p_1} \), \( \vec{p_2} \), \( \vec{p_3} \) は正規直交基底となるので、直交行列\[
P = \left( \vec{p_1}, \vec{p_2}, \vec{p_3} \right) = \frac{1}{\sqrt{6}} \left( \begin{array}{ccc} \sqrt{3} & 1 & \sqrt{2} \\ 0 & -2 & \sqrt{2} \\ - \sqrt{3} & 1 & \sqrt{2} \end{array} \right)
\]を用いて、\[
P^{-1} AP = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 6 \end{array} \right)
\]と対角化することができます。
Step4:直交行列 \( P \) を用いて標準形に変換
よって、 \( y_1 \), \( y_2 \), \( y_3 \) を\[
\vec{y} = \left( \begin{array}{ccc} y_1 \\ y_2 \\ y_3 \end{array} \right) = {}^t\! P \left( \begin{array}{ccc} x_1 \\ x_2 \\ x_3 \end{array} \right) = {}^t\! P \vec{x}
\]とおくことで*5、\[
y_1^2 + 3 y_2^2 + 6 y_3^2
\]と標準形を求められる。
また、標準形の形(と2次形式を表現する固有値)より、2次形式は必ず正となる。
よって正定値である。
(固有値に正の値(1,3,6)しかないため)
解答2
Step1:2次形式を表す実対称行列を作成
\( A \) 、ベクトル \( \vec{x} \) をそれぞれ\[
A = \left( \begin{array}{ccc} 3 & 2 & 2 \\ 2 & 3 & -2 \\ 2 & -2 & -1 \end{array} \right) \ \ \ \vec{x} = \left( \begin{array}{ccc} x_1 \\ x_2 \\ x_3 \end{array} \right)
\]とすると、\[
3 x_1^2 + 3 x_2^2 - x_3^2 + 4 x_1 x_2 + 4 x_1 x_3 - 4 x_2 x_3 = {}^t\! \vec{x} A \vec{x}
\]と変形できる。
Step2:行列の固有値を求める
固有値を \( t \) とすると、固有方程式は、\[\begin{align*}
|A-tE| = & \left| \begin{array}{ccc} 3-t & 2 & 2 \\ 2 & 3-t & -2 \\ 2 & -2 & -1-t \end{array} \right|
\\ = & \left| \begin{array}{ccc} 5-t & 5-t & 0 \\ 2 & 3-t & -2 \\ 2 & -2 & -1-t \end{array} \right|
\\ = & (5-t) \left| \begin{array}{ccc} 1 & 1 & 0 \\ 2 & 3-t & -2 \\ 2 & -2 & -1-t \end{array} \right|
\\ = & (5-t) \left| \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1-t & -2 \\ 0 & -4 & -1-t \end{array} \right|
\\ = & (5-t) \left| \begin{array}{ccc} 1-t & -2 \\ -4 & -1-t \end{array} \right|
\end{align*} \]となる。
ここで、\[\begin{align*} &
\left| \begin{array}{ccc} 1-t & -2 \\ -4 & -1-t \end{array} \right|
\\ = & \left| \begin{array}{ccc} 1-t & -2 \\ -4 & -1-t \end{array} \right|
\\ = & (t+1)(t-1) - 8
\\ = & t^2 - 9
\\ = & (t+3)(t-3)
\end{align*} \]となるので、\[
|A - tE| = (5-t)(t-3)(t+3)= 0
\]を満たす \( t \) が固有値となり、固有値は5, 3, -3となる。
Step3:大きさ1の直交する固有ベクトルを求め、対角化
(1) 固有値が5のとき\[ \begin{align*}
(A-5E) = &
\left( \begin{array}{ccc} -2 & 2 & 2 \\ 2 & -2 & -2 \\ 2 & -2 & -6 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 2 & -2 & 2 \\ 0 & 0 & -4 \\ 0 & 0 & 0 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & -1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{array} \right)
\end{align*} \]となる。\[
\left\{ \begin{array}{l} x - y = 0 \\ z = 0 \end{array}\right.
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 1 \\ 0 \end{array} \right)
\]と表せる。
固有ベクトル \( \vec{p_1} \) は大きさを1に正規化したベクトル、\[
\vec{p_1} = \frac{1}{\sqrt{2}} \left( \begin{array}{ccc} 1 \\ 1 \\ 0 \end{array} \right)
\]となる。
(2) 固有値が3のとき\[ \begin{align*}
(A-3E) = &
\left( \begin{array}{ccc} 0 & 2 & 2 \\ 2 & 0 & -2 \\ 2 & -2 & -4 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 0 & 2 & 2 \\ 2 & 0 & -2 \\ 2 & 0 & -2 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 1 & 0 & -1 \\ 0 & 1 & 1 \\ 0 & 0 & 0 \end{array} \right)
\end{align*} \]となる。\[
\left\{ \begin{array}{l} x - z = 0 \\ y - z = 0 \end{array}\right.
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = k \left( \begin{array}{ccc} 1 \\ 1 \\ 1 \end{array} \right)
\]と表せる。
固有ベクトル \( \vec{p_2} \) は大きさを1に正規化したベクトル、\[
\vec{p_2} = \frac{1}{\sqrt{3}} \left( \begin{array}{ccc} 1 \\ 1 \\ 1 \end{array} \right)
\]となる。
(3) 固有値が-3のとき\[ \begin{align*}
(A+3E) = &
\left( \begin{array}{ccc} 6 & 2 & 2 \\ 2 & 6 & -2 \\ 2 & -2 & 2 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 0 & 8 & -4 \\ 0 & 8 & -4 \\ 2 & -2 & 2 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 0 & 0 & 0 \\ 0 & 2 & -1 \\ 2 & 0 & 1 \end{array} \right) \\ \to \ &
\left( \begin{array}{ccc} 2 & 0 & 1 \\ 0 & 2 & -1 \\ 0 & 0 & 0 \end{array} \right)
\end{align*} \]となる。\[
\left\{ \begin{array}{l} 2x + z = 0 \\ 2y - z = 0 \end{array}\right.
\]を解くと、任意定数 \( k \) を用いて\[
\left( \begin{array}{ccc} x \\ y \\ z \end{array} \right) = k \left( \begin{array}{ccc} -1 \\ 1 \\ 2 \end{array} \right)
\]と表せる。
固有ベクトル \( \vec{p_3} \) は大きさを1に正規化したベクトル、\[
\vec{p_3} = \frac{1}{\sqrt{6}} \left( \begin{array}{ccc} -1 \\ 1 \\ 2 \end{array} \right)
\]となる。
よって、\( \vec{p_1} \), \( \vec{p_2} \), \( \vec{p_3} \) は正規直交基底となるので、直交行列\[
P = \left( \vec{p_1}, \vec{p_2}, \vec{p_3} \right) = \frac{1}{\sqrt{6}} \left( \begin{array}{ccc} \sqrt{3} & \sqrt{2} & -1 \\ \sqrt{3} & - \sqrt{2} & 1 \\ 0 & \sqrt{2} & 2 \end{array} \right)
\]を用いて、\[
P^{-1} AP = \left( \begin{array}{ccc} 5 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & -3 \end{array} \right)
\]と対角化することができます。
Step4:直交行列Pを用いて標準形に変換
よって、 \( y_1 \), \( y_2 \) を\[
\vec{y} = \left( \begin{array}{ccc} y_1 \\ y_2 \end{array} \right) = {}^t\! P \left( \begin{array}{ccc} x_1 \\ x_2 \end{array} \right) = {}^t\! P \vec{x}
\]とおくことで、\[
5 y_1^2 + 3 y_2^2 - 3 y_3^2
\]と標準形を求められる。
また、標準形の形(と2次形式を表現する固有値)より、2次形式は正も負もとりうる。
よって正定値でも負定値でもない。
(固有値に正の値(5,3)と負の値(-3)が混在している)
6.さいごに
今回は、2次形式についてまとめていきました。
次回は、2次形式の知識を利用して2次曲線のグラフを書きかたについてまとめていきたいと思います。
関連広告・スポンサードリンク