うさぎでもわかる微分方程式　Part09　定数変化法を用いた2階非同次線形微分方程式の一般解の求め方

こんにちは、ももやまです。

前回は非同次の定数係数の2階線形微分方程式の特殊解、一般解を未定係数法を用いて求める方法説明しました。

今回は、非同次の定数係数線形微分方程式の4つの解き方

• 未定係数法
• 定数変化法
• 微分演算子法
• ラプラス変換を用いる方法

の中でも定数係数に限らない2階線形微分方程式の特殊解、一般解を求めるときに使える定数変化法について説明していきたいと思います。

定数変化法を含む残りの3つの方法の長所・短所も載せておくので、特殊解をどう求めようか迷った人はご覧ください。

※1. 今回は定数変化法の説明のため、定数変化法を用いて計算をしていますが、実際の試験などでは、まず未定係数法が使えないか考えましょう。
※2. 3階以上だと定数変化法による計算は大変なため、本記事では2階の場合のみ説明します。

もしダメそうなら今回説明する定数変化法などで計算しましょう。

前回の微分方程式の記事はこちら！　未定係数法を用いて特殊解を求める方法について説明しています。

スポンサードリンク

１．同次方程式の基本解と一般解

まずは、復習をしましょう。

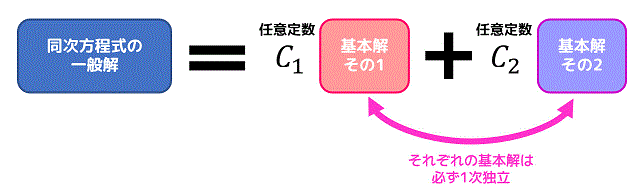
同次式の2階線形微分方程式\[
\frac{d^2 y}{dx^2} + P(x) \frac{dy}{dx} + Q(x) y = 0
\]の一般解は、2つの（1次独立な）基本解 \( y_1 \), \( y_2 \) を用いて\[
y = C_1 y_1 + C_2 y_2
\]の形で表すことができましたね。

今回は、同次方程式の一般解から定数変化法を用いることで、非同次の2階線形微分方程式\[
\frac{d^2 y}{dx^2} + P(x) \frac{dy}{dx} + Q(x) y = R(x)
\]の一般解を求める方法について説明したいと思います。

スポンサードリンク

２．定数変化法のやり方

ここでは、

• 連立方程式を逆行列を用いて解く方法
  （うさぎでもわかる線形代数　第03羽）
• ロンスキアン

の2つの知識を使います。もし忘れている場合は復習しておきましょう。

非同次の2階線形微分方程式\[
\frac{d^2 y}{dx^2} + P(x) \frac{dy}{dx} + Q(x) y = R(x)
\]の同次方程式\[
\frac{d^2 y}{dx^2} + P(x) \frac{dy}{dx} + Q(x) y = 0
\]の一般解は、基本解 \( y_1 \), \( y_2 \)、任意定数 \( C_1 \), \( C_2 \) を用いて\[
y = C_1 y_1 + C_2 y_2
\]と求められますね。（ここまでが復習）

定数変化法の考え方は、1階線形微分方程式のときと同じく、任意定数 \( C_1 \), \( C_2 \) がもし \( x \) の関数 \( z_1(x) \), \( z_2 (x) \) であると仮定したら解けないかな、と考えます。

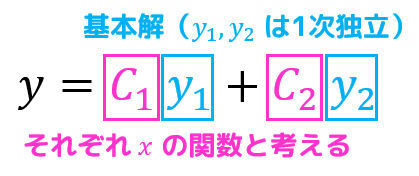
同次方程式の一般解\[
y = C_1 y_1 + C_2 y_2
\]の任意定数 \( C_1 \), \( C_2 \) をそれぞれ \( z_1(x) \), \( z_2(x) \) とおきかえると、\[
y = z_1 (x) y_1 + z_2 (x) y_2
\]となります。

（以降 \( z_1 (x) \) を \( z_1 \)、\( z_2 (x) \) を \( z_2 \) と表記します。）

両辺を \( x \) で微分すると、積の微分公式より\[\begin{align*}
y' & = z_1' y_1 + z_1 y_1' + z_2' y_2 + z_2 y_2'
\\ & = \textcolor{red}{z_1' y_1 + z_2' y_2} + z_1 y_1' +  z_2 y_2'
\end{align*} \]と変形できます。

ここで、\[
\textcolor{red}{z_1' y_1 + z_2' y_2} = 0 \tag{1}
\]とおきます。（この式をおくのがポイント！）

すると、\[
y' = z_1 y_1' +  z_2 y_2'
\]となりますね。

さらに \( y' \) の両辺を \( x \) で微分すると、\[\begin{align*}
y'' & = (z_1 y_1')' +  (z_2 y_2')'
\\ & = z_1' y_1' + z_1 y_1'' + z_2' y_2' + z_2 y_2''
\\ & = z_1 y_1'' + z_2 y_2'' + z_1' y_1' + z_2' y_2'
\end{align*}\]となります。

よって、\[\begin{align*}
\frac{dy}{dx} & = y'
\\ & = z_1 y_1' +  z_2 y_2'
\end{align*}\]\[\begin{align*}
\frac{d^2y}{dx^2} & = y''
\\ & = z_1 y_1'' + z_2 y_2'' + z_1' y_1' + z_2' y_2'
\end{align*}\]が求まります。

また、\( y_1 \), \( y_2 \) は同次方程式の解なので、\[
\left\{ \begin{array}{l} \textcolor{red}{y_1'' + P(x) y_1' + Q(x) y_1} = 0 \\ \textcolor{blue}{y_2'' + P(x) y_2' + Q(x) y_2} = 0 \end{array}\right.
\]が成立します。。

よって、非同次2階線形微分方程式は\[ \begin{align*}
& \frac{d^2 y}{dx^2} + P(x) \frac{dy}{dx} + Q(x) y
\\ = \ & y'' + P(x) y' + Q(x) y
\\ = \ & (  z_1 y_1'' + z_2 y_2'' + z_1' y_1' + z_2' y_2' ) + (z_1 y_1' +  z_2 y_2') P(x) +  (z_1 y_1 + z_2 y_2) Q(x)
\\ = \ & z_1 (\textcolor{red}{y_1'' + P(x) y_1' + Q(x) y_1}) + z_2  (\textcolor{blue}{y_2'' + P(x) y_2' + Q(x) y_2}) + z_1' y_1' + z_2' y_2'
\\ = \ & z_1 \cdot \textcolor{red}{0} + z_2 \cdot \textcolor{blue}{0} + z_1' y_1' + z_2' y_2'
\\ = \ & z_1' y_1' + z_2' y_2'
\\ = \ & R(x)
\end{align*} \]と変形でき、式\[
z_1' y_1' + z_2' y_2' = R(x) \tag{2}
\]を得ることができます。

ここで、(1)で仮定した式と(2)を合わせて\[
\left\{ \begin{array}{l} y_1 z_1' + y_2 z_2' = 0 \\  y_1' z_1' + y_2' z_2' = R(x) \end{array}\right.
\]の2つの式が得られますね。

（行列で表すために \( y \) と \( z \) を入れ替えてます。）

この2つの式を行列を用いて表すと、\[
\left( \begin{array}{ccc} y_1 z_1' + y_2 z_2' \\ y_1' z_1' + y_2' z_2' \end{array} \right) = \left( \begin{array}{ccc} 0 \\ R(x) \end{array} \right)
\]となるので、\[
\left( \begin{array}{ccc} y_1 & y_2 \\ y_1' & y_2' \end{array} \right)  \left( \begin{array}{ccc} z_1' \\ z_2' \end{array} \right) = \left( \begin{array}{ccc} 0 \\ R(x) \end{array} \right)
\]と表現、つまり\[
A \vec{x} = \vec{b}
\]の形に持ち込むことができます。

ここまでくれば、連立方程式の解、つまり\[
\vec{x} = \left( \begin{array}{ccc} z_1' \\ z_2' \end{array} \right)
\]を解くのは簡単ですよね。

基本解 \( y_1 \), \( y_2 \) の2組は必ず1次独立な関係なので、ロンスキアン \( W(y_1, y_2) \) には、\[\begin{align*}
W(y_1, y_2 ) & = |A|
\\ & = \left| \begin{array}{ccc} y_1 & y_2 \\ y_1' & y_2' \end{array} \right|
\\ & \not = 0
\end{align*}\]の関係式が成立します。

そのため、行列 \( A \) には逆行列が存在します。なので、\[
A \vec{x} = \vec{b}
\]を、\[
A^{-1} A \vec{x} = A^{-1} \vec{b} \]\[
\vec{x} = A^{-1} \vec{b} \]\[
\left( \begin{array}{ccc} z_1' \\ z_2' \end{array} \right) =  \left( \begin{array}{ccc} y_1 & y_2 \\ y_1' & y_2' \end{array} \right)^{-1}  \left( \begin{array}{ccc} 0 \\ R(x) \end{array} \right)
\]と変形することで \( z_1' \), \( z_2' \) を計算することができます。

ここで、2次の逆行列 \( A^{-1} \) は、\[\begin{align*}
A^{-1} & = \left( \begin{array}{ccc} y_1 & y_2 \\ y_1' & y_2' \end{array} \right)^{-1}
\\ & = \frac{1}{|A|} \left( \begin{array}{ccc} y_2' & -y_2 \\ -y_1' & y_1 \end{array} \right)
\\ & = \frac{1}{ W( y_1 , y_2 )} \left( \begin{array}{ccc} y_2' & -y_2 \\ -y_1' & y_1 \end{array} \right)
\\ & = \frac{1}{ W( y_1 , y_2 )} \left( \begin{array}{ccc} y_2' & -y_2 \\ -y_1' & y_1 \end{array} \right)
\end{align*}\]と計算できますね。

（2次の逆行列は公式として覚えておきましょう。逆行列の仕組みや計算方法を忘れてしまった人はこちらから復習を。）

よって、\( z_1' \), \( z_2' \) を\[\begin{align*}
\left( \begin{array}{ccc} z_1' \\ z_2' \end{array} \right) & = \left( \begin{array}{ccc} y_1 & y_2 \\ y_1' & y_2' \end{array} \right)^{-1} \left( \begin{array}{ccc} 0 \\ R(x) \end{array} \right)
\\ & = \frac{1}{ W( y_1 , y_2 )} \left( \begin{array}{ccc} y_2' & -y_2 \\ -y_1' & y_1 \end{array} \right) \left( \begin{array}{ccc} 0 \\ R(x) \end{array} \right)
\\ & = \frac{1}{ W( y_1 , y_2 )} \left( \begin{array}{ccc} - y_2 R(x) \\ y_1 R(x) \end{array} \right)
\end{align*} \]と計算できるので、\[
z_1' = \frac{d z_1}{dx} = - \frac{y_2 R(x)}{W(y_1, y_2)} \]\[
z_2' = \frac{d z_2}{dx} = \frac{y_1 R(x)}{W(y_1, y_2)}
\]となり、直接積分形に持ち込めます。

さらに上の2式を \( x \) で積分すると、\[
z_1 = \int - \frac{y_2 R(x)}{W(y_1, y_2)} \ dx + C_1 \]\[
z_2 = \int \frac{y_1 R(x)}{W(y_1, y_2)} \ dx + C_2
\]となります。

（\( C_1 \), \( C_2 \) は任意定数です。）

最後に \( z_1 \), \( z_2 \) を\[
y = z_1 (x) y_1 + z_2 (x) y_2
\]に代入することにより、非同次形の一般解を\[
y = - y_1 \left( \int \frac{y_2 R(x)}{W(y_1, y_2)} \ dx + C_1 \right) + y_2 \left( \int \frac{y_1 R(x)}{W(y_1, y_2)} \ dx + C_2 \right)
\]で求めることができます。

[特殊解を1つ求めなさいという問題が出た場合]

試験などで「特殊解を1つ求めなさい。」と指示された場合は、\( z_1 \), \( z_2 \) の積分定数 \( C_1 \), \( C_2 \) を省略し、\[
y = - y_1 \int \frac{y_2 R(x)}{W(y_1, y_2)} \ dx + y_2  \int \frac{y_1 R(x)}{W(y_1, y_2)} \ dx
\]とすることで特殊解を1つ求めることができます。

※ 指定されたとき以外は、任意定数を付けて一気に一般解を求めましょう。

実際に、例題で解を求める流れを確認しましょう。

例題1

微分方程式\[
\frac{d^2 y}{dx^2} - 5 \frac{dy}{dx} + 6y = e^x
\]の一般解を求めたい。

(1) 同次方程式\[
\frac{d^2 y}{dx^2} - 5 \frac{dy}{dx} + 6y = 0
\]の基本解を求め、さらにそれぞれの基本解が1次独立になることを確認してから一般解を求めなさい。

(2) 定数変化法を用いて、微分方程式の一般解を求めなさい。

解説1

(1)

まずは復習。

特性方程式は\[
k^2 - 5k + 6 = 0
\]となるので、\[
(k-2)(k-3) = 0
\]とすることで、\( k = 2 \), \( k = 3 \) と求められ、基本解が \( y_1 = e^{2x} \), \( y_2 = e^{3x} \) と求められる。

ここで、ロンスキアン \( W(y_1, y_2) \) が\[\begin{align*}
W(y_1, y_2 ) & = \left| \begin{array}{ccc} y_1 & y_2 \\ y_1' & y_2' \end{array} \right|
\\ & = \left| \begin{array}{ccc} e^{2x} & e^{3x} \\ 2e^{2x} & 3e^{3x} \end{array} \right|
\\ & = e^{2x} \cdot 3e^{3x} - e^{3x} \cdot 2e^{2x}
\\ & = 3e^{5x} - 2e^{5x}
\\ & = e^{5x} \not = 0
\end{align*} \]となるので、2つの基本解が1次独立となることがわかる。

また、一般解は任意定数 \( C_1 \), \( C_2 \) を用いて\[\begin{align*}
y & = C_1 y_1 + C_2 y_2
\\ & = C_1 e^{2x} + C_2 e^{3x}
\end{align*} \]と表せる。

(2)

※ここからの途中式では、\( y_1 \), \( y_1' \), \( y_1'' \), \( y_2 \), \( y_2' \), \( y_2'' \) に具体値を入れるとぐちゃぐちゃになるので、変形が完了するまで代入しないことを強くおすすめします。

同次方程式の一般解\[
y = C_1 y_1 + C_2 y_2
\]の任意定数 \( C_1 \), \( C_2 \) をそれぞれ \( z_1(x) \), \( z_2(x) \) とおきかえると、\[
y = z_1 (x) y_1 + z_2 (x) y_2
\]となる。

（ただし \( z_1 (x) \) を \( z_1 \)、\( z_2 (x) \) を \( z_2 \) と表記する。）

両辺を \( x \) で微分すると、\[\begin{align*}
y' & = z_1' y_1 + z_1 y_1' + z_2' y_2 + z_2 y_2'
\\ & = \textcolor{red}{z_1' y_1 + z_2' y_2} + z_1 y_1' +  z_2 y_2'
\end{align*} \]となる。

ここで、\[
\textcolor{red}{z_1' y_1 + z_2' y_2} = 0 \tag{1}
\]とおくと、\[
y' = z_1 y_1' +  z_2 y_2'
\]となる。

さらに両辺を \( x \) で微分すると、\[\begin{align*}
y'' & = (z_1 y_1')' +  (z_2 y_2')'
\\ & = z_1' y_1' + z_1 y_1'' + z_2' y_2' + z_2 y_2''
\\ & = z_1 y_1'' + z_2 y_2'' + z_1' y_1' + z_2' y_2'
\end{align*}\]となる。

よって、\[\begin{align*}
\frac{dy}{dx} & = y'
\\ & = z_1 y_1' +  z_2 y_2'
\end{align*}\]\[\begin{align*}
\frac{d^2y}{dx^2} & = y''
\\ & = z_1 y_1'' + z_2 y_2'' + z_1' y_1' + z_2' y_2'
\end{align*}\]が求まります。

また、\( y_1 \), \( y_2 \) は同次方程式の解なので、\[
\left\{ \begin{array}{l} \textcolor{red}{y_1'' - 5 y_1' + 6 y_1} = 0 \\ \textcolor{blue}{y_2'' - 5 y_2' + 6 y_2} = 0 \end{array}\right.
\]が成立します。。

よって、非同次2階線形微分方程式は\[ \begin{align*}
& \frac{d^2 y}{dx^2} - 5 \frac{dy}{dx} + 6 y
\\ = \ & y'' - 5 y' + 6 y
\\ = \ & (  z_1 y_1'' + z_2 y_2'' + z_1' y_1' + z_2' y_2' ) - 5(z_1 y_1' +  z_2 y_2') + 6(z_1 y_1 + z_2 y_2)
\\ = \ & z_1 (\textcolor{red}{y_1'' - 5 y_1' + 6y_1}) + z_2  (\textcolor{blue}{y_2'' - 5 y_2' + 6 y_2}) + z_1' y_1' + z_2' y_2'
\\ = \ & z_1 \cdot \textcolor{red}{0} + z_2 \cdot \textcolor{blue}{0} + z_1' y_1' + z_2' y_2'
\\ = \ & z_1' y_1' + z_2' y_2'
\\ = \ & e^x
\end{align*} \]と変形でき、式\[
z_1' y_1' + z_2' y_2' = e^x \tag{2}
\]を得る。

ここで、(1), (2)より\[
\left\{ \begin{array}{l} y_1 z_1' + y_2 z_2' = 0 \\  y_1' z_1' + y_2' z_2' = e^x \end{array}\right.
\]の2つの式を行列を用いて\[
\left( \begin{array}{ccc} y_1 & y_2 \\ y_1' & y_2' \end{array} \right)  \left( \begin{array}{ccc} z_1' \\ z_2' \end{array} \right) = \left( \begin{array}{ccc} 0 \\ e^x \end{array} \right)
\]、つまり\[
\left( \begin{array}{ccc} e^{2x} & e^{3x} \\ 2e^{2x} & 3e^{3x} \end{array} \right)  \left( \begin{array}{ccc} z_1' \\ z_2' \end{array} \right) = \left( \begin{array}{ccc} 0 \\ e^x \end{array} \right)
\]と表せる。

※ ここで \( y_1 \), \( y_1' \), \(   y_1'' \) などに具体値を代入しましょう。

さらに問題(1)より、\[ W(y_1, y_2) =  \left| \begin{array}{ccc} e^{2x} & e^{3x} \\ 2e^{2x} & 3e^{3x} \end{array} \right| \not = 0 \]が成立するので、行列\[
\left( \begin{array}{ccc} e^{2x} & e^{3x} \\ 2e^{2x} & 3e^{3x} \end{array} \right)
\]には逆行列が存在し、その逆行列は\[\begin{align*}
\left( \begin{array}{ccc} e^{2x} & e^{3x} \\ 2e^{2x} & 3e^{3x} \end{array} \right)^{-1} & =  \frac{1}{W(y_1,y_2)} \left( \begin{array}{ccc} 3e^{3x} & -e^{3x} \\ -2e^{2x} & e^{2x} \end{array} \right)
\\ & = \frac{1}{e^{5x}} \left( \begin{array}{ccc} 3e^{3x} & -e^{3x} \\ -2e^{2x} & e^{2x}
\end{array} \right)
\end{align*}\]と求められる。

よって、\[\begin{align*}
\left( \begin{array}{ccc} z_1' \\ z_2' \end{array} \right) & = \left( \begin{array}{ccc} e^{2x} & e^{3x} \\ 2e^{2x} & 3e^{3x} \end{array} \right)^{-1}  \left( \begin{array}{ccc} 0 \\ e^x \end{array} \right)
\\ & = \frac{1}{e^{5x}} \left( \begin{array}{ccc} 3e^{3x} & -e^{3x} \\ -2e^{2x} & e^{2x}
\end{array} \right) \left( \begin{array}{ccc} 0 \\ e^x \end{array} \right)
\\ & = \frac{1}{e^{5x}} \left( \begin{array}{ccc} -e^{4x} \\ e^{3x} \end{array} \right)
\\ & = \left( \begin{array}{ccc} -e^{-x} \\ e^{-2x} \end{array} \right)
\end{align*}\]が成立する。

さらに上の2式を \( x \) で積分すると、\[\begin{align*}
z_1  & = \int - e^{-x} \ dx
\\ & = e^{-x} + C_1
\end{align*} \]\[\begin{align*}
z_2  & = \int e^{-2x} \ dx
\\ & = - \frac{1}{2} e^{-2x} + C_2
\end{align*} \]となるので、一般解は\[\begin{align*}
y & = z_1 e^{2x} + z_2 e^{3x}
\\ & = \left( e^{-x} + C_1 \right) e^{2x} +  \left( - \frac{1}{2} e^{-2x} + C_2 \right) e^{3x}
\\ & = e^{x} + C_1 e^{2x} - \frac{1}{2} e^{x} + C_2 e^{3x}
\\ & = \frac{1}{2} e^x + C_1 e^{2x} + C_2 e^{3x}
\end{align*}\]と求められる。

[特殊解の1つを意図的に求めたい場合]

「特殊解を1つ求めなさい。」と指示された場合は、\( z_1 \), \( z_2 \) の積分定数を省略することで求められます。

今回の場合は、\[\begin{align*}
z_1  & = \int - e^{-x} \ dx
\\ & = e^{-x}
\end{align*} \]\[\begin{align*}
z_2  & = \int e^{-2x} \ dx
\\ & = - \frac{1}{2} e^{-2x}
\end{align*} \]なので、特殊解の1つは\[\begin{align*}
y & = z_1 e^{2x} + z_2 e^{3x}
\\ & = e^{-x} \cdot e^{2x} - \frac{1}{2} e^{-2x} \cdot e^{3x}
\\ & = e^{x} - \frac{1}{2} e^{x}
\\ & = \frac{1}{2} e^{x}
\end{align*}\]と求められます。

スポンサードリンク

３．練習問題

では、3問だけですが練習してみましょう。

1問は定数係数の2階線形微分方程式、残り2問は定数係数ではない2階線形微分方程式に関する問題です。

練習1

2階線形微分方程式\[
\frac{d^2 y}{dx^2} + a^2 y = b \sin ax
\]の一般解を求めたい。つぎの(1), (2)の問いに答えなさい。

ただし、\( a \), \( b \) は定数とし、\( a \not = 0 \), \( b \not = 0 \) である。

(1) 同次方程式\[
\frac{d^2 y}{dx^2} + a^2 y = 0
\]の基本解を求め、さらに求めた基本解の組が1次独立となることを確認してから一般解を求めなさい。

(2) 微分方程式の特殊解を1つ求めなさい。

(3) 微分方程式の一般解を求めなさい。

練習2

2階線形微分方程式\[
\frac{d^2 y}{dx^2} + \frac{x}{x+1} \frac{dy}{dx} - \frac{1}{x+1} y = x+1
\]の一般解を求めたい。

(1) 同次方程式\[
\frac{d^2 y}{dx^2} + \frac{x}{x+1} \frac{dy}{dx} - \frac{1}{x+1} y = 0
\]の基本解が \( y_1 = x \), \( y_2 = e^{-x} \) となることを確認しなさい。

(2) 微分方程式の一般解を求めなさい。

練習3

2階線形微分方程式\[
\frac{d^2 y}{dx^2} + \frac{2}{x} \frac{dy}{dx} + y = \frac{1}{x}
\]の一般解を求めたい。

(1) 同次方程式\[
\frac{d^2 y}{dx^2} + \frac{2}{x} \frac{dy}{dx} + y = 0
\]の基本解が \( y_1 = \frac{1}{x} \sin x \), \( y_2 = \frac{1}{x} \cos x \) となることを確認しなさい。

(2) 微分方程式の一般解を求めなさい。

４．練習問題の答え

解答1

(1)

特性方程式は\[
k^2 + a^2 = 0
\]となるので、\( k = \pm ai \) と求められ、基本解が \( y_1 = \cos ax \), \( y_2 = \sin ax \) と求められる。

ここで、ロンスキアン \( W(y_1, y_2) \) が\[\begin{align*}
W(y_1, y_2 ) & = \left| \begin{array}{ccc} y_1 & y_2 \\ y_1' & y_2' \end{array} \right|
\\ & = \left| \begin{array}{ccc} \cos ax & \sin ax \\ -a \sin ax & a \cos ax \end{array} \right|
\\ & = a \cos^2 ax + a \sin^2 ax
\\ & = a \not = 0
\end{align*} \]となるので、2つの基本解が1次独立となることがわかる。

また、一般解は任意定数 \( C_1 \), \( C_2 \) を用いて\[\begin{align*}
y & = C_1 y_1 + C_2 y_2
\\ & = C_1 \cos ax + C_2 \sin ax
\end{align*} \]と表せる。

(2)

同次方程式の一般解は、任意定数 \( C_1 \), \( C_2 \) を用いて\[
y = C_1 y_1 + C_2 y_2
\]とあらわせる。

ここで、\( C_1 \), \( C_2 \) をそれぞれ \( z_1(x) \), \( z_2(x) \) とおきかえると、\[
y = z_1 (x) y_1 + z_2 (x) y_2
\]となる。

（ただし \( z_1 (x) \) を \( z_1 \)、\( z_2 (x) \) を \( z_2 \) と表記する。）

両辺を \( x \) で微分すると、\[\begin{align*}
y' & = z_1' y_1 + z_1 y_1' + z_2' y_2 + z_2 y_2'
\\ & = \textcolor{red}{z_1' y_1 + z_2' y_2} + z_1 y_1' +  z_2 y_2'
\end{align*} \]となる。

ここで、\[
\textcolor{red}{z_1' y_1 + z_2' y_2} = 0 \tag{1}
\]とおくと、\[
y' = z_1 y_1' +  z_2 y_2'
\]となる。

さらに両辺を \( x \) で微分すると、\[\begin{align*}
y'' & = (z_1 y_1')' +  (z_2 y_2')'
\\ & = z_1' y_1' + z_1 y_1'' + z_2' y_2' + z_2 y_2''
\\ & = z_1 y_1'' + z_2 y_2'' + z_1' y_1' + z_2' y_2'
\end{align*}\]となります。

よって、\[\begin{align*}
\frac{dy}{dx} & = y'
\\ & = z_1 y_1' +  z_2 y_2'
\end{align*}\]\[\begin{align*}
\frac{d^2y}{dx^2} & = y''
\\ & = z_1 y_1'' + z_2 y_2'' + z_1' y_1' + z_2' y_2'
\end{align*}\]が求まります。

また、\( y_1 \), \( y_2 \) は同次方程式の解なので、\[
\left\{ \begin{array}{l} \textcolor{red}{y_1'' + a^2 y_1} = 0 \\ \textcolor{blue}{y_2'' + a^2 y_2} = 0 \end{array}\right.
\]が成立する。

よって、非同次2階線形微分方程式は\[ \begin{align*}
& \frac{d^2 y}{dx^2} + a^2 y
\\ = \ & y'' + a^2 y
\\ = \ & (  z_1 y_1'' + z_2 y_2'' + z_1' y_1' + z_2' y_2' ) + a^2 (z_1  y_1 + z_2  y_2 )
\\ = \ & z_1 \left(\textcolor{red}{y_1'' + a^2 y_1} \right) + z_2  \left( \textcolor{blue}{y_2'' + a^2 y_2} \right) + z_1' y_1' + z_2' y_2'
\\ = \ & z_1 \cdot \textcolor{red}{0} + z_2 \cdot \textcolor{blue}{0} + z_1' y_1' + z_2' y_2'
\\ = \ & z_1' y_1' + z_2' y_2'
\\ = \ & b \sin ax
\end{align*} \]と変形でき、式\[
z_1' y_1' + z_2' y_2' = b \sin ax \tag{2}
\]を得る。

ここで、(1), (2)より\[
\left\{ \begin{array}{l} y_1 z_1' + y_2 z_2' = 0 \\  y_1' z_1' + y_2' z_2' = b \sin ax \end{array}\right.
\]の2つの式を行列を用いて\[
\left( \begin{array}{ccc} y_1 & y_2 \\ y_1' & y_2' \end{array} \right)  \left( \begin{array}{ccc} z_1' \\ z_2' \end{array} \right) = \left( \begin{array}{ccc} 0 \\ b \sin ax \end{array} \right)
\]、つまり\[
\left( \begin{array}{ccc} \cos ax & \sin ax \\ -a \sin ax & a \cos ax \end{array} \right)  \left( \begin{array}{ccc} z_1' \\ z_2' \end{array} \right) = \left( \begin{array}{ccc} 0 \\ b \sin ax \end{array} \right)
\]と表せる。

さらに\[ W(y_1, y_2) =  \left| \begin{array}{ccc} \cos ax & \sin ax \\ -a \sin ax & a \cos ax \end{array} \right| \not = 0 \]が成立するので、行列\[
\left( \begin{array}{ccc} \cos ax & \sin ax \\ -a \sin ax & a \cos ax \end{array} \right)
\]には逆行列が存在し、その逆行列は\[\begin{align*}
\left( \begin{array}{ccc} \cos ax & \sin ax \\ -a \sin ax & a \cos ax \end{array} \right)^{-1} & =  \frac{1}{W(y_1,y_2)} \left( \begin{array}{ccc} a \cos ax & - \sin ax \\ a \sin ax & \cos ax \end{array} \right)
\\ & = \frac{1}{a} \left( \begin{array}{ccc} a \cos ax & - \sin ax \\ a \sin ax & \cos ax \end{array} \right)
\end{align*}\]と求められる。

よって、\[\begin{align*}
\left( \begin{array}{ccc} z_1' \\ z_2' \end{array} \right) & = \left( \begin{array}{ccc} \cos ax & \sin ax \\ -a \sin ax & a \cos ax \end{array} \right)^{-1}  \left( \begin{array}{ccc} 0 \\ b \sin ax \end{array} \right)
\\ & =  \frac{1}{a} \left( \begin{array}{ccc} a \cos ax & - \sin ax \\ a \sin ax & \cos ax
\end{array} \right) \left( \begin{array}{ccc} 0 \\ b \sin ax \end{array} \right)
\\ & = \frac{1}{a} \left( \begin{array}{ccc} - b \sin^2 ax \\ b \sin ax \cos ax  \end{array} \right)
\\ & = \left( \begin{array}{ccc} - \frac{b}{a} \sin^2 ax \\ \frac{b}{a} \sin ax \cos ax \end{array} \right)
\end{align*}\]が成立する。

さらに上の2式を \( x \) で積分すると、\[\begin{align*}
z_1  & = - \frac{b}{a} \int \sin^2 ax \ dx
\\ & =  - \frac{b}{2a} \int 1 - \cos 2ax \ dx
\\ & = - \frac{b}{2a} \left( x - \frac{1}{2a} \sin 2ax \right)
\\ & = - \frac{b}{2a} x + \frac{b}{4a^2} \sin ax
\end{align*} \]\[\begin{align*}
z_2  & = \frac{b}{a} \int \sin ax \cos ax \ dx
\\ & = \frac{b}{2a} \int \sin 2ax \ dx
\\ & = \frac{b}{2a} \cdot \left( - \frac{1}{2a} \cos 2ax \right)
\\ & = - \frac{b}{4a^2} \cos 2ax
\end{align*} \]となる*1。

（特殊解を求めるため、任意定数 \( C_1 \), \( C_2 \) を省略しています。）

よって、特殊解は\[\begin{align*}
y & = z_1 \cos ax + z_2 \sin ax
\\ & = \left(  - \frac{b}{2a} x + \frac{b}{4a^2} \sin 2ax \right) \cos ax - \frac{b}{4a^2} \cos 2ax \cdot \sin ax
\\ & = - \frac{b}{2a} x \cos ax + \frac{b}{4a^2} \left( \sin 2ax \cos ax - \cos 2ax \sin ax \right)
\\ & = - \frac{b}{2a} x \cos ax + \frac{b}{4a^2} \left( \sin 2ax \cos ax - \cos 2ax \sin ax \right)
\\ & = - \frac{b}{2a} x \cos ax + \frac{b}{4a^2} \sin \left( 2ax - ax \right)
\\ & = - \frac{b}{2a} x \cos ax + \frac{b}{4a^2} \sin ax
\end{align*}\]となる*2。

よって、特殊解の1つは\[
y = - \frac{b}{2a} x \cos ax + \frac{b}{4a^2} \sin ax
\]となる。

※ \( \sin ax \) が基本解なので、\( \sin ax \) の項を打ち消して特殊解を\[
y = - \frac{b}{2a} x \cos ax
\]とするのもあり。

計算途中で三角関数の変形

• 倍角（半角）の公式
• 加法定理

を用いています。忘れた人は、下の記事で確認しておきましょう。

www.momoyama-usagi.com

(3)

一般解は、「同次形の一般解」と「特殊解の1つ」の和で求められる。

よって、任意定数 \( C_1 \), \( C_2 \)を用いて\[
y = C_1 \cos ax + C_2 \sin ax - \frac{b}{2a} x \cos ax + \frac{b}{4a^2} \sin ax
\]となる。

もしくは、\( \frac{b}{4a^2} \sin ax \) を \( C_2 \sin ax \) の中に含めて\[
y = C_1 \cos ax + C_2 \sin ax - \frac{b}{2a} x \cos ax
\]としてもOK。

解答2

(1)

微分方程式の基本解となることを示すためには、

• 2つの解が微分方程式を満たすこと … (i)
• 2つの解が1次独立であること … (ii)

を示せばよい。

まず、2つの解が微分方程式を満たすことを示す。

\[
y_1' = 1, \ \ \ y_1'' = 0
\]となるので、\[
0 + \frac{x}{x+1} - \frac{1}{x+1} \cdot x = 0 \]\[
\frac{x}{x+1} - \frac{x}{x+1} = 0
\]となり、\( y_1 \) は微分方程式の解となる。

また、\[
y_2' = - e^{-x} , \ \ \ y_2' = e^{-x}
\]となるので、\[
e^{-x} + \frac{x}{x+1} \cdot (- e^{-x}) - \frac{1}{x+1} \cdot e^{-x} = 0 \]\[
\frac{x+1}{x+1} e^{-x} - \frac{x}{x+1} e^{-x} - \frac{1}{x+1} e^{-x} = 0
\]となり、\( y_2 \) も微分方程式の解となる。

また、

よって、\( y_1 \), \( y_2 \) の解は微分方程式を満たし、(i) が示された。

さらに、ロンスキアン \( W(y_1, y_2) \) が\[\begin{align*}
W(y_1, y_2 ) & = \left| \begin{array}{ccc} y_1 & y_2 \\ y_1'  & y_2' \end{array} \right|
\\ & = \left| \begin{array}{ccc} x & e^{-x} \\ 1 & - e^{-x} \end{array} \right|
\\ & = x \cdot \left( - e^{-x} \right) - e^{-x} \cdot 1
\\ & = - e^{-x} (x+1) \not = 0
\end{align*} \]となるので、\( y_1 \), \( y_2 \) は1次独立な解であることが示されたので、(ii) も示された。

よって、(i), (ii) より、\( y_1 = x \), \( y_2 = e^{-x} \) が微分方程式の基本解であることが示された。

(2)

同次方程式の一般解は、任意定数 \( C_1 \), \( C_2 \) を用いて\[
y = C_1 y_1 + C_2 y_2
\]とあらわせる。

ここで、\( C_1 \), \( C_2 \) をそれぞれ \( z_1(x) \), \( z_2(x) \) とおきかえると、\[
y = z_1 (x) y_1 + z_2 (x) y_2
\]となる。

（ただし \( z_1 (x) \) を \( z_1 \)、\( z_2 (x) \) を \( z_2 \) と表記する。）

両辺を \( x \) で微分すると、\[\begin{align*}
y' & = z_1' y_1 + z_1 y_1' + z_2' y_2 + z_2 y_2'
\\ & = \textcolor{red}{z_1' y_1 + z_2' y_2} + z_1 y_1' +  z_2 y_2'
\end{align*} \]となる。

ここで、\[
\textcolor{red}{z_1' y_1 + z_2' y_2} = 0 \tag{1}
\]とおくと、\[
y' = z_1 y_1' +  z_2 y_2'
\]となる。

さらに両辺を \( x \) で微分すると、\[\begin{align*}
y'' & = (z_1 y_1')' +  (z_2 y_2')'
\\ & = z_1' y_1' + z_1 y_1'' + z_2' y_2' + z_2 y_2''
\\ & = z_1 y_1'' + z_2 y_2'' + z_1' y_1' + z_2' y_2'
\end{align*}\]となります。

よって、\[\begin{align*}
\frac{dy}{dx} & = y'
\\ & = z_1 y_1' +  z_2 y_2'
\end{align*}\]\[\begin{align*}
\frac{d^2y}{dx^2} & = y''
\\ & = z_1 y_1'' + z_2 y_2'' + z_1' y_1' + z_2' y_2'
\end{align*}\]が求まります。

また、\( y_1 \), \( y_2 \) は同次方程式の解なので、\[
\left\{ \begin{array}{l} \textcolor{red}{y_1'' + \frac{x}{x+1} y_1' - \frac{1}{x+1} y_1} = 0 \\ \textcolor{blue}{y_2'' + \frac{x}{x+1} y_2' - \frac{1}{x+1}  y_2} = 0 \end{array}\right.
\]が成立する。

よって、非同次2階線形微分方程式は\[ \begin{align*}
& \frac{d^2 y}{dx^2} + \frac{2}{x} \frac{dy}{dx} + y
\\ = \ & y'' + \frac{x}{x+1} y' - \frac{1}{x+1} y
\\ = \ & (  z_1 y_1'' + z_2 y_2'' + z_1' y_1' + z_2' y_2' ) + \frac{x}{x+1} (z_1 y_1' +  z_2 y_2') - \frac{1}{x+1} (z_1 y_1 + z_2 y_2)
\\ = \ & z_1 \left(\textcolor{red}{y_1'' + \frac{x}{x+1} y_1' - \frac{1}{x+1} y_1} \right) + z_2  \left( \textcolor{blue}{y_2'' + \frac{x}{x+1} y_2' - \frac{1}{x+1} y_2} \right) + z_1' y_1' + z_2' y_2'
\\ = \ & z_1 \cdot \textcolor{red}{0} + z_2 \cdot \textcolor{blue}{0} + z_1' y_1' + z_2' y_2'
\\ = \ & z_1' y_1' + z_2' y_2'
\\ = \ & x+1
\end{align*} \]と変形でき、式\[
z_1' y_1' + z_2' y_2' = x+1 \tag{2}
\]を得る。

ここで、(1), (2)より\[
\left\{ \begin{array}{l} y_1 z_1' + y_2 z_2' = 0 \\  y_1' z_1' + y_2' z_2' = x+1 \end{array}\right.
\]の2つの式を行列を用いて\[
\left( \begin{array}{ccc} y_1 & y_2 \\ y_1' & y_2' \end{array} \right)  \left( \begin{array}{ccc} z_1' \\ z_2' \end{array} \right) = \left( \begin{array}{ccc} 0 \\ x+1 \end{array} \right)
\]、つまり\[
\left( \begin{array}{ccc} x & e^{-x} \\ 1 & - e^{-x} \end{array} \right)  \left( \begin{array}{ccc} z_1' \\ z_2' \end{array} \right) = \left( \begin{array}{ccc} 0 \\ x+1 \end{array} \right)
\]と表せる。

さらに問題(1)より、\[ W(y_1, y_2) =  \left| \begin{array}{ccc} x & e^{-x} \\ 1 & - e^{-x} \end{array} \right| \not = 0 \]が成立するので、行列\[
\left( \begin{array}{ccc} x & e^{-x} \\ 1 & - e^{-x} \end{array} \right)
\]には逆行列が存在し、その逆行列は\[\begin{align*}
\left( \begin{array}{ccc} x & e^{-x} \\ 1 & - e^{-x} \end{array} \right)^{-1} & =  \frac{1}{W(y_1,y_2)} \left( \begin{array}{ccc} - e^{-x} & -e^{-x} \\ -1 & x \end{array} \right)
\\ & = \frac{1}{- e^{-x} (x+1)} \left( \begin{array}{ccc} - e^{-x} & -e^{-x} \\ -1 & x
\end{array} \right)
\\ & = \frac{1}{x+1} \left( \begin{array}{ccc} 1 & 1 \\ e^x & - x e^x
\end{array} \right)
\end{align*}\]と求められる。

よって、\[\begin{align*}
\left( \begin{array}{ccc} z_1' \\ z_2' \end{array} \right) & = \left( \begin{array}{ccc} x & e^{-x} \\ 1 & - e^{-x} \end{array} \right)^{-1}  \left( \begin{array}{ccc} 0 \\ x+1 \end{array} \right)
\\ & =  \frac{1}{x+1} \left( \begin{array}{ccc} 1 & 1 \\ e^x & - x e^x
\end{array} \right) \left( \begin{array}{ccc} 0 \\ x+1 \end{array} \right)
\\ & = \frac{1}{x+1} \left( \begin{array}{ccc} x+1 \\ - x e^x(x+1) \end{array} \right)
\\ & = \left( \begin{array}{ccc} 1 \\ - x e^x \end{array} \right)
\end{align*}\]が成立する。

さらに上の2式を \( x \) で積分すると、\[\begin{align*}
z_1  & = \int 1 \ dx
\\ & = x + C_1
\end{align*} \]\[\begin{align*}
z_2  & = \int - x e^x \ dx
\\ & = - x e^x + e^x
\\ & = (1-x) e^x + C_2
\end{align*} \]となるので、一般解は\[\begin{align*}
y & = z_1 x + z_2 e^{-x}
\\ & = \left( x + C_1 \right) x +  \left( (1-x) e^x + C_2 \right) e^{-x}
\\ & = x^2 + C_1 x + (1-x) + C_2 e^{-x}
\\ & = C_1 x + C_2 e^{-x} + x^2 - x + 1
\end{align*}\]と求められる。

解答3

(1)

微分方程式の基本解となることを示すためには、

• 2つの解が微分方程式を満たすこと … (i)
• 2つの解が1次独立であること … (ii)

を示せばよい。

まず、2つの解が微分方程式を満たすことを示す。\[\begin{align*}
y_1' = - \frac{1}{x^2} \sin x + \frac{1}{x} \cos x
\end{align*}\]\[\begin{align*}
y_1'' & = \frac{2}{x^3} \sin x - \frac{1}{x^2} \cos x - \frac{1}{x^2} \cos x - \frac{1}{x} \sin x
\\ & = \frac{2}{x^3} \sin x - \frac{2}{x^2} \cos x - \frac{1}{x} \sin x
\end{align*}\]となるので、\[
\left( \frac{2}{x^3} \sin x - \frac{2}{x^2} \cos x - \frac{1}{x} \sin x \right) + \frac{2}{x} \left( - \frac{1}{x^2} \sin x + \frac{1}{x} \cos x \right) + \frac{1}{x} \sin x = 0 \]\[
\textcolor{red}{\frac{2}{x^3} \sin x} \textcolor{blue}{- \frac{2}{x^2} \cos x} \textcolor{green}{- \frac{1}{x} \sin x} \textcolor{red}{- \frac{2}{x^3} \sin x} \textcolor{blue}{ + \frac{2}{x^2} \cos x} \textcolor{green}{+ \frac{1}{x} \sin x} = 0
\]となり、\( y_1 \) は微分方程式の解となる。

また、\[\begin{align*}
y_2' = - \frac{1}{x^2} \cos x - \frac{1}{x} \sin x
\end{align*}\]\[\begin{align*}
y_2'' & = \frac{2}{x^3} \cos x + \frac{1}{x^2} \sin x + \frac{1}{x^2} \sin x - \frac{1}{x} \cos x
\\ & = \frac{2}{x^3} \cos x + \frac{2}{x^2} \sin x - \frac{1}{x} \cos x
\end{align*}\]となるので、\[
\left( \frac{2}{x^3} \cos x + \frac{2}{x^2} \sin x - \frac{1}{x} \cos x \right) + \frac{2}{x} \left( - \frac{1}{x^2} \cos x - \frac{1}{x} \sin x \right) + \frac{1}{x} \cos x = 0 \]\[
\textcolor{red}{ \frac{2}{x^3} \cos x } \textcolor{blue}{ + \frac{2}{x^2} \sin x} \textcolor{green}{ - \frac{1}{x} \cos x} \textcolor{red}{ - \frac{2}{x^3} \cos x } \textcolor{blue}{ - \frac{2}{x^2} \sin x} \textcolor{green}{ + \frac{1}{x} \cos x } = 0
\]となり、\( y_2 \) は微分方程式の解となる。

よって、\( y_1 \), \( y_2 \) の解は微分方程式を満たし、(i) が示された。

さらに、ロンスキアン \( W(y_1, y_2) \) が\[\begin{align*}
W(y_1, y_2 ) & = \left| \begin{array}{ccc} y_1 & y_2 \\ y_1'  & y_2' \end{array} \right|
\\ & = \left| \begin{array}{ccc} \frac{1}{x} \sin x & \frac{1}{x} \cos x \\ - \frac{1}{x^2} \sin x + \frac{1}{x} \cos x  & - \frac{1}{x^2} \cos x - \frac{1}{x} \sin x \end{array} \right|
\\ & = \frac{1}{x} \sin x \left( - \frac{1}{x^2} \cos x - \frac{1}{x} \sin x \right) - \frac{1}{x} \cos x \left( - \frac{1}{x^2} \sin x + \frac{1}{x} \cos x \right)
\\ & = \textcolor{red}{- \frac{1}{x^3} \sin x \cos x} - \frac{1}{x^2} \sin^2 x \textcolor{red}{+ \frac{1}{x^3} \sin x \cos x } - \frac{1}{x^2} \cos^2 x
\\ & = - \frac{1}{x^2} \left( \sin^2 x + \cos^2 x \right)
\\ & = - \frac{1}{x^2} \not = 0
\end{align*} \]となるので、\( y_1 \), \( y_2 \) は1次独立な解であることが示されたので、(ii) も示された。

よって、(i), (ii) より、\( y_1 = \frac{1}{x} \sin x \), \( y_2 = \frac{1}{x} \cos x \) が微分方程式の基本解であることが示された。

(2)

同次方程式の一般解は、任意定数 \( C_1 \), \( C_2 \) を用いて\[
y = C_1 y_1 + C_2 y_2
\]とあらわせる。

ここで、\( C_1 \), \( C_2 \) をそれぞれ \( z_1(x) \), \( z_2(x) \) とおきかえると、\[
y = z_1 (x) y_1 + z_2 (x) y_2
\]となる。

（ただし \( z_1 (x) \) を \( z_1 \)、\( z_2 (x) \) を \( z_2 \) と表記する。）

両辺を \( x \) で微分すると、\[\begin{align*}
y' & = z_1' y_1 + z_1 y_1' + z_2' y_2 + z_2 y_2'
\\ & = \textcolor{red}{z_1' y_1 + z_2' y_2} + z_1 y_1' +  z_2 y_2'
\end{align*} \]となる。

ここで、\[
\textcolor{red}{z_1' y_1 + z_2' y_2} = 0 \tag{1}
\]とおくと、\[
y' = z_1 y_1' +  z_2 y_2'
\]となる。

さらに両辺を \( x \) で微分すると、\[\begin{align*}
y'' & = (z_1 y_1')' +  (z_2 y_2')'
\\ & = z_1' y_1' + z_1 y_1'' + z_2' y_2' + z_2 y_2''
\\ & = z_1 y_1'' + z_2 y_2'' + z_1' y_1' + z_2' y_2'
\end{align*}\]となります。

よって、\[\begin{align*}
\frac{dy}{dx} & = y'
\\ & = z_1 y_1' +  z_2 y_2'
\end{align*}\]\[\begin{align*}
\frac{d^2y}{dx^2} & = y''
\\ & = z_1 y_1'' + z_2 y_2'' + z_1' y_1' + z_2' y_2'
\end{align*}\]が求まります。

また、\( y_1 \), \( y_2 \) は同次方程式の解なので、\[
\left\{ \begin{array}{l} \textcolor{red}{y_1'' + \frac{2}{x} y_1' + y_1} = 0 \\ \textcolor{blue}{y_2'' + \frac{2}{x} y_2' +  y_2} = 0 \end{array}\right.
\]が成立します。。

よって、非同次2階線形微分方程式は\[ \begin{align*}
& \frac{d^2 y}{dx^2} + \frac{2}{x} \frac{dy}{dx} + y
\\ = \ & y'' + \frac{2}{x} y' + y
\\ = \ & (  z_1 y_1'' + z_2 y_2'' + z_1' y_1' + z_2' y_2' ) + \frac{2}{x} (z_1 y_1' +  z_2 y_2') + (z_1 y_1 + z_2 y_2)
\\ = \ & z_1 \left(\textcolor{red}{y_1'' + \frac{2}{x} y_1' + y_1} \right) + z_2  \left( \textcolor{blue}{y_2'' + \frac{2}{x} y_2' + y_2} \right) + z_1' y_1' + z_2' y_2'
\\ = \ & z_1 \cdot \textcolor{red}{0} + z_2 \cdot \textcolor{blue}{0} + z_1' y_1' + z_2' y_2'
\\ = \ & z_1' y_1' + z_2' y_2'
\\ = \ & e^x
\end{align*} \]と変形でき、式\[
z_1' y_1' + z_2' y_2' = \frac{1}{x} \tag{2}
\]を得る。

ここで、(1), (2)より\[
\left\{ \begin{array}{l} y_1 z_1' + y_2 z_2' = 0 \\  y_1' z_1' + y_2' z_2' = \frac{1}{x}\end{array}\right.
\]の2つの式を行列を用いて\[
\left( \begin{array}{ccc} y_1 & y_2 \\ y_1' & y_2' \end{array} \right)  \left( \begin{array}{ccc} z_1' \\ z_2' \end{array} \right) = \left( \begin{array}{ccc} 0 \\ \frac{1}{x} \end{array} \right)
\]つまり\[
\left( \begin{array}{ccc} \frac{1}{x} \sin x & \frac{1}{x} \cos x \\ - \frac{1}{x^2} \sin x + \frac{1}{x} \cos x & - \frac{1}{x^2} \cos x - \frac{1}{x} \sin x \end{array} \right)  \left( \begin{array}{ccc} z_1' \\ z_2' \end{array} \right) = \left( \begin{array}{ccc} 0 \\ \frac{1}{x} \end{array} \right)
\]と表せる。

さらに問題(1)より、\[ W(y_1, y_2) =  \left| \begin{array}{ccc} \frac{1}{x} \sin x & \frac{1}{x} \cos x \\ - \frac{1}{x^2} \sin x + \frac{1}{x} \cos x & - \frac{1}{x^2} \cos x - \frac{1}{x} \sin x \end{array} \right| \not = 0 \]が成立するので、行列\[
\left( \begin{array}{ccc} \frac{1}{x} \sin x & \frac{1}{x} \cos x \\ - \frac{1}{x^2} \sin x + \frac{1}{x} \cos x & - \frac{1}{x^2} \cos x - \frac{1}{x} \sin x \end{array} \right)
\]には逆行列が存在し、その逆行列は\[\begin{align*}
&  \left( \begin{array}{ccc} \frac{1}{x} \sin x & \frac{1}{x} \cos x \\ - \frac{1}{x^2} \sin x + \frac{1}{x} \cos x & - \frac{1}{x^2} \cos x - \frac{1}{x} \sin x \end{array} \right)^{-1}
\\ = \ & - \frac{1}{ \frac{1}{x^2} } \left( \begin{array}{ccc} - \frac{1}{x^2} \cos x - \frac{1}{x} \sin x & - \frac{1}{x} \cos x \\  \frac{1}{x^2} \sin x - \frac{1}{x} \cos x & \frac{1}{x} \sin x  \end{array}\right)
\\ = \ & - x^2 \left( \begin{array}{ccc} - \frac{1}{x^2} \cos x - \frac{1}{x} \sin x & - \frac{1}{x} \cos x \\  \frac{1}{x^2} \sin x - \frac{1}{x} \cos x & \frac{1}{x} \sin x  \end{array}\right)
\end{align*}\]と求められる。

よって、\[\begin{align*}
\left( \begin{array}{ccc} z_1'  \\ z_2'  \end{array} \right) & = \left( \begin{array}{ccc} \frac{1}{x} \sin x & \frac{1}{x} \cos x \\ - \frac{1}{x^2} \sin x + \frac{1}{x} \cos x & - \frac{1}{x^2} \cos x - \frac{1}{x} \sin x \end{array} \right)^{-1}  \left( \begin{array}{ccc} 0 \\ \frac{1}{x} \end{array} \right)
\\ & = - x^2 \left( \begin{array}{ccc} - \frac{1}{x^2} \cos x - \frac{1}{x} \sin x & - \frac{1}{x} \cos x \\  \frac{1}{x^2} \sin x - \frac{1}{x} \cos x & \frac{1}{x} \sin x  \end{array}\right) \left( \begin{array}{ccc} 0 \\ \frac{1}{x} \end{array} \right)
\\ & = - x^2 \left( \begin{array}{ccc} - \frac{1}{x^2} \cos x  \\ \frac{1}{x^2} \sin x  \end{array}\right)
\\ & = \left( \begin{array}{ccc} \cos x  \\ - \sin x  \end{array} \right)
\end{align*}\]が成立する。

さらに上の2式を \( x \) で積分すると、\[\begin{align*}
z_1  & = \int \cos x \ dx
\\ & = \sin x + C_1
\end{align*} \]\[\begin{align*}
z_2  & = \int - \sin x \ dx
\\ & = \cos x + C_2
\end{align*} \]となるので、一般解は\[\begin{align*}
y & = z_1 \frac{1}{x} \sin x + z_2 \frac{1}{x} \cos x
\\ & = \left( \sin x + C_1 \right) \frac{1}{x} \sin x +  \left( \cos x + C_2 \right) \frac{1}{x} \cos x
\\ & = \frac{1}{x} \sin^2 x + C_1 \frac{1}{x} \sin x + \frac{1}{x} \cos^2 x + C_2 \frac{1}{x} \cos x
\\ & = \frac{1}{x} \left( \sin^2 x + \cos^2 x \right) + C_1 \frac{1}{x} \sin x + C_2 \frac{1}{x} \frac{1}{x}
\\ & = \frac{1}{x} + C_1 \frac{1}{x} \sin x + C_2 \frac{1}{x} \cos x
\end{align*}\]と求められる。

５．さいごに

今回は、非同次の2階線形微分方程式を定数変化法で解く方法について説明しました。

定数変化法は時間がかかるため、未定係数法で計算ができないかどうかをまずチェックして、計算ができなさそうなら定数変化法を使うようにしましょう。

次回は、連立微分方程式を解く方法について説明したいと思います。