スポンサードリンク
こんにちは、ももやまです。
今回はコンパイラの処理の流れについて、字句解析と意味解析を中心にまとめていきたいと思います。
前提としてオートマトンや文脈自由文法の知識があると理解が早まるかと思います。
(ただし、前提知識がなくてもわかるように補足しています)
前回の計算機システムの記事(Part10)はこちら!
目次
スポンサードリンク
1.コンパイラの処理の流れ
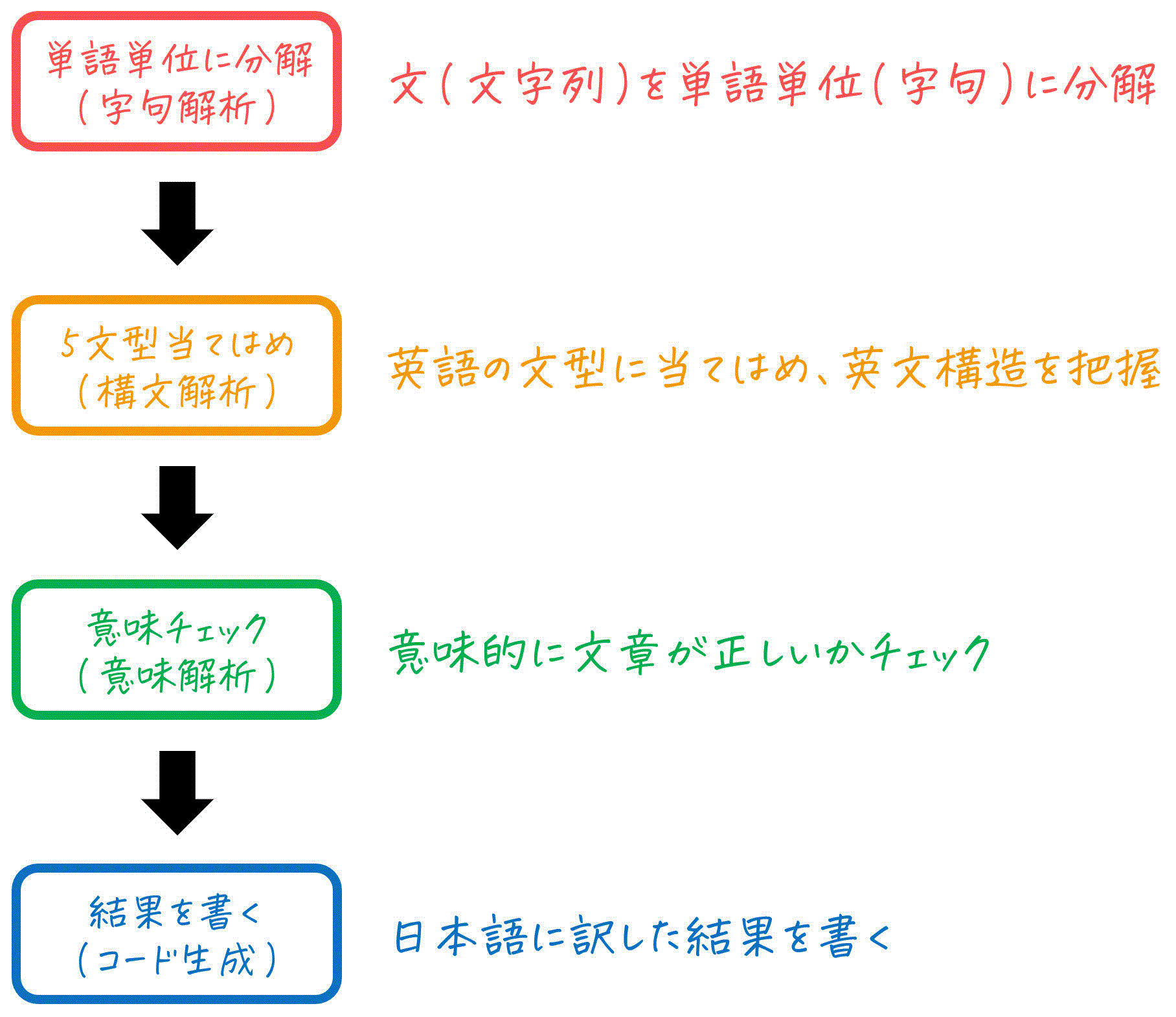
まず、コンパイラの処理の大まかな流れ(Cプログラム test.c を実行可能な機械語ファイル (test.exe もしくは test.out )にするまでの流れ)を見ていきましょう。
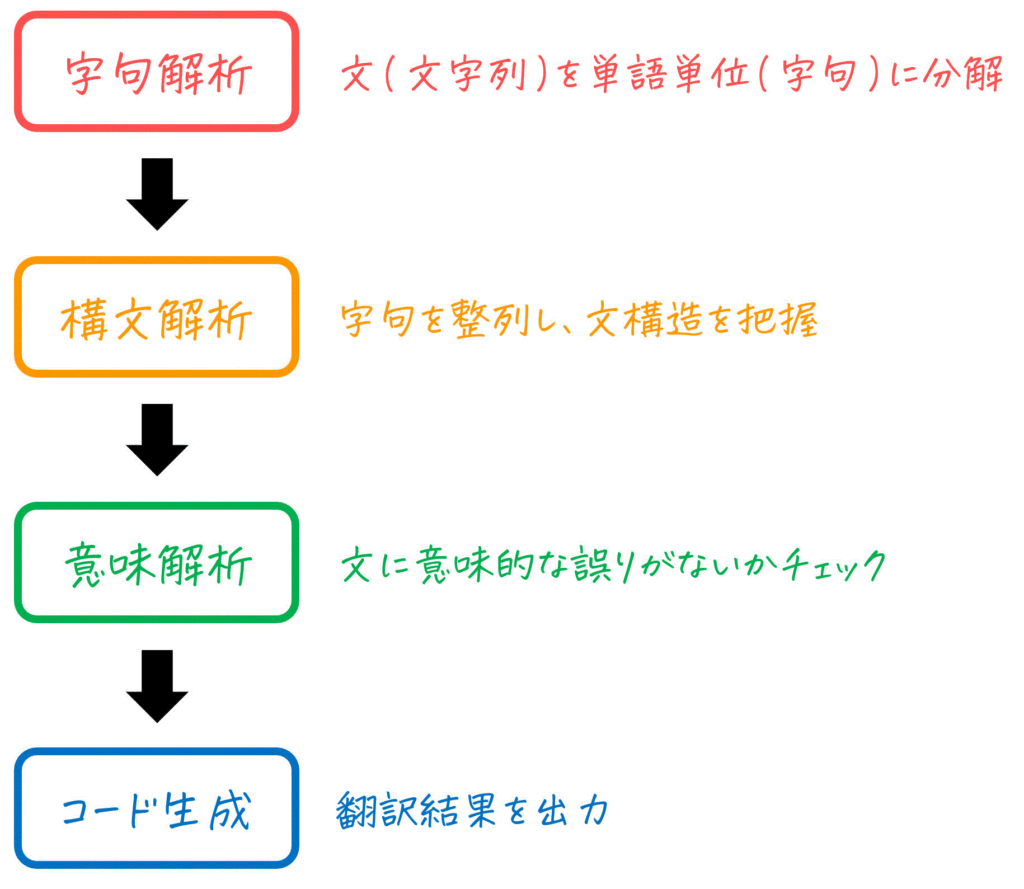
ただ、いきなりこんなこと言われても「わからん!!」ってなると思います。なので、各工程を「英文を日本語に直す過程」に当てはめてみました!
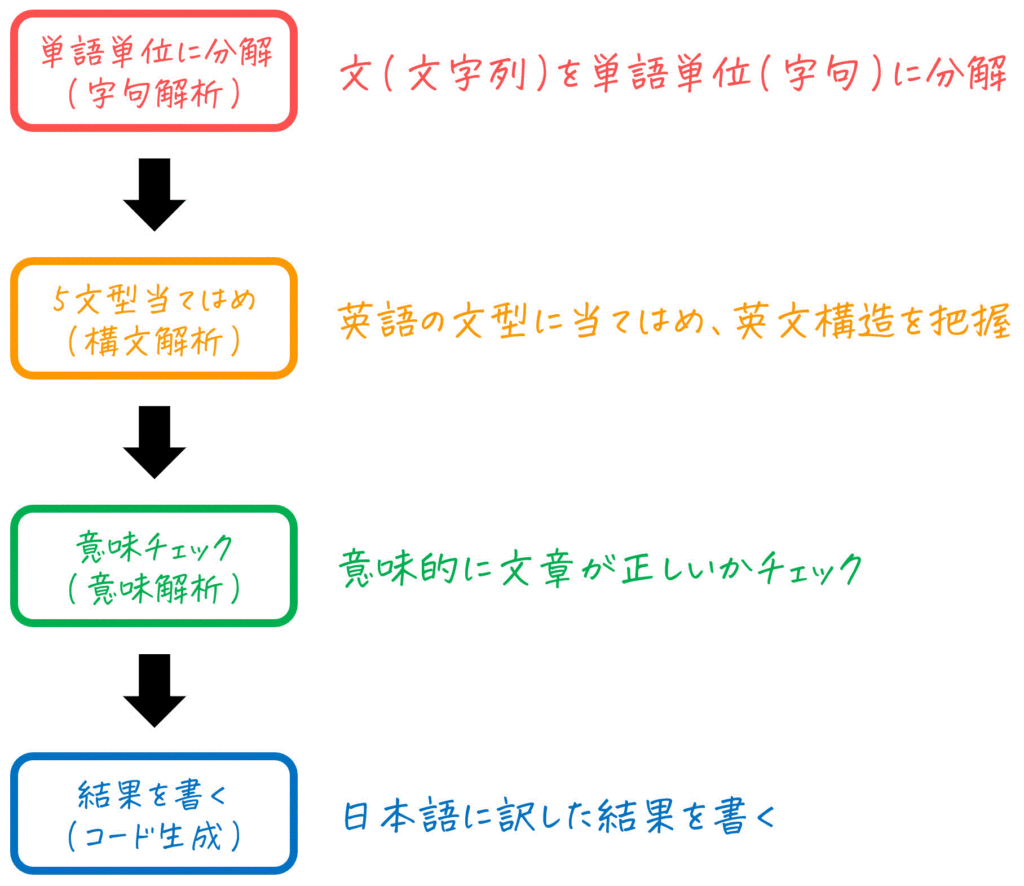
流れを大まかに把握できたところで、各工程で具体的にどんなことをするかを見ていきましょう!
スポンサードリンク
2.字句解析
皆さんは英語を日本語に翻訳するときに、(頭の中やテスト用紙などを用いて)英文に出てくる各英単語が「どんな品詞を持って、どんな意味を持つのか」を考えながら翻訳していたと思います。

プログラミングでも、実行可能な形(機械語)にコンパイルをするために、プログラムファイルを単語単位に分割し、その単語がどんな属性(自然言語でいう品詞)を持つのかを機械的にチェックします。
この過程が、字句解析なのです!
(1) 字句とは?
まずは字句解析の「字句」ってなんぞや。というところから見ていきましょう。
自然言語(日本語とか英語とか)で出てくる文章は、単語の塊で構成されていますね。
例えば下の文であれば、I, like, this, rabbit, too が単語になりますね。さらに、各単語の品詞は下のようになりますね。

プログラミング言語にも、自然言語における単語のようなものが存在します。この単語のようなものを字句と呼びます。
C言語の場合、6つの字句に分類することができます。
その1 識別子
識別子は、変数や関数などの名前を表します。
1文字目は英字かアンダーバー _ で、2文字目以降は英字・数字・_ で始まる必要があります。
例えば、test123, dasshi_chan, __init__ などは識別子ですが、4chome のように最初が数字で始まっていたり、dasshi-chan のように途中で英字・数字・_ 以外が入っている場合は識別子とは言えません。
その2 キーワード
決まった意味で用いる語のことをキーワード(予約語)と呼びます*1。
C言語では、int, if, else, break, while, for, return, double, void のようなプログラム上で意味をなす語がキーワードとなっています。
キーワードとなるような語は識別子として用いることができません。
つまり、int, double のような単語を関数名や変数名として使おうとするとエラーが出ます。
その3 定数
ある特定の型の定数を表します。
整数定数、浮動小数点定数、文字定数の3つにわかれます。
整数定数の例:334(10進数)、0114514(8進数)、0xDEAD(16進数)など
浮動小数点定数の例:3.14, 2.71, 1.23e6 ( \( 1.23 \times 10^{6} \) ) など
文字定数の例: 'a', 'E', '\n' (改行) など
その4 文字列定数
" で囲まれた文字列は文字列定数となります。
例えば、"z", "Hello World!", "Hey, I am a rabbit." などが文字列定数となります。
その5 区切り子
(, {, ;, ; などの記号を区切り子と呼びます。
その6 演算子
四則演算 +, -, *, / 、論理演算 &&, || 、等号不等号 =, <, <=、さらに ++ や += などの演算を表す記号は演算子と呼ばれます。
(2) 字句と正規表現とオートマトン
(a) 字句と正規表現
字句は正規表現を用いて表すことができます。
例えば、識別子は1文字目が英字 or _ で、2文字目以降がが英数字 or _ となるものでしたね。
これを正規表現を用いて書くと [A-Za-z_][0-9A-Za-z_]* と書くことができますね。
正規表現の復習
[文字列] とすることで文字列にかかれているいずれか1文字を表すことができます。
例えば [A-Za-z_] であれば A-Z (大文字アルファベット1文字)、a-z (小文字アルファベット1文字)、_(アンダーバー)のいずれかを表します。
また、 * は0回以上の繰り返し、+ は1回以上の繰り返しを表します。
正規表現についてはこちらの記事にまとめているので、正規表現について復習したい人はぜひお読みください!
(b) 正規表現とオートマトン
正規表現は有限オートマトン(以下オートマトンと表記します)を用いて表すことができます。
例えば、識別子かどうか判定する非決定性オートマトン(NFA)*2は下のように表すことができますね。
(識別子は1文字目が英字 or _ で、2文字目以降がが英数字 or _ となるもの、正規表現で表すと [A-Za-z_][0-9A-Za-z_]* )
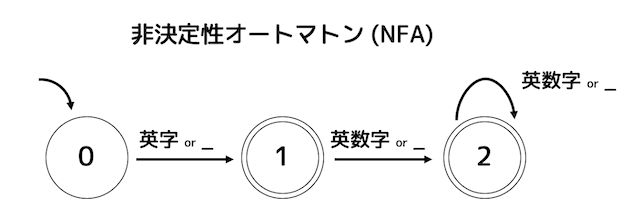
さらに決定性オートマトン(DFA)にすると下のような形となります。
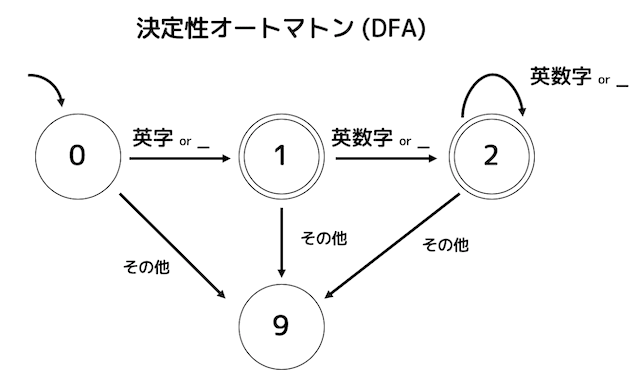
なので、字句は正規表現だけでなく、オートマトンを用いても表すことができますね!
オートマトンの復習
オートマトンについて少し復習しておきましょう。
オートマトンは、ある文字列が条件に一致するか一致しないかを図(状態遷移図)や表など(状態遷移表)で表したものを指します。
そしてオートマトンの◎は受理状態(True)、○は非受理状態(False)を表しています。さらに中に書かれている数字や文字は状態の名前(変数名みたいなもん)を表しています。
状態遷移図には、何も書かれていないただの矢印(⤵)がありますね。これを初期状態と呼びます。いわゆるスタート地点です。
状態遷移図を読む際には、初期状態から文字列を1文字ずつ矢印をたどりながら状態遷移を動かしていきます。文字列をたどり終わったとき、◎の位置にいれば受理(条件に一致)、○の位置にいれば非受理(条件に非一致)となります。
なお、非決定性オートマトンの場合は文字列をたどっていく最中に状態遷移がなくなることがあります。
状態遷移ができなくなった場合も非受理(条件に非一致)となります。
つまり、文字列をすべてたどることができて、かつ最後に◎の位置にいれば受理状態となります。
念のため、先程のオートマトンで状態遷移図を読む練習をしましょう。

何も書かれていない謎の矢印が0を指していますね。つまり、初期状態(スタート地点)が0であることを示しています。
例えば、AED であれば、1文字目の A で 0から1へ、2文字目の E で1から2へ、3文字目の D で2から2へ遷移しますね。
文字列をたどり終わったときに2の状態にいますね。この状態は◎なので、たしかに AED は条件に合致し、受理される(つまり識別子である)ことがわかりますね。
もう1つ、3chome で試してみましょう。
すると、1文字目の 3 ででいきなり遷移できる場所がなくなりますよね。
なので、 3chome は受理しない(つまり識別子ではない)ことがわかりますね。
オートマトンについてもっと詳しく知りたい人はこちらの記事をご覧ください。
また、オートマトンと正規表現についてはこちらの記事に書いてあるのでこちらもよろしければご覧ください。
(2) 字句解析とは
いよいよ本題です。
字句解析は、ソースプログラム上にかかれている文字を字句単位、つまり計算機上でわかる単語単位にに分割していく作業を表します。
字句解析を行う部分のことを字句解析器(スキャナ)と呼びます。
字句解析器は有限オートマトンを用いて構成することができます。
ではここで字句とオートマトンについて3問ほど練習してみましょう。
練習1
C言語において、次の(1)~(4)は何個の字句で構成されているか。
(1) find_n()
(2) "I have a pen, I have an apple, oh, apple pen."
(3) num++
(4) 33-4
練習2
つぎのC言語プログラムの関数 is_aho は引数 n が3の倍数、もしくは3のつく数かを判定する関数である。
int is_aho(int n) {
if(n % 3 == 0) {
return 1;
}
while(n > 0) {
if(n % 10 == 3) {
return 1;
}
else {
n /= 10;
}
}
return 0;
}
このプログラムの字句を切りだし、合計何個の字句から構成されているかを答えなさい。(さらに答えが3の倍数、もしくは3のつく数であればアホになりなさい。)
練習3
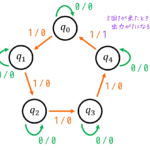
つぎの状態遷移図で表されるオートマトンが(1)~(6)の文字列を受理するかどうかを判定しなさい。さらに、受理する場合はどの状態で受理されるかも答えなさい。
※ . は(改行以外の)任意の1文字を表す。
(1) ab
(2) AB
(3) ab19
(4) a
(5) a9b
(6) 9ab
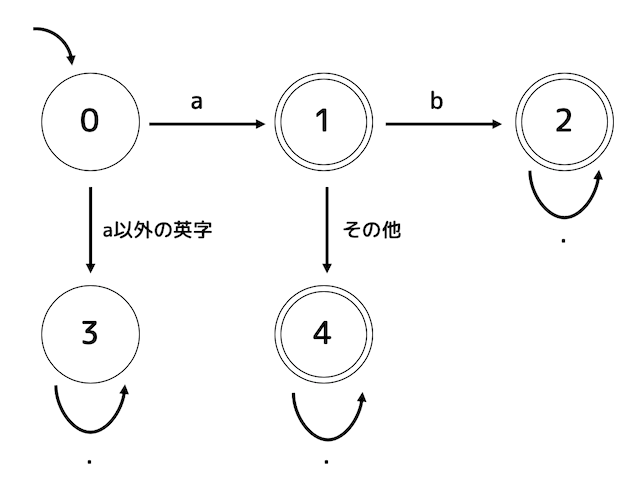
解答1
(1) find_n, (, ) で分けられるので3個
(2) "" で囲まれているのは1つの文字列定数なので1個
(3) num で1つ、++ で1つなので2個
(4) 33 で1つ、- で1つ、4で1つなので3個
解答2
int is_aho(int n) { // int is_aho ( int n ) { 合計 7個
if(n % 3 == 0) { // if ( n % 3 == 0 ) { 合計 9個
return 1; // return 1 ; 合計 3個
} // } 合計 1個
while(n > 0) { // while ( n > 0 ) { 合計 7個
if(n % 10 == 3) { // if ( n % 10 == 3 ) { 合計 9個
return 1; // return 1 ; 合計 3個
} // } 合計 1個
else { // else { 合計 2個
n /= 10; // n /= 10 ; 合計 4個
} // } 合計 1個
} // } 合計 1個
return 0; // return 0 ; 合計 3個
} // } 合計 1個
より合計52個。残念、アホにはならなかった。
解答3
初期状態は0。なのでスタート地点は0。
(1) ab(状態2で受理)
a で状態0→状態1、b で状態1→状態2に遷移する。
よって状態2で受理。
(2) AB (受理しない)
アルファベットの大文字と小文字は別物なのに注意。A で状態0→状態3、B で状態3→状態3に遷移する。よって受理しない。
(3) ab19(状態2で受理)
a で状態0→状態1、b で状態1→状態2に、1 で状態2→状態2、9 で状態2→状態2に遷移する。
よって状態2で受理。
(4) a(状態1で受理)
a で状態0→状態1に遷移するので状態1で受理する。
(5) a9b(状態4で受理)
a で状態0→状態1、9 で状態1→状態4、bで状態変化しないため、状態4で受理。
(6) 9ab(受理しない)
9 の遷移先が見つからないため、最後まで文字列を遷移させることができない。
よって受理しない。
スポンサードリンク
3.構文解析
(1) 構文解析とは
英文の各単語の意味や品詞全て把握できていたとしても、「英文の構造(5文型)」のどれに当てはまるのかが分からないと、(複雑な文章の) 和訳はは実現できません。
そのため、(複雑な) 英文を正確に和訳する際には、「構文解釈」が必要になってきます。
(皆さんも高校生の頃、「構文解釈」をしてきた思い出があるかと思います。)

コンパイラも同じように、ただ字句を解析しただけではコンピュータ上では意味がわかりません。そのため、機械語の実行可能なファイルへの変換もできません。
そこで、字句がどのような関係を持つかを調べるために、「英文の構文解釈」みたいなことをします。これが構文解析です。
(2) BNF記法とは
構文解析を行うために必要な構文はBNF記法(文脈自由文法を定義するために使われる文法)で書かれています。
なので、構文解析の話をする前にBNF記法で使われる記号について簡単にですが解説したいと思います。
※文脈自由文法がわかっていること前提で説明するため、もし文脈自由文法がわからない or わすれてしまった人はこちらの記事で復習しましょう!
(a) 非終端記号を表す < >
< > で囲まれた記号は非終端記号を表します。
(非終端記号は変数みたいなものだと思ってください。)
例えば、<式>, <項> のように表記することができます。
※注意
下の説明をわかりやすくするため、大文字1文字 A, B のような記号は < > で囲われていなくても非終端記号であると仮定します。
(b) 構文を定義する ::=
置き換えルールを定義する記号です。
例えば、文脈自由文法で \( A \to B + C \) と定義される文法は、
A ::= B + C
と書くことができます。
(念の為解説すると、「A から B+C を生成できますよ〜」の「から」に相当する部分が ::= となる)
(c) 複数の文法を表記 |
| を使うことで1つの式に2つ以上の規則を定義することができます。
例えば、
A ::= B + C A ::= B
の2つの規則を
A ::= B + C | B
のように1つにまとめることができます。
念のため、BNF記法に関する練習問題を1問だけ解いてみましょう。
基本情報の過去問です。
練習4
次のBNFで定義されるビット列Sであるものはどれか。
<S> ::= 01 | 0<S>1
ア:000111
イ:010010
ウ:010101
エ:011111
解答4
問題のBNFは、
<S> ::= 01 <S> ::= 0<S>1
の2つの規則を表していますね。
規則を適用していくと、\[
S \to 0S1 \to 00S11 \to 000111
\]と変形できるので答えはア。
(3) 構文規則の定義
構文解析をするために、構文規則を定義する必要があります。
構文規則は先程説明したBNF記法の文脈自由文法で表記されます。
つまり、BNF記法で表された生成規則、非終端記号、終端記号、出発記号の4つの項目で構文規則は定義されています。
例えば下のように4つの項目は定義されます。
生成規則
<式> ::= <式> + <項> | <項> <項> ::= <項> * <因子> | <因子> <因子> ::= ( <式> ) | 数字
非終端記号 <式>, <項>, <因子>
終端記号 +, *, (, ), 数字(0以上)
出発記号 <式>
では、早速この規則を使って2つほど構文解析をしてみましょう!
(4) Let's 構文解析(解析木と構文木を書いてみよう)
では、早速上の構文規則から 1+2*3 の構文解析を、解析木や構文木と呼ばれるものを書きながらしていきましょう。
(i) 解析木の書き方
解析木は、出発記号(今回の場合は <式>)からどのようにして目的の式(今回の場合は 1+2*3)になるのかを下のように図で表したものです。
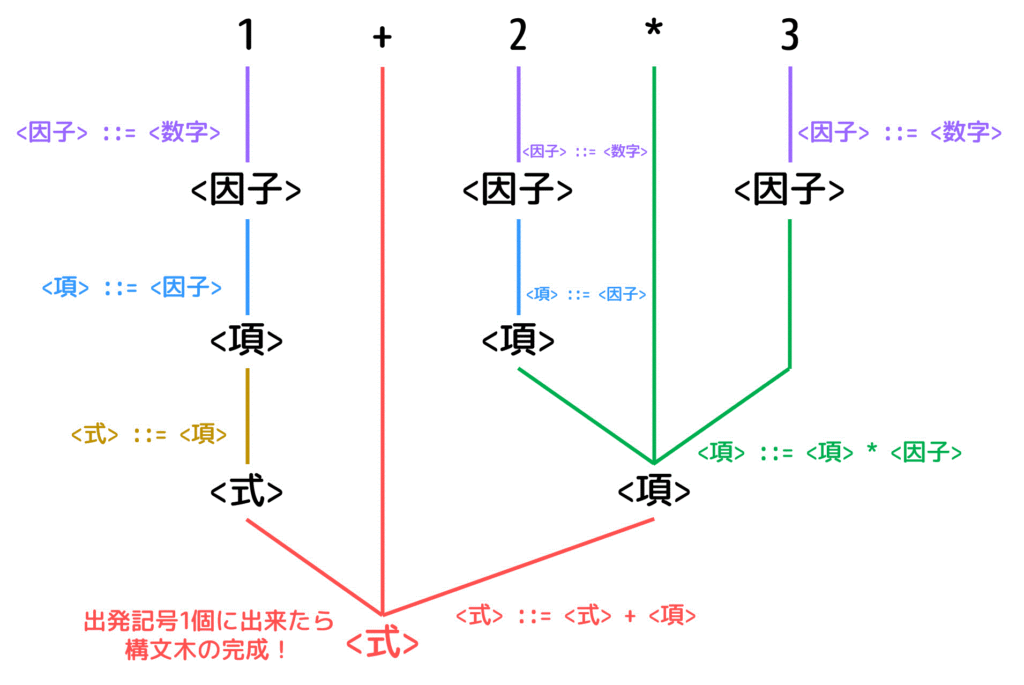
(生成規則を逆にたどりながら「出発記号」に戻していく)
解析木を書く際には、「目的の式 1+2*3 は出発記号 <式> からどの生成規則を使って導出されていくのか」というのを求めながら書いていきます。言い換えると、解析木を書く作業は目的の式から、生成規則を逆に(もとに戻す方法へ)辿っていき、出発記号に戻すパズルみたいなものだと思っていただけたらOKです[1]例えば、\( A \to B + C \) に対して、\( B + C \) を \( A \) に戻すことを「生成規則を逆へたどる」と思っていただけたらOKです。。
ここからは、実際にどのように「生成規則を逆に辿っていき、目的式 1+2*3 を出発記号 <式> に戻していくか」を実際に下の例に対して見ていきましょう。
生成規則
<式> ::= <式> + <項> | <項> <項> ::= <項> * <因子> | <因子> <因子> ::= ( <式> ) | 数字
非終端記号 <式>, <項>, <因子>
終端記号 +, *, (, ), 数字(0以上)
出発記号 <式>
注意:生成規則を逆に適用していく際には、記号の順番を入れ替えてはいけません。
[OKな例]A ::= B+C を逆に適用 → B+C を A に書き換え[NGな例]
A ::= B+C を逆に適用 → C+B を A に書き換え(
B+C の記号を入れ替えて C+B にしているためNG)
[Step1]
まず、1 + 2 * 3 つまり 数字, +, * に対して生成規則を逆に適用できないかを確認します。
すると、<因子> ::= 数字 を逆に適用、つまり数字から <因子>への書き換えが出来ますね。
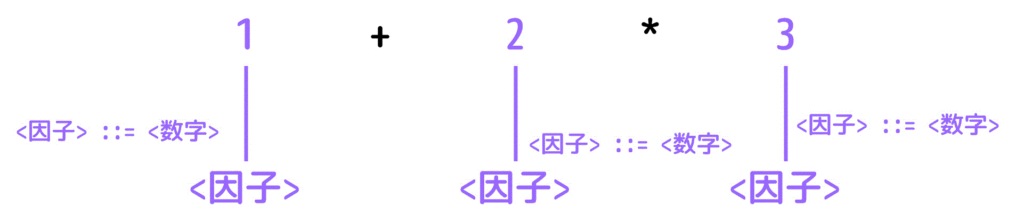
[Step2]
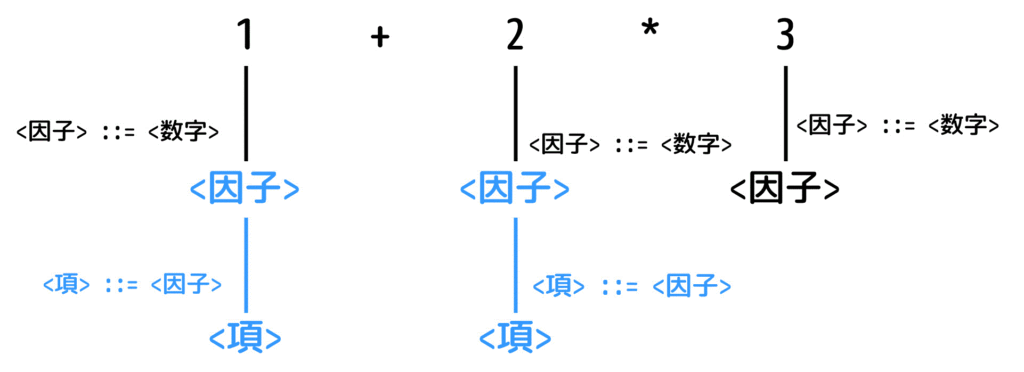
つぎに、<項> ::= <因子> を逆に適用、つまり<因子>から<項>への書き換えをします。
[Step3]
つぎに、1から生成規則を逆に適用している部分には <式> ::= <項> を逆に適用し、<項>から<式>へ書き換えます。
また、2, 3から生成規則を逆に適用している部分は、<項> ::= <項> * <因子> を逆に適用し、<項> * <因子> を <項> に書き換えます。
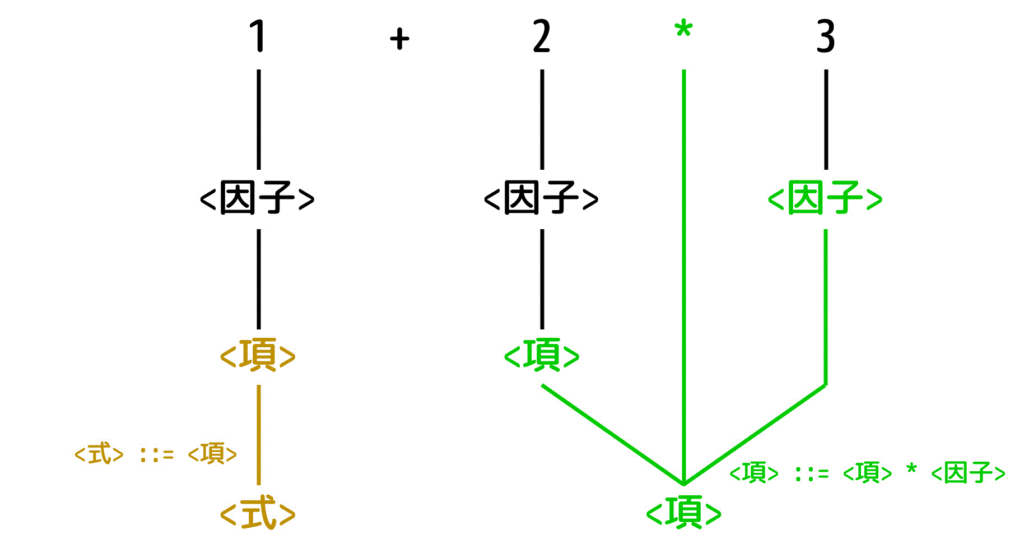
[Step4]
最後に <式> ::= <式> + <項> を逆に適用し、<式> + <項> を <式> に書き換えます。
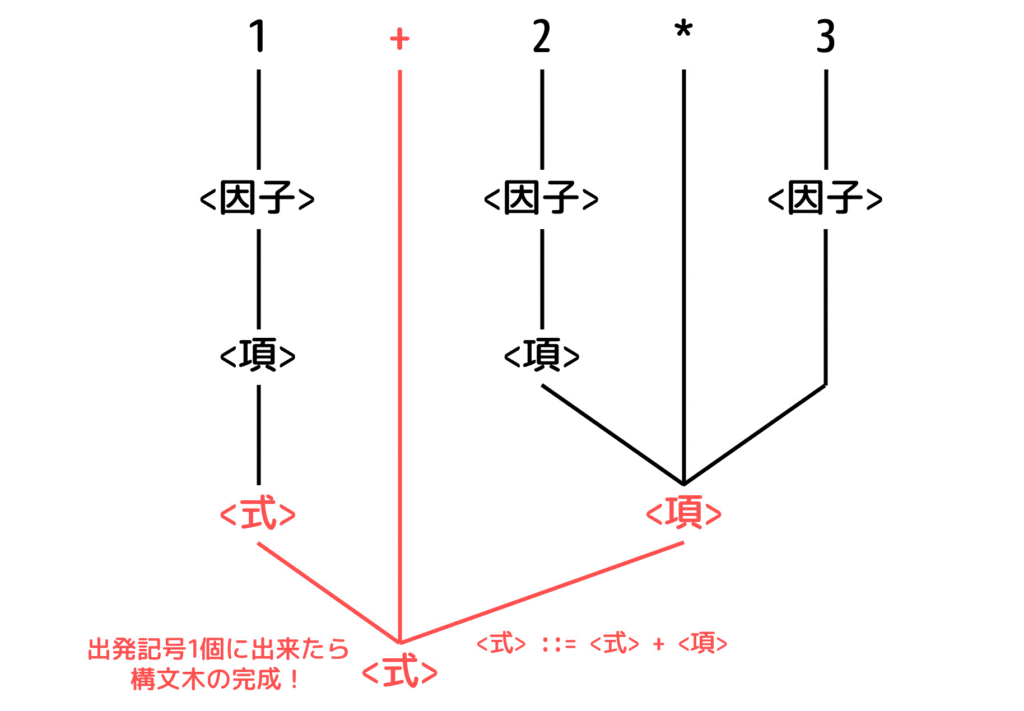
これで、1+2*3 を出発記号 <式> に書きかえることが出来たため、解析木の完成です!
[余談]
下の図ように、出発記号 <式> が一番上に来るように解析木を書いてもOKです。
(むしろこの書き方のほうが主流な気がします。)
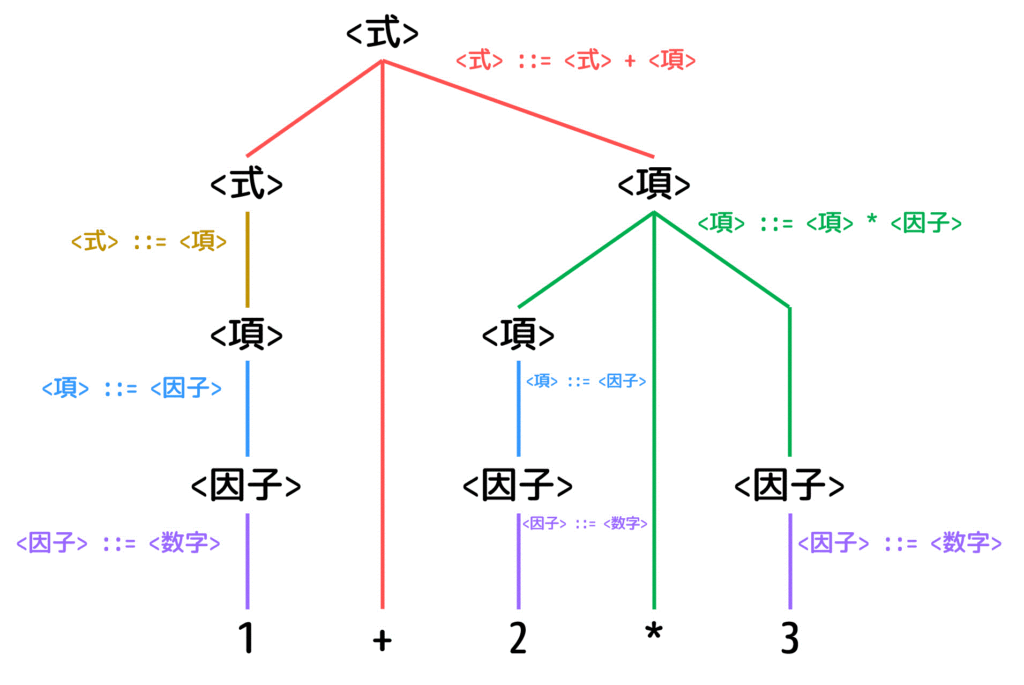
(ii) 構文木の書き方
(i)で求めた解析木から非終端記号(と今回はありませんが演算の順番を表す括弧 () )を取り除くことで構文木を求めることができます。
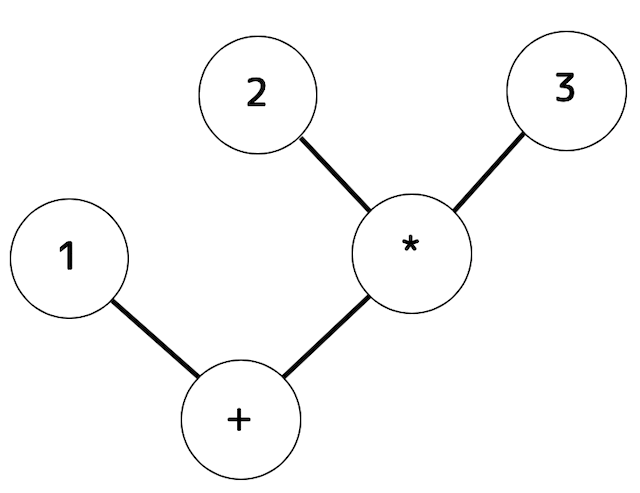
構文木の向きを変えて下のように表すとより木構造っぽくなりますね。
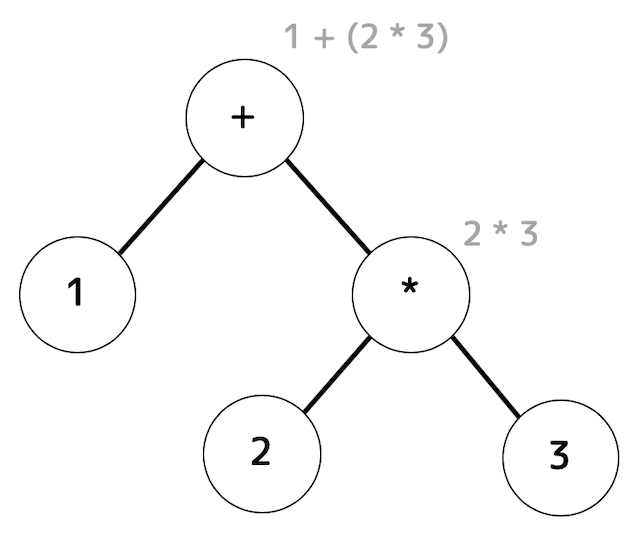
構文解析を行い、字句を木構造で表すことで、計算機上でも意味のある形になりますね。
ではここで練習を1問してみましょう。
練習5
先程と同じ規則、つまり
生成規則
<式> ::= <式> + <項> | <項> <項> ::= <項> * <因子> | <因子> <因子> ::= ( <式> ) | 数字
非終端記号 <式>, <項>, <因子>
終端記号 +, *, (, ), 数字(0以上)
出発記号 <式>
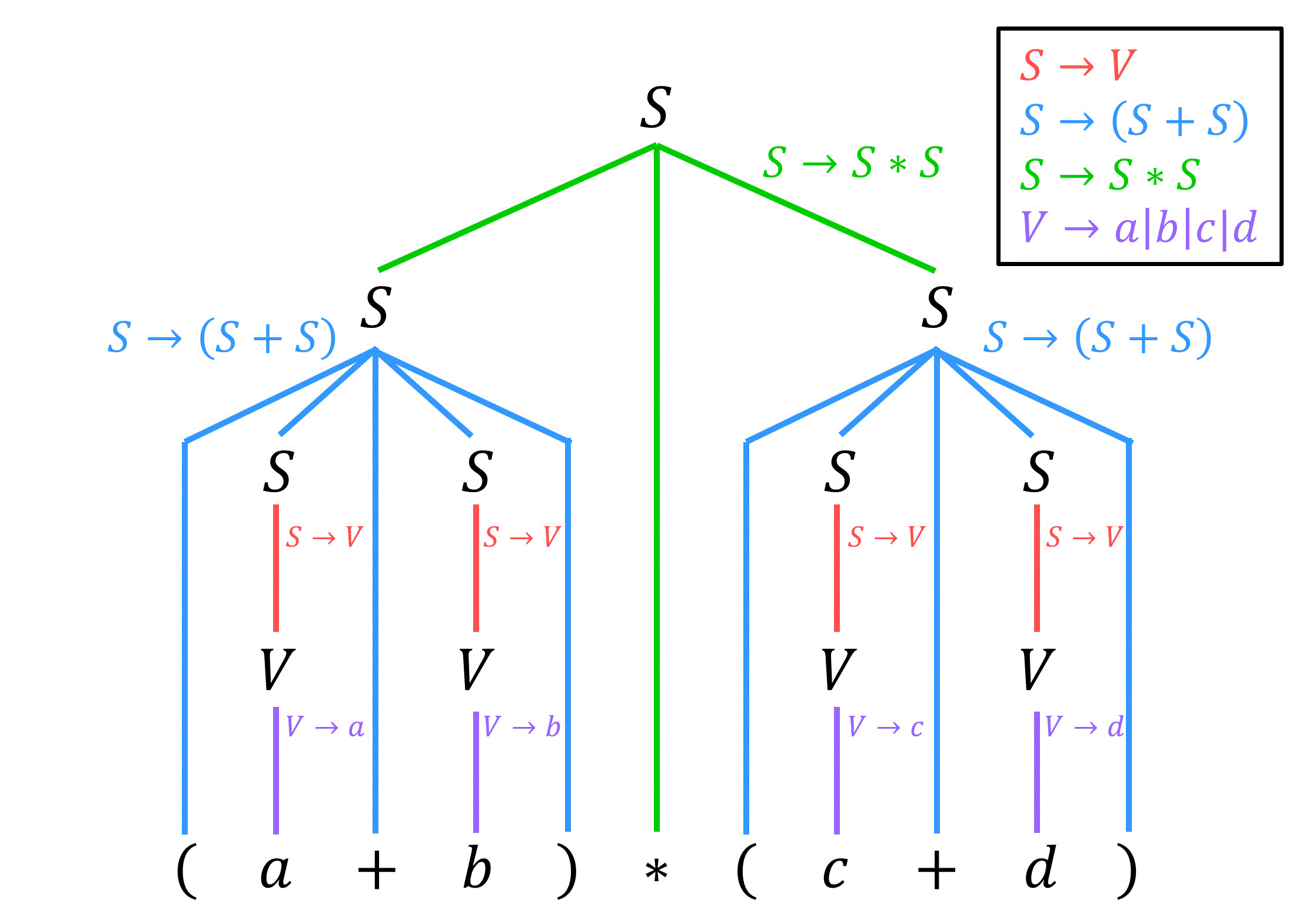
を用いて、(1+2)*3 の解析木、構文木を作成しなさい。
解答5
解析木は下のようになる。
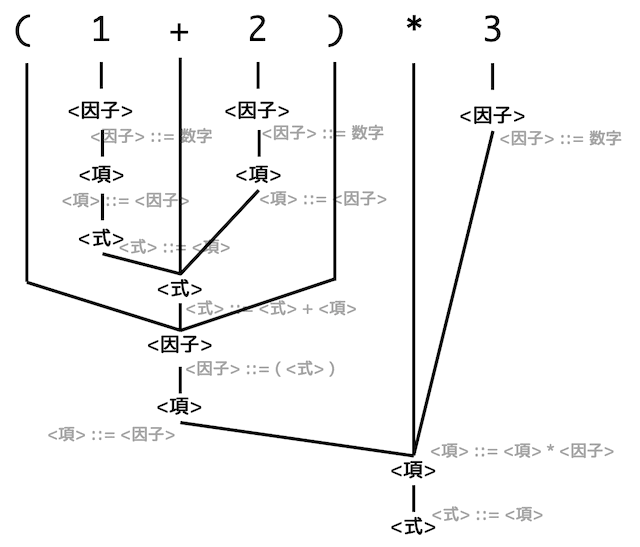
解析木から非終端記号や演算順番の括弧 () を除去すると下のような構文木ができる。
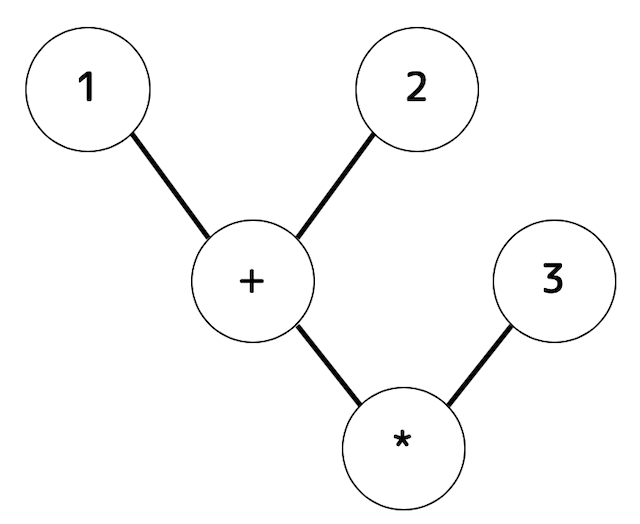
向きをちょっと変えてより木構造っぽくすると下のような構文木が完成する。
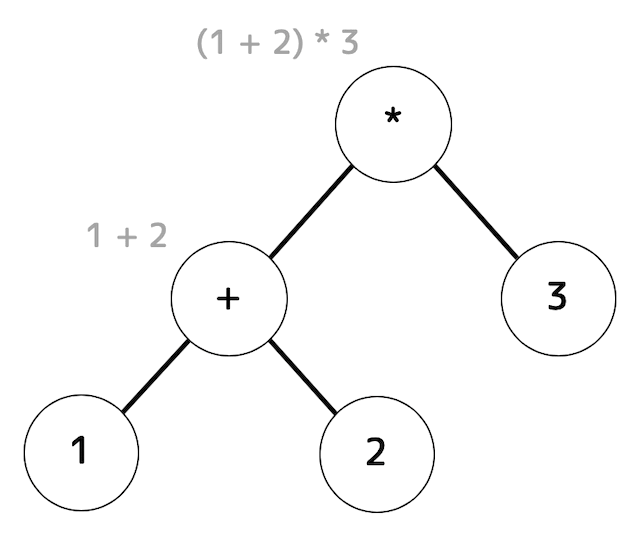
(4) 演算子の優先順位
先程、1+2*3 を構文解析し、下のような構文木を得ましたね。

括弧とか何もつけていないのにも関わらず、1+2*3 が 1+(2*3) (つまり掛け算を優先的に処理)になっていましたね。
現実世界でも皆さんは、足し算 + よりも掛け算 * のほうを先に計算しますよね。
このように、うまく生成規則を決めることで演算子の優先順位をコントロールすることができるのです!
余談ですが、論理演算の場合も、論理和(or のこと、記号だと || )よりも論理積(andのこと、記号だと &&)のほうが優先的に処理されます。
論理演算の場合も四則演算と同じように和よりも積が優先されるのです!
(5) 左結合・右結合
皆さんは 5 - 2 - 1 をどのように計算しますか?
おそらく全員が 5-2 を先に計算してから[
5-2-1 = (5-2) - 1 = 3 - 1 = 2
]と頭の中で計算しているはずです。
このように、左から順番に処理していく演算子は左結合と呼ばれます。
一方右側から順番に処理するような演算子、つまり右結合な演算子はあるのでしょうか?
実は皆さんあまり使いませんが、
a = b = c = 5;
の a = b = c = 5 のような代入処理は右結合、つまり右から順番に行われるのです。
括弧を用いて計算順序をわかりやすくすると、a = (b = (c = 5)) のように処理されます。
余裕があれば
#include <stdio.h>
int main(void){
int a,b,c;
(a = b) = c = 5; // わざと代入演算子の代入順序に逆らう
printf("(%d,%d,%d)",a,b,c);
return 0;
}
を実行してみてください。エラーが出ます。
さらに (a = b) = c = 5; を a = b = c = 5; にしてみてください。今度はちゃんと実行されるはずです。
左結合・右結合では当然構文木も変わってきます。
2つの結合の違いを下に表しました。
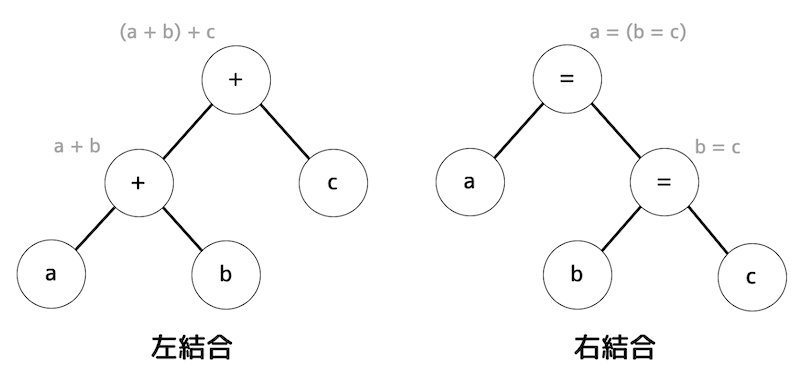
では、最後にもう1問練習してみましょう。
練習6
練習5と同じ生成規則、つまり
<式> ::= <式> + <項> | <項> <項> ::= <項> * <因子> | <因子> <因子> ::= ( <式> ) | 数字
非終端記号 <式>, <項>, <因子>
終端記号 +, *, (, ), 数字(0以上)
出発記号 <式>
がある。これについて次の問いに答えなさい。
(1) 1+2+3 の解析木、構文木を書きなさい。
(2) 1*2*3 の解析木、構文木を書きなさい。
(3) +, * が左結合であることを構文木から確認しなさい。
解答6
(1)
解析木
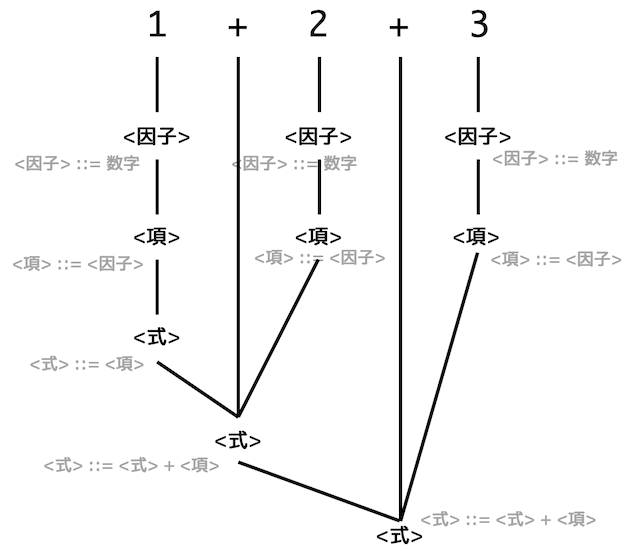
構文木
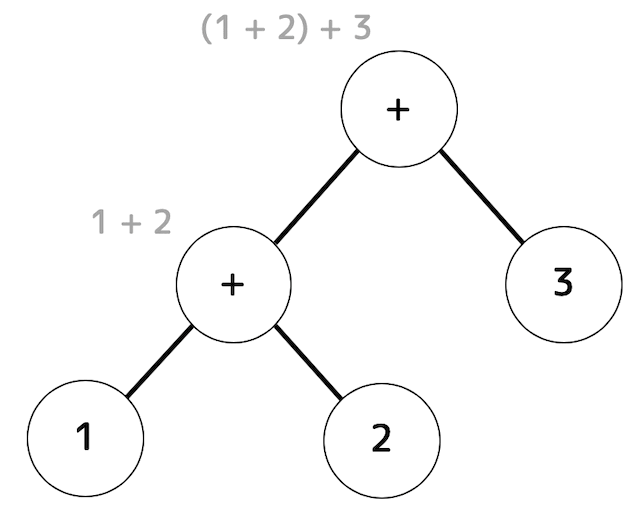
(2)
解析木
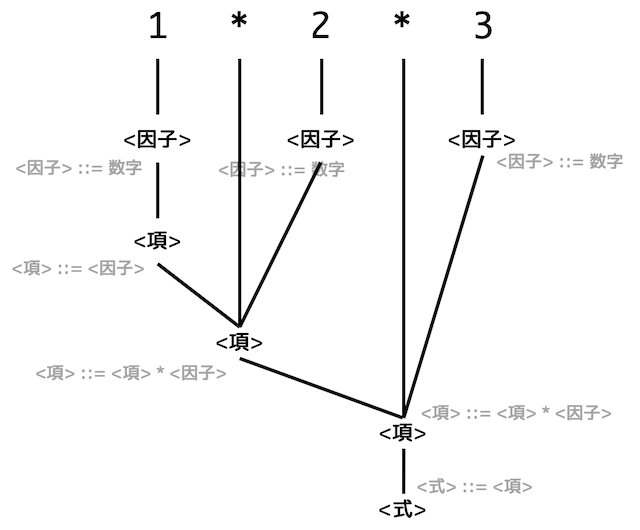
構文木
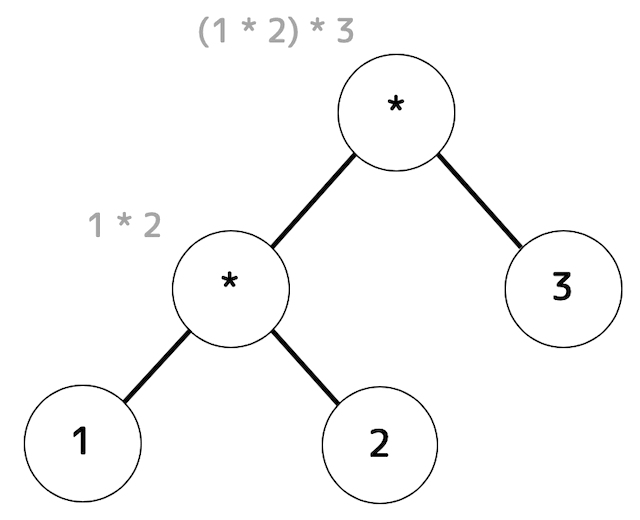
(3)
1+2+3 と 1*2*3 の2式はともに (1+2)+3), (1*2)*3 の計算順序になることが構文木からわかりますね。
なので、左結合(左から順番に計算している)ことが確認できますね。
お知らせ) 解析木・構文木の記事を追記しました!
もし解析木や構文木の具体的な書き方や、さらなる練習問題にチャレンジしたい人はこちらの記事をご覧ください!
4.意味解析
皆さんは、英文を(テストやら入試で)訳したあとに、意味的にこの文章おかしいなぁって思ったことありますよね。
1つ例を出してみます。
This train consists of 12 cars.
JR西日本 大阪駅で流れてくる放送より
この電車は、12両で構成されています。
この「英語→日本語訳」には、文法的にも単語の意味的にも誤っている部分はありません。しかし、駅で「12両構成されています」というアナウンスが流れてきたらびっくりしますよね。
コンパイラでも同じようにプログラムの文法的にはあってるんだけど、意味的におかしくないか??というのを確認します。この工程を意味解析と呼びます。
コンパイラの世界の「意味的におかしい」とは、具体的には下のようなコードを表します。
int a = 3.5; // 整数型に小数を代入しようとしている
char c1 = `a`, c2 = `b`, c3;
c3 = c1 * c2; // 文字列型の演算を行おうとしている
このような「意味的なおかしさ」は、構文解析では検知できないため、警告を出したり自動で適した型を変えたりします[2]適した型に変えるとは、int a = 3.5 は double a = 3.5 に、文字列型の演算はすべてint型に変えるような操作のことをいいます。。
5.コードの最適化・コード生成
あとはコードを生成するのみです!(英語→日本語の翻訳で言う「答えを書く部分」に相当。)
ですが、この際にコンパイラはソースコードの無駄な操作をカットするということを行います。この無駄な操作をカットするのが最適化です。
1つ例を出してみましょう。例えば、
int x = 20, y = 30;
x = 50;
x = y * 2;
のようなプログラムの場合、x の値は3行目の x = y * 2; で決まっていて、上2行の x の値の代入は全く意味がありませんよね。
この場合、上2行部分は「無駄な操作」なので、コンパイラは最適化の際に無駄な上2行をカットしちゃいます。
このコードの最適化が終わると、コンピュータ上で実行可能な機械語コードが生成されます!
と同時にコンパイルの役目もここで終わりです。
6.さいごに
今回はコンパイラの処理の流れを「字句解析」および「構文解析」を中心にまとめました。
これで計算機についてまた1つ新たな知識が増えましたね!
次回からはオペレーティングシステム(OS)関連のまとめに入りたいと思います。
関連広告・スポンサードリンク