こんにちは、ももやまです。
ほとんどの人がオートマトンという言葉を大学入学前に聞いたことはないと思います。大学などの授業で初めてオートマトンを習うとき、初めての概念で不安になってしまう人も多いと思います。
そこで今回は、オートマトンと言語理論ってどんなことを習うのかについてを簡単にですがダイジェスト方式でまとめていきたいと思います。
（この範囲もオートマトンで習うだろって意見もあるかもしれませんが今回は私の偏見で昔習ったなぁというのを入れています。）
ダイジェスト方式なので詳しい説明はあまりしていません。より詳しい説明がみたい人はリンクを貼っていると思うのでリンク先の記事をご覧ください。
１．基本用語説明
オートマトンについて説明する前にオートマトンで出てくる言語について説明しましょう。
(1) アルファベット 
皆さんはアルファベットと言ったら、「a,b,c,d…,z」をまず思い浮かべると思います。
しかし、オートマトンの世界ではアルファベットの意味は皆さんが普段使うアルファベットとは異なります。
オートマトンの世界上では、文字列上で使われる文字の集合を表し、 で表されます。
例えば、\[ \Sigma = \{ a,b \} \]とすれば、a,bだけの文字列 "aababaa", "baaab", "abb" などを表すことができます（要するにa,bしか使われない世界線の完成ってわけよ）。
(2) 文字列・語
上で少し説明しましたが、オートマトンにおける文字列・語はアルファベット 上の文字（記号）を0文字以上（空文字も含まれることに注意！）並べたものを表します。
具体例をいくつかあげてみましょう。
(a) のときの文字列の例
,
,
,
など
(b) のときの文字列の例
,
,
,
など
(c) のときの文字列の例
男女, 男男女男, 男女男男女男女, 女男女男女男男女 など
わかりやすく言うと、アルファベット は、その国で使われる文字*1を表し、文字列（語）はアルファベット（文字）を並べたもの、ということができます。
(3) 文字列（語）の特殊な記号
オートマトンでは、文字列（語）を表記するときに特別な表記をするものがあります。
(i) 空文字を表す記号 
文字列は、 を0文字以上並べたものを指します。ですが、0文字、つまり空文字のときは本当にそこに文字が並べられているかわからなくなってしまうことがあります。
そこで、空の文字列のことを と表します。
(ii) 連続する文字を表す記号
が1000文字続いているようなものをわざわざ
を1000個書いて表現すると日が暮れてしまいます。
なので、連続する文字は のように指数を使って表します。
例：,
,
(iii) 文字列の長さ
とある語 の長さ（文字の数）を
で表します。
例えば だと5文字なので長さ
は5、
だと4文字なので
、
だと
となります。
また、空文字 の長さは0 、つまり
となります。
(iv) 語（文字列）の連接
すでにある文字列 に文字列
を付け加え
とすることを文字列の連接と呼びます。
例えば に
を連接すると
になり、
に
を連接すると
となります。
語（文字列）の連接には順番があるので注意しましょう。
（ に
を連接すると
に、逆だと
になる）
(v) すべての文字列の集合 
上の文字を使って表現できるあらゆる文字列の集合を
と表します。全体集合みたいなもんです。
例えば、 だと、\[
\Sigma = \{a,b \} \\
\Sigma^* = \{ \varepsilon, \ a, \ b, \ aa, \ ab, \ bb, \cdots \}
\]のように の文字と
の文字を使ったあらゆる文字列の集合が
となります（空文字も含まれるところに注意）。
(vi) 空文字を除くすべての文字列の集合 
（あらゆる文字列の集合）から空文字
を取り除いたものを
と表します。言い換えて、
上の文字を使って表現できる1文字以上のあらゆる文字列の集合と思ってもOKです。
例えば、 だと、\[
\Sigma = \{a,b \} \\
\Sigma^+ = \{ \ a, \ b, \ aa, \ ab, \ bb, \cdots \}
\]のように の文字と
の文字を使ったあらゆる文字列の集合が
となります（ただし1文字以上））。
(4) 言語
言語 とは、文字列の集合を表します。例えば、\[
L = \{ aaa, aabba, abbaababa \}
\]のように表されます。
また、言語 は必ず
の部分集合となります。
(5) オートマトン
オートマトンとは、ある文字列が言語 が含まれるか含まれないかを判定するための機械のことを表します。文字列が言語
に含まれていれば*2文字列は受理(accept)、含まれていなければ*3文字列は却下(reject)されます。
オートマトンと言語理論でよく使う記号を下にまとめてみたので参考までにどうぞ。
２．有限オートマトン
各種用語の説明が終わったのでいよいよ有限オートマトンの説明に入りましょう。
有限オートマトンには決定性有限オートマトン(DFA)と非決定性有限オートマトン(NFA)の2つにわかれます。
決定性(DFA)・非決定性(NFA)を問わず有限オートマトンを表現する際には状態遷移図が用いられます。状態遷移図を用いることによって視覚的にわかりやすく受理/拒否を判定することができます。
また、後ほど説明しますが有限オートマトンが書けることとある言語 が正則（正規言語）であることは同値なので、有限オートマトンを書くことができればある言語
が正則であることを示すことができます。
(1) 決定性オートマトン(DFA)
決定性オートマトン(DFA)は、現在の状態と次の文字が決まれば次の状態が必ず1通りになる、つまり状態遷移図のたどり方が1本道となるようなオートマトンを表します。
決定性オートマトンの状態遷移図は下のように表せます。
（今回は ）
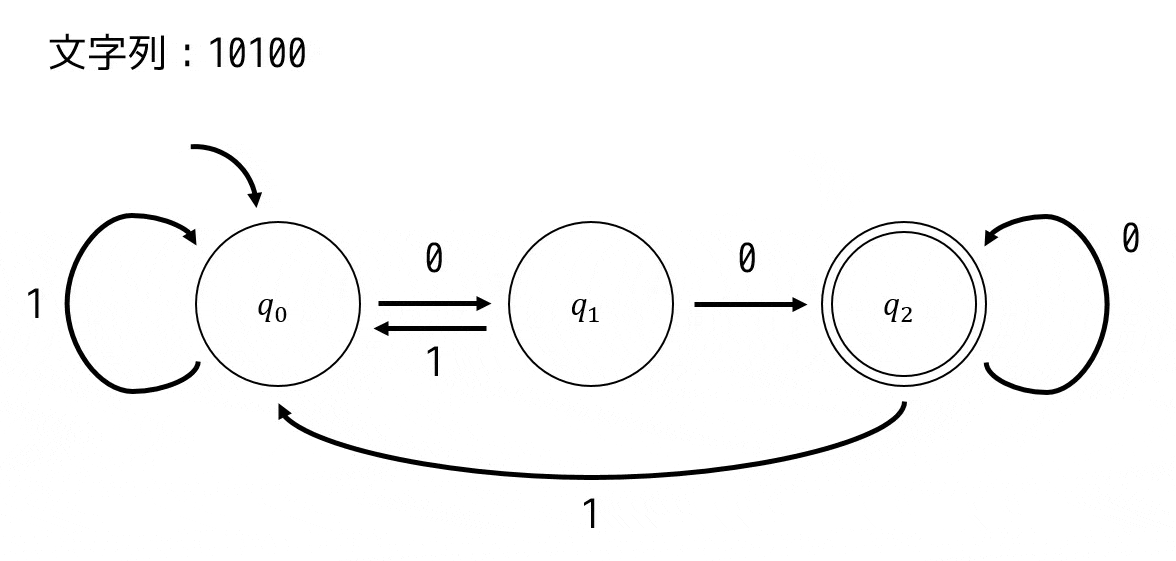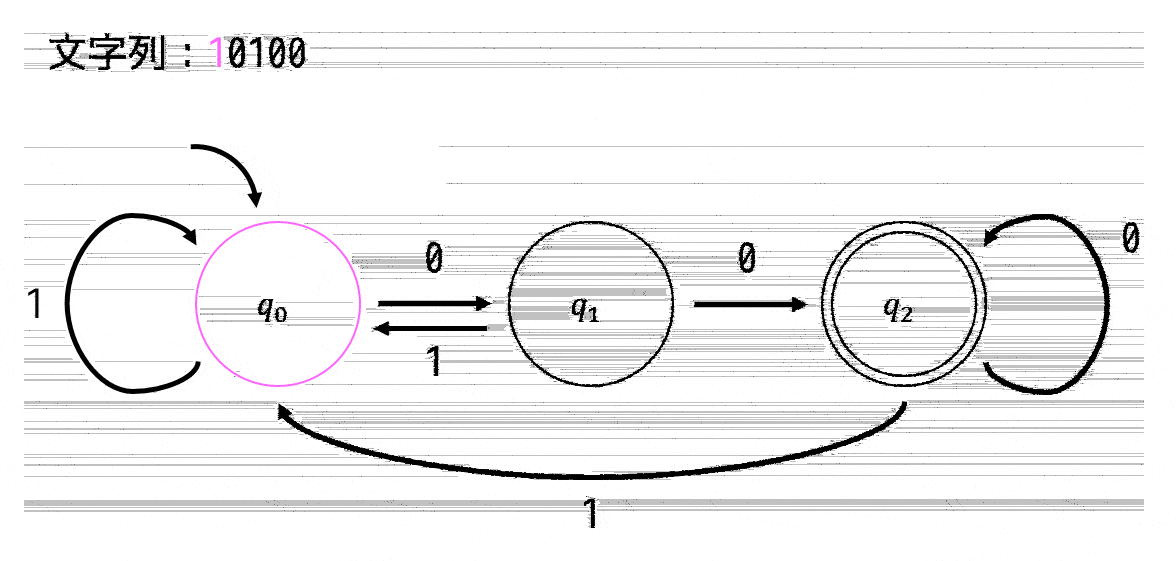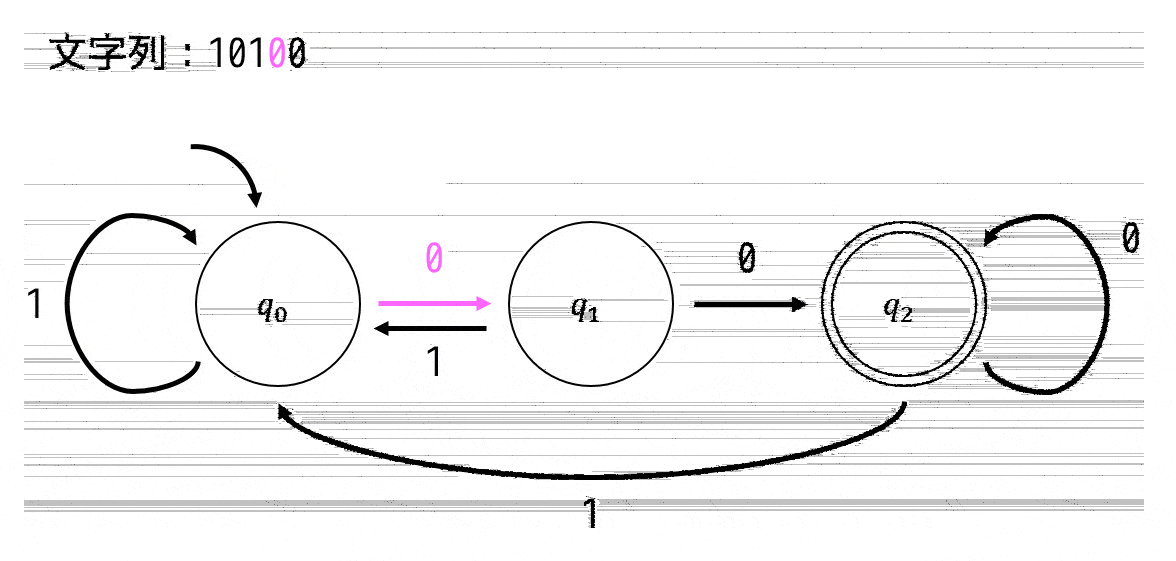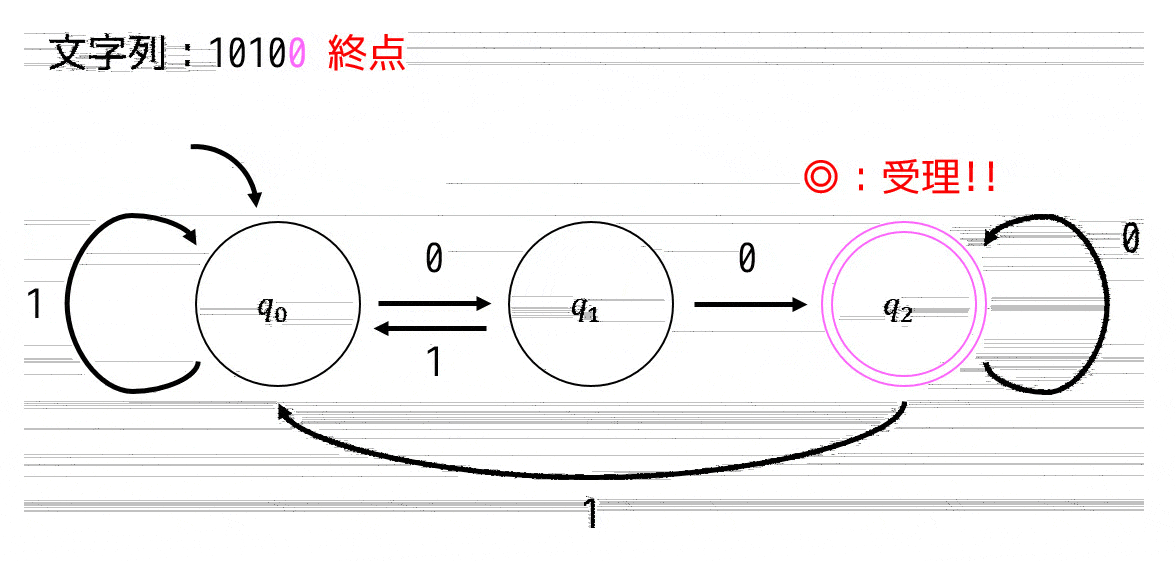
現在の状態と次の文字からの遷移先はそれぞれ1本しかないため、,
,
のどの要素からも
内の文字すべての行き先（つまり0による行き先と1による行き先）が1つずつ矢印で示されています。
また、状態遷移の様子を図ではなく、表で示すこともできます。
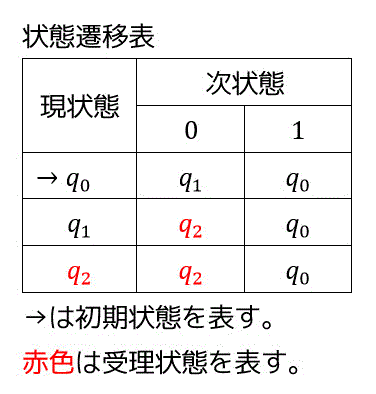
表を見ると現状態と次の文字からの遷移先がそれぞれ1つずつしかないことがわかりますね。
決定性オートマトンについての記事はこちら↓
(2) 非決定性オートマトン(NFA)
非決定性オートマトンは、現在の文字と次の文字の遷移先が決定性オートマトンのように1つとは限らず、2つ以上あることや全くないこともありえるオートマトンです（つまりたどり方が1本道とは限らない）。
初期状態も決定性オートマトンでは必ず1つでしたが、非決定性オートマトンでは2つ以上許容されるので、図のように2つに分離して1つの非決定性オートマトンと考えることもできます。
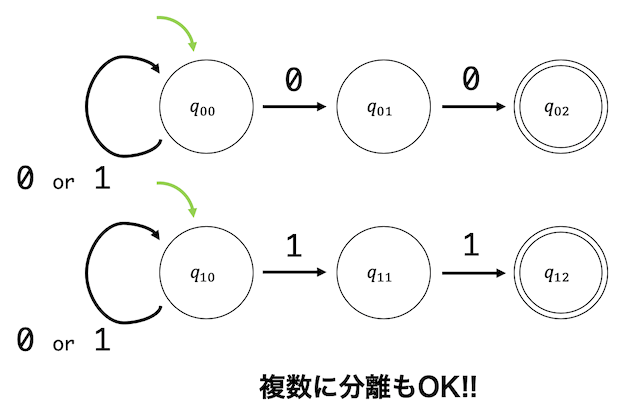
すべての非決定性オートマトンは状態遷移表を書くことによって決定性オートマトンに変換することができます。言い換えると、非決定性でもいいから言語 を表現するようなオートマトンが書けることで言語
が正則であることを示すことができます。
非決定性オートマトン(NFA)についての記事はこちら↓
有限オートマトンの記述は、特定の言語だけが受理できるように（言い換えると特定の言語以外は受理されないように）パズルを組み立てて行く過程に似ています。
パズルを組み立てる練習をすることで「あ、このパターンだ！」ってわかるようになってくるので、ぜひ練習しましょう！
３．言語の演算
有限オートマトンで記述することができる言語 ,
,
を用いて以下のような演算を行うことができます。
(1) 補集合演算
(2) 和集合演算
(3) 積集合演算
(4) 差集合演算
(5) 連接演算
(6) 閉包演算
これらの演算は、演算元の言語がすべて正則であれば、演算先の言語もすべて正則となり、有限オートマトンで表すことができます。
言語の演算についてはこちらから↓（前編・後編わけてあります）
前編（補集合・和集合・積集合・差集合演算）
後編（補集合・和集合・積集合・差集合演算）
４．決定性オートマトンの最小化
決定性オートマトンは下のような余分な状態を探し出し、1つにまとめることで上のような最小状態の決定性オートマトンを作り出すことができます。
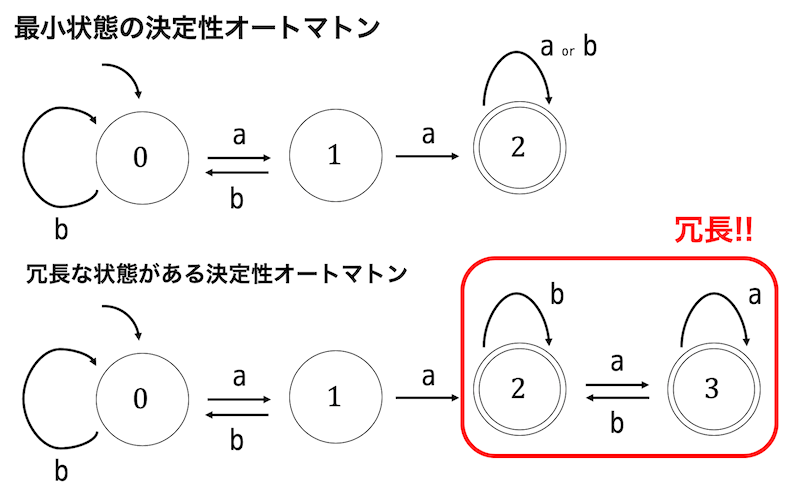
特に3で説明した言語の演算後（とくに連接）は、冗長な状態が増えてしまいます。そこで決定性オートマトンを最小化するようなアルゴリズムを適用することで最小化し、冗長な状態をなくすことができます。
オートマトンの最小化についての記事はこちら↓
５．言語が正則・正則でない判定・証明
ある言語が正則（正規言語）であるかどうかの判定は非常に重要です。
正則であることを示すためには、有限オートマトンを書くことができればOKでしたね。
しかし、正則でないことを示すのは大変ですよね。有限オートマトンが書けないことを示すのもきついし……
そこで使われるのがMyhill-Nerodeの定理です。この定理と背理法を応用させることにより、とある言語が有限オートマトンで表せないこと、つまり正則でないことを示すことができるのです。
Myhill-Nerodeの定理を正則でない言語の証明法はこちらからどうぞ↓
また、ある言語が正則かどうかは練習を行うことである程度見極めることができるようになります。
正則言語の判定練習はこちらから↓（今までの総復習となっております）
６．文脈自由文法
有限オートマトンで記述することができる言語には限りがありますよね。
そこで使われるのが文脈自由文法です。文脈自由文法を用いることでより多くの言語を表現、カバーすることができます。
文脈自由文法とは、下のような4つの状態から構成されるような文法を表します。
特に生成規則 が特殊なものについては、正則文法、チョムスキー標準形、グライバッハ標準形などの名前がつけられています。
文脈自由文法についてはこちらからどうぞ↓
７．正規表現
ある文字列が言語 が含まれるか含まれないかを判定するために正規表現を使う方法もあります。正規表現とは、\[
(01)^* 11 (0|1)^+
\]のように、 や
や
などの特別な記号を使って言語
に含まれるような文字列を書く方法です。
また、とある言語 が正則（正規言語）であれば、必ず正規表現で表すことができます。つまり、
- ある言語
が正則
- 言語
- 言語
- 言語
この4つはすべて同値と言えます。
正規表現についてはこちらの記事をご覧ください！
８．さいごに
今回はオートマトンで習うような概念をダイジェスト方式でお送りしました。
より詳しい説明がみたい方はリンク先の記事をご覧ください。