スポンサードリンク
離散数学・グラフ理論って高校数学(特に微積)とはちょっと離れた不思議な数学系科目ですよね。
なので、独特で不思議な(数学の)世界観で少し迷子になってしまうかもしれません。
そこで、この私が、離散数学のグラフ理論分野を試験前日でも3時間あれば総復習ができるように10題の練習問題を作成しました!
前編では基本的な事項を確認するためのフォーム型の問題を3問用意しました!
- 90分間で問題を解く。さらにフォーム編の答えを回答フォームに入力する。
- フォーム編は、答えを送信後、間違った箇所を確認し、解説を見てどこで間違えたのか(理解ができていないのか)を確認する。
- 記述編は、解説を見ながら自己採点を行い、どこで間違えた(理解ができていないのか)を確認する。
- 間違えた箇所を参考書や記事などで練習する。
- 時間があれば、合っている箇所も確認する。(青色と赤色の枠部分)
- 寝る。
時間がある人はじっくり、時間がない人は素早くこの記事にてグラフ理論の復習をしましょう!
目次
スポンサードリンク
グラフの基本についての復習記事
問題1、問題2、問題3ではグラフ理論の基本的な用語などを確認するための復習問題です。もし、この基本的な用語を忘れてしまったなぁって思った人は、こちらの3つの記事を読んで先に復習しましょう。
スポンサードリンク
問題1. 正誤問題
次の(1)~(8)それぞれにある[X], [Y]の文章について、その正誤の組み合わせとして正しいものを下の選択肢1~4から1つ選びなさい。
(1) 次数
[Y] あるグラフの最大次数と最小次数が等しいならば、それは完全グラフである。
- [X] 正 [Y] 正
- [X] 正 [Y] 誤
- [X] 誤 [Y] 正
- [X] 誤 [Y] 誤
解答: 4 (1点)
[X] 次数の合計は必ず偶数となるため、誤り。 → 握手定理。(辺が0本のときの次数の合計は0、また、1つ辺を足すと必ず次数の合計は2増えるため、奇数になることがない。) [Y] 最大次数と最小次数が等しいグラフは、どの点における次数も等しいグラフ。そのようなグラフは完全グラフではなく、正則グラフである。よって誤り。
(2) 同型
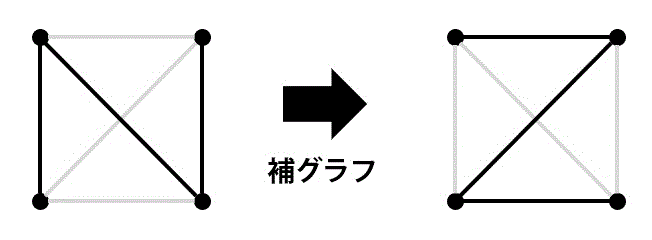
[Y] あるグラフとその補グラフが同型になることがある。
- [X] 正 [Y] 正
- [X] 正 [Y] 誤
- [X] 誤 [Y] 正
- [X] 誤 [Y] 誤
解答: 4 (1点)
[X] 例えば、下の2つは点の数、辺の数がともに等しい。ただし、同型ではない。よって、誤り[1]仮に[X]が正しい場合、それぞれの頂点数ごとに互いに同型でない木が1種類しか存在しないことになる。。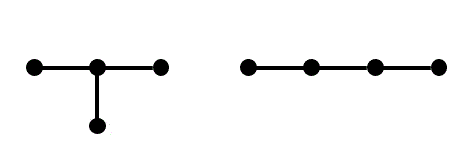

(3) 完全グラフ・オイラーグラフ・ハミルトングラフ
[Y] オイラーグラフでかつハミルトングラフであるようなグラフは存在しない。
- [X] 正 [Y] 正
- [X] 正 [Y] 誤
- [X] 誤 [Y] 正
- [X] 誤 [Y] 誤
解答: 2 (1点)
[X] 完全グラフ \( K_3 \) は点の数と辺の数が等しい。よって正しい。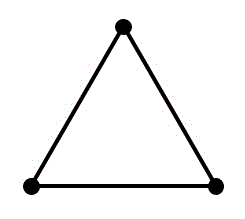
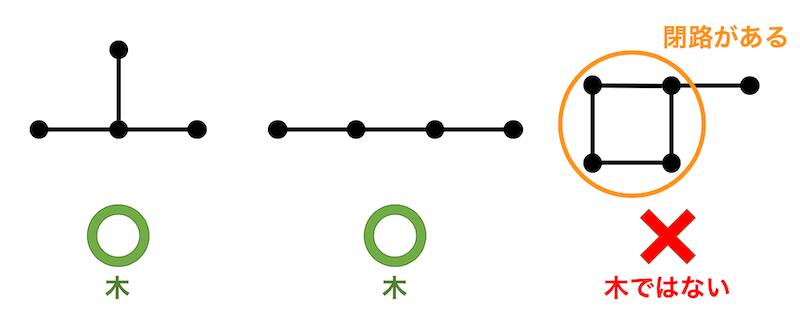
(4) 木1
[Y] 木は必ず2部グラフとなる。
- [X] 正 [Y] 正
- [X] 正 [Y] 誤
- [X] 誤 [Y] 正
- [X] 誤 [Y] 誤
解答: 3 (1点)
[X] 木の場合、必ず (辺数) = (点数) - 1 が成立する。よって点数と辺数が等しい木は存在しないため誤り。 [Y] 2部グラフは、長さが奇数の閉路を持たないグラフのことである。ここで木は閉路が存在しないため、必ず2部グラフとなる。よって正しい。- グラフが閉路を持たず、連結である。(そのため、必ず2部グラフとなり、彩色数も2となる)
- グラフの位数(点数)が \( n \) のとき、辺数が \( n - 1 \) となる。
- グラフの辺を1本でも消すと連結ではなくなる。
- グラフのどの2点間の道は1通りしかない(たどり方は必ず1通り)
(5) 木2
[Y] 根付き木のある頂点 \( u \) の親を \( v \) とすると、\( v \) は \( u \) の先祖であると言える。
- [X] 正 [Y] 正
- [X] 正 [Y] 誤
- [X] 誤 [Y] 正
- [X] 誤 [Y] 誤
解答: 1 (1点)
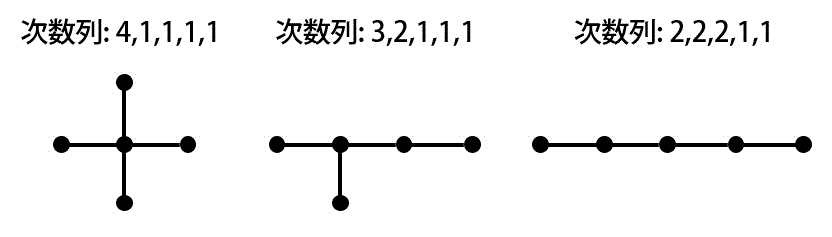
[X] 点数が5ということは、辺数が4なので、次数の合計が8となる。そのため、点数が5の木の次数列の組み合わせとして、次の3パターンが考えられる。
- 4,1,1,1,1
- 3,2,1,1,1
- 2,2,2,1,1
それぞれの次数列ごとに(互いに同型でない)グラフは1種類しかないため、正しい。
あるノードを先祖としたとき、先祖のノードからより深い方向(子の方向)にたどっていったときにあるノードすべてを子孫と呼ぶ。
言い換えると、子孫のノードからより浅い方向(親の方向)にたどっていったときにあるノードすべてが先祖となる。
木についての復習はこちらから!
(6) 橋・閉路・回路
[Y] 閉路は回路の部分集合である。(閉路は回路の一種である。)
- [X] 正 [Y] 正
- [X] 正 [Y] 誤
- [X] 誤 [Y] 正
- [X] 誤 [Y] 誤
そのため、スタート点に戻るためには必ず橋を1往復(つまり同じ辺を2回通ることを)しなければならない。よってオイラーグラフは必ず橋を持たない。
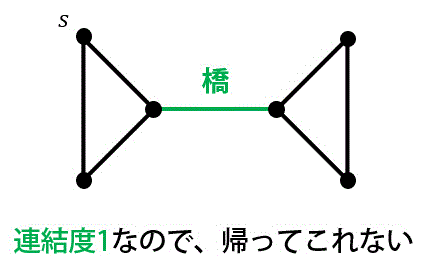
回路:同じ辺を2回以上通らずたどりはじめの点に戻るようにたどったもの
閉路:同じ点を2回以上通らずたどりはじめの点に戻るようにたどったもの
※ 閉路は必ず回路となる。
(7) マッチング
[Y] 完全グラフは完全マッチングを持つ。
- [X] 正 [Y] 正
- [X] 正 [Y] 誤
- [X] 誤 [Y] 正
- [X] 誤 [Y] 誤
正解: 2
[X] 正しい。すべての点の次数が1となる最大マッチング(全部の点に対して、1つの辺がつながっている)を完全マッチングと呼ぶ。 [Y] 誤り。頂点数が奇数のときは完全マッチングを持たない。(イメージ:例えば5人で2人組を作りなさいって言われたら、余る人が出ますよね)
極大マッチング:マッチングの中でこれ以上辺(ペア)を追加できないもの
最大マッチング:あるグラフに追加できる上限数分の辺(ペア)を追加したもの
(最大マッチングであるものは必ず極大マッチングであるが、極大マッチングだからといって最大マッチングであるとは限らない*5。)
完全マッチング:どの点にも辺がつながっている(ペアになっている)マッチング
(完全マッチングであれば必ず最大マッチングとなる)
マッチングについてさらに復習したい人はこちら。
(8) 彩色数・彩色指数
[Y] 2部グラフの彩色指数は必ず2である。
- [X] 正 [Y] 正
- [X] 正 [Y] 誤
- [X] 誤 [Y] 正
- [X] 誤 [Y] 誤
解答: 2 (1点)
[X] 完全グラフはどの点ともつながっているグラフなので、点の数だけ色を分ける必要がある。そのため、彩色数は点の数と等しくなる。 [Y] 2部グラフでは、彩色指数ではなく、彩色数が2となる。※ 彩色指数は、隣の辺が同じ色にならないようにグラフの辺を塗り分けるために必要な色数のこと。
彩色数:隣の点が同じ色にならないように塗り分ける場合に必要な色の数
彩色指数:隣の辺が同じ色にならないように塗り分ける場合に必要な色の数
彩色数: \( n \)
彩色指数: \( n \) が奇数のときは \( n \)、\( n \) が偶数のときは \( n - 1 \)
彩色に関する問題についてさらに復習したい人はこちら。
スポンサードリンク
問題2. グラフの基礎1
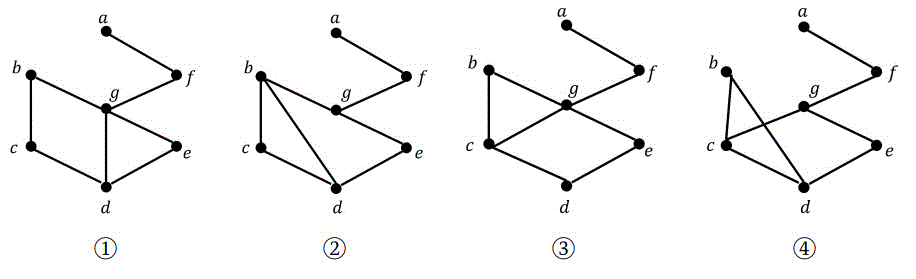
つぎの点集合 \( V \)、辺集合 \( E \) で表されるグラフがある。\[
V = \{ a, b, c, d, e, f, g \}
\]\[
E = \{ (a,f), (b,c), (b,g), (c,d), (d,e), (d,g), (e,g), (f,g)
\]次の(1)~(5)の問いに答えなさい。(配点 10)
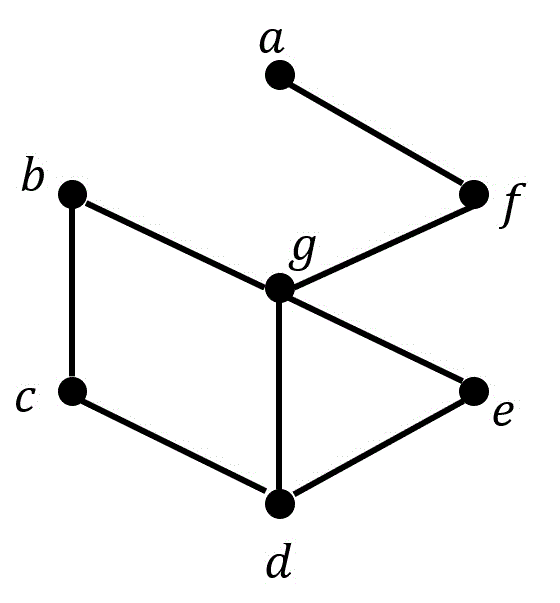
(1) グラフ \( G \) を描画したものはどれか。番号で答えなさい。
(2) グラフ \( G \) の頂点数と辺数を答えなさい。
(3) グラフ \( G \) の最大次数と最小次数を答えなさい。
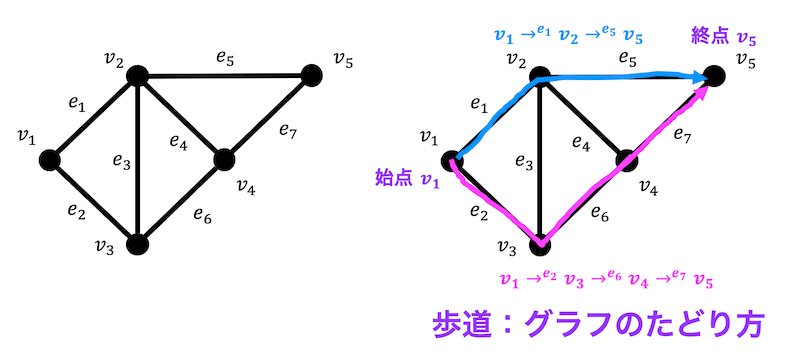
(4) 始点が点 \( c \)、終点が点 \( f \) までの歩道のうち、長さが最も大きくなる小道を求め、その長さを答えなさい。
(5) グラフ \( G \) のカット点、および橋をすべて答えなさい。答えは下の選択肢の番号で答えること。
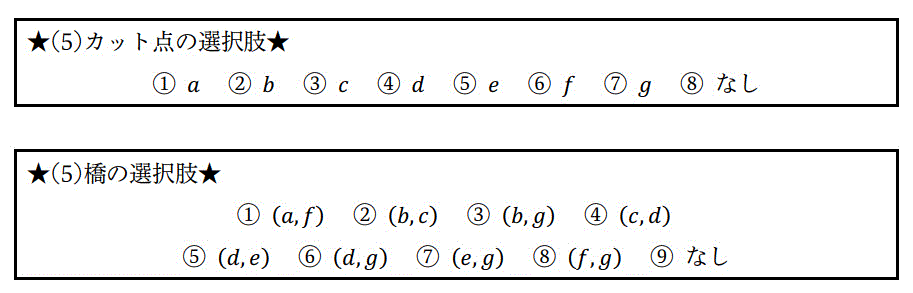
(1) 解答: 1(2点)
この問題を間違えると、連鎖的に他の問題も間違えてしまうので、慎重に解きましょう。
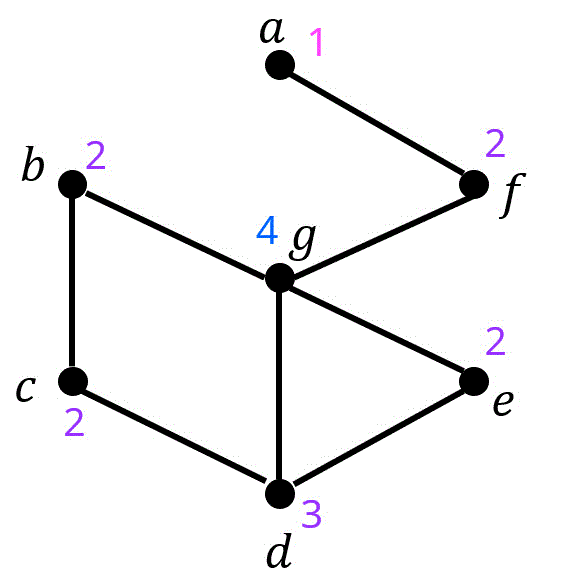
(2) 頂点数: 7、辺数: 8(1点×2)
(1)で書いたグラフの頂点数、辺数を書いても、集合 \( V \), \( E \) の要素数を数えてもOK。
(3) 最大次数: 4、最小次数: 1(1点×2)
各点の次数は、下の通り。
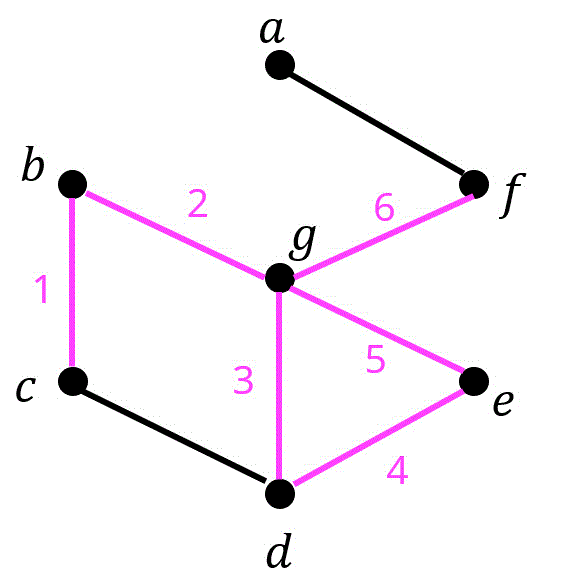
(4) 解答: 6
\( c \to b \to g \to d \to e \to g \to f \) とたどるのが最長。
(5) カット点: 6, 7
削除すると連結成分の数が増えるような点がカット点。
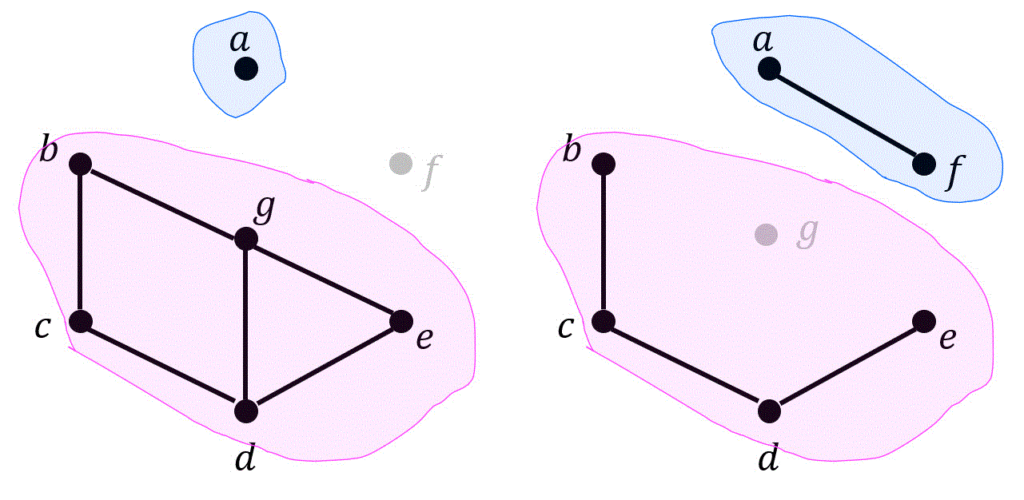
橋: 1, 8
削除すると連結成分の数が増えるような辺が橋。
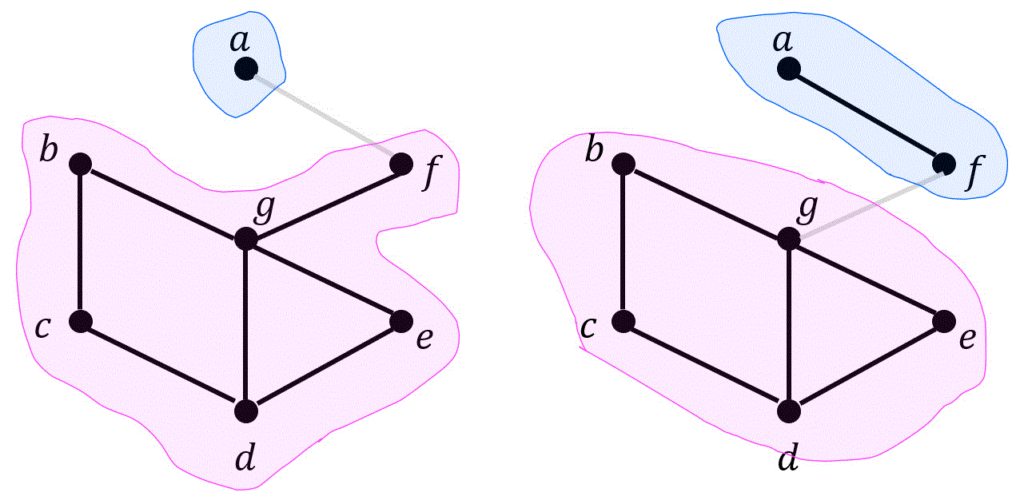
カット点:削除すると連結成分の数が増えるような点のこと。
橋:削除すると連結成分の数が増えるような辺のこと。
グラフの連結性や、カット点、橋についてさらに復習したい人はこちらの記事をご覧ください!
問題3. グラフの基礎2
次の①~⑧のグラフについて、(1)~(6)にあてはまるグラフをすべて選びなさい。ただし、当てはまるグラフがない場合は⑨と答えること。(配点 12)
(1) 隣接行列\[
A = \left( \begin{array}{ccc} 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{array} \right)
\]で表されるグラフと同型なグラフ
(2) 完全グラフ
(3) 3次の正則グラフ
(4) ハミルトングラフではないグラフ
(5) 互いに同型な1組のグラフ
(6) 彩色数が2のグラフ
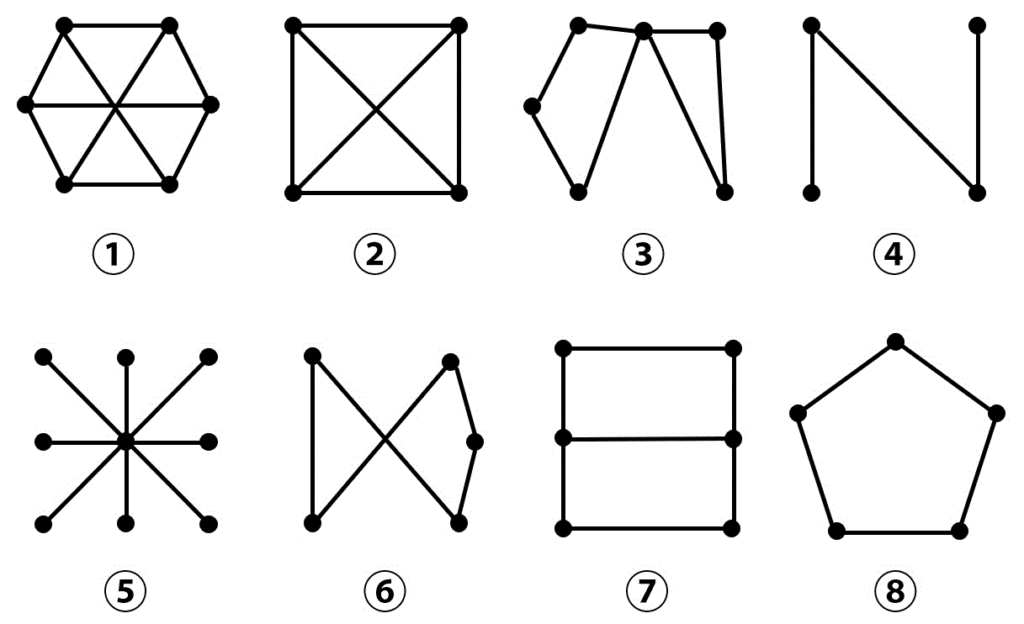
(1) 4
(2) 2
(3) 1, 2
(4) 3, 4, 5
(5) 5, 8
(6) 1, 4, 5, 7
(1) 落ち着いて、隣接行列をグラフにしましょう。
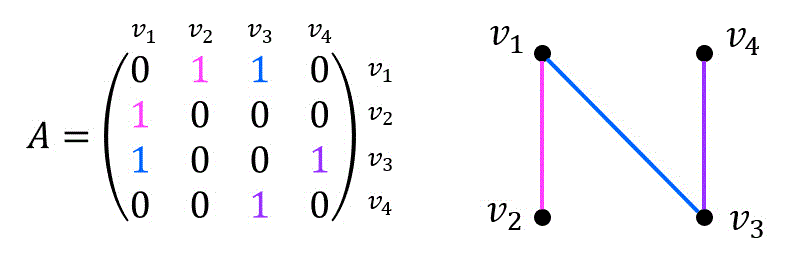
(2), (3) まずは、各点の次数を書きましょう。
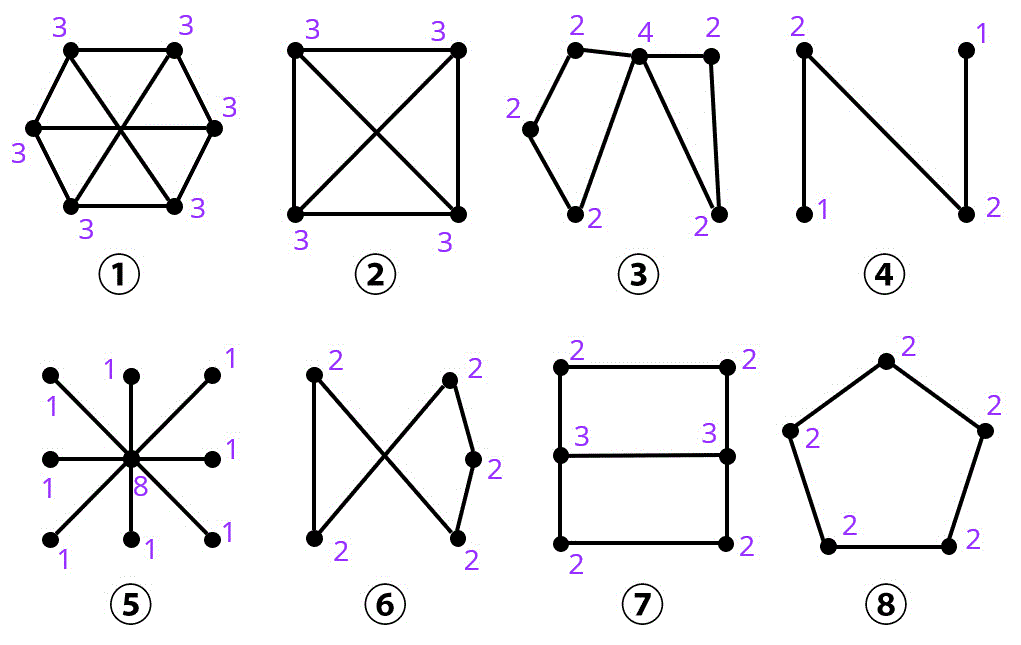
(2) 完全グラフ → 全部の点の次数が 「(頂点数) - 1」となっているようなグラフを選べばOK。(2だけ)
(3) 3次の正則グラフ → 全部の点の次数が3となっているグラフを選びましょう。(1, 2が答え)
(4) ハミルトングラフでないグラフを確認すればよいので、すべての点を一筆書きでたどることができ、かつスタート地点に戻れないようなグラフを選べばOK。(3, 4, 5が答え)
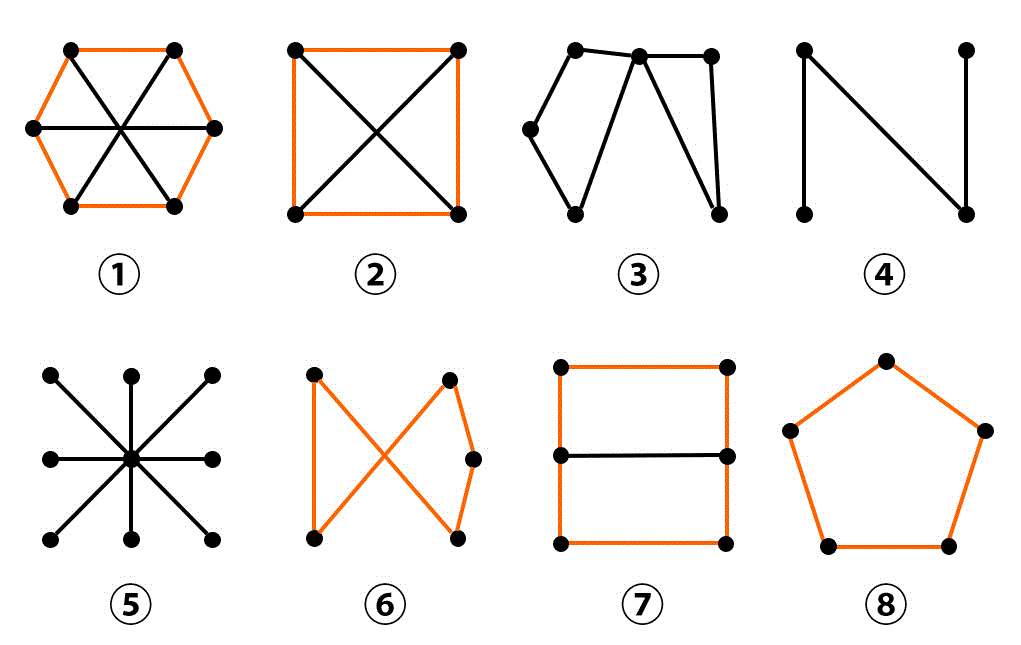
(5) 次数列の組み合わせを書いて明らかに同型でない組み合わせを消去するのがおすすめ。すると、
- 3,3,3,3,3,3
- 3,3,3,3
- 4,2,2,2,2,2
- 2,2,1,1
- 8,1,1,1,1,1,1,1,1
- 2,2,2,2,2
- 3,3,2,2,2,2
- 2,2,2,2,2
となるので、6と8以外の候補が残らない。よって答えは6-8。
(6) 彩色数が2となるグラフは、2部グラフです。また、2部グラフは長さが奇数の閉路を持たないグラフですね。なので、長さが奇数の閉路を持たないグラフを探せばOK。
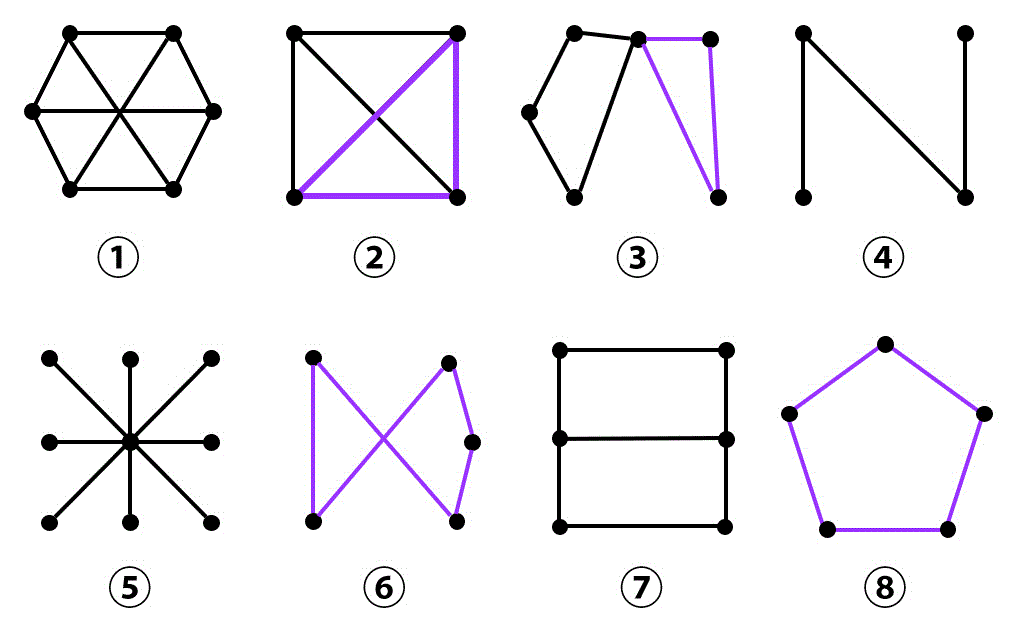
すると、2, 3, 6, 8は長さが奇数の閉路を持つ。よって残った1, 4, 5, 7が答え。
※ Welch-Powellの点彩色アルゴリズムで判定してもいいですが、時間がかかるのでおすすめしません。
2部グラフの彩色数は必ず2である。
注釈
| ↑1 | 仮に[X]が正しい場合、それぞれの頂点数ごとに互いに同型でない木が1種類しか存在しないことになる。 |
|---|