うさぎでもわかる微分方程式　Part14　ラプラス変換のいろは

こんにちは、ももやまです。

今回は、ラプラス変換を用いた微分方程式について説明する前に、ラプラス変換とはどのようなものなのかについて説明していきたいと思います。

[確認]

今回の記事では、

• 部分積分（省略公式による計算含む）
• 広義積分
• ロピタルの定理
• 部分分数分解
• 複素数計算の基礎

の知識を使います。

リンクをクリックすると、該当する知識に関する記事に飛ぶので、自信がない人は復習することをおすすめします。

前回の微分方程式の記事はこちら！

（微分演算子に関する記事です。ラプラス変換とはあまり関係ないです）

うさぎでもわかる微分方程式　Part13　微分演算子を用いた特殊解の求め方

2020.4.27

こんにちは、ももやまです。 今回は、非同次の定数係数線形微分方程式の4つの解き方 未定係数法 定数変化法 微分演算子法 ラプラス変換を用いる方法 の中でも演算子を使った方法について...

スポンサードリンク

１．ラプラス変換とは

いきなりですが、ラプラス変換の定義から説明します。

定義域が \( 0 \leqq t \lt \infty \) のある関数 \( f(t) \)（時間関数と呼ばれることが多いです）に対し、\[\begin{align*}
F(s) & = \int^{\infty}_{0} f(t) e^{-st} \ dt
\\ & = \lim_{R \to \infty} \int^{R}_{0} f(t) e^{-st} \ dt
\end{align*}\]の広義積分の形で表される \( s \) の関数 \( F(s) \) のことを、\( f(t) \) のラプラス変換と呼び、\(  \mathcal{L}[f(t)] \) と表記します。

（変数 \( s \) は複素数範囲で考えるのが基本ですが、実数範囲として考えている参考書もあります。今回は実数範囲として考えたあと、複素数範囲でも考えていきましょう*1。）

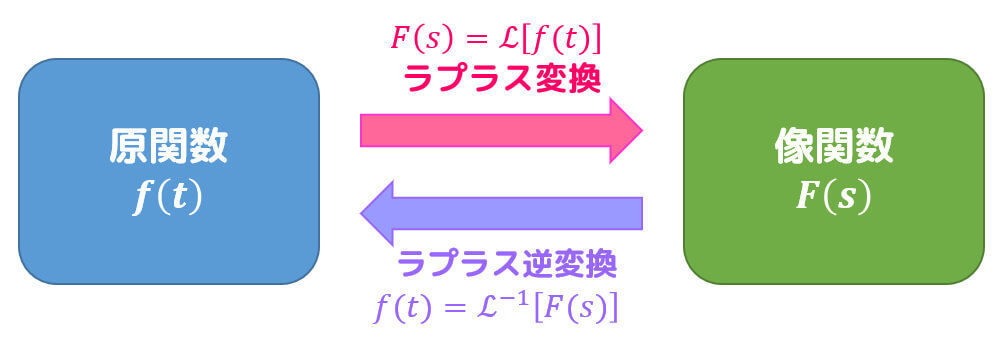
また、ラプラス変換を行う元の関数 \( f(t) \) のことを原関数、ラプラス変換後の関数 \( F(s) \) のことを像関数と呼び、1対1に対応しています。

ラプラス変換が\[
\int^{\infty}_{0} e^{-st} \ dt
\]の形で定義されている理由としては、関数 \( e^{-t} \) が下の図のように \( t \) を大きくすればするほど0に収束する関数となっているからです。

また、積分範囲を実数全体 \( - \infty \lt t \lt \infty \) にしてしまうと \( e^{-t} \) が \( t \to - \infty \) のときに発散してしまうため、積分範囲を0を含む正の実数に限定して定義されています。

実際に積分計算をして収束することを確かめてみましょう。

\( s \) が実数であると仮定すると、\[\begin{align*}
\int^{\infty}_{0} e^{-st} \ dt & = \lim_{R \to \infty} \int^{R}_{0} e^{-st} \ dt
\\ & = \lim_{R \to \infty} \left[ - \frac{1}{s} e^{-st} \right]^{R}_{0}
\\ & = \lim_{R \to \infty}  - \frac{1}{s} \left( e^{-Rs} - e^0 \right)
\\ & = \lim_{R \to \infty}  \frac{1}{s} \left( 1 - \frac{1}{e^{Rs}} \right)
\\ & = \frac{1}{s} \ \ \ \left( s \gt 0 \  のとき \ \lim_{R \to \infty} \frac{1}{ e^{Rs} } = 0 \right)
\end{align*}\]と、\( s \gt 0 \) であれば確かに収束しますね。

（\( s = 0 \) であれば分母が0に、\( s \lt 0 \) であれば無限大に発散）

また、\( s \) が複素数 \( s = a + bi \) であれば、\[\begin{align*}
\lim_{R \to \infty} \frac{1}{ e^{Rs} } & = \lim_{R \to \infty} \frac{1}{ e^{R (a+bi)} }
\\ & = \lim_{R \to \infty} \frac{1}{ e^{aR} e^{ibR} }
\\ & = 0 \ \ \left( a \gt 0 \  のとき \ \lim_{R \to \infty} \frac{1}{ e^{aR} e^{ibR} } = 0 \right)
\end{align*}\]と計算できるので、\( \mathrm{Re} (s) \gt 0 \) であれば収束することがわかりますね。

（なお、これ以降出てくるすべてのラプラス変換の定義域は \( s \) の部分を \( \mathrm{Re} (s) \gt 0 \) に変えれば複素数範囲でも成立します。）

ということで、まずはラプラス変換を実際に定義に基づいて計算してみましょう。

例題1

つぎの(1), (2)で表される関数 \( f(t) \) のラプラス変換 \(  \mathcal{L}[f(t)] \) を求めなさい。（\( s \) の収束領域も求めること）

(1) \(  \mathcal{L}[t] \)

(2) \(  \mathcal{L}[t^2] \)

解説1

(1)

\[\begin{align*}
\mathcal{L}[t] & = \int^{\infty}_{0} t e^{-st} \ dt
\\ & = \lim_{R \to \infty} \int^{R}_{0} t e^{-st} \ dt
\\ & = \lim_{R \to \infty} \left[ - \frac{1}{s} t e^{-st} - \frac{1}{s^2} e^{-st} \right]^{R}_{0}
\\ & = \lim_{R \to \infty} \left( - \frac{1}{s} \frac{R}{e^{Rs}} - \frac{1}{s^2} \frac{1}{e^{Rs} }+ \frac{1}{s^2} \right)
\\ & = \frac{1}{s^2} - \frac{1}{s^2}\lim_{R \to \infty} \frac{R}{ e^{Rs} } - \frac{1}{s^2}\lim_{R \to \infty} \frac{1}{ e^{Rs} }
\\ & = \frac{1}{s^2} - \frac{1}{s^2} \lim_{R \to \infty} \frac{Rs+1}{ e^{Rs} }
\end{align*}\]となる。

（部分積分の際に、部分積分の省略公式をもちいています。）

ここで、ロピタルの定理を使うことで、\( s \gt 0 \) のとき\[\begin{align*}
\lim_{R \to \infty} \frac{Rs+1}{ e^{Rs} } & = \lim_{R \to \infty} \frac{s}{ Re^{Rs} }
\\ & = 0
\end{align*}\]となるので、\[\begin{align*}
\mathcal{L}[t] & = \int^{\infty}_{0} t e^{-st} \ dt
\\ & = \frac{1}{s^2} - \frac{1}{s^2} \lim_{R \to \infty} \frac{Rs+1}{ e^{Rs} }
\\ & = \frac{1}{s^2}
\end{align*}\]と求めることができる。

（収束領域：\( s \gt 0 \)）

なお、\( s \) が複素数であれば、\( s = a+bi \) として、\[\begin{align*}
\lim_{R \to \infty} \frac{s}{ Re^{Rs} } & = \lim_{R \to \infty} \frac{s}{ Re^{(a+bi)s} }
\\ & = \lim_{R \to \infty} \frac{s}{ Re^{as} e^{bis} }
\end{align*}\]となるので、\( a \gt 0 \) のとき、つまり \( \mathrm{Re} (s) \gt 0 \) が収束範囲となる。

(2)

同じように計算していきましょう。

\[\begin{align*}
\mathcal{L}[t^2] & = \int^{\infty}_{0} t^2 e^{-st} \ dt
\\ & = \lim_{R \to \infty} \int^{R}_{0} t^2 e^{-st} \ dt
\\ & = \lim_{R \to \infty} \left[ - \frac{1}{s} t^2 e^{-st} - \frac{2}{s^2} t e^{-st} - \frac{2}{s^3} e^{-st} \right]^{R}_{0}
\\ & = \lim_{R \to \infty} \left( - \frac{1}{s} \frac{R^2}{e^{Rs}} - \frac{2}{s^2} \frac{R}{e^{Rs} } - \frac{2}{s^3} \frac{1}{e^{Rs} } + \frac{2}{s^3} \right)
\\ & = \frac{2}{s^3} - \frac{1}{s^3} \lim_{R \to \infty} \frac{R^2 - 2R - 2}{ e^{Rs} }
\end{align*}\]となる。

ここで、ロピタルの定理を使うことで、\( s \gt 0 \) のとき、\[\begin{align*}
\lim_{R \to \infty} \frac{R^2 - 2R - 2}{ e^{Rs} } & = \lim_{R \to \infty} \frac{2R}{ Re^{Rs} }
\\ & = \lim_{R \to \infty} \frac{2}{e^{Rs} }
\\ & = 0
\end{align*}\]となるので、\[\begin{align*}
\mathcal{L}[t^2] & = \int^{\infty}_{0} t^2 e^{-st} \ dt
\\ & = \frac{2}{s^3} - \frac{1}{s^3} \lim_{R \to \infty} \frac{R^2 - 2R - 2}{ e^{Rs} }
\\ & = \frac{2}{s^3}
\end{align*}\]と求めることができる。

（収束領域：\( s \gt 0 \)）

なお、\( s \) が複素数の場合の収束領域は(1)と同じように計算することで収束領域は \( \mathrm{Re} (s) \gt 0 \) となる。

収束領域については、実際にラプラス変換（逆変換も）を計算する際に気にする必要は基本的にはありません。（問題文で聞かれたら別ですが…）

スポンサードリンク

２．ラプラス逆変換

ラプラス変換を行う前の関数である原関数 \( f(t) \) とラプラス変換を行った後の関数である像関数 \( F(x) \) は1対1に対応しているのでしたね。

1対1に対応していることを利用することで、ラプラス変換後の関数 \( F(s) \) からラプラス変換前の関数 \( f(t) \) に戻すラプラス逆変換 \( \mathcal{L}^{-1} \) が定義されます。

先程、\( f(t) = 1 \) をラプラス変換した結果が \( F(s) = \frac{1}{s} \) であることを確認しましたね。

ラプラス変換前・変換後の関数は1対1の関係にあるため、\( F(s) = \frac{1}{s} \) をラプラス逆変換した結果は\[\begin{align*}
f(t) & = \mathcal{L}^{-1} \left[ \frac{1}{s} \right]
\\ & = 1
\end{align*}\]と求めることができます。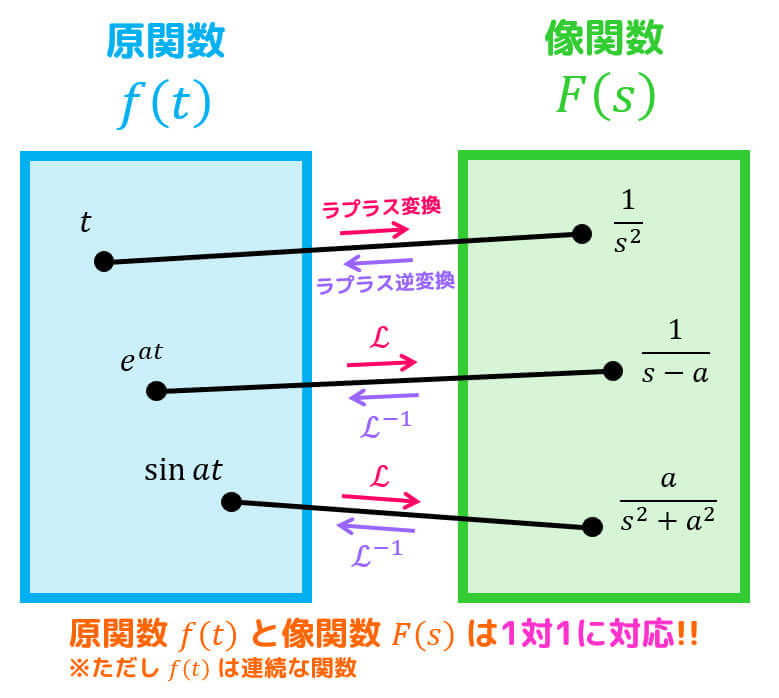

余談：ラプラス逆変換を逆ラプラス変換と呼ぶ人もいます。

スポンサードリンク

３．重要なラプラス変換の4つの法則

つぎに、ラプラス変換でとても重要な4つの法則について説明していきたいと思います。

重要度が高い順に紹介したいと思います。

その1　線形の法則

ラプラス変換を行う上で、最も重要な法則となります。

積分計算と同じように定数倍・足し算（引き算）を分離できるという法則です！

ラプラス変換の線形性を用いることで、例えば \( f(t) = 2t + 3 \) のラプラス変換を、\[
\mathcal{L}[2t+3] = 2 \mathcal{L}[t] + 3 \mathcal{L}[1]
\]のように計算することができます。

線形性の証明は積分式の簡単な変形のみで行えます。

2つまとめた形が成り立つことを示しちゃいましょう。\[\begin{align*}
\mathcal{L}[a \ f(t)+b \ g(t)] & = \int^{\infty}_{0} \left( a \ f(t) + b \ g(t) \right) e^{-st} \ dt
\\ & = \int^{\infty}_{0} a \ f(t) e^{-st} \ dt + \int^{\infty}_{0} b \ g(t) e^{-st} \ dt
\\ & = a \int^{\infty}_{0}  f(t) e^{-st} \ dt + b \int^{\infty}_{0} g(t) e^{-st} \ dt
\\ & = a \int^{\infty}_{0}  f(t) e^{-st} \ dt + b \int^{\infty}_{0} g(t) e^{-st} \ dt
\\ & = a \mathcal{L}[f(t)] + b \mathcal{L}[g(t)]
\end{align*}\]よって、線形性が成り立つことが示されました。

逆変換でも線形の法則は成り立つ！

また、ラプラス逆変換であっても、\[
\mathcal{L}^{-1}[a \ f(t)+b \ g(t)] = a \mathcal{L}^{-1}[f(t)] + b \mathcal{L}^{-1}[g(t)]
\]と、定数倍・足し算を分離することができます。

その2　微分の法則

ラプラス変換を用いた微分方程式を解く際に必ず使う法則です。

2階微分 \( f''(t) \) まで証明してみましょう。

\[\begin{align*}
\mathcal{L}[f'(t)] & = \int^{\infty}_{0} f'(t) e^{-st} \ dt
\\ & = \lim_{R \to \infty} \int^{R}_{0} f'(t) e^{-st} \ dt
\\ & = \lim_{R \to \infty} \left( \left[ f(t) e^{-st} \right]^{R}_{0} - \int^{R}_{0} s f(t) e^{-st} \ dt \right)
\\ & = \lim_{R \to \infty} \left( f(R) e^{-sR} - f(0) e^0 \right) + s \int^{\infty}_{0} f(t) e^{-st} \ dt
\\ & = - f(0) + s F(s)
\\ & = sF(s) - f(0)
\end{align*}\]となり、1回微分のときが示されました。

2階微分の証明は、1回微分のときの法則を2回使うことで簡単に示せます。

\[\begin{align*}
\mathcal{L}[f''(t)] & = \mathcal{L}[\left( f'(t) \right)']
\\ & = s \mathcal{L}[f'(t)] - f'(0)
\\ & = s \left( sF(s) - f(0) \right) - f'(0)
\\ & = s^2 F(s) - s \ f(0) - f'(0)
\end{align*}\]と変形することで示すことができます。

なお、3階微分以降の証明であっても、2階微分のときと同様に証明することができます。

その3　移動の法則

\( e^{at} f(t) \) の形をしたラプラス変換を求める際に使う法則です。

ラプラス変換の元が \( e^{at} \) 倍されたら、結果の \( s \) の部分が \( s-a \) になると覚えましょう！

なお、証明するのはすごく簡単です。

\[\begin{align*}
\mathcal{L}[e^{at} f(t)] & = \int^{\infty}_{0} e^{at} f(t) e^{-st} \ dt
\\ & = \int^{\infty}_{0} f(t) e^{-(s-a)t} \ dt
\\ & = F(s-a)
\end{align*}\]と簡単に示せます。

ラプラス変換を用いて微分方程式を解く場合、

• その1：線形の法則
• その2：微分の法則
• その3：移動の法則

の3つが抑えられていればOKです！

その4　相似の法則

ラプラス変換を用いる際にはあまり用いませんが、相似法則についても確認しましょう。

なお、ラプラス逆変換の場合でも使えます。

証明は簡単です。

ラプラス変換の場合の式のみ示してみましょう。

\( at = u \) とおく。すると、\( a \ dt = du \), \( dt = \frac{1}{a} du \) となる。

すると、\[\begin{align*}
\mathcal{L}[f(at)] & = \int^{\infty}_{0} f(at) e^{-st} \ dt
\\ & = \int^{\infty}_{0} f(u) e^{- \frac{s}{a} u } \cdot \frac{1}{a} \ du
\\ & = \frac{1}{a} \int^{\infty}_{0} f(u) e^{- \frac{s}{a} u } \ du
\\ & = \frac{1}{a} F \left( \frac{s}{a} \right)
\end{align*}\]と示せます。

どっちかというと相似の法則というよりは置換の法則に見えますね。

４．代表的なラプラス変換の導出

ここからは、よく出てくる関数のラプラス変換を定義\[\begin{align*}
\mathcal{L}[f(t)] & = \int^{\infty}_{0} f(t) e^{-st} \ dt
\end{align*}\]に従って求めていきたいと思います。

（収束領域も確認していきましょう。）

(1) べき関数 t^n のラプラス変換

第1章で \( t \), \( t^2 \) のラプラスを計算しました。

では、\( t^n \) のラプラス変換はどうなるでしょうか。

実際に誘導に沿って計算してみましょう。

例題2

0以上の整数 \( n \) に対し、ラプラス変換 \(  \mathcal{L}[t^n] \) を求めたい。

つぎの(1)～(3)の問いに答えなさい。

(1) \( n = 0 \) のときのラプラス変換、つまり \(  \mathcal{L}[1] \) を求めなさい。
(2) \(  \mathcal{L}[t^n] \) を \(  \mathcal{L}[t^{n-1}] \) を用いて表しなさい。
(3) \(  \mathcal{L}[t^n] \) を求めなさい。

解説2

(1)

\[\begin{align*}
\mathcal{L}[1] & =
\int^{\infty}_{0} e^{-st} \ dt \\ & = \lim_{R \to \infty} \int^{R}_{0} e^{-st} \ dt
\\ & = \lim_{R \to \infty} \left[ - \frac{1}{s} e^{-st} \right]^{R}_{0}
\\ & = \lim_{R \to \infty}  - \frac{1}{s} \left( e^{-Rs} - 1 \right)
\\ & = \frac{1}{s} - \frac{1}{s} \lim_{R \to \infty} \frac{1}{ e^{Rs} }
\\ & = \frac{1}{s}
\end{align*}\]と計算できる。（先程も計算しましたね…）

（ただし、収束範囲は \( s \) が実数なら \( s \gt 0 \)、複素数なら \( \mathrm{Re} (s) \gt 0 \) が条件）

(2)

\[\begin{align*}
\mathcal{L}[t^n] & =
\int^{\infty}_{0} t^n e^{-st} \ dt \\ & = \lim_{R \to \infty} \int^{R}_{0} t^n e^{-st} \ dt
\\ & = \lim_{R \to \infty} \left[ - \frac{1}{s} t^n e^{-st} \right]^{R}_{0} - \frac{1}{s} \int^{R}_{0} - t^{n-1} e^{-st}
\\ & = \lim_{R \to \infty} - \frac{1}{s} \frac{R^n}{e^{Rs} } - \lim_{R \to \infty} \frac{n}{s} \int^{R}_{0} - t^{n-1} e^{-st}
\\ & = 0 + \lim_{R \to \infty} \frac{n}{s} \int^{R}_{0} - t^{n-1} e^{-st}
\\ & = \frac{n}{s} \int^{\infty}_{0} - t^{n-1} e^{-st}
\\ & = \frac{n}{s} \mathcal{L}[t^{n-1}]
\end{align*}\]と計算できる。

(3)

(1), (2)より\[\begin{align*}
\mathcal{L}[t^n] & = \frac{n}{s} \mathcal{L}[t^{n-1}]
\\ & = \frac{n}{s} \times \frac{n-1}{s} \mathcal{L}[t^{n-2}]
\\ & = \frac{n}{s} \times \frac{n-1}{s} \times \frac{n-2}{s} \mathcal{L}[t^{n-3}]
\\ & = \frac{n}{s} \times \frac{n-1}{s} \times \frac{n-2}{s} \times \cdots \times \frac{2}{s} \mathcal{L}[t^1]
\\ & = \frac{n}{s} \times \frac{n-1}{s} \times \frac{n-2}{s} \times \cdots \times \frac{2}{s} \times \frac{1}{s} \mathcal{L}[t^0]
\\ & = \frac{n}{s} \times \frac{n-1}{s} \times \frac{n-2}{s} \times \cdots \times \frac{2}{s} \times \frac{1}{s} \times \frac{1}{s}
\\ & = \frac{n!}{ s^{n+1} }
\end{align*}\]と計算することができる。

(2) 指数関数 e^at のラプラス変換

つぎに指数関数 \( e^{at} \) のラプラス変換 \(  \mathcal{L}[e^{at}] \) を求めてみましょう。（\( a \) は実数としましょう）

例題2

関数 \( f(t) = e^{at} \) のラプラス変換 \(  \mathcal{L}[e^{at}] \) を求めなさい。（\( s \) の収束領域も求めること）

解説2

\[\begin{align*}
\mathcal{L}[e^{at}] & =
\int^{\infty}_{0} e^{at} e^{-st} \ dt \\ & = \lim_{R \to \infty} \int^{R}_{0} e^{(a-s)t} \ dt
\\ & = \lim_{R \to \infty} \left[ \frac{1}{a-s} e^{(a-s)t} \right]^{R}_{0}
\\ & = \lim_{R \to \infty} \frac{1}{a-s} e^{(a-s)R} - \frac{1}{a-s} \cdot e^0
\\ & = \frac{1}{s-a} + \lim_{R \to \infty} \frac{1}{a-s} e^{(a-s)R}
\\ & = \frac{1}{s-a} \ \ \left( s \gt a \  のとき \ \lim_{R \to \infty} \frac{1}{a-s} e^{(a-s)R} = 0 \right)
\end{align*}\]と計算できる。

（収束領域：\( s \) が実数なら \( s \gt a \)、複素数なら \( \mathrm{Re} (s) \gt a \)）

(3) 三角関数 sin(at), cos(at) のラプラス変換

つぎに三角関数のラプラス変換\[
\mathcal{L}[\sin at], \ \ \ \mathcal{L}[\cos at]
\]を求めてみましょう。

（\( a \) は実数と仮定）

\( e^{\textcolor{red}{ia}t} \) のラプラス変換を実部と虚部にわけて求めると、\[\begin{align*}
\mathcal{L}[e^{\textcolor{red}{ia}t}] & = \frac{1}{ s- \textcolor{red}{ia} }
\\ & = \frac{s+ai}{(s-ia)(s+ia)}
\\ & = \frac{s+ai}{s^2 + a^2}
\\ & = \textcolor{deepskyblue}{ \frac{s}{s^2 + a^2} } + i \textcolor{magenta}{ \frac{a}{s^2 + a^2} }
\end{align*} \]となりますね。

ここで、オイラーの公式\[
e^{iat} = \cos at + i \sin at
\]を使うことで、\[\begin{align*}
\mathcal{L}[e^{\textcolor{red}{ia}t}] & = \textcolor{deepskyblue}{\mathcal{L}[\cos at]} + i \textcolor{magenta}{\mathcal{L}[\sin at]}
\\ & = \textcolor{deepskyblue}{ \frac{s}{s^2 + a^2} } + i \textcolor{magenta}{ \frac{a}{s^2 + a^2} }
\end{align*}\]と変形できるので、うまく実部と虚部に分離され、\[
\textcolor{magenta}{ \mathcal{L}[\sin at] = \frac{a}{s^2 + a^2} } \\
\textcolor{deepskyblue}{ \mathcal{L}[\cos at] = \frac{s}{s^2 + a^2} }
\]を導出することができます。

(4) 双曲線関数 sinh(at), cosh(at) のラプラス変換

最後に双曲線関数のラプラス変換\[
\mathcal{L}[\sinh at], \ \ \ \mathcal{L}[\cosh at]
\]を求めてみましょう。

※双曲線関数とは\[
\sinh at = \frac{ e^{at} - e^{-at} }{2} \\
\cosh at = \frac{ e^{at} + e^{-at} }{2}
\]のことを表します。

\( e^{\textcolor{red}{a}t} \) のラプラス変換は\[\begin{align*}
\mathcal{L}[e^{\textcolor{red}{a}t}] & = \frac{1}{s-\textcolor{red}{a}}
\end{align*}\]なので、\[\begin{align*}
\mathcal{L}[\sinh at] & = \mathcal{L} \left[\frac{ e^{at} - e^{-at} }{2} \right]
\\ & = \frac{1}{2} \mathcal{L}[e^{at}] -  \frac{1}{2} \mathcal{L}[e^{-at}]
\\ & = \frac{1}{2} \left( \frac{1}{s-a} - \frac{1}{s+a} \right)
\\ & = \frac{1}{2} \frac{2a}{s^2-a^2}
\\ & = \frac{a}{s^2-a^2}
\end{align*}\]\[\begin{align*}
\mathcal{L}[\cosh at] & = \mathcal{L}\left[ \frac{ e^{at} + e^{-at} }{2} \right]
\\ & = \frac{1}{2} \mathcal{L}[e^{at}] + \frac{1}{2} \mathcal{L}[e^{-at}]
\\ & = \frac{1}{2} \left( \frac{1}{s-a} + \frac{1}{s+a} \right)
\\ & = \frac{1}{2} \frac{2s}{s^2-a^2}
\\ & = \frac{s}{s^2-a^2}
\end{align*}\]と導出することができます。

なお、収束領域は

• \( e^{at} \) のラプラス変換の収束領域：\( s \gt a \)
• \( e^{-at} \) のラプラス変換の収束領域：\( s \gt -a \)

の2つをともに満たす必要があるため、\( s \gt |a| \)（複素数範囲：\( \mathrm{Re} (s) \gt |a| \)）と求めることができます。

※なお、本ブログでは双曲線関数を使うような例題、練習問題は出さないようにしています。

５．覚えるべき法則・公式

ここからは、実際に期末試験、院試などでラプラス変換・ラプラス逆変換を行う際に頭にいれておくべき法則、公式を紹介したいと思います。

(1) 重要な3法則

ただラプラス変換、逆変換を求めるだけであれば法則1、法則3だけで十分です。

しかし、微分方程式に応用する場合は法則2も必ず頭にいれておく必要があります。

(2) 重要な変換公式

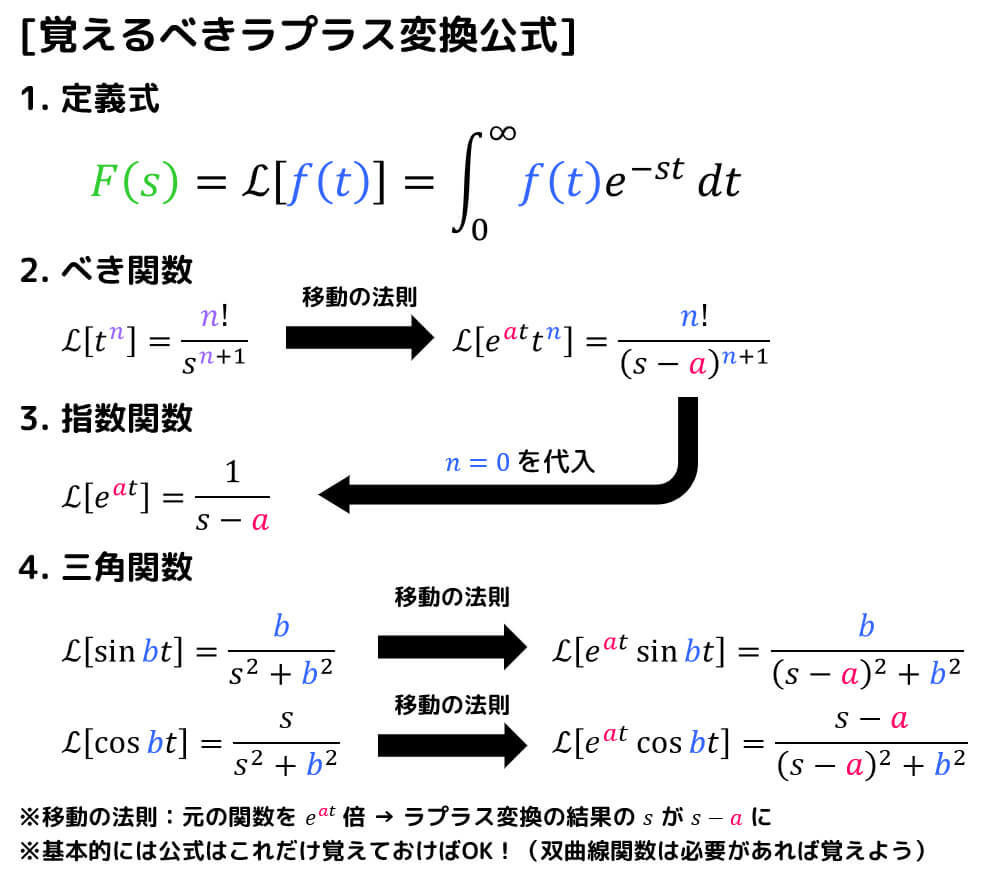
ラプラス変換・逆変換を単に求める場合、および微分方程式に利用する場合は収束領域を頭にいれておく必要はありません。

基本的には、

• べき関数 \( t^n \)
• 指数関数 \( e^{at} \)
• 三角関数 \( \sin bt \), \( \cos bt \)
• 移動の法則
• （双曲線関数 \( \sinh bt \), \( \cosh bt \)）

の4(5)つを覚えておけばOKです。

また、最初から移動法則を適用させた形、つまり

• \( e^{at} t^n \)
• \( e^{at} \sin bt \)
• \( e^{at} \cos bt \)

を覚えるのもアリです。

（\( a = 0 \) や \( n = 0 \) を代入することで残りの公式が導出できる）

(2) ラプラス変換表について

実際にラプラス変換、逆変換を用いる際には、ある関数 \( f(t) \) と、ラプラス変換後の関数 \( F(s) \) の対応が書かれたラプラス変換表を使って行うことも多いです。ラプラス変換の公式

ラプラス変換の基本法則・基本公式をまとめたプリントを作成したので、もし必要な人は下のボタンからダウンロードしてください！

６．公式を用いたラプラス変換・逆変換の求め方

では、実際にラプラス変換、逆変換を求めてみましょう。

例題3　ラプラス変換

つぎの(1)～(5)のラプラス変換 \(  \mathcal{L}[f(t)] \) を計算しなさい。

（公式を用いても構わない）

(1)\[
f(t) = 1 + 2t + 3t^2
\]

(2)\[
f(t) = e^{3t} + e^{-2t}
\]

(3)\[
f(t) = \sin 5t
\]

(4)\[
f(t) = t^2 e^{3t}
\]

(5)\[
f(t) = e^{-t} \cos t
\]

解説3

(1)

公式\[
\mathcal{L}[t^\textcolor{blue}{n}] = \frac{\textcolor{blue}{n}!}{ s^{\textcolor{blue}{n}+1} }
\]を用いる。

\[\begin{align*}
\mathcal{L}[f(t)] & = \mathcal{L}[1+2t+3t^2]
\\ & = \mathcal{L}[1] + 2 \mathcal{L}[t] + 3 \mathcal{L}[2]
\\ & = \frac{ \textcolor{blue}{0} !}{s^{\textcolor{blue}{0}+1}} + 2 \cdot \frac{ \textcolor{blue}{1} !}{s^{\textcolor{blue}{1}+1}} + 3 \cdot \frac{ \textcolor{blue}{2} !}{s^{\textcolor{blue}{2}+1}}
\\ & = \frac{1}{s} + 2 \cdot \frac{1}{s^2} + 3 \cdot \frac{2}{s^3}
\\ & = \frac{1}{s} + \frac{2}{s^2} + \frac{6}{s^3}
\end{align*}\]と求められる。

(2)

公式\[
\mathcal{L}[e^{ \textcolor{red}{a} n}] = \frac{1}{s - \textcolor{red}{a} }
\]を用いる。

\[\begin{align*}
\mathcal{L}[f(t)] & = \mathcal{L}[ e^{3t} + e^{-2t} ]
\\ & = \frac{1}{s - \textcolor{red}{3} } + \frac{1}{s - (\textcolor{red}{-2}) }
\\ & = \frac{1}{s-3} + \frac{1}{s+2}
\\ & = \frac{2s-1}{(s-3)(s+2)}
\end{align*}\]と求められる。

(3)

公式\[
\mathcal{L}[\sin \textcolor{red}{a} t] = \frac{\textcolor{red}{a}}{s^2 + \textcolor{red}{a}^2}
\]を用いる。

\[\begin{align*}
\mathcal{L}[f(t)] & = \mathcal{L}[ \sin \textcolor{red}{5} t ]
\\ & = \frac{\textcolor{red}{5}}{s^2 + \textcolor{red}{5}^2}
\\ & = \frac{5}{s^2 + 25}
\end{align*}\]と求められる。

(4)

公式\[
\mathcal{L}[t^\textcolor{blue}{n} e^{\textcolor{red}{a}t}] = \frac{\textcolor{blue}{n}!}{(s-\textcolor{red}{a})^{\textcolor{blue}{n}+1}}
\]を用いる。

\[\begin{align*}
\mathcal{L}[f(t)] & = \mathcal{L}[ t^\textcolor{blue}{n} e^{\textcolor{red}{a}t} ]
\\ & = t^\textcolor{blue}{2} e^{\textcolor{red}{3}t}
\\ & = \frac{\textcolor{blue}{2}!}{(s-\textcolor{red}{3})^{\textcolor{blue}{2}+1}}
\\ & = \frac{2}{(s-3)^3}
\end{align*}\]と求められる。

(5)

公式\[
\mathcal{L}[e^{\textcolor{red}{a}t} \cos \textcolor{blue}{b} t] = \frac{ s-\textcolor{red}{a} }{ (s-\textcolor{red}{a})^2 + \textcolor{blue}{b}^2}
\]を用いる。

\[\begin{align*}
\mathcal{L}[f(t)] & = \mathcal{L}[ e^{\textcolor{red}{-1}t} \cos \textcolor{blue}{1} t ]
\\ & = \frac{ s- ( \textcolor{red}{-1} ) }{ (s- (\textcolor{red}{-1}))^2 + \textcolor{blue}{1}^2}
\\ & = \frac{s+1}{(s+1)^2+1}
\end{align*}\]と求められる。

復習　部分分数分解

公式を用いてラプラス逆変換を計算する際には、部分分数分解を使うことが多いです

部分分数分解がよくわからない（忘れてしまった）という人は必ず下の記事で復習しましょう。

www.momoyama-usagi.com

※部分分数分解に自信ある人も要注意！！

意外と、\[
\frac{1}{(s-a)^2} = \frac{A}{s-a} + \frac{B}{(s-a)^2}
\]のように、分母に \( (s-a)^2 \) の項が入っていたり\[
\frac{1}{s^2+1} = \frac{As + B}{s^2 +1}
\]のように分母に \( s^2 \) の項が入っている場合の部分分数分解を忘れてしまっている（もしくは間違えている）人が多いので気を付けましょう。

（あれってなった人は上の記事で復習復習！！）

例題4　ラプラス逆変換

つぎの(1)～(5)のラプラス逆変換 \(  \mathcal{L}^{-1}[F(s)] \) を計算しなさい。

（公式を用いても構わない）

(1)\[
F(s) = \frac{1}{s-1} + \frac{1}{s-2}
\]

(2)\[
F(s) = \frac{1}{(s-1)(s-2)(s-3)}
\]

(3)\[
F(s) = \frac{1}{(s+1)(s-1)^2}
\]

(4)\[
F(s) = \frac{1}{(2s-3)^4}
\]

(5)\[
F(s) = \frac{1}{s^2-4s+5}
\]

解説4

(1)

公式\[
\mathcal{L} [e^{ \textcolor{red}{a} t} ] = \frac{ 1 }{ s - \textcolor{red}{a} }
\]から、ラプラス逆変換\[
\mathcal{L}^{-1} \left[  \frac{ 1 }{ s - \textcolor{red}{a} } \right] = e^{ \textcolor{red}{a} t}
\]が導ける。

（ラプラス変換を逆に適用させたのがラプラス逆変換）

よって、\[\begin{align*}
\mathcal{L}^{-1} \left[ F(s) \right] & = \mathcal{L}^{-1} \left[ \frac{1}{s-1} + \frac{1}{s-2} \right]
\\ & = \mathcal{L}^{-1} \left[ \frac{1}{s - \textcolor{red}{1} } \right] + \mathcal{L}^{-1} \left[ \frac{1}{s - \textcolor{red}{2} } \right]
\\ & = e^{ \textcolor{red}{1} t} + e^{ \textcolor{red}{2} t}
\\ & = e^{t} + e^{2t}
\end{align*}\]と計算できる。

(2)

まず、\[
\frac{1}{(s-1)(s-2)(s-3)}
\]を部分分数分解する。

すると、\[\begin{align*}
& \frac{1}{(s-1)(s-2)(s-3)}
\\ = \ & \frac{1}{2}  \frac{1}{s-1} - \frac{1}{s-2} + \frac{1}{2} \frac{1}{s-3}
\end{align*}\]と変形できる。

よって、\[\begin{align*}
\mathcal{L}^{-1} \left[ F(s) \right] & = \mathcal{L}^{-1} \left[ \frac{1}{(s-1)(s-2)(s-3)} \right]
\\ & =  \mathcal{L}^{-1} \left[\frac{1}{2}  \frac{1}{s-1} - \frac{1}{s-2} + \frac{1}{2} \frac{1}{s-3} \right]
\\ & = \frac{1}{2} \mathcal{L}^{-1} \left[ \frac{1}{s - \textcolor{red}{1}} \right] - \mathcal{L}^{-1} \left[ \frac{1}{s - \textcolor{red}{2}} \right] + \frac{1}{2} \mathcal{L}^{-1} \left[ \frac{1}{s - \textcolor{red}{3}} \right]
\\ & = \frac{1}{2} e^{ \textcolor{red}{1} t} - e^{ \textcolor{red}{2} t} + \frac{1}{2} e^{ \textcolor{red}{3} t}
\\ & = \frac{1}{2} e^{t} - e^{2t} + \frac{1}{2} e^{3t}
\end{align*}\]と計算できる。

(3)

まず、\[
\frac{1}{(s+1)(s-1)^2}
\]を部分分数分解する。

すると、\[\begin{align*}
& \frac{1}{(s+1)(s-1)^2}
\\ = \ & \frac{1}{4} \frac{1}{s+1} - \frac{1}{4} \frac{1}{s-1} + \frac{1}{2} \frac{1}{(s-1)^2}
\end{align*}\]と変形できる。

また、公式\[
\mathcal{L}[t^\textcolor{blue}{n} e^{\textcolor{red}{a}t}] = \frac{\textcolor{blue}{n}!}{(s-\textcolor{red}{a})^{\textcolor{blue}{n}+1}}
\]から、ラプラス逆変換\[
\mathcal{L}^{-1} \left[  \frac{\textcolor{blue}{n}!}{(s-\textcolor{red}{a})^{\textcolor{blue}{n}+1}} \right] = t^\textcolor{blue}{n} e^{\textcolor{red}{a}t}
\]が導ける。

よって、\[\begin{align*}
\mathcal{L}^{-1} \left[ F(s) \right] & = \mathcal{L}^{-1} \left[ \frac{1}{(s+1)(s-1)^2} \right]
\\ & =  \mathcal{L}^{-1} \left[ \frac{1}{4} \frac{1}{s+1} - \frac{1}{4} \frac{1}{s-1} + \frac{1}{2} \frac{1}{(s-1)^2} \right]
\\ & = \frac{1}{4} \mathcal{L}^{-1} \left[ \frac{1}{s - (\textcolor{red}{-1}) } \right] - \frac{1}{4} \mathcal{L}^{-1} \left[ \frac{1}{s - \textcolor{red}{1} } \right] + \frac{1}{2} \mathcal{L}^{-1} \left[ \frac{\textcolor{blue}{1}!}{(s-\textcolor{red}{1})^{\textcolor{blue}{1}+1}} \right]
\\ & = \frac{1}{4} e^{ \textcolor{red}{-1} t} - \frac{1}{4} e^{ \textcolor{red}{1} t} + \frac{1}{2} t^{ \textcolor{blue}{1} } e^{ \textcolor{red}{1} t}
\\ & = \frac{1}{4} e^{-t} - \frac{1}{4} e^{t} + \frac{1}{2} t e^{t}
\end{align*}\]と計算できる。

(4)

(3)と同じ公式\[
\mathcal{L}^{-1} \left[  \frac{\textcolor{blue}{n}!}{(s-\textcolor{red}{a})^{\textcolor{blue}{n}+1}} \right] = t^\textcolor{blue}{n} e^{\textcolor{red}{a}t}
\]を用いる。

よって、\[\begin{align*}
\mathcal{L}^{-1} \left[ F(s) \right] & = \mathcal{L}^{-1} \left[ \frac{1}{(2s-3)^4} \right]
\\ & = \mathcal{L}^{-1} \left[ \frac{1}{2^4 \left(s- \frac{3}{2} \right)^4} \right]
\\ & = \frac{1}{16} \mathcal{L}^{-1} \left[ \frac{1}{\textcolor{blue}{3}!} \frac{\textcolor{blue}{3}!}{\left( s- \frac{3}{2} \right)^{\textcolor{blue}{3} +1} } \right]
\\ & = \frac{1}{16 \cdot 6} \mathcal{L}^{-1} \left[ \frac{\textcolor{blue}{3}!}{\left( s- \frac{3}{2} \right)^{\textcolor{blue}{3} +1} } \right]
\\ & = \frac{1}{96} t^\textcolor{blue}{3} e^{\textcolor{red}{\frac{3}{2}}t}
\end{align*}\]と計算できる。

(5)

公式\[
\mathcal{L}[e^{\textcolor{red}{a}t} \sin \textcolor{blue}{b} t] = \frac{ \textcolor{blue}{b} }{ (s-\textcolor{red}{a})^2 + \textcolor{blue}{b}^2}
\]から、ラプラス逆変換\[
\mathcal{L}^{-1} \left[ \frac{ \textcolor{blue}{b} }{ (s-\textcolor{red}{a})^2 + \textcolor{blue}{b}^2} \right] = e^{\textcolor{red}{a}t} \sin \textcolor{blue}{b} t
\]が導ける。

よって、\[\begin{align*}
\mathcal{L}^{-1} \left[ F(s) \right] & = \mathcal{L}^{-1} \left[ \frac{1}{s^2-4s+5} \right]
\\ & = \mathcal{L}^{-1} \left[ \ \frac{1}{(s-2)^2+1} \right]
\\ & = \mathcal{L}^{-1} \left[ \ \frac{ \textcolor{blue}{1} }{ (s- \textcolor{red}{2} )^2+ \textcolor{blue}{1}} \right]
\\ & = e^{\textcolor{red}{2} t} \sin \textcolor{blue}{1} t
\\ & = e^{2t} \sin t
\end{align*}\]と計算できる。

７．さいごに

今回は、ラプラス変換のいろは、基礎に関するお話をしました。

次回は、いよいよラプラス変換を用いて微分方程式を解いていきたいと思います！

（なお、次回が微分方程式の最終回です！）