スポンサードリンク
こんにちは! ももやまです!
今回は離散数学(情報数学)ってどんなことするの? 何の役にたつの? というのを少しまとめてみました。わかりやすく書いたので厳密な定義では説明できてません……
スポンサードリンク
1.離散数学って何? 前提科目は?
高校時代、数学の様々な科目を履修したはずです。二次関数、図形と方程式、三角関数、指数関数、対数関数、微積、理系の人なら複素数平面などなど……。
でも離散数学という名前だけではどんなことをするのか全然わかりませんよね。
ということで、まずは離散数学とはどんな数学なのかを見てみましょう。
微分積分学の極限に関係しない数学。すなわち〈連続の数学〉に対して離散的な構造を扱う数学。計算可能性の理論,符号理論,オートマトンの理論,計算量の理論,証明論,組合せ論などの幅広い分野が含まれる。
有限でかつ離散的な,非計量の分野を対象とする数学。集合論,整数論,グラフ理論,組合せ論などの分野が含まれる。………
引用:コトバンク「離散数学」
読んでみると、微積とは全く関係ない内容というのがわかりますね。しかし、離散的な構造を扱うというところが少しわかりにくいかもしれないので、少しわかりやすく説明しましょう。
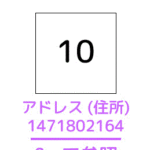
突然ですが、1と2の間にある実数、整数、自然数を1つ思い浮かべてみてください。
1と2の間にある実数は1.5とか1.8のような数値はすぐに浮かび上がりますが、1と2の間にある整数や自然数は思い浮かびませんよね。1と2の間の整数や自然数は存在しないので……。
離散的というのは、実数のような連続した数字ではなく、整数や自然数のように飛び飛びのような状態を表します。なので離散数学は、整数とは自然数をメインに扱う科目だと思ってください。*1
微分積分では基本的に実数を扱ってきたので微分積分をメインで習ってきた人は少し違う数学だなと思うかもしれません。
高校数学でも離散数学の基礎となる分野があります。例えば、
- 数学1 集合と論理
- 数学A 場合の数と確率(場合の数が大事)
- 数学A 整数の性質
- 数学B 数列
は離散数学でも役に立つ知識なのでこれらの分野が苦手という人は少し復習しておくといいかもしれません。
スポンサードリンク
2.どんなこと習うの?
離散数学で習う内容を8つくらいにわけてみました。
大学によって、離散数学で習う内容は違うので参考までにどうぞ。
(1) 集合について
皆さんは数学1(数学A)で集合分野を習ったと思います。例えばですが、\( \cup \) と \( \cap \) そして \( \in \) と\( \subset \) の違いは覚えてますか? 覚えてない人は離散数学の勉強をする前に確認をしておきましょう。
高校の数学に加えて、集合の中に集合が入ったり、べき集合など新たな概念が登場します。プログラミングでいう配列、リストが集合に相当します。
集合分野をまとめた記事はこちらです!
\( \cup \) と \( \cap \) そして \( \in \) と\( \subset \) の違いとかも書いているのでぜひ見てください!
(2) 命題論理について
この分野は情報系の学部や学科にいる人は100%確実に使います。
真理値表の書き方、「ならば」の意味などを習います。
また、この内容がわかると一部の論理パズルが効率的に解ける様になって楽しいです!
情報系の学部、学科では命題論理の知識はほぼ確実に必要なのでこの分野は確実にマスターしましょう!
この分野をまとめた記事はこちらです!
最後に論理パズルを1問用意したのでぜひ見てください!
(3) 述語論理について
命題論理に加えて、「ある変数」、「すべての変数」においてこの論理式は成立するか? みたいなことを習うのが述語論理です。
しかし、術後論理では \( \forall \) や \( \exists \) のような顔文字でしか見慣れないような記号が大量に出てくるのに加えて式が長くなりがちなので理解するのが少し難しいかもしれません。
そこで、述語論理を習うことで、日本語で長ったらしい条件を記号でスマートに書けるようになります。大学の先生はこの述語論理を使って条件を書く人が結構いるので \( \forall, \exists \) で書かれた論理式を少なくとも読めるようにしましょう。
書ける必要はありません。(私も読みにくいので日本語で書く派です)
この分野をまとめた記事はこちらです!
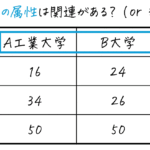
(4) 二項関係について
2つの変数 \( x \) と \( y \) の関係の性質について学びます。
数学Aの整数知識があると理解が楽かもしれません。
反射性、対称性のような見慣れない言葉が出てきます。まずは反射性、対称性などがどんな性質をもっているのかについて理解しましょう。性質が成り立つかの判定で整数知識を使うので、整数が苦手な人は整数知識を少しだけ復習しておきましょう。
この分野をまとめた記事はこちらです!
(5) 半順序関係について
今まで数学で2つの未知数を比較することはありましたよね。そのとき、「比較できない」なんてことはありませんでしたよね。このようなどんなもの同士でも比較できる関係のことを全順序関係といいます。
この分野では、「全順序関係」ではないもの、つまり「比較できないもの」があるかもしれない関係について学びます。このような関係を「半順序関係」といいます。
このような「半順序関係」を表すのに「ハッセ図」というのがよく使われます。
この分野をまとめた記事はこちらです!
(6) 写像(関数) 全射・単射など
皆さんは関数は中学生のときに習いましたよね。
「関数ってなに?」という質問をもしされたらあなたは答えることはできますか?
この分野では、関数とはどんなものなのか、そして関数をさらに広くした写像という概念を習います。さらに写像の中でも、全射・単射な写像ってどんなものなの? というのもここで習います。
この分野をまとめた記事はこちらです!
また、写像は線形代数にも出てきます。線形写像における写像はこちらをご覧ください。
(7) 数学的帰納法
これは数学Bで習う数学的帰納法と概念は全く同じです!
ただ、先生によっては帰納法の書き方が少し違うので先生の話はきっちり聞きましょう!
この分野のまとめはこちら!
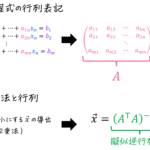
(8) 漸化式・差分方程式
数学Bで漸化式を習いましたよね?
この分野は漸化式の解き方について学びます。
差分方程式と言う人もいますが、差分方程式と漸化式はほぼ同じものだと思ってOKです。厳密に言えば違いますが…
高校のころ、漸化式を解くときにいくつかのパターンを習ったと思うのですが、あまり覚えていない人もいますよね…。
なので、微分方程式っぽく解いてみよう! というのがこの科目の特徴です。
この分野がわかることで、再帰関数(情報系の大学なら確実に習います)の計算時間などを見積もることができます。
この分野のまとめはこちら!
スポンサードリンク
3.実際どこに使われているの?
離散数学の知識はグラフ理論、組合せ論などの分野に応用することができます。
大学によっては離散数学という名前でグラフ理論を学ぶところもあるかもしれません。
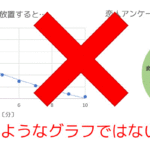
皆さんはグラフというと棒グラフや折れ線グラフのようなものを想像するかもしれませんが、グラフ理論のグラフは棒グラフや折れ線グラフのようなグラフではありません。
皆さんは地図、路線図などを見たことはありますか?
計算機(PC)上でこれらの図を表すためには、その図にどんな点(例えば路線図なら駅)があるのか、その点はどこにつながっているのか(駅と駅の線路はどうつながっているか)、などを集合を使って表現してやる必要があります。このように点と集合と辺の集合が集まったものをグラフといいます。
グラフ理論の特徴として、とにかく覚える用語が多いというのがあります。とにかく用語の意味を覚えましょう。
グラフ理論の用語をまとめた記事をこちらで紹介しているので用語についてはこちらの記事をご覧ください。
グラフ理論の基礎1(基本用語まとめ1)
グラフ理論の基礎2(基本用語まとめ2)
グラフ理論の基礎3(基本用語まとめ3)
下にグラフ理論(組合せ論?)の応用例を5つほど示してみました。
(1) 最短経路
皆さんは乗り換えアプリを使ってますか?
乗り換えアプリがないと乗る電車がわからずに間違った電車に乗っちゃったりしますよね……。
このような、乗り換えの最短経路(例「新宿→横浜」、「大阪→天王寺」)などは、離散数学のグラフ理論の知識を使って算出されています。
↓こんな感じに乗り換えアプリとかは一瞬で最短経路(時間)を調べてくれますよね!
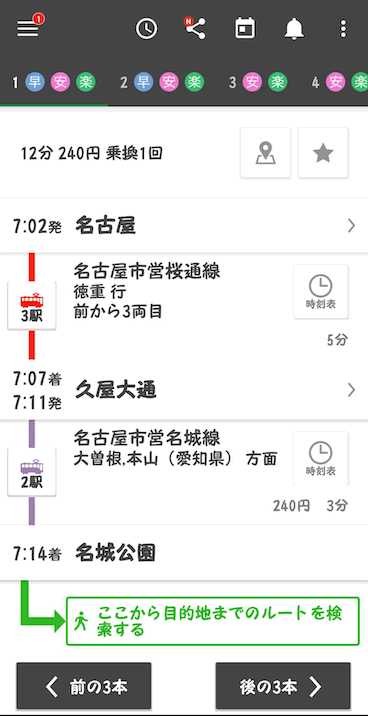
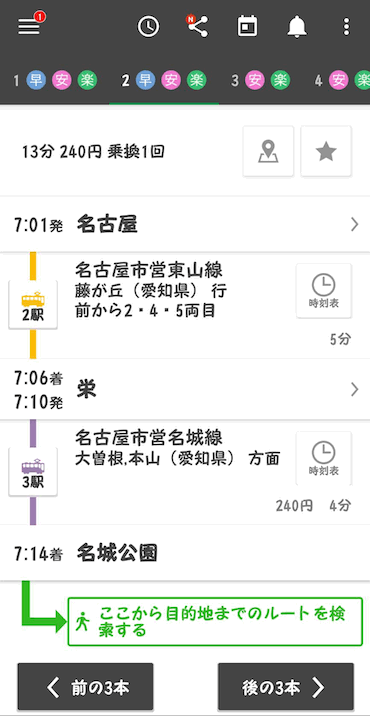
最短経路の求め方についてはこちらの記事にまとめているのでぜひご覧ください!
(2) 彩色

例えば次の近畿の2府5県を次のようなルールで4色で塗り分けてみてください
- 赤・青・緑・黄の4色で塗り分けること
- 1つの県(府)は必ず1色で塗ること
- 隣り合っている県同士で色が同じにならないこと
このような彩色問題もグラフを使って解いちゃうことができます!
彩色問題についてはこちらにまとめているのでぜひご覧ください!
地図の引用元: Craft Map
(3) 一筆書き
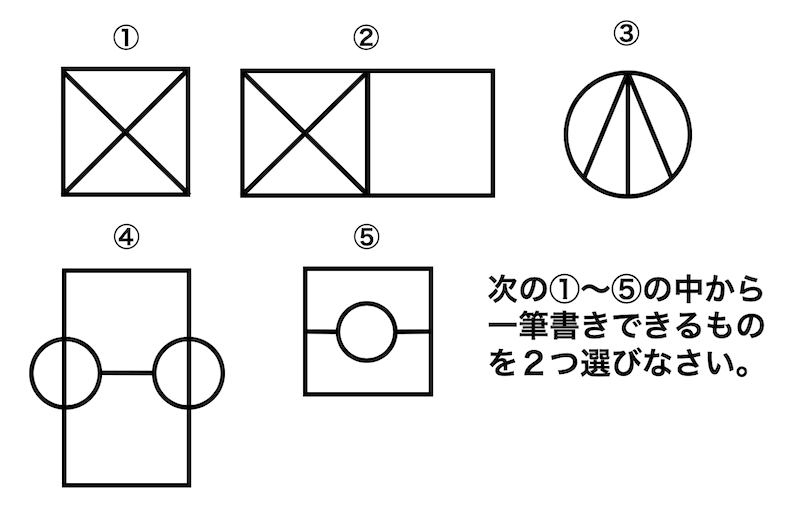
引用元:パズル算数クイズ
この5つの図形の中で一筆書きできるものを2つ挙げてみましょう*2。
グラフ理論では、図形の一筆書きができる条件なども習います!
詳しくはこちらをご覧ください!
(上の一筆書きの問題の答えの解説はこちらの記事に載せています。)
ちなみにこれは北嶺中学校の中学入試の問題です。
(4) 迷路
皆さんは迷路を作ったり迷路を解いたことはありますか?
迷路の道はグラフ理論で習う「木構造」で表現することができます。迷路を解く際には木構造をうまく解く(探索する)ことで経路を解くことができたりします。
迷路生成アルゴリズムを紹介した面白い動画があったので貼っておきます。
(5) ダンジョンマップ
皆さんは「不思議のダンジョンシリーズ」のゲームをしたことありますか? あの1,000回遊べるRPGって言われてるあれです。ローグライクゲームと呼ぶらしいです。
トルネコとかシレンとかポケモンとかチョコボとか色々ありますよね。
あのゲームに出てくるダンジョンマップ、毎回異なったマップが自動生成される不思議に思いませんか? しかもクリアできない詰みマップになることなんてほとんどありませんよね。
あのダンジョンマップが生成されるときはグラフ理論の知識が応用されています。今度不思議の(な)ダンジョンを遊ぶときは少し気にしてみてください()
余談ですが、最近「チョコボの不思議なダンジョン エブリバディ!」が出ましたね。子供のころチョコボの不思議なダンジョン1と2の両方にハマったのが懐かしい()
もちろん他にもグラフ理論、離散数学が使われている分野は存在します。*3
組合せ論についてはまたいつかまとめてみたいと思います。
4.さいごに
今回は「離散数学ってどんな科目なの?」、「離散数学って何の役にたつの?」についてまとめてみました。
離散数学の得意不得意は、他の微分積分のような科目(解析学)の得意不得意とは独立していることが多いです。微積が得意で離散数学が苦手という人もいればその逆もいます(もちろん得意な人もいますが…)。なので数学嫌だ!という人は離散数学は好き、得意になってもらえたらありがたいです。
これから離散数学を習う人も、すでに離散数学を履修済みな人も離散数学について興味をもってもらえたらうれしいです。
ではまた次回。
関連広告・スポンサードリンク