
スポンサードリンク
こんにちは、ももやまです。
今まで求めてきたフーリエ級数では、周期が一定の関数(波形) \( f(t) \) を \( \sin \) や \( \cos \) などの周期関数で表すことができましたね。
しかし、現実世界では周期が一定で変わらない波なんてそんな都合のいいものはありません。例えばですが、心電図なども常に周期が変わっていますよね[1]常に心拍数が一定(例えば60)なんて人はいませんよね。仮にいたとしたらそれ機械人間ですよ笑。。
そこで、周期が一定の関数(波形) だけでなく、一定ではない非周期関数に対しても適用できるようにしたものがフーリエ変換なのです!
目次
スポンサードリンク
1. (復習) 複素フーリエ級数展開
まず、フーリエ変換の導出に使う複素フーリエ級数展開について復習をしましょう。
周期 \( T \) の関数 \( f(t) \) の複素フーリエ級数展開は以下のように求められる。\[
f(t) = \sum^{\infty}_{k = - \infty} c_k e^{ik \omega t}
\]\[
c_k = \frac{1}{T} \int^{T}_{0} f(t) e^{- i k \omega t} \ dt , \ \ \ \omega = \frac{ 2 \pi }{T}
\]
[注意点]
※1 \( k = 0 \) のときに \( c_k \) の分母が0になるときは、\( c_0 \) を別途計算する必要あり。
※2 積分範囲は1周期分であればどこでもOK。例えば \( 0 \to T \) のかわりに \( -T/2 \to T/2 \) としてもOK。
複素フーリエ級数がちょっとイマイチだよ or 複素フーリエ級数をもっと復習したいよという方は、下の記事にて復習をしましょう!
スポンサードリンク
2. フーリエ変換へ
では、皆さんお待ちかねのフーリエ変換の導出過程に参りましょう。
まず、周期 \( T \) の関数 \( f(t) \) の複素フーリエ級数展開はこのような式で求められるのでしたね。\[
f(t) = \sum^{\infty}_{k = - \infty} c_k e^{ik \omega t}
\]\[
c_k = \int^{T}_{0} f(t) e^{- i k \omega t} , \ \ \ \omega = \frac{ 2 \pi }{T}
\]
ここで、\( c_k \) の積分範囲は1周期分ならどこでもOKなので、積分範囲を \( -T/2 \to T/2 \) と書き換えましょう。さらに \( T = \frac{ 2 \pi }{ \omega } \) を代入して積分式の前の \( 1/T \) も \( T \) を使わない表記に書き換えてあげます。つまり、\[\begin{align*}
c_k & = \frac{1}{T} \int^{ \frac{T}{2} }_{ - \frac{T}{2} } f(t) e^{- i k \omega t} \ dt
\\ & = \frac{1}{ \frac{ 2 \pi }{ \omega } } \int^{ \frac{T}{2} }_{ - \frac{T}{2} } f(t) e^{- i k \omega t} \ dt
\\ & = \frac{ \omega }{ 2 \pi } \int^{ \frac{T}{2} }_{ - \frac{T}{2} } f(t) e^{- i k \omega t} \ dt
\end{align*}\]とします。
さらに周期が一定ではないというのを、周期 \( T \) を極限まで長くすると言い換えます。つまり \( T \) を無限大まで大きくしていくことを考えます。
ここで、\( \omega = \frac{ 2 \pi }{ T } \) なので \( T \) を大きくすればするほど \( \omega \) は非常に小さい数となりますね。この非常に小さい数 \( \omega \) を \( d \omega \) とおきましょう。
どこまで \( T \) を大きくしていくかについてですが、ここで、\( e^{i k \omega t} \) の中にも \( \omega \) が含まれているほか、\( k \) という \( - \infty < k < \infty \) を取る文字に着目しましょう。
今回は \( k \omega \) の角速度が \( \omega \) になる程度まで周期 \( T \) を無限大まで近づけることにしましょう。
つまり、複素フーリエ級数の \( T \), \( \omega \), \( k \omega \) を以下のように置き換かえます。
| 複素フーリエ級数 | 置き換え後 |
|---|---|
| \( T \) | \( T \to \infty \) |
| \( \omega \) | \( d \omega \) |
| \( k \omega \) | \( \omega \) |
すると、\[\begin{align*}
c_k & = \frac{ \omega }{ 2 \pi } \int^{ \frac{T}{2} }_{ - \frac{T}{2} } f(t) e^{- i k \omega t} \ dt
\\ & = \frac{ d \omega }{ 2 \pi } \int^{ \infty }_{ - \infty } f(t) e^{ - i \omega t} \ dt
\end{align*}\]と変形することができますね。
さらに、変形した \( c_k \) の式を \( f(t) \) の複素フーリエ級数の式に代入します。すると、\[\begin{align*}
f(t) & = \sum^{\infty}_{k = - \infty} c_k e^{i \omega t}
\\ & = \sum^{\infty}_{k = - \infty} \frac{ d \omega }{ 2 \pi } \left( \int^{ \infty }_{ - \infty } f(t) e^{ - i \omega t} \ dt \right) e^{i \omega t}
\\ & = \frac{ 1 }{ 2 \pi } \sum^{\infty}_{k = - \infty} \left( \int^{ \infty }_{ - \infty } f(t) e^{ - i \omega t} \ dt \right) e^{i \omega t} \ d \omega
\end{align*}\]となりますね。
ここで、シグマ式の中の部分\[
\sum^{\infty}_{k = - \infty} \left( \int^{ \infty }_{ - \infty } f(t) e^{ - i \omega t} \ dt \right) e^{i \omega t} \ d \omega
\]は、下の図の黄色い面積部分と一致しますね。
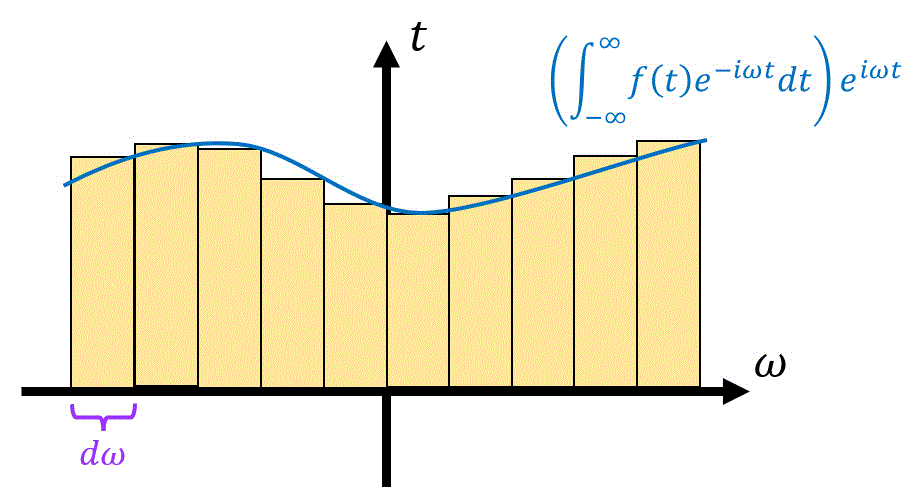
\( d \omega \) は微小な数なので、黄色い面積部分は、積分の形\[
\int^{\infty}_{- \infty} \left( \int^{ \infty }_{ - \infty } f(t) e^{ - i \omega t} \ dt \right) e^{i \omega t} \ d \omega
\]に書き換えることができますね!
よって、以下のように積分内に \( f(t) \) が含まれる式から \( f(t) \) が出てくる式を導出することができます。\[\begin{align*}
f(t) & = \sum^{\infty}_{k = - \infty} c_k e^{ik \omega t}
\\ & = \frac{ 1 }{ 2 \pi } \sum^{\infty}_{k = - \infty} \left( \int^{ \infty }_{ - \infty } f(t) e^{ - i \omega t} \ dt \right) e^{i \omega t} \ d \omega
\\ & = \frac{ 1 }{ 2 \pi } \int^{\infty}_{- \infty} \textcolor{deepskyblue}{ \underbrace{ \left( \int^{ \infty }_{ - \infty } f(t) e^{ - i \omega t} \ dt \right) }_{ F( \omega ) } } e^{i \omega t} \ d \omega \tag{☆}
\end{align*}\]
上の☆式の青部分\[
F( \omega ) = \textcolor{deepskyblue}{ \int^{ \infty }_{ - \infty} f(t) e^{ - i \omega t} } \ dt
\]がフーリエ変換の式の定義となるのです…!
また☆式より、\( F ( \omega ) \) から \( f(t) \) に戻す式も導出できます。\[\begin{align*}
f(t) & = \frac{ 1 }{ 2 \pi } \int^{\infty}_{- \infty} \left( \int^{ \infty }_{ - \infty } f(t) e^{ - i \omega t} \ dt \right) e^{i \omega t} \ d \omega
\\ & = \frac{ 1 }{ 2 \pi } \int^{\infty}_{- \infty} F ( \omega ) e^{i \omega t} \ d \omega
\end{align*}\]
この式がフーリエ逆変換の式となります…!
1つの式から、フーリエ変換、フーリエ逆変換の2つの公式を導出できるのは不思議ですね!

\[
F( \omega ) = \int^{\infty}_{- \infty} f(t) e^{- i \omega t} \ dt
\]
[フーリエ逆変換](フーリエ変換された関数 \( F ( \omega ) \) を元の関数 \( f ( t ) \) に戻す)
\[
f(t) = \frac{1}{2 \pi} \int^{\infty}_{- \infty} F ( \omega ) e^{i \omega t} \ d \omega
\]
積分の中身に複素数 \( i \) が入っており、「そのまま計算しても大丈夫なのか?」と思うかもしれませんが、何事もなかったのように普通に計算してOKです!(厳密にはよくないんですけどね…)
スポンサードリンク
3. 例題を解いてみよう!
では、早速例題でフーリエ変換の計算に慣れてみましょう。
ただし、フーリエ変換では無限範囲の積分を行うことが多いため、広義積分の知識が必須となります。広義積分がまだ怪しいよという方は、下の記事にて広義積分の復習をしてからこちらの例題に戻りましょう。
広義積分大丈夫だよって人は例題に突入しましょう!
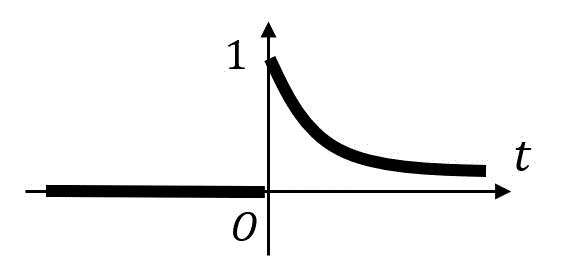
次の関数 \( f(t) \) のフーリエ変換 \( F( \omega ) \) を求めなさい。\[\begin{align*}
f(t) = \left\{ \begin{array}{l}
e^{-at} \ & ( t \geqq 0 ) \\
0 \ & ( t \lt 0 )
\end{array}\right.
\end{align*}\]
[解説]
おとなしくフーリエ変換の公式に入れましょう。\( f(t) \) が0になるは積分しても0なので、計算しなくてOKです。(今回は例題なのでわかりやすく記述します。)
今回の場合は、\( - \infty \leqq t < 0 \) のときは \( f(t) = 0 \) なので積分範囲にいれなくてOKです。
\[\begin{align*}
F ( \omega ) & = \int^{ \infty }_{0} e^{-at} \cdot e^{- i \omega t} \ dt + \int^{ 0 }_{ - \infty } 0 \cdot e^{- i \omega t} \ dt
\\ & = \int^{ \infty }_{0} e^{- (a+ i \omega) t} \ dt
\\ & = \lim_{R \to \infty} \int^{ R }_{0} e^{- (a+ i \omega) t} \ dt
\\ & = \lim_{R \to \infty} \left[ \frac{1}{-(a + i \omega)} e^{- (a+ i \omega) t} \right]^{R}_{0}
\\ & = \lim_{R \to \infty} \left[ - \frac{1}{a + i \omega} e^{- (a+ i \omega) t} \right]^{R}_{0}
\\ & = \lim_{R \to \infty} \left\{ \frac{1}{a + i \omega} \left( - e^{-R (a + i \omega)} + 1 \right) \right\}
\\ & = \lim_{R \to \infty} \left\{ \frac{1}{a + i \omega} \left( 1 - \frac{1}{e^{R (a + i \omega)}} \right) \right\}
\\ & = \lim_{R \to \infty} \left\{ \frac{1}{a + i \omega} \left( 1 - \frac{1}{ e^{Ra} ( \cos \omega R + i \sin \omega R ) } \right) \right\}
\\ & = \frac{1}{a + i \omega}
\end{align*}\]となる[2]\( \cos \omega R + i \sin \omega R \) は必ず有限の値になる。。
4. フーリエ余弦変換と正弦変換
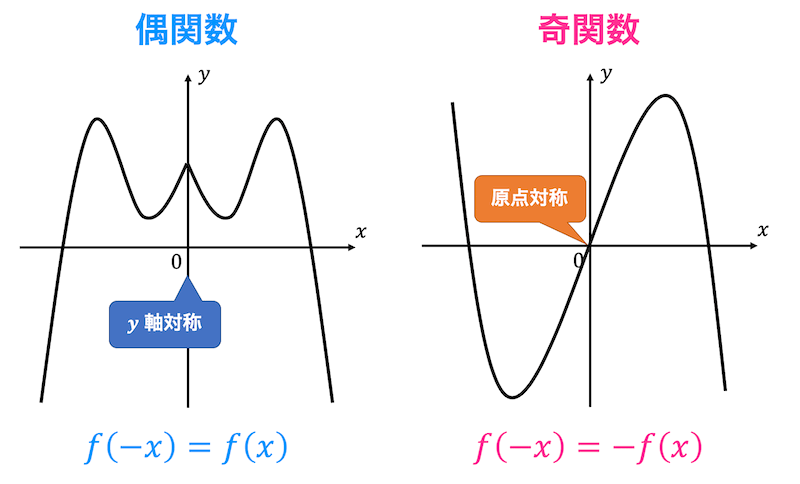
ここでは、偶関数・奇関数のお話をします。もし「偶関数とか奇関数ってなんだっけ」と思った人は、下の記事にて復習をしましょう。
実関数のフーリエ級数展開では、展開元の関数 \( f(t) \) が偶関数 or 奇関数だと計算が少し楽になるのでしたね。
同じように、フーリエ変換においても \( f(t) \) が偶関数 or 奇関数の場合は少し簡単な計算公式に変換することが可能です。
フーリエ変換元の関数 \( f(t) \) が偶関数もしくは奇関数のとき、フーリエ変換を以下のように計算することもできる。
(1) \( f(t) \) が偶関数のとき(フーリエ余弦変換)\[
F ( \omega ) = 2 \int^{\infty}_{ 0 } f(t) \cos \omega t \ dt
\]
(2) \( f(t) \) が奇関数のとき(フーリエ正弦変換)\[
F ( \omega ) = - 2i \int^{\infty}_{ 0 } f(t) \sin \omega t \ dt
\]
[仕組み]
フーリエ変換の公式を、オイラーの公式を用いて分解してみましょう。\[\begin{align*}
F ( \omega ) & = \int^{\infty}_{- \infty} f(t) e^{- i \omega t}\ dt
\\ & = \int^{\infty}_{- \infty} f(t) ( \cos \omega t - i \sin \omega t )\ dt
\\ & = \int^{\infty}_{- \infty} f(t) \cos \omega t \ dt - i \int^{\infty}_{- \infty} f(t) \sin \omega t \ dt
\end{align*}\]
ここで、\( \cos \omega t \) は偶関数、\( \sin \omega t \) は奇関数になりますね。
(1) \( f(t) \) が偶関数のとき
\( f(t) \) が偶関数のとき、\( f(t) \cos \omega t \), \( f(t) \sin \omega t \) が偶関数、奇関数になるかは下のようになりますね。
- \( f(t) \cos \omega t \) は (偶関数) × (偶関数) より偶関数
- \( f(t) \sin \omega t \) は (偶関数) × (奇関数) より奇関数
ここで、ある関数 \( f(x) \) が奇関数のときは、\[
\int^{R}_{-R} f(x) \ dx = 0
\]となり、\( f(x) \) が偶関数のときは\[
\int^{R}_{-R} f(x) \ dx = 2 \int^{R}_{0} f(x) \ dx
\]でしたね。
よって、\[\begin{align*}
F ( \omega ) & = \int^{\infty}_{- \infty} f(t) e^{- i \omega t}\ dt
\\ & = \underbrace{ \int^{\infty}_{- \infty} f(t) \cos \omega t \ dt }_{中身が偶関数} - i \underbrace{ \int^{\infty}_{- \infty} f(t) \sin \omega t \ dt }_{中身が奇関数なので \ 0}
\\ & = 2 \int^{\infty}_{0} f(t) \cos \omega t \ dt
\end{align*}\]となりますね。
このように \( f(t) \) が偶関数のときは、フーリエ余弦変換による計算でもフーリエ変換を計算することができます。
(2) \( f(t) \) が奇関数のとき
\( f(t) \) が奇関数のとき、\( f(t) \cos \omega t \), \( f(t) \sin \omega t \) が偶関数、奇関数になるかは下のようになりますね。
- \( f(t) \cos \omega t \) は (奇関数) × (偶関数) より奇関数
- \( f(t) \sin \omega t \) は (奇関数) × (奇関数) より偶関数
よって、\[\begin{align*}
F ( \omega ) & = \int^{\infty}_{- \infty} f(t) e^{- i \omega t}\ dt
\\ & = \underbrace{ \int^{\infty}_{- \infty} f(t) \cos \omega t \ dt }_{中身が奇関数なので \ 0} - i \underbrace{ \int^{\infty}_{- \infty} f(t) \sin \omega t \ dt }_{中身が偶関数}
\\ & = - 2i \int^{\infty}_{0} f(t) \sin \omega t \ dt
\end{align*}\]となりますね。
このように \( f(t) \) が偶関数のときは、フーリエ余弦変換による計算でもフーリエ変換を計算することができます。
ここで、1問例題を見てみましょう。
次の関数 \( f(t) \) のフーリエ変換 \( F( \omega ) \) を(1), (2)の誘導に従って解きなさい。\[\begin{align*}
f(t) = \left\{ \begin{array}{l}
t \ & ( - \pi \leqq t \leqq \pi ) \\
0 \ & ( それ以外 )
\end{array}\right.
\end{align*}\]
(1) \( f(t) \) は偶関数、奇関数のどちらか。
(2) \( f(t) \) をフーリエ余弦変換、フーリエ正弦変換のいずれかを用いてフーリエ変換 \( F ( \omega ) \) を計算しなさい。
(1)
図を書くと、原点対称になっていることがわかる。つまり、\( f(t) = - f(-t) \) が成立しているので、\( f(t) \) は奇関数である。
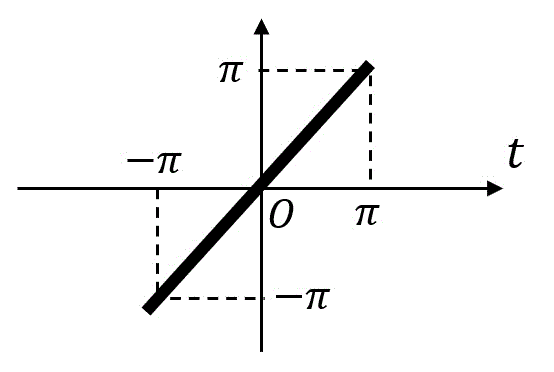
(2)
\( f(t) \) は奇関数なので、フーリエ正弦変換を用いてフーリエ変換を算出する。\[\begin{align*}
F ( \omega ) & = -2i \int^{\pi}_{0} t \sin \omega t \ dt
\\ & = -2i \left[ \frac{1}{\omega} t ( - \cos \omega t ) - \frac{1}{\omega^2} ( - \sin \omega t) \right]^{\pi}_{0}
\\ & = -2i \left[ - \frac{1}{\omega} t \cos \omega t + \frac{1}{\omega^2} \sin \omega t)\right]^{\pi}_{0}
\\ & = -2i \left( - \frac{1}{\omega} \pi \cos \pi \omega + \frac{1}{ \omega^2 } \sin \pi \omega \right)
\\ & = -2i \cdot \frac{- \pi \omega \cos \pi \omega + \sin \pi \omega}{ \omega^2 }
\\ & = \frac{ 2 \pi \omega \cos \pi \omega - 2 \sin \pi \omega }{ \omega^2 } i
\end{align*}\]
5. フーリエ変換で成り立つ5つの法則
最後にフーリエ変換で成り立つ5つの法則と、法則が成り立つ仕組み(厳密な証明ではない)を確認しておきましょう。こんな法則が成り立つんだ〜程度の理解でOKです。
※ ここでは \( f(t) \) のフーリエ変換を \( \mathcal{F} [ f(t) ] \) と書くことにしましょう。
(1) 線形の性質
積分計算と同じように、定数倍、足し算引き算を分離することができるという法則です。
(a) 足し算、引き算の分離が可能\[
\mathcal{F} [ f(t) + g(t) ] = \mathcal{F} [ f(t) ] + \mathcal{F} [ g(t) ]
\]
(b) 定数倍の分離も可能\[
\mathcal{F} [ k f(t) ] = k \mathcal{F} [ f(t) ]
\]
(a), (b) 合わせて参考書では以下のように書かれることがほとんど。\[
\mathcal{F} [ a \ f(t) + b \ g(t) ] = a \mathcal{F} [ f(t) ] + b \mathcal{F} [ g(t) ]
\]
[仕組み]
\[\begin{align*}
\mathcal{F} [a \ f(t) + b \ g(t) ] & = \int^{\infty}_{- \infty} \left(a \ f(t) + b \ g(t) \right) \ dt
\\ & = \int^{\infty}_{- \infty} a \ f(t) \ dt + \int^{\infty}_{- \infty} b \ g(t) \ dt
\\ & = a \int^{\infty}_{- \infty} f(t) \ dt + b \int^{\infty}_{- \infty} g(t) \ dt
\\ & = a \ \mathcal{F} [f(t)] + b \ \mathcal{F} [g(t)]
\end{align*}\]
なお、逆変換の場合においても線形の法則は成り立ちます。
フーリエ逆変換の場合でも線形の法則は成り立つ。\[
\mathcal{F}^{-1} [ a \ F( \omega ) + b \ G( \omega ) ] = a \mathcal{F}^{-1} [ F( \omega )] + b \mathcal{F}^{-1} [ G( \omega ) ]
\]
※ \( F ( \omega) \) のフーリエ逆変換を \( \mathcal{F}^{-1} [ F ( \omega ) ] \) と記した
(2) 微分の性質
次に、フーリエ変換元の関数 \( f(t) \) を \( t \) で微分すると、変換先 \( F ( \omega ) \) がどのようになるかを見ていきましょう。
\[
\mathcal{F} \left[ \frac{d}{dt} f(t) \right] = i \omega \ \mathcal{F} [ f(t) ]
\]※ \( t \to \pm \infty \) のときに \( f(t) \to 0 \) になることを仮定
[仕組み]
\( t \to \pm \infty \) のときに \( f(t) \to 0 \) に収束することを仮定します。すると、\[\begin{align*}
\frac{d}{dt} f(t) & = \frac{d}{dt} \left( \int^{\infty}_{- \infty} F ( \omega ) e^{\textcolor{red}{i \omega} t} \ d \omega \right)
\\ & = \textcolor{red}{i \omega} F ( \omega ) e^{ i \omega t} \ d \omega
\\ & = i \omega f(t)
\end{align*}\]より、\[
\mathcal{F} \left[ \frac{d}{dt} f(t) \right] = i \omega \ \mathcal{F} [ f(t) ]
\]となる。
(3) 移動の性質
\( t \) を定数 \( a \) だけシフトさせるとフーリエ変換がどのようになるかを確認しましょう。
\[
\mathcal{F} [ f(t-a) ] = e^{- i a \omega} \mathcal{F} [ f(t) ]
\]
[仕組み]
途中で \( x = t-a \) と置換積分します。(積分範囲は変化なし、また \( dx = dt \) となる。)
\[\begin{align*}
\mathcal{F} [ f(t-a) ] & = \int^{\infty}_{- \infty} f(t-a) e^{- i \omega t } \ dt
\\ & = \int^{\infty}_{- \infty} f(x) e^{- i \omega (x+a) } \ dx
\\ & = \int^{\infty}_{- \infty} f(x) e^{- i \omega x } e^{-i \omega a} \ dx
\\ & = e^{-i \omega a} \int^{\infty}_{- \infty} f(x) e^{- i \omega x } \ dx
\\ & = e^{-i \omega a} \mathcal{F} [ f(t) ]
\end{align*}\]
(4) 相似の性質
最後に相似の法則について確認しておきましょう。
\[
\mathcal{F} [ f(kt) ] = \frac{1}{|k|} F \left( \frac{ \omega }{ k } \right)
\]
[仕組み]
\( k > 0 \) のときと \( k < 0 \) のときに分けておこないます。
(i) \( k > 0 \) のとき
\( kt = x \) とする。すると、\( k \ dt = dx \) となる。\[\begin{align*}
\mathcal{F} [ f(kt) ] & = \int^{\infty}_{- \infty} f(kt) e^{- i \omega t } \ dt
\\ & = \int^{\infty}_{- \infty} f(x) e^{- i \omega \frac{x}{k} } \cdot \frac{1}{k} \ dx
\\ & = \frac{1}{k} \int^{\infty}_{- \infty} f(x) e^{- i \frac{ \omega}{k} x } \ dx
\\ & = \frac{1}{k} F \left( \frac{ \omega }{ k } \right)
\end{align*}\]
(ii) \( k < 0 \) のとき
\( kt = x \) とする。すると、\( k \ dt = dx \) となる。さらに \( k < 0 \) なため、積分範囲が \( \infty \to - \infty \) に切り替わる。\[\begin{align*}
\mathcal{F} [ f(kt) ] & = \int^{\infty}_{- \infty} f(kt) e^{- i \omega t } \ dt
\\ & = \int^{- \infty}_{\infty} f(x) e^{- i \omega \frac{x}{k} } \cdot \frac{1}{k} \ dx
\\ & = - \frac{1}{k} \int^{\infty}_{- \infty} f(x) e^{- i \frac{ \omega}{k} x } \ dx
\\ & = - \frac{1}{k} F \left( \frac{ \omega }{ k } \right)
\end{align*}\]
(i), (ii) をまとめると、\[
\mathcal{F} [ f(kt) ] = \frac{1}{|k|} F \left( \frac{ \omega }{ k } \right)
\]となる。
(5) 共役の性質
フーリエ変換後の関数 \( F( \omega \) \) の \( \omega \) の正負を入れ替えると \( F( \omega \) \) の共役複素数となります。
\[
F( \omega ) = \overline{ F ( - \omega ) }
\]
※ \( \overline{ F ( - \omega ) } \) は \( F ( - \omega ) \) の共役複素数
[仕組み]
\( F ( \omega ) \) と \( F ( - \omega ) \) のフーリエ逆変換をそれぞれ計算します。
\[\begin{align*}
F( \omega ) & = \int^{\infty}_{- \infty} f(t) e^{- i \omega t} \ dt
\\ & = \int^{\infty}_{- \infty} f(t) (\cos \omega t - i \sin \omega t) \ dt
\\ & = \int^{\infty}_{- \infty} f(t) \cos \omega t \ dt \textcolor{red}{-} i \int^{\infty}_{- \infty} f(t) \sin \omega t \ dt
\end{align*}\]
\[\begin{align*}
F( - \omega ) & = \int^{\infty}_{- \infty} f(t) e^{- i ( - \omega ) t} \ dt
\\ & = \int^{\infty}_{- \infty} f(t) e^ {i \omega t} \ dt
\\ & = \int^{\infty}_{- \infty} f(t) (\cos \omega t + i \sin \omega t) \ dt
\\ & = \int^{\infty}_{- \infty} f(t) \cos \omega t \ dt \textcolor{red}{+} i \int^{\infty}_{- \infty} f(t) \sin \omega t \ dt
\end{align*}\]
となり、たしかに \( F ( \omega ) \) と \( F ( - \omega ) \) は共役の関係になっていますね。
フーリエ変換の性質は、ラプラス変換に似ている部分も多いので、興味ある人は下の記事にてラプラス変換についても勉強してみてください…!
6. 練習問題
では、2問ほどフーリエ変換の練習問題を用意したので、練習してみましょう。
★問題★
練習1
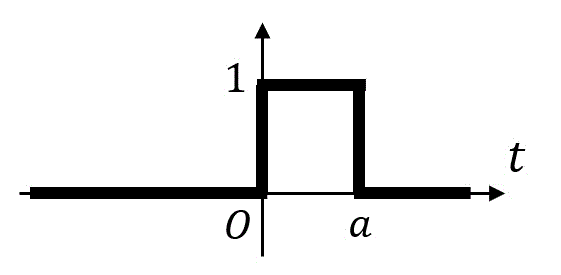
次の関数 \( f(t) \) のフーリエ変換 \( F( \omega ) \) を求めなさい。\[\begin{align*}
f(t) = \left\{ \begin{array}{l}
1 \ & ( 0 \leqq t \leqq a ) \\
0 \ & ( それ以外 )
\end{array}\right.
\end{align*}\]
※ 可能であれば標本化関数\[
\frac{ \sin \theta }{ \theta } = \mathrm{sinc} \ \theta
\]の形で答えてみましょう。
練習2
次の関数 \( f(t) \) のフーリエ変換 \( F( \omega ) \) を(1), (2)のどちらかの方法を用いて解きなさい。\[\begin{align*}
f(t) = \left\{ \begin{array}{l}
e^{-at} \ & ( t \geqq 0 ) \\
e^{at} \ & ( t < 0 )
\end{array}\right.
\end{align*}\]
(1) フーリエ正弦変換、フーリエ余弦変換の性質を使わずに解きなさい。
(2) フーリエ正弦変換、フーリエ余弦変換のうち、適切な方を使ってフーリエ変換を求めなさい。
※ 時間のある人は2パターン両方解いてみよう!
★解答★
解答1
おとなしくフーリエ変換の公式に入れましょう。今回は、\( 0 \leqq t \leqq a \) のとき以外は \( f(t) = 0 \) なので、\( 0 \leqq t \leqq a \) の部分のみをフーリエ変換すればOKです。\[\begin{align*}
F ( \omega ) & = \int^{a}_{0} 1 \cdot e^{- i \omega t} \ dt
\\ & = \int^{a}_{0} e^{- i \omega t} \ dt
\\ & = \left[ \frac{1}{- i \omega} e^{- i \omega t} \right]^{a}_{0}
\\ & = - \frac{1}{i \omega} e^{- i \omega a} + \frac{1}{ i \omega }
\\ & = \frac{1 - e^{- i \omega a}}{ i \omega }
\\ & = \frac{e^{ - \frac{i \omega a}{2} }(e^{ \frac{i \omega a}{2} } - e^{ - \frac{i \omega a}{2} })}{ i \omega }
\\ & = \frac{2 e^{ - \frac{i \omega a}{2} }}{\omega } \cdot \frac{e^{ \frac{i \omega a}{2} } - e^{ - \frac{i \omega a}{2} }}{2i}
\\ & = \frac{2 e^{ - \frac{i \omega a}{2} }}{\omega } \cdot \sin \frac{ \omega a }{2}
\\ & = a e^{ - \frac{i \omega a}{2} } \cdot \frac{ \sin \frac{ \omega a }{2} }{ \frac{ \omega a }{2} }
\\ & = a e^{ - \frac{i \omega a}{2} } \mathrm{sinc} \ \frac{ \omega a }{2}
\end{align*}\]
解答2
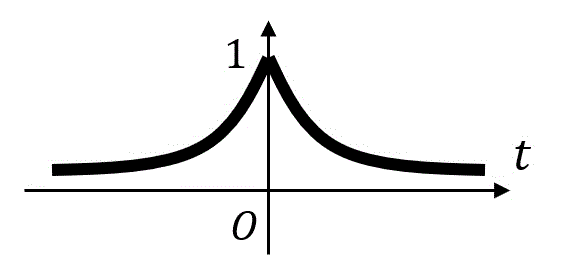
図はこんな感じ。
(1) 普通に計算
おとなしくフーリエ変換の公式に入れましょう。積分の式が2つになるのが少し大変かもしれません。\[\begin{align*}
F ( \omega ) & = \int^{\infty}_{0} e^{-at} e^{- i \omega t} \ dt + \int^{0}_{-\infty} e^{at} e^{i \omega t} \ dt
\end{align*}\] の計算をすればOK。
ここでそれぞれの積分を別々に計算する。
\[\begin{align*}
\int^{\infty}_{0} e^{-at} e^{- i \omega t} \ dt
& = \int^{ \infty }_{0} e^{- (a+ i \omega) t} \ dt
\\ & = \lim_{R \to \infty} \int^{ R }_{0} e^{- (a+ i \omega) t} \ dt
\\ & = \lim_{R \to \infty} \left[ \frac{1}{-(a + i \omega)} e^{- (a+ i \omega) t} \right]^{R}_{0}
\\ & = \lim_{R \to \infty} \left[ - \frac{1}{a + i \omega} e^{- (a+ i \omega) t} \right]^{R}_{0}
\\ & = \lim_{R \to \infty} \left\{ \frac{1}{a + i \omega} \left( - e^{-R (a + i \omega)} + 1 \right) \right\}
\\ & = \lim_{R \to \infty} \left\{ \frac{1}{a + i \omega} \left( 1 - e^{-aR} e^{- i \omega R} \right) \right\}
\\ & = \lim_{R \to \infty} \left\{ \frac{1}{a + i \omega} \left( 1 - \underbrace{e^{-aR}}_{0 \ に収束} \underbrace{ ( \cos R \omega - i \sin R \omega ) }_{どんなに大きくても \ 1} \right) \right\}
\\ & = \frac{1}{a + i \omega}
\end{align*}\]
\[\begin{align*}
\int^{0}_{- \infty} e^{at} e^{- i \omega t} \ dt
& = \int^{0}_{- \infty} e^{(a - i \omega) t} \ dt
\\ & = \lim_{R \to \infty} \int^{ 0 }_{-R} e^{(a - i \omega) t} \ dt
\\ & = \lim_{R \to \infty} \left[ \frac{1}{(a - i \omega)} e^{(a - i \omega) t} \right]^{ 0 }_{-R}
\\ & = \lim_{R \to \infty} \left[ \frac{1}{a - i \omega} e^{(a - i \omega) t} \right]^{ 0 }_{-R}
\\ & = \lim_{R \to \infty} \left\{ \frac{1}{a - i \omega} \left( 1 - e^{-R (a - i \omega)} \right) \right\}
\\ & = \lim_{R \to \infty} \left\{ \frac{1}{a - i \omega} \left( 1 - e^{-aR} e^{ i \omega R} \right) \right\}
\\ & = \lim_{R \to \infty} \left\{ \frac{1}{a - i \omega} \left( 1 - \underbrace{e^{-aR}}_{0 \ に収束} \underbrace{ ( \cos R \omega + i \sin R \omega ) }_{どんなに大きくても \ 1} \right) \right\}
\\ & = \frac{1}{a - i \omega}
\end{align*}\]
より、フーリエ変換は\[\begin{align*}
F ( \omega ) & = \int^{infty}_{0} e^{-at} e^{- i \omega t} \ dt + \int^{0}_{-\infty} e^{at} e^{i \omega t} \ dt
\\ & = \frac{1}{a + i \omega} + \frac{1}{a - i \omega}
\\ & = \frac{(a - i \omega) + (a + i \omega)}{(a + i \omega)(a - i \omega) }
\\ & = \frac{2a}{a^2 - i^2 \omega^2}
\\ & = \frac{2a}{a^2 + \omega^2}
\end{align*}\]と計算できる。
(2) フーリエ余弦変換 or 正弦変換の使用
図を書くと、y軸対称になっていることがわかる。つまり、\( f(t) = f(-t) \) が成立しているので、\( f(t) \) は偶関数である。
偶関数なので、フーリエ余弦変換を利用することでフーリエ変換を計算することができる。\[\begin{align*}
f( \omega ) & = 2 \int^{\infty}_{0} e^{-at} \cos \omega t \ dt
\\ & = 2 \int^{\infty}_{0} e^{-at} \frac{ e^{i \omega t} + e^{-i \omega t} }{2} \ dt
\\ & = \int^{\infty}_{0} e^{-at} \left( e^{i \omega t} + e^{-i \omega t} \right) \ dt
\\ & = \int^{\infty}_{0} e^{(-a+ i \omega ) t} \ dt + \int^{\infty}_{0} e^{-(a+ i \omega) t } \ dt
\end{align*}\]
ここで、\[\begin{align*}
\int^{\infty}_{0} e^{(-a+ i \omega ) t} \ dt
& = \lim_{R \to \infty} \int^{ R }_{0} e^{(-a+ i \omega ) t} \ dt
\\ & = \lim_{R \to \infty} \left[ \frac{1}{- a + i \omega} e^{(-a+ i \omega ) t} \right]^{ R }_{0}
\\ & = \lim_{R \to \infty} \frac{1}{-a + i \omega} \left( e^{(-a+ i \omega )R} - 1 \right)
\\ & = \lim_{R \to \infty} \frac{1}{a - i \omega} \left( 1 - e^{-aR} e^{-i \omega R} \right)
\\ & = \lim_{R \to \infty} \frac{1}{a - i \omega} \left( 1 - \underbrace{e^{-aR}}_{0 \ に収束} \underbrace{ \left( \cos \omega R - \sin \omega R \right) }_{どんなに大きくても \ 1} \right)
\\ & = \frac{1}{a - i \omega}
\end{align*}\]と計算できる。
また(1)より\[
\int^{\infty}_{0} e^{-(a+ i \omega) t } \ dt = \frac{1}{a + i \omega}
\]となる。
よって、フーリエ変換 \( F ( \omega ) \) は、\[\begin{align*}
f( \omega ) & = 2 \int^{\infty}_{0} e^{-at} \cos \omega t \ dt
\\ & = \int^{\infty}_{0} e^{(-a+ i \omega ) t} \ dt + \int^{\infty}_{0} e^{-(a+ i \omega) t } \ dt
\\ & = \frac{1}{a - i \omega} + \frac{1}{a + i \omega}
\\ & = \frac{2a}{a^2 + \omega^2}
\end{align*}\]と計算できる。
(分母のiを消す部分の計算過程は(1)をご確認ください)
7. さいごに
今回は、フーリエ変換について、複素フーリエから導出する過程、および実際に計算する方法を例題や練習問題を用いて説明していきました。
フーリエ変換は多くの理系大学生が学ぶ分野で、様々な分野で使われるので確実に理解しておきましょう…!
関連広告・スポンサードリンク







![うさぎでもわかる計算機システム Part01 2進数 [基本情報対応]](https://www.momoyama-usagi.com/wp-content/uploads/2021/05/20190612102246-1-150x150.gif)