スポンサードリンク
こんにちは、ももやまです!
そろそろ1年生も終わりになる時期だと思います。
しかし、「あぁぁ解析学わかんねぇ難しすぎる」って思ってる人、諦めないでください!!
この私が、1年後期の解析学を試験前日でも4時間あれば総復習ができるように10題の練習問題を作成しました!
前編では基本的な事項を確認するためのフォーム型の問題を5問用意しました!
- 50分間で問題を解く。答えを回答フォームに入力する。
- 答えを送信後、間違った箇所を確認し、解説を見てどこで間違えたのか(理解ができていないのか)を確認する。
- 間違えた箇所を参考書や記事などで練習する。
- 時間があれば、合っている箇所も確認する。(青色と赤色の枠部分)
- 寝る。
時間がある人はじっくり、時間がない人は素早くこの記事にて1年後期の解析の復習をしましょう!
本記事では、練習問題の解説を載せております。さらに、要点を
- 試験で必要な知識:青色の枠
- 試験で必要な解き方:赤色の枠
などでまとめております。
目次
スポンサードリンク
1. 小問集合
次の2変数関数の極限を計算したい。(i)~(iv)の問いに答えなさい。\[
\lim_{(x,y) \to (0,0)} \frac{xy^2}{2x^2 + 3y^4}
\]
(1) 2変数関数の極値
次の2つの極限を計算したときの結果を \( a \), \( b \) とする。\[
a = \lim_{x \to 0} \left( \lim_{y \to 0} \frac{x^2y}{2x^4 + 3y^2} \right)
\]\[
b = \lim_{y \to 0} \left( \lim_{x \to 0} \frac{x^2y}{2x^4 + 3y^2} \right)
\]このとき、\( a \), \( b \) に成り立つ関係として正しいものを選択肢から選び、[ 1 ]にマークしなさい。
★ [ 1 ] の解答群 ★
0. \( a = b \)
1. \( a \not = b \)
2. \( a \) は収束するが \( b \) は発散する
3. \( a \) は発散するが \( b \) は収束する
4. \( a \) も \( b \) も発散する
解答:0 [1点]
1年前期の解析学や、数3と同じ
\[\begin{align*}
a & = \lim_{x \to 0} \left( \lim_{y \to 0} \frac{x^2y}{2x^4 + 3y^2} \right)
\\ & = \lim_{x \to 0} \frac{x \cdot 0}{2x^4 }
\\ & = \lim_{x \to 0} 0
\\ & = 0
\end{align*}\]
\[\begin{align*}
b & = \lim_{y \to 0} \left( \lim_{x \to 0} \frac{x^2y}{2x^4 + 3y^2} \right)
\\ & = \lim_{y \to 0} \frac{0 \cdot y^2}{3y^2}
\\ & = \lim_{y \to 0} 0
\\ & = 0
\end{align*}\]となる。
よって、\( a = 0 \), \( b = 0 \) より成り立つ関係式は \( a = b \) が答え。(マーク番号0)
点 \( (x,y) \) を \( y = mx^2 \) に沿って原点 \( (0,0) \) に近づける。\[
\lim_{ \substack{x \to 0 \\ y = mx^2} } \frac{ xy^2 }{2x^2 + 3y^4 } = \left[ \ \ \ 2 \ \ \ \right]
\]
このときの極限値を \( m \) を用いて表したものとして、正しいものを選択肢から選び、[ 2 ] にマークしなさい。
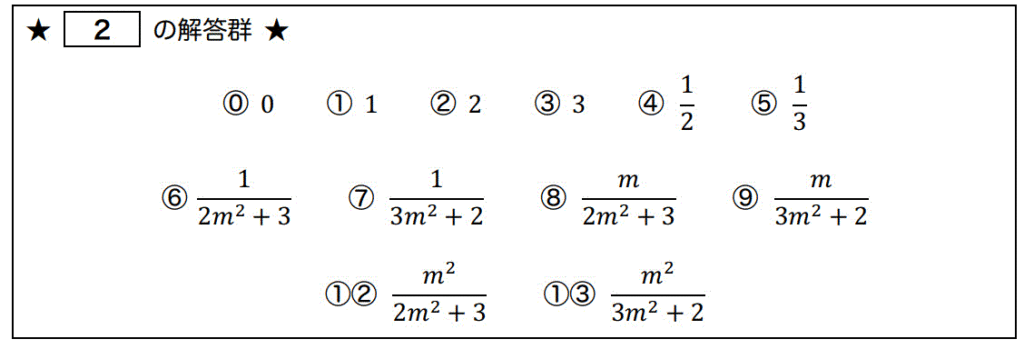
解答:9 [1点]
\( y = mx^{ 2 } \) としてから \( x \to 0 \) に極限を飛ばしましょう。\[\begin{align*}
\lim_{ \substack{x \to 0 \\ y = mx^2} } \frac{x^2y}{2x^4 + 3y^2} & = \lim_{x \to 0} \frac{x^2 \cdot (mx^2)}{2x^4 + 3 (mx^2)^2}
\\ & = \lim_{x \to 0} \frac{mx^4}{2x^4 + 3m^2 x^4}
\\ & = \lim_{x \to 0} \frac{m}{2+ 3m^2}
\\ & = \frac{m}{2+ 3m^2}
\\ & = \frac{m}{3m^2+ 2}
\end{align*}\]となるため、マーク番号9が答え。
つぎの2変数関数の極限値\[
c = \lim_{(x,y) \to (0,0)} \frac{x^2y}{2x^4 + 3y^2}
\]に関する文章の空欄( ア )、( イ )を正しく埋める選択肢の組み合わせとして正しいものを1つ選び、[ 3 ] にマークしなさい。

解答: 3 [1点]
(ii)で、\( y = mx^2 \) とおいてから \( x \to 0 \) としたときに\[
c = \lim_{ \substack{x \to 0 \\ y = mx^2} } \frac{x^2 y }{2x^4 + 3y^2 } = \frac{m}{3m^2+ 2}
\]となっていましたね。
ここで、\( m \) は問題文で勝手におかれた極限とは関係のない変数ですね。なので、\( m \) の値を変えると計算結果が変わるという現象が発生します。
\( m \) の値が変わったら \( c \) の値も変化するってことは極限とは言えません。なので答えは3です。
2変数関数 \( f(x,y) \) の極値\[
c = \lim_{(x,y) \to (0,0)} f(x,y)
\]は、\( y = mx^a \) もしくは極座標変換( \( x = r \cos \theta \), \( y = r \sin \theta \) )をすれば求められる。
ここで、2変数関数が極値を持つための条件は \( c \) の値が新たにおいた変数(\( m \), \( r \) , \( \theta \))に依存しないことである。
\[
f(x,y) = \left\{ \begin{array}{l} \ \ \frac{x^2y}{2x^4 + 3y^2} \ \ & (x,y) \not = (0,0) \\ \ \ \ \ \ \ 0 & (x,y) = (0,0) \end{array}\right.\]
は原点 (0,0) において連続か。解答群の中から正しいものを1つ選び、[ 4 ] にマークしなさい。
★ [ 4 ] の解答群 ★
0. \( f(x,y) \) は原点において連続である
1. \( f(x,y) \) は原点において連続ではない
2. \( f(x,y) \) は原点において連続かどうかはわからない
解答: 1 [1点]
\( (x,y) \) を原点 \( (0,0) \) まで近づけると、(iii) より、\( m \) の値によって依存するような値\[
\frac{m}{3m^2 + 2}
\]を取るのでしたね。
なので、原点で連続ではありません。よって答えは1。
2変数関数 \( f(x,y) \) \[
f(x,y) = \left\{ \begin{array}{l} \ \ g(x,y) \ \ & (x,y) \not = (0,0) \\ \ \ \ \ \ \ k & (x,y) = (0,0) \end{array}\right.
\]が原点 (0,0) において連続であるかどうかは、極限\[
\lim_{(x,y) \to (0,0)} g(x,y)
\]が存在し、その極限が \( k \) となることを確認すればOK。
(極限が \( k \) となれば連続、\( k \) 以外の値を取ったり、極値が存在しない場合は連続ではない)
2変数関数の極限についての復習記事はこちら!
(2) C2級関数とは
2変数関数 \( f(x,y) \) が \( C_2 \) 級関数であるとき、\( f_{xy} = f_{yx} \) が成り立つ。つまり、偏微分の順序を入れ替えても計算結果が変わらない。ここで、\( C_2 \) 級関数とはどのような関数か。正しいものを1つ選び、マーク番号 [ 5 ] にマークしなさい。
[ 5 ] の選択肢⓪ 1回偏微分可能な関数
① 2回偏微分可能な関数
② 3回偏微分可能な関数
③ 1次以下の偏導関数がすべて連続な関数
④ 2次以下の偏導関数がすべて連続な関数
⑤ 3次以下の偏導関数がすべて連続な関数
⑥ 1回偏微分可能かつ1次以下の偏導関数がすべて連続な関数
⑦ 2回偏微分可能かつ2次以下の偏導関数がすべて連続な関数
⑧ 3回偏微分可能かつ3次以下の偏導関数がすべて連続な関数
解答:7 [1点]
- 2回偏微分可能(2次までの偏導関数が存在)
- 2次までの偏導関数がすべて連続
の2つを満たしたものを \( C_{2} \) 級関数といいます。
※ \( f_{xx} \), \( f_{xy} \), \( f_{yx} \), \( f_{yy} \) がすべて存在して連続であれば \( C_2 \) 級関数ということができます。
(3) 全微分
関数 \( f(x,y) \) を全微分した結果 \( df \) として正しい式を選び、マーク番号 [ 6 ] にマークしなさい。

解答: 2 [1点]
公式を復習しといてください。
関数 \( f(x,y) \) の全微分 \( df \) は次のようになる。\[
df = \frac{ \partial f }{ \partial x } dx + \frac{ \partial f }{ \partial y } dy
\]
全微分についてさらに復習したい方はこちらをご覧ください!
(4) 2変数の極値
2変数関数 \( f(x,y) \) がある点 \( (a,b) \) において極大値を持つとする。このとき成立する関係式として正しいものを2つ選び、マーク番号 [ 7 ] にマークしなさい。
ただし、行列 \( X \) を\[
X = \left| \begin{array}{ccc} f_{xx} (a,b) & f_{xy}(a,b) \\ f_{yx}(a,b) & f_{yy}(a,b) \end{array} \right|
\]とする。なお、この行列式 \( |X| \) は [ 8 ] と呼ばれる。

★ 解答 ★
No.07 0,5 [完答1点]
No.08 5 [1点]
公式を確認してください。
2変数関数 \( f(x,y) \) がある点(停留点) \( (a,b) \) において極値を持つかどうかは下の行列式\[X = \left| \begin{array}{ccc} f_{xx} (a,b) & f_{xy}(a,b) \\ f_{yx}(a,b) & f_{yy}(a,b) \end{array} \right|\]の値を確認すればOK。(この行列 \( X \) はヘッシアン・ヘッセ行列などと呼ばれる)
- \( X > 0 \) … 点 \( (a,b) \) は極値
- \( X < 0 \) … 点 \( (a,b) \) は極値ではない
- \( X = 0 \) … 点 \( (a,b) \) は極値かどうかわからない(試験に出ない)
また、点 \( (a,b) \) が極値であるとき、その極値が極大値・極小値のどちらになるかは、\( f_{xx} \) の値を計算することで確認可能。
- \( f_{xx} (a,b) > 0 \) … 点 \( (a,b) \) は極小値
- \( f_{xx} (a,b) < 0 \) … 点 \( (a,b) \) は極大値
2変数関数の極値(条件なし)についてのより詳細な記事はこちら!
(5) 陰関数の極値
次の陰関数に関する文章の空欄 ( ア )、( イ )を正しく埋める選択肢の組み合わせとして正しいものを1つ選び、[ 9 ] にマークしなさい。
陰関数で与えられた方程式 \( f(x,y) = 0 \) からなる関数の導関数 \( \frac{dy}{dx} \) が存在するための条件は( ア )である。また、( ア )を満たすとき、導関数 \( \frac{dy}{dx} \) は( イ )で求めることができる。
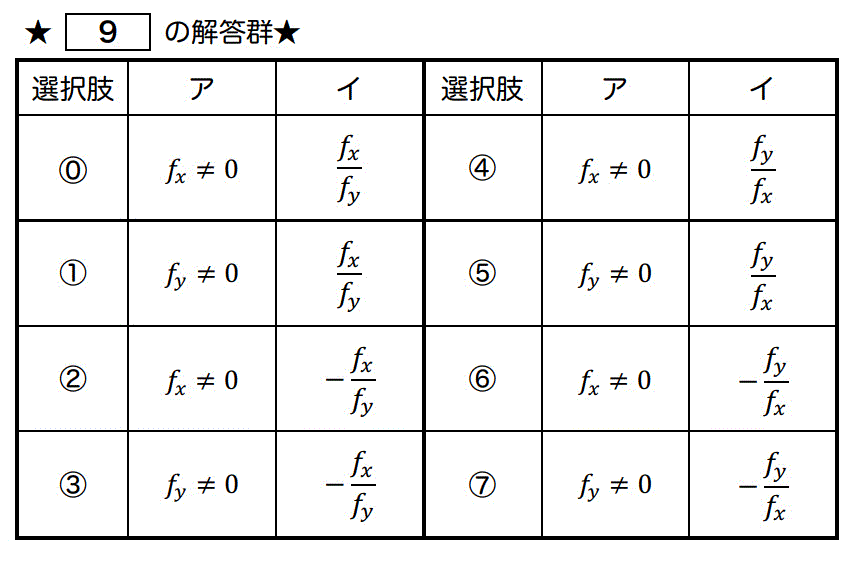
解答: 3 [1点]
方程式 \( f(x,y) = 0 \) で定まる関数 \( y = g(x) \) があるとする。
式の両辺を \( x \) で微分すると、\[
\frac{d}{dx} f(x,g(x) ) = f_x + \frac{dy}{dx} f_y = 0
\]となるので、\[
\frac{dy}{dx} = - \frac{f_x}{f_y}
\]を導くことができる。。
また、\( - \frac{f_x}{f_y} \) の分母が0になったら陰関数は存在しないので \( f_{y} \not = 0 \) が陰関数が存在する条件となり、組み合わせとして正しい選択肢は3となる。
方程式 \( f(x,y) = 0 \) で定まる関数 \( y = g(x) \) の導関数は、\( f_y \not = 0 \) のとき、下のように求めることができる。\[
\frac{dy}{dx} = - \frac{f_x}{f_y}
\]
陰関数表示された関数の導関数を偏微分を用いて求める方法はこちら!
(6) ヤコビアン計算
ある関数の2重積分を求めるために \( x = ar \cos \theta \), \( y = br \sin \theta \) と変数変換を行った。このときのヤコビ行列式の値として正しいものを [ 10 ] にマークしなさい。
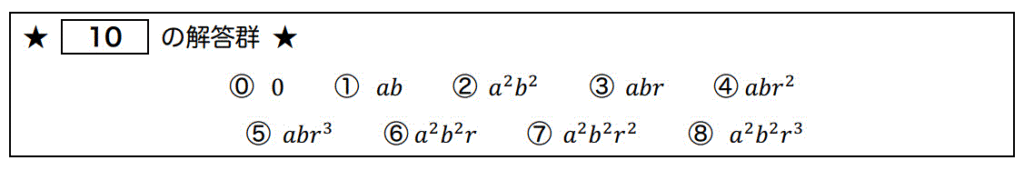
解答: 3 [1点]
\( x = ar \cos \theta \), \( y = br \sin \theta \) と変数変換を行ったときのヤコビ行列式(ヤコビアン)は、\[ \begin{align*}
J & = \left| \begin{array}{ccc} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \end{array} \right|
\\ & = \left| \begin{array}{ccc} a \cos \theta & - ar \sin \theta \\ b \sin \theta & br \cos \theta \end{array} \right|
\\ & = abr \cos^2 \theta + abr \sin^2 \theta
\\ & = abr \left( \cos^2 \theta + \sin^2 \theta \right)
\\ & = abr
\end{align*} \]と計算できるので答えは \( abr \) となり、マーク番号3が答え。
※ この変数変換は範囲 \( D \) が楕円になっているときに使えます。
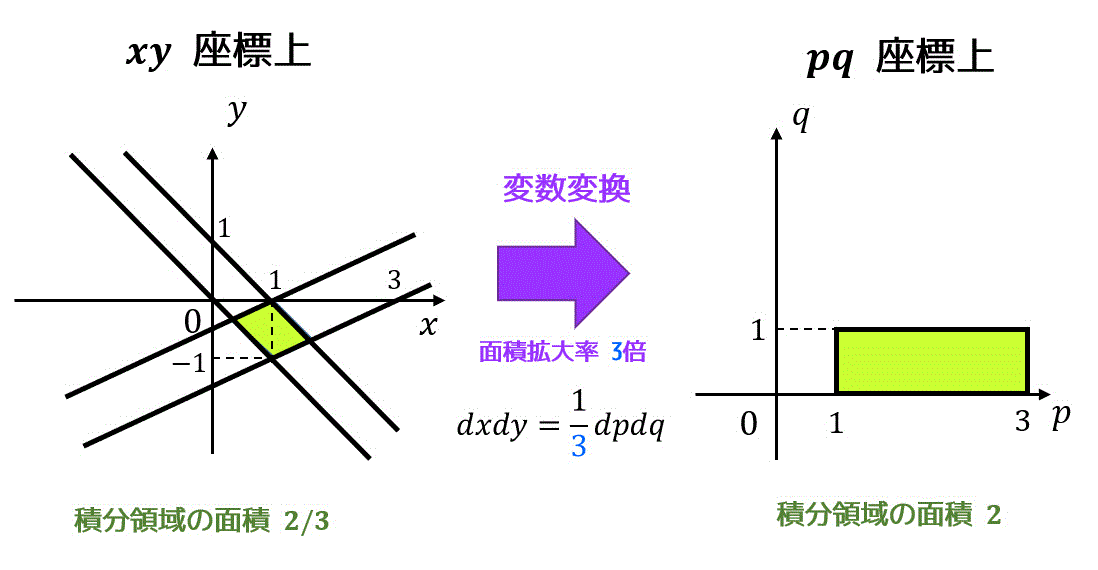
被積分関数が \( x \), \( y \) の2重積分の変数を \( x = x(p,q) \), \( y = y(p,q) \) でおく。
このときのヤコビアン \( J \) を下のように計算できる。\[\begin{align*}
J = \left| \begin{array}{ccc} \frac{\partial x}{\partial p} & \frac{\partial x}{\partial q} \\ \frac{\partial y}{\partial p} & \frac{\partial y}{\partial q} \end{array} \right|
\end{align*}\]
また、ヤコビアン \( J \) を用いて、変数変換の前後の関係は下のように書き表せる。\[
dxdy = |J| \ dpdq
\]※ 絶対値が付くところに要注意!
ヤコビアンについてのより詳細な記事はこちら!
スポンサードリンク
2.偏微分・合成関数の微分
(1) 偏微分
つぎの [ 11 ] ~ [ 14 ] に当てはまる答えを下の解答群から選び、マークしなさい。
[2010年度EMaT 微分・積分問4]2変数関数\[
f(x,y) = \log (x^2 + y^2)
\]を考える。ただし \( (x,y) \not = (0,0) \) とする。
(i) 偏導関数は、\[
\frac{ \partial f }{ \partial x} = \left[ \ \ 11 \ \ \right] , \ \ \
\frac{ \partial f }{ \partial y} = \left[ \ \ 12 \ \ \right]
\]となる。
(ii) さらに、\[
\frac{ \partial^2 f }{ \partial y \partial x } = \left[ \ \ 13 \ \ \right] \]\[
\frac{ \partial^2 f }{ \partial x^2} + \frac{ \partial^2 f }{ \partial y^2} = \left[ \ \ 14 \ \ \right] \]と計算できる。

★解答★
No.11: 4 [1点]
No.12: 5 [1点]
No.13: 13 [2点]
No.14: 0 [2点]
(i) 偏微分は、微分する変数以外はすべて定数と考えるのがポイント!
\( f(x,y) \) を \( x \) について微分する場合は、\( \textcolor{red}{x} \) 以外はすべて定数となる。\[
\log ( \textcolor{red}{x}^2 + y^2)
\]※色のついていない文字はすべて定数だと思って計算すればOK
よって、\[\begin{align*}
\frac{ \partial f }{ \partial \textcolor{red}{x}} & = \frac{(\textcolor{red}{x}^2 + y^2)'}{\textcolor{red}{x}^2+y^2}
\\ & = \frac{2x}{x^2+y^2}
\end{align*}\]と計算できるため、答えは4。
同じように \( y \) について微分する場合は、\( \textcolor{blue}{y} \) 以外はすべて定数としてみればOK。\[
\log ( x^2 + \textcolor{blue}{y}^2)
\]※色のついていない文字はすべて定数だと思って計算すればOK
よって、\[\begin{align*}
\frac{ \partial f }{ \partial \textcolor{blue}{y}} & = \frac{(x^2 + \textcolor{blue}{y}^2)'}{x^2 + \textcolor{blue}{y}^2}
\\ & = \frac{2y}{x^2+y^2}
\end{align*}\]と計算できるため、答えは5。
ある2変数関数 \( f(x,y) \) の偏導関数は、微分する係数以外を定数として考えることで、1変数関数の微分をするときと同じ感覚で求められる。
\[
\frac{ \partial f }{\partial x} \to ( x \ \mathrm{以外の変数を定数と考え、微分} )
\]\[
\frac{ \partial f }{\partial y} \to ( y \ \mathrm{以外の変数を定数と考え、微分})
\]
(ii) 2次偏導関数は、1次の偏導関数をさらに偏微分すればOK。
例えば、\[
\frac{ \partial^2 f }{ \partial x^2}
\]であれば、\( \frac{ \partial f }{ \partial x } \) をさらに \( x \) で偏微分すればOK。
また、\[
\frac{ \partial^2 f }{ \textcolor{red}{\partial y \partial x} }
\]であれば、\( \frac{ \partial f }{ \partial x } \) をさらに \( y \) で偏微分すればOKです。
※ 赤色部分に要注意! 偏微分した順に右から書いていきます。
なので、\[\begin{align*}
\frac{ \partial^2 f }{ \partial y \partial x } & = \frac{ \partial }{ \partial y} \left( \frac{ \partial f }{ \partial x} \right)
\\ & = \frac{ \partial }{ \partial \textcolor{blue}{y}} \left( \frac{2x}{x^2+\textcolor{blue}{y}^2} \right)
\\ & = \frac{- 2x \cdot 2y}{(x^2 + y^2)^2}
\\ & = \frac{ -4xy }{(x^2+y^2)^2}
\end{align*}\]と計算でき、答えは13。
また、\[\begin{align*}
\frac{ \partial^2 f }{ \partial x^2} & = \frac{ \partial }{ \partial x} \left( \frac{ \partial f }{ \partial x} \right)
\\ & = \frac{ \partial }{ \partial \textcolor{red}{x}} \left( \frac{2 \textcolor{red}{x}}{ \textcolor{red}{x}^2+y^2} \right)
\\ & = \frac{2 \cdot (x^2 + y^2) - 2x \cdot 2x}{ (x^2+y^2)^2 }
\\ & = \frac{2x^2 + 2y^2 - 4x^2}{ (x^2+y^2)^2 }
\\ & = \frac{-2x^2 + 2y^2}{ (x^2+y^2)^2 }
\end{align*}\]
\[\begin{align*}
\frac{ \partial^2 f }{ \partial y^2} & = \frac{ \partial }{ \partial y} \left( \frac{ \partial f }{ \partial y} \right)
\\ & = \frac{ \partial }{ \partial \textcolor{blue}{y}} \left( \frac{2 \textcolor{blue}{y}}{ x^2+ \textcolor{blue}{y}^2} \right)
\\ & = \frac{2 \cdot (x^2 + y^2) - 2y \cdot 2y}{ (x^2+y^2)^2 }
\\ & = \frac{2x^2 + 2y^2 - 4y^2}{ (x^2+y^2)^2 }
\\ & = \frac{2x^2 - 2y^2}{ (x^2+y^2)^2 }
\end{align*}\]
と計算できるので、\[\begin{align*}
\frac{ \partial^2 f }{ \partial x^2} + \frac{ \partial^2 f }{ \partial y^2} & = \frac{-2x^2 + 2y^2}{ (x^2+y^2)^2 } + \frac{2x^2 - 2y^2}{ (x^2+y^2)^2 }
\\ & = 0
\end{align*}\]となる。
ある2変数関数 \( f(x,y) \) の第2次偏導関数(2階偏微分)は、1回偏微分したもの\[
\frac{\partial f}{\partial x}, \ \ \ \frac{\partial f}{\partial y}
\]を、さらにもう1回偏微分すれば求められる。
偏微分の適用順: \( x \) → \( x \) \[
\frac{ \partial^2 f }{ \partial x^2 } = \frac{\partial }{ \partial x} \left( \frac{\partial f}{\partial x} \right)
\]
偏微分の適用順: \( x \) → \( y \) \[
\frac{ \partial^2 f }{ \partial y \partial x } = \frac{\partial }{ \partial y} \left( \frac{\partial f}{\partial x} \right)
\]
偏微分の適用順: \( y \) → \( x \) \[
\frac{ \partial^2 f }{ \partial x \partial y } = \frac{\partial }{ \partial x} \left( \frac{\partial f}{\partial y} \right)
\]
偏微分の適用順: \( y \) → \( y \) \[
\frac{ \partial^2 f }{ \partial y^2 } = \frac{\partial }{ \partial y} \left( \frac{\partial f}{\partial y} \right)
\]
※ 期末試験で出題されるような関数は、偏微分の順序を入れ替えても答えが変わらない(\( C^2 \) 級関数)、つまり\[
\frac{ \partial^2 f }{ \partial y \partial x } = \frac{ \partial^2 f }{ \partial x \partial y}
\]なので、順番はあまり気にしなくてOK
偏微分の基本をもう1度復習したい方はこちら!
(2) 合成関数の微分1
\( t \) について2回微分可能な関数 \( f(t) \)、および2変数関数 \( g(x,y) = f(2x-4y) \) がある。
このとき、以下の式が成り立つように [ 15 ] ~ [ 17 ] にあてはまる-9以上9以下の数字を答えなさい。\[
\frac{\partial g}{\partial x} = \left[ \ \ 15 \ \ \right] f'(2x-4y), \ \ \ \frac{\partial g}{\partial y} = \left[ \ \ 16 \ \ \right] f'(2x-4y)
\]\[
\frac{\partial^2 g}{\partial x \partial y} + \frac{\partial^2 g}{\partial y^2} = \left[ \ \ 17 \ \ \right] \frac{\partial^2 g}{\partial x^2}
\]
★解答★
No.15: 2 [1点]
No.16: -4 [1点]
No.17: 2 [1点]
2変数関数 \( g(x,y) \) を1変数関数 \( f(t) \) でおいたときの偏微分公式をまずは確認しましょう。
2変数関数 \( g(x,y) \) を \( t = t(x,y) \) 1変数関数 \( f(t) \) におきかえる。\[
g(x,y) = f(t)
\]
このとき、2階までの微分は次のように計算できる。
[1回微分]\[\begin{align*}\frac{ \partial g}{ \partial x } & = \frac{\partial t}{\partial x} \frac{ d f }{ d t} \\
\\ & = \frac{\partial t}{\partial x} f'(t)
\end{align*}\]\[\begin{align*}
\frac{ \partial g}{ \partial x } & = \frac{\partial t}{\partial x} \frac{ d f }{ d t} \\
\\ & = \frac{ \partial t }{ \partial x} f'(t)
\end{align*}\] [2回微分]
\[\begin{align*}
\frac{ \partial^2 g}{ \partial x^2 } & = \frac{\partial t}{\partial x} \frac{\partial t}{\partial x} \frac{ d^2 f }{ d t^2} \\
\\ & = \frac{\partial t}{\partial x} \frac{\partial t}{\partial x} f''(t)
\end{align*}\]
\[\begin{align*}
\frac{ \partial^2 g}{ \partial y \partial x } & = \frac{ \partial^2 g}{ \partial x \partial y }
\\ & = \frac{\partial t}{\partial x} \frac{\partial t}{\partial y} \frac{ d^2 f }{ d t^2} \\
\\ & = \frac{\partial t}{\partial x} \frac{\partial t}{\partial y} f''(t)
\end{align*}\]
\[\begin{align*}
\frac{ \partial^2 g}{ \partial y^2 } & = \frac{\partial t}{\partial y} \frac{\partial t}{\partial y} \frac{ d^2 f }{ d t^2} \\
\\ & = \frac{\partial t}{\partial y} \frac{\partial t}{\partial y} f''(t)
\end{align*}\]
今回は、\( g(x,y) = f(2x-4y) \) とおいているので、\( t = 2x - 4y \) としたときを考えればOK。
ここで、\( \frac{\partial t}{ \partial x } \), \( \frac{\partial t}{ \partial y } \) はそれぞれ\[
\frac{\partial t}{ \partial x } = 2 , \ \ \ \frac{\partial t}{ \partial y } = - 4
\]と計算できる。
よって、1回目の微分は\[\begin{align*}
\frac{\partial g}{ \partial x } & = \frac{\partial t}{ \partial x } \frac{ d f }{ d t}
\\ & = 2 f'(t)
\end{align*}\]
\[\begin{align*}
\frac{\partial g}{ \partial y } & = \frac{\partial t}{ \partial y } \frac{ d f }{ d t}
\\ & = -4 f'(t)
\end{align*}\]と計算できる。
また、2回目の微分は\[\begin{align*}
\frac{\partial^2 g}{ \partial x^2 } & = \frac{\partial t}{\partial x} \frac{\partial t}{\partial x} \frac{ d^2 f }{ d t^2}
\\ & = 4 f'(t)
\end{align*}\]
\[\begin{align*}
\frac{\partial^2 g}{ \partial x \partial y } & = \frac{\partial t}{\partial x} \frac{\partial t}{\partial y} \frac{ d^2 f }{ d t^2}
\\ & = -8 f'(t)
\end{align*}\]
\[\begin{align*}
\frac{\partial^2 g}{ \partial y^2 } & = \frac{\partial t}{\partial y} \frac{\partial t}{\partial y} \frac{ d^2 f }{ d t^2}
\\ & = 16 f'(t)
\end{align*}\]となるので、\[\begin{align*}
\frac{\partial^2 g}{\partial x \partial y} + \frac{\partial^2 g}{\partial y^2} & = -8 f'(t) + 16 f'(t)
\\ & = 8 f'(t)
\\ & = 2 \cdot 4 f'(t)
\\ & = 2 \frac{\partial^2 g}{ \partial x^2 }
\end{align*}\]と計算できる。
(3) 合成関数の微分2
\( u, v \) について2回微分可能な2変数関数 \( g(u,v) \)、および2変数関数 \( g(x,y) = f(x+y,xy) \) がある。
ここで、\( u = x+2y \), \( v = xy \) とおいたとき、以下の式が成り立つように [ 18 ] ~ [ 19 ] に当てはまる式を解答群の中から1つ選びなさい。\[
\frac{\partial g}{\partial y} (x,y) = \left[ \ \ 18 \ \ \right] \frac{\partial f}{\partial u} (x+y,xy) + \left[ \ \ 19 \ \ \right] \frac{\partial f}{\partial v} (x+y,xy)
\]
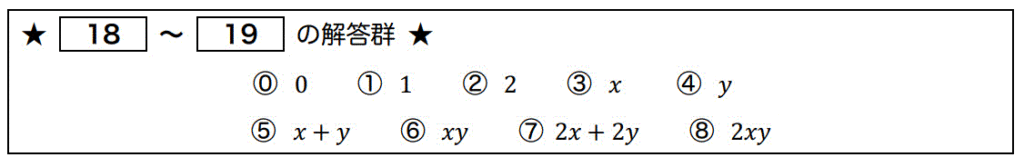
★解答★
No.18: 2 [1点]
No.19: 3 [1点]
2変数関数 \( g(x,y) \) を2変数関数 \( f(t) \) でおいたときの偏微分公式をまずは確認しましょう。
2変数関数 \( f(x,y) \) を \( u \), \( v \) を用いて \( g(u,v) \) ににおきかえる。\[
g(u,v) = f(x,y)
\]
このとき、1階微分は次のように計算できる。
\[
\frac{\partial g}{ \partial x} = \frac{\partial u}{\partial x} \frac{ \partial f }{ \partial u} + \frac{\partial v}{\partial x} \frac{ \partial f }{ \partial v}
\]
\[ \frac{\partial g}{ \partial y} = \frac{\partial u}{\partial y} \frac{ \partial f }{ \partial u} + \frac{\partial v}{\partial y} \frac{ \partial f }{ \partial v}
\]
今回は、\( u = x+2y \), \( v = xy \) とおいているので、\[
\frac{du}{dy} = 2 , \ \ \ \frac{dv}{dy} = x
\]となる。よって、\( \frac{\partial g}{\partial y } \) の計算式は下のようになる。
\[\begin{align*}
\frac{ \partial g }{ \partial y } & = \frac{ \partial u }{ \partial y } \frac{ \partial f }{ \partial u } + \frac{ \partial v }{ \partial y } \frac{ \partial f }{ \partial v }
\\ & = 2 \frac{ \partial f }{ \partial u } + x \frac{ \partial f }{ \partial v }
\end{align*}\]となるため、マーク番号は順番に2, 3。
合成関数の偏微分についてさらに復習したい人はこちら!
スポンサードリンク
問題3.偏微分の応用
(1) 2変数マクローリン展開
つぎの [ 20 ] ~ [ 24 ] に当てはまる数字を -9 ~ 9 の範囲でマークしなさい。(配点 5)
2変数関数\[
f(x,y) = \frac{1}{1+x-y}
\]を2次の項までマクローリン展開すると、\[
f(x,y) = 1 + \left[ \ \ 20 \ \ \right] x + \left[ \ \ 21 \ \ \right] y + \left[ \ \ 22 \ \ \right] x^2 + \left[ \ \ 23 \ \ \right] xy + \left[ \ \ 24 \ \ \right] y^2
\]となる。
★解答★
[ 20 ]:-1(1点)[ 21 ]:1(1点)
[ 22 ]:1(1点)
[ 23 ]:-2(1点)
[ 24 ]:1(1点)
2次までの2変数マクローリン展開の公式をまずは確認しましょう。
ある関数 \( f(x,y) \) の2次までの2変数マクローリン展開(点(0,0)におけるテイラー展開)は、下のように計算できる。\[\begin{align*}
f(x,y) = f(0,0) + \frac{ \partial f }{ \partial x } (0,0) x + \frac{ \partial f }{ \partial y } (0,0) y + \frac{1}{2} \left( \frac{ \partial^2 f }{ \partial x^2 } (0,0) \ x^2 + 2 \frac{ \partial^2 f }{ \partial x \partial y } (0,0) \ xy + \frac{ \partial^2 f }{ \partial y^2 } (0,0) y^2 \right)
\end{align*}\]
※ \( \frac{ \partial^2 f }{ \partial x \partial y } \) の偏微分順序は問わない。なので、\( x \) → \( y \) の順に偏微分しても、\( y \) → \( x \) の順に偏微分してもOK。
まずは、公式に当てはめて偏微分をしていく。
\[
f(x,y) = \frac{1}{1+x-y} = (1+x-y)^{-1}
\]なので、\[
f_{x}= - (1+x-y)^{-2}, \ \ \ f_{x} (0,0) = -1 \]\[
f_{y}= (1+x-y)^{-2}, \ \ \ f_{y} (0,0) = 1 \]\[
f_{xx}= 2 (1+x-y)^{-3}, \ \ \ f_{xx} (0,0) = 2 \]\[
f_{xy}= -2 (1+x-y)^{-3}, \ \ \ f_{xy} (0,0) = -2 \]\[
f_{yy}= 2 (1+x-y)^{-3}, \ \ \ f_{yy} (0,0) = 2 \]\[
\]となるので、\[\begin{align*}
f(x,y) & = 1 + f_{x} (0,0) x + f_{y} (0,0) y + \frac{1}{2} \left( f_{xx} (0,0) x^2 + 2 f_{xy} (0,0) xy + f_{yy} (0,0) y^2 \right)
\\ & = 1 -x + y + x^2 - 2xy + y^2
\\ & = 1 + (-1) x + 1y + 1 x^2 + (-2) xy + y^2
\end{align*}\]となる。
※ スペースの関係上、偏微分を省略記法 \( f_x \) や \( f_{xx} \) などで書いています。
[別解]\( t = - (x - y) \) とすることで、1変数関数(1年前期解析学レベル)のマクローリン展開に持ち込むことも可能。\[
f(t) = \frac{1}{1-t}
\]のマクローリン展開を求める。すると、\[
f(t) = 1 + t + t^2 + \cdots
\]となるので、\( t = -x + y \) を代入しもとに戻すと\[\begin{align*}
f(x,y) & = 1 + (-x+y) + (-x+y)^2
\\ & = 1 -x + y + x^2 - 2xy + y^2
\\ & = 1 + (-1) x + 1y + 1 x^2 + (-2) xy + y^2
\end{align*}\]となる。
2変数 \( x \), \( y \) を \( t \) などの文字を用いて1変数にすることで、1変数関数のマクローリン展開と同じ感覚で2変数マクローリン展開を求めることができる。
2変数関数のマクローリン展開についてさらに復習したい方はこちら!
(2) 接平面の方程式
つぎの [ 25 ] ~ [ 28 ] に当てはまる答えを下の解答群から選びなさい(配点 5)
\[
z = f(x,y) = \tan^{-1} \frac{y}{x}
\]の \( f(1,1) \) における接平面の方程式を求めたい。\[
f(1,1) = \left[ \ \ 25 \ \ \right]
\]なので接平面の方程式は\[
z = \left[ \ \ 26 \ \ \right] x + \left[ \ \ 27 \ \ \right] y + \left[ \ \ 25 \ \ \right] + \left[ \ \ 28 \ \ \right]
\]となる。

★解答★
[ 25 ]:17(1点)[ 26 ]:9(2点)
[ 27 ]:3(2点)
[ 28 ] : 0(2点)
接平面の方程式を確認しましょう。
2変数関数 \( f(x,y) \) の点 \( (a,b) \) における接平面の公式は下のように求められる。
\[
z = \frac{\partial f}{ \partial x} (a,b) (x-a) + \frac{\partial f}{ \partial y} (a,b) (y-b) + f(a,b)
\]
[修正 2022/02/13] 接平面の公式を誤って記載していたものを修正しました。大変申し訳ありません。
\( f(1,1) \) は、1年前期の解析学の復習。\[\begin{align*}
f(1,1) & = \tan^{-1} \frac{1}{1}
\\ & = \tan^{-1} 1
\\ & = \frac{\pi}{4}
\end{align*}\]よって、No.25の答えは17。
ここで、\[\begin{align*}
\frac{\partial f}{\partial x} & = \frac{1}{1 + \left( \frac{y}{x} \right)^2 } \cdot \left( - \frac{y}{x^2} \right)
\\ & = - \frac{1}{1 + \frac{y^2}{x^2}} \cdot \frac{y}{x^2}
\\ & = - \frac{x^2}{x^2 + y^2} \cdot \frac{y}{x^2}
\\ & = - \frac{y}{x^2 + y^2}
\end{align*}\]
ここで、\[\begin{align*}
\frac{\partial f}{\partial y} & = \frac{1}{1 + \left( \frac{y}{x} \right)^2 } \cdot \left( \frac{1}{x} \right)
\\ & = - \frac{1}{1 + \frac{y^2}{x^2}} \cdot \frac{1}{x}
\\ & = - \frac{x^2}{x^2 + y^2} \cdot \frac{1}{x}
\\ & = - \frac{x}{x^2 + y^2}
\end{align*}\]
となるので、\[
\frac{\partial f}{\partial x} (1,1) = - \frac{1}{2}, \ \ \ \frac{\partial f}{\partial y} (1,1) = \frac{1}{2}
\]と計算できる。あとは公式に当てはめるだけ。\[\begin{align*}
z & = \frac{\partial f}{\partial x} (1,1) (x-1) + \frac{\partial f}{\partial y} (1,1) (y-1) + f(1,1)
\\ & = - \frac{1}{2} (x-1) + \frac{1}{2} (y-1) + \frac{ \pi }{ 4 }
\\ & = - \frac{1}{2} x + \frac{1}{2} y + \frac{ \pi }{4} + 0
\end{align*}\]となり、No.26, No.27の答えは順番に9, 3, 0。
接平面についてさらに復習したい方はこちら!
問題4.2重積分
つぎの [ 29 ] ~ [ 32 ] に当てはまる選択肢として正しいものをそれぞれの解答群の中から選びなさい。(配点 10)
[2009年度EMaT 微分・積分問6]2重積分\[
\iint_{D} x e^{y^{2}} \ dxdy \]\[
D = \{ (x,y) \mid 0 \leqq x \leqq 1, \ x^2 \leqq y \leqq 1\ \}
\]の値を求める。積分範囲 \( D \) を変更すると、\[
D = \{ (x,y) \mid 0 \leqq y \leqq 1, \ \left[ \ \ 29 \ \ \right] \leqq x \leqq \left[ \ \ 30 \ \ \right] \ \}
\]となる。よって、\[\begin{align*}
\iint_{D} x e^{y^{2}} \ dxdy & = \int^{1}_{0} \left( \int^{ \left[ \ \ 30 \ \ \right] }_{ \left[ \ \ 28 \ \ \right] } x e^{y^{2}} \ dx \right) \ dy
\\ & = \int^{1}_{0} \left[ \ \ 31 \ \ \right] \ dy
\\ & = \left[ \ \ 32 \ \ \right]
\end{align*}\]と積分を計算することができる。

★解答★
[ 29 ]:0(2点)[ 30 ]:4(2点)
[ 31 ]:3(3点)
[ 32 ]:5(3点)
積分順序を変更する際には、ごり押しでやってもいいのですが、積分範囲を図示してみましょう。
今回は、\( y \) → \( x \) の積分順序を \( x \) → \( y \) に変えたいので、\( 0 \leqq y \leqq 1 \) のもとで、\( D \) と同じ領域を表す \( x \) の範囲を考えます。
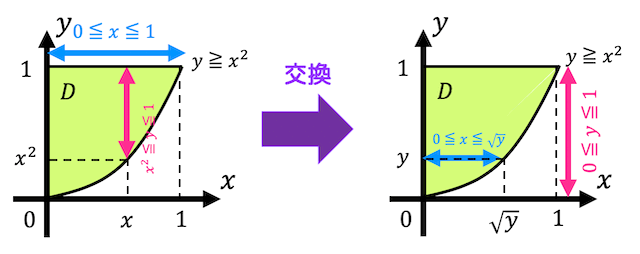
すると、\[
D = \{ (x,y) \mid 0 \leqq y \leqq 1, \ 0 \leqq x \leqq \sqrt{y} \ \}
\]と変換できるので、No.28のマーク番号は0、No.29のマーク番号は4となる。
よって、\[ \begin{align*}
\iint_{D} x e^{y^{2}} \ dxdy & = \int^{1}_{0} \left( \int^{ \sqrt{y} }_{ 0 } x e^{y^{2}} \ dx \right) \ dy
\\ & = \int^{1}_{0} \left( \int^{ \sqrt{y} }_{ 0 } x e^{y^{2}} \ dx \right) \ dy
\\ & = \int^{1}_{0} \left( e^{y^{2}}\int^{ \sqrt{y} }_{ 0 } x \ dx \right) \ dy
\\ & = \int^{1}_{0} \left( e^{y^{2}} \left[ \frac{1}{2} x^2 \right]^{ \sqrt{y} }_{ 0 } \right) \ dy
\\ & = \int^{1}_{0} e^{y^{2}} \cdot \frac{1}{2} y \ dy
\\ & = \int^{1}_{0} \frac{y}{2} e^{y^{2}} \ dy \ \ \ \left( \left[ \ \ 25 \ \ \right] \to 3 \right)
\\ & = \frac{1}{4} \int^{1}_{0} 2y e^{y^{2}} \ dy
\\ & = \frac{1}{4} \left[ e^{ y^{2} } \right]^{1}_{0} \ dy
\\ & = \frac{1}{4} \left( e - 1 \right)
\\ & = \frac{e-1}{4} \ \ \ \left( \left[ \ \ 26 \ \ \right] \to 5 \right)
\end{align*} \]となるため、No.30のマーク番号は 3 、No.31のマーク番号は 5 となる。
\[D = \{ (x,y) \mid 0 \leqq x \leqq 1, \ \textcolor{red}{x^2 \leqq y \leqq 1} \ \}\]のように、積分範囲にもう1つの積分変数が含まれている場合、必ず積分範囲にもう1つの積分定数が含まれている方から積分しなければならない。
また、積分順序を入れ替えたほうが積分が早く計算出来そうだと思った場合は、積分範囲を入れ替えることもできる。
2重積分の基礎についてさらに復習したい人はこちら!
問題5.2重積分の応用
つぎの [ 33 ] ~ [ 35 ] に当てはまる選択肢として正しいものをそれぞれの解答群の中から選びなさい。(配点 8)
放物面 \( z = x^2 + y^2 \) のうち、2つの平面 \( z = 0 \), \( z = 1 \) にある部分の曲面積を求めたい。ここで、\( z = f(x,y) \) とすると、曲面積は\[
\iint_{D} \sqrt{ 1 + \left( \frac{ \partial f }{ \partial x } \right)^2 + \left( \frac{ \partial f }{ \partial y } \right)^2 } \ dxdy \]\[
D = \{ (x,y) \mid x^2 + y^2 \leqq 1 \ \}
\]で求めることができる。
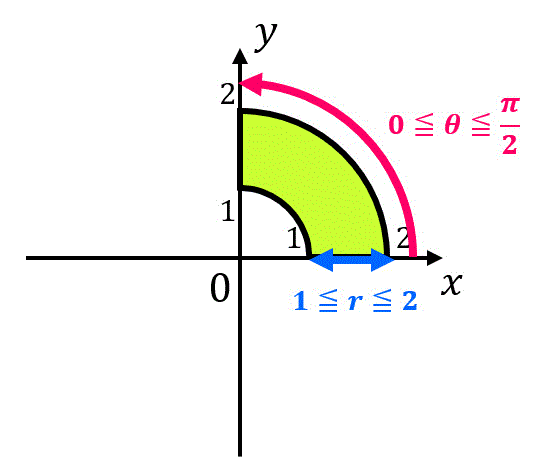
さらに \( x = r \cos \theta \), \( y = r \sin \theta \) とすると範囲を\[
D' = \{ (x,y) \mid \left[ \ \ 33 \ \ \right] \ \}
\]と変換することができる。よって、\[\begin{align*}
\iint_{D} \sqrt{ 1 + \left( \frac{ \partial f }{ \partial x } \right)^2 + \left( \frac{ \partial f }{ \partial y } \right)^2 } \ dxdy & = \iint_{D'} \left[ \ \ 34 \ \ \right] \ dr d \theta
\\ & = \left[ \ \ 35 \ \ \right]
\end{align*} \]と計算できる。

★解答★
No.33 → 1 (3点)
No.34 → 7 (3点)
No.35 → 3 (3点)
まず、積分範囲 \( D' \) を求めるために \( D \) の積分範囲 \( x^2 + y^2 \leqq 1 \) に \( x = r \cos \theta \), \( y = r \sin \theta \) を代入する。すると、\[\begin{align*}
x^2 + y^2 & \leqq 1 \\
r^2 \cos^2 \theta + r^2 \sin^2 \theta & \leqq 1 \\
r^2 ( \cos^2 \theta + \sin^2 \theta) & \leqq 1 \\
r^2 & \leqq 1
\end{align*}\]となる。さらに \( r \geqq 0 \) なので \( r \) の範囲は \( 0 \leqq r \leqq 1 \) となる。
また、\( \theta \) の範囲はとくに制限がないため、1周分 \( 0 \leqq \theta \leqq 2 \pi \) が接気分範囲となる。よって、積分範囲 \( D' \) は\[
D' = \{ (r, \theta ) \mid 0 \leqq r \leqq 1, \ 0 \leqq \theta \leqq 2 \pi \ \}
\]となる。( [ 32 ] の答えは 1 )
次にNo.33-No.34の空欄を埋めていく。
まず、ヤコビアン \( J \) は\[\begin{align*}
J & = \left| \begin{array}{ccc} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \end{array} \right|
\\ & = \left| \begin{array}{ccc} \cos \theta & - r \sin \theta \\ \sin \theta & r \cos \theta \end{array} \right|
\\ & = r \cos^2 \theta + r \sin^2 \theta
\\ & = r ( \cos^2 \theta + \sin^2 \theta )
\\ &= r
\end{align*}\]となるので、関係式\[
dxdy = r \ dr d \theta
\]が成り立つ。
ここで、\[
\frac{ \partial f }{ \partial x } = 2x , \ \ \ \frac{ \partial f }{ \partial y } = 2y
\]なので、\[ \begin{align*} &
\iint_{D} \sqrt{ 1 + \left( \frac{ \partial f }{ \partial x } \right)^2 + \left( \frac{ \partial f }{ \partial y } \right)^2 } \ dxdy \\ = & \iint_{D} \sqrt{ 1 + \left( 2x \right)^2 + \left( 2y \right)^2 } \ dxdy
\\ = & \iint_{D} \sqrt{ 1 + 4x^2 + 4y^2 } \ dxdy
\\ = & \iint_{D’} r \sqrt{ 1 + 4r^2 } \ dr d \theta
\\ = & \iint_{D’} r \sqrt{ 1 + 4r^2 } \ dr d \theta
\\ = & \int^{2 \pi}_{0} 1 \ d \theta \cdot \int^{1}_{0} r \sqrt{1 + 4r^2} \ dr
\end{align*} \]と変形できる。(マークNo.33の答えは7)
あとはそれぞれの積分を計算するだけ\[ \begin{align*}
\int^{1}_{0} r \sqrt{ 1 + 4r^2 } \ dr & = \frac{1}{8} \int^{1}_{0} 8r \sqrt{ 1 + 4r^2 } \ dr
\\ & = \frac{1}{8} \left[ \frac{2}{3} ( 1 + 4r^2 )^{ \frac{3}{2} } \right]^{1}_{0}
\\ & = \frac{1}{8} \cdot \frac{2}{3} \left( 5 \sqrt{5} - 1 \right)
\\ & = \frac{1}{12} \left( 5 \sqrt{5} - 1 \right)
\end{align*} \] \[
\int^{2 \pi}_{0} 1 \ d \theta = 2 \pi
\]となるので、\[\begin{align*}
\iint_{D} \sqrt{ 1 + 4x^2 + 4y^2 } \ dxdy & = \iint_{D'} r \sqrt{ 1 + 4r^2 } \ dr d \theta
\\ & = \int^{2 \pi}_{0} 1 \ d \theta \cdot \ \int^{1}_{0} r \sqrt{ 1 + 4r^2 } \ dr
\\ & = 2 \pi \cdot \frac{1}{12} \left( 5 \sqrt{5} - 1 \right)
\\ & = \frac{1}{6} \left( 5 \sqrt{5} - 1 \right) \pi
\end{align*} \]となるのでNo.34の答えは 3 となる。
ある2重積分の被積分関数 \( x \), \( y \) を \( r = \cos \theta \), \( r = \sin \theta \) と変数変換したときのヤコビアンは \( J = r \) となる。
つまり、\( dxdy = r \ dr d \theta \) の関係式が成り立つ。
※ 試験頻出なのでぜひ覚えておいてください、導出もできますが時間短縮になります。
極座標変換 \( x = r \cos \theta \), \( y = r \sin \theta \) を用いた変数変換について復習したい人はこちら!
曲平面の求め方について復習したい人はこちら!
関連広告・スポンサードリンク