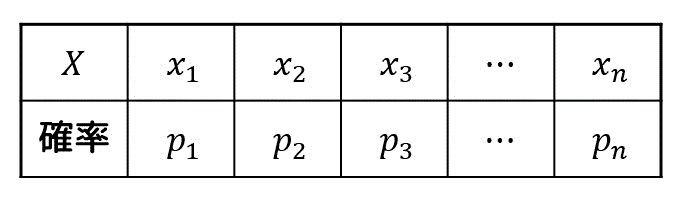
スポンサードリンク
こんにちは、ももやまです。
今回は
- モーメント母関数の求め方
- モーメント母関数を用いた平均・分散の求め方
の2つについて説明していきます。
[注意]
この記事では、
の内容を使います。不安な人はリンク先で復習することをおすすめします。
目次
スポンサードリンク
1.モーメント(積率)
(1) モーメントとは
モーメントは、確率分布 \( X \) が
- どのような分布を示すのか
- どんな風にデータがバラバラになっているか
を数字で表現したものあり、積率とも呼ばれます。
(2) モーメントの定義
ある点 \( x = a \) 周りの \( k \) 次のモーメントは、
- それぞれの確率変数 \( X \) における \( (X-a)^k \) の値
(期待値を求めるときの \( X \) が \( (X-a)^k \) に変化) - \( X \) となる確率
で求めることができ、\( E \left( (X-a)^k \right) \) と表されます。
皆さんが今まで求めてきた平均(期待値)・分散は、モーメントの中でも特殊な場合で、具体的には
- 確率の和 (1) → 原点周りの0次のモーメント*1
- 平均 → 原点周りの1次のモーメント
- 分散 → 平均周りの2次のモーメント
に相当します。
(3) 定義に従ったモーメントの求め方
モーメントの求め方を離散型と連続型の確率分布に分けて説明しましょう。
(i) 離散型の場合
ある確率変数 \( X \) が取りうる値の範囲を \( x_1 \), \( x_2 \), …, \( x_n \) とし、それぞれの確率を \( p_1 \), \( p_2 \), …, \( p_n \)、つまり\[
P (X = x_k) = p_k
\]となっている確率分布があるとします。
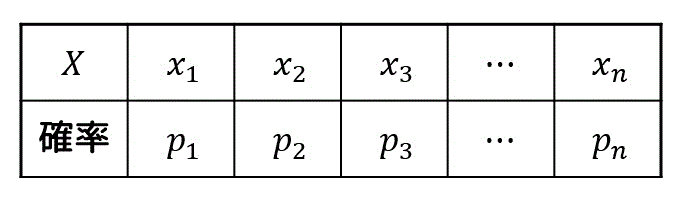
例えば、平均 \( E(X) \) であれば、\[\begin{align*}
E(X) & = \sum^{n}_{i=1} \textcolor{red}{x_i} p_i
\\ & = \textcolor{red}{x_1} p_1 + \textcolor{red}{x_2} p_2 + \cdots + \textcolor{red}{x_n} p_n
\end{align*}\]で求めることができますね。
この \( \textcolor{red}{x_i} \) の部分を \( \textcolor{red}{(x_i-a)^k} \) としたものが \( k \) 次のモーメントとなります。
式で表すと、\[\begin{align*}
E \left( (X - a)^k \right) & = \sum^{n}_{i=1} \textcolor{red}{(x_i - a)^k} p_i
\\ & = \textcolor{red}{(x_1 - a)^k} p_1 + \textcolor{red}{(x_2 - a)^k} p_2 + \cdots + \textcolor{red}{(x_n - a)^k} p_n
\end{align*}\]となります。
早速例題で2次のモーメントまで求めてみましょう。
\( X \) の確率分布表は下のようになる。
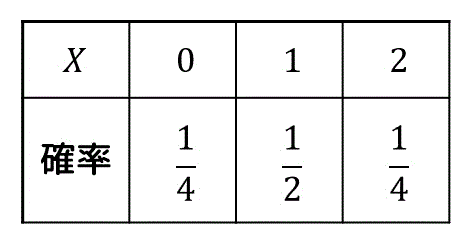
解説1
(1)
0次のモーメント:1
答えは明らかだが、念のため計算をする。\[\begin{align*}
E(X^0) & = E(1)
\\ & = \frac{1}{4} + \frac{1}{2} + \frac{1}{4}
\\ & = 1
\end{align*}\]と計算できる。
1次のモーメント:1
平均を求めるのと同じ。\[\begin{align*}
E(X) & = 0 \cdot \frac{1}{4} + 1 \cdot \frac{1}{2} + 2 \cdot \frac{1}{4}
\\ & = 1
\end{align*}\]と計算できる。
2次のモーメント:3/2
計算あるのみ。\[\begin{align*}
E(X^2) & = 0^2 \cdot \frac{1}{4} + 1^2 \cdot \frac{1}{2} + 2^2 \cdot \frac{1}{4}
\\ & = \frac{3}{2}
\end{align*}\]と計算できる。
(2)
分散 \( V(X) \) は、\[
V(X) = E ( X^2 ) - \left\{ E (X) \right\}^2
\]で求められる*2。
(つまり、2次のモーメント - 1次のモーメントの2乗 が分散)
よって、\[\begin{align*}
V(X) & = E(X^2) - \left\{ E(X) \right\}^2
\\ & = \frac{3}{2} - 1^2
\\ & = \frac{1}{2}
\end{align*}\]となる。
(2) 連続型の場合
ある確率密度関数 \( f(x) \) で表される確率分布 \( X \) の期待値は、\[
\int^{\infty}_{- \infty} \textcolor{red}{x} f(x) \ dx
\]で計算できるのでしたね*3。
この \( \color{red}{x} \) を \( \color{red}{(x-a)^k} \) としたものが \( k \) 次のモーメントとなります。
式で表すと、\[\begin{align*}
E \left( (x - a)^k \right) = \int^{\infty}_{- \infty} \textcolor{red}{(x-a)^k} f(x) \ dx
\end{align*}\]となります。
解説2
(1)
0次のモーメント:1
計算するまでもないが、念のため。\[\begin{align*}
E( X^0 ) & = E(1)
\\ & = \int^{\infty}_{0} 2 e^{-2x} \ dx
\\ & = \lim_{R \to \infty} \int^{R}_{0} 2 e^{-2x} \ dx
\\ & = \lim_{R \to \infty} \left[ - e^{-2x} \right]^{R}_{0}
\\ & = \lim_{R \to \infty} \left( - e^{-2R} + 1 \right)
\\ & = \lim_{R \to \infty} \left( 1 - \frac{1}{e^{2R}} \right)
\\ & = 1
\end{align*}\]となる。
(積分範囲が0からになっているのは、0以下のときは確率が0だから。)
1次のモーメント:1/2
\[\begin{align*}
E( X) & = \int^{\infty}_{0} x \cdot 2 e^{-2x} \ dx
\\ & = \lim_{R \to \infty} \int^{R}_{0} 2x e^{-2x} \ dx
\\ & = \lim_{R \to \infty} \left[ - x e^{-2x} - \frac{1}{2} e^{-2x} \right]^{R}_{0}
\\ & = \lim_{R \to \infty} \left( - R e^{-2R} - \frac{1}{2} e^{-2R} + \frac{1}{2} \right)
\\ & = \lim_{R \to \infty} \left( \frac{1}{2} - \frac{R}{e^{2R}} - \frac{1}{2e^{2R}} \right)
\\ & = \frac{1}{2}
\end{align*}\]となる。
2次のモーメント:1/2
\[\begin{align*}
E( X^2) & = \int^{\infty}_{0} x^2 \cdot 2 e^{-2x} \ dx
\\ & = \lim_{R \to \infty} \int^{R}_{0} 2x^2 e^{-2x} \ dx
\\ & = \lim_{R \to \infty} \left[ - x^2 e^{-2x} - x e^{-2x} - \frac{1}{2} e^{-2x} \right]^{R}_{0}
\\ & = \lim_{R \to \infty} \left( - R^2 e^{-2R} - R e^{-2R} - \frac{1}{2} e^{-2R} + \frac{1}{2} \right)
\\ & = \lim_{R \to \infty} \left( \frac{1}{2} - \frac{R^2}{e^{2R}} - \frac{R}{2e^{2R}} - \frac{1}{2e^{2R}} \right)
\\ & = \frac{1}{2}
\end{align*}\]となる。
なお、広義積分の計算のとき、
を使っています。
(2)
分散 \( V(X) \) は、\[
V(X) = E ( X^2 ) - \left\{ E (X) \right\}^2
\]で求められるので、\[\begin{align*}
V(X) & = E(X^2) - \left\{ E(X) \right\}^2
\\ & = \frac{1}{2} - \left( \frac{1}{2} \right)^2
\\ & = \frac{1}{2} - \frac{1}{4}
\\ & = \frac{1}{4}
\end{align*}\]となる。
ある点 \( x = a \) 周りの \( k \) 次のモーメント \( E \left( (X-a)^k \right) \) は、
- それぞれの確率変数 \( X \) における \( (X-a)^k \) の値
(期待値を求めるときの \( X \) が \( (X-a)^k \) に変化) - \( X \) となる確率
で求めることができる。
[離散型確率分布の場合]\[\begin{align*}
E \left( (X - a)^k \right) & = \sum^{n}_{i=1} (x_i - a)^k p_i
\\ & = (x_1 - a)^k p_1 + (x_2 - a)^k p_2 + \cdots + (x_n - a)^k p_n
\end{align*}\]で求められる。
\[\begin{align*}
E \left( (x - a)^k \right) = \int^{\infty}_{- \infty} (x-a)^k f(x) \ dx
\end{align*}\]で求められる。
スポンサードリンク
2.モーメント母関数
モーメント母関数は、
- それぞれの確率変数 \( X \) における \( e^{tX} \) の値
(期待値を求めるときの \( X \) が \( e^{tX} \) に変化) - \( X \) となる確率
の積で求めることができ、 \( E ( e^{tX} ) \) と表されます。
モーメント母関数とは、あらゆるモーメントを生み出すことができる関数です。
では、離散型と連続型の確率変数に分けてモーメント母関数の出し方について説明していきましょう。
(1) 離散型の確率変数の場合
まずは、離散型の確率変数 \( X \) のモーメント母関数の求め方について説明しましょう。
先程と同じように、ある確率変数 \( X \) が取りうる値の範囲を \( x_1 \), \( x_2 \), …, \( x_n \) とし、それぞれの確率を \( p_1 \), \( p_2 \), …, \( p_n \) とします。
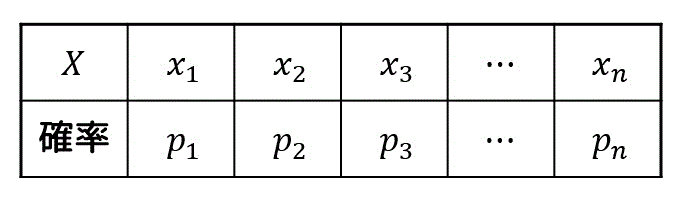
期待値の部分に掛けていた \( x_i \) の部分を \( e^{tx_i} \) に変えればいいので、モーメント母関数を求める式は、\[\begin{align*}
E \left( e^{tX} \right) & = \sum^{n}_{i=1} \textcolor{red}{e^{tx_i} p_i}
\\ & = \textcolor{red}{e^{tx_1}} p_1 + \textcolor{red}{e^{tx_2}} p_2 + \cdots \textcolor{red}{e^{tx_n} }p_n
\end{align*}\]となります。
早速例題で2次のモーメントまで求めてみましょう。
解説3
\( X \) の確率分布表は下のようになる。

よって、モーメント母関数は\[\begin{align*}
E \left( e^{tX} \right) & = e^{0t} \cdot \frac{1}{4} + e^{1t} \cdot \frac{1}{2} + e^{2t} \cdot \frac{1}{4}
\\ & = \frac{1}{4} + \frac{1}{2} e^{t} + \frac{1}{4} e^{2t}
\end{align*}\]となる。
(2) 連続型の確率変数の場合
連続型の確率変数でのモーメント母関数についても確認しましょう。
期待値の部分に掛けていた \( x \) の部分を \( e^{tx} \) に変えればいいので、モーメント母関数を求める式は、\[\begin{align*}
E \left( e^{tX} \right) = \int^{\infty}_{- \infty} \textcolor{red}{ e^{tx} } f(x) \ dx
\end{align*}\]となります。
解説4
モーメント母関数は\[\begin{align*}
E \left( e^{tX} \right) & = \int^{\infty}_{0} e^{tx} \cdot 2e^{-2x} \ dx
\\ & = \lim_{R \to \infty} \int^{R}_{0} 2e^{(t-2)x}
\\ & = \lim_{R \to \infty} \left[ \frac{2}{2-t} e^{(t-2)x} \right]^{R}_{0}
\\ & = \lim_{R \to \infty} \frac{2}{2-t} \left( 1 - e^{(t-2)R} \right)
\\ & = \frac{2}{2-t} \ \ \ \left( \because t<2 \right)
\end{align*}\]と計算できる。
(第3章で説明しますが、モーメント母関数に \( t = 0 \) を代入すると、必ず1になるので、必ず検算しましょう。)
モーメント母関数 \( E ( e^{tX} ) \) は、
- それぞれの確率変数 \( X \) における \( e^{tX} \) の値
(期待値を求めるときの \( X \) が \( e^{tX} \) に変化) - \( X\) となる確率
の積で求めることができる。
[離散型確率分布の場合]\[\begin{align*}
E \left( e^{tX} \right) & = \sum^{n}_{i=1} e^{tx_i} p_i
\\ & = e^{tx_1} p_1 + e^{tx_2} p_2 + \cdots + e^{tx_n} p_n
\end{align*}\]で求められる。
\[\begin{align*}
E \left( e^{tX} \right) = \int^{\infty}_{- \infty} e^{tx} f(x) \ dx
\end{align*}\]で求められる。
スポンサードリンク
3.モーメント母関数を用いたモーメントの求め方
モーメント母関数を用いることで、原点 \( x = 0 \) まわりの \( k \) 次のモーメントを簡単に計算することができます。
ここで、\( e^{tx} \) のマクローリン展開について考えましょう。
\( e^{x} \) のマクローリン展開は、\[\begin{align*}
e^{x} & = \sum^{\infty}_{k = 0} \frac{1}{k!} x^{k}
\\ & = 1 + x + \frac{1}{2!} x^2 + \frac{1}{3!} x^3 + \cdots
\end{align*}\]なので、\( x \to tx \) とすることで\[\begin{align*}
e^{tx} & = \sum^{\infty}_{k = 0} \frac{1}{k!} (tx)^{k}
\\ & = 1 + tx + \frac{1}{2!} (tx)^2 + \frac{1}{3!} (tx)^3 + \cdots
\\ & = 1 + tx + \frac{1}{2!} t^2 x^2 + \frac{1}{3!} t^3 x^3 + \cdots
\end{align*}\]となりますね。
\( e^{tx} \) のマクローリン展開から、モーメント母関数 \( E \left( e^{tX} \right) \) を\[\begin{align*}
E \left( e^{tX} \right) & = E \left( 1 + tx + \frac{1}{2!} t^2 x^2 + \frac{1}{3!} t^3 x^3 + \cdots + \cdots \right)
\\ & = E(1) + t \textcolor{red}{E(X)} + \frac{1}{2!} t^2 \textcolor{blue}{E(X^2)} + \frac{1}{3!} t^3 \textcolor{green}{E(X^3)} + \cdots
\\ & = \sum^{\infty}_{k = 0} \frac{1}{k!} t^k E (X^k)
\end{align*}\]と分解できますね。
また、モーメント母関数 \( g(t) \) を \( t = 0 \) でマクローリン展開すると、\[\begin{align*}
g(t) & = g(0) + t \textcolor{red}{g'(0)} + \frac{1}{2!} t^2 \textcolor{blue}{g''(0)} + \frac{1}{3!} t^3 \textcolor{green}{g'''(0)} + \cdots
\\ & = \sum^{\infty}_{k = 0} \frac{1}{k!} g^{(k)} (0)
\end{align*}\]となるので、\[
E(1) = g(0) = 1\]\[
\textcolor{red}{E(X) = g'(0)} \]\[
\textcolor{blue}{E(X^2) = g''(0)} \]\[
\textcolor{green}{E(X^3) = g'''(0)}
\]のように各次のモーメント母関数 \( g(t) \) さえわかってしまえば、微分して0を代入するだけでモーメントを求めることができます!
(なお、\( g(0) = 1 \) は手軽にできるモーメント母関数の検算テクニックの1つなので必ずチェックしましょう!)
モーメント母関数 \( E \left( tX \right) \) を\[\begin{align*}
E \left( e^{tX} \right) \\ & = E(1) + t \textcolor{red}{E(X)} + \frac{1}{2!} t^2 \textcolor{blue}{E(X^2)} + \frac{1}{3!} t^3 \textcolor{green}{E(X^3)} + \cdots
\\ & = \sum^{\infty}_{k = 0} \frac{1}{k!} t^k E (X^k)
\end{align*}\]と \( t \) の多項式に分解することで各項における原点のモーメントを求めることができる。
具体的には、\[
g(t) = E \left( e^{tX} \right)
\]とし、\[
E(1) = g(0) = 1 \]\[
\textcolor{red}{E(X) = g'(0)} \]\[
\textcolor{blue}{E(X^2) = g''(0)} \]\[
\textcolor{green}{E(X^3) = g'''(0)}
\]のように項の回数分微分してから \( t = 0 \) を代入することで求められる。
早速例題でその威力を確かめてみましょう。
解説5
2次のモーメントを求めるために\[
f(t) = \frac{2}{2-t}
\]を2回微分し、それぞれに \( t = 0 \) を代入する。
0次のモーメント\[
f(0) = 1
\]より、1。
(ここが1にならない場合、モーメント母関数で計算ミスをしている)
1次のモーメント\[
f'(t) = \frac{2}{(2-t)^2} , \ \ \ f'(0) = \frac{1}{2}
\]より、1/2。
2次のモーメント\[
f''(t) = \frac{4}{(2-t)^3} , \ \ \ f''(0) = \frac{1}{2}
\]より、1/2。
4.練習問題(指数分布とモーメント)
最後に1問だけ練習してみましょう。
指数分布\[
f(x) = \left\{ \begin{array}{l} \lambda e^{- \lambda x} \ \ \left( x \geqq 0 \right) \\ 0 \ \ \ \ \ \ \ \ \ \ \left( x < 0 \right) \end{array}\right.
\]で表されるような確率変数 \( X \) がある。ただし、\( \lambda > 0 \) である。
(1) モーメント母関数 \( E \left( e^{tX} \right) \) を求めなさい。必要なら \( t < \lambda \) を用いてよい。
(2) 2次までのモーメントを求めなさい。
(3) 分散 \( V(X) \) を求めなさい。
5.練習問題の答え
(1)
モーメント母関数は\[\begin{align*}
E \left( e^{tX} \right) & = \int^{\infty}_{0} e^{tx} \cdot \lambda e^{- \lambda x} \ dx
\\ & = \lim_{R \to \infty} \int^{R}_{0} 2e^{(t- \lambda )x}
\\ & = \lim_{R \to \infty} \left[ \frac{\lambda}{\lambda -t} e^{(t- \lambda )x} \right]^{R}_{0}
\\ & = \lim_{R \to \infty} \frac{\lambda}{ \lambda -t} \left( 1 - e^{(t- \lambda )R} \right)
\\ & = \frac{\lambda}{\lambda -t} \ \ \ \left( \because t< \lambda \right)
\end{align*}\]と計算できる。
(\( t = 0 \) を代入し、1になるかを確認)
(2)
\( g(t) \) を\[
g(t) = E \left( e^{tX} \right) = \frac{\lambda}{\lambda -t}
\]とする。
0次のモーメント:1(確率の和は必ず1)
1次のモーメント\[
g'(t) = \frac{\lambda}{( \lambda - t )^2} , \ \ \ g'(0) = \frac{1}{\lambda}
\]より、\[\begin{align*}
E(X) & = g'(0)
\\ & = \frac{1}{\lambda}
\end{align*}\]と求められる。
2次のモーメント\[
g''(t) = \frac{2 \lambda}{( \lambda - t )^3} , \ \ \ g''(0) = \frac{2}{\lambda^2}
\]より、\[\begin{align*}
E(X^2) & = g''(0)
\\ & = \frac{2}{\lambda^2}
\end{align*}\]と求められる。
(3)
分散は「2次のモーメント - 1次のモーメントの2乗」で求められる。
よって、\[\begin{align*}
V(X) & = E(X^2) - \left\{ E(X) \right\}^2
\\ & = \frac{2}{\lambda^2} - \left( \frac{1}{\lambda} \right)^2
\\ & = \frac{1}{\lambda^2}
\end{align*}\]となる。
このように、確率密度関数が \( e^{ax} \) の形になっていて、定義通りに分散を出そうとすると計算がきつい*4問題でも、モーメント母関数を使えばあっという間に求めることができます!
6.さいごに
今回は、
- モーメントとは
- モーメント母関数の求め方
- モーメント母関数を用いたモーメントの出し方
の3つについて説明しました。
確率密度関数が \( e^{ax} \) の形のときは、積極的にモーメント母関数から平均、分散を求めることで計算時間の短縮をすることができるので積極的に使っていきましょう!
*1:なので0次のモーメントを試験で聞かれたら、何がなんだろうが答えは「1」です。サービス問題だねやったぁ!
*2:平均 \( \mu \) 周りの2次のモーメント\[
\sum^{n}_{i = 1} (x_i - \mu)^2 p_i
\]で求めてもいいが、せっかく(1)の誘導がついてるので、誘導に従いましょう。
*3:高校の確率分布と統計的な推測の場合、積分範囲に無限大が含まれるのを防ぐため、確率分布 \( X \) に \( m \leqq X \leqq M\) のような制限をつけて\[
\int^{M}_{m} x f(x) \ dx
\]で表現しています。
*4:部分積分を複数回繰り返す必要があるため
関連広告・スポンサードリンク